Markov Chains: Joint, Conditional, and Marginal Distributions

Popcorn and ice cream

state_names = c("ice cream", "popcorn")

P = rbind(
  c(0.2, 0.8),
  c(0.4, 0.6)
)

Transition matrix

plot_transition_matrix(P, state_names)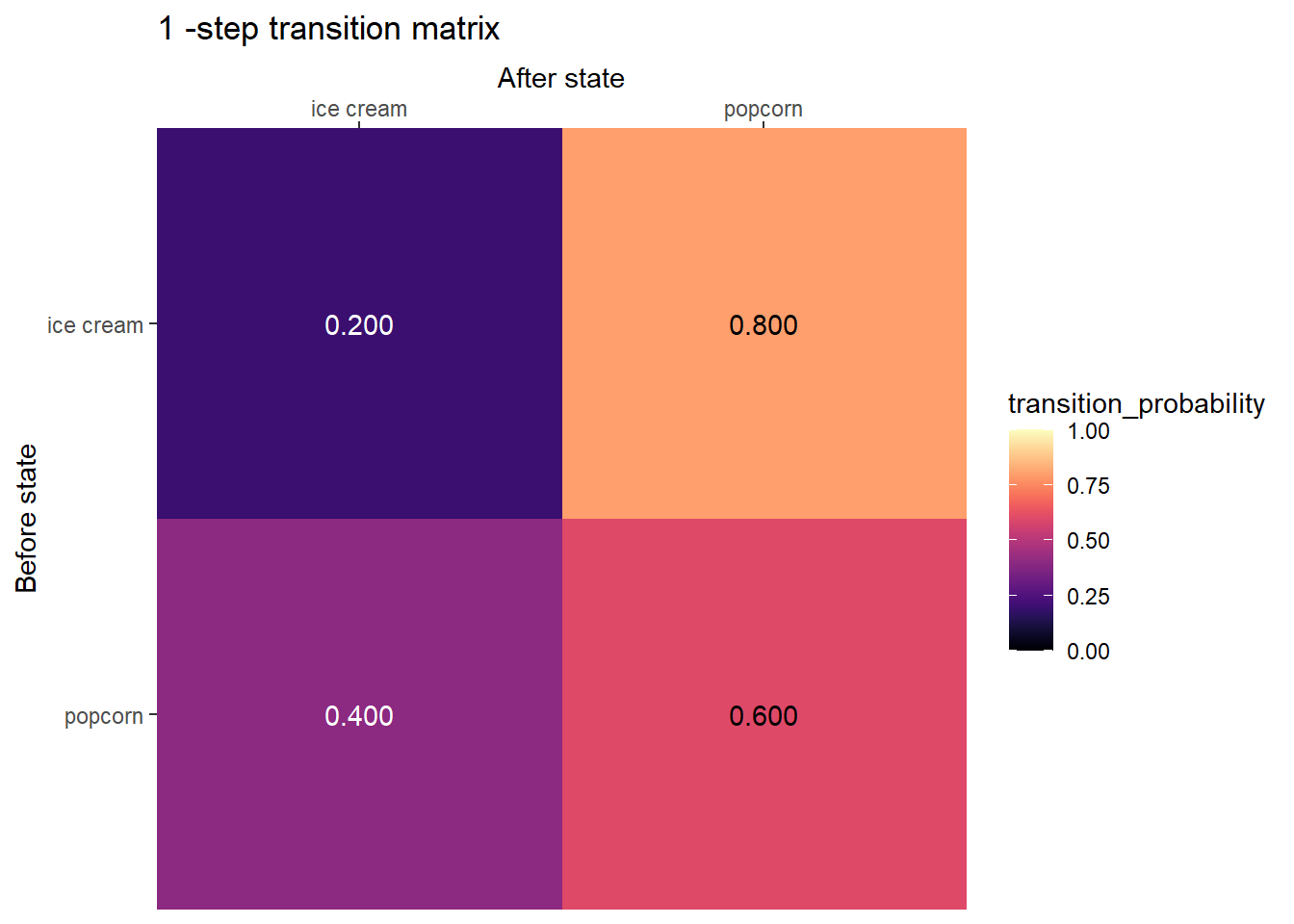

2-step transition matrix

P %*% P
     [,1] [,2]
[1,] 0.36 0.64
[2,] 0.32 0.68
library(expm)
P %^% 2
     [,1] [,2]
[1,] 0.36 0.64
[2,] 0.32 0.68
plot_transition_matrix(P, n_step = 2)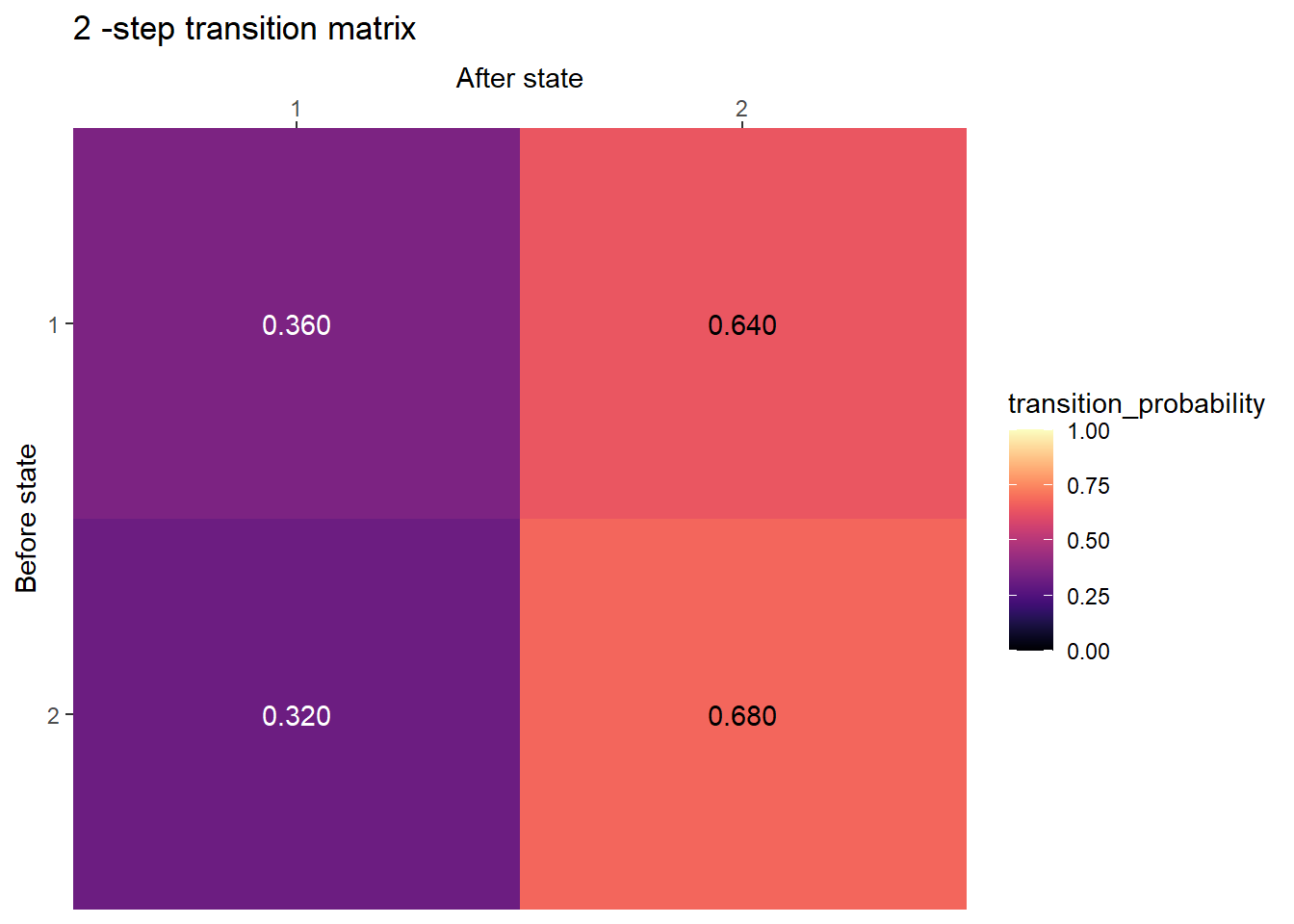

3-step transition matrix

P %^% 3
      [,1]  [,2]
[1,] 0.328 0.672
[2,] 0.336 0.664
plot_transition_matrix(P, n_step = 3)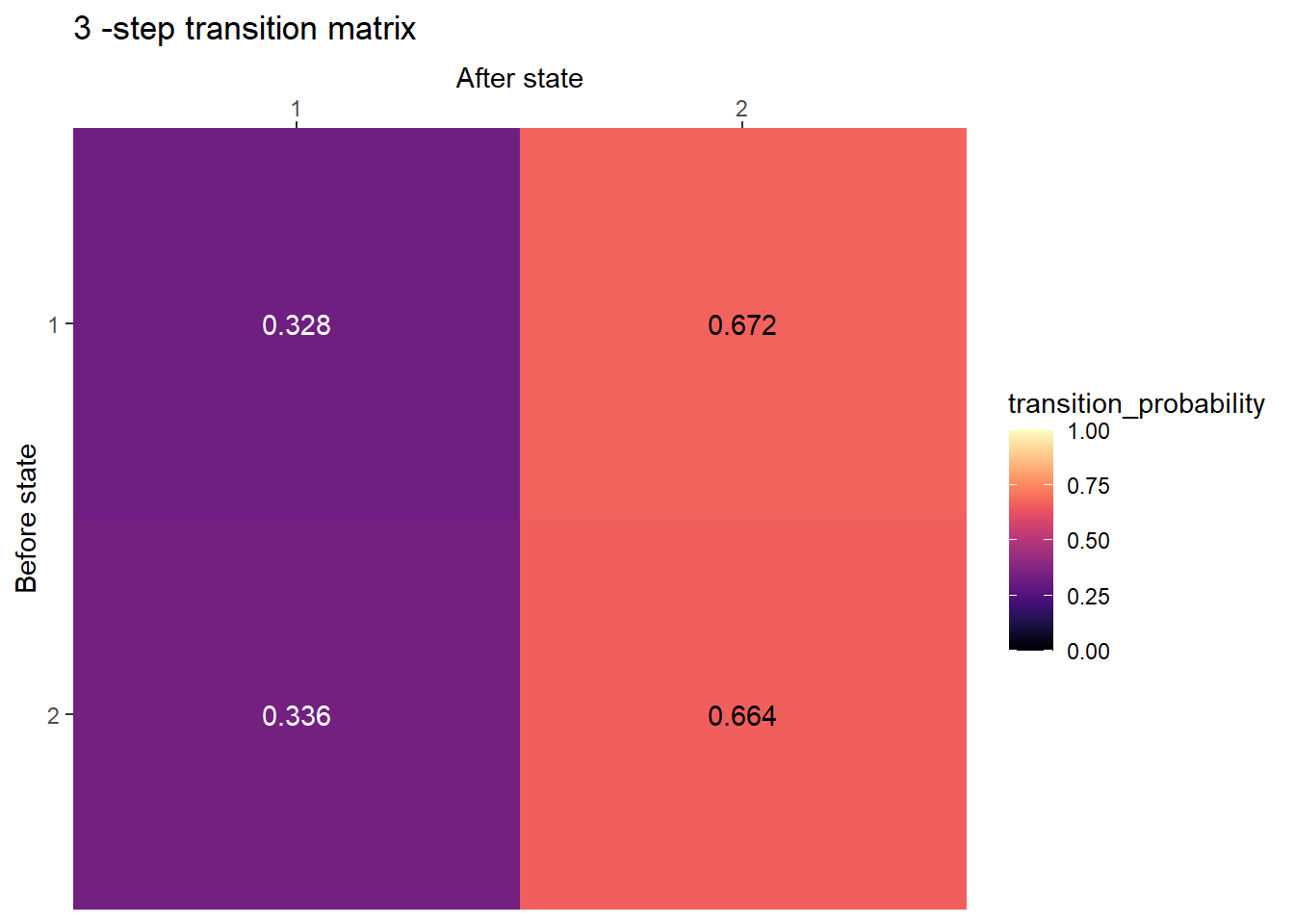

Weather chain

state_names = c("RR", "NR", "RN", "NN")

P = rbind(c(.7, 0, .3, 0),
          c(.5, 0, .5, 0),
          c(0, .4, 0, .6),
          c(0, .2, 0, .8)
)

Transition matrix

plot_transition_matrix(P, state_names)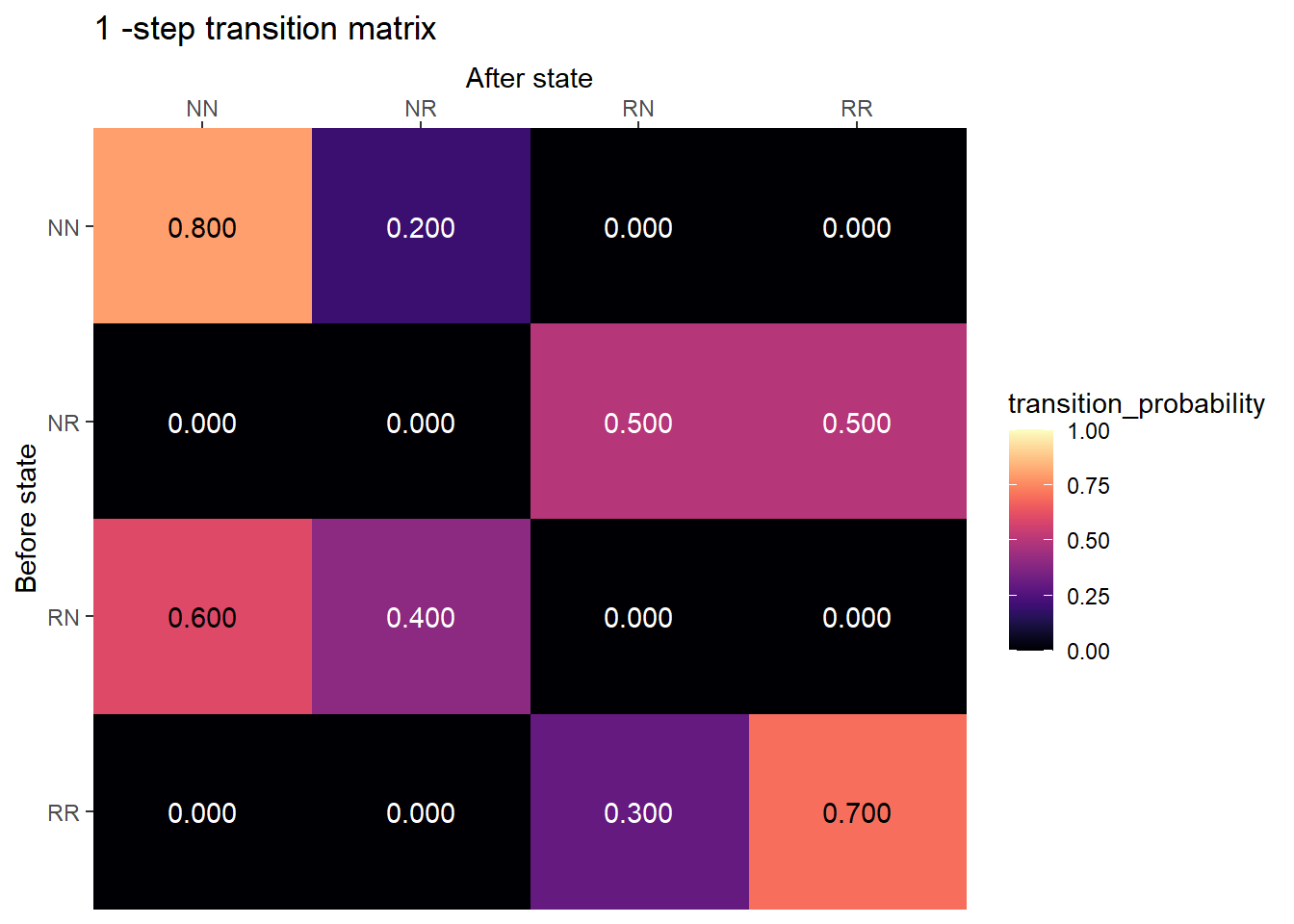

2-step transition matrix

plot_transition_matrix(P, state_names, n_step = 2)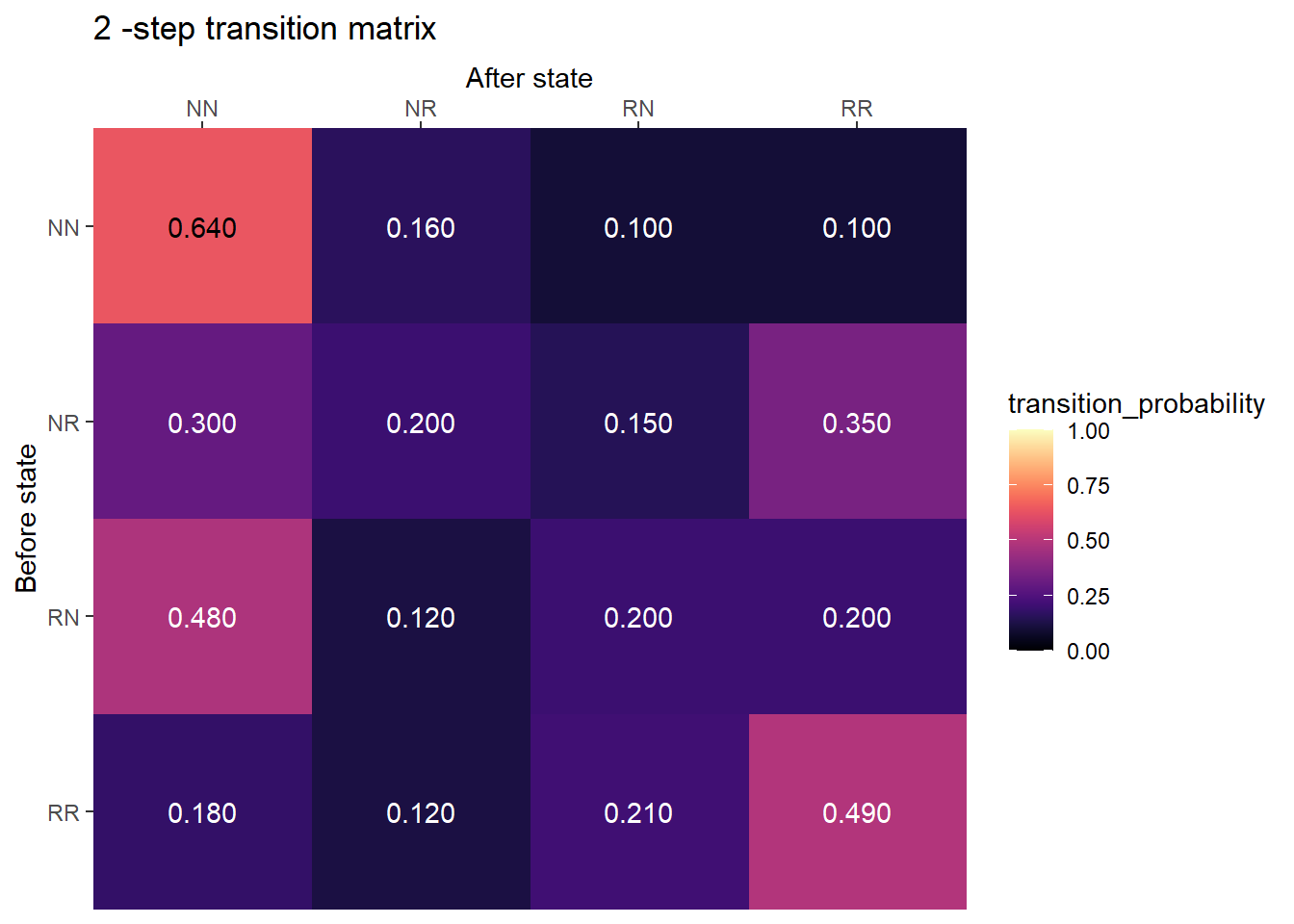

2-step transition matrix

plot_transition_matrix(P, state_names, n_step = 3)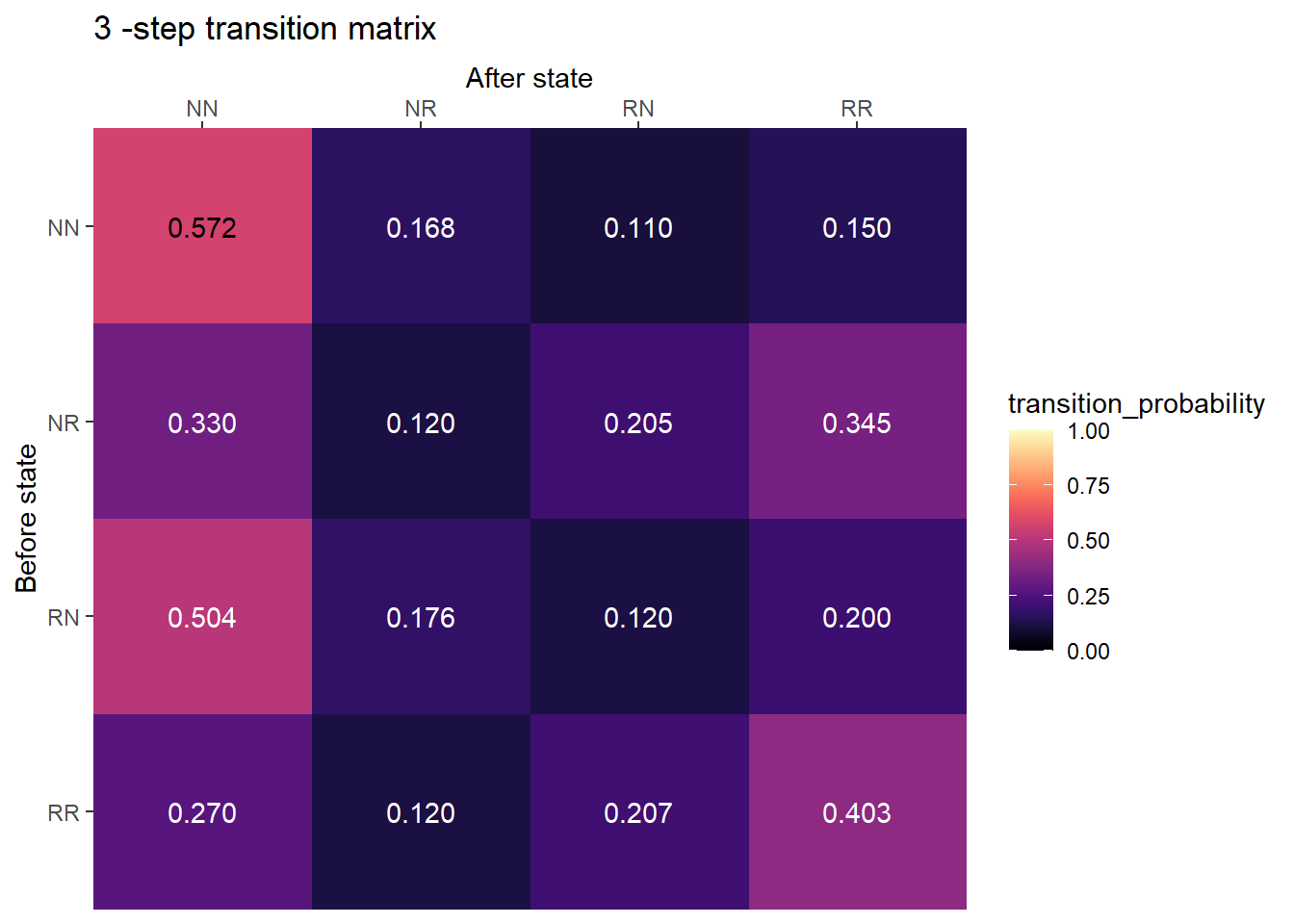

Ping pong

state_names = c("AB", "AC", "BC")

P = rbind(c(0, .7, .3),
          c(.8, 0, .2),
          c(.6, .4, 0)
)

Initial players chosen at random

pi_0 = c(1/3, 1/3, 1/3)

pi_0 %*% P
          [,1]      [,2]      [,3]
[1,] 0.4666667 0.3666667 0.1666667
plot_DTMC_marginal_bars(pi_0, P, state_names, last_time = 10)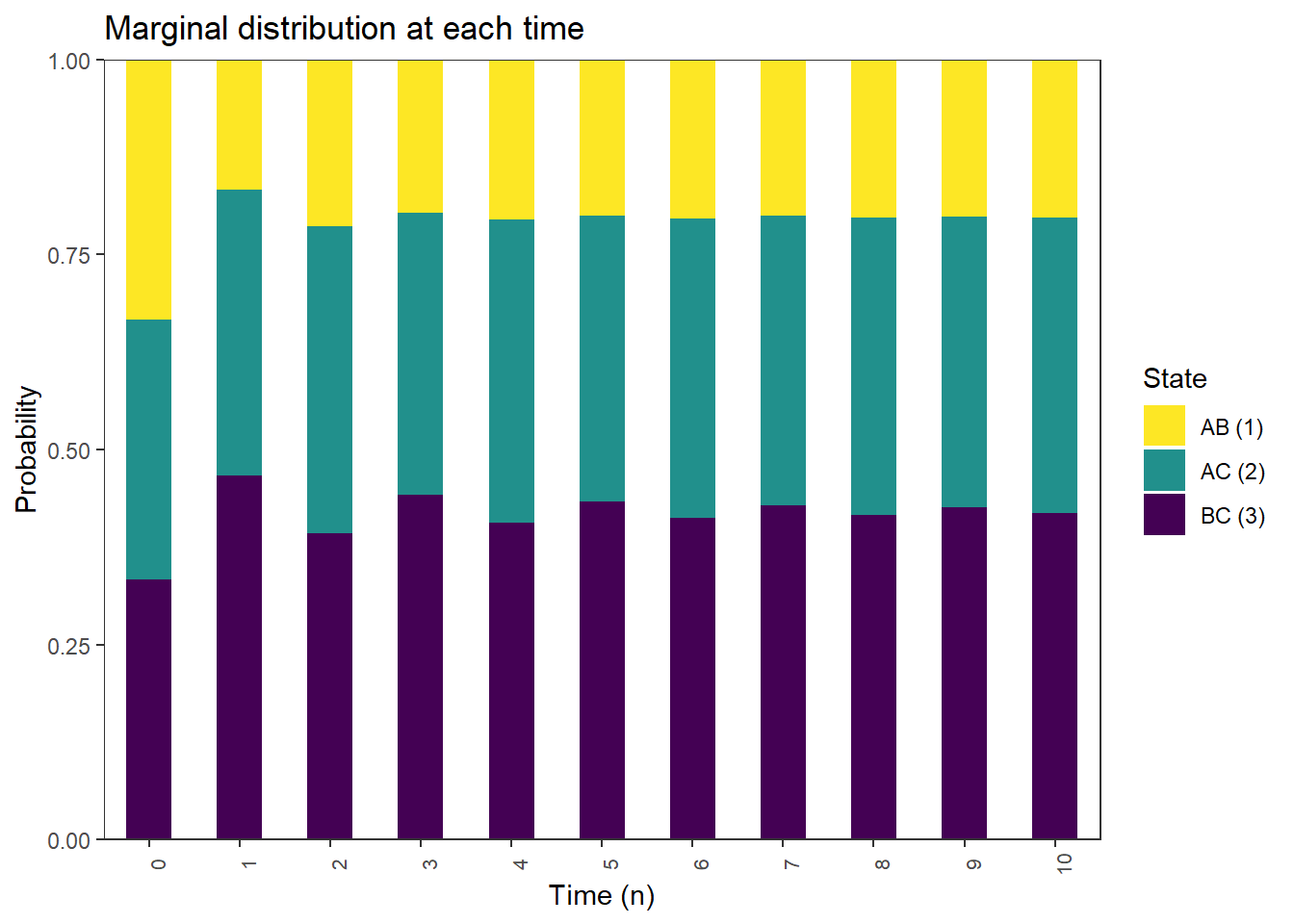

Player A’s initial opponent chosen at random

pi_0 = c(1/2, 1/2, 0)

pi_0 %*% P
     [,1] [,2] [,3]
[1,]  0.4 0.35 0.25
plot_DTMC_marginal_bars(pi_0, P, state_names, last_time = 10)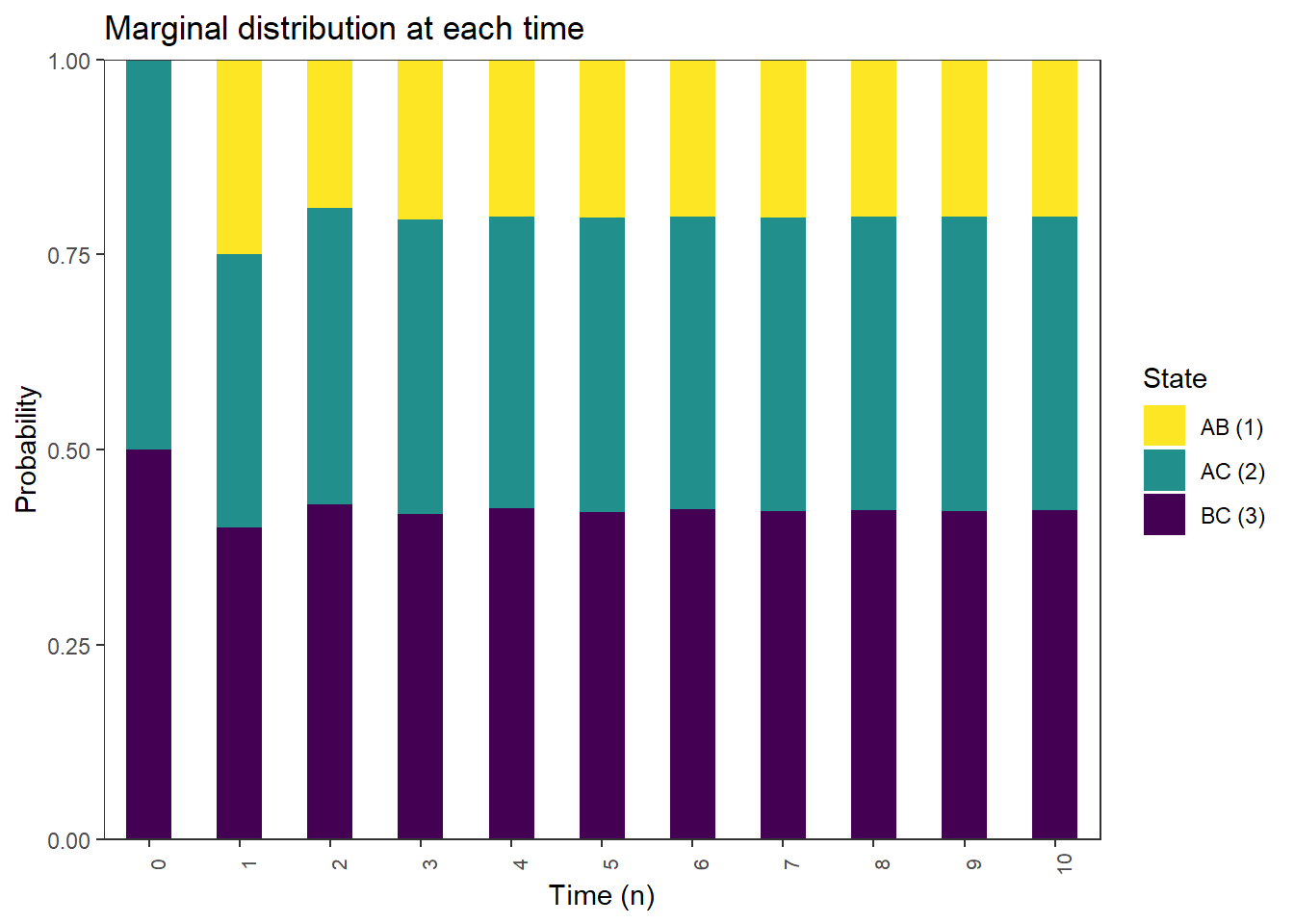

Player A and B play initially

pi_0 = c(1, 0, 0)

pi_0 %*% P
     [,1] [,2] [,3]
[1,]    0  0.7  0.3
plot_DTMC_marginal_bars(pi_0, P, state_names, last_time = 10)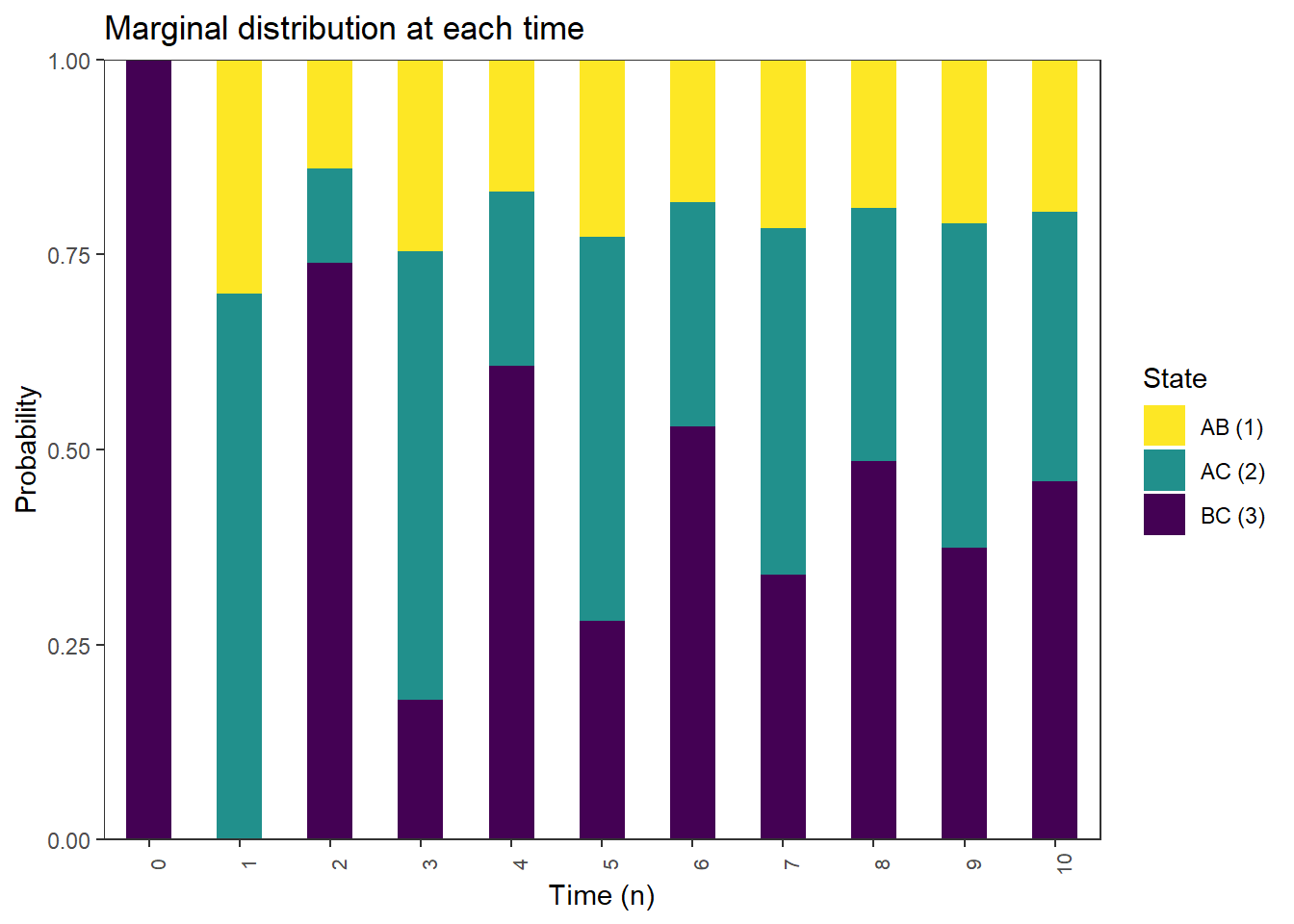

Ehrenfest urn chain

M = 3

state_names = 0:M

P = rbind(c(0, 1, 0, 0),
         c(1/3, 0, 2/3, 0),
         c(0, 2/3, 0, 1/3),
         c(0, 0, 1, 0)
)

Molecules initially distributed at random between A and B

Marginal distribution of \(X_0\)

pi_0 = dbinom(0:M, M, 0.5)

pi_0
[1] 0.125 0.375 0.375 0.125

Marginal distribution of \(X_1\)

pi_0 %*% P
      [,1]  [,2]  [,3]  [,4]
[1,] 0.125 0.375 0.375 0.125

Marginal distribution of \(X_2\)

pi_0 %*% (P %^% 2)
      [,1]  [,2]  [,3]  [,4]
[1,] 0.125 0.375 0.375 0.125

Marginal distribution of \(X_3\)

pi_0 %*% (P %^% 3)
      [,1]  [,2]  [,3]  [,4]
[1,] 0.125 0.375 0.375 0.125
plot_DTMC_marginal_bars(pi_0, P, state_names, last_time = 10)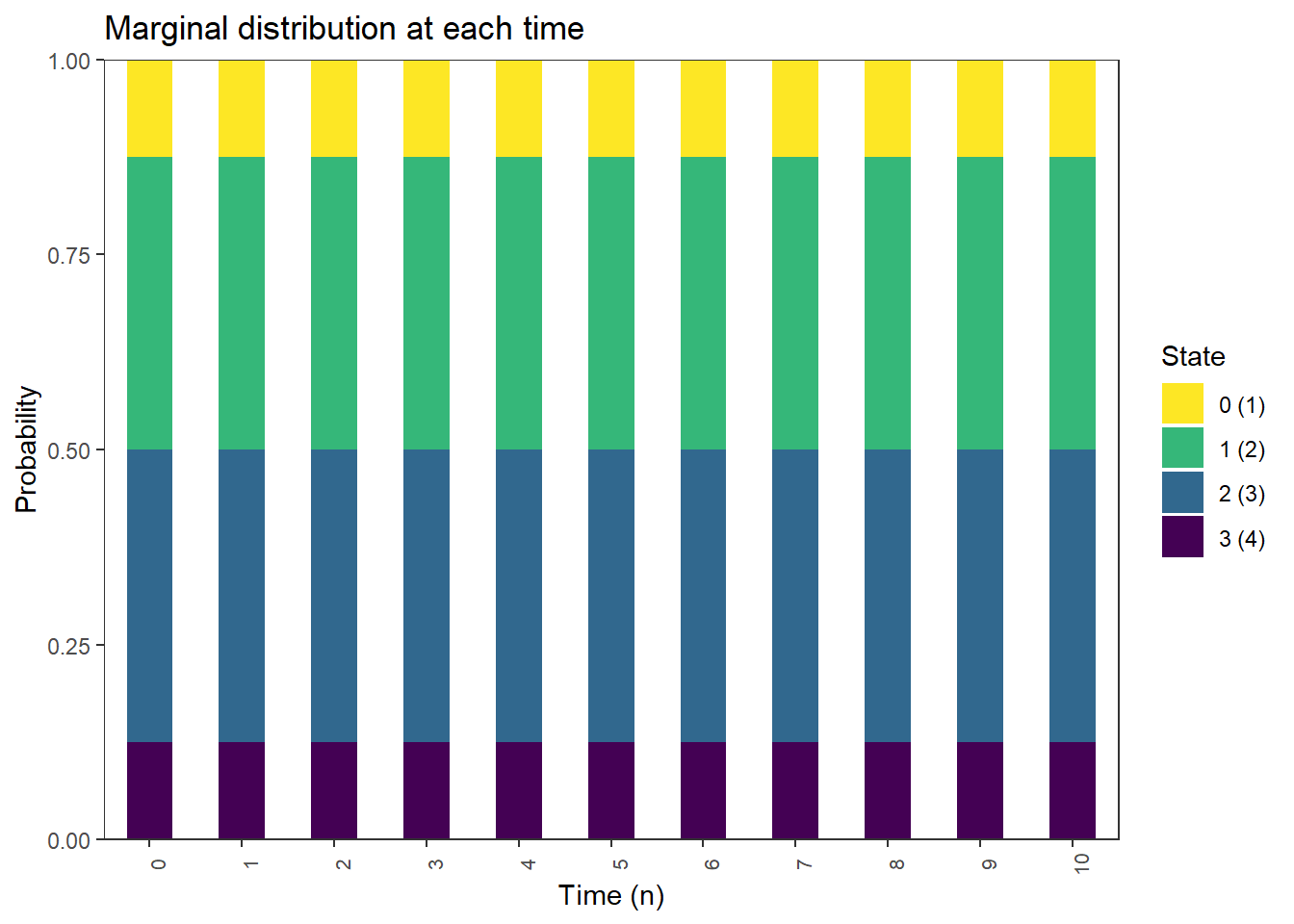

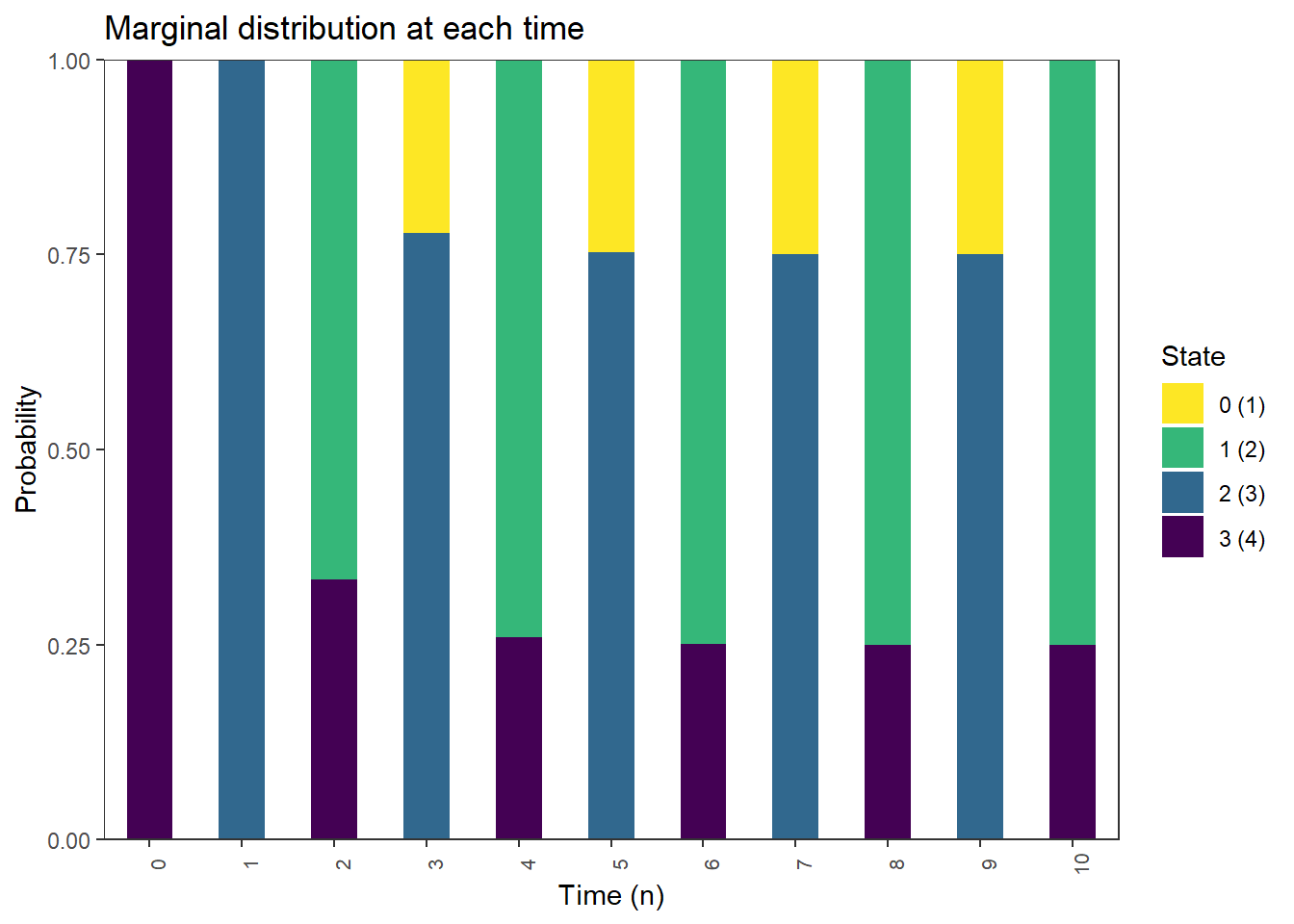
Molecules initially all in A

Marginal distribution of \(X_0\)

pi_0 = c(rep(0, M), 1)

pi_0
[1] 0 0 0 1

Marginal distribution of \(X_1\)

pi_0 %*% P
     [,1] [,2] [,3] [,4]
[1,]    0    0    1    0

Marginal distribution of \(X_2\)

pi_0 %*% (P %^% 2)
     [,1]      [,2] [,3]      [,4]
[1,]    0 0.6666667    0 0.3333333

Marginal distribution of \(X_3\)

pi_0 %*% (P %^% 3)
          [,1] [,2]      [,3] [,4]
[1,] 0.2222222    0 0.7777778    0
plot_DTMC_marginal_bars(pi_0, P, state_names, last_time = 10)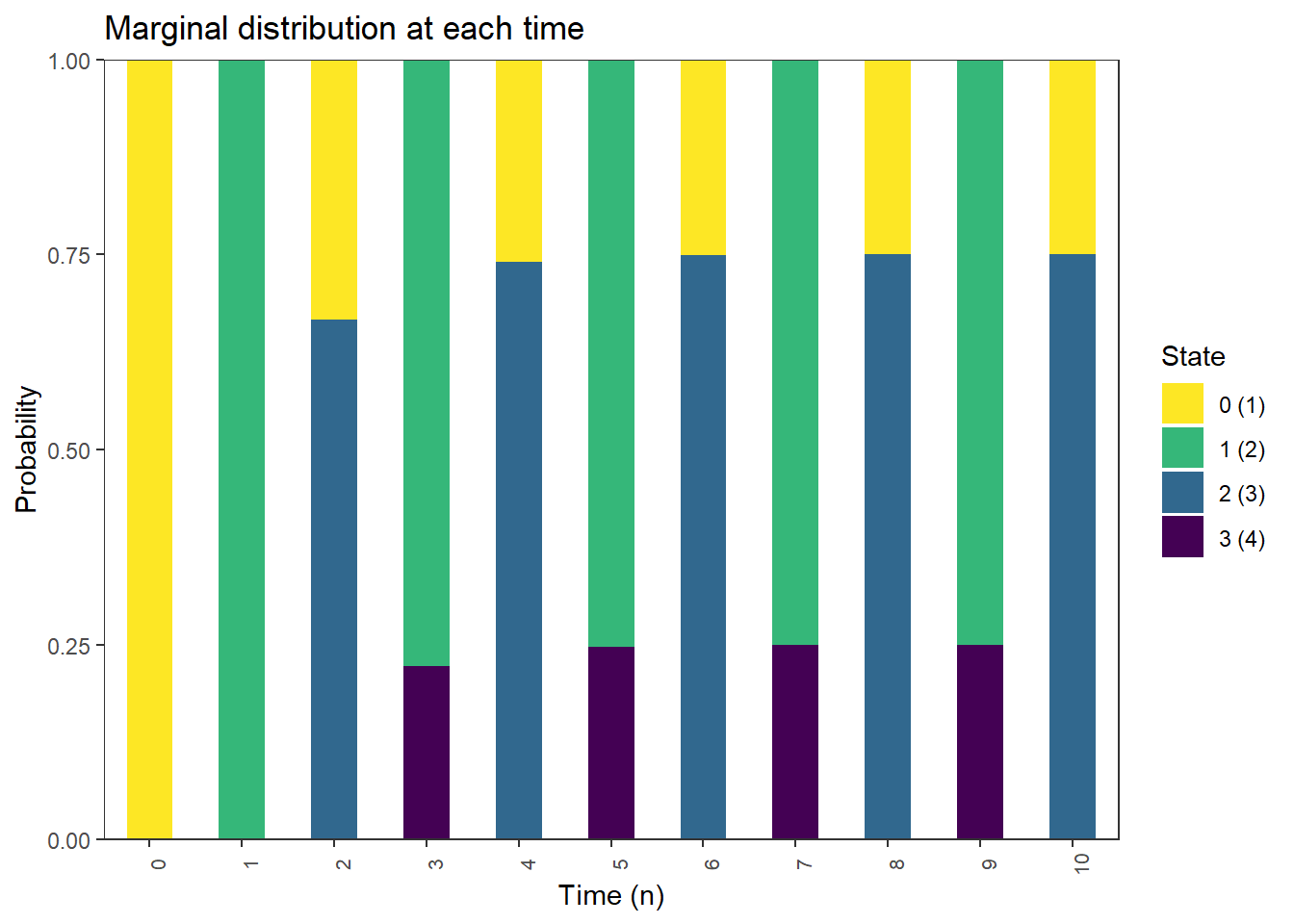

Molecules initially all in B

Marginal distribution of \(X_0\)

pi_0 = c(1, rep(0, M))

pi_0
[1] 1 0 0 0

Marginal distribution of \(X_1\)

pi_0 %*% P
     [,1] [,2] [,3] [,4]
[1,]    0    1    0    0

Marginal distribution of \(X_2\)

pi_0 %*% (P %^% 2)
          [,1] [,2]      [,3] [,4]
[1,] 0.3333333    0 0.6666667    0

Marginal distribution of \(X_3\)

pi_0 %*% (P %^% 3)
     [,1]      [,2] [,3]      [,4]
[1,]    0 0.7777778    0 0.2222222
plot_DTMC_marginal_bars(pi_0, P, state_names, last_time = 10)