state_names = c("start", "middle across", "outer edge across",
"diagonal not middle", "diagonal middle", "corners",
"absorbing")
P = rbind(
c(0, 1/4, 0, 0, 1/2, 0, 1/4),
c(0, 0, 2/9, 4/9, 0, 2/9, 1/9),
c(0, 1/4, 0, 0, 1/2, 0, 1/4),
c(0, 1/4, 0, 0, 1/2, 0, 1/4),
c(0, 0, 2/9, 4/9, 0, 1/9, 2/9),
c(0, 1/2, 0, 0, 1/2, 0, 0),
c(0, 0, 0, 0, 0, 0, 1)
)Miscellaneous Markov Math
Mouse and cat
See https://fivethirtyeight.com/features/how-many-pennies-should-you-pinch/ and https://www.jtash.com/riddler-delirious-ducks
mtta = mean_time_to_absorption(P, state_names)
mtta |> kbl() |> kable_styling()| start_state | mean_time_to_absorption |
|---|---|
| start | 4.905405 |
| middle across | 5.675676 |
| outer edge across | 4.905405 |
| diagonal not middle | 4.905405 |
| diagonal middle | 4.972973 |
| corners | 6.324324 |
T_pmf = pmf_of_time_to_absorption(P, state_names, start_state = "start")
T_pmf |> head(10) |> kbl() |> kable_styling()| n | prob_absorb_at_time_n |
|---|---|
| 1 | 0.2500000 |
| 2 | 0.1388889 |
| 3 | 0.1250000 |
| 4 | 0.0879630 |
| 5 | 0.0810185 |
| 6 | 0.0573560 |
| 7 | 0.0528549 |
| 8 | 0.0374228 |
| 9 | 0.0344865 |
| 10 | 0.0244175 |
ggplot(T_pmf |>
filter(prob_absorb_at_time_n > 0),
aes(x = n,
y = prob_absorb_at_time_n)) +
geom_line(linewidth = 1)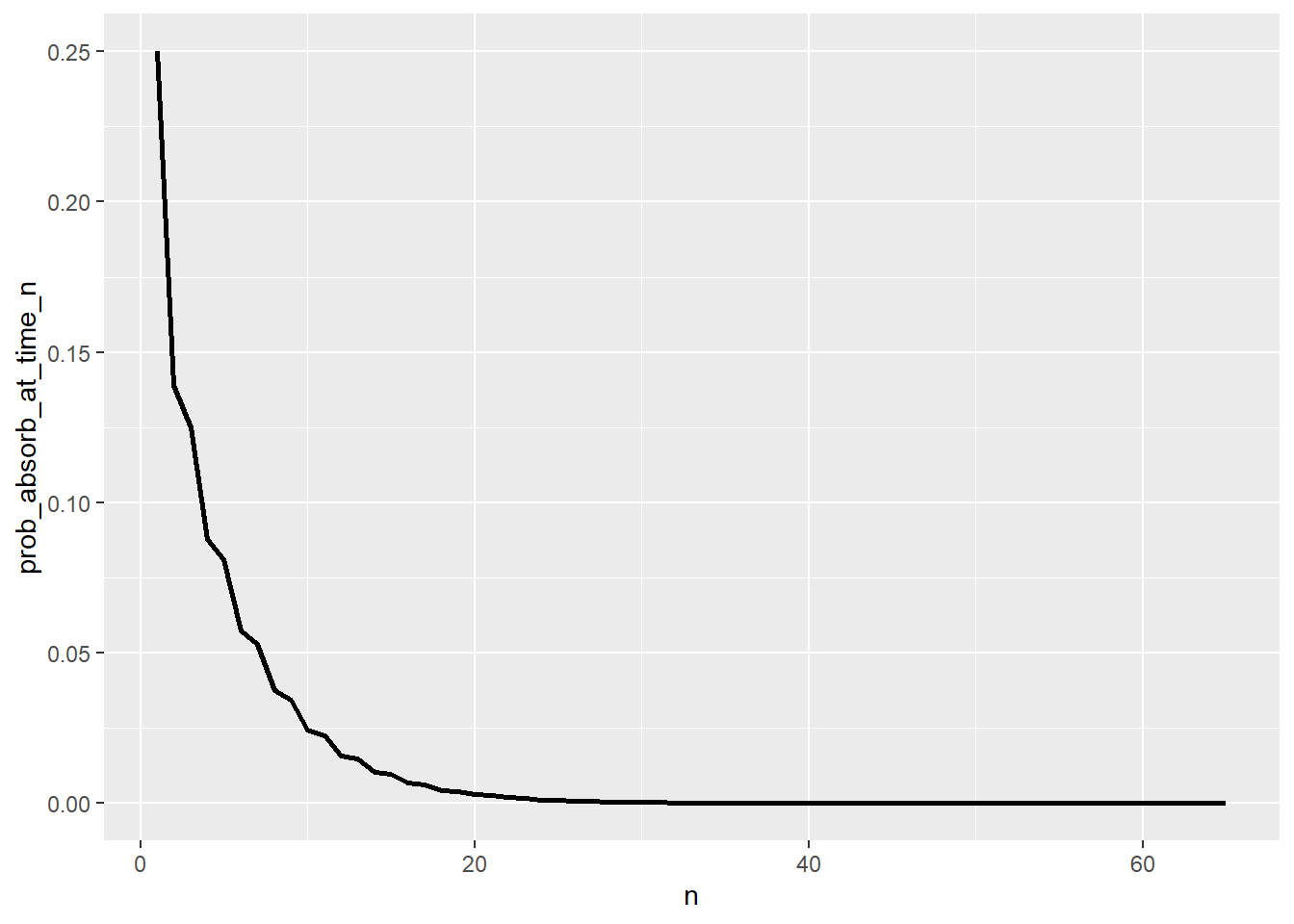
sum(T_pmf[, 1] * T_pmf[, 2])[1] 4.905344