Discrete Time Markov Chains: Stationary Distributions

1. Consider a retail store that sells a particular item (say a TV). Each day they experience customer demand of 0 units of the item with probability 0.6, 1 unit with probability 0.3, and 2 units with probability 0.1 (provided enough units are on the shelf), independently from day to day. The shelf space in the store has room for at most 5 units of the item. If at the end of the day there are fewer than 2 units left then the store restocks the shelf so that it has a total of 5 units on it at the start of the next day. Let \(X_n\) be the number of units on the shelf at the end of day \(n\), before restocking.

   1. Set up — by hand — a system of equations you would solve to find the stationary distribution.
   2. Use software to find the stationary distribution.

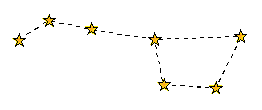
2. A particle makes a random walk between the stars in the Big Dipper. Starting from each star, the particle is equally likely to move to one of its neighboring stars (see the dotted lines in the picture below), independently of all previous moves. Find the stationary distribution of the particle’s position, without setting up or solving a system of equations.