Q = rbind(
c(-2, 2),
c(10, -10)
)Continuous Time Markov Chains: Transition Probabilities and Kolmogorov Equations
Busy machine
t = 1 / 60
10 / 12 + 2 / 12 * exp(-12 * t)[1] 0.969788510 / 12 - 10 / 12 * exp(-12 * t)[1] 0.1510577library(expm)Loading required package: Matrix
Attaching package: 'expm'The following object is masked from 'package:Matrix':
expmexpm(Q * 1 / 60) [,1] [,2]
[1,] 0.9697885 0.03021154
[2,] 0.1510577 0.84894229t = 1 / 6
10 / 12 + 2 / 12 * exp(-12 * t)[1] 0.855889210 / 12 - 10 / 12 * exp(-12 * t)[1] 0.7205539expm(Q * 1 / 6) [,1] [,2]
[1,] 0.8558892 0.1441108
[2,] 0.7205539 0.2794461t = 1
10 / 12 + 2 / 12 * exp(-12 * t)[1] 0.833334410 / 12 - 10 / 12 * exp(-12 * t)[1] 0.8333282expm(Q * 1) [,1] [,2]
[1,] 0.8333344 0.1666656
[2,] 0.8333282 0.1666718t = 2
10 / 12 + 2 / 12 * exp(-12 * t)[1] 0.833333310 / 12 - 10 / 12 * exp(-12 * t)[1] 0.8333333expm(Q * 2) [,1] [,2]
[1,] 0.8333333 0.1666667
[2,] 0.8333333 0.1666667Machine repair
Q = [[-0.2, 0.05, 0.15],
[ 0, -1, 1],
[ 1.5, 0.5, -2]]
pi0 = [1, 0, 0]
states = [1, 2, 3]
X = ContinuousTimeMarkovChain(Q, pi0, states)plt.figure();
X[1 / 60].sim(10000).plot()
plt.show();
Q = rbind(
c(-0.2, 0.05, 0.15),
c(0, -1, 1),
c(1.5, 0.5, - 2)
)
expm(Q * 1 / 60) [,1] [,2] [,3]
[1,] 0.9967031105 0.0008353086 0.002461581
[2,] 0.0002046696 0.9835394306 0.016255900
[3,] 0.0245475853 0.0081381834 0.967314231expm(Q * 1.5 / 60) [,1] [,2] [,3]
[1,] 0.9950815971 0.001254325 0.003664078
[2,] 0.0004564517 0.975461238 0.024082310
[3,] 0.0364886266 0.012063978 0.951447396expm(Q * 1) [,1] [,2] [,3]
[1,] 0.8821068 0.04523439 0.07265883
[2,] 0.2909738 0.44448084 0.26454534
[3,] 0.6295971 0.14682136 0.22358158plt.figure();
X[10].sim(10000).plot()
plt.show();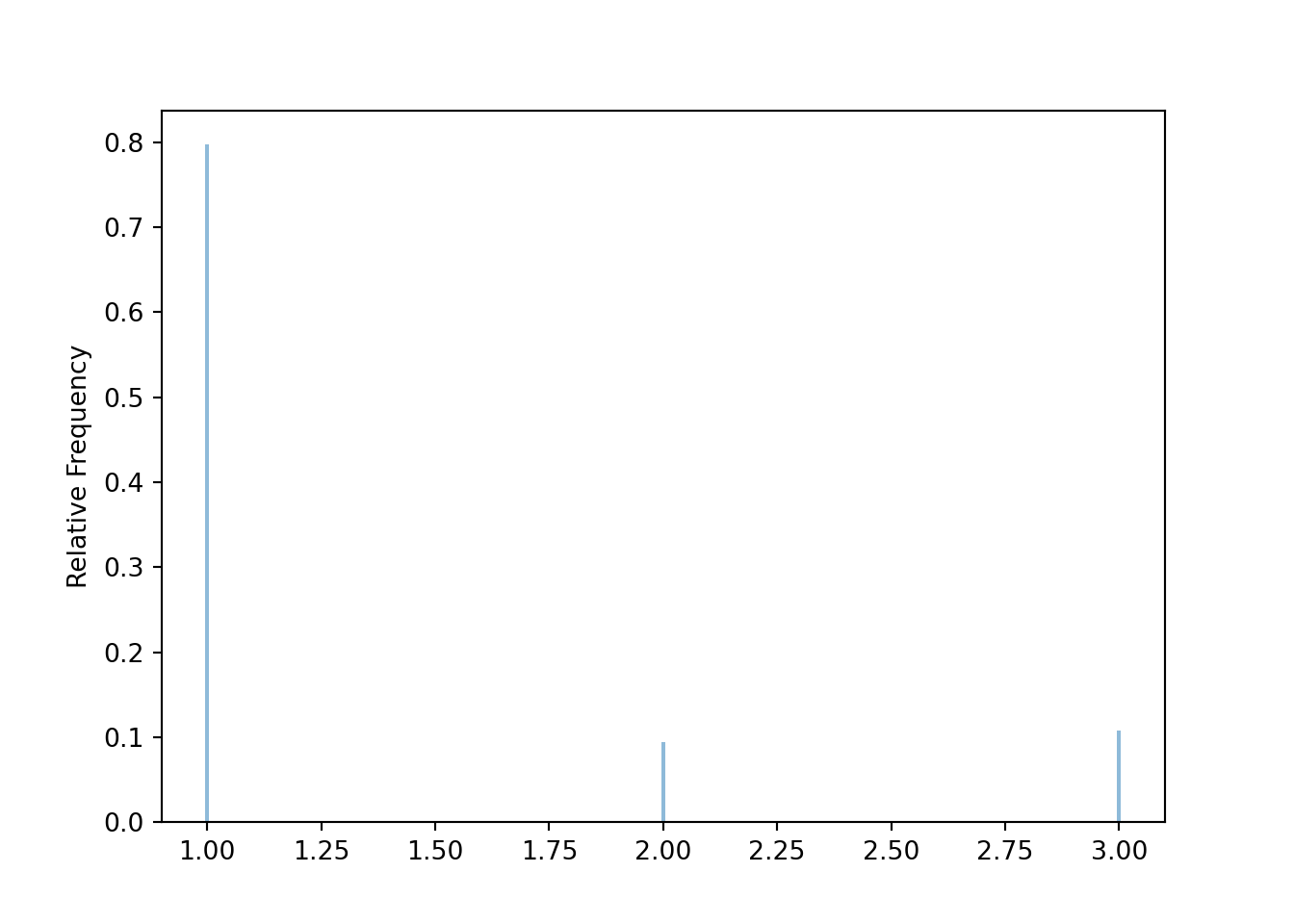
expm(Q * 10) [,1] [,2] [,3]
[1,] 0.8000763 0.09328615 0.1066376
[2,] 0.7994811 0.09365426 0.1068647
[3,] 0.7998819 0.09340639 0.1067117