Exercise 3 Optimal scaling of nominal questionnaire data
| Data file | Nishisato.csv |
| R package | aspect |
3.1 Objectives
In this exercise, we will attempt to find “optimal” scores for nominal responses. Unlike ordinal responses considered in Exercise 2, nominal categories do not assume any particular order. Consequently, optimal scores assigned to them are not expected to monotonically increase or decrease - there is simply no restrictions on their sign or order.
As before, in assigning “optimal” scores, we will maximize the sum of the item correlations (and therefore the test score’s “internal consistency” measured by Cronbach’s alpha).
3.2 Worked Example – Optimal scaling of Nishisato attitude items
This example considers responses to 4 attitude items from N=23 respondents (Nishisato, 1994). Optimal scaling of these data is considered in detail in McDonald (1999, p. 435-441).
1. How old are you? (20-29 / 30-39 / 40+)
2. Children today are not as disciplined as when I was a child (agree / cannot tell / disagree)
3. Children today are not as fortunate as when I was a child (agree / cannot tell / disagree)
4. Religion should be taught in school (agree / indifferent / disagree)By looking at the items, we may tentatively propose that they measure something in common, perhaps nostalgic feelings about the past (?), if agreeing to items 2, 3 and 4, and older age were keyed positively. To put this initial intuition to the test, we will conduct optimal scaling.
Step 1. Importing and examining data
We begin by importing data file Nishisato.csv. Unlike in the previous exercises, this file is not in the internal R format but is a comma-separated text file (.csv). Files in foreign to R formats are not “loaded” but “read” instead. We can use function read.csv(file, header = TRUE, sep = ",",...) dedicated to reading files of this format. Note that by default, the function assumes that the file has variable names (header=TRUE)`. Because this is an external file, we need to place it into an internal to R object - a data frame. We will call this data frame (arbitrarily) attitude.
## item1 item2 item3 item4
## 1 40+ agree disagree disagree
## 2 30-39 agree cannot tell agree
## 3 30-39 agree disagree agree
## 4 20-29 disagree disagree indifferent
## 5 40+ agree disagree agree
## 6 20-29 cannot tell agree agreeExamine the item names (item1, item2, item3, item4) and responses. You can see that the responses are not coded as numbers, they are actually strings corresponding to the response options, for example “cannot tell”. We leave them like that, as in this analysis, we will not make use of any ordering of the response options, considering them purely nominal categories.
Step 2. Running the optimal scaling procedure
We will again use package aspect, so load it into memory now.
When using function corAspect(data, aspect = "aspectSum", level = "nominal", ...), we will maximize the sum of items’ correlations, so use the default setting aspect="aspectSum". For the level of measurement, we will also use the default, level="nominal".
opt2 <- corAspect(attitude, aspect = "aspectSum", level="nominal")
# Summary output for the optimal scaling analysis
summary(opt2)##
## Correlation matrix of the scaled data:
## item1 item2 item3 item4
## item1 1.0000000 0.7960663 0.3873563 0.7034011
## item2 0.7960663 1.0000000 0.3333116 0.4785331
## item3 0.3873563 0.3333116 1.0000000 0.3999385
## item4 0.7034011 0.4785331 0.3999385 1.0000000
##
##
## Eigenvalues of the correlation matrix:
## [1] 2.5896793 0.7535762 0.5116607 0.1450839
##
## Category scores:
## item1:
## score
## 20-29 1.4526531
## 30-39 -0.3425303
## 40+ -1.0122570
##
## item2:
## score
## agree -0.6607173
## cannot tell 1.4369605
## disagree 1.6078784
##
## item3:
## score
## agree -0.5216552
## cannot tell 1.8973623
## disagree -0.5281230
##
## item4:
## score
## agree -0.4235185
## disagree -0.7718009
## indifferent 1.6643455The output displays the “Correlation matrix of the scaled data”, which are correlations of the item scores after optimal scaling. These are all positive and surprisingly high, ranging between 0.33 and 0.79. Further, “Eigenvalues of the correlation matrix” (from Principal Components Analysis) are displayed. The first eigenvalue here (2.59) is substantially larger than the remaining eigenvalues, indicating just one dimension.
Finally, “Category scores” show the scores that the optimal scaling procedure assigned to the response categories. For example, for those between 20 and 29 years of age, the score suggested is 1.45; those between 30 and 39 will get -.34 and those who are 40 or older will get -1.01. These and other values are chosen so that the scaled item’s mean in the sample is 0, and the correlations between the items are maximized.
Step 3. Viewing transformation plots
We obtain transformation plots by calling
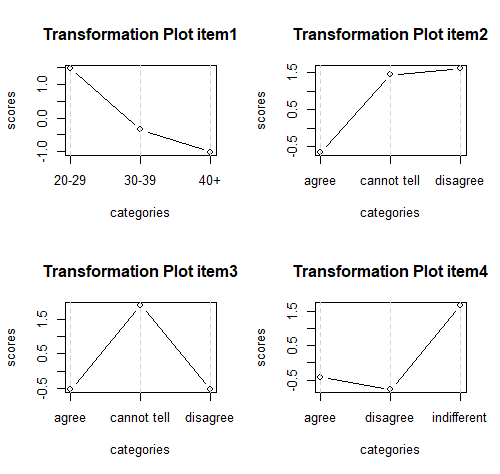
The transformation plot for item1 (age) makes it obvious that although the relationship is monotonic, it is not perfectly linear.
QUESTION 1. Interpret category score assignments and transformation plots for the other items. Items 3 and 4 are the most interesting because they have non-monotonic relationships, and thus depart completely from our initial intuition about potential Likert scaling of items.
QUESTION 2. What kind of person would get the highest score on the total attitude scale (how old would they be, how would they respond to the other items?). What kind of person would get the lowest score?
QUESTION 3. Now, providing the established scaling, what do you think the resulting scale measures?
This completes the exercise.
3.3 Solutions
Q1. Output for item2 (Children today are not as disciplined as when I was a child: Agree / Cannot tell / Disagree) suggests that for those agreeing, the score will be -.66; those who ‘cannot tell’ will get 1.44 and those who disagree will get only slightly more, 1.61.
Output for item3 (Children today are not as fortunate as when I was a child: Agree / Cannot tell / Disagree) shows that those who ‘cannot tell’ will get the score 1.90, and those who agree or disagree will get very similar scores, -.52 or -.53, respectively.
Output for item4 (Religion should be taught in school: Agree / Indifferent / Disagree) shows that those who are ‘indifferent’ will get the score 1.66, and those who agree or disagree will get negative scores, -.42 or -.77 respectively.
Q2. The highest score on the scale will be obtained by those aged 20-29, disagreeing with the idea that children today are not as disciplined as when they were a child, and not providing any definitive opinion on the other two statements (“Children today are not as fortunate as when I was a child”, and “Religion should be taught in school”). The lowest score on the scale will be obtained by those aged 40+, feeling that children today are not as disciplined, and disagreeing with the other two statements (“Children today are not as fortunate as when I was a child”, and “Religion should be taught in school”). [In fact, there is very little difference in score whether one agrees or disagrees with the last two statements].
Q3. Are the score assignments consistent with the conjecture that what is measured is a form of conservatism marked by aging and nostalgia/dogmatism? To some extent, yes, because on one end of the scale we have young people who do not have any concerns about lowering discipline standards for children, feel it is impossible to tell whether children today are more or less fortunate, and are indifferent to whether religion is taught in school or not (more liberal/open-minded). On the other end of the scale we have older people who feel that discipline standards for children have deteriorated, and have opinions on whether children today are more or less fortunate, and whether religion should be taught in school or not (more nostalgic about the past and dogmatic).