Exercise 22 Testing for longitudinal measurement invariance in repeated test measurements
| Data file | SDQ_repeated.csv |
| R package | lavaan |
22.1 Objectives
The objective of this exercise is to fit a full structural model to repeated observations. This model will allow testing for significance of treatment effect (mean difference in latent constructs for pre-treatment and post-treatment data). You will learn how to implement measurement invariance constraints, which are essential to make sure that the scale of measurement is maintained over time.
22.2 Study of clinical change in externalising problems after treatment
Data for this exercise is an anonymous sample from the Child and Adolescent Mental Health Services (CAMHS) database. The sample includes children and adolescents who were referred for psychological/psychiatric help with regard to various problems. In order to evaluate the outcomes of these interventions, the patients’ parents completed the Strengths and Difficulties Questionnaire (SDQ) twice – at referral and then at follow-up, typically 6 months from the referral (from 4 to 8 months on average), in most cases post treatment, or well into the treatment.
The Strengths and Difficulties Questionnaire (SDQ) is a screening questionnaire about 3-16 year olds. It exists in several versions to meet the needs of researchers, clinicians and educationalists (http://www.sdqinfo.org/). In Exercises 1, 5 and 7, we worked with the self-rated version of the SDQ. Today we will work with the parent-rated version, which allows recording outcomes for children of any age. Just like the self-rated version, the parent-rated version includes 25 items measuring 5 facets.
The participants in this study are parents of N=579 children and adolescents (340 boys and 239 girls) aged from 2 to 16 (mean=10.4 years, SD=3.2). This is a clinical sample, so all patients were referred to the services with various presenting problems.
22.3 Worked Example - Quantifying change on a latent construct after an intervention
To complete this exercise, you need to repeat the analysis from a worked example below, and answer some questions.
You will work with the facet scores as indicators of broader difficulties. The three facets of interest here are Conduct problems, Hyperactivity and Pro-social behaviour. These three facets together are thought to measure a broad construct referred to as Externalizing problems, with pro-social behaviour indicating the low end of this construct (it is a negative indicator).
Step 1. Reading and examining data
Download the data file SDQ_repeated.csv, and save it in a new folder. In RStudio, create a new project in the folder you have just created. Start a new script.
This time, the data file is not in the internal R format, but rather a comma-separated text file. The first row contains variables names, and each subsequent row is data for one individual on these variables. To read this file into a data frame, use the dedicated function for .csv files read.csv(). Let’s name this data frame SDQ.
A new object SDQ should appear in your Environment panel. Examine this object using functions head() and names().
Variables p1_conduct, p1_hyper and p1_prosoc are parent-rated scores on the 3 subscales at Time 1, pre-treatment; and variables p2_conduct, p2_hyper and p2_prosoc are parent-rated scores on the 3 subscales at Time 2, post-treatment.
Let’s use function describe() from package psych to get full descriptive statistics for all variables:
## vars n mean sd median trimmed mad min max range skew kurtosis
## age_at_r 1 579 10.42 3.22 10 10.50 4.45 2 16 14 -0.18 -1.00
## gender 2 579 1.41 0.49 1 1.39 0.00 1 2 1 0.35 -1.88
## p1_hyper 3 579 6.26 3.06 6 6.48 4.45 0 10 10 -0.38 -1.01
## p1_emo 4 579 5.15 2.85 5 5.15 2.97 0 10 10 0.00 -1.01
## p1_conduct 5 579 4.50 2.81 4 4.43 2.97 0 10 10 0.18 -0.96
## p1_peer 6 579 3.41 2.47 3 3.27 2.97 0 10 10 0.43 -0.61
## p1_prosoc 7 579 6.48 2.46 7 6.61 2.97 0 10 10 -0.40 -0.61
## p2_hyper 8 579 5.45 3.14 6 5.52 4.45 0 10 10 -0.09 -1.23
## p2_emo 9 579 3.98 2.83 4 3.83 2.97 0 10 10 0.38 -0.81
## p2_conduct 10 579 3.92 2.88 3 3.74 2.97 0 10 10 0.46 -0.77
## p2_peer 11 579 3.13 2.47 3 2.92 2.97 0 10 10 0.62 -0.34
## p2_prosoc 12 579 6.77 2.43 7 6.94 2.97 0 10 10 -0.45 -0.52
## se
## age_at_r 0.13
## gender 0.02
## p1_hyper 0.13
## p1_emo 0.12
## p1_conduct 0.12
## p1_peer 0.10
## p1_prosoc 0.10
## p2_hyper 0.13
## p2_emo 0.12
## p2_conduct 0.12
## p2_peer 0.10
## p2_prosoc 0.10QUESTION 1. Note mean differences at Time 1 (pre-treatment) and Time 2 (post-treatment) for the focal constructs Conduct Problems, Hyperactivity and Pro-social. Do the means increase or decrease? How do you interpret the changes?
Step 2. Fitting a basic structural model for repeated measures
Given that the three SDQ subscales – Conduct problems, Hyperactivity and Pro-social behaviour – are thought to measure Externalizing problems, we will fit the same measurement model at each time point.
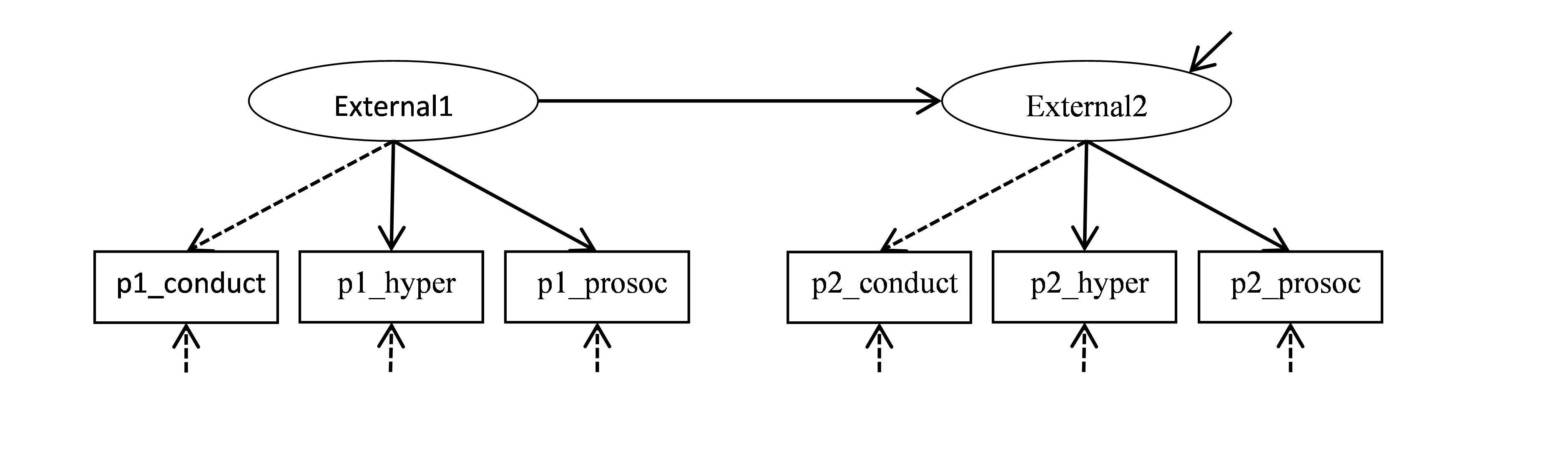
Figure 22.1: Basic model for change in Externalizing problems.
This model specifies that p1_conduct, p1_hyper and p1_prosoc (scores on the 3 subscales at Time 1) are indicators of the factor External1; and that p2_conduct, p2_hyper and p2_prosoc (scores on the 3 subscales at Time 2) are indicators of the factor External2. These parts represent the 2 measurement models. External1 is interpreted as the extent of externalizing problems at referral (Time 1), and External2 is the extent of externalizing problems at follow-up (Time 2). The structural model specifies that External2 is linearly dependent on (regressed on) External1.
First, load the lavaan package.
Now let’s code the model in Figure 22.1 by translating the following sentences into syntax:
• External1 is measured by p1_conduct and p1_hyper and p1_prosoc
• External2 is measured by p2_conduct and p2_hyper and p2_prosoc
• External2 is regressed on External1
Using lavaan contentions, we specify this model (let’s call it Model0) as follows:
Model0 <- '
# Time 1 measurement model
External1 =~ p1_conduct + p1_hyper + p1_prosoc
# Time 2 measurement model
External2 =~ p2_conduct + p2_hyper + p2_prosoc
# Structural model
External2 ~ External1 'By default, External1 and External2 will be scaled by adopting the scale of their first indicators (p1_conduct and p2_conduct respectively). So, it will set the loadings of p1_conduct and p2_conduct to 1. On the diagram, I made these fixed loading paths in dashed rather than solid lines.
To fit this basic model, we need lavaan function sem(). We need to pass to this function the model name (model = Model0), and the data (data = SDQ). Because in this exercise we are interested in change between Time 1 and Time 2, we need to bring means and intercepts into the analysis. This can be done by either declaring means/intercepts of the variables in the model using lavaan convention ~ 1 (this is convenient when you need labels for specific intercepts and we will do this later), or, by simply setting meanstructure=TRUE in the sem() function:
fit0 <- sem(model = Model0, data = SDQ, meanstructure=TRUE)
# ask for summary output including fit indices
summary(fit0, fit.measures=TRUE)## lavaan 0.6-19 ended normally after 35 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 19
##
## Number of observations 579
##
## Model Test User Model:
##
## Test statistic 466.618
## Degrees of freedom 8
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 2229.698
## Degrees of freedom 15
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.793
## Tucker-Lewis Index (TLI) 0.612
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -7603.738
## Loglikelihood unrestricted model (H1) -7370.429
##
## Akaike (AIC) 15245.476
## Bayesian (BIC) 15328.341
## Sample-size adjusted Bayesian (SABIC) 15268.023
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.315
## 90 Percent confidence interval - lower 0.291
## 90 Percent confidence interval - upper 0.339
## P-value H_0: RMSEA <= 0.050 0.000
## P-value H_0: RMSEA >= 0.080 1.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.075
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## External1 =~
## p1_conduct 1.000
## p1_hyper 0.917 0.049 18.868 0.000
## p1_prosoc -0.711 0.040 -17.985 0.000
## External2 =~
## p2_conduct 1.000
## p2_hyper 0.971 0.047 20.840 0.000
## p2_prosoc -0.709 0.037 -19.184 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## External2 ~
## External1 1.003 0.046 21.889 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .p1_conduct 4.504 0.117 38.576 0.000
## .p1_hyper 6.264 0.127 49.263 0.000
## .p1_prosoc 6.484 0.102 63.394 0.000
## .p2_conduct 3.924 0.120 32.771 0.000
## .p2_hyper 5.454 0.130 41.845 0.000
## .p2_prosoc 6.769 0.101 67.004 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .p1_conduct 2.216 0.204 10.885 0.000
## .p1_hyper 4.586 0.311 14.762 0.000
## .p1_prosoc 3.183 0.211 15.077 0.000
## .p2_conduct 2.251 0.203 11.078 0.000
## .p2_hyper 4.127 0.292 14.117 0.000
## .p2_prosoc 2.867 0.193 14.820 0.000
## External1 5.678 0.472 12.029 0.000
## .External2 0.337 0.189 1.780 0.075Examine the output. Note that the factor loadings for p1_conduct and p2_conduct are fixed to 1, and the other loadings are freely estimated. As expected, the loadings for p1_prosoc and p2_prosoc are negative, because being pro-social indicates the lack of externalising problems. Also note that the variance for External1 and residual variance for External2 (.External2) are freely estimated, as are the unique (error) variances of all the indicators (.p1_conduct, .p1_hyper, etc.)
There is also output called ‘Intercepts’. For every DV, its intercept is printed (beginning with ‘.’, for example .p1_conduct), and for every IV, its mean is printed.
Note that the mean of External1 and the intercept of External2 are fixed to 0. This is the default way of giving the origin of measurement to the common factors. Lavaan did this automatically, just as it automatically gave the unit of measurement to the factors by adopting the unit of their first indicators. With the scale of common factors set, the intercepts of all indicators (observed variables) are freely estimated – and thus they have Standard Errors (Std.Err). These intercepts correspond to the expected scale scores on Conduct, Hyperactivity and Pro-social for those with the average (=0) scores on External at the respective time point.
Now examine the chi-square statistic, and other measures of fit.
QUESTION 2. Report and interpret the chi-square test, SRMR, CFI and RMSEA. Would you accept or reject Model0?
To help you understand the reasons for misfit, request the modification indices (sort them in descending order):
## lhs op rhs mi epc sepc.lv sepc.all sepc.nox
## 37 p1_hyper ~~ p2_hyper 248.442 3.524 3.524 0.810 0.810
## 41 p1_prosoc ~~ p2_prosoc 156.286 1.839 1.839 0.609 0.609
## 38 p1_hyper ~~ p2_prosoc 45.346 1.208 1.208 0.333 0.333
## 40 p1_prosoc ~~ p2_hyper 41.278 1.175 1.175 0.324 0.324
## 36 p1_hyper ~~ p2_conduct 40.656 -1.231 -1.231 -0.383 -0.383
## 33 p1_conduct ~~ p2_hyper 31.941 -1.073 -1.073 -0.355 -0.355
## 32 p1_conduct ~~ p2_conduct 31.520 0.985 0.985 0.441 0.441
## 35 p1_hyper ~~ p1_prosoc 12.271 0.662 0.662 0.173 0.173
## 27 External2 =~ p1_conduct 12.270 -3.019 -7.425 -2.643 -2.643
## 39 p1_prosoc ~~ p2_conduct 10.351 0.503 0.503 0.188 0.188
## 34 p1_conduct ~~ p2_prosoc 10.057 0.471 0.471 0.187 0.187
## 44 p2_hyper ~~ p2_prosoc 9.982 0.565 0.565 0.164 0.164
## 24 External1 =~ p2_conduct 9.980 -2.442 -5.819 -2.020 -2.020
## 43 p2_conduct ~~ p2_prosoc 4.580 -0.359 -0.359 -0.141 -0.141
## 25 External1 =~ p2_hyper 4.580 1.464 3.489 1.112 1.112
## 28 External2 =~ p1_hyper 4.105 1.376 3.385 1.106 1.106
## 31 p1_conduct ~~ p1_prosoc 4.105 -0.359 -0.359 -0.135 -0.135
## 29 External2 =~ p1_prosoc 0.959 -0.513 -1.263 -0.513 -0.513
## 30 p1_conduct ~~ p1_hyper 0.959 0.222 0.222 0.070 0.070
## 42 p2_conduct ~~ p2_hyper 0.538 0.168 0.168 0.055 0.055
## 26 External1 =~ p2_prosoc 0.538 -0.364 -0.867 -0.357 -0.357QUESTION 3. What do the modification indices tell you? Which two changes in the model would produce the greatest decrease in the chi-square? How do you interpret these model changes?
Let us now modify the model allowing the unique factors (errors) of p1_hyper and p2_hyper, and errors of p1_prosoc and p2_prosoc correlate. Modify Model0 as follows, creating Model1:
Model1 <- '
# Time 1 measurement model
External1 =~ p1_conduct + p1_hyper + p1_prosoc
# Time 2 measurement model
External2 =~ p2_conduct + p2_hyper + p2_prosoc
# Structural model
External2 ~ External1
# MODIFIED PART: correlated errors for repeated measures
p1_hyper ~~ p2_hyper
p1_prosoc ~~ p2_prosoc 'Now fit the modified model Model1 and ask for the summary output:
## lavaan 0.6-19 ended normally after 44 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 21
##
## Number of observations 579
##
## Model Test User Model:
##
## Test statistic 1.490
## Degrees of freedom 6
## P-value (Chi-square) 0.960
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## External1 =~
## p1_conduct 1.000
## p1_hyper 0.793 0.044 17.853 0.000
## p1_prosoc -0.627 0.036 -17.575 0.000
## External2 =~
## p2_conduct 1.000
## p2_hyper 0.865 0.043 20.209 0.000
## p2_prosoc -0.640 0.033 -19.227 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## External2 ~
## External1 0.885 0.040 22.276 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## .p1_hyper ~~
## .p2_hyper 3.459 0.278 12.444 0.000
## .p1_prosoc ~~
## .p2_prosoc 1.827 0.170 10.771 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .p1_conduct 4.504 0.117 38.576 0.000
## .p1_hyper 6.264 0.128 49.094 0.000
## .p1_prosoc 6.484 0.102 63.381 0.000
## .p2_conduct 3.924 0.120 32.771 0.000
## .p2_hyper 5.454 0.131 41.689 0.000
## .p2_prosoc 6.769 0.101 67.154 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .p1_conduct 1.200 0.211 5.680 0.000
## .p1_hyper 5.216 0.343 15.229 0.000
## .p1_prosoc 3.429 0.223 15.350 0.000
## .p2_conduct 1.396 0.200 6.962 0.000
## .p2_hyper 4.742 0.323 14.678 0.000
## .p2_prosoc 3.057 0.202 15.129 0.000
## External1 6.694 0.500 13.389 0.000
## .External2 1.666 0.196 8.494 0.000QUESTION 4. Report and interpret the chi-square for the model with correlated errors for repeated measures (Model1). Would you accept or reject Model1? What are the degrees of freedom for Model1 and how do they compare to Model0?
Step 3. Fitting a full measurement invariance model for repeated measures
Our structural model with correlated errors fits well, but this model cannot be used to measure change in externalising problems because it does not ensure measurement invariance across time. The scale of measurement of Externalizing factor might have changed, and if so, we cannot compare Externalising constructs at Time 1 and Time 2 (it is like comparing temperatures measured in Celsius and Fahrenheit). To ensure equivalent measurement across time, we need constraints on the measurement parameters: factor loadings (unit of measurement), intercepts (origin of measurement) and unique/error variances (error of measurement) of respective indicators at Time 1 and Time 2.
These constraints are easy to implement by giving the corresponding parameters the same label (look at small symbols in red in Figure 22.2). To constrain the loadings of p1_hyper and p2_hyper to be the same across time, we give them the same label (for instance, lh, standing for ‘loading hyper’ – but you can use any label you want); to constrain the intercepts of p1_hyper and p2_hyper to be the same, we give them the same label (ih, standing for ‘intercept hyper’); and to constrain the error variances of p1_hyper and p2_hyper to be the same, we give them the same label (eh, standing for ‘error hyper’). We do the same for the other indicators, giving the same labels to the loadings, intercepts and error variances at Time 1 and Time 2.
NOTE that the loadings for p1_conduct and p2_conduct do not need to be constrained equal by using labels because they are fixed to 1 by default, therefore they are already equal.
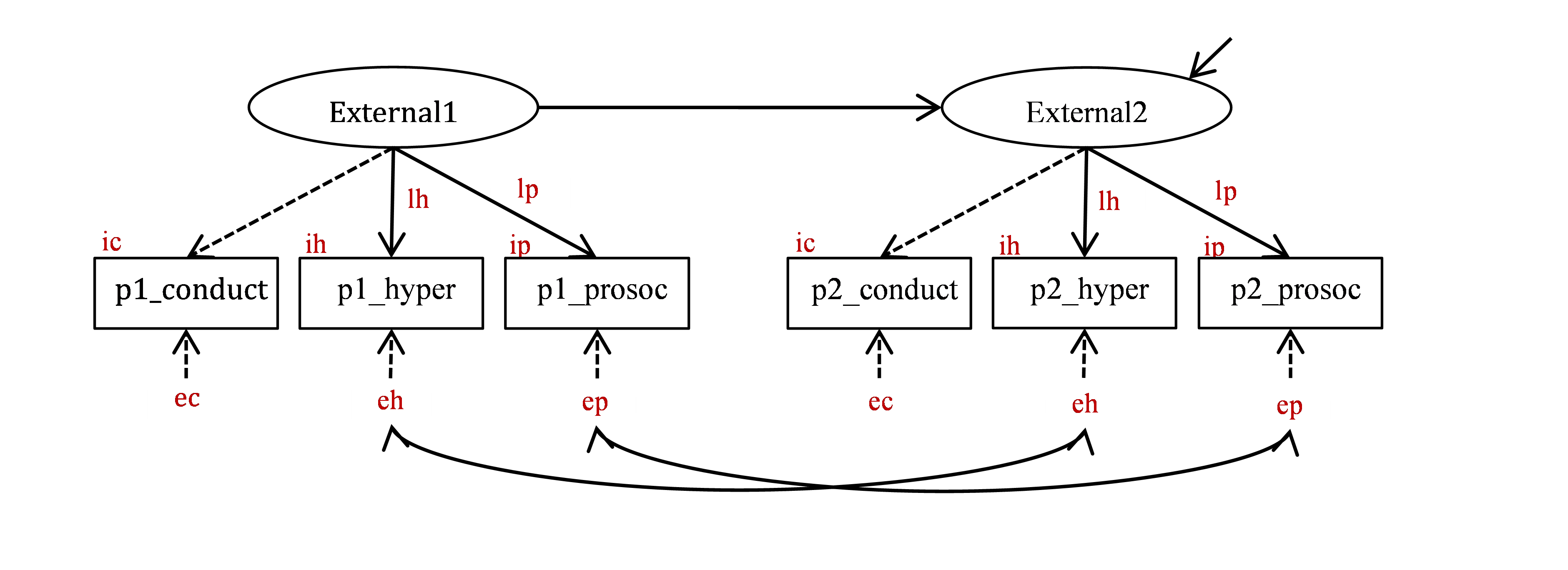
Figure 22.2: Full measurement invariance model for change in Externalizing problems.
You should already know how to specify labels for path coefficients. Factor loadings are path coefficients. Simply add multipliers in front of indicators in measurement =~ statements, like so: lh*p1_hyper. To specify labels for variances, add multipliers in variance ~~ statements, like so: p1_hyper ~~ eh*p1_hyper.
To specify labels for intercepts, use multipliers in statements ~ 1. For example, to label the intercept of p1_hyper as ih, write p1_hyper ~ ih*1.
OK, here is the full measurement invariance model (Model2) corresponding to Figure 22.2. [Please type it in yourself, using bits of your previous models, but do not just copy and paste my text! You need to make your own mistakes and correct them.]
Model2 <- '
# Time 1 measurement model with labels
External1 =~ p1_conduct + lh*p1_hyper + lp*p1_prosoc
# error variances
p1_conduct ~~ ec*p1_conduct
p1_hyper ~~ eh*p1_hyper
p1_prosoc ~~ ep*p1_prosoc
# intercepts
p1_conduct ~ ic*1
p1_hyper ~ ih*1
p1_prosoc ~ ip*1
# Time 2 measurement model with labels
External2 =~ p2_conduct + lh*p2_hyper + lp*p2_prosoc
# error variances
p2_conduct ~~ ec*p2_conduct
p2_hyper ~~ eh*p2_hyper
p2_prosoc ~~ ep*p2_prosoc
# intercepts
p2_conduct ~ ic*1
p2_hyper ~ ih*1
p2_prosoc ~ ip*1
# Structural model
External2 ~ External1
#correlated errors for repeated measures
p1_hyper ~~ p2_hyper
p1_prosoc ~~ p2_prosoc 'Model2 tests the following combined hypothesis:
• H1. Two measurements of Externalising are fully invariant across time.
• H2. And, because we have not changed the origin of measurement for External2 (its intercept was set to 0 by default, remember?), Model2 also assumes that there is no change in Externalising from Time 1 to Time 2 (because the mean of External1 was also set to 0).
Now fit Model2 (assign the results to new object fit2), and examine the output.
## lavaan 0.6-19 ended normally after 42 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 21
## Number of equality constraints 8
##
## Number of observations 579
##
## Model Test User Model:
##
## Test statistic 103.584
## Degrees of freedom 14
## P-value (Chi-square) 0.000
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## External1 =~
## p1_condct 1.000
## p1_hyper (lh) 0.840 0.038 22.356 0.000
## p1_prosoc (lp) -0.625 0.029 -21.901 0.000
## External2 =~
## p2_condct 1.000
## p2_hyper (lh) 0.840 0.038 22.356 0.000
## p2_prosoc (lp) -0.625 0.029 -21.901 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## External2 ~
## External1 0.888 0.032 27.610 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## .p1_hyper ~~
## .p2_hyper 3.398 0.279 12.173 0.000
## .p1_prosoc ~~
## .p2_prosoc 1.844 0.170 10.863 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .p1_condct (ic) 4.283 0.110 39.027 0.000
## .p1_hyper (ih) 5.917 0.123 48.276 0.000
## .p1_prosoc (ip) 6.583 0.093 70.683 0.000
## .p2_condct (ic) 4.283 0.110 39.027 0.000
## .p2_hyper (ih) 5.917 0.123 48.276 0.000
## .p2_prosoc (ip) 6.583 0.093 70.683 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .p1_condct (ec) 1.258 0.125 10.025 0.000
## .p1_hyper (eh) 5.048 0.284 17.743 0.000
## .p1_prosoc (ep) 3.253 0.172 18.896 0.000
## .p2_condct (ec) 1.258 0.125 10.025 0.000
## .p2_hyper (eh) 5.048 0.284 17.743 0.000
## .p2_prosoc (ep) 3.253 0.172 18.896 0.000
## External1 6.567 0.454 14.471 0.000
## .External2 2.110 0.224 9.436 0.000Note that all parameter labels that you introduced are printed in the output next to the respective parameter. Also note that every pair of parameters that you constrained equal are indeed equal!
QUESTION 5. Report and interpret the chi-square test for the full measurement invariance model (Model2). Would you accept or reject this model?
Now we need to understand what the chi-square result means with respect to the combined hypotheses that Model2 tested. Rejection of the model could mean that the measurement invariance is violated (H1 is wrong) or that there is a significant change in the Externalising score from Time 1 to Time 2 (H2 is wrong). To help us understand which hypothesis is wrong, let us obtain the modification indices.
## Warning: lavaan->modindices():
## the modindices() function ignores equality constraints; use lavTestScore()
## to assess the impact of releasing one or multiple constraints.## lhs op rhs mi epc sepc.lv sepc.all sepc.nox
## 24 External1 ~1 73.030 5.966 2.328 2.328 2.328
## 25 External2 ~1 73.030 -0.667 -0.247 -0.247 -0.247
## 38 External2 =~ p1_hyper 4.519 -0.070 -0.190 -0.061 -0.061
## 44 p1_conduct ~~ p2_prosoc 1.898 -0.173 -0.173 -0.085 -0.085
## 52 p2_hyper ~~ p2_prosoc 1.630 -0.164 -0.164 -0.041 -0.041
## 37 External2 =~ p1_conduct 1.568 0.045 0.121 0.043 0.043
## 46 p1_hyper ~~ p2_conduct 1.552 -0.205 -0.205 -0.081 -0.081
## 48 p1_prosoc ~~ p2_conduct 1.383 -0.151 -0.151 -0.075 -0.075
## 41 p1_conduct ~~ p1_prosoc 1.323 0.147 0.147 0.073 0.073
## 35 External1 =~ p2_hyper 1.199 0.040 0.102 0.032 0.032
## 50 p2_conduct ~~ p2_hyper 1.154 0.175 0.175 0.069 0.069
## 10 External2 =~ p2_conduct 0.965 -0.039 -0.104 -0.036 -0.036
## 1 External1 =~ p1_conduct 0.965 0.039 0.099 0.035 0.035
## 51 p2_conduct ~~ p2_prosoc 0.910 0.125 0.125 0.062 0.062
## 47 p1_hyper ~~ p2_prosoc 0.859 0.116 0.116 0.029 0.029
## 34 External1 =~ p2_conduct 0.748 -0.034 -0.088 -0.030 -0.030
## 39 External2 =~ p1_prosoc 0.723 -0.024 -0.065 -0.027 -0.027
## 49 p1_prosoc ~~ p2_hyper 0.143 0.047 0.047 0.012 0.012
## 45 p1_hyper ~~ p1_prosoc 0.051 0.029 0.029 0.007 0.007
## 36 External1 =~ p2_prosoc 0.028 0.005 0.013 0.005 0.005
## 43 p1_conduct ~~ p2_hyper 0.008 -0.014 -0.014 -0.006 -0.006
## 42 p1_conduct ~~ p2_conduct 0.007 -0.021 -0.021 -0.017 -0.017
## 40 p1_conduct ~~ p1_hyper 0.004 0.011 0.011 0.004 0.004The largest modification index should appear first in the output. Compare its size to the chi-square of the model, because the MI shows by how much the chi-square will reduce if the respective parameter was freely estimated.
QUESTION 6. What is the largest modification index? How does it compare to the chi-square and other modification indices? Try to interpret what this index suggests. Do you think it points to H1 being wrong, or H2 being wrong?
Step 4. Measuring change in Externalising Problems factor
Now, hopefully you agree that the reason for misfit of Model2 was fixing the mean of External1 and the intercept of External2 to the same value – zero. This basically allows no change in the Externalising score due to the intervention, setting the regression intercept to 0, like in this equation:
External2 = 0 + B1*External1This is indeed unreasonable. More reasonable would be to assume that after treatment, externalising problems reduced. To allow this change between Externalising score at Time 1 and Time 2 in the model, we need to free the intercept of External2. This can be done by adding the following new line to Model2, making Model3.
NA*1 means that we are “freeing” the intercept of External2 (we have no particular value or label to assign to it). Now, Model3 would test the hypothesis H1 (full measurement invariance across Time).
Create and fit Model3 (assign its results to fit3), examine the output, and answer the following questions.
## lavaan 0.6-19 ended normally after 44 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 22
## Number of equality constraints 8
##
## Number of observations 579
##
## Model Test User Model:
##
## Test statistic 24.219
## Degrees of freedom 13
## P-value (Chi-square) 0.029
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## External1 =~
## p1_condct 1.000
## p1_hyper (lh) 0.866 0.037 23.389 0.000
## p1_prosoc (lp) -0.625 0.028 -22.133 0.000
## External2 =~
## p2_condct 1.000
## p2_hyper (lh) 0.866 0.037 23.389 0.000
## p2_prosoc (lp) -0.625 0.028 -22.133 0.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|)
## External2 ~
## External1 0.918 0.030 30.138 0.000
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## .p1_hyper ~~
## .p2_hyper 3.417 0.280 12.223 0.000
## .p1_prosoc ~~
## .p2_prosoc 1.823 0.170 10.728 0.000
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|)
## .p1_condct (ic) 4.550 0.113 40.169 0.000
## .p1_hyper (ih) 6.150 0.127 48.553 0.000
## .p1_prosoc (ip) 6.416 0.095 67.667 0.000
## .p2_condct (ic) 4.550 0.113 40.169 0.000
## .p2_hyper (ih) 6.150 0.127 48.553 0.000
## .p2_prosoc (ip) 6.416 0.095 67.667 0.000
## .External2 -0.672 0.073 -9.181 0.000
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .p1_condct (ec) 1.333 0.120 11.096 0.000
## .p1_hyper (eh) 4.962 0.284 17.479 0.000
## .p1_prosoc (ep) 3.260 0.172 18.978 0.000
## .p2_condct (ec) 1.333 0.120 11.096 0.000
## .p2_hyper (eh) 4.962 0.284 17.479 0.000
## .p2_prosoc (ep) 3.260 0.172 18.978 0.000
## External1 6.411 0.444 14.431 0.000
## .External2 1.656 0.194 8.547 0.000QUESTION 7. What is the (unstandardized) intercept of External2 (treatment effect)? Recall that we expected a negative effect, since the interventions were aiming to reduce problems. Is the effect as expected?
QUESTION 8. What is the (unstandardized) regression coefficient of External2 on External1? How will you interpret this value in relation to the unit of measurement of External1?
Finally, carry out the chi-square difference test to compare nested models Model2 and Model3. (HINT. Use function anova(fit2,fit3)).
QUESTION 9. How would you interpret the results of this test? Is Model3 significantly better than Model2? Which model would you retain?
Step 5. Saving your work
After you finished work with this exercise, save your R script by pressing the Save icon in the script window, and giving the script a meaningful name, for example “SDQ change after intervention”. To keep all of the created objects, which might be useful when revisiting this exercise, save your entire ‘work space’ when closing the project. Press File / Close project, and select Save when prompted to save your ‘Workspace image’ (with extension .RData).
22.4 Solutions
Q1. The means decrease for Conduct and Hyperactivity, and increase for Pro-social. This is to be expected since the SDQ Hyperactivity and Conduct scales measure problems (the higher the score, the larger the extent of problems), and SDQ Pro-social measures positive pro-social behaviour. Reduction in the problem scores is to be expected after treatment.
Q2. Chi-square = 466.618 (df = 8); P-value < .001. We have to reject the model because the chi-square is highly significant. CFI=0.793, which is much lower than 0.95 (the threshold for good fit), and lower than 0.90 (the threshold for adequate fit). RMSEA =0.315, which is much greater than 0.05 (for good fit) and 0.08 (adequate fit). Finally, SRMR = 0.075, which is just below the threshold for adequate fit (0.08). All indices except SRMR indicate very poor model fit.
Q3. Two largest modification indices (MI) by far can be found in the covariance ~~ statements: p1_hyper~~p2_hyper (mi=248.422) and p1_prosoc~~p2_prosoc (mi=156.286).
The first MI tells you that if you repeat the analysis allowing p1_hyper and p2_hyper correlate (actually, because these are DVs, the correlation will be between their errors/unique factors), the chi square will fall by about 248. But is this reasonable to allow errors/unique factors for the same measures at Time 1 and Time 2 correlate? Consider how the variance on the Hyperactivity facet is explained by both, the common Externalising factor, and the remaining unique content of the facet (the unique factor). Because the same Hyperactivity scale was administered on two different occasions, its unique content not explained by the common Externalising factor would be still shared between the occasions. Therefore, the unique factors at Time 1 and Time 2 cannot be considered independent. The correlated errors will correct for this lack of local independence. Similarly, we should allow correlated errors across time for the Pro-social construct (p1_prosoc and p2_prosoc). A correlated error for p1_conduct and p2_conduct is not needed since M.I. did not suggest it.
Q4. Model1: Chi-square = 1.490 (df=6), P-value = 0.960. The chi-square test is not significant and we accept the model with correlated errors for repeated measures. The degrees of freedom for Model1 are 6, and the degrees of freedom for Model0 were 8. The difference, 2 df, corresponds to the 2 additional parameters we introduced – the two error covariances. By adding 2 parameters, we reduced df by 2.
Q5. Model2: Chi-square = 103.584 (df = 14); P-value < 0.001. The test is highly significant and we have to reject the model.
Q6. The largest modification index by far is 73.030. It is of the same magnitude as the chi-square for this model (103.584), and much larger than other MIs, which are all in single digits. This index pertains to both External1~1 and External2~1. These are mean/intercept statements. Remember that the mean of External1 and the intercept of External2 were fixed to 0 by default? The modification index says that if you either freed the mean of External1 or freed the intercept of External2, the chi-square would improve dramatically. This points to the hypothesis of no change in the Externalising score between Time 1 and Time 2 (H2) being wrong.
Q7. The intercept of External2 is -.672, significant (p<.001) and negative as we expected, indicating reduction in Externalizing problems on average. [Note that this value is on the same scale as the facet Conduct problems, since the Externalising factors borrowed the unit of measurement from this facet.] This result shows that the interventions reduced the extent of externalising problems in children.
Q8. The regression coefficient is 0.918 (look for External2 ~ External1 in the output). This indicates that per one unit change in External1, External2 changes by 0.918 units. Since both External1 and External2 are measured on the same scale, the closeness of the regression coefficient to 1 indicates that the children largely retain their relative ordering on Externalising problems after intervention.
Q9.
##
## Chi-Squared Difference Test
##
## Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
## fit3 13 14793 14854 24.219
## fit2 14 14870 14927 103.584 79.365 0.36789 1 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The chi-square difference of 79.365 on 1 degree of freedom is highly significant. Therefore Model3 is significantly better than Model2, and we should retain Model3.