Exercise 11 EFA of personality scale scores
| Data file | neo.csv |
| R package | psych |
11.1 Objectives
The objective of this exercise is to conduct Exploratory Factor Analysis of a multifaceted personality questionnaire, using a published correlation matrix of its scale scores. Specifically, we will look to establish a factor structure of one of the most popular personality measures, NEO PI-R (Costa & McCrae, 1992).
11.2 Study of factor structure of personality using NEO PI-R
The NEO PI-R is based on the Five Factor model of personality, measuring five broad domains, namely Neuroticism (N), Extraversion (E), Openness (O), Agreeableness (A) and Conscientiousness (C). In addition, NEO identifies 6 facet scales for each broad factor, measuring 30 subscales in total. The facet subscales are listed below:
| Neuroticism | Extraversion | Openness | Agreeableness | Conscientiousness |
|---|---|---|---|---|
| N1 Anxiety | E1 Warmth | O1 Fantasy | A1 Trust | C1 Competence |
| N2 Angry Hostility | E2 Gregariousness | O2 Aesthetics | A2 Straightforwardness | C2 Order |
| N3 Depression | E3 Assertiveness | O3 Feelings | A3 Altruism | C3 Dutifulness |
| N4 Self-Consciousness | E4 Activity | O4 Ideas | A4 Compliance | C4 Achievement Striving |
| N5 Impulsiveness | E5 Excitement-Seeking | O5 Actions | A5 Modesty | C5 Self-Discipline |
| N6 Vulnerability | E6 Positive Emotions | O6 Values | A6 Tender-Mindedness | C6 Deliberation |
The NEO PI-R Manual reports correlations of the 30 facets based on N=1000 subjects. Despite having no access to the actual scale scores for the 1000 subjects, the correlation matrix is all we need to perform factor analysis of the subscales.
11.3 Worked Example - EFA of NEO PI-R correlation matrix
To complete this exercise, you need to repeat the analysis from a worked example below, and answer some questions.
Step 1. Downloading and examining the observed correlations
I recommend to download data file neo.csv into a new folder, and in RStudio, associate a new project with this folder. Create a new script, where you will type all commands.
The data this time is actually a correlation matrix, stored in the comma-separated (.csv) format. You can preview the file by clicking on neo.csv in the Files tab in RStudio, and selecting View File. This will not import the data yet, just open the actual .csv file. You will see that the first row contains the NEO facet names - “N1”, “N2”, “N3”, etc., and the first entry in each row is again the facet names. To import this correlation matrix into RStudio preserving all these facet names for each row and each column, we will use function read.csv(). We will say that we have headers (header=TRUE), and that the row names are contained in the first column (row.names=1).
We have just read the data into a new object named neo, which appeared in your Environment tab. Examine the object by either pressing on it, or calling function View(neo).
You will see that the data are indeed a correlation matrix, with values 1 on the diagonal.
Step 2. Examining suitability of data for factor analysis
First, load the package psych to enable access to its functionality. Conveniently, most functions in this package easily accommodate analysis with correlation matrices as well as with raw data.
Before you start EFA, request the Kaiser-Meyer-Olkin (KMO) index – the measure of sampling adequacy (MSA):
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = neo)
## Overall MSA = 0.87
## MSA for each item =
## N1 N2 N3 N4 N5 N6 E1 E2 E3 E4 E5 E6 O1 O2 O3 O4
## 0.89 0.91 0.92 0.93 0.89 0.92 0.86 0.77 0.89 0.86 0.79 0.87 0.86 0.73 0.84 0.85
## O5 O6 A1 A2 A3 A4 A5 A6 C1 C2 C3 C4 C5 C6
## 0.79 0.77 0.90 0.87 0.85 0.83 0.81 0.86 0.91 0.88 0.93 0.88 0.90 0.87QUESTION 1. What is the overall measure of sampling adequacy (MSA)? Interpret this result.
Step 3. Determining the number of factors
In the case of NEO PI-R, we have a clear prior hypothesis about the number of factors underlying the 30 facets of NEO. The instrument was designed to measure the Five Factors of personality; therefore we would expect the facets to be indicators of 5 broad factors.
We will use function fa.parallel() to produce a scree plot for the observed data, and compare it to that of a random (i.e. uncorrelated) data matrix of the same size. This time, in addition to the actual data (our correlation matrix, neo), we need to supply the sample size (n.obs=1000) to enable simulation of random data, because from the correlation matrix alone it is impossible to know how big the sample was. We will also change the default estimation method to maximum likelihood (fm="ml"), because the sample is large and the scale scores are reported to be normally distributed. We will again display only eigenvalues for principal components (fa="pc").
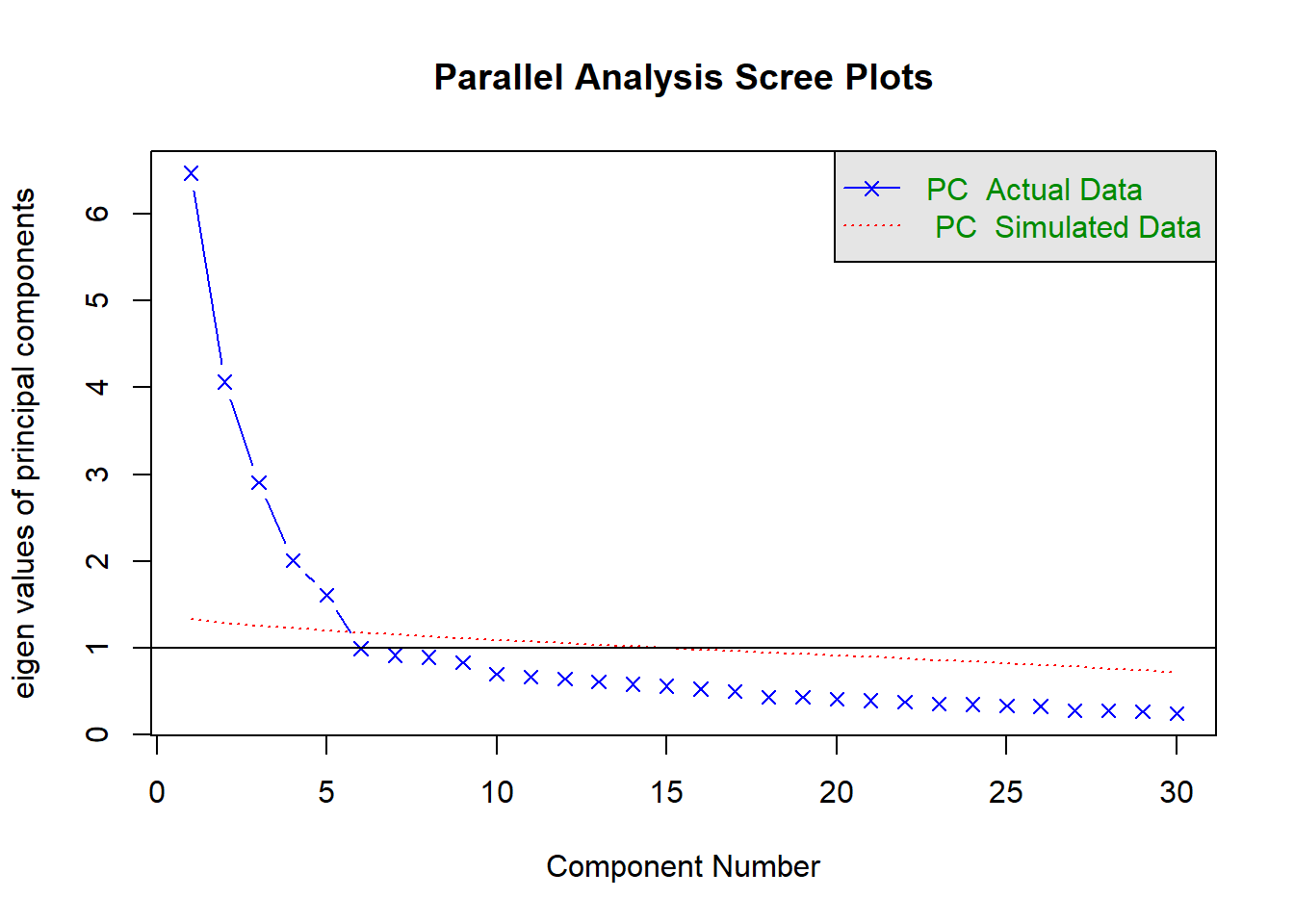
## Parallel analysis suggests that the number of factors = NA and the number of components = 5Remember that when interpreting the scree plot, you retain only the factors on the blue (real data) scree plot that are ABOVE the red (simulated random data) plot, in which we know there is no common variance, only random variance, i.e. “scree” (rubble).
QUESTION 2. Examine the Scree plot. Does it support the hypothesis that 5 factors underlie the data? Why? Does your conclusion correspond to the text output of the parallel analysis function?
Step 4. Fitting an exploratory 5-factor model and checking the model fit
We will use function fa(), which has the following general form
fa(r, nfactors=1, n.obs = NA, rotate="oblimin", fm="minres" …),
and requires data (argument r), and the number of observations if the data is correlation matrix (n.obs). Other arguments have defaults, and we will change the number of factors to extract from the default 1 to the expected number of factors, nfactors=5, and the estimation method (fm="ml"). We are happy with the oblique rotation method, rotate="oblimin".
Specifying all necessary arguments, we can simply call the fa() function to test the hypothesized 5-factor model. However, it will be very convenient to store the factor analysis results in a new object, which can be “interrogated” later when we need to extract specific parts of the results. So, we will assign the results of fa() to an object named (arbitrarily) FA_neo.
## Loading required namespace: GPArotation##
## Factor analysis with Call: fa(r = neo, nfactors = 5, n.obs = 1000, fm = "ml")
##
## Test of the hypothesis that 5 factors are sufficient.
## The degrees of freedom for the model is 295 and the objective function was 1.47
## The number of observations was 1000 with Chi Square = 1443.45 with prob < 1.8e-150
##
## The root mean square of the residuals (RMSA) is 0.03
## The df corrected root mean square of the residuals is 0.04
##
## Tucker Lewis Index of factoring reliability = 0.863
## RMSEA index = 0.062 and the 10 % confidence intervals are 0.059 0.066
## BIC = -594.34
## With factor correlations of
## ML1 ML4 ML3 ML2 ML5
## ML1 1.00 -0.41 -0.12 -0.13 -0.07
## ML4 -0.41 1.00 0.07 0.21 0.08
## ML3 -0.12 0.07 1.00 0.01 -0.16
## ML2 -0.13 0.21 0.01 1.00 0.32
## ML5 -0.07 0.08 -0.16 0.32 1.00Examine the summary output. Try to answer the following questions (you can refer to instructional materials of your choice for help; I recommend McDonald’s Test Theory). I will indicate which parts of the output you need to answer each question.
QUESTION 3. Find the chi-square statistic testing the 5-factor model (look for “Likelihood Chi Square”). How many degrees of freedom are there? What is the chi square statistic, and p value, for the tested model? Would you retain or reject this model based on the chi-square test? Why?
Next, let’s examine the model residuals, which are direct measures of model (mis)fit. First, you can evaluate the root mean square of the residuals (RMSR), which is a summary of all residuals.
QUESTION 4. Find and interpret the RMSR in the output.
Package psych has a nice function residuals.psych() that pulls the residuals from the saved factor analysis results (object FA_neo) and prints them in a user-friendly way.
The above call will print residuals matrix with uniqunesses on the diagonal. These are discrepancies between the observed item variances (equal 1 in this standardized solution) and the variances explained by the 5 common factors, or communalities (uniquness = 1-communality). To remove these values on the diagonal out of sight, use:
## N1 N2 N3 N4 N5 N6 E1 E2 E3 E4 E5
## N1 NA
## N2 0.00 NA
## N3 0.01 0.01 NA
## N4 0.00 -0.04 0.01 NA
## N5 -0.03 0.02 -0.02 0.02 NA
## N6 0.04 0.00 -0.02 0.00 0.00 NA
## E1 0.02 0.00 0.00 -0.02 -0.03 0.02 NA
## E2 0.04 -0.02 -0.01 -0.03 -0.06 0.08 0.09 NA
## E3 0.02 0.02 0.02 -0.06 -0.02 -0.01 0.04 0.08 NA
## E4 -0.02 0.00 0.01 0.03 -0.04 0.02 -0.06 0.01 0.01 NA
## E5 -0.01 -0.04 0.02 0.01 0.01 0.00 -0.04 0.09 -0.10 0.04 NA
## E6 -0.02 -0.01 -0.03 0.03 0.01 -0.01 -0.01 -0.06 -0.05 0.06 0.04
## O1 0.04 -0.03 0.01 0.00 0.02 -0.01 -0.03 -0.05 -0.03 -0.04 0.03
## O2 -0.05 0.01 -0.02 -0.01 0.01 0.03 0.00 0.03 -0.01 0.01 -0.02
## O3 0.00 0.04 0.00 -0.01 0.02 -0.03 0.03 -0.02 -0.01 -0.05 -0.05
## O4 0.01 -0.01 0.00 -0.02 -0.05 0.00 -0.03 0.08 0.00 0.06 0.04
## O5 0.01 -0.03 0.01 0.02 0.00 -0.02 0.00 -0.06 0.01 0.00 0.06
## O6 0.04 0.04 0.00 0.01 -0.03 -0.02 0.00 -0.03 -0.05 0.04 0.01
## A1 -0.02 0.02 0.00 -0.01 0.02 0.02 0.03 0.02 0.03 0.03 -0.05
## A2 -0.03 0.05 -0.01 -0.03 0.03 0.02 -0.04 -0.02 -0.01 0.04 -0.01
## A3 0.01 0.00 0.02 0.00 0.04 -0.04 0.02 -0.08 0.01 -0.02 -0.01
## A4 0.01 -0.06 0.01 0.02 -0.04 0.02 -0.03 0.05 -0.04 0.04 0.00
## A5 -0.03 0.02 0.02 0.00 -0.01 -0.07 -0.02 -0.06 -0.03 0.02 0.03
## A6 0.00 0.01 0.02 -0.02 0.01 -0.01 -0.02 0.01 0.01 -0.02 0.03
## C1 0.02 0.02 -0.01 0.02 0.05 -0.04 -0.01 -0.04 0.00 -0.05 -0.03
## C2 0.00 -0.02 -0.01 0.00 0.02 0.01 0.01 0.02 -0.02 -0.01 0.05
## C3 -0.01 0.01 0.01 0.00 0.02 0.00 0.04 0.02 0.03 -0.02 -0.05
## C4 -0.01 0.00 0.00 0.02 0.01 0.01 0.01 0.00 0.04 0.07 -0.01
## C5 0.01 -0.02 0.00 0.00 -0.03 -0.01 -0.03 0.00 -0.05 0.02 0.06
## C6 0.06 -0.02 -0.01 -0.02 -0.09 0.02 0.03 0.04 0.00 -0.07 0.00
## E6 O1 O2 O3 O4 O5 O6 A1 A2 A3 A4
## E6 NA
## O1 0.01 NA
## O2 0.03 -0.03 NA
## O3 0.03 0.05 0.03 NA
## O4 -0.02 0.00 0.04 -0.02 NA
## O5 -0.01 0.00 0.02 -0.04 -0.03 NA
## O6 -0.01 0.02 -0.08 -0.01 0.09 0.01 NA
## A1 -0.03 0.01 -0.01 -0.02 -0.03 -0.02 0.08 NA
## A2 0.01 -0.05 0.04 -0.03 0.05 -0.01 0.00 0.05 NA
## A3 0.02 0.02 -0.04 0.01 -0.03 0.02 -0.02 -0.03 0.01 NA
## A4 0.03 0.01 0.00 -0.04 0.05 0.00 0.01 0.00 0.00 -0.01 NA
## A5 0.02 -0.05 0.02 0.04 0.05 -0.01 -0.04 -0.01 0.06 -0.02 0.01
## A6 -0.04 0.01 0.01 0.00 -0.02 0.01 0.03 0.02 -0.01 0.05 -0.03
## C1 0.00 0.04 -0.05 0.05 -0.06 0.01 0.06 0.02 0.01 0.04 -0.03
## C2 0.01 -0.01 0.06 0.00 -0.01 -0.01 -0.03 -0.03 0.00 -0.03 0.01
## C3 -0.04 0.00 -0.02 0.03 -0.05 0.00 -0.02 0.05 0.02 0.00 -0.03
## C4 -0.01 -0.05 0.03 -0.04 0.03 0.01 -0.03 0.02 0.00 -0.02 0.04
## C5 0.01 0.04 -0.01 -0.01 0.05 -0.01 0.02 -0.01 0.00 -0.01 0.01
## C6 -0.01 0.00 -0.01 0.04 -0.05 0.00 0.00 -0.06 -0.05 0.01 -0.01
## A5 A6 C1 C2 C3 C4 C5 C6
## A5 NA
## A6 0.04 NA
## C1 -0.09 0.02 NA
## C2 0.00 -0.01 -0.02 NA
## C3 -0.01 -0.03 0.03 -0.04 NA
## C4 0.01 -0.03 -0.04 -0.02 0.01 NA
## C5 0.03 0.02 0.00 0.06 -0.02 0.01 NA
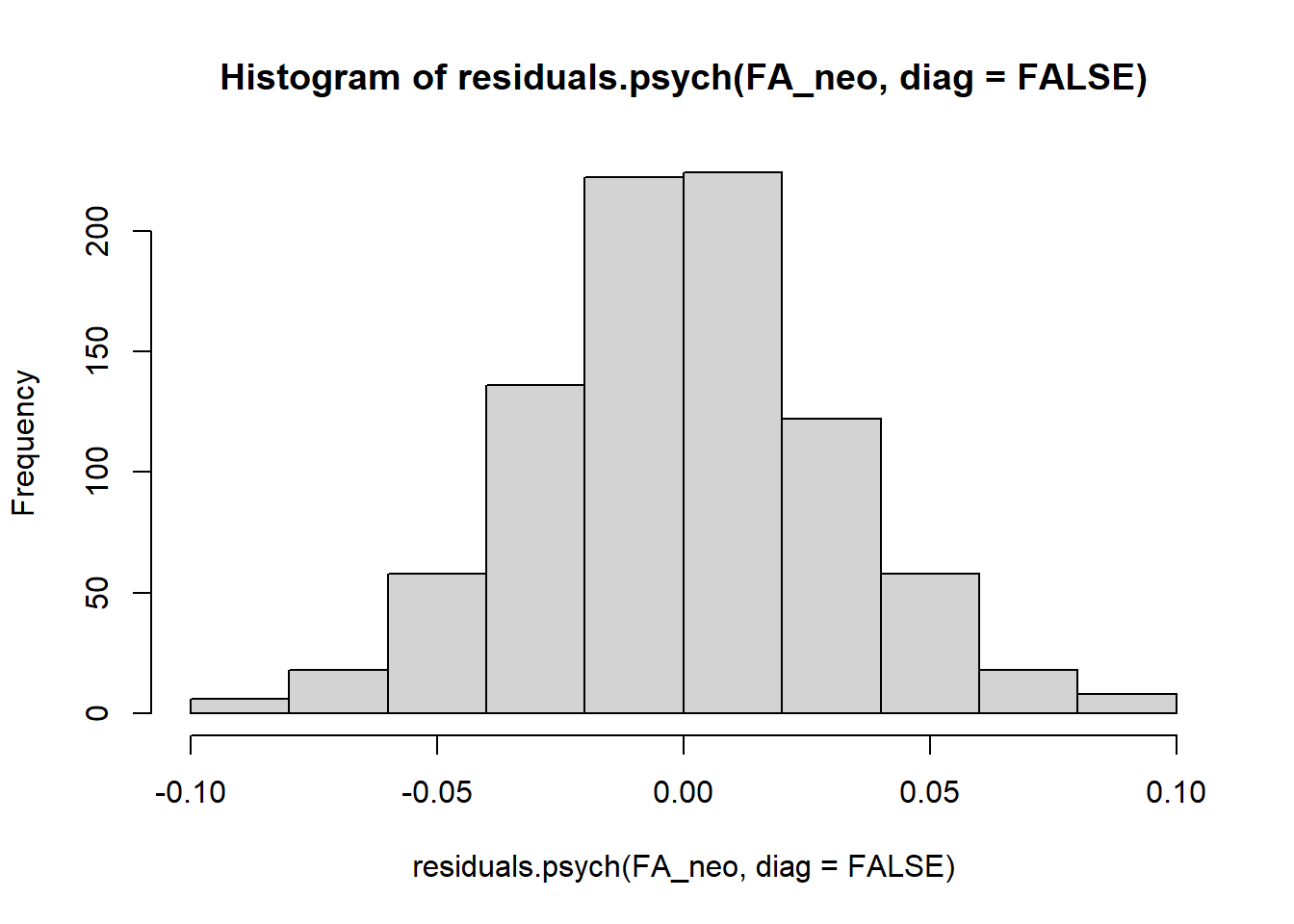
## C6 -0.07 0.03 0.08 0.04 0.02 -0.04 -0.04 NAQUESTION 5. Examine the residual correlations. What can you say about them? Are there any non-trivial residuals (greater than 0.1 in absolute value)?
Step 5. Interpreting parameters of the 5-factor exploratory model
Having evaluated the model suitability and fit, we are ready to obtain and interpret its parameters - factor loadings, unique variances, and factor correlations. You can call object FA_neo, or, to obtain just the factor loadings in a convenient format, call:
##
## Loadings:
## ML1 ML4 ML3 ML2 ML5
## N1 0.798
## N2 0.578 -0.437 -0.123
## N3 0.783 -0.109
## N4 0.694 0.100
## N5 0.373 -0.252 -0.282 0.295
## N6 0.650 -0.251
## E1 0.170 0.690 0.105
## E2 -0.155 0.547
## E3 -0.290 0.227 -0.406 0.250 0.164
## E4 0.394 -0.382 0.358
## E5 -0.478 0.380
## E6 -0.116 0.696
## O1 -0.317 -0.144 0.114 0.474
## O2 0.129 0.183 0.699
## O3 0.331 0.342 0.418
## O4 -0.173 0.153 0.427
## O5 -0.149 -0.127 0.710
## O6 -0.123 -0.157 0.325
## A1 -0.282 0.422 0.306 0.111
## A2 0.219 0.627
## A3 0.208 0.353 0.635 -0.109
## A4 0.728 0.112
## A5 0.197 0.518 -0.122
## A6 0.457 0.373
## C1 -0.294 0.555 0.104
## C2 0.662 -0.135
## C3 0.619 0.273
## C4 0.715 -0.170 0.159
## C5 -0.180 0.727
## C6 -0.116 0.496 0.276 -0.229
##
## ML1 ML4 ML3 ML2 ML5
## SS loadings 3.228 3.020 2.834 2.612 1.855
## Proportion Var 0.108 0.101 0.094 0.087 0.062
## Cumulative Var 0.108 0.208 0.303 0.390 0.452Note that in the factor loadings matrix, the factor labels do not always correspond to the column number. For example (factor named ML1 is in 1st column, but ML2 is in 4th column. This does not matter, but just pay attention to the factor name that you quote.)
QUESTION 6. Examine the standardized factor loadings (pattern matrix), and name the factors you obtained based on which facets load on them.
Examine the factor loading matrix again, this time looking for cross-loading facets (facets with loadings greater than 0.32 on factor(s) other than its own). Note that in the above output, loadings under 0.1 are suppressed by default. You can control the cutoff value for printing loadings, and set it to 0.32 using function print():
## Factor Analysis using method = ml
## Call: fa(r = neo, nfactors = 5, n.obs = 1000, fm = "ml")
## Standardized loadings (pattern matrix) based upon correlation matrix
## ML1 ML4 ML3 ML2 ML5 h2 u2 com
## N1 0.80 0.60 0.40 1.0
## N2 0.58 -0.44 0.59 0.41 2.0
## N3 0.78 0.70 0.30 1.1
## N4 0.69 0.53 0.47 1.1
## N5 0.37 0.42 0.58 3.7
## N6 0.65 0.64 0.36 1.4
## E1 0.69 0.59 0.41 1.2
## E2 0.55 0.33 0.67 1.3
## E3 -0.41 0.50 0.50 3.7
## E4 0.39 -0.38 0.36 0.49 0.51 3.2
## E5 -0.48 0.38 0.38 0.62 2.0
## E6 0.70 0.55 0.45 1.1
## O1 0.47 0.41 0.59 2.2
## O2 0.70 0.48 0.52 1.2
## O3 0.33 0.34 0.42 0.48 0.52 3.1
## O4 0.43 0.28 0.72 1.7
## O5 0.71 0.51 0.49 1.2
## O6 0.32 0.15 0.85 2.0
## A1 0.42 0.41 0.59 2.9
## A2 0.63 0.46 0.54 1.3
## A3 0.35 0.63 0.61 0.39 1.9
## A4 0.73 0.56 0.44 1.1
## A5 0.52 0.32 0.68 1.5
## A6 0.46 0.37 0.36 0.64 2.1
## C1 0.56 0.58 0.42 1.6
## C2 0.66 0.41 0.59 1.1
## C3 0.62 0.52 0.48 1.4
## C4 0.72 0.59 0.41 1.2
## C5 0.73 0.69 0.31 1.2
## C6 0.50 0.40 0.60 2.2
##
## ML1 ML4 ML3 ML2 ML5
## SS loadings 3.52 3.31 2.89 2.80 2.01
## Proportion Var 0.12 0.11 0.10 0.09 0.07
## Cumulative Var 0.12 0.23 0.32 0.42 0.48
## Proportion Explained 0.24 0.23 0.20 0.19 0.14
## Cumulative Proportion 0.24 0.47 0.67 0.86 1.00
##
## With factor correlations of
## ML1 ML4 ML3 ML2 ML5
## ML1 1.00 -0.41 -0.12 -0.13 -0.07
## ML4 -0.41 1.00 0.07 0.21 0.08
## ML3 -0.12 0.07 1.00 0.01 -0.16
## ML2 -0.13 0.21 0.01 1.00 0.32
## ML5 -0.07 0.08 -0.16 0.32 1.00
##
## Mean item complexity = 1.8
## Test of the hypothesis that 5 factors are sufficient.
##
## df null model = 435 with the objective function = 13.03 with Chi Square = 12873.19
## df of the model are 295 and the objective function was 1.47
##
## The root mean square of the residuals (RMSR) is 0.03
## The df corrected root mean square of the residuals is 0.04
##
## The harmonic n.obs is 1000 with the empirical chi square 857.09 with prob < 3.2e-56
## The total n.obs was 1000 with Likelihood Chi Square = 1443.45 with prob < 1.8e-150
##
## Tucker Lewis Index of factoring reliability = 0.863
## RMSEA index = 0.062 and the 90 % confidence intervals are 0.059 0.066
## BIC = -594.34
## Fit based upon off diagonal values = 0.98
## Measures of factor score adequacy
## ML1 ML4 ML3 ML2 ML5
## Correlation of (regression) scores with factors 0.94 0.93 0.92 0.92 0.88
## Multiple R square of scores with factors 0.89 0.87 0.85 0.85 0.78
## Minimum correlation of possible factor scores 0.78 0.75 0.69 0.69 0.56Note. I use a 0.32 cut-off for non-trivial loadings since this translates into 10% of variance shared with the factor in an orthogonal solution. This value is quite arbitrary, and many use 0.3 instead.
QUESTION 7. Refer to the NEO facet descriptions in the supplementary document to hypothesize why any non-trivial cross-loadings may have occurred.
Examine columns h2 and u2 of the factor loading matrix. The h2 column is the facet’s communality (proportion of variance due to all of the common factors), and u2 is the uniqueness (proportion of variance unique to this facet). The communality and uniqueness sum to 1.
QUESTION 8. Based on communalities and uniquenesses, which facets are the best and worst explained by the factor model we just tested?
QUESTION 9. Refer to the earlier summary output to find and interpret the factor correlation matrix. Which factors correlate the strongest?
Step 6. Saving your work
After you finished work with this exercise, save your R script by pressing the Save icon in the script window. To keep all the created objects (such as FA_neo), which might be useful when revisiting this exercise, save your entire work space. To do that, when closing the project by pressing File / Close project, make sure you select Save when prompted to save your “Workspace image”.
11.4 Solutions
Q1. MSA = 0.87. The data are “meritorious” according to Kaiser’s guidelines (i.e. very much suitable for factor analysis). Refer to Exercise 7 to remind yourself of this index and its interpretation.
Q2. There is a clear change from a steep slope (“mountain”) and a shallow slope (“scree” or rubble) in the Scree plot. The first five factors form a mountain; factor #6 and all subsequent factors belong to the rubble pile and therefore we should proceed with 5 factors. Parallel analysis confirms this decision – five factors of the blue plot (observed data) are above the red dotted line (the simulated random data).
Q3. Chi-square=1443.45 on DF=295 (p=1.8E-150). The p value is given in the scientific format, with 1.8 multiplied by 10 to the power of -150. It is so tiny (divided by 10 to the power of 150) that we can just say p<0.001. We should reject the model, because the probability of observing the given correlation matrix in the population where the 5-factor model is true (the hypothesis we are testing) is vanishingly small (p<0.001). However, chi-square test is very sensitive to the sample size, and our sample is large. We must judge the fit based on other criteria, for instance residuals.
Q4.
The root mean square of the residuals (RMSR) is 0.03 The RMSR of 0.03 is a very small value, indicating that the 5-factor model reproduces the observed correlations well.
Q5. All residuals are very small (close to zero), and none are above 0.1 in absolute value. Since the 30x30 matrix of residuals is somewhat hard to eyeball, you can create a histogram of the values pulled by residuals.psych():
Q6. ML1=Neuroticism; ML4=Conscientiousness, ML3=Agreeableness, ML2=Extraversion, ML5=Openness (see the salient loadings marked in Q7).
Q7. As illustrated in Figure 11.1, there are several cross-loadings for facets of Agreeableness (factor ML3) and Extraversion (factor ML2). For instance, E4 (Activity), described as “pace of living” loads on Extraversion as expected (0.36) but loads slightly stronger on Conscientiousness (0.39) and negatively on Agreeableness (-0.38). Perhaps the need to meet deadlines and achieve (part of Conscientiousness) has an effect on the “pace of living”, as well as the need to “get ahead” (the low end of Agreeableness).
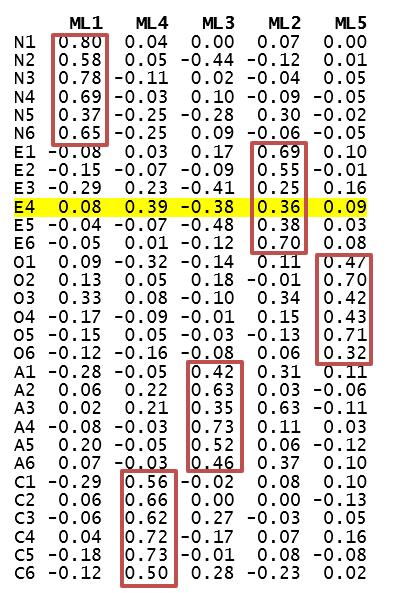
Figure 11.1: Loading matrix with marker items.
Q8. Facets O6 (Values) and O4 (Ideas) are worst explained by the factors in this model. Their communalities (see column “h2”) are only 15% and 28% respectively. O6 Values is an unusual scale, quite different from other NEO scales. It has attitudinal rather than behavioural statements, such as “I believe letting students hear controversial speakers can only confuse and mislead them”. Facets N3 (Depression) and C5 (Self-Discipline) are best explained by the factors in this model.
Q9. Overall, the five factors correlate quite weakly, but they are not orthogonal. ML1 (Neuroticism) correlates negatively with all other factors; the remaining factors correlate positively with each other. The strongest correlation is between ML1 (Neuroticism) and ML4 (Conscientiousness) (r=–.41).