Exercise 2 Optimal scaling of ordinal questionnaire data
| Data file | SDQ.RData |
| R package | aspect |
2.1 Objectives
Previously, in Exercise 1, we scored the Strength and Difficulties Questionnaire (SDQ) using the so-called “Likert scaling” approach, whereby response categories “not true”-“somewhat true”-“certainly true” were assigned consecutive integers 0-1-2. Apart from reflecting the apparently increasing degree of agreement in these response options, the assignment of the integers was arbitrary, as there was no particular reason we assigned 0-1-2 as opposed to, for instance, 1-2-3. Such an arbitrary way of scoring item responses is also called “measurement by fiat”. In this exercise, we will attempt to find “optimal” scores for ordinal responses to the SDQ. “Optimal” means that scores we assign to responses are not just any scores, but they are “best” out of all other possible scores in terms of fulfilling some statistical criterion.
There are many ways to “optimize” item scores; here, we will maximize the ratio of the variance of the total score to the sum of the variances of the item scores. In psychometrics, fulfilling this criterion results in maximizing the sum of the item correlations (and therefore the test score’s “internal consistency” measured by Cronbach’s alpha).
2.2 Worked Example – Optimal scaling of SDQ Emotional Symptoms items
We begin by loading data frame SDQ kept in file SDQ.RData. Please refer to Exercise 1 for explanation of all variables in this data frame.
## [1] "Gender" "consid" "restles" "somatic" "shares" "tantrum"
## [7] "loner" "obeys" "worries" "caring" "fidgety" "friend"
## [13] "fights" "unhappy" "popular" "distrac" "clingy" "kind"
## [19] "lies" "bullied" "helpout" "reflect" "steals" "oldbest"
## [25] "afraid" "attends" "consid2" "restles2" "somatic2" "shares2"
## [31] "tantrum2" "loner2" "obeys2" "worries2" "caring2" "fidgety2"
## [37] "friend2" "fights2" "unhappy2" "popular2" "distrac2" "clingy2"
## [43] "kind2" "lies2" "bullied2" "helpout2" "reflect2" "steals2"
## [49] "oldbest2" "afraid2" "attends2"We will use package aspect, which makes optimal scaling easy by offering a range of very useful options and built-in plots.
Step 1. Selecting items for analysis
To analyse only the items measuring Emotional Symptoms, it is convenient to create a list of item (variable) names, and then refer to only these items in the data frame:
# pick only items designed to measure Emotional Symptoms
items_emotion <- c("somatic","worries","unhappy","clingy","afraid")
# preview the Emotional Symptoms item responses
head(SDQ[items_emotion])## somatic worries unhappy clingy afraid
## 1 2 1 0 1 0
## 2 2 0 0 1 0
## 3 0 0 0 0 1
## 4 0 0 0 1 1
## 5 2 1 0 1 0
## 6 1 0 0 1 0Step 2. Dropping cases with missing responses
Before performing optimal scaling, we will drop cases with missing responses on at least one of the items, as the package aspect does not appear to support missing values. There are only 5 such cases with mising responses.
## somatic worries unhappy clingy
## Min. :0.0000 Min. :0.0000 Min. :0.0000 Min. :0.0000
## 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:0.0000 1st Qu.:0.0000
## Median :0.0000 Median :0.0000 Median :0.0000 Median :1.0000
## Mean :0.6106 Mean :0.6211 Mean :0.3172 Mean :0.8421
## 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:1.0000 3rd Qu.:1.0000
## Max. :2.0000 Max. :2.0000 Max. :2.0000 Max. :2.0000
## NA's :2 NA's :1 NA's :1
## afraid
## Min. :0.00
## 1st Qu.:0.00
## Median :0.00
## Mean :0.48
## 3rd Qu.:1.00
## Max. :2.00
## NA's :3Step 3. Running the optimal scaling procedure
Function corAspect() performs optimal scaling by optimizing various criteria on the correlation matrix. Here is the standard call for this function: corAspect(data, aspect = "aspectSum", level = "nominal", ...). First, we need to supply data, which will be our working data frame, items. Second, we need to choose the criterion (aspect) to optimize. Here, we will maximize the sum of items’ correlations, so use the default setting aspect="aspectSum". Third, we need to supply the level of measurement for the analysed variables. A nominal scale level (default) assumes that the variables are nominal categories and involves no restrictions on the resulting scores. An ordinal scale level requires preserving order of the scores, and numerical variables additionally require equal distances between the scores. In this example, the response categories “not true”-“somewhat true”-“certainly true” clearly reflect an increasing order of agreement, which we want to preserve, so we set level="ordinal".
opt <- corAspect(items, aspect = "aspectSum", level="ordinal")
# Summary output for the optimal scaling analysis
summary(opt)##
## Correlation matrix of the scaled data:
## somatic worries unhappy clingy afraid
## somatic 1.0000000 0.3480251 0.3651134 0.2258002 0.3113325
## worries 0.3480251 1.0000000 0.4612166 0.4020225 0.3901405
## unhappy 0.3651134 0.4612166 1.0000000 0.3598932 0.4603964
## clingy 0.2258002 0.4020225 0.3598932 1.0000000 0.3865003
## afraid 0.3113325 0.3901405 0.4603964 0.3865003 1.0000000
##
##
## Eigenvalues of the correlation matrix:
## [1] 2.4961448 0.7844417 0.6270432 0.5887536 0.5036166
##
## Category scores:
## somatic:
## score
## 0 -0.8864022
## 1 0.5836441
## 2 2.0454937
##
## worries:
## score
## 0 -0.8348282
## 1 0.4234660
## 2 2.1441015
##
## unhappy:
## score
## 0 -0.5895239
## 1 1.3910873
## 2 2.7286027
##
## clingy:
## score
## 0 -1.1851447
## 1 0.2510005
## 2 1.6576948
##
## afraid:
## score
## 0 -0.7821442
## 1 1.0234825
## 2 1.8943502The output displays the “Correlation matrix of the scaled data”, which are correlations of the item scores after optimal scaling. These can be compared to correlations between the original variables calculated using cor(items). Further, “Eigenvalues of the correlation matrix” are displayed. Eigenvalues are the variances of principal components (from Principal Components Analysis), and are very helpful in indicating the number of dimensions measured by this set of items. The result here, with the first eigenvalue substantially larger than the remaining eigenvalues, indicates just one dimension, as we hoped.
Finally, “Category scores” show the scores that the optimal scaling procedure assigned to the item categories. For example, the result suggests to score item somatic by assigning the score -0.8864022 to response “not true”, the score 0.5836441 to response “somewhat true” and the score 2.045493 to response “certainly true”. The values are chosen so that the scaled item’s mean in the sample is 0, and the correlations between the items are maximized.
Step 4. Viewing transformation plots
Package aspect makes it very easy to obtain transformation plots, which show the category score assignments graphically.
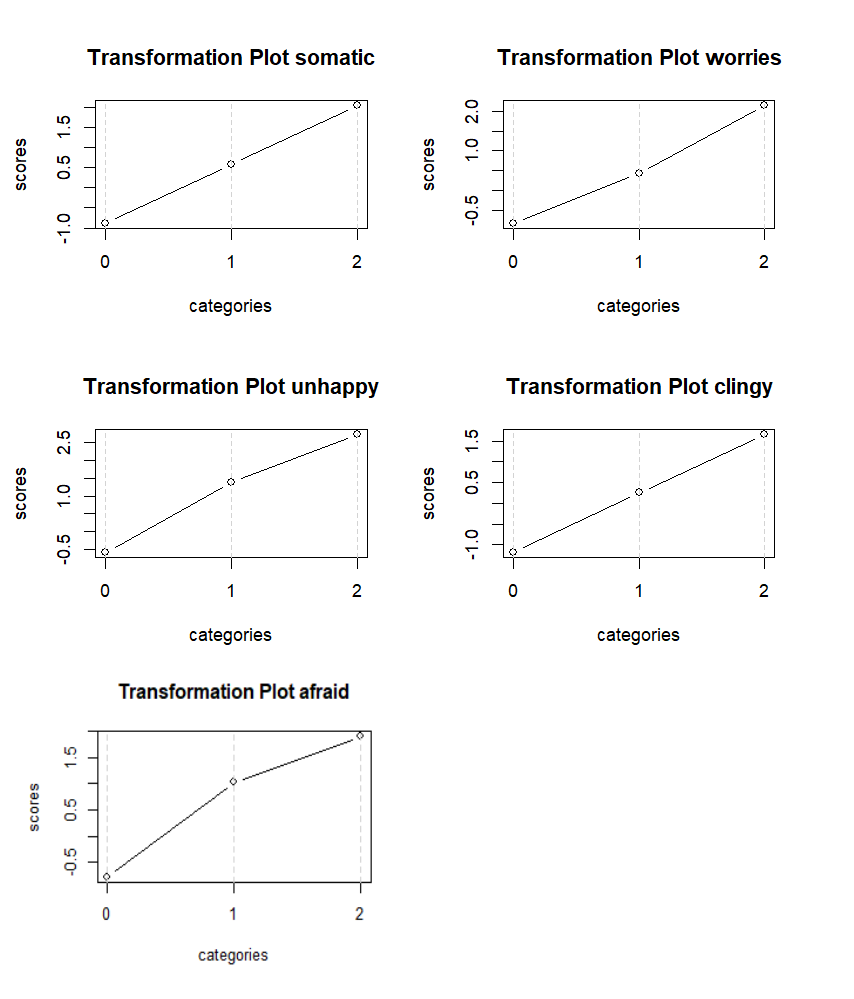
Looking at the transformation plots, it can be seen that 1) the scores for subsequent categories increase almost linearly; 2) the categories are roughly equidistant. We conclude that for scoring ordinal items in the SDQ Emotional Symptoms scale, Likert scaling is appropriate, and not much can be gained by optimal scaling over basic Likert scaling.
2.3 Further practice – Optimal scaling of the remaining SDQ subscales
Following the steps in the worked example, perform optimal scaling of the remaining SDQ scales. Refer to Exercise 1 for the list of items in each scale. You should not need to worry about some items being counter-indicative of their scales, because optimal scaling should take care of this by assigning scores that monotonically decrease when the category increases.