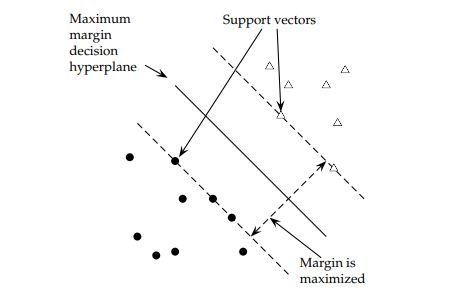
10.1 Maximal Margin Classifier
The maximal margin classifier is the optimal hyperplane defined in the (rare) case where two classes are linearly separable. Given an \(n \times p\) data matrix \(X\) with a binary response variable defined as \(y \in [-1, 1]\) it might be possible to define a p-dimensional hyperplane \(h(X) = \beta_0 + \beta_1X_1 + \beta_2X_2 \dots + \beta_pX_p = x_i^T \beta + \beta_0 = 0\) such that all observations of each class fall on opposite sides of the hyperplane. This separating hyperplane has the property that if \(\beta\) is constrained to be a unit vector, \(||\beta|| = \sum\beta^2 = 1\), then the product of the hyperplane and response variables are positive perpendicular distances from the hyperplane, the smallest of which may be termed the hyperplane margin, \(M\),
\[y_i (x_i^{'} \beta + \beta_0) \ge M.\]
The maximal margin classifier is the hyperplane with the maximum margin, \(\max \{M\}\) subject to \(||\beta|| = 1\). A separating hyperplane rarely exists. In fact, even if a separating hyperplane does exist, its resulting margin is probably undesirably narrow. Here is the maximal margin classifier.1
Maximum marginal classifier
The data set has two linearly separable classes, \(y \in [-1, 1]\) described by two features, \(X1\) and \(X2\)2. The code is unimportant - just trying to produce the visualization.
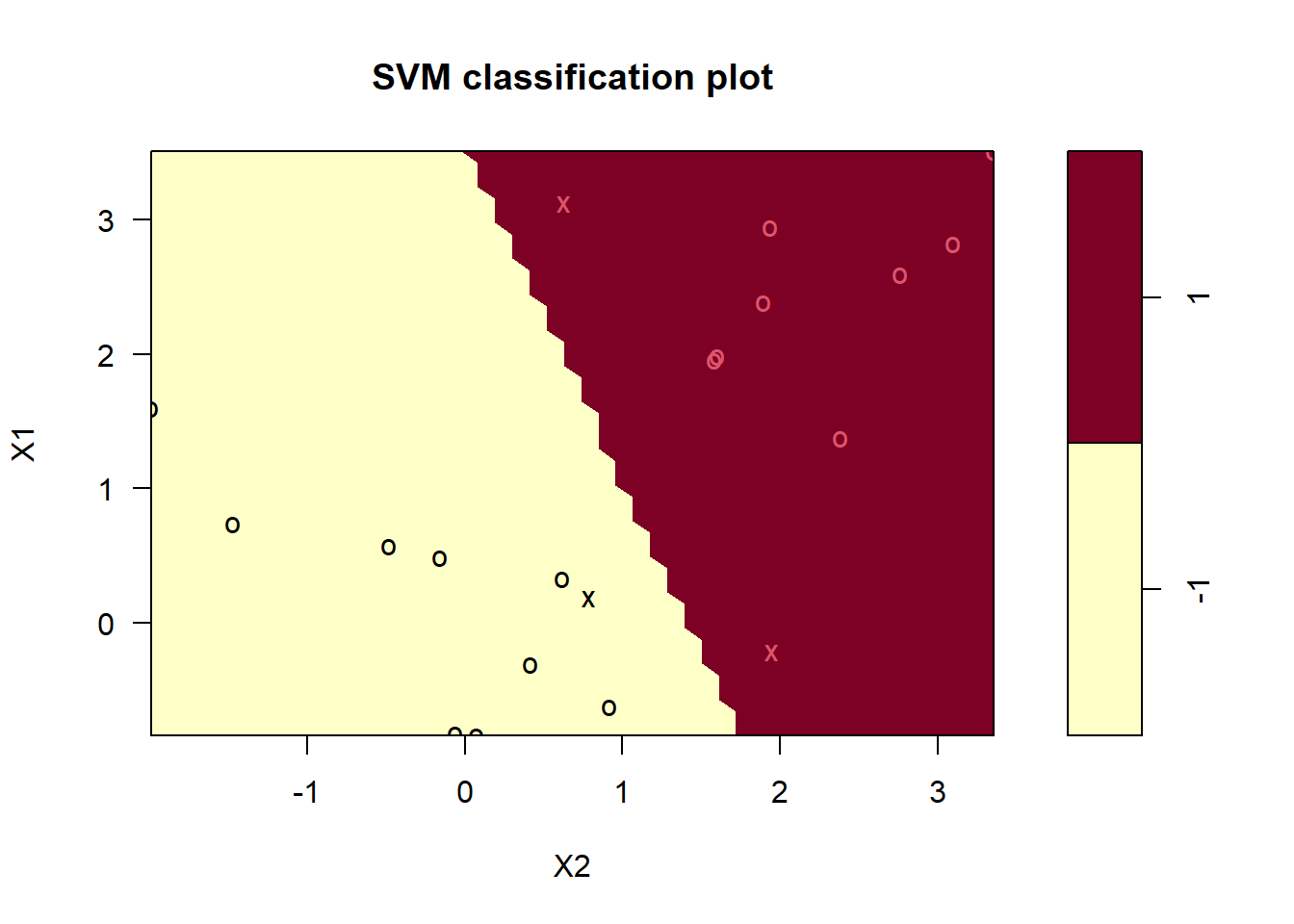
Image from https://nlp.stanford.edu/IR-book/pdf/15svm.pdf.↩︎
Any more features and we won’t be able to visualize it↩︎