7.2 Lasso
Lasso stands for “least absolute shrinkage and selection operator”. Like ridge, lasso adds a penalty for coefficients, but instead of penalizing the sum of squared coefficients (L2 penalty), lasso penalizes the sum of absolute values (L1 penalty). As a result, for high values of \(\lambda\), coefficients can be zeroed under lasso.
The loss function for lasso is
\[L = \sum_{i = 1}^n \left(y_i - x_i^{'} \hat\beta \right)^2 + \lambda \sum_{j=1}^k \left| \hat{\beta}_j \right|.\]
Example
Continuing with prediction of mpg from the other variables in the mtcars data set, follow the same steps as before, but with ridge regression. This time specify parameter alpha = 1 for ridge regression (it was 0 for ridge, and for elastic net it will be something in between and require optimization).
set.seed(1234)
mdl_lasso <- train(
mpg ~ .,
data = training,
method = "glmnet",
metric = "RMSE",
preProcess = c("center", "scale"),
tuneGrid = expand.grid(
.alpha = 1, # optimize a lasso regression
.lambda = seq(0, 5, length.out = 101)
),
trControl = train_control
)## Warning in nominalTrainWorkflow(x = x, y = y, wts = weights, info = trainInfo, :
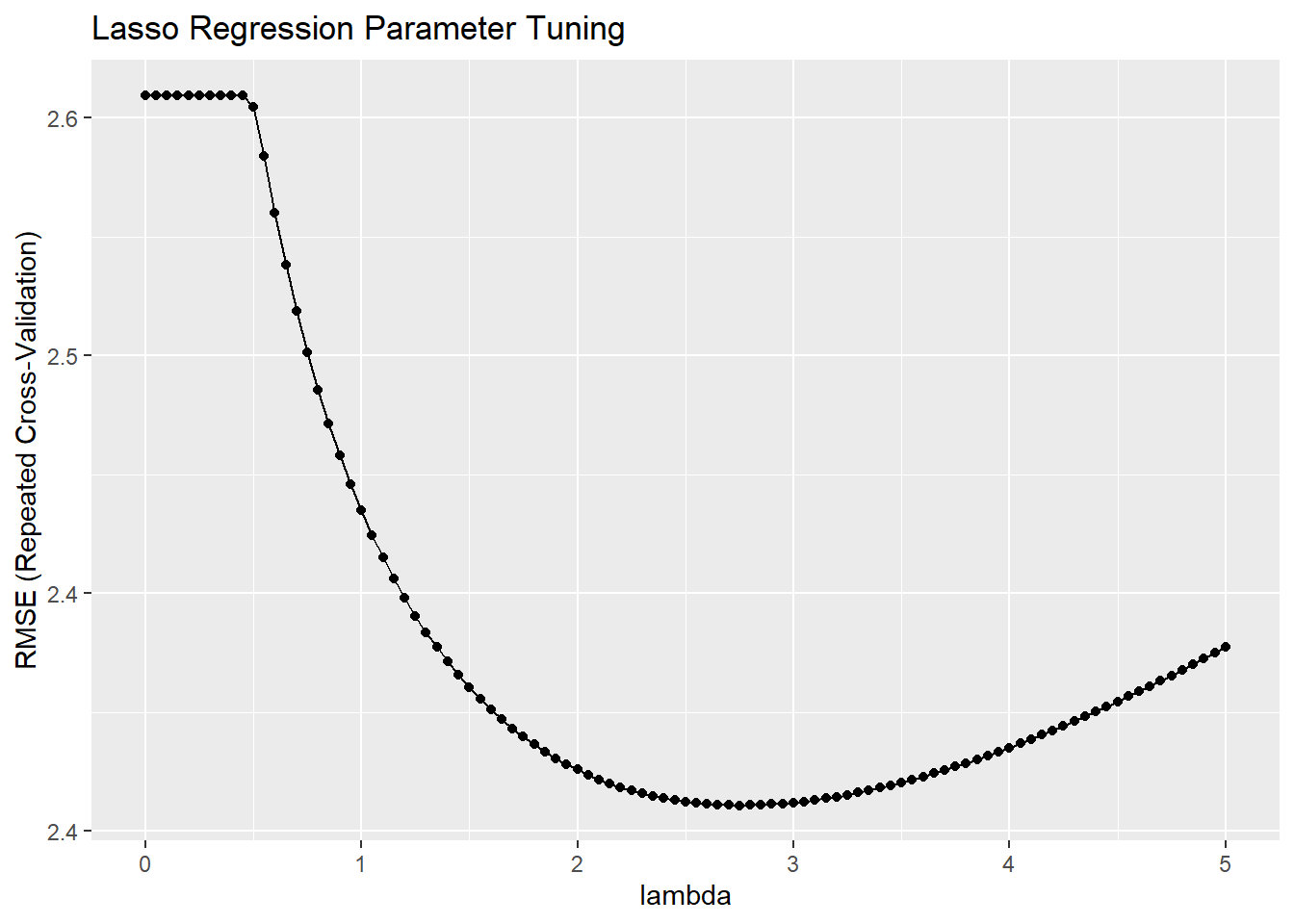
## There were missing values in resampled performance measures.## alpha lambda
## 14 1 0.65The summary output shows the model did not tune alpha because I held it at 1 for lasso regression. The optimal tuning values (at the minimum RMSE) were alpha = 1 and lambda = 0.65. You can see the RMSE minimum on the the plot.