1.5 Likelihood

The likelihood function is the likelihood of a parameter \(\theta\) given an observed value of the random variable \(X\). The likelihood function is identical to the probability distribution function, except that it reverses which variable is considered fixed. E.g., the binomial probability distribution expresses the probability that \(X = x\) given the success probability \(\theta = \pi\).

\[f(x|\pi) = \frac{n!}{x!(n-x)!} \pi^x (1-\pi)^{n-x}.\]

The corresponding likelihood function expresses the probability that \(\pi = p\) given the observed value \(x\).

\[L(p|x) = \frac{n!}{x!(n-x)!} p^x (1-p)^{n-x}.\]

You usually want to know the value of \(\theta\) at the maximum of the likelihood function. When taking derivatives, any multiplicative constant is irrevelant and can be discarded. So for the binomial distribution, the likelihood function for \(\pi\) may instead be expressed as

\[L(p|x) \propto p^x (1-p)^{n-x}\]

Calculating the maximum is usually simplified using the log-likelihood, \(l(\theta|x) = \log L(\theta|x)\). For the binomial distribution, \(l(p|x) = x \log p + (n - x) \log (1 - p)\). Frequently you derive loglikelihood from a sample. The overall likelihood is the product of the individual likelihoods, and the overall loglikelihood is the log of the overall likelihood.

\[l(\theta|x) = \log \prod_{i=1}^n f(x_i|\theta)\]

Here are plots of the binomial log-likelihood of \(pi\) for several values of \(X\) from a sample of size \(n = 5\).

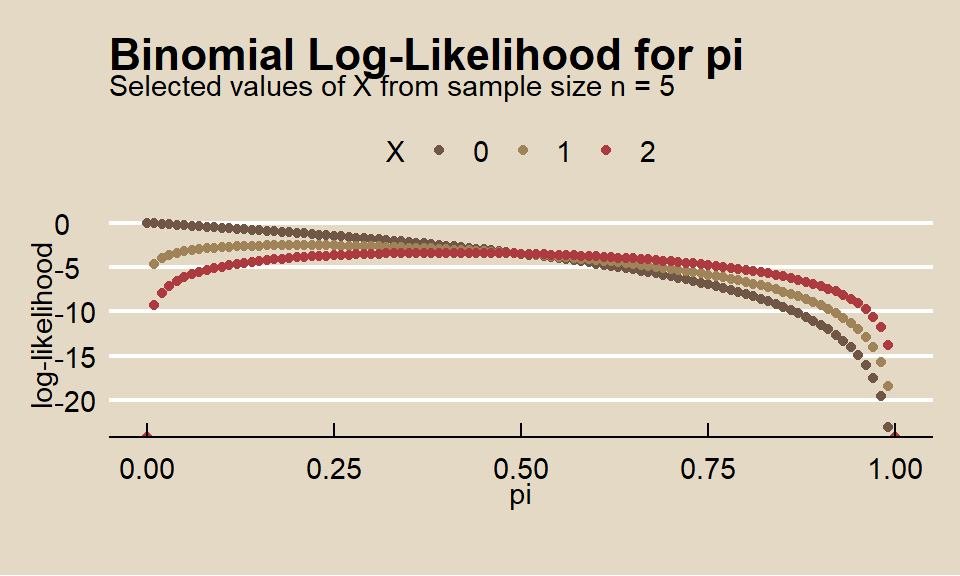
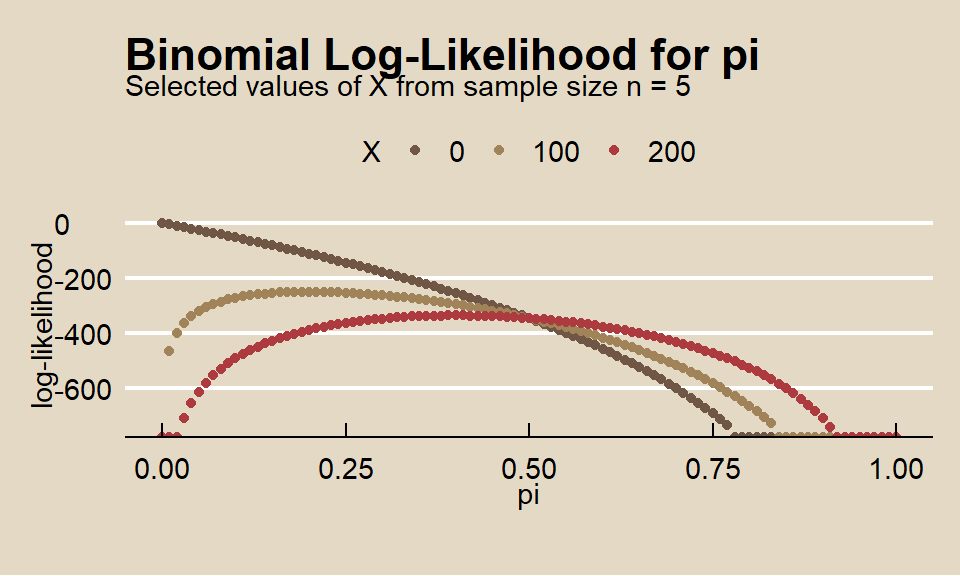
As the total sample size \(n\) grows, the loglikelihood function becomes more sharply peaked around its maximum, and becomes nearly quadratic (i.e. a parabola, if there is a single parameter). Here is the same plot with \(n = 500\).

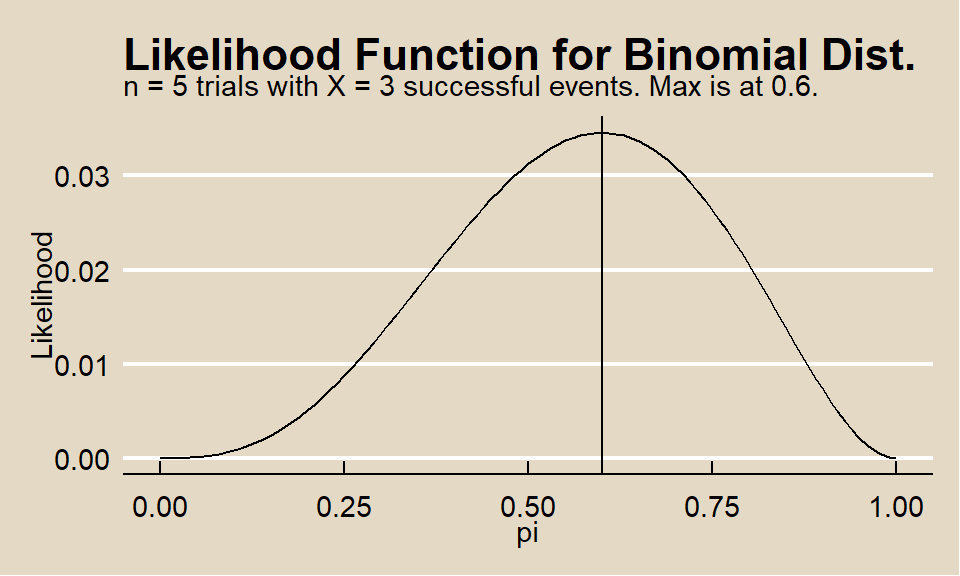
The value of \(\theta\) that maximizes \(l\) (and \(L\)) is the maximum-likelihood estimator (MLE) of \(\theta\), \(\hat{\theta}\). E.g., suppose you have an experiment of \(n = 5\) Bernoulli trials \(\left(X \sim Bin(5, \pi) \right)\) with and \(X = 3\) successful events. A plot of \(L(p|x) = p^3(1 - p)^2\) shows the MLE is at \(p = 0.6\).

This approach is called maximum-likelihood estimation. MLE usually involves setting the derivatives to zero and solving for \(theta\).