1.1 行列式の定義と性質

行列式は正方行列に対して定義される．いかに簡単に行列式の定義を示す（厳密な定義については割愛する）．

Definition 1.1 (行列式) $A = (\boldsymbol a_{1},\ldots,\boldsymbol a_{n}) \in \mathbb R^{n\times n}$ について，次の性質を満たす写像 $\det:\mathbb R^{n\times n} \longrightarrow \mathbb R$ を行列式という．行列式を記号で $\det A, \det(A), |A|$ などと表す．

$A'$ を $A$ の $i$ 番目の列ベクトルに $\boldsymbol b \in \mathbb R^{n}$ に足したもの， $A^\ast$ を $A$ の $i$ 番目の列ベクトルを $\boldsymbol b$ で置き換えたものとする．この時， $\det A' = \det A + \det A^\ast$ が成り立つ．
$A'$ を $A$ の $i$ 番目の列ベクトルを $c$ 倍したものとする．この時， $\det A' = c \det A$ が成り立つ．
$A'$ を $A$ の $i$ 番目の列ベクトルを $j$ 番目の列ベクトルで置き換えたものとする．この時， $\det A' = 0$ が成り立つ．
$A'$ を $A$ の $i$ 番目の列ベクトルと $j$ 番目の列ベクトルを交換したものとする．この時， $\det A' = - \det A$ が成り立つ．
$\det I_n = 1$ が成り立つ．

1.1.1 $n=2,3$ の場合の計算方法

$2$ 次と $3$ 次正方行列の場合の行列式の具体的な計算方法について紹介する．

1.1.1.1 $n=2$

$A$ を $2$ 次正方行列とする．

$\begin{align} A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \end{align}$

この時 $A$ の行列式 $\det A$ は

$\det A = a_{11} a_{22} - a_{21} a_{12}$

として求められる．

1.1.1.2 $n=3$

$A$ を $3$ 次正方行列とする．

$A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ \end{pmatrix}$

この時 $A$ の行列式 $\det A$ は

$\begin{align} \det A &= a_{11} a_{22} a_{33} + a_{21} a_{32} a_{13} + a_{31} a_{12} a_{23} \\ &- a_{13} a_{22} a_{31} - a_{23} a_{32} a_{11} - a_{33} a_{12} a_{21} \end{align}$

として求められる．この計算式は次の図のように，同じ行列を縦に並べてイメージするとわかりやすい．

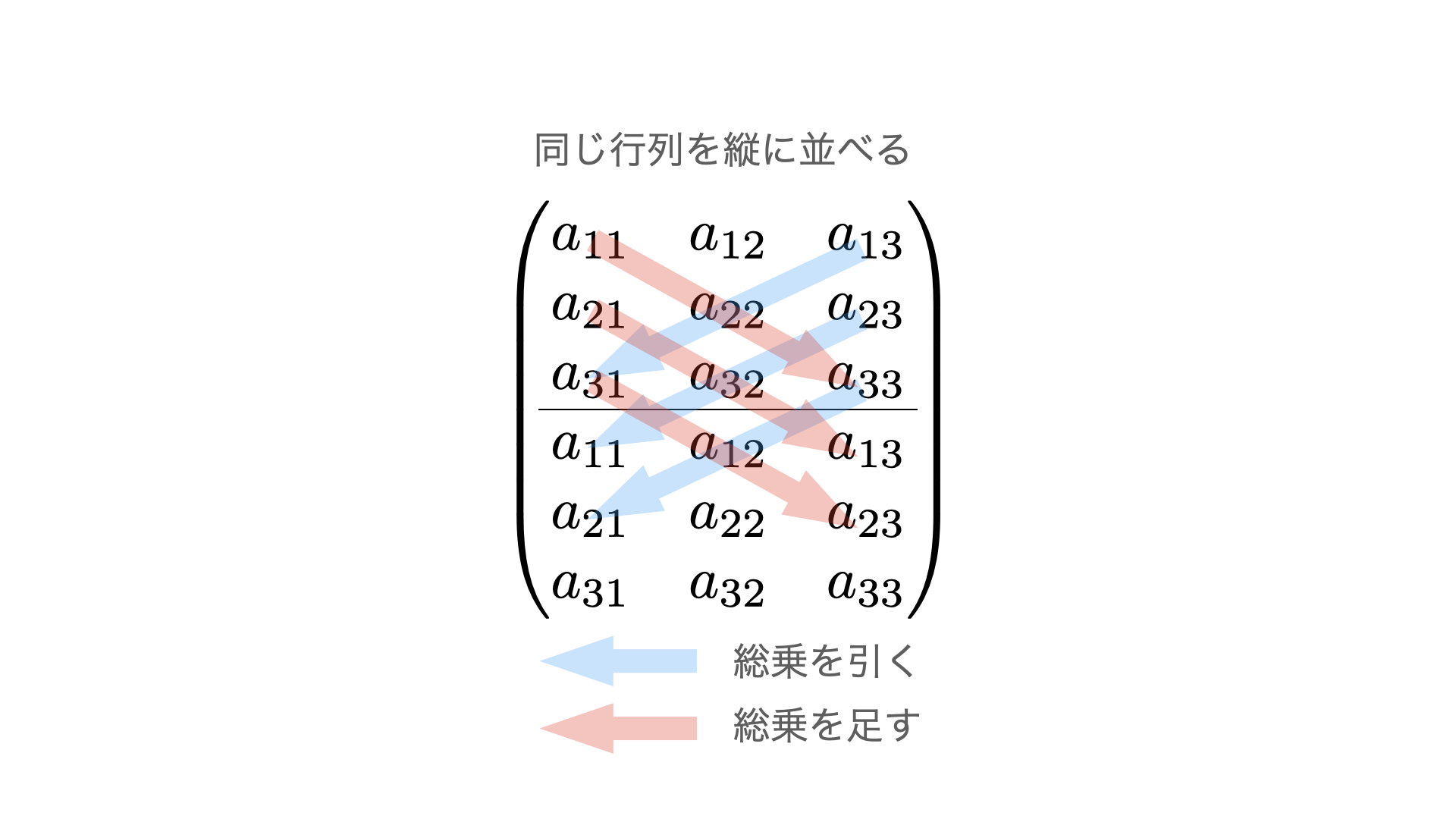
図2-1:3次正方行列の行列式の求め方

1.1.2 性質

行列式については以下の性質がよく知られている．

Theorem 1.1 (行列式の性質) 行列式は以下の性質を満たす．

$A \in \mathbb R^{n\times n}, c \in \mathbb R$ について， $\det(cA) = c^n \det A$
$A$ が対角行列のとき， $\det A = \prod_{i=1}^n a_{ii}$
$A$ を $n$ 次の上三角行列（あるいは下三角行列）とする．このとき， $\det A = \prod_{i=1}^{n} a_{ii}$ ．
$A,B \in \mathbb R^{n\times n}$ ならば $\det (AB) = \det A \det B$
$A \in \mathbb R^{n\times n}$ で正則のとき $\det A^{-1} = \frac{1}{\det A}$
$A \in \mathbb R^{n\times n}$ で正則行列 $\Leftrightarrow \det A \neq 0$
$A \in \mathbb R^{n\times n}$ に対して $\det A^{\top} = \det A$
$P \in \mathbb R^{n\times n}$ が直交行列のとき， $\det P = \pm 1$ ．特に $\det P = 1$ であれば回転行列である．
$A \in \mathbb R^{n\times n}$ が対称行列のとき， $A$ が正定値行列であれば $\det A \leq a_{11} a_{22} \cdots a_{nn}$

6番目の性質である「 $A \in \mathbb R^{n\times n}$ で正則行列 $\Leftrightarrow \det \neq 0$ 」は逆行列の存在確認方法としても有用である．

Exercise 1.1 (行列式の計算) 次の行列式を求めよ

$\begin{align} \begin{pmatrix} 2 & 1 \\ 4 & -1 \end{pmatrix} \end{align}$