4.9 Boxplot（箱ひげ図）

箱ひげ図はHistogramと同じく，データの分布を可視化する手法の一つである．Histogramよりも大雑把にデータの分布を表現するため，1変数のみについて確認するのであればHistogramの方が良い．

Boxplotとは次のような図である．

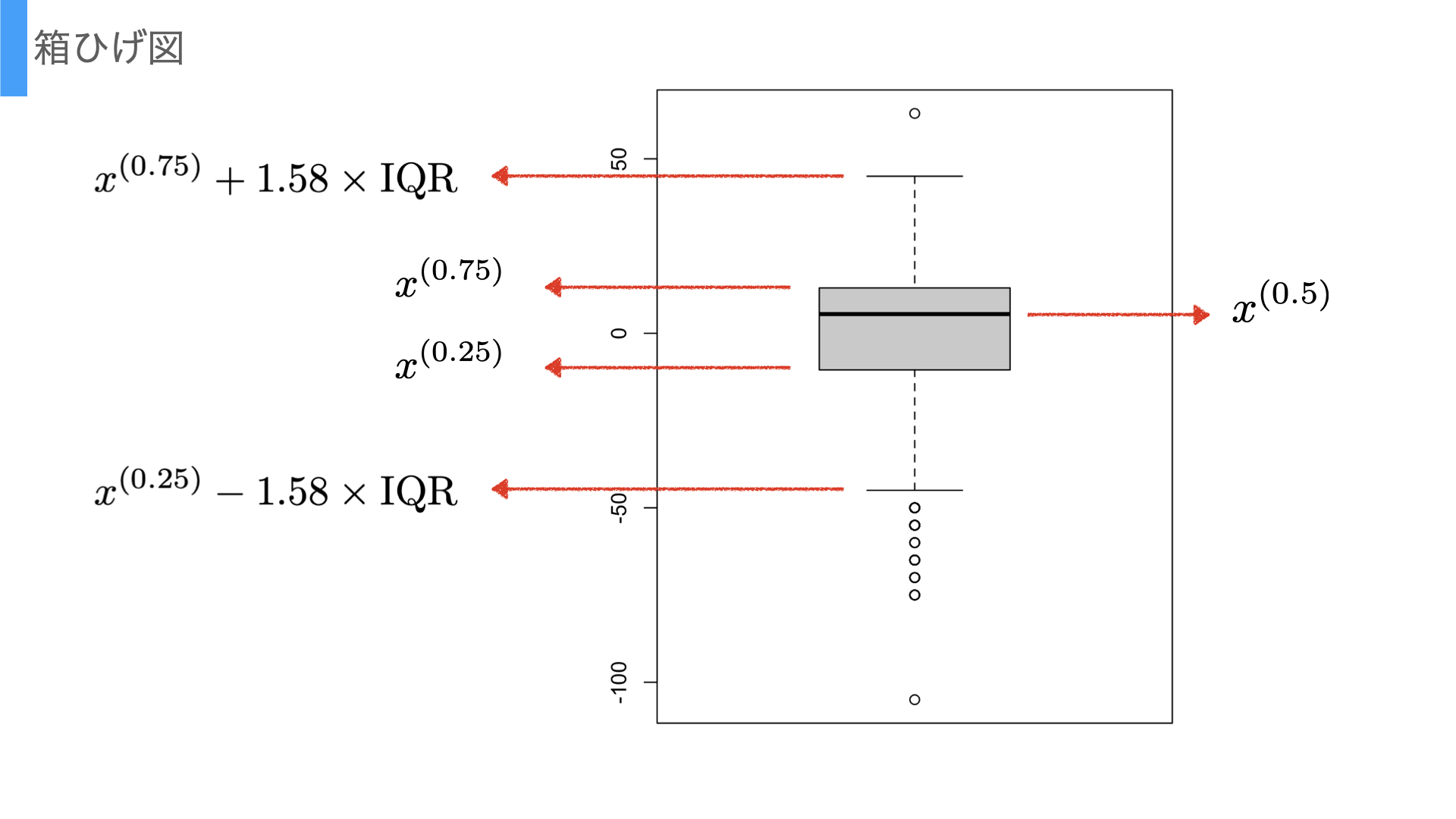図にある\(x^{(p)}\)とは\(100p\%\)点を意味している．%点とはデータを数値の小さい順に並び替えた時に小さい方から全体の何%の位置にいるかということである．

Boxplotのnotch（髭の部分）は流儀により定義が異なるが，Rのデフォルトの設定では，\(x^{(0.25/0.75)} \pm 1.58 \times \text{IQR}\)となっている．ここで\(\text{IQR}\)とは，Inter Quantile Rangeの頭文字を取ったもので，25%点と75%点の距離を指している． また，このnotchよりも大きいまたは小さいデータをOutlier（外れ値）として，データの分布を考慮するとやや特異な点である可能性を示唆している点である．

さて，実際には質的変数のラベルごとに量的変数の分布を概観したいとき，Boxplotを用いると良い． ここでは，先ほどの集計に利用したanswersのデータを引き続き利用する．

1変数だけでBoxplotを作成する時はboxplot関数に変数を渡せば良い．

boxplot(answers$height)

### 質的変数との掛け合わせ

さて，実際に質的変数のラベルごとにBoxplotを描くには以下のように実装すれば良い．ここでは，Rでもともと提供されているboxplotとggplotを利用する場合を紹介する．

boxplotを利用する場合は，データを引数に渡す際に，量的変数~質的変数というふうに指定すれば良い． answersにあるheightをclubごとにBoxplotを描きたい場合は以下のようになる．

boxplot(height~club, data=answers)

これを見ると，Basketballのクラブの人は他のクラブと比べて身長が高い人がいると考えられる． ただし，この図からわかるように箱ひげ図にはサンプル数については何ら考慮していないため，実はデータが数個しかなかったということもあり得る． あらかじめ数を集計しておき，そのような組み合わせがないかどうか確認しておくことが重要である．

次にggplotを利用する場合を紹介する．

answers %>% 
  ggplot(aes(x=club, y=height, fill=club)) +
  geom_boxplot()

特に色などの指定をせずともggplotの方は色分けをした状態で出力される． また，notchの部分に横棒がないなど細かな違いはあるが，概ね同じである．

Exercise 4.5 (Boxplot) answersのmajorごとのincomeの分布をBoxplotを用いて可視化しなさい．