Capítulo 10 La trilla
William Sealy Gosset tenía la misión de corroborar la calidad de la cerveza producida por Guinness, cosa de rutina, si no fuera porque las muestras con las que trabajaba eran pequeñas y el único instrumento que existía por aquel entonces para evaluar el error de una media era la distribución normal, de uso exclusivo para muestras grandes; no había un instrumento estadístico para pesos pluma. Es decir, así se comportaban las medias muestrales, consideradas errores o desviaciones, cuando estaban compuestas por más de cien casos. ¿Y eso qué?, si recuerdas, estuvimos a punto de fracasar cuando pronosticamos el error para las medias obtenidas por los soldados de Tucídides; la razón es que las muestras eran muy pequeñas, de 5 soldados, y lógicamente su distribución de errores es diferente a la distribución de errores de una curva normal. Ni siquiera hace falta mucha explicación de este fenómeno, no es la misma variación cuando cuentan 5 soldados que cuando lo hacen 100; cien es mejor que uno, diría Surowiecki (2005). Había pues, que construir distribuciones20 con base en muestras pequeñas para trillar; separar la paja del trigo, la buena cerveza de la mala. En otras palabras, comparar si la media observada es un error aceptable o está fuera del rango de lo que se considera un error normal. Mira la figura 10.1, la diferencia entre una distribución normal y una t de Student, sin ser muy grande, es detectable a simple vista. La distribución t es, en el centro, más baja que la curva normal. ¿Adivinas por qué?, hay menos valores allí, se han desplazado a los extremos, los cuales son más pronunciados que en la curva normal; como consecuencia de la muestra de tan sólo \(5\) casos hay mayor dispersión o variabilidad. El \(95\%\) de las muestras están contenidas en \(2.77\) desviaciones estándar y no en \(1.96\), como sucede con la distribución normal21. Por cierto, se llama t de student porque se asemeja a una t, volteada de cabeza, naturalmente, y de Student por el seudónimo con el que firmaba sus investigaciones el jefe cervecero William Sealy. La Compañía Guinness le permitía a sus investigadores publicar sus hallazgos, siempre y cuando no mencionaran el nombre de la empresa ni cerveza ni el nombre real del investigador; el motivo era esconder la ventaja competitiva que le brindaba contar con profesionales de la estadística para revisar sus procedimientos de producción.
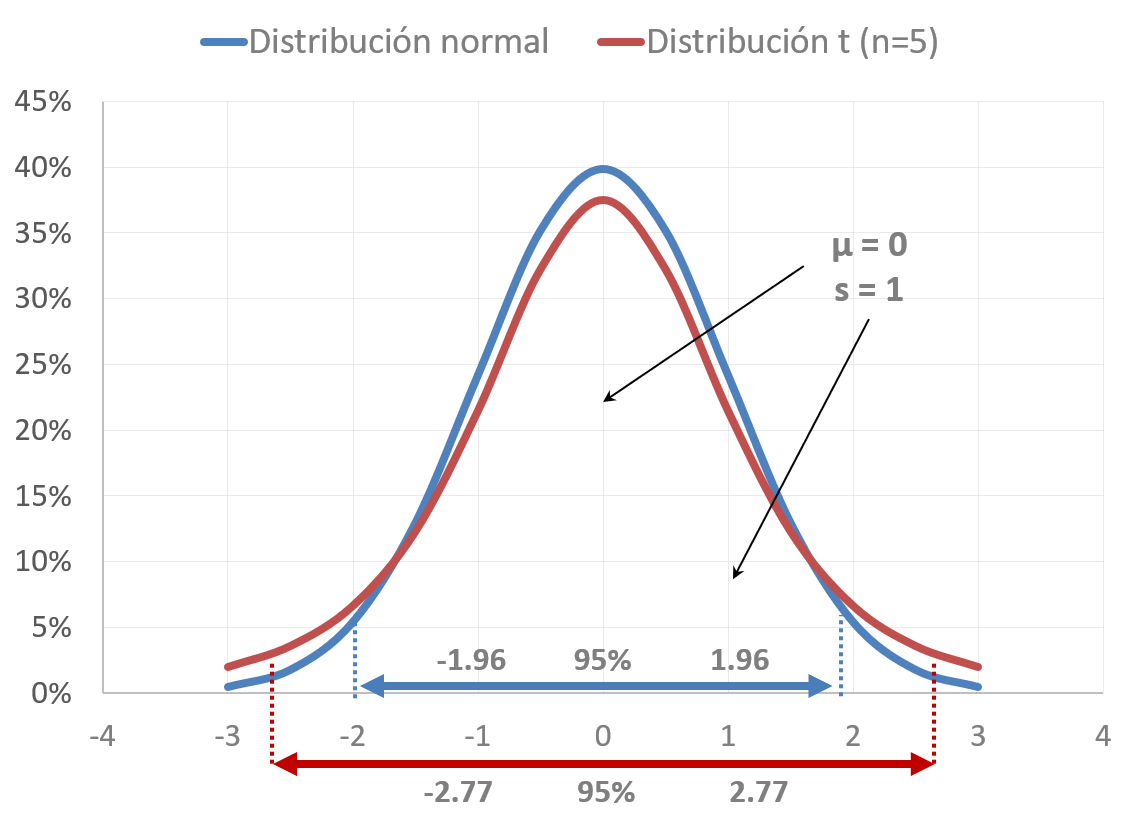
Figura 10.1: Comparación entre una distribución normal y una t
¿En cuáles situaciones necesita el investigador de mercados hacer la trilla?, cuando quiere comparar la satisfacción o calidad de sus servicios y productos. En el primer caso se trata de los conocidos estudios de satisfacción del consumidor, el investigador necesita saber si el nivel promedio de satisfacción cambia de período a período y si el cambio es significativo, estadísticamente hablando. En el otro caso, es vital que el producto cumpla con la calidad necesaria, ya sea que se trate de uno nuevo o de un cambio en su fórmula, empaque, contenido, etc. Vamos a ver cómo opera la prueba t o t-test en las pruebas de producto llamadas Tal como me gusta. Antes déjame explicarte, al estilo del perico jefe, que clase de estudios son éstos. Un hombre impresionantemente grande se acerca a una prostituta y le dice que desea contratar su servicio. Te pago lo que me pidas, pero tiene que ser Tal como me gusta, dice el hombre. La mujer piensa inmediatamente que un hombre tan corpulento algún perjuicio podría representar para su integridad física y declina a tan suculenta oferta; no obstante, le dice que espere allí en lo que le consigue alguna otra mujer dispuesta a asumir el riesgo. El hombre asiente con la cabeza, y la mujer parte rauda y veloz a reunirse con otras mujeres para contarles sobre el generoso ofrecimiento. Todas las mujeres al ver a semejante hombre rechazan también la oferta, pero sienten pena por él y deciden ir con La Rosita Arenas, quién tenía fama de aguantadora y echada pa’delante, a enterarla de la oferta del cliente. Ésta al enterarse, sin pensárselo dos veces, va con el hombre y se mete al cuarto de hotel acompañada por él. Todas las mujeres deseosas de saber el desenlace y la suerte de la valerosa Rosita, se arremolinan y pegan la oreja en la puerta del cuarto. Así transcurren unos cuantos minutos sin que se oiga sonido alguno, hasta que de pronto se escucha un desmadre total de vidrios que se rompen, sillas y multitud de otros artefactos que se estrellan contra la pared haciéndose añicos. Al instante se abre la puerta violentamente y sale corriendo el hombre desnudo, llevando entre sus manos su ropa y calzado, y tras él la Rosita vuelta una furia. Las mujeres, sin aguantarse más la curiosidad, le preguntan: ¿cómo quería? Quería fiado el hijo de la chingada, responde la Rosita.
La cuestión es ¿cómo logramos que el cliente obtenga justo lo que quiere?; claro, siempre y cuando no se le ocurra pedir fiado. Las escalas de Tal como me gusta (TCG) o en inglés Just about right (JAR) se utilizan con este objetivo, principalmente en las pruebas organolépticas, las cuales son muy demandadas en la industria de alimentos, bebidas, pastelitos, etc. Con ellas se puede evaluar qué tanto se aproxima el producto a lo que el cliente desea. La idea es evaluar qué tan cerca está el producto del punto ideal en cuanto a sal, dulzor, color, intensidad de sabor, tostado, gas, y muchas otras variables en las cuales más es malo y menos también. Por ejemplo, hagamos de cuenta que se evalúa un jugo, se pide al entrevistado que lo pruebe y nos diga ¿qué tan dulce sabe?, usando una escala de 5 puntos donde:
- Es “Mucho menos dulce de lo que me gusta”
- Es “Menos dulce de lo que me gusta”
- Es “Tal como me gusta”
- Es “Más dulce de lo que me gusta”
- Es “Mucho más dulce de lo que me gusta”
Si la respuesta es que el dulzor es tal como a él le gusta, el producto está en el punto ideal; si al entrevistado le resulta más, o menos, dulce de lo que le gusta, seguramente habrá que hacer cambios a la formulación del producto. Este tipo de escalas son populares debido a su simpleza y claridad para el investigador y para el entrevistado, además su tratamiento estadístico es fácil; sin embargo, como pasa con todas las escalas, su utilización no está exenta de críticas (véase Varela and Ares 2014). Sea como sea, esta escala se utiliza mucho, pero se hace en combinación con la escala de agrado general (hedónica), quizá para subsanar algunas de las debilidades que tiene y darle mayor validez. La escala de agrado general puede ser de 1 a 5, 1 a 7, 0 a 10 puntos, o cualquier otra. Siguiendo con nuestro ejemplo, la pregunta sería: En general, ¿qué tanto le agrada el jugo que acaba de probar? Dígamelo en una escala del 0 al 10, donde 0 significa que le desagrada totalmente y 10 que le agrada totalmente. Lo dicho, analizar la escala TCG no tiene complicación, sólo se necesita sumar y restar. !Verás!, se agrupan a los sujetos que contestaron 1 y 2: Mucho menos dulce de lo que me gusta y Menos dulce de lo que me gusta; a los que contestaron 4 y 5: Más dulce de lo que me gusta y Mucho más dulce de lo que me gusta; y se dejan aparte los sujetos que contestaron 3: Tal como me gusta. Los tres grupos formados se pueden describir como los que piensan que le falta dulce a la bebida, los que piensan que es ideal, y los que consideran que le sobra dulzor (véase figura 10.2).
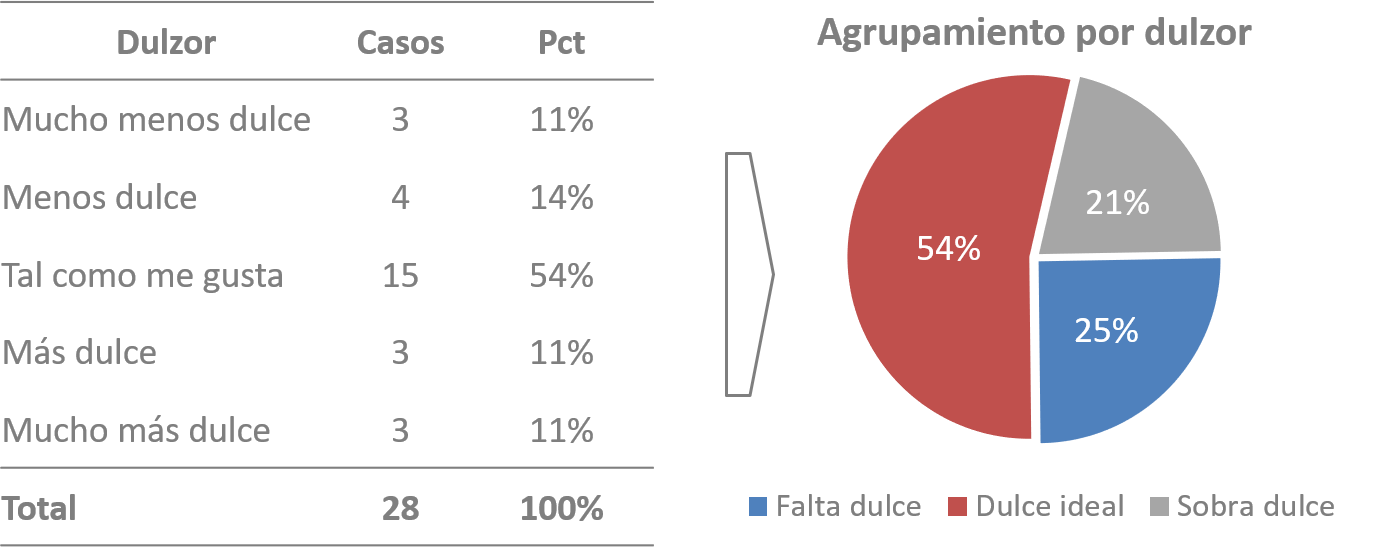
Figura 10.2: Agrupación de respuestas de la escala TCG
Ten presente que lo ideal es que ni le sobre ni le falte azúcar (dulce); en síntesis, que la mayoría de los sujetos estén en el grupo ideal: Tal como me gusta. Como en gustos se rompen géneros, es casi imposible que todos estén de acuerdo en ello, por lo tanto una regla de oro es que al menos el \(75\%\) caiga en la categoría Tal como me gusta y otra es que el porcentaje de alguno de los grupos que mencionan que el producto es más dulce o menos dulce de lo que les gusta no sea superior al \(20\%\); si alguna de estas reglas se rompe, entonces hay que analizar la posibilidad de hacer cambios en la formulación del producto. En nuestro gráfico puedes ver que estamos \(11\%\) por debajo del estándar: \(54\%–75\%=21\%\) ¿Entonces qué hay que corregir?, ¿le quitamos o le ponemos más dulce al jugo? El sentido común diría que hay que subirle pues el \(25\%\) dijo que faltaba, pero como dicen que el sentido común es la cosa peor repartida del mundo, preferimos no fiarnos de él y en su lugar emplear la técnica Penalty Analysis o Análisis de Penalización, también conocida como Mean Drop, caída de media; más adelante te vas a dar cuenta porqué estos nombres.
La idea del Penalty Analysis es relacionar el nivel de agrado general con cada uno de los grupos, con el fin de determinar a cuál de ellos le agrada más el producto. Para no perder el hilo, continuemos con el mismo ejemplo; los resultados se pueden ver en la tabla 10.1. ¿Te das cuenta que el grupo ideal (Tal como me gusta) tiene la media más alta de agrado en general: \(7.87\)? (recuerda que la escala va de 0 a 10, de desagrado a agrado); mientras que la media del grupo que dice que le falta dulce es de \(5.29\) y la del que piensa que le sobra es de \(5.83\). Aparentemente, que le falte azúcar al producto es más grave a que le sobre, la media de agrado general cae; por esa razón se dice que se castiga o penaliza al producto. Para calcular la caída se substrae a la media del grupo ideal, la media de cada uno de los otros grupos; la caída de falta de dulce es \(2.58\): \(7.87–5.29=2.58\); y la de azúcar de sobra es \(2.04\): \(7.87–5.83=2.04\). Toda vez que en estadística la relevancia de un resultado se relaciona con el tamaño de la muestra o número de sujetos, es menester ponderar esta caída. Lo que se hace en la columna que dice Caída ponderada es multiplicar el porcentaje de cada grupo por el porcentaje de caída en el grupo. Ejemplo, la caída por falta de dulce es de \(2.58\) lo cual equivale a una caída de \(33\%\) de la media ideal: \(\frac{2.58}{7.87}=.33\); multiplicando este porcentaje por el tamaño del grupo nos da \(8\%\): \(.33\times .25=.08\). En términos prácticos, significa que si corregimos la falta de dulce el promedio de agrado general se ajustaría un \(8\%\). Nuestro análisis se basa en una sola característica del producto, pero en la práctica se llegan a evaluar hasta una decena de características (acidez, color, suavidad, etc.) y probar más de un producto a la vez. En estos casos algunos investigadores crean un solo indicador ponderado; o lo que es lo mismo, uno global para ordenar las características según su grado de penalización. Lo que hacen es crear 2 grupos, juntan el 1, 2, 4 y 5 de la escala de TCG y dejan solo el 3 (Tal como me gusta) y emplean la misma técnica de penalización. En otras palabras, no importa si al producto le sobra o le falta, lo importante es saber qué tanto cae la media en global.
| Dulzor | Casos | Pct | Media_agrado | Caída | Caída_pct | Caída_pon |
|---|---|---|---|---|---|---|
| Falta dulce | 7 | 25% | 5.29 | 2.58 | 33% | 8% |
| Tal como me gusta | 15 | 54% | 7.87 | 0.00 | 0 | 0 |
| Sobra dulce | 6 | 21% | 5.83 | 2.04 | 26% | 5% |
| Total | 28 | 100% | 6.79 | NA | NA | NA |
Ya estamos listos para pasar al tema principal. Observa la ecuación (10.1), es muy sencilla, de hecho se usa para probar la diferencia de una sola muestra, de allí el nombre de prueba t de una sola muestra. No hay ningún problema para interpretarla; lo que comunica es que se resta la media muestral, \(\tilde{x}\), a la media poblacional, \(\mu\). Ya conocemos la media muestral, \(6.79\) (véase tabla 10.1), no así la media poblacional. Normalmente, ésta se deriva de decenas de pruebas de producto hechas por la propia agencia de investigación o empresa y se conoce como norma. Lo que intentamos identificar es qué tan diferente es la muestra de la norma que usamos para evaluar si el producto tiene la suficiente calidad. Hagamos de cuenta que nuestra norma para pruebas de producto es \(7.92\); entonces, la diferencia es \(-1.13\): \(6.79-7.92=-1.13\). Es necesario que tomes consciencia de lo que representa esta insignificante resta: la media poblacional es el cero absoluto (véase sección 6), de allí parten las puntuaciones que se desvían positiva o negativamente; la media muestral es sólo un caso que se desvía de la media poblacional. ¿Qué tanto se desvía esa muestra?, ¿está dentro de los dos o tres típicos errores estándar? Para contestar se debe evaluar a cuántos errores estándar equivale la desviación de \(-1.13\); la división entre el error estándar es la solución. Para variar, surge la duda sobre cuál desviación estándar debemos usar, ¿la muestral o la poblacional? En sentido estricto, deberíamos usar la desviación estándar de la población, porque lo que deseamos saber es qué tan alejada está la media muestral de la media poblacional, y no al revés. Pero la desviación estándar de la población muy rara vez se conoce, por lo cual los investigadores optan por usar la muestral para estimar el error estándar. El denominador \(\frac{s}{\sqrt{n}}\), lo sabes, representa el tamaño del error estándar; así que la operación es muy obvia: la ecuación determina cuántos errores estándar caben dentro de la diferencia que hay de la media muestral a la poblacional. Si esos errores son más de tres, ya puedes irte olvidando de que no hay diferencias; sí las hay. La media de satisfacción general con lo dulce del jugo es baja, estadísticamente hablando. ¿En qué nos apoyamos para hacer esta afirmación? Con base en la teoría estadística, la cual menciona que el \(68\%\) de los resultados se encuentran dentro de un error estándar, el 95% dentro de dos errores estándar22 y el \(99\%\) dentro de tres errores estándar. Dependiendo de la confianza que uno le desea dar a los resultados es que se escoge el número de desviaciones suficientes para determinar si hay diferencias.
\[\begin{equation} t=\frac{\tilde{x}-\mu}{s/\sqrt{n}} \tag{10.1} \end{equation}\]
En la tabla 10.2 hemos colocado las estadísticas necesarias para probar si la diferencia de la muestra es distinta a la norma que usamos para controlar el proceso de calidad de nuestros productos. Sustituyendo en la ecuación (10.1), se aprecia que hay más de tres errores estándar lejos de la media poblacional: \(\frac{-1.13}{0.372}=-3.038\)23. Sabiendo que de acuerdo con la distribución normal, el \(95\%\) de las muestras o desviaciones se encuentran entre \(0\) (recuerda el cero es la media verdadera) y \(1.96\) errores estándar, se puede decir que con un \(95\%\) de confianza la muestra es diferente a la norma; no hay forma de que se haya alejado tanto de lo que se considera una distribución normal. Se puede alegar que la muestra es pequeña (\(28\) casos) lo cual amerita utilizar otro tipo de distribución, y efectivamente, hay razón para dudar; sin embargo, da la casualidad que comparando contra las probabilidades de la distribución t, también es significativa. Una muestra de \(28\) casos es significativa, usando una probabilidad del \(95\%\), después de \(2.05\) errores estándar24, y en nuestro análisis hay más de tres.
| Dulzor | Casos | Pct | Media_agrado | Desviación_stdr | Error_stdr |
|---|---|---|---|---|---|
| Falta dulce | 7 | 25% | 5.29 | 1.38 | 0.522 |
| Tal como me gusta | 15 | 54% | 7.87 | 1.19 | 0.307 |
| Sobra dulce | 6 | 21% | 5.83 | 2.64 | 1.077 |
| Total | 28 | 100% | 6.79 | 1.97 | 0.372 |
Una duda que atormenta constantemente al investigador novato es: cómo es que se pueden comparar medias procedentes de distintas escalas con el mismo método. La respuesta reside en lo que llamamos estandarización; el procedimiento no es distinto al que se usa para sacar porcentajes u obtener medias. La diferencia radica en que, en lugar de dividir por casos se hace por la desviación estándar o error estándar. Mediante este truco se puede comparar cualquier cantidad en términos de sus desviaciones o errores. Por ejemplo, si una persona tiene una media de ingreso anual de \(500\) mil pesos y la media general (contando a todos los empleados) en su empresa es de \(80\) mil pesos, con una desviación estándar de \(50\) mil, se puede calcular qué tan alejada está esa persona de todos los demás empleados usando la ecuación (10.2); muy similar a la prueba de una sola media, ¡¿no te parece?! Nota que en lugar de restar la media muestral se resta la media del ingreso del empleado a la media poblacional; lo otro es igual, se divide entre la desviación estándar. Este hipotético empleado está en el límite de toda la distribución, está a casi tres desviaciones estándar por encima de la media de todos los empleados: \(\frac{500-80}{150}=2.8\); su ingreso excede a más del \(95\%\) de los empleados de la empresa. Este ejercicio de estandarización se llama puntuación \(Z\). La \(Z\) se refiere a una desviación o error estándar: \(2Z\) son dos desviaciones estándar, \(3Z\) tres desviaciones estándar, etc. Ese es el gran secreto que permite verificar si hay diferencias significativas usando cualquier tipo de distribución (normal, t, binomial, etc.), sin importar lo que se mide: dulzor, satisfacción, intención de compra, o lo que sea.
\[\begin{equation} z=\frac{x-\tilde{x}}{s} \tag{10.2} \end{equation}\]
Perdón que nos hayamos extendido tanto, era necesario conocer toda esta teoría y razonar adecuadamente sobre la naturaleza de un error estándar. Analicemos la ecuación (10.3) que se utiliza para probar la diferencia entre dos medias. Parece muy distinta a la ecuación (10.1) de la prueba de una media, pero no lo es. Es exactamente la misma cosa; aunque en este caso se suman las variaciones de las dos muestras antes de estimar el tamaño del error. Por principio de cuentas, el numerador no cambia, sigue tratándose de la diferencia entre dos medias: \(\tilde{x_{1}}-\tilde{x_{2}}\), sólo que, ahora ambas son muestras; ninguna representa un valor real (poblacional). Las repercusiones son inmediatas, hay dos errores muestrales involucrados, no solo uno como en la ecuación (10.1); eso es lo que expresa el denominador de la ecuación (10.3): la suma de dos desviaciones. ¿Por qué no se hace igual en la ecuación (10.1); es decir, sumar la desviación de la muestra y la de la población? No se puede, recuerda que la población no tiene error, es un valor real. Hay error cuando se trata de muestras, no de poblaciones. Si estamos de acuerdo en ese punto, también debemos estarlo en que dos muestras, dos desviaciones o mayor desviación. Sin duda un elemento que confunde mucho a los que no tenemos espíritu gaussiano es la raíz cuadrada; ¿por qué los términos no dividen entre la raíz de \(n\), que es la forma en que se calcula el error?: \(\frac{s}{\sqrt{n}}\). Bueno, sí lo hacen, pero no antes de sumar las desviaciones. Matemáticamente, el error estándar se calcula también así: \(\sqrt{\frac{s^2}{n}}\); es una simple manipulación matemática25. ¿Ves alguna diferencia entre la fórmula anterior y esta: \(\sqrt{\frac{s_{1}^2}{n_{1}}+\frac{s_{2}^2}{n_{2}}}\); en absoluto, es transparente, se trata de la suma de la variación de las dos muestras, antes de calcular su error estándar. En concreto, se suma la variación de la muestra 1: \(\frac{s_{1}^2}{n_{1}}\) a la de la muestra 2: \(\frac{s_{2}^2}{n_{2}}\); se dividen entre \(n\) porque cualquier varianza depende del tamaño de la muestra. Muestras más grandes, variaciones más pequeñas, pero ¿qué tan pequeñas?, ¿recuerdas los barcos de papel?, del tamaño de una raíz cuadrada. Esa es la razón de extraer la raíz a la suma de esas desviaciones y no simplemente sumar los errores por separado; si lo hiciéramos así, romperíamos con la teoría de la distribución de las probabilidades del error.
\[\begin{equation} t=\frac{\tilde{x_{1}}-\tilde{x_{2}}} {\sqrt{\frac{s_{1}^{2}} {n_{1}}+\frac{s_{2}^{2}} {n_{2}}}} \tag{10.3} \end{equation}\]
Aún nos queda por explicar cómo se comparan dos medias: los que quieren un jugo más dulce y los que piden que no sea tan dulce. Los datos de análisis se encuentran en la tabla 10.2. ¿Cuántos errores caben dentro de la diferencia entre las medias? El cálculo matemático es muy directo. La diferencia entre una media y la otra es \(0.54\): \(5.83-5.29=0.54\); el error total o dentro de los grupos es \(1.19\): \(\frac{2.64^2}{6}=1.16+\frac{1.38^2}{7}=0.272\); \(1.16+0.272=1.433\); \(\sqrt{1.433}=1.19\). Así el valor t es igual a \(0.450\): \(\frac{0.54}{1.19}=0.450\). Ese valor es tan pequeño que ni siquiera amerita que lo contrastemos contra las tablas de la distribución probabilística \(t\). Indudablemente, no hay diferencias entre las medias. Da lo mismo hacer un jugo más dulce o menos dulce; los dos grupos están igual de insatisfechos. Estas afirmaciones las hacemos con base en lo que sabemos de distribuciones; un error estándar conlleva a una probabilidad de que se repita el mismo resultado en el \(68\%\) de los casos. O sea, es casi un volado; sería mucho atrevimiento decir que sí hay diferencias. En dos errores estándar (en la distribución t cambian estas probabilidades) se encuentran el \(95\%\) de los resultados; es muy lógico decir que sí existen diferencias cuando rebasamos este número de errores. Cuando hay más de tres errores estándar, el 99% de los resultados estarán dentro de los posibles resultados. Científicamente, las afirmaciones estadísticas no se hacen a ojo de buen cubero, sino comparando el valor resultante contra las distribuciones probabilísticas generadas por computadora, ya sea \(Z\), \(t\), \(Chi\) \(Cuadrado\) u otra26.
La clásica ilustración de dos curvas separadas índica que las medias son diferentes; no se traslapan. En nuestro ejercicio imaginario las curvas sí se traslapan (véase figura 10.3). Las medias son diferentes, pero los errores muestrales son tan grandes, derivado de las pequeñas muestras, que prácticamente una curva está encima de la otra. Las medias de ambas curvas no tienen ni un error estándar de separación entre ellas. En realidad, el error estándar \(0.450\) refleja casi un error estándar de una sola muestra, porque sumamos las desviaciones de las dos muestras en el denominador de la ecuación; es decir, duplicamos el error. En la figura 10.3 es notable que la separación se aproxima a un error estándar. ¿Entiendes que una diferencia entre las medias con una confianza del \(95\%\) equivale a cuatro errores estándar?, dos por cada muestra. Esa es la imagen clásica de la que hablamos.
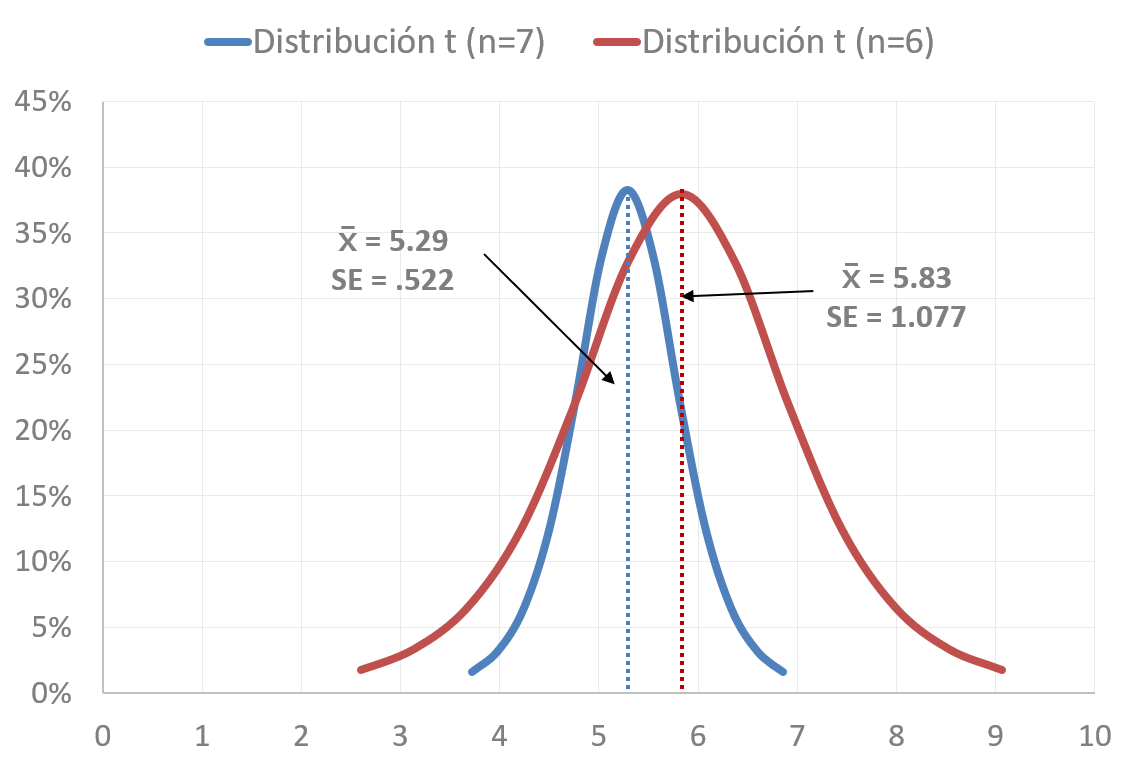
Figura 10.3: Diferencia entre dos medias
Hacer tablas de distribuciones que dieran cuenta de la dispersión que hay alrededor de la media verdadera con muestras pequeñas. En el pasado se empleaban tablas que reflejaban la probabilidad que había de encontrar un resultado dentro de uno, dos y hasta tres errores estándar; el profesionista comparaba el número de desviaciones que había en su investigación contra esas tablas y determinaba la probabilidad que había de que el resultado se volviera a repetir. Si la probabilidad de encontrarlo era baja, porque estaba a muchos errores estándar alejado de la media de esa distribución, declaraba una diferencia significativa, si no, sencillamente decía que no había diferencias.↩
Ten presente que en una distribución estadística la desviación estándar se llama error estándar. Las probabilidades de encontrar determinado valor dentro de uno, dos o tres errores estándar en una distribución \(t\) cambian constantemente derivado de la gran variación que hay en las muestras pequeñas. Ésto no sucede en la distribución normal debido a la ley de los grandes números o teorema del límite central.↩
Para ser exactos, utilizando una distribución normal (o sea una muestra grande), el \(95\%\) de las muestras caeran dentro de \(1.96\) errores estándar.↩
Cálculo del error estándar: \(\frac{1.97}{\sqrt{28}}=0.372\).↩
Las tablas estadísticas de donde se extraen estas probabilidades y sus errores (áreas debajo de la curva), tienen muy poco uso en la actualidad. En su lugar se usan programas estadísticos u hojas de cálculo que tienen funciones que calculan automáticamente todos esos valores (v.gr. Excel).↩
Observa que \(s^2\) es la varianza, no la desviación estándar; este cambio permite sacar la raíz cuadrada sin alterar el resultado. Intenta calcular el error estándar con las dos fórmulas para tu tranquilidad.↩
Estas distribuciones se encontraban en tablas dentro de todos los libros de texto de estadística; la comparación se hacía utilizando esas tablas. Hoy en día es raro hacerlo así, el programa de estadística señala al instante si el valor encontrado es significativo o no. Por otro lado, Excel que es el programa más universal que hay, tiene todas esas funciones estadísticas.↩