Capítulo 14 Camino arriba, camino abajo, uno y el mismo
No importa si subes o bajas, el camino es uno y el mismo; el trabajo es encontrarlo. La regresión lineal te ayuda a encontrar ese camino a través del método de los mínimos cuadrados; inventado por el Príncipe de las matemáticas Gauss. En pocas palabras, se trata de encontrar un promedio general, representado por una línea recta que esté a la mínima distancia de todas las observaciones; sin importar si están por arriba o por abajo del promedio. ¿Suena complicado?, quizá, pero entender el concepto es de lo más fácil que puedas imaginar. Así que ¡al camino!, que como decía Miguel de Cervantes: “El que lee mucho y anda mucho, ve mucho y sabe mucho”.
Imagina que eres el orgulloso dueño de un nuevo restaurante llamado Yupi’s Pizza, y que un cliente te pregunta cuánto tiempo tarda en llegar su pedido de pizzas. Para responder necesitas conocer el tiempo que se tarda un repartidor en llegar desde el establecimiento hasta el lugar donde se encuentra ese cliente. Por fortuna, tienes datos de las primeras diez entregas con la distancia en kilómetros que hay entre la pizzería y el lugar donde se han entregado varios pedidos, y el tiempo en minutos que dilataron en llegar los repartidores (véase tabla 14.1).
| Entregas | Distancia_km | Tiempo_min |
|---|---|---|
| 1 | 3 | 5 |
| 2 | 12 | 10 |
| 3 | 4 | 5 |
| 4 | 7 | 9 |
| 5 | 6 | 8 |
| 6 | 14 | 15 |
| 7 | 15 | 20 |
| 8 | 16 | 18 |
| 9 | 11 | 12 |
| 10 | 8 | 9 |
Sabes que ese cliente se encuentra a \(14km\) de distancia. ¿Qué tiempo le responderías? Una rápida inspección te ubica en la sexta entrega de la tabla de datos. ¡Exacto!, \(15min\); es lo que se aprecia que le lleva a un repartidor recorrer esa distancia. Te imaginas una tabla dónde se encontraran las respuestas o toda clase de preguntas del tipo causa y efecto. En otras palabras, una en la que se supiera en qué medida una cosa depende de otra; en este caso el tiempo de entrega que depende de la distancia. No, no existe tal tabla. ¿Sabes por qué no existe?, porque es imposible. Las posibilidades son simplemente infinitas. Qué pasa si regresa el repartidor y te dice que se tardó \(2min\) más de lo previsto, o sea \(17min\), ¿qué le vas a decir al próximo cliente cuando te pregunte cuánto tiempo tardará su pedido, suponiendo que está exactamente a \(14km\) de distancia? ¿Le dirás \(15min\) o \(17min\)? Gracias a la lectura de este libro, has aprendido que el promedio es el indicador más exacto, así que poniendo en práctica los conocimientos adquiridos, \(16min\) parece la mejor respuesta (\(\frac{15+17}{2}=16\)). Sucede, y confiado le dices a este otro cliente que su pedido llegará en \(16min\). De regreso el repartidor te dice que fueron \(12min\), no \(16min\), los que tardó en llevar la pizza a su destino. No hay problema, vuelves a sacar otro promedio para estar preparado por si otro cliente, ubicado a la misma distancia, quiere conocer el tiempo de entrega. La media (promedio) es una apuesta segura para una variable. Hasta ahora la distancia es única e invariable: \(14km\), pero ¿qué pasa cuando la distancia cambia?, la media se vuelve inútil. Si un cuarto cliente que vive a \(10km\) de distancia pregunta el tiempo de llegada de su pizza, no hay forma de saber cuál es la respuesta. Primero, porque en la tabla 14.1 no hay ningún pedido a esa distancia; segundo porque entre tantas distancias y tiempos de entregas es difícil saber cuáles escoger para obtener algún promedio más o menos exacto. Además, eso de estar promediando una y otra vez es muy molesto. ¿Te das cuenta qué las posibilidades son muchas? ¿No sería mejor tener una especie de entregómetro, el cual se pudiera consultar cada vez que se necesitara conocer el tiempo de entrega a la distancia que fuera?
Voy a escarbar un poco en la forma de pensar de la mayoría de nosotros los mortales. Para casi cualquiera es incuestionable que la distancia afecta el tiempo de entrega de la pizza. Hay una interacción entre estas dos variables; a mayor distancia uno se tarda más en llegar a donde quiera que sea que pretenda llegar. Esa interacción se representa matemáticamente con una multiplicación (véase sección 2), ya podemos decir que \(distancia \times tiempo = entrega\). Usemos esta primera ecuación para conocer el tiempo de llegada de la primera entrega: \(14km\times 15min=210\), el tiempo de entrega sería de \(210\). ¿Qué significa ese número? No es ni kilometros ni minutos, más bien es \(min/km\). Eso no sirve para fabricar un entregómetro. El truco es quitar los \(km\) o sea dividir por ellos, de tal forma que la medida resultante sea sólo tiempo: \(\frac{210}{14}=15min\). Aunque no hay nada malo en el procedimiento anterior, estamos caminando en círculos; hemos vuelto al mismo lugar. Véamos, se cumple la condición de que ambas variables tiempo y distancia interactúan, por eso decidimos multiplicarlas. Por otro lado, también estamos razonando adecuadamente al ubicar en el denominador a la variable independiente; esa es la que explica. Recuerda que el as bajo la manga de los investigadores es la división (véase sección 4). Sin embargo, el resultado sirve para cuantificar una única variable; de la cual, además, ya sabíamos que era \(15min\). Asimismo, no tenemos una razón fija que explique la cantidad de cambio del tiempo de entrega en razón de la distancia. Algo que se puede obtener, y sin tanto brinco, dividiendo únicamente el tiempo sobre la distancia: \(\frac{15min}{14km}=1.07\). La razón fija es que por cada kilometro el tiempo se incrementa en \(1.07min\). Ese sí sería un buen número, muy cerca al entregómetro que estamos buscando. Así para cada distancia nueva que tuviéramos sólo tendríamos que multiplicarla por \(1.07min\) para conocer el tiempo de entrega. Por ejemplo, si nos piden el tiempo de llegada a una distancia de \(10km\), la respuesta es \(10.7min\): \(1.07\times 10km=10.7min\). Desafortunadamente, esta forma de pensar no funciona en un charco lleno de ranas (véase sección 13); es decir, multivariable. Forzosamente se necesitan tomar en cuenta todas las variables como si fueran una sola y conocer si efectivamente interactúan o no; en otras palabras, si se relacionan. Con este último método que nos hemos inventado no estamos tomando en cuenta la interacción de las variables distancia y tiempo. Una forma muy inteligente de construir el entregómetro respetando los procedimientos matemáticos: interacción-explicación es la siguiente: multipliquemos distancia y tiempo, y dividamos por la distancia, pero hagamos lo mismo que con el numerador, multipliquemos la distancia por la misma distancia; o sea elevémosla al cuadrado. Este artificio nos asegura que la proporción original va a permanecer inalterada: si arriba multiplicamos por distancia, también lo hacemos abajo: \(\frac{14km\times 15min}{14km\times 14km}=\frac{210}{196}=1.07\). Es exactamente la misma proporción que cuando sólo usamos las cantidades sencillas de tiempo sobre distancia; salvo que ahora tenemos todo un mundo de posibilidades y lo podemos hacer involucrando muchas observaciones (tiempos y distancias diferentes). ¡Felicidades!, si entendiste este procedimiento, ya sabes qué es la regresión lineal o el método de mínimos cuadrados de Gauss.
La mayoría de las veces los problemas a los que nos enfrentamos no son tan claros ni tan sencillos. En el caso anterior cualquiera entiende que la distancia afecta el tiempo de entrega de la pizza. Por otro lado, los datos son pocos y es fácil manipularlos; incluso hacer una gráfica sencilla para ver la relación que hay entre la distancia y el tiempo (véase figura 14.1). En ella, cada punto azul, incluido el rojo, es una entrega que da cuenta de la relación entre la distancia y el tiempo, es notorio que ambas crecen casi uniformemente; a más distancia mayor tiempo. La regresión lineal en particular y la estadística en general están hechas para analizar problemas más complejos, donde no son tan obvias ni tan claras las relaciones multivariables o simplemente en las cuales la cantidad de datos que hay que analizar son muy grandes. Gauss ideó el instrumento de la regresión lineal o mejor dicho de los mínimos cuadrados30 para encontrar la razón o proporción en que una variable afectaba a otra u otras. Lo hizo de una forma tan sencilla y elegante que una vez comprendido el método uno diría que no hizo nada, pero es todo un portento de pensamiento. Muy similar al que usaría cualquiera de nosotros, sólo que sumándonos a todos y elevando el resultado al cuadrado; más adelante verás a qué me refiero.
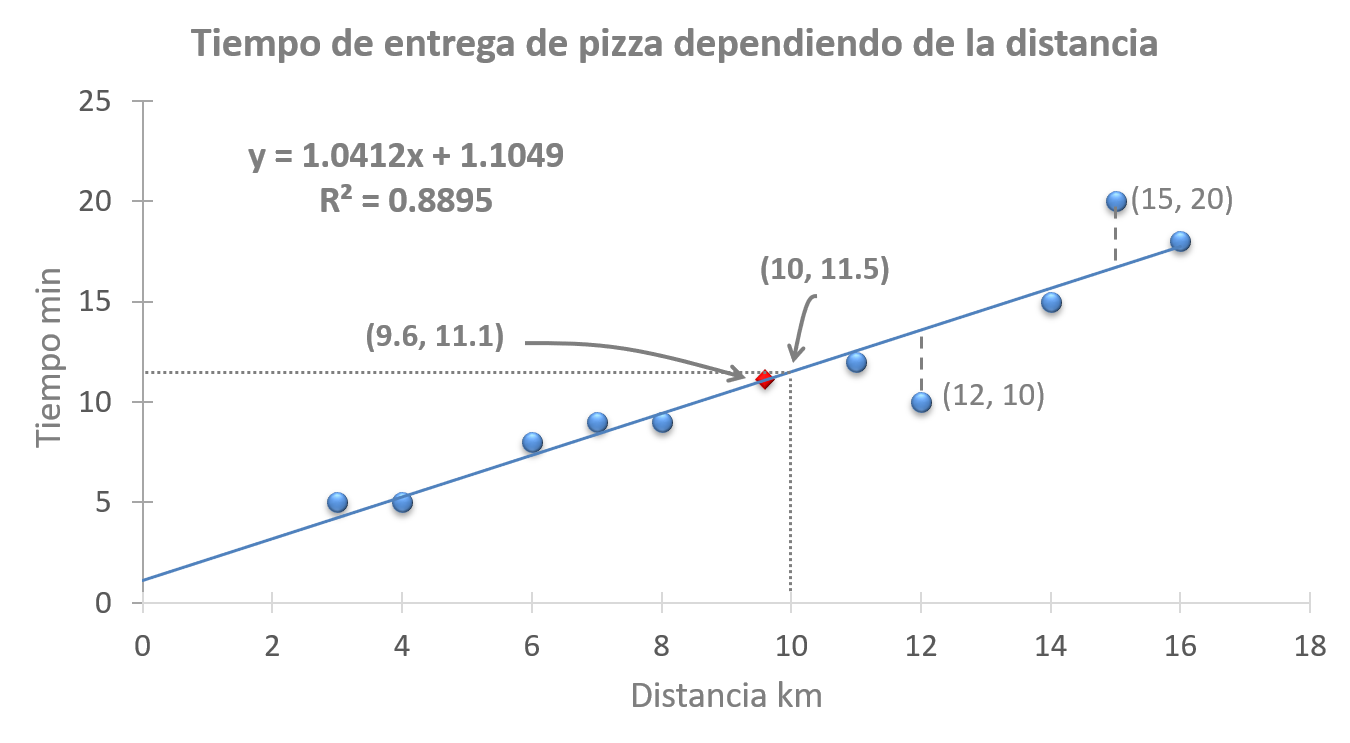
Figura 14.1: Tiempo de entrega de pizzas
Antes de proseguir, me gustaría ejemplificar el uso de la regresión lineal múltiple en la investigación de mercados. En los estudios de satisfacción del cliente es difícil conocer cuáles variables son las que afectan la satisfacción en general y sobre todo cuánto. Ese cuánto se llama coeficiente de regresión y es la cantidad que varía la variable dependiente en función de la independiente. En otras palabras, qué tanto aumenta o disminuye la satisfacción general cuando se alteran las variables independientes que pueden ser precio, calidad, atención, amabilidad, puntualidad, servicio o cualesquier otro aspecto del producto o servicio. A los aspectos que determinan la satisfacción en general los mercadólogos les llaman drivers y son claves para proporcionar una experiencia más satisfactoria al cliente; lo que en términos prácticos significa retenerlo y que siga comprando los servicios o productos de la empresa. Ese coeficiente de regresión también se llama beta de regresión porque se representa con la letra griega beta: \(\beta\). En la figura 14.2 cada uno de los círculos representa un driver que afecta la satisfacción en general del cliente con la línea aérea. El número que hay dentro de cada círculo es el coeficiente de regresión o beta de ese driver. Si sumas estos coeficientes vas a obtener \(100\%\); eso se debe a que hemos ajustado todas las betas para que en total sumen \(100\%\). ¡Atención!, no es que los coeficientes resultantes del análisis de regresión múltiple sumen \(100\%\), es más, ni siquiera están expresados en porcentajes; lo que sucede es que para las personas es más fácil interpretar esos números ajustados que si les decimos que el coeficiente de regresión o beta es de \(.30\), \(75\), o la cantidad de la variable que sea que represente ese coeficiente. Algunas agencias de investigación en lugar de ajustar a \(100\%\) sólo indican el orden en el que las variables independientes afectan a la satisfacción general (variable dependiente). Mencionan algo parecido a el atributo A afecta en primer lugar a la satisfacción general, en segundo lugar el que más afecta es el atributo B, y así sucesivamente. Desde nuestro punto de vista, eso está mal hecho pues no es lo mismo decir a sus órdenes General que órdenes generales. Por si no entendiste mi lenguaje cantinfleado, ahí te va de nuevo: si \(x1\) afecta en \(90\%\) y \(x2\) en \(10\%\) es más sencillo decidir prioridades, que si sólo se sabe que \(x1\) es primero y \(x2\) es segundo.

Figura 14.2: Drivers de la satisfacción en general
La correlación y la regresión están estrechamente relacionados. Haz de recordar que la suma de los productos cruzados (véase sección 13) es la forma de cuantificar la variación conjunta de dos variables; en nuestro caso la distancia y el tiempo. En la columna Variacion_xy, la cual representa la multiplicación de las columnas Distancia_x y Tiempo_y de la tabla 14.2, se puede notar que en conjunto ambas variables tienen una suma de variación total o, más bien dicho, de covarianza de \(202.4\). Hay una variación muy ordenada, si la distancia aumenta, el tiempo también. En la figura 14.1 es más que evidente dicha relación; excepto por la segunda entrega (el punto rojo de la gráfica), ésta tiene un resultado negativo; en la columna Variacion_xy se aprecia su valor: \(-2.64\). Cuando se suman los productos cruzados esta entrega resta importancia a la relación. En buen cristiano diríamos que no corresponde el tiempo de entrega con la distancia. El repartidor hizo menos tiempo del esperado; quizá iba montado en una Kawasaki Ninja de carreras. En resumen, los productos cruzados dan cuenta de la relación e importancia entre la distancia y el tiempo de entrega, pero no dicen en qué medida o proporción. Para ello, es necesario meter la variable explicativa, la distancia. Ésta la elevamos al cuadrado por dos razones principales: la primera es que si no lo hiciéramos, la suma daría cero; puedes checarlo en la columna Distancia_x; esta columna representa la variación o desviación de la distancia con relación a su promedio: \(distancia-distancia\ media\). Gauss pensó que lo mejor era operar con la variación total de esa variable elevándola al cuadrado; ¿ya empiezas a ver porqué el método de mínimos cuadrados?31 La segunda es porque queremos obtener una razón que no se altere, y para lograrlo debemos hacer lo mismo que hicimos con el Tiempo_y (variación del tiempo: \(tiempo-tiempo\ medio\)), el cual lo multiplicamos por la Distancia_x. Entonces, debemos multiplicar la Distancia_x por ella misma; o sea elevarla al cuadrado como aparece en la columna Distancia_x2. Lo que sigue es dividir la suma de los productos cruzados entre la suma de la variación al cuadrado de esa distancia: \(\frac{202.4}{194.4}=1.041\).
| Entrega | Dist | Tiempo | Dist_x | Tiempo_y | Dist_x2 | Var_xy |
|---|---|---|---|---|---|---|
| 1 | 3 | 5 | -6.6 | -6.1 | 43.56 | 40.26 |
| 2 | 12 | 10 | 2.4 | -1.1 | 5.76 | -2.64 |
| 3 | 4 | 5 | -5.6 | -6.1 | 31.36 | 34.16 |
| 4 | 7 | 9 | -2.6 | -2.1 | 6.76 | 5.46 |
| 5 | 6 | 8 | -3.6 | -3.1 | 12.96 | 11.16 |
| 6 | 14 | 15 | 4.4 | 3.9 | 19.36 | 17.16 |
| 7 | 15 | 20 | 5.4 | 8.9 | 29.16 | 48.06 |
| 8 | 16 | 18 | 6.4 | 6.9 | 40.96 | 44.16 |
| 9 | 11 | 12 | 1.4 | 0.9 | 1.96 | 1.26 |
| 10 | 8 | 9 | -1.6 | -2.1 | 2.56 | 3.36 |
| media | 9.6 | 11.1 | — | — | — | — |
| suma | — | — | 0 | 0 | 194.4 | 202.4 |
La ecuación de la regresión lineal (14.1) es multipropósito; sirve para hacer un entregómetro, calcular el nivel de satisfacción del cliente, pronosticar si una pareja se va a divorciar debido a su mala comunicación, economía, falta de sexo o atracción, y prácticamente cualquier otra cosa que se te ocurra medir. Lo que recien acabamos de calcular es la beta \(\beta_{1}\). En la figura 14.1 se puede apreciar la misma ecuación con las betas calculadas. Todavía falta calcular la beta cero (\(\beta_{0}\)) ¿Qué papel juega esta misteriosa beta? Bueno, es la llamada constante de medición, es la cantidad que habría en caso de que la distancia fuera cero; esto es teórico, no corresponde necesariamente con la realidad, pero es un buen comienzo para entender cuánto puede crecer o decrecer la variable dependiente. Para calcular este valor nos apoyamos en un simple hecho: la línea de regresión tiene que pasar por el promedio de la variable independiente (x) y la dependiente (y). El promedio de la distancia es \(9.6km\) y del tiempo es \(11.1min\) (tabla 14.2); puedes corroborarlo en la gráfica 14.1. Usando nuestros conocimientos básicos de álgebra y sustituyendo en la ecuación (14.1) encontramos la beta que nos falta: \(11.1=(1.0412\times9.6)+\beta_{0}\); \(\beta_{0}=-9.9955+11.1\); \(\beta_{0}=1.1049\). Allí lo tienes, está listo nuestro instrumento de medición.
\[\begin{equation} \hat{y}=\beta_{1}x+\beta_{0}+e \tag{14.1} \end{equation}\]
¿Qué te parece si probamos el nuevo entregómetro? Según nuestros cálculos, sustituyendo en la fórmula las betas que obtuvimos, llevar la pizza a 10 kilómetros de distancia tardaría 11.51 minutos: \((1.0412\times 10)+1.1049=11.51\). La misma coordenada (10, 11.5) que se señala en la figura 14.1. El pronóstico es que el repartidor estará entregando el pedido en \(11.5min\). ¿Será exacto el tiempo? Muy probablemente no. Por eso es que se usa ese símbolo de error \(e\) al final de la ecuación (14.1), el cual señala que existe un error adicional que se debe sumar al cálculo para hacer una estimación exacta del tiempo. Conceptualmente ese error es la distancia que hay entre las estimaciones del punto medio o línea de regresión y los datos reales u observados; y se calcula de la misma forma que cualquier error estándar. La manera más directa de evaluar la magnitud del error es a través de la \(R^2\); que no es otra cosa que la correlación al cuadrado. Si esta medida se acerca a \(1\), el ajuste es perfecto; es decir, todas las observaciones caen en la línea de regresión o, lo que es lo mismo, son iguales a la media. En el caso de nuestro entregómetro la \(R^2 =.88\) sugiere un ajuste muy alto; las observaciones están muy cerca de la media (figura 14.1). La otra manera, más técnica, es a través del cálculo del error estándar. Analiza con calma la ecuación (14.2), es la misma ecuación (9.2); aunque en este caso la desviación se origina de la media estimada \(\hat{y}\), y se divide entre el numero de casos \(n\) menos \(2\), por los dichosos grados de libertad. Se sabe que un error estándar equivale al \(68\%\) de confianza y dos al \(95\%\). Para darle un aire de cientificidad al asunto, se puede decir que la estimación que hicimos del tiempo, cuando hay que entregar la pizza a \(10km\) de distancia es de \(11.51min\), pero puede ser 1.81 minutos antes o después. Eso sería si queremos confiar un 68% en el pronóstico; si deseamos tener mayor confianza, el 95% que es la usual, tendríamos que restar y sumar dos errores estándar a \(11.51 min\); para obtener un intervalo con esa confianza. Así que el repartidor puede llegar entre \(7.89min\) y \(15.13min\). Si todavía tienes dudas acerca de cómo obtuvimos ese error estándar, se desprende de la suma total de los errores al cuadrado: \(\sum(\hat{y}-y)^{2}=26.20\) (véase la suma de la columna Diferencia_y2 de la tabla 14.3), dividido entre \(n-2\), y extrayendo la raíz cuadrada al resultado: \(SE=\sqrt{\frac{26.20}{8}}\); \(SE=1.81min\). En la práctica, el error no se utiliza mucho debido a que no es algo que el cliente esté interesado en conocer, no es vital, o simplemente escapa a su conocimiento.
\[\begin{equation} SE=\sqrt{\frac{\sum(\hat{y}-y)^{2}}{n-2}} \tag{14.2} \end{equation}\]
En general, todo lo que se aleja de la línea de regresión es considerado un error (véase sección 6) debido a que esta línea es en realidad una media, un origen (véase sección 5); y es muy fácil comprobarlo. Analiza la tabla 14.3, la columna Estimado_y es el valor calculado o estimado para cada entrega con base a la ecuación lineal (14.1); en otras palabras, se trata del tiempo promedio. La diferencia de ese promedio (media) con el valor real está en la columna Diferencia_y; sumando estas diferencias se obtiene cero, lo mismo que sucede con la varianza (sección 6). Eso es prueba más que suficiente de que se trata de una media. Ahora, piensa en el repartidor de la moto Kawasaki Ninja, en realidad no sabes por qué razón la distancia y el tiempo son tan dispares en relación a las otras mediciones; por qué se alejan tanto de la media de regresión. Esa ignorancia no hay forma de explicarla, no por lo menos hasta que te enteras que, efectivamente, el repartidor iba montado en una moto de carreras. Gráficamente ese error se representa con líneas punteadas que se conectan con la pendiente de la recta; por ejemplo, la entrega 2 y 7, coordenadas (12, 10) y (15, 20), respectivamente, de la figura 14.1. Date cuenta de que las líneas punteadas son verticales, pues es una distancia que se suma o resta al tiempo estimado \(\hat{y}\) (eje \(y\)).
| Entrega | Dist_x | Tiempo_y | Est_y | Dif_y | Dif_y2 |
|---|---|---|---|---|---|
| 1 | 3 | 5 | 4.23 | -0.77 | 0.59 |
| 2 | 12 | 10 | 13.6 | 3.60 | 12.96 |
| 3 | 4 | 5 | 5.27 | 0.27 | 0.07 |
| 4 | 7 | 9 | 8.39 | -0.61 | 0.37 |
| 5 | 6 | 8 | 7.35 | -0.65 | 0.42 |
| 6 | 14 | 15 | 15.68 | 0.68 | 0.46 |
| 7 | 15 | 20 | 16.72 | -3.28 | 10.76 |
| 8 | 16 | 18 | 17.76 | -0.24 | 0.06 |
| 9 | 11 | 12 | 12.56 | 0.56 | 0.31 |
| 10 | 8 | 9 | 9.43 | 0.43 | 0.18 |
| suma | — | — | — | 0.00 | 26.20 |
Permíteme finalizar con unos cuantos apuntes más. Primero, respecto a la significancia estadística, ésta proporciona una certeza de la fuerza con la que la variable independiente afecta a la dependiente. Tal vez, eso sea lo primero que aprende un estudiante sobre la estadística, sin duda, algo muy importante. Desafortunadamente, lo aprende como una receta de cocina, sin tener mucha idea de lo que implica. Como se dijo anteriormente, la correlación y la regresión son muy parecidas, tanto que es fácil confundirse con lo que hace una y hace la otra. Ambas obtienen resultados a partir de la suma de los productos cruzados, pero la correlación se obtiene dividiendo entre la varianza total; dando cuenta del porcentaje de explicación que da la interacción de dos variables, cuando interactúan efectivamente. La regresión, por su parte, se consigue dividiendo entre la suma total de la variación de la variable independiente. Eso conlleva a una suspicacia: la variable independiente la elegimos nosotros. La distancia determina el tiempo de entrega de la pizza, pero nada nos impide analizar las cosas a la inversa; esto es, determinar qué tanto afecta el tiempo a la distancia. Eso marca una gran diferencia entre correlación y regresión. Como dicen comúnmente, que dos variables estén asociadas no significa que una sea causa de la otra. Por eso es que la medida por excelencia de la significancia estadística de una regresión es la correlación: una variable causa a la otra y además están asociadas. En palabras de Olivia Newton John: “Hopelessly devoted to you”. La regresión lineal simple o múltiple asume algunos supuestos que debes revisar que se cumplan, como la distribución normal de los errores y su independencia; dale pues una revisada a esos conceptos para que te sientas más seguro de lo que estás haciendo. Una beta depende del tipo de variables de medición; para hacer pronósticos se requiere manejar el resultado tal cual. Sin embargo, en muchos casos lo que se necesita es una beta estandarizada; esa va de -1 a 1, donde -1 significa que la variable independiente afecta totalmente a la variable dependiente de forma negativa, mientras que 1 significa lo mismo, pero positivamente. Esto no es algo que deba preocuparte, todos los programas estadísticos reportan ambos tipos de betas.
El término regresión fue tomado de Francis Galton. Fuera del nombre regresión, no hay otra cosa en común con el método estadístico de los mínimos cuadrados que construyó Carl Friedrich Gauss. Quizá sólo se llamó así al método por la similitud gráfica con la pendiente de una línea que mostraba Galton en su obra.↩
La realidad es que este método es más obligado para facilitar la derivación de la ecuación de la línea recta que otra cosa.↩