Capítulo 11 Un sombrero seleccionador

¿Recuerdas el sombrero de Harry Potter?, ¿ese que le decía a cada nuevo estudiante a qué casa de estudios de la academia Hogwarts debería ir? El sombrero analizaba los pensamientos de cualquier estudiante y sentenciaba victorioso: Gryffindor, Hufflepuff, Ravenclaw o Slytherin. Mediante este mágico procedimiento se clasificaba a los estudiantes de acuerdo a la clase a la que pertenecían. En ciencia, y sin magia de por medio, también se busca encontrar evidencia de la clase a la que pertenece cada sujeto, cosa o fenómeno natural. La chi cuadrado $X^2$ es el procedimiento estadístico más conocido para verificar si algo o alguien es o no de determinada clase. Este sombrero seleccionador estadístico dice rechazado si encuentra evidencia de que lo que observa no es normal y aceptado si sí lo es. ¿Qué tan útil puede ser un sombrero con estas características?, ¿cómo se utiliza en marketing? y, sobre todo, ¿cómo funciona? No prolonguemos más el suspenso, y vamos directo al grano.

La tabla 11.1, llamada tabla de contingencia o de datos cruzados, es el instrumento más universal que hay para clasificar sujetos o cosas con base a sus frecuencias. Su uso está plenamente justificado por su practicidad y utilidad. Por ejemplo, de un solo vistazo descubrimos que el champú Pantene es el jefe de la categoría; tiene los porcentajes²⁷ más altos en casi todos los atributos. ¿Qué más se deduce a partir de una inspección visual? Bueno, los atributos en los cuales Pantene tiene las calificaciones más altas y bajas: Tiene publicidad y Quita la caspa, respectivamente. Asimismo, Caprice y Head & Shoulders tienen porcentajes muy parecidos entre ellos, pero ¿cuáles son los atributos más importantes de estas dos marcas?, eso no se detecta tan rápido. No obstante, lo útil que resultan este tipo de tablas, analizar los datos en conjunto no es tan simple ni directo como parece. Es más, la cosa se complica si queremos observar las interacciones (asociaciones) entre marcas y atributos. Para tener una apreciación clara de las fortalezas y debilidades de las marcas en esos atributos, los investigadores de mercado utilizan el archirequetecontraconocido método de normalización de datos.

Tabla 11.1: Imagen de marcas de champú
Atributos	Pantene	Caprice	Head_S	Total
Tiene publicidad	93	42	41	176
Es de calidad	79	37	35	151
Hace espuma adecuada	78	46	31	155
Tiene fragancia agradable	83	35	29	147
Es para toda la familia	70	42	29	141
Deja el cabello suave	71	33	32	136
Da brillo al cabello	74	34	28	136
Deja el cabello sedoso	74	27	21	122
Es para cabello reseco	77	35	19	131
Quita la caspa	26	17	35	78
Total	725	348	300	1373

¿Normalización?, déjame explicarlo trivialmente, cuando vemos una mujer u hombre extremadamente atractiva(o), nos viene a la mente cualquier cosa, excepto, que se trata de una persona normal; con respecto a su belleza, ella o él sobresalen de las demás personas. La situación se repite independientemente de la característica que se observe (v.gr. la inteligencia). La naturaleza se manifiesta de forma tal que casi todos somos más o menos normales. Es decir, hay pocas personas extremadamente bellas o feas, pocas muy inteligentes o brutas, ¿me explico?; normal significa estar en el promedio. Por otro lado, ya sabes que el promedio (media) es el origen de donde parten las diferencias; tan es así, que para determinar si algo o alguien es diferente, lo único que debemos hacer es compararlo con el promedio. Ese promedio, en términos de la $X^2$, se llama esperado. Volvamos a pensar en esa persona atractiva, ¿cuánta gente esperas encontrarte en la calle con esos rasgos tan finos?; no mucha, ¡¿no es así?! Esperado, normal, y promedio son la misma cosa. Observa la tabla 11.2, el $79\%$ de la gente opina que Pantene Es una marca de calidad vs. un $37\%$ que dijo lo mismo de Caprice. ¿Es normal que la gente se exprese así de ambas marcas? Podría serlo, después de todo Pantene es la marca líder; aunque queda la duda de qué tan normal puede ser. ¿Qué hay del atributo Es para toda la familia?, Caprice no parece estar tan abajo de Pantene: $42\%$ vs. $70\%$, respectivamente. ¿Qué tan normal es esto?, ¿cómo puede ser que Head & Shoulders tenga un porcentaje mayor que Pantene en el atributo Quita la caspa?, $35\%$ vs. $26\%$, respectivamente; no parece normal, ¿o sí? La respuesta a todas estas preguntas It’s not blowing in the wind, parte del promedio esperado; de aquello que nos parece normal o justo.

Tabla 11.2: Imagen de champú en tres atributos
Atributos	Pantene	Caprice	Head_S	Media
Es de calidad	79	37	35	50
Es para toda la familia	70	42	29	47
Quita la caspa	26	17	35	26
Media	58	32	33	41

Sumando los porcentajes de puntuación de todas las celdas de la tabla 11.2 y dividiendo entre el número de celdas, descubrimos que la media de desempeño general es $41\%$ (véase la intersección de la fila y columna Media). Ya tenemos un promedio para evaluar si una celda cualquiera es normal o diferente. Hagámoslo con Pantene y el atributo Es de calidad: $79\%-41\%=38\%$. La conclusión es que Pantene en Calidad está muy bien, muy por arriba del promedio. Demasiado fácil para ser cierto, ¡¿no crees?! ¿Cómo está Pantene en Quita la caspa?, tiene un desempeño de $-15\%$: $26\%-41\%=-15\%$; o sea, no está tan bien, queda por debajo de la media. Sorprendentemente, también Caprice está mal: $-24\%$ ($17\%-41\%=-24\%$) y Head & Shoulders: $-6\%$ ($35\%-41\%=-6\%$). Resulta extraño, por decirlo de alguna manera, todos saben que Head & Shoulders es un champú para la caspa; ¿por qué está por debajo del promedio? Pantene, lo mismo que Caprice y Head & Shoulders, tiene sus propios estándares; no se aprecia justo comparar una marca que vende muchos millones con otras que poseen menos de la mitad del mercado de champú ni comparar el desempeño de una marca en un atributo específico utilizando un promedio que involucra a todas las marcas y atributos. Pantene jamás ha mencionado que Es para toda la familia, lo cual es algo que sí hace Caprice, o que Quita la caspa, que definitivamente es algo que no hace, pero Head & Shoulders sí. Es como competir en un decatlón, siendo que lo único que has hecho en toda tu vida es correr. El promedio general no sirve como instrumento de comparación. Se necesita otra medida que tome en cuenta únicamente a la marca y el atributo del que se trata. Lo justo es que se dé a cada quien según sus capacidades o necesidades. No se puede medir a todos con el mismo rasero.

El gran misterio de la $X^2$ es que considera exclusivamente la interacción entre clases para determinar el valor esperado donde se intersectan. Por ejemplo, para saber qué tanto le corresponde a Pantene en Calidad, multiplica el promedio de la marca por el promedio del atributo y divide entre el promedio global; así se obtiene el valor normal, promedio o esperado. ¿Por qué entre el promedio global? Esa división logra dos cosas, primero, devuelve el resultado de esa multiplicación (interacción o intersección) a sus unidades originales; y segundo, dimensiona la cantidad del promedio global que corresponde a esa interacción. ¿Se entiende? En la tabla 11.2 la calificación promedio de cada marca, tomando en cuenta todos los atributos, se presenta en la fila titulada Media; el promedio de Pantene es $58\%$: $\frac{79\%+70\%+26\%}{3}=58\%$, el mismo procedimiento se ha aplicado para obtener el promedio de Caprice ($32\%$) y Head & Shoulders ($33\%$). El cálculo para cada atributo se ha obtenido de forma similar, obviamente, promediando las marcas; estas medias se observan en la columna Media. Poniendo en práctica el conocimiento que tenemos de teoría de conjuntos, en el cual una intersección se representa con una multiplicación, multipliquemos el promedio de Pantene por el promedio de Es de calidad $58\times 50=2900$; eso entre $41$ da $71$: $\frac{2900}{41}=71$. Este número es lo normal, lo que se espera de esa interacción o intersección entre la marca Pantene y el atributo Es de calidad. El promedio esperado es un buen instrumento para evaluar qué tan bien califica la marca en ese atributo. Si Pantene tiene $79\%$ en Es de calidad y se espera que tenga $71\%$, está bien, por lo menos en numeros sanos, un $8\%$ arriba del promedio esperado: $79\%-71\%=8\%$. Para saber en qué estado se encuentran las demás marcas en cada atributo, se repite la misma acción. Por ejemplo, Head & Shoulders en el atributo Quita la caspa está $14\%$ por encima del promedio esperado: $\frac{33\times 26}{41}=21$; $35-21=14$. ¿Verdad que checa perfecto con lo que pensábamos de esta marca? ¿Que hay de Caprice? En el atributo Es para toda la familia tiene un buen desempeño, $5\%$ arriba del promedio: $\frac{32\times 47}{41}=37$; $42-37=5$. En resumen, para determinar si una marca, o cualquier otra cosa, está mejor o peor que el promedio, hay que comparar su porcentaje, calificación, o frecuencia con la que tendría o se espera en condiciones normales. En estadística, la calificación, porcentaje o frecuencia que se analiza se llama observado y al promedio esperado se le dice esperado; elemental, mi querido lector. La figura 11.1 es un buen recordatorio del procedimiento que se usa para calcular el valor esperado. La cruz señala que hay que multiplicar el reglón $R$ por la columna $C$; el valor obtenido es la interacción que se deposita en la celda central de esa multiplicación y se divide por el valor total de abajo para obtener el esperado.

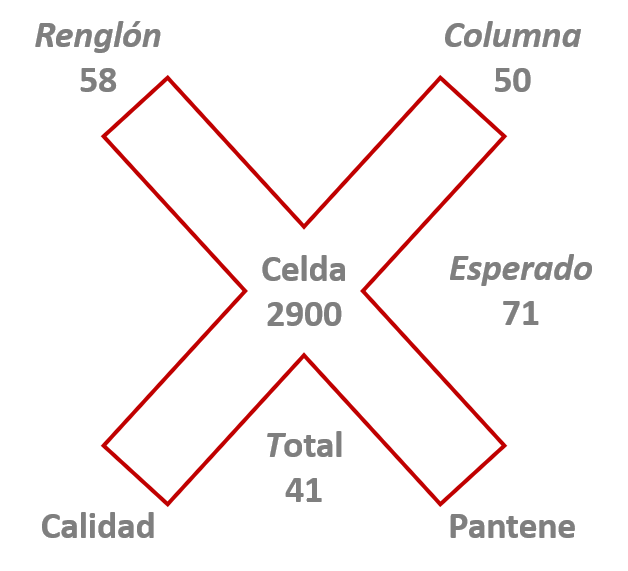
Figura 11.1: Procedimiento para obtener un valor esperado

Te tengo una buena noticia, no es necesario calcular previamente ninguna media para obtener el valor esperado, tampoco porcentajes; de hecho, no se debe. Te hemos traído por el camino complicado sólo para demostrarte que el valor esperado es un promedio. Asimismo, queríamos enseñarte que un promedio es lo mismo que una suma, pero en su forma condensada, estandarizada; si procedes con sumas en lugar de promedios, llegas a la misma solución. Ve la tabla 11.3, la suma total de Pantene es 175 y de Es de calidad 151, aplicando la fórmula nos da un esperado de $71\%$: $\frac{175\times 151}{370}=71$. Diferentes caminos, mismo destino. No te fijes en los decimales, por favor.

Tabla 11.3: Imagen de champú en tres atributos sin promediar
Atributos	Pantene	Caprice	Head_S	Suma
Es de calidad	79	37	35	151
Es para toda la familia	70	42	29	141
Quita la caspa	26	17	35	78
Suma	175	96	99	370

Es sensacional haber llegado hasta aquí. Con el procedimiento que acabamos de aprender, identificar las fortalezas y debilidades de cada marca es muy sencillo. La figura 11.2 contiene las diferencias que hay entre un valor observado y esperado para cada celda. Hemos utilizado los datos de la tabla 11.1 para realizar el cálculo, por lo que no debes esperar que coincidan con los ejemplos anteriores. Por otra parte, nota que en este caso estamos usando las sumas totales por renglones y columnas; esas sumas se llaman frecuencias marginales. Anteriormente, las diferencias se presentaban en gráficas separadas, una por cada marca; actualmente eso parece excesivo, dada la enorme cantidad de información que tiene que revisar diariamente un analista y el escaso tiempo del que dispone para ello. Considero que una simple figura ordenada por los valores más importantes y con base a la marca del cliente es más que suficiente. Suponiendo que Pantene fuera el cliente, es notorio que Deja el cabello sedoso, Es para cabello reseco, y Tiene fragancia agradable son atributos importantes para la marca. Por el contrario, Quita la caspa, Es para toda la familia, y Hace espuma adecuada son atributos poco importantes para Pantene. Algunos analistas consideran los valores negativos como debilidades de una marca y los positivos como fortalezas; en ninguno de los dos casos es adecuada esta forma de pensar, los atributos deben estar alineados a la estrategia de comunicación. Es obvio que Pantene no quiere ser conocida como una marca que Quita la caspa ni tampoco Para toda la familia; por lo tanto, es inapropiado pensar que son debilidades de la marca. En cambio, si tiene la mira puesta en el atributo Hace espuma adecuada, debería de reforzar ese atributo. La misma lógica aplica para cualquier marca. El desfase entre estrategia y producto o servicio a veces no parece importante, pero tiene un impacto profundo. Un buen amigo mío, quien trabaja en una empresa cuyo principal producto es champú, lo explica así: un hombre le pregunta a una sexoservidora: ¿Cuánto quieres por tus servicios? La mujer contesta: $500 pesos por hacer el amor en una cama, $200 por hacerlo en petate²⁸ y $100 por hacerlo en el suelo. A lo cual el hombre contesta, en un tono decidido: Bien, quiero $500 pesos. Entonces, la mujer, sin ocultar su emoción, le dice: ¡Anda pillín!, te gusta hacerlo en la cama. No, lo que deseo es hacerlo 5 veces en el suelo, revira el hombre. En otras palabras, una marca puede tener puntuaciones muy altas en atributos que a los consumidores poco les importa y, consecuentemente, no inciden en la decisión de compra que toman.

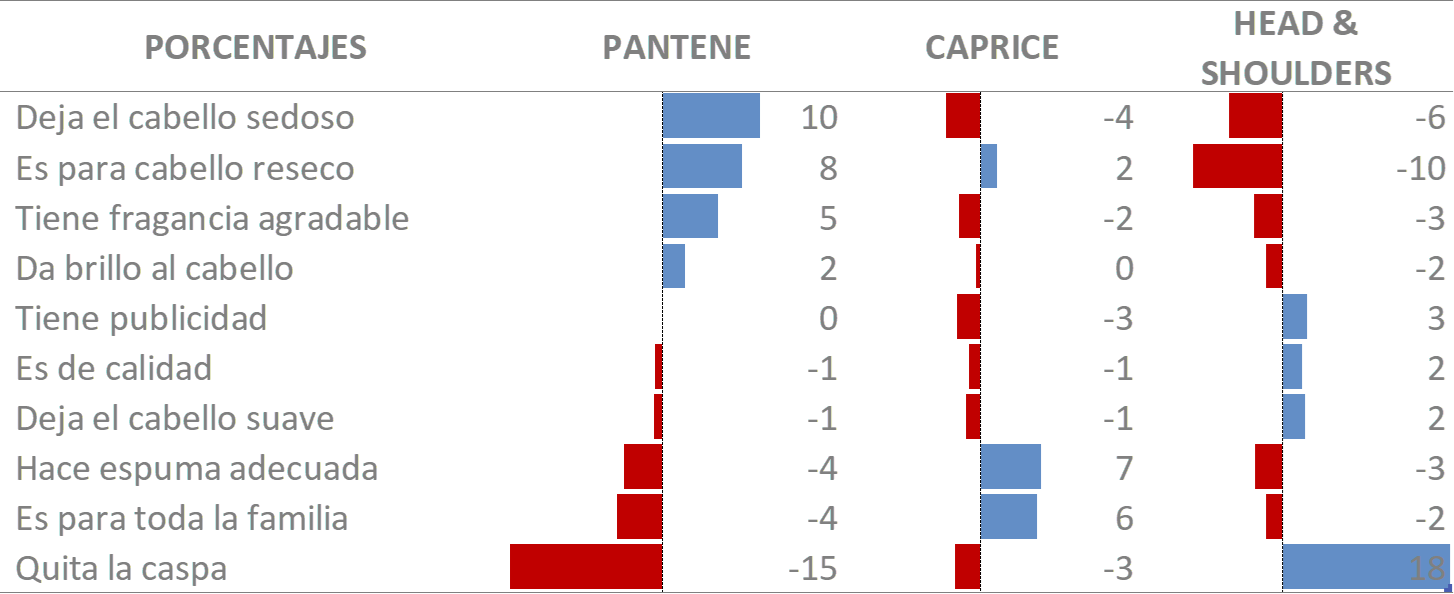
Figura 11.2: Perfil de marca (diferencias)

Todavía queda una cosa por resolver: cómo clasifica la Chi Cuadrado; para ello debemos analizar la ecuación (11.1). El Chi Cuadrado es simplemente la suma de todas esas diferencias al cuadrado; elevarlas al cuadrado es lo que hace posible la magia de sumarlas sin que se anulen y que su suma sea cero. Por otro lado, nota que se trata del acumulado de la cantidad de veces que cabe el esperado en la diferencia de cada celda. Exacto, como una varianza (véase sección 6), sólo que, en lugar de dividir por casos, lo hacemos por los valores esperados. Por ejemplo, Pantene tiene un valor $x^2$ en Deja el cabello sedoso de $1.55$: su diferencia entre el observado y el esperado es $10$ (véase figura 11.2), su esperado es $64$: $725\times 122=88450$; $\frac{88450}{1373}=64$, por lo cual su valor $x^2$ es igual a $\frac{(10)^2}{64}= 1.55$. Para dar nuestro veredicto debemos verificar si este valor, sumado a los de las otras celdas (marcas), está fuera de lo normal. Toda la estadística parte de un simple principio, un resultado es significativo si es diferente de los datos obtenidos al azar. La Chi Cuadrado no es un tipo de distribución distinta a la campana de Gauss o distribución normal, más bien, se deriva de ella²⁹ y, básicamente, tiene la misma función: sirve para contrastar si un resultado está dentro de los parámetros normales de desviación. Si la suma de ese chi cuadrado es mayor a lo esperado, el sombrero del Chi Cuadrado dice rechazado; si no es mayor dice aceptado. Suena extraño, pero así es, se acepta algo cuando no hay diferencias y se rechaza si las hay. Es más que obvio que las marcas y los atributos están asociados de forma diferenciada: Pantene se asocia a cabello sedoso, Head & Shoulders a Quita la caspa, y Caprice a Es para toda la familia; nuestro sombrero diría rechazado. El procedimiento para verificar si hay o no diferencias significativas (aceptación o rechazo) raramente se hace manualmente, por lo cual no enseñamos cómo se hace; todos los programas estadísticos dan por default la significancia estadística. Lo importante es que tomes consciencia de que estás midiendo qué tanto se alejan los resultados de los esperados al azar. Azar significa que todo se reparta igual; como cuando empiezas un nuevo juego de Monopoly.

\[\begin{equation} x^2=\sum_{i=1}^{n}\frac{(o_{i}-e_{i})^2}{e_{i}} \tag{11.1} \end{equation}\]

Tengo una frase nemotécnica que nos recuerda el procedimiento para obtener los valores esperados y explica la ecuación de la Chi Cuadrado. Dice así: El Caballo Renco Entre todas las Caballerizas es el más Esperado, o su acrónimo CRECE. El primer paso del Caballo (Caballo por Chi) es multiplicar el renglón por la columna, por eso está Renco. La multiplicación obedece a la interacción que hay entre la marca y el atributo, o lo que sea que representen los renglones y columnas de la tabla; el resultado es la variación conjunta. La división (Entre) tiene la encomienda de determinar a qué proporción equivale la variación conjunta de la variación total; o sea, la suma de todas las celdas (Caballerizas por celdas). ¿Por qué todas las celdas? En la Chi Cuadrado cada celda o interacción representa una muestra. Por esa razón se suman los errores de todas las celdas para determinar si hay o no diferencias significativas. Sin embargo, confunde la forma en que se obtienen esos errores, ¿por qué dividir entre el esperado, si el esperado es un promedio? En eso quedamos, ¿o no? Es un caso curioso, que tiene una explicación escurridiza. Una celda, cualquier celda, cuenta con un solo valor, ese valor es todo, su media y su variación. ¿Cuál es el promedio de edad de una quinceañera?, quince años. ¿Y cuál es su variación de edad?, cero, no la hay porque no hay más valores. Da la casualidad de que cero es también la media, es el instrumento de comparación para registrar la variación. El valor esperado representa la media y la variación; cumple con ambas funciones. Todos estos elementos están contenidos en la ecuación (11.1). Tiene sentido ¡¿No crees?!

Usar porcentajes en las tablas de contingencia, cuando se efectúa un análisis de $X^2$, no es lo más ortodoxo; lo recomendable es usar frecuencias absolutas. Sin embargo, el uso de porcentajes en investigación de mercados es muy útil porque permite dimensionar los resultados; particularmente, si se normalizan.↩
Tapete tejido de palma.↩
Imagina que tienes una tabla de dos marcas y dos atributos: Caprice y Head & Shoulders cruzados con Es para toda la familia y Quita la caspa. A este tipo de tabla se le conoce como tabla de $2\times2$ porque cuenta con dos columnas y dos renglones. La gran mayoría de los investigadores sabe que para declarar diferencias estadísticamente significativas, en una tabla de $2\times2$, el número mágico chi cuadrado debe ser mayor a $3.84$. Incluso los anglosajones utilizan una nemotecnia para acordarse de este número: The three (3) little pigs (.) ate (8) like the four (4) horsemen. Este número tiene mucho sentido cuando uno se da cuenta de que la Chi Cuadrado proviene de una distribución normal. Si recuerdas el $95\%$ de los resultados se encuentran dentro de $2$ errores estándar, para ser exactos dentro de $1.96$. Si elevamos al cuadrado esa cantidad, adivina qué, se convierte en $3.84$: $1.96^2=3.84$. ¿Por qué si hay dos atributos o dos marcas se cuentan los errores de una sola población? Por los famosos grados de libertad. Volvamos a nuestro ejemplo imaginario, si Caprice tuviera $10$ casos y el total de casos fuera $15$, ¿cuántos casos debería tener Head & Shoulders?, No puede tener otro número distinto a $5$. Ha perdido su poder de independencia, ya no puede variar, no tiene libertad para hacerlo. Lo mismo sucedería si fuera esta marca la conocida y Caprice la desconocida. En una tabla de $2\times2$ existe sólo un grado de libertad, porque conociendo el valor de una celda las otras se determinan automáticamente. En palabras simples, la Chi Cuadrado es la distribución que resulta de elevar al cuadrado los errores de la distribución normal. Elevar al cuadrado estos valores le da esa forma tan característica parecida a la serpiente boa de El Principito en su lado derecho, sin cola, debido a que se trata de puros valores positivos. No hace falta decir que para comparar un resultado con esta distribución no es necesario que tenga una distribución normal. La comparación se hace de la suma total de todas las celdas porque cada fila y columna de la tabla cuentan como si fueran muestras independientes. Claro, restando los grados de libertad que se determinan como: $gl=(r-1)(k-1)$, $r$ es el número de renglones y $k$ el número de columnas.↩