Capítulo 15 De tin, marín, de do pingüé…

Si la gente hiciera sus elecciones o compras usando el clásico De tin, marín, de do pingüe… nadie dedicado a la mercadotecnia tendría chamba; investigadores de mercado, publicistas, mercadólogos, vendedores, etc. serían una especie extinta. Si algo sabemos de la forma en que los consumidores hacen sus elecciones o compras es que no lo hacen al azar; consideran una serie de aspectos que van desde concretos hasta sutiles. Gracias a la Gestalt, también sabemos que todos los componentes de un producto o servicio así como el ambiente que le rodea interactúan en mayor o menor grado para influir en cualquier decisión de compra. Entender cómo se hacen las decisiones de compra es muy importante porque de ello depende gran parte del éxito de un producto o servicio. El conjoint analysis es una buena técnica para estimar la probabilidad de este éxito porque se aproxima a la forma en que el consumidor decide acerca de las opciones de compra que tiene. Cómo dice la Gestalt, éste evalúa de forma integral, viendo las cosas en su totalidad y no por sus partes. Los anglosajones norteamericanos dicen que conjoint significa considered jointly, es decir, considerado junto o en conjunto. Así pues, el conjoint analysis se utiliza para evaluar productos o servicios tomando en cuenta todas las características o atributos de forma conjunta, no separada. Cuál de las siguientes preguntas te parece más sensata para evaluar la disposición de compra de una laptop:

¿Qué tan dispuesto(a) está a comprar una laptop a un precio de $30 mil pesos?
¿Qué tan dispuesto(a) está a comprar una laptop con un terabyte de disco duro?
¿Qué tan dispuesto(a) está a comprar una laptop con 32 gb de memoria ram?
¿Qué tan dispuesto(a) está a comprar una laptop con pantalla 4k?
¿Qué tan dispuesto(a) está a comprar una laptop de la marca Apple?
¿Qué tan dispuesto(a) está a comprar una laptop a un precio de 30 mil pesos, con un terabyte de disco duro, 32 gb de memoria ram, pantalla 4k, de la marca Apple?

Sin duda la pregunta 6 es la más sensata. Puede que una característica de nuestra hipotética computadora pese más que las otras en la decisión de compra del consumidor, pero la decisión final no dependerá de esa sola característica, sino del conjunto de todas ellas. A través del conjoint analysis se puede evaluar qué tanto pesa cada característica sin necesidad de hacerlo para cada una de ellas por separado. Determinar la demanda (preferencia) del producto o servicio completo y, lo que es más importante, gracias a la sofisticación del método, recrear todas sus combinaciones o configuraciones y estimar su participación de mercado (preferencia); sin importar si una configuración específica fue o no evaluada directamente por el consumidor. ¿Suena complejo?, sí, lo es; no te voy a mentir. Es uno de esos métodos que todavía se apoyan en software comercial para implementarlo, pero se debe, más que a su complejidad, a la falta de comprensión de la técnica, los procedimientos metodológicos y estadísticos involucrados y lo laborioso que puede resultar preparar el informe final, el cual incluye un simulador. La empresa que más ha trabajado sobre este tema en particular es Sawtooth Software; además de vender software para llevar a cabo estudios de conjoint, es, posiblemente, la que más y mejor material bibliográfico, vídeos, y tutoriales puede proporcionar para aprender conjoint. Por otra parte, una de las lecturas más accesibles para el público con conocimiento básico estadístico que desea aprender esta técnica es Rao (2014); altamente recomendable.

El conjoint analysis es muy extenso y tiene múltiples variantes (tipos de conjoint), sin contar los métodos estadísticos utilizados actualmente; eso nos impide enseñarte hacer conjoint analysis en un espacio tan pequeño como el de este capítulo. Sin embargo, podemos encaminarte y orientarte para que encares el problema de manera firme y con confianza. Para empezar, déjame decirte que es perfectamente asimilable en el curso de un taller de 6 a 8 horas³² y que, pese a su sofisticación, es posible elaborarlo con Excel, lo cual no recomendamos, sino sólo como herramienta de aprendizaje. Si un investigador de mercados quiere hacer un estudio utilizando la técnica de conjoint, hay tres cosas absolutamente indispensables que debe entender bien. La primera, obvio, es que necesita conocer qué es conjoint analysis; lo cual resulta fácil, ya que hay toneladas de información en Internet, amén de una extensa bibliografía sobre él. Este vídeo puede ayudarte a comprenderlo. No obstante, por aquello de no te entumas, aquí tienes nuestra interpretación de conjoint. Casi todos los productos o servicios son clasificados sin ningún problema por el consumidor. Éste no confunde la categoría de donas con la de bísquets o bolillos, por ejemplo. Se infiere que el consumidor también detecta las diferencias que hay entre marcas, productos y/o servicios, las cuales pueden deberse a distintos atributos, beneficios, precio, o cualquier otra característica. ¿Quién confunde una dona de chocolate con una de fresa, o glaseada, o con chispas de chocolate? Nadie, ¡¿verdad?! Los fans de la serie Los Simpson saben que a Homero le gustan más las donas glaseadas de fresa con chispas que las de chocolate, cajeta, o cualquier otra. Sin embargo, ¿sabrán qué es más importante para Homero, el sabor a fresa, las chispas, o el glaseado? No lo creo. Este tipo de preguntas son las que se pueden responder con la técnica de conjoint analysis. Y fabricar donas de acuerdo con los gustos de Homero; quizá hasta ofrecer un nuevo tipo de dona mejorada.

Hace algunas décadas el procedimiento para conocer la preferencia se hacía por partes. Por ejemplo, si se trataba de evaluar un vestido, se pedía al consumidor que calificara o dijera su preferencia por la composición de la tela, luego el color, en seguida el diseño, posteriormente el precio, etc. (toma en cuenta que se evaluaban varias opciones de telas, colores, diseños, y así sucesivamente), todo por separado. Al final, se manufacturaba el producto de acuerdo con los elementos mejor evaluados. El resultado de este tipo de investigación podría ser insospechado; no es difícil imaginarse que se corría el riesgo de crear un Frankenstein. A esa técnica se le llamaba de composición. Actualmente, el procedimiento es más natural y efectivo. Se hacen los productos dummy (prototipos) o tarjetas simulando, esto es describiendo, productos o servicios completos, y se pide al consumidor que los evalúe, uno por uno o en subgrupos, ya sea calificando su preferencia o seleccionando el que más le agrada. A través de modelos estadísticos se deriva la importancia de las características que influyen en las preferencias del consumidor; esa técnica se llama de descomposición. La teoría que está detrás de los modelos de conjoint se basa en la suposición de que los consumidores ponderan los distintos aspectos que ofrece un producto o servicio, antes de decidir su compra. Indudablemente, es un enfoque muy racionalista. En la práctica, la gente adquiere productos y servicios con base a algo más que sus características. Las emociones generadas a través de la publicidad o comunicación juegan un papel preponderante en la conducta del consumidor. No obstante, el enfoque de conjoint analysis es la forma más técnica y adecuada de tomar decisiones sobre la configuración y fabricación de productos o servicios ofertados al consumidor; además de su uso extendido para determinar el precio más adecuado para ellos. Otra de las ventajas del conjoint es su habilidad para responder preguntas del tipo ¿Qué tal si…? Es decir, creando productos o servicios virtuales es posible obtener respuesta a preguntas sobre la preferencia que tendrían en el mercado, independientemente de que hayan o no sido evaluados directamente por el consumidor. A eso se le denomina simulación, y nos da una buena estimación de la participación que podrían obtener en el mercado. Es como checar a través de Internet el valor de un objeto que se quiere empeñar sin tener que llevarlo a valuar directamente a la casa de empeño. Una última observación, el conjoint analisys es tutti frutti; esto quiere decir que hay de varios tipos; sin embargo, dos son los más básicos y esenciales: conjoint tradicional y CBC (Choice Based Conjoint). El conjoint tradicional es el primer modelo que existió, con él, se sientan las bases de su desarrollo posterior; por eso mismo es importante conocerlo. El segundo, el CBC es por mucho el más utilizado; éste representa el paradigma de los modelos discretos o de selección, que está más apegado a la forma en que los consumidores hacen sus elecciones en contraste con el conjoint tradicional, el cual utiliza escalas de medición para estimar la preferencia de los consumidores. Más adelante hablaremos sobre ambos tipos de conjoint. Espero que con esta breve explicación hayamos cubierto el requisito de entender lo que es conjoint analysis.

Los dos requisitos restantes son más complicados, pero mucho más interesantes. El segundo exige conocer qué son los diseños experimentales y estímulos o tratamientos o perfiles. Todos estos términos significan lo mismo, aunque se utilizan en diferentes contextos. Estímulos se utiliza más en psicología; tratamientos en el cultivo de elotes (agronomía); y perfiles en investigación de mercados, por lo que de aquí en adelante nos referiremos a perfiles casi exclusivamente. La sección 15.1 trata este tema. El tercer requisito es cómo analizar los datos, esto se puede hacer a través de regresión lineal múltiple, regresión logística o multinomial, mejor conocida como modelos logit, y modelos jerárquicos bayesianos o hierarchical bayes models, entre otros menos famosos.

15.1 Esa torta no está en el menú

¿Sabías que John Napier pasó 20 años de su vida desarrollando las tablas de logaritmos? Ese esfuerzo significó un inmenso ahorro de tiempo para miles de científicos; quienes se la pasaban gran parte de su vida haciendo cálculos. ¡Dios bendiga a San Juan Napier!, habrán dicho. Tal vez los que hacemos investigación de mercados hubiésemos tenido que cambiarle el nombre a Addelman (1962) para llamarlo San Addelman, debido a los diseños experimentales que nos obsequió; útiles para nuestras investigaciones con conjoint analysis o análisis conjunto. Pero no pudo ser, porque a diferencia de lo que pasó en la época de Napier, en la cual las reglas de cálculo y luego las calculadoras tardaron cientos de años en llegar, en nuestros tiempos, en cuestión de un par de décadas, ya teníamos varios programas para generar diseños experimentales. El diseño no es para cualquiera, al menos para los que no saben cómo funcionan las cosas. Los logaritmos que inventó Napier fueron una idea extremadamente ingeniosa de alguien que entendía bien lo que significaban para la comunidad científica. Los diseños experimentales son otra de esas cosas útiles para el quehacer científico. Sin embargo, para utilizarlos, pasa igual que con las tablas de logaritmos, necesitamos conocer cómo funcionan. Como sugiere el nombre, un diseño es la creación de un objeto con propiedades útiles y/o estéticas. Nota que un objeto, en el caso de la mercadotecnia, no es exclusivamente un producto también puede representar un servicio. De eso trata esta sección, de aprender cómo se generan los diseños experimentales para estudios de conjoint analysis.

Bueno, empecemos desde el génesis. Un perfil es una descripción o modelo ficticio de un producto o servicio que se diseña para evaluar su preferencia y determinar qué atributos influyen más en ella. En la imagen 15.1 tenemos 3 perfiles: el perfil de un Mini Cooper con motor de 2.0 lts., transmisión estándar, que usa combustible de gasolina; y los perfiles de un Beetle y Honda. Cada uno de ellos con sus propias características. Eso estuvo muy fácil, ¡¿verdad?! De lo anterior se deduce que para hacer un conjoint es necesario, primeramente —como decía mi hijo pequeño— decidir qué características o atributos del producto o servicio se van a evaluar. En los perfiles anteriores se tomó la decisión de incluir 4 atributos o factores, como también se les denomina en la terminología del conjoint analysis:

Marca del vehículo
Tipo de motor
Tipo de transmisión
Alimentación de combustible.

Figura 15.1: Perfiles de autos

El sentido común nos dice que para evaluar qué tanto impacta el tipo de transmisión (estándar o automática) a las ventas del Mini, el entrevistado tiene que calificar o evaluar una versión de esta marca con transmisión estándar y otra versión con transmisión automática. Si no, ¿cómo se puede determinar cuánta gente prefiere un Mini con uno u otro tipo de transmisión?, lógico, ¡¿no es así?! El problema se torna aún más interesante cuando también deseamos saber qué tanto cambia la preferencia por el Mini con base al tipo de combustible que usa. Vamos a decir que queremos saber en cuál situación el consumidor lo escoge más: cuándo es alimentado con gasolina, diésel, o mediante batería eléctrica y gasolina, es decir, híbrido. Como lo imaginas, el consumidor tiene que evaluar al Mini con estas otras tres variantes. La misma situación se repite para conocer la preferencia por el tipo de motor. La cosa no se detiene allí, el mismo razonamiento aplica para Beetle y Honda.

Toma en cuenta que no podemos evaluar parcialmente al Mini; al menos en nuestro tipo de conjoint³³. En otras palabras, preguntarle al entrevistado su preferencia por un Mini Cooper con transmisión estándar y luego pedir que nos diga qué tanto lo prefiere de gasolina. El perfil se debe evaluar completo, o sea, el entrevistado debe valorar al Mini Cooper con motor de 2.0 litros, transmisión estándar, y alimentado con gasolina. En resumen, si quieres saber cómo se afecta la preferencia por cada automóvil, es menester combinar todas las variantes: 3 marcas, 3 tipos de motor, 2 tipos de transmisión y 3 tipos de alimentación de combustible. Nota que estamos utilizando la marca del auto como otra variante más. De esta manera el auto que el consumidor (encuestado) selecciona o prefiere depende de la marca, el tipo de motor, transmisión y combustible. Siendo este el caso, ¿cuántos perfiles completos hay cuando hacemos todas las combinaciones posibles? El cálculo es simple: $3\times3\times2\times3=54$; cincuenta y cuatro combinaciones en total. En concreto, hay $54$ diferentes tipos de automóviles de entre los cuales el consumidor puede escoger.

¿Qué crees que pasaría si deseamos evaluar más atributos? Tal vez, determinar cómo cambia la preferencia si el auto es convertible y totalmente eléctrico; en ese caso, los atributos o factores cambian de 4 a 6 y las variantes o niveles son ahora 4 más (2 más por ser o no ser convertible y otras 2 si es o no eléctrico). ¿Te das cuenta de que entre más atributos y variantes hay en cada uno de ellos el número de perfiles va in crescendo? Efectivamente, ahora tenemos $3\times3\times2\times3\times2\times2=216$; doscientos dieciséis perfiles completos o tipos de automóviles. Mi primera pregunta es, ¿qué empresa armadora de autos se puede dar el lujo de fabricar $216$ diferentes tipos de autos? None, isn’t it? Bueno, esto no es una limitante nada más para las armadoras, también lo es para los consumidores que entrevistamos, ¿qué consumidor está lo bastante chiflado como para aguantar una entrevista en la cual se le pide que diga su preferencia por $216$ diferentes tipos de autos? ¿Lo ves?, el quid de la cuestión, y por la cual tenemos que usar una computadora para diseñar los perfiles de nuestro estudio, es que si el investigador lo hiciera a mano se pasaría gran parte de su vida combinando las variantes de cada atributo para ir armando perfiles. Y así como sucedía con las estampitas con las que jugábamos de niños, tendría que revisarlos uno a uno para hacer un reconocimiento sobre cuáles ya tiene y cuáles no: “Sí, sí, sí, a ver espérame…no, ese no lo tengo”. La otra, naturalmente, es que ningún consumidor nos daría una entrevista si le decimos que necesitamos que nos diga su preferencia sobre $216$ autos. Pese a ello, en la práctica se hacen estudios que llegan a cientos o miles de combinaciones, ¿cómo es posible ésto?

Para conservar una relación cordial con el consumidor (entrevistado), el investigador decidió que lo más prudente era presentarle sólo una parte del total de los perfiles y así nació —es un decir, pues estos diseños existen desde hace mucho— lo que en conjoint se llama diseño factorial fraccionado (DFF) o incompleto. Claro está que, si éste se llama incompleto, el que contiene todos los perfiles se llama completo; elemental mi estimado lector. El problema con los DFF’s es que, como puedes suponer, algunas o más bien muchas combinaciones (tipos de auto, en nuestro ejemplo) van a estar ausentes. Paréntesis. Esto me recuerda a un jefe que tuve y su discusión con un tortero. Mi jefe pedía al tortero que le hiciera una torta con jamón, pollo, huevo, chorizo, queso de puerco, pierna, salchicha, etcétera. El tortero nomás no quería, argumentando que no tenía de ese tipo de tortas, únicamente contaba con las que aparecían en el menú. No obstante, se podían divisar todos los ingredientes para preparar esa torta tan especial. Llegó a tal grado la discusión que mi jefe, queriendo hacer valer su estatus, le gritaba totalmente histérico al tortero: “Qué no sabes con quien estás hablando. Ni más ni menos que con el dueño de una de las agencias de investigación de mercados más grandes de México”, jajajaja. ¡Pobre tortero!, quizá hasta el día de hoy se está preguntando qué es eso de investigación de mercados. ¡Qué tiempos aquellos! Claro que, si hubiera conocido de diseños, habría hecho la torta que mi jefe le pedía. La moraleja de la historia es que lo importante no es el menú, sino los ingredientes. Asegúrate de incluirlos en el estudio para fabricar la torta tan deseada.

¿En qué íbamos?, ¡ah, sí!, el truco es que las combinaciones resultantes del DFF deben hacerse de tal forma que cada nivel (ya sabes, variante) de un atributo se aparee por lo menos el mismo número de veces con cada uno de los niveles de cualquier otro atributo. Con eso, aseguramos que un nivel de un atributo no aparezca más veces con un nivel en particular. A eso se le denomina diseño ortogonal (independiente) pues impide que un nivel se relacione con otro de forma ventajosa. Por ejemplo, ¿qué pasa si a ti te gusta mucho el Beetle y este auto aparece más de la cuenta con transmisión automática? Aunque a ti te gusten más los autos estándar, siempre que elijas el Beetle estarás escogiendo también la transmisión automática. Es de puro sentido común que estas dos variantes no son independientes: si escoges a uno escoges al otro. Es como el compromiso matrimonial, pides la mano de la novia, pero sabes que te la vas a llevar completa, ¿me captas?

La principal virtud de estos diseños es que con ellos se pueden estimar los efectos principales o generales. Aunque San Addelman dice que no es una condición necesaria, pues basta con que las variantes de un atributo con otro se encuentren apareados en la misma proporción —recuerda que anteriormente dijimos mismo número de veces, no proporción; no es lo mismo 4 manzanas que un cuarto de manzana—. Los efectos principales permiten determinar el valor que el consumidor le asigna a cada nivel y, por supuesto, la importancia de cada atributo o factor. Dicho de otra forma, ¿qué importa más, la marca, el tamaño de motor, el tipo de transmisión, o el combustible? Y dentro de cada factor, qué nivel vale más para el consumidor. Por ejemplo, ¿cuál es la marca más rentable, Mini, Beetle, u Honda? La principal desventaja de un DFF, derivado de la ausencia de otros perfiles, es la imposibilidad de saber qué tanto impacta a la preferencia una combinación específica de esas variantes. Por ejemplo, si hay una asociación o interacción que tendría un éxito inusitado, digamos la marca con el tipo de transmisión, no se sabe; lo único que se puede determinar es cuál marca y tipo de transmisión son los más preferidos. Parece que es lo mismo, ¿verdad?, pero no es así. Hay combinaciones mortales. Sabes que Leo Messi es un gran jugador, pero no es lo mismo Leo Messi con el Barcelona que Leo Messi con la Selección Argentina, en un equipo es mortífero, en el otro es bueno, pero no letal. En general, la mayoría de los estudios de conjoint se hacen para estimar los efectos principales; por dicha razón es tan llevado y traído el famoso diseño ortogonal de factorial fraccionado. Espero que no te hayas perdido hasta este momento, como su nombre lo indica, los diseños se llaman fraccionados porque sólo son una fracción del total de perfiles posibles; en nuestro caso tenemos $54$ perfiles y podemos reducirlo hasta la mitad, es decir, $\frac{1}{2}$ fracción que equivale a $27$ perfiles. Hacer diseños factoriales fraccionados es simple cuando el número de niveles de cada atributo o factor es igual; esos diseños se conocen como diseños factoriales simétricos, la literatura está llena de ellos. La cosa se complica cuando el número de niveles es distinto para cualesquiera de los atributos, en este caso se debe hacer un diseño factorial asimétrico. Si a todo eso le agregas que debe ser fraccionado, a nadie le debe de extrañar por qué a muchos investigadores de mercado les cuesta trabajo concebir y llevar a cabo un estudio de conjoint.

Ahora, perdóname por hacerte la vida un poco más complicada, tradicionalmente se presentaba al entrevistado un perfil de un diseño fraccionado y se le pedía que dijera con qué probabilidad compraría ese producto o servicio; el entrevistado debía dar su respuesta en una escala de 0 a 10, donde 0 significaba que definitivamente no lo compraría y 10 que definitivamente sí lo compraría, o en cualquier otro tipo de escala. Tenía que hacer lo mismo con cada uno de los perfiles restantes y los resultados de esas evaluaciones se analizaban con el método de regresión lineal múltiple; ese fue el primer conjoint y por eso se le llama tradicional o de calificación, pero pronto apareció el CBC (Choice Based Conjoint). La diferencia más importante del conjoint tradicional con el CBC es que éste no utiliza calificaciones para evaluar, sino que se basa en selecciones discretas, por eso también se le llama conjoint de modelos discretos. Al encuestado se le pide que seleccione un perfil de un conjunto de ellos. Toma nota que esta forma de preguntar también es un cambio drástico con el conjoint tradicional, no se le pide al entrevistado que evalúe un perfil a la vez, lo que se hace es combinar varios perfiles y presentarlos al mismo tiempo para que el consumidor diga cuál de todos ellos prefiere o compraría. ¡Atención!, porque este es el punto fino de la discusión, en el cbc no cambia nada, se sigue diseñando igual que en el conjoint tradicional, pero ahora hay que combinar los perfiles. Sí, los mismos perfiles que siempre se han utilizado, se evalúan en paquete, no uno por uno; como en la figura 15.1 en la cual el consumidor escogió la opción de enmedio, el Beetle. Eso, en la práctica, es lo que hacen los programas comerciales: diseñar y combinar los perfiles; además de arrojar estadísticas de la eficiencia del diseño resultante. Naturalmente, hay muchas formas de escoger y combinar los perfiles, por lo que hay que buscar las que cumplan con los criterios que comentamos con anterioridad: frecuencia y proporcionalidad.

Crear este tipo de diseños es fácil con el software comercial, sólo es cuestión de indicar los ingredientes que quieres para que te preparen tu torta. SPSS, Sawtooth, SAS, entre otros, tienen muchos pasos por default que te facilitan la vida. En el caso de lenguajes como R, se tiene que especificar el diseño. De ninguna manera aconsejamos hacer el procedimiento en Excel, pero creemos que nada mejor que éste para ver lo que está sucediendo dentro de estos programas y paquetes estadísticos. ¿Te animas a hacer el ejercicio con los perfiles de autos que tenemos? Si sí, continúa, si no, pasa a la sección 15.2. De acuerdo, el concepto es simple, se llama producto cartesiano a la operación de dos conjuntos que resulta en otro conjunto, cuyos elementos son todos los pares ordenados que pueden formarse de manera que el primer elemento del par ordenado pertenezca al primer conjunto y el segundo elemento pertenezca al segundo conjunto. Se supone que uno debe comprender esta definición, pero no siempre es así; es mejor demostrar qué explicar. Observa la figura 15.2, el conjunto de cachorros de la primera columna (conjunto 1) se mezcla con cada uno de los cachorros de la segunda columna (conjunto 2) dando lugar a un tercer conjunto de parejas de cachorros (pares ordenados). ¿Qué pasa cuando se tienen más de dos conjuntos, como en el conjoint analysis en el cual cada atributo es un conjunto de niveles o características? El truco para crear las tarjetas cuando se tienen más de dos conjuntos es combinar el primer producto cartesiano con el siguiente conjunto. Es decir, el primer conjunto total con el tercer conjunto; luego, el segundo producto cartesiano con el cuarto y así sucesivamente. En el ejemplo de automóviles debemos combinar cada marca con cada tipo de motor. El conjunto resultante se combina nuevamente con el conjunto del tipo de transmisión y se continúa así hasta que ya no haya más conjuntos por combinar.

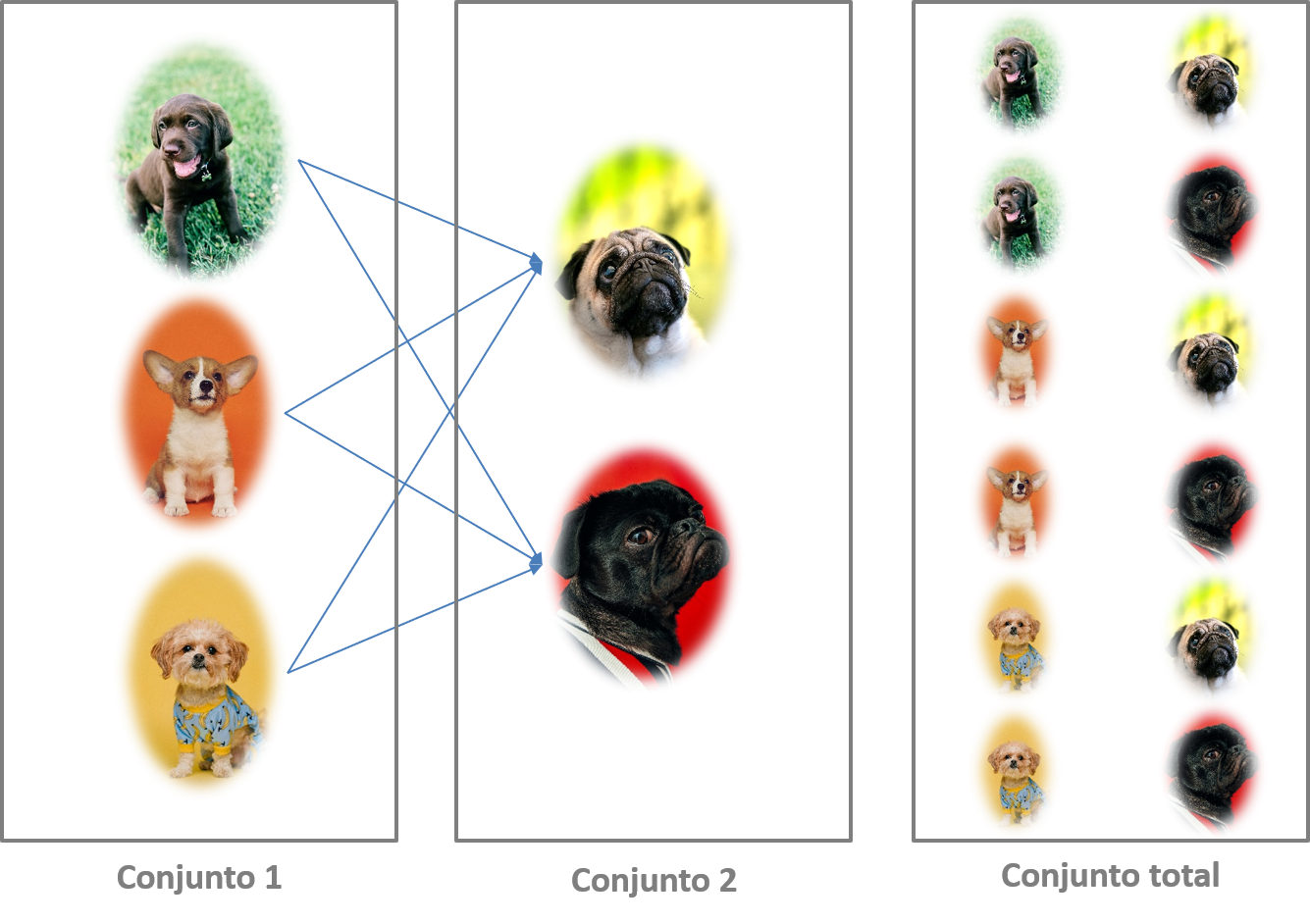
Figura 15.2: Producto cartesiano

Para hacer en Excel estas operaciones necesitas incluir unas cuantas funciones. Observa la imagen 15.3, en la columna A hemos escrito todas las marcas, una en cada fila y en las columnas los niveles de cada atributo (v.gr. los tres primeros tipos de motor: 2.4 lts., 2.0 lts., y 1.8 lts.); dejando una columna al final de cada uno de ellos (v.gr. columna E, perfil_i1). En esas columnas se insertarán los resultados de los productos cartesianos. Entonces, el primer paso es crear esa matriz o tabla con los nombres de los niveles de cada uno de los factores. Toma en cuenta que el orden en el que entran es como al final van a quedar los perfiles. En otras palabras, primero aparecerá la marca del automóvil, luego el tipo de motor, seguido del tipo de transmisión y finalmente el combustible que usa. Ese acomodo se hace a discreción; supongo que lo adecuado es poner los atributos más importantes al principio, como la marca, por ejemplo. El segundo paso es insertar las funciones. La primera función $A2&B$1 encadena las etiquetas de la columna A con las de la fila 1; por lo que se fijan, para que no cambien estas referencias. Observa que las funciones de la columna F y de la columna I son casos idénticos, sólo que esta vez están encadenando el resultado de la columna E (perfil i1) y columna H (perfil i2), respectivamente. O sea, el resultado de los productos cartesianos anteriores. No olvides insertar una tabla en tus datos para que las fórmulas se extiendan automáticamente sin que tengas que arrastrarlas manualmente. Excel sólo rellena automáticamente hacia abajo, no lo hace lateralmente. Por consiguiente, debes copiar la primera fórmula de cada nuevo atributo a las columnas de sus niveles restantes (no arrastres las fórmulas, así no funciona el llenado automático, tienes que copiarlas, forzosamente).

Figura 15.3: Funciones de Excel para generar un producto cartesiano

El tercer paso es convertir la matriz de celdas que contienen el resultado de esos encadenamientos en una lista, dentro de sus correspondientes columnas E, H y L (perfil_i1, perfil_i2 y perfil completo, respectivamente). Para ello utilizamos una segunda función, un poquito más complicada, pero divertida. DESREF se usa para copiar el contenido de una celda origen a otra celda de destino; sus argumentos son tres: la celda de dónde se debe partir, cuántas filas y cuántas columnas hay que avanzar para llegar a la celda que se quiere copiar (celda origen). La función que se inserta en la celda E2 pide desplazarse desde la celda $B$2 (Nota que es una referencia fija; siempre nos vamos a desplazar a partir de esa celda cuando se trate del mismo atributo). Para precisar cuántas filas y columnas nos debemos desplazar del punto de referencia es necesario utilizar otro par de funciones más: ENTERO y RESIDUO. La función ENTERO precisa cuántas filas hay que desplazarse y la función RESIDUO cuántas columnas. Observa que dentro del par de funciones anteriores hay otra función que está ajustando constantemente el número de filas y columnas que hay que moverse. Esta es FILA(), la cual señala el número de fila en la que se está; de tal forma que se puede utilizar el resultado de esa función como si fuera un número y restarlo, sumarlo, dividirlo, etc. En este caso en particular, se resta con la misma referencia de fila, pero fija FILA($B$2); es decir, la fila 2. Como es fija podríamos haber usado simplemente el número 2, pero no tendría mucha emoción esta pequeña explicación; digo yo. Como lo indica su nombre, la función ENTERO elimina todos los decimales y deja exclusivamente los enteros. En resumen, lo que estamos haciendo es dividir el resultado de la resta (FILA()-FILA($B$2)) entre 3, lo puedes ver como $(2-2)/3=0$; el siguiente valor de la celda de abajo E3 sería $(3-2)/3=0$; y el de la celda E4 que sigue abajo sería $(4-2)/3=0$, porque los decimales resultantes son removidos por la función ENTERO dejando sólo el cero. El truco de ese denominador es que cuando se llega a la cuenta de tres filas hacia abajo cambia el número de fila; ahora resulta que en la celda E5 hay que moverse una fila $(5-2)/3=1$. ¿¡Lo ves!?, la virtud que tiene ese denominador es cambiar el ENTERO cada tres filas (Por favor, haz el ejercicio para que lo puedas entender). De esa manera siempre nos estamos moviendo una fila hacia abajo cada vez que hemos recorrido 3 filas. Se usa como denominador el 3 porque ese es el número de niveles que se tiene en tipo de motor. En el caso de transmisión se usa el denominador 2; y se utiliza 3 nuevamente en el atributo combustible. RESIDUO devuelve los enteros que quedan después de una división. En el caso de la celda E2, el primer número que regresa es 0 (2-2 entre 3 da como residuo 0); el segundo es 1 (3-2 entre 3 tiene un residual de 1); el tercer número es 2 (4-2 entre 3 tiene residual de 2). Aquí también hay un cambio cada tres filas, pero éste es constante e igual; independientemente de los renglones que se avancen hacia abajo el resultado será 0, 1 y 2 y se reiniciará de nueva cuenta. Sé que puede parecer complicado, pero si lo haces vas a entenderlo perfectamente. El último paso es extender la tabla hasta que el número total de filas sea igual al total de combinaciones (i.e. $54$) más una fila debido a la fila de encabezados. La tabla debe rellenar en automático las celdas con las fórmulas. Ahora ya tienes un listado completo de perfiles en la columna L (véase figura 15.4). No pierdas de vista que hemos ocultado todas las demás filas para poder presentar exclusivamente los tres primeros y tres últimos perfiles.

Figura 15.4: Diseño de perfiles usando el producto cartesiano

Lo que sigue es seleccionar una fracción de esos perfiles porque es demasiada información como para que cualquier persona pueda manifestar su preferencia por cada uno de ellos. Haz una selección aleatoria simple³⁴ y verifica que los niveles se distribuyan uniformemente en todos los perfiles. Por ejemplo, si la marca Mini aparece 5 veces las otras dos marcas también deben estar presentes el mismo número de veces; a eso se le denomina estímulos balanceados. Haz varias muestras y compáralas; quizá usando tablas dinámicas de Excel. Checar la ortogonalidad o independencia es un poco más sofisticado pues se deben utilizar procedimientos estadísticos como Chi Cuadrado (sección 11). Este procedimiento es muy demandante como para hacerlo muestra por muestra en Excel o sin la ayuda de un programa especializado. No obstante, si no tienes acceso a uno, en la práctica funciona bien una muestra elegida con criterios de balance. Por otro lado, la mayoría de las veces no se puede llegar a un diseño perfecto, por lo cual se administran distintas versiones de perfiles a distintos entrevistados. Por ejemplo, a 50 personas se le muestran 27 perfiles; suponiendo que el diseño fue fraccionado por la mitad; a otras 50 personas 27 perfiles distintos. En la práctica significa tener dos cuestionarios por cada grupo de entrevistados. Los datos se mezclan y analizan como si se tratara de una sola muestra; eso es posible debido a la técnica de descomposición. Perdona que no expongamos la forma de hacer ese muestreo ni cómo verificar que sea un diseño balanceado para no hacer más cansada esta sección. Es suficiente con que conozcas los principios subyacentes a la creación y selección de los estímulos (perfiles). Si te parece ahora vamos a la práctica, a ver cómo se usan esos perfiles en el conjoint tradicional, también llamado, perfil completo.

15.2 De perfil completo

Una pregunta difícil para las mujeres ¿Qué vale más, un hombre con dinero, uno guapo, o uno divertido? En la oficina hicimos un conjoint analysis tradicional para saber qué opinaba el maravilloso sexo femenino. Pero antes de explicarte cómo le hicimos y para que no te hagas bolas, necesitamos presentarte algunos conceptos básicos del conjoint, éstos son:

Factores o atributos. Son las características del producto o servicio, estos por supuesto varían en cada producto. En el ejemplo anterior la marca del automóvil es un atributo.
Niveles. Son el número de opciones en cada atributo. Repitiendo el ejemplo anterior, la marca del automóvil tiene tres niveles u opciones: Mini, Beetle y Honda.
Estímulos o perfiles. Para evaluar la utilidad (valor) que tiene cada nivel, es necesario presentar a los sujetos estímulos que representen diferentes productos para que los califiquen, ordenen o seleccionen de acuerdo con su grado de preferencia o intención de compra.
Utilidad. Es la base conceptual para medir el valor. No tiene una equivalencia directa a alguna otra medida, ni siquiera dentro del mismo conjoint, dado que la utilidad depende de los atributos o niveles que se miden y por supuesto de la escala o nivel de medición empleado. Esto es un poco difícil de entender, pero piensa en atributos como felicidad y amor. Puedes saber si eres feliz o si estás enamorado y más o menos en qué grado lo eres o estás, aunque no puedes comparar felicidad con amor, simplemente son conceptos distintos. Por eso, en un estudio puedes tener diferentes grados de utilidad para cada atributo.

Ahora sí, procedamos con la explicación. Queríamos saber qué tipo de hombre prefieren las mujeres y cuáles son los atributos más importantes que debe tener. Pensamos en 3 atributos con 2 niveles por cada uno de ellos, riqueza: adinerado o pobre, atractivo: guapo o feo, y romanticismo: divertido o aburrido. Es menester presentar los estímulos (perfiles completos) a las mujeres para que evalúen su tipo de hombre. Los estímulos, como sabes, se generan combinando las distintas características de cada atributo. Por ejemplo, podemos decir que un estímulo sería un hombre feo, pobre, pero muy divertido; otro sería un hombre guapo, pobre y aburrido. Seguramente ya te disté cuenta de que hay varias posibles combinaciones que recrean distintos tipos de hombres con distinto atractivo para nuestras amigas de la oficina, a quienes llamaremos Lucy, Martha y Eva. El número de combinaciones (estímulos) totales depende del número de atributos y niveles de cada uno de ellos; el total de ejemplares masculinos es ocho, $2\times2\times2=8$³⁵.

Mostramos estos perfiles (ocho tarjetas) a tan distinguidas damas y les pedimos que los jerarquizaran, poniendo en primer lugar el perfil más deseado y en octavo lugar el menos deseado. Esa es una forma simple de preguntar la preferencia y lo hicimos así debido a que eran muy pocos perfiles. En la vida real lo más probable es que se tengan muchos más perfiles (aunque no se hable de hombres) y se use una escala del tipo: Dígame que tan dispuesta(o) o indispuesta (o) estaría en comprar un(a) (SE MENCIONA LA CATEGORÍA, POR EJEMPLO, JUGO) con estas características (SE MUESTRA EL PERFIL), use una escala del 1 al 5, en la cual 1 es definitivamente no compraría ese jugo y 5 es definitivamente compraría ese jugo. En la tabla 15.1 se aprecia la forma en que las mujeres de la oficina ordenaron los perfiles.

Tabla 15.1: Ordenación de perfiles de hombres
Perfil	Romanticismo	Atractivo	Riqueza	Lucy	Martha	Eva
1	Divertido	Guapo	Rico	2	1	1
2	Divertido	Guapo	Pobre	4	2	3
3	Divertido	Feo	Rico	1	3	4
4	Divertido	Feo	Pobre	6	4	5
5	Aburrido	Feo	Rico	5	6	7
6	Aburrido	Guapo	Pobre	7	7	6
7	Aburrido	Feo	Pobre	8	8	8
8	Aburrido	Guapo	Rico	3	5	2

¿Ves el perfil 1 y el 7?, ambos representan el mejor y el peor ejemplar masculino, respectivamente. Por tal razón todas las mujeres coincidieron en poner el perfil 7 en octavo lugar; ¿quién se puede interesar en un hombre aburrido, feo y pobre? En la práctica esta situación es casi constante, hay estímulos que son muy deseables y/o poco deseables. El investigador soluciona este tipo de problemas restringiendo dichos perfiles, eliminándolos de la muestra o prohibiéndolos que aparezcan desde el diseño de estímulos. No tendríamos nada que decir respecto a dicho procedimiento si no fuera porque se llega a excesos que evidencian la falta de conocimiento de lo que es un diseño experimental; de tal forma que no es raro obtener resultados extraños, por decir lo menos. Nuestra recomendación es que no impongas nada, a menos que sea absolutamente necesario (i.e. que el estímulo sea totalmente increíble, demasiado bueno para ser real). En otras ocasiones, los clientes se empeñan en tener combinaciones o mezclas poco usuales (v.gr. hacer competir presentaciones de bebidas dirigidas a niños con presentaciones familiares; las características varían en muchos sentidos) eso también impacta al diseño de estímulos. La recomendación es explicar lo más claro posible lo que se puede obtener al hacer el estudio como lo visualiza el cliente. Pero independientemente de ello, hay que tener siempre en mente que un diseño experimental no es igual que la vida real; en el primero se deben controlar las variables para obtener resultados óptimos, eso implica que no podemos hacer ajustes a nuestro antojo. La vida, por su parte, no acepta controles, combina lo que se le pega la regalada gana y procede de la misma forma. La moraleja es: no se pueden hacer cambios a los diseños sin pagar la cuota respectiva en la confiabilidad del estudio, a veces es aceptable, pero otras no.

El análisis de datos es directo utilizando el método estadístico de regresión lineal múltiple (véase sección 14). La sutileza del análisis radica en el arreglo de la base de datos. Mira la tabla 15.2, siempre que un perfil cuenta con una característica se codifica con 1 si no cuenta con la característica se codifica con 0. Recuerdas que el perfil 1 tenía todo: divertido, guapo y rico, bien esa es la razón por la que se codifica todo con 1. El perfil 7 era un fracaso de hombre: aburrido, feo y pobre, por eso se codifica todo con cero. El mismo arreglo se hace con las respuestas de Martha y Eva, en la misma base de datos. No lo ejemplificamos para no terminar con una base de datos kilométrica. Es probable, que en este momento ya hayas caído en la cuenta de lo laborioso que puede resultar un análisis de conjoint sin el software adecuado o si se hace con Excel³⁶. El arreglo de la base de datos, la cual siempre se tiene que hacer en cualquier tipo de conjoint, es un buen ejemplo del trabajo implicado.

Tabla 15.2: Codificación de variables mudas de las respuestas de Lucy
Sujeto	Perfil	Romanticismo	Atractivo	Riqueza	Orden
Lucy	1	1	1	1	2
Lucy	2	1	1	0	4
Lucy	3	1	0	1	1
Lucy	4	1	0	0	6
Lucy	5	0	0	1	5
Lucy	6	0	1	0	7
Lucy	7	0	0	0	8
Lucy	8	0	1	1	3

Después del arreglo de la base de datos, lo que sigue es efectuar el análisis de regresión lineal múltiple, utilizando como variable dependiente el Orden que dieron las mujeres a cada perfil y como variables independientes el Romanticismo, el Atractivo, y la Riqueza. Los valores obtenidos (betas de regresión) se pueden ver en el cuadro de análisis de abajo. Las betas más altas representan mayor preferencia porque invertimos la escala que iba de 1 a 8 para que el más preferido fuera el perfil con la calificación 8 y el menos preferido el perfil con la calificación de 1. Esas betas son nuestros tan anhelados valores de utilidad. Lo más importante es en primer lugar, en contra del sentido común, el Romanticismo, tiene una beta de 3.0. En segundo lugar, la Riqueza, su beta de regresión es de 2.3. Por último, lo Atractivo que tiene una beta de 1.8. En México explicamos este hallazgo diciendo: "Verbo mata carita, aunque jamás habríamos sospechado que también dinero.

## 
## Call:
## lm(formula = Orden ~ Romanticismo + Atractivo + Riqueza, data = tradicional)
## 
## Coefficients:
##  (Intercept)  Romanticismo     Atractivo       Riqueza  
##       0.9167        3.0000        1.8333        2.3333

Por supuesto, puedes ver cuál tipo de hombre tiene mejores posibilidades. Por ejemplo el perfil 3 es feo, pero divertido y rico vs. el perfil 6 quien es guapo, pero sin dinero y aburrido, ¿quién tiene más posibilidades de ser amado por alguna de nuestras chicas de la oficina? Es cuestión de armar la ecuación (14.1) y extraer su valor de utilidad.

El valor del perfil 3 sería:

$.91+3*1+1.83*0+2.33*1=6.25$

El valor del perfil 6 sería:

$.91+3*0+1.83*1+2.33*0=2.75$.

Concluyendo, es más preferido el perfil 3 que el 6; el primero llega casi a 8 (6.25), la calificación más alta, en tanto que el segundo se acerca más a 1 (2.75), la calificación más baja que puede haber. ¡¿Se entiende, no es así?!

Como te habrás dado cuenta, puedes calcular la importancia de cada factor y las utilidades para cada nivel; incluso lo puedes hacer por cada una de las mujeres que nos respondieron. Las utilidades son sumamente importantes porque se usan para configurar un tipo de hombre específico (producto o servicio). A esas configuraciones los mercadólogos le llaman escenarios (véase sección 15.4) ya que es posible estimar la preferencia con distintos supuestos ¿Te imaginas si tuvieras dinero, fueras guapo y te expresaras como Agustín Lara? Ese sí que sería el mejor escenario. Existen más modelos de conjoint analysis, el que utilizamos aquí se llama de perfil completo o tradicional, y se usa la regresión lineal múltiple para analizarlo. Actualmente, su uso en el mundo de la investigación es poco frecuente, pero es necesario entenderlo porque ilustra claramente cómo opera el análisis de conjunto o conjoint analysis. El más usado es, sin duda, por lo menos en Latinoamérica, el CBC (Choice Based Conjoint) o modelo discreto, tema de la siguiente sección.

15.3 Contar, básicamente contar (CBC)

La mayoría de los modelos de investigación de mercados utilizan métodos poco naturales para recopilar la información de un consumidor (v.gr. el conjoint tradicional)³⁷ con base en preguntas que requieren de un esfuerzo cognitivo del consumidor, superior al que emplea para resolver problemas cotidianos reales; como seleccionar una marca. Este inconveniente es historia para el CBC (Choice Based Conjoint) porque el consumidor sólo tiene que escoger el producto que desea y el investigador hace todo lo demás para determinar los gustos del consumidor. Por tal razón, el CBC es tan solicitado en el mundo de la investigación; porque se aproxima a la forma real en la que los consumidores hacen sus selecciones de productos o servicios.

Mira el estímulo o tarea, así se dice en el lenguaje del conjoint, que aparece en la figura 15.5. Hay que elegir un café de grano de los tres que se presentan, cada uno de ellos cuenta con 3 características:

La marca. Starbucks, Vips, y Los Portales
Tipo de café. Con cafeína o descafeinado.
Tipo de cultivo. Orgánico o inorgánico (cultivado con fertilizantes).

Figura 15.5: Estímulo o tarea de CBC

Para elegir un café se deben considerar cada uno de los 3 aspectos y decidir sobre el producto deseado; no se permite elegir una marca, digamos Starbucks, luego el tipo de café y finalmente la forma de cultivo, de forma separada. Lo que se presenta, es todo lo que hay en el menú, y de allí hay que escoger. Pero ¿qué pasa si no está la marca que a uno le gusta o está la marca, pero no en el tipo de café que acostumbra? Bueno, el CBC permite generar una opción extra, aparte de esas 3, que incluye el Ninguno; no elegiría ninguno de éstos, como en la figura 15.6.

Figura 15.6: Estímulo o tarea de CBC

Con base en las selecciones que se hacen podemos saber qué marca, tipo de café y cultivo son los más importantes, qué es lo primero que se toma en cuenta a la hora de comprar un café y cuál es el procedimiento que se sigue para ello. En un momento más vamos a ilustrar cómo, pero antes déjanos explicar algunos conceptos específicos del CBC.

Concepto. Cada producto con su configuración particular es un concepto, recuerda que también se le dice perfil. La figura 15.5 contiene 3 conceptos: el concepto de café VIPS descafeinado y cultivado con fertilizantes; el concepto de café Los Portales con cafeína y cultivado sin fertilizantes; y el concepto Starbucks descafeinado y cultivado con fertilizantes.
Tarea. Cuando los conceptos se presentan simultáneamente al entrevistado para que elija uno de entre todos ellos, se dice que se está realizando una tarea.
Atributos. En nuestro ejemplo tenemos 3 atributos; la marca, el tipo de café y la forma de cultivo.
Niveles. Cada Atributo debe tener por lo menos 2 opciones de otra forma no funciona para llevar a cabo el conjoint; cada opción representa un nivel distinto; la marca tiene 3 niveles distintos: Vips, Los Portales y Starbucks; el atributo tipo de café tiene 2 niveles: con cafeína y descafeinado; y el tipo de cultivo 2: usando fertilizantes o de forma natural.

Ya podemos continuar. Sabes que las combinaciones posibles son más de tres (doce para ser exactos) lo que arroja más conceptos. Claro que se puede pedir al entrevistado que resuelva más de una tarea con 3 conceptos cada una. Para presentar los 12 conceptos suena conveniente pedirle al entrevistado que resuelva cuatro tareas de tres conceptos cada una de ellas. También se podrían presentar los doce conceptos de una sola vez; aunque no se aconseja porque la elección se vuelve más complicada. Algunos mercadólogos dicen que cuando hay un gran número de opciones la gente compra menos; no vaya a ser que los entrevistados se decanten por el concepto de “NINGUNO”. En realidad el número de conceptos que se deben presentar en una sola tarea es más de criterio que de otra cosa; así como la planogramación en un autoservicio se hace con base a criterios propios de la tienda, tampoco existe una fórmula para decidir cuál es el número ideal. Sin embargo, reflexiona sobre lo siguiente, en la naturaleza las redes tienen un promedio de tres nodos prominentes, pasa también con los nombres de las marcas que una persona puede recordar en promedio, y con muchas otras cosas. Para mí el ideal ronda en tres, pero no hay problema si usas más. Obviamente, esto tiene un costo en la exactitud del estudio. Vamos a apegarnos al primer plan y generar otras 3 tareas con los conceptos restantes:

Figura 15.7: Estímulo o tarea de CBC

Observa el cambio de los perfiles en la tarea 2; así como la rotación de las marcas, ahora Los Portales está al inicio y Vips al final (figura 15.7).

Figura 15.8: Estímulo o tarea de CBC

La misma tónica se encuentra en las tareas 3 y 4 (figuras 15.8 y 15.9).

Figura 15.9: Estímulo o tarea de CBC

A falta de voluntarios, yo mismo seré el conejillo de indias. En la primera tarea elegí la marca Los Portales porque me gusta su sabor más que el de Vips y Starbucks, pero sobre todo porque no era descafeinado y su producción era orgánica. En la segunda tarea escogí Starbucks porque contenía lo mismo que Los Portales. Es decir, era un café no descafeinado y orgánico. En la tercera tarea me decidí por Vips por las mismas razones; mientras que en la última tarea me fue más difícil decidirme porque si bien me gusta el café sin descafeinar no me agradó mucho que fuera cultivado con fertilizantes. Recuerda que también puede haber dicho en la última tarea que no quería ninguno de esos productos, pero para hacer más simple esta explicación opté por no incluir dicha opción en las tareas. En el cuadro 15.10 vienen los resultados de mi autoconjoint.

Figura 15.10: Resultados de cuatro tareas de CBC

Nota que el título de la tabla dice diseño equilibrado y balanceado. Eso es uno de los puntos más críticos a la hora de diseñar un conjoint. Siempre que se preparan los estímulos se debe verificar que el resultado de las combinaciones que se hacen están balanceadas y equilibradas. En pocas palabras, todos los atributos deben aparecer el mismo número de veces y en las mismas combinaciones. Una inspección rápida revela que Vips aparece el mismo número de veces que las otras marcas y que además se combina con los otros atributos de la misma forma que las otras marcas. O sea, Vips con cafeína en sus dos formas de cultivo con fertilizantes y orgánico y Vips descafeinado en ambos tipos de cultivo. Lo mismo pasa con Starbucks y Los Portales. Cuando se logra este equilibrio se dice que el diseño es ortogonal; es decir, ningún atributo depende de otro. No te atormentes, estas combinaciones no se hacen a mano, los programas de conjoint las hacen automáticamente; además proporcionan una prueba de la eficiencia del diseño. Ojo, mucho ojo, si el diseño no pasa esta prueba, tampoco lo hará el estudio de campo. Por otro lado, cuando los atributos y sus niveles son muchos, la creación de tareas puede ser complicada si no se hace con un programa para conjoint; no obstante, hay estrategias para emprender tan loable labor a mano (véase Chrzan and Bryan 2000)

Hecha la advertencia anterior, continuemos con el análisis de resultados. Los círculos del cuadro 15.10 reflejan mis preferencias en cada tarea. De las cuatro veces (tareas) que se me presentó la marca Vips, la elegí una sola vez, por lo que la probabilidad de elección de esta marca es de $25\%$ ($\frac{1}{4}=.25$). Lo mismo sucedió con Los Portales por lo que su probabilidad de selección fue exactamente de $25\%$. En el caso de Starbucks tuve el tino de seleccionarla 2 de 4 veces que apareció por lo que la probabilidad de que elija Starbucks es de $50\%$ ($\frac{2}{4}=.50$). En la figura 15.11 se presentan estos resultados.

Figura 15.11: Resultados de conteo de CBC por marca

En cuanto al tipo de café, siempre que pude escogí sin descafeinar, por lo que la probabilidad de selección fue $66\%$ y la de descafeinado fue de $0\%$. ¡Ah, caray!, y por qué no nos da $100\%$; la razón es que esta probabilidad se obtiene de dividir el número de veces que se elige un nivel entre el número total de veces que aparece, y como en una misma tarea los niveles “con cafeína” y “descafeinado” aparecen más de una vez, el resultado no suma $100\%$. Lo que se hace en estos casos es ajustar los porcentajes resultantes al $100\%$. La figura 15.12 contiene estos otros resultados.

Figura 15.12: Resultados de conteo de CBC por tipo de café

En el caso del tipo de producción, prefiero el café orgánico por lo que su probabilidad de selección es del $50\%$ vs. un $16\%$ en que preferí la producción con fertilizantes (figura 15.13).

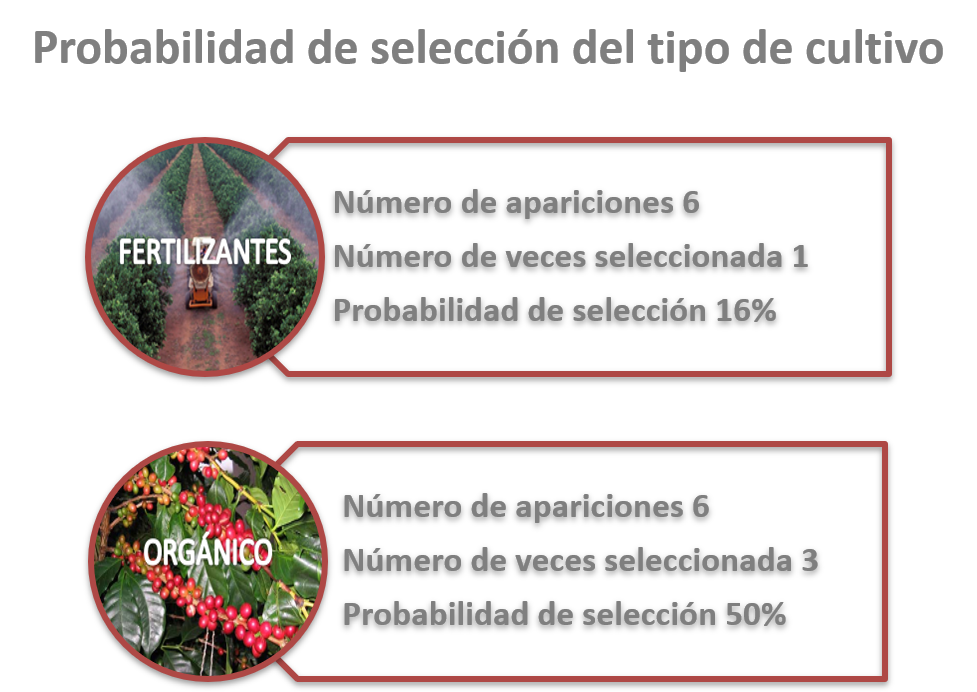
Figura 15.13: Resultados de conteo de CBC por tipo de cultivo

Viendo las cosas así, las implicaciones se hacen claras: una muestra de consumidores es más exacta que la respuesta de un solo sujeto; los resultados son mucho, pero mucho más confiables. No se necesita mostrar forzosamente las cuatro tareas a cada sujeto, de hecho, con una sola sería suficiente, pero tendríamos que distribuir las cuatro a un mismo número de sujetos. Por ejemplo, si tenemos 20 sujetos, a 5 les presentamos la tarea 1, a otros 5 la tarea 2, y así sucesivamente. Confío en que esta explicación te muestre porqué el diseño debe ser equilibrado y balanceado; si algunas marcas aparecen más que otras o aparecen más a menudo con otras características habrá un tremendo sesgo al analizar los resultados ya que en automático la selección de un atributo/nivel jala a los otros con los que se junta. El análisis de conteo del CBC es muy fácil y proporciona una buena idea de por dónde andan las preferencias de los entrevistados. Sin embargo, los métodos estadísticos que se usan para analizar los datos del CBC son mucho más refinados que un simple conteo; uno de los más empleados es la regresión logística multinomial. Chapman and Feit (2019) es una excelente lectura para aprender a hacer este tipo de análisis aplicado al conjoint CBC usando R.

15.4 Qué tal si…

Una desventaja de usar software de pago para llevar a cabo CBC u otro tipo de conjoint, es la dependencia que se tiene a este software a la hora de presentar los resultados con un cliente. Muchos investigadores entregan únicamente una serie de gráficos que muestran la importancia de los atributos y sus niveles. Asimismo, configuran diversos escenarios del tipo: qué participación o preferencia tendría el producto o marca A, si su precio fuera $x$ o $y$, si tuviera el atributo $x$, $y$ o $z$, entre otros. A eso se le llama simulación de escenarios. La desventaja deriva en que para hacer esas configuraciones se requiere del software en cuestión, de tal forma que por cuestiones de licencia no se puede dar acceso completo a un cliente. Además del inconveniente que puede ser explicarle cómo funciona dicho simulador. Consecuentemente, la alternativa que tiene el investigador es presentar un número limitado de escenarios en gráficas fijas (los más importantes quizá o los solicitados explícitamente por el cliente).

En cualquier tipo de conjoint lo más arduo es estimar los valores de utilidad, una vez logrado esto, se puede armar un simple simulador en Excel, usando funciones como validación de listas para hacer el cambio de niveles sin que el cliente tenga que teclearlos, búsqueda vertical, entre unas cuántas funciones más. Cómo en todo, hay métodos más sofisticados para hacer este simulador, pero la ganancia que se obtiene es muy poca como para tomarse la molestia. Claro que si tienes el software que ya lo hace pues aprovéchalo al máximo. La figura 15.14 es la versión casera de este simulador hecho en Excel; muy sencillo, pero efectivo. Con él puedes armar todos los escenarios que se te ocurran, y, más importante aun, el cliente puede quedárselo para armar sus propios escenarios; sin necesidad de tener que explicarle cómo funciona. Esa es la ventaja de Excel, todo mundo sabe cómo trabajar con él.

Figura 15.14: Simulador de un estudio de CBC

Nosotros mismos hemos impartido talleres de esta naturaleza.↩
Como se dijo anteriormente, hay muchas variantes de conjoint analysis; sin embargo, una de las más comunes es la de perfil completo.↩
Una selección aleatoria simple en Excel se obtiene fácilmente usando la función aleatorio.entre(1,54); los argumentos se deben a que tenemos 54 perfiles. La función se copia en el mismo número de filas que se requieran, dependiendo del tamaño de muestra elegido. En caso de obtener perfiles repetidos simplemente se sustituye por el perfil anterior o posterior de la lista completa.↩
Una pregunta recurrente es cuántos perfiles debe evaluar un entrevistado. No hay una respuesta simple para ello; más bien depende del número de atributos y niveles que se tengan. Una fórmula sencilla que señala el mínimo de perfiles requeridos con base a esas variables es: Mínimo de perfiles = Total de niveles - (Total de atributos + 1). Sin embargo, mi receta es más empírica y de sentido común. Siempre procuro que el entrevistado evalúe no menos de 16 y no más de 24 perfiles. Esto se debe a la cantidad de información que puede procesar y el tiempo que le lleva contestar la encuesta. Claro está que no debe ser así forzosamente. Un buen investigador siempre debe usar su criterio más allá de las cuestiones técnicas. Si se equivoca habrá aprendido algo útil; si lo hace bien, sin equivocarse, también irá afinando su sensibilidad.↩
R es sin duda una de las cosas más importantes que les ha pasado a los investigadores sociales; es un lenguaje de programación orientado a los científicos de datos. Realizar un análisis de conjoint con R es fácil; desafortunadamente, aprenderlo lleva algo de tiempo. Te aconsejo seriamente que empieces de ya.↩
Esta aseveración es particularmente cierta en el neuromarketing; por suerte, parece que la efervescencia por estas técnicas empieza a descender.↩