5.9 MACD

Moving average convergence/divergence (MACD) is the difference between a short-period (fast) EMA and a long-period (slow) SMA: \[MACD_t(S,L)=ema_t(P, S)-ema_t(P, L).\]

For its usage, we compare it with its exponential smoothed line. This line is called the : \[sig_{t}(S,L,K)=ema_t(MACD(S,L), K).\] Usually, \(K=9\) days, \(S=12\) days and \(L=26\) days. Note that MACD sometimes appear as the percetnage format \[MACD_t(S,L)= ema_t(P, S)-ema_t(P, L))/ema_t(P, L).\]

Here is the short code for MACD:

myMACD <- function (price,S,L,K){
  MACD <- EMA(price,S) - EMA(price,L)
  signal <- EMA(MACD,K)
  output <- cbind(MACD,signal)
  colnames(output) <- c("MACD","signal")
  return(output)
}

Let us apply our code:

macd <- myMACD(Cl(AAPL), 12, 26,9)
tail(macd,n=5)

##                 MACD    signal
## 2012-12-21 -2.208678 -2.072365
## 2012-12-24 -2.178151 -2.093522
## 2012-12-26 -2.211121 -2.117042
## 2012-12-27 -2.188278 -2.131289
## 2012-12-28 -2.207780 -2.146587

5.9.1 TTR

We use MACD function in TTR package:

macd <- MACD(Cl(AAPL), nFast=12, nSlow=26,
             nSig=9, percent=FALSE)
tail(macd,n=5)

##                 macd    signal
## 2012-12-21 -2.208678 -2.072365
## 2012-12-24 -2.178151 -2.093522
## 2012-12-26 -2.211121 -2.117042
## 2012-12-27 -2.188278 -2.131289
## 2012-12-28 -2.207780 -2.146587

where nFast, nSlow, and nSig are S, L, and K in our formula. The percent is whether MACD is in percentage form or in difference form.

5.9.2 Trading signal

Buy signal arises when MACD crosses from below to above the signal line.

Sell signal arrises when MACD crosses from above to below the signal line.

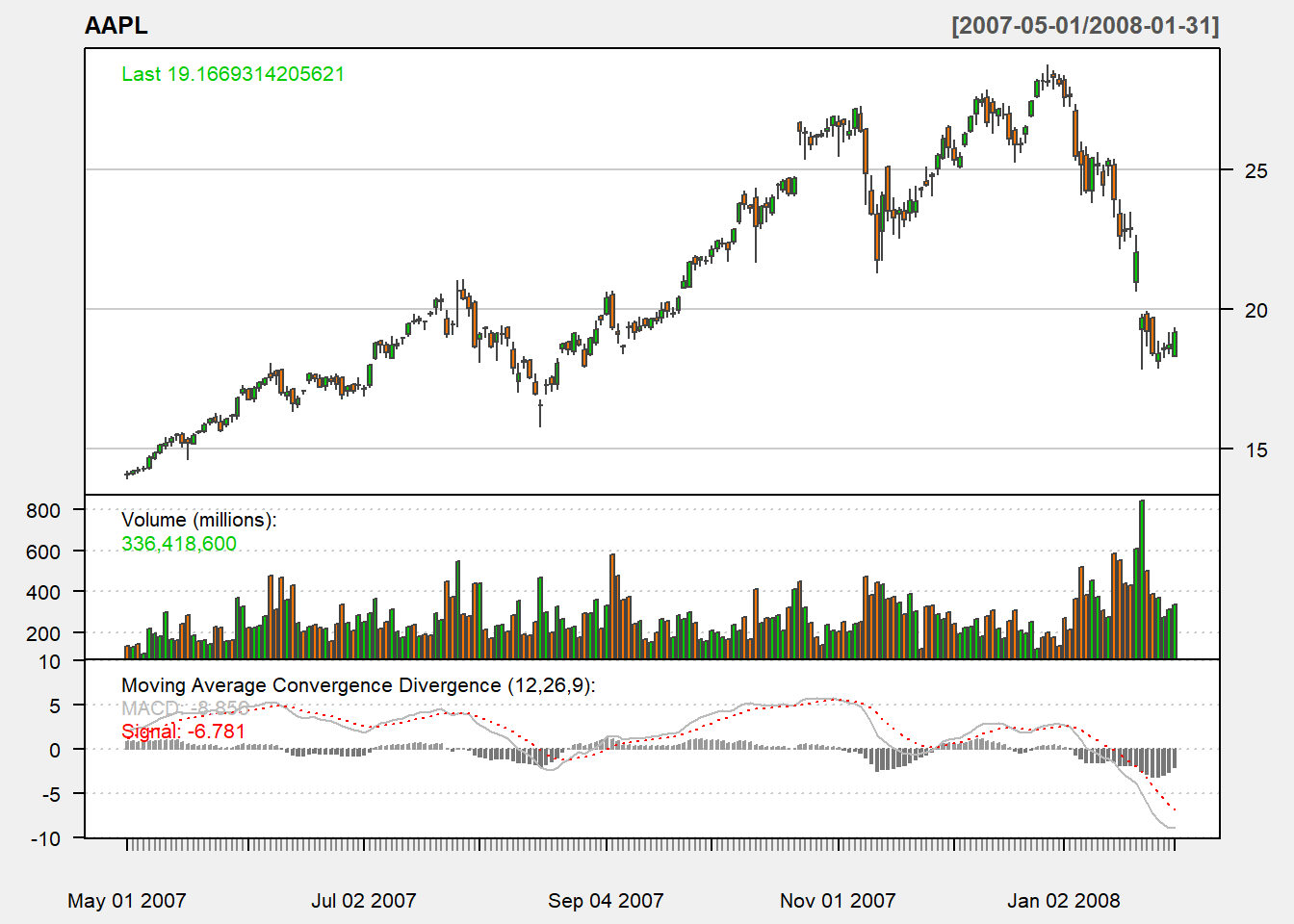
5.9.3 Charting

chartSeries(AAPL,
            subset='2007-05::2008-01',
            theme=chartTheme('white'))
addMACD(fast=12,slow=26,signal=9,type="EMA")