Chapter 10 Population Projection III: Temporal Environmental Stochasticity
Each of us a cell of awareness
imperfect and incomplete
Genetic blends with uncertain ends
on a fortune hunt that’s far too fleet
Note: The example code in this chapter relies on code executed in previous chapters. This code is available in a ready-to-run block in Appendix II (19.0.4).
Stochasticity refers to randomness. In population ecology, stochasticity is studied in two dominant forms: environmental and demographic (Caswell 2001). The former refers to randomness in the environment leading to random changes in the projection matrix over time and/or space. The latter refers to random divergence in vital rates caused by the differing fates of individuals within populations of finite size. In this chapter, we will concern ourselves only with the former kind of stochasticity.
Most of the literature on environmental stochasticity in matrix projection analysis is focused on randomness with respect to time. Temporally random sequences can come in a variety of forms, but we will be concerned with two in this chapter: iid sequences and discrete-state Markov chains. We will begin with the former.
10.1 The iid stochastic sequence
The iid (independent and identically distributed) sequence is one in which the choice of matrix for a particular point in time does not depend on any other time. The matrix used for projection at some point in time is drawn at random from a distribution of such matrices, with each matrix having some probability of being chosen (Caswell 2001). These probabilities do not need to be equal, but they must not vary for any reason. Alternatively, in the case of function-based MPMs, the kernel used to populate the matrices has a set of terms that vary across time, and these terms are shuffled randomly according to some distribution at each time step. Thus, the choice of matrix is not predictable - knowing the composition of the matrix at one point in time tells you nothing of its composition at any other point in time.
How exactly does such randomness change the projection? In comparison to equation (9.1), which shows a deterministic projection, an environmental stochastic projection is given as the following.
\[\begin{equation} \mathbf{n_t} = \mathbf{A_t A_{t-1} \cdots A_1 n_0} \tag{10.1} \end{equation}\]
Here, each \(\mathbf{A_i}\) is a randomly sampled matrix, each of which has the same dimensions. If we project the population forward a large number of time steps, then we generally find certain stable conditions forming in the long run. These stable conditions are predicted by the strong and weak ergodic theorems (Caswell 2001).
Package lefko3 includes a number of functions to facilitate matrix projection analysis assuming temporal stochasticity (we shall refer to this in general as stochastic analysis from now on). Currently, we include functions to estimate stochastic population growth rate, long-run stage structure, long-run reproductive value, stochastic sensitivity and elasticity, and stochastic life table response experiments. Two projection functions are also included that can be used to assess more interesting questions with or without stochasticity.
Let’s utilize the raw MPMs developed in chapter 4 to illustrate the sorts of stochastic analyses that we can perform. These are the same matrices utilized in the last chapter (chapter 9). Particularly, we will use the lefkoMat objects named cypmatrix2r, cypmatrix2rp, cypmatrix3r, and cypmatrix3rp. However, the function-based MPMs, IPMs, age-by-stage MPMs, and Leslie MPMs that we have created so far can also be used in all cases.
Let’s start off by taking a look at summaries of these objects.
summary(cypmatrix2r)
>
> This ahistorical lefkoMat object contains 5 matrices.
>
> Each matrix is square with 11 rows and columns, and a total of 121 elements.
> A total of 120 survival transitions were estimated, with 24 per matrix.
> A total of 40 fecundity transitions were estimated, with 8 per matrix.
> This lefkoMat object covers 1 population, 1 patch, and 5 time steps.
>
> The dataset contains a total of 74 unique individuals and 320 unique transitions.
>
> Survival probability sum check (each matrix represented by column in order):
> [,1] [,2] [,3] [,4] [,5]
> Min. 0.000 0.050 0.050 0.000 0.050
> 1st Qu. 0.100 0.140 0.140 0.100 0.140
> Median 0.689 0.870 0.864 0.610 0.882
> Mean 0.552 0.629 0.629 0.528 0.627
> 3rd Qu. 1.000 1.000 1.000 0.960 1.000
> Max. 1.000 1.000 1.000 1.000 1.000
summary(cypmatrix2rp)
>
> This ahistorical lefkoMat object contains 15 matrices.
>
> Each matrix is square with 11 rows and columns, and a total of 121 elements.
> A total of 266 survival transitions were estimated, with 17.733 per matrix.
> A total of 70 fecundity transitions were estimated, with 4.667 per matrix.
> This lefkoMat object covers 1 population, 3 patches, and 5 time steps.
>
> The dataset contains a total of 74 unique individuals and 320 unique transitions.
>
> Survival probability sum check (each matrix represented by column in order):
> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
> Min. 0.000 0.000 0.000 0.000 0.000 0.000 0.050 0.050 0.000 0.050 0.000 0.000
> 1st Qu. 0.075 0.025 0.075 0.025 0.075 0.075 0.140 0.140 0.100 0.140 0.100 0.100
> Median 0.180 0.100 0.180 0.100 0.180 0.180 0.909 0.778 0.686 0.857 0.750 0.575
> Mean 0.457 0.361 0.471 0.328 0.417 0.464 0.631 0.611 0.530 0.631 0.562 0.523
> 3rd Qu. 0.955 0.769 1.000 0.592 0.781 1.000 1.000 1.000 0.955 1.000 1.000 1.000
> Max. 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000 1.000
> [,13] [,14] [,15]
> Min. 0.000 0.000 0.000
> 1st Qu. 0.075 0.075 0.100
> Median 0.180 0.180 0.750
> Mean 0.432 0.450 0.562
> 3rd Qu. 0.875 1.000 1.000
> Max. 1.000 1.000 1.000
summary(cypmatrix3r)
>
> This historical lefkoMat object contains 4 matrices.
>
> Each matrix is square with 121 rows and columns, and a total of 14641 elements.
> A total of 242 survival transitions were estimated, with 60.5 per matrix.
> A total of 54 fecundity transitions were estimated, with 13.5 per matrix.
> This lefkoMat object covers 1 population, 1 patch, and 4 time steps.
>
> The dataset contains a total of 74 unique individuals and 320 unique transitions.
>
> Survival probability sum check (each matrix represented by column in order):
> [,1] [,2] [,3] [,4]
> Min. 0.000 0.000 0.000 0.000
> 1st Qu. 0.000 0.000 0.000 0.000
> Median 0.000 0.000 0.000 0.000
> Mean 0.173 0.179 0.166 0.198
> 3rd Qu. 0.100 0.100 0.100 0.100
> Max. 1.000 1.000 1.000 1.000
summary(cypmatrix3rp)
>
> This historical lefkoMat object contains 12 matrices.
>
> Each matrix is square with 121 rows and columns, and a total of 14641 elements.
> A total of 516 survival transitions were estimated, with 43 per matrix.
> A total of 70 fecundity transitions were estimated, with 5.833 per matrix.
> This lefkoMat object covers 1 population, 3 patches, and 4 time steps.
>
> The dataset contains a total of 74 unique individuals and 320 unique transitions.
>
> Survival probability sum check (each matrix represented by column in order):
> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
> Min. 0.000 0.0000 0.0000 0.000 0.000 0.000 0.00 0.000 0.000 0.0000 0.000
> 1st Qu. 0.000 0.0000 0.0000 0.000 0.000 0.000 0.00 0.000 0.000 0.0000 0.000
> Median 0.000 0.0000 0.0000 0.000 0.000 0.000 0.00 0.000 0.000 0.0000 0.000
> Mean 0.107 0.0945 0.0851 0.101 0.158 0.158 0.14 0.169 0.119 0.0851 0.119
> 3rd Qu. 0.000 0.0000 0.0000 0.000 0.100 0.100 0.05 0.100 0.000 0.0000 0.000
> Max. 1.000 1.0000 1.0000 1.000 1.000 1.000 1.00 1.000 1.000 1.0000 1.000
> [,12]
> Min. 0.000
> 1st Qu. 0.000
> Median 0.000
> Mean 0.144
> 3rd Qu. 0.000
> Max. 1.000
We see that these four MPMs cover three patches of one population, and that cypmatrix2r and cypmatrix3r do not distinguish the patches while cypmatrix2rp and cypmatrix3rp do. Objects cypmatrix2r and cypmatrix2rp are ahistorical, while cypmatrix3r and cypmatrix3rp are historical. Because these are raw MPMs and there are six total monitoring occasions covered, we see five matrices estimated in the ahistorical population-level set and four matrices estimated in the historical population-level set. The patch-level MPMs create five and four matrices per patch for the ahistorical and historical cases, respectively. Finally, there are 11 life history stages, which we see below.
cypmatrix2r$ahstages
> stage_id stage original_size original_size_b original_size_c min_age max_age
> 1 1 SD 0.0 NA NA 0 NA
> 2 2 P1 0.0 NA NA 0 NA
> 3 3 P2 0.0 NA NA 0 NA
> 4 4 P3 0.0 NA NA 0 NA
> 5 5 SL 0.0 NA NA 0 NA
> 6 6 D 0.0 NA NA 0 NA
> 7 7 XSm 1.0 NA NA 0 NA
> 8 8 Sm 3.0 NA NA 0 NA
> 9 9 Md 6.0 NA NA 0 NA
> 10 10 Lg 11.0 NA NA 0 NA
> 11 11 XLg 19.5 NA NA 0 NA
> repstatus obsstatus propstatus immstatus matstatus entrystage indataset
> 1 0 0 1 0 0 1 0
> 2 0 0 0 1 0 1 0
> 3 0 0 0 1 0 0 0
> 4 0 0 0 1 0 0 0
> 5 0 0 0 1 0 0 0
> 6 0 0 0 0 1 0 1
> 7 1 1 0 0 1 0 1
> 8 1 1 0 0 1 0 1
> 9 1 1 0 0 1 0 1
> 10 1 1 0 0 1 0 1
> 11 1 1 0 0 1 0 1
> binhalfwidth_raw sizebin_min sizebin_max sizebin_center sizebin_width
> 1 0.0 0.0 0.0 0.0 0
> 2 0.0 0.0 0.0 0.0 0
> 3 0.0 0.0 0.0 0.0 0
> 4 0.0 0.0 0.0 0.0 0
> 5 0.0 0.0 0.0 0.0 0
> 6 0.5 -0.5 0.5 0.0 1
> 7 0.5 0.5 1.5 1.0 1
> 8 1.5 1.5 4.5 3.0 3
> 9 1.5 4.5 7.5 6.0 3
> 10 3.5 7.5 14.5 11.0 7
> 11 5.0 14.5 24.5 19.5 10
> binhalfwidthb_raw sizebinb_min sizebinb_max sizebinb_center sizebinb_width
> 1 NA NA NA NA NA
> 2 NA NA NA NA NA
> 3 NA NA NA NA NA
> 4 NA NA NA NA NA
> 5 NA NA NA NA NA
> 6 NA NA NA NA NA
> 7 NA NA NA NA NA
> 8 NA NA NA NA NA
> 9 NA NA NA NA NA
> 10 NA NA NA NA NA
> 11 NA NA NA NA NA
> binhalfwidthc_raw sizebinc_min sizebinc_max sizebinc_center sizebinc_width
> 1 NA NA NA NA NA
> 2 NA NA NA NA NA
> 3 NA NA NA NA NA
> 4 NA NA NA NA NA
> 5 NA NA NA NA NA
> 6 NA NA NA NA NA
> 7 NA NA NA NA NA
> 8 NA NA NA NA NA
> 9 NA NA NA NA NA
> 10 NA NA NA NA NA
> 11 NA NA NA NA NA
> group comments alive almostborn
> 1 0 Dormant seed 1 0
> 2 0 1st yr protocorm 1 0
> 3 0 2nd yr protocorm 1 0
> 4 0 3rd yr protocorm 1 0
> 5 0 Seedling 1 0
> 6 0 Dormant adult 1 0
> 7 0 Extra small adult (1 shoot) 1 0
> 8 0 Small adult (2-4 shoots) 1 0
> 9 0 Medium adult (5-7 shoots) 1 0
> 10 0 Large adult (8-14 shoots) 1 0
> 11 0 Extra large adult (>14 shoots) 1 0Let’s move on now to the first of the stochastic analyses: the estimation of the stochastic population growth rate, \(a\).
10.1.1 Stochastic population growth rate
Function slambda3() estimates the log stochastic population growth rate in its instantaneous form (\(a = \text{log} \lambda _{S}\)). This is estimated as the mean log discrete population growth rate across a user-specified number of random draws of the annual matrices provided as input in the function.
\[\begin{equation} a = \text{log} \lambda _{S} = \frac{1}{T} \sum _{t=1}^{T} \text{log} \frac{N _{t}}{N _{t-1}} \tag{10.2} \end{equation}\]
Here, \(N _t\) is the population size in occasion \(t\), and \(T\) is the number of occasions projected forward, set to 10,000 by default. Function slambda3() does not shuffle across patches or populations, instead shuffling within patches, or shuffling annual matrices calculated as element-wise means of patch matrices within the same population and the same time. The methodology is based on Morris & Doak (2002), though accounts for spatial averaging of patches and can easily handle large and sparse matrices.
Let’s estimate the stochastic population growth rate. We will use set.seed() prior to each run to make sure that our exact results are replicable (function set.seed() allows us to set the seed for R’s pseudo-random number generator, thus yielding the same “random” sequence of matrix draws).
# Raw ahistorical stochastic log lambda
set.seed(42)
cypmatrix2rp_slam <- slambda3(cypmatrix2rp)
cypmatrix2rp_slam
> pop patch a var sd se
> 1 1 A -0.03349084 4.2171941 2.0535808 0.020535808
> 2 1 B 0.09728146 1.3439679 1.1592963 0.011592963
> 3 1 C 0.06638145 1.1461344 1.0705766 0.010705766
> 4 1 0 0.04221328 0.7354604 0.8575899 0.008575899
# Raw historical stochastic log lambda
set.seed(42)
cypmatrix3rp_slam <- slambda3(cypmatrix3rp)
cypmatrix3rp_slam
> pop patch a var sd se
> 1 1 A -0.18490427 6.3024809 2.5104742 0.025104742
> 2 1 B -0.07213781 2.4096979 1.5523202 0.015523202
> 3 1 C -0.05559008 2.8068160 1.6753555 0.016753555
> 4 1 0 -0.12545093 0.8018269 0.8954479 0.008954479
The output above is for the ahistorical and historical patch-level MPMs. The final entry in each case, labeled as patch 0, corresponds to the population (where the population MPM is one in which the matrix for each year is an equally weighted mean of each patch’s matrix for that year). Unlike in deterministic analysis, population growth rate is not estimated for each matrix, but rather for each patch or population. This is because the growth rate is estimated by a random shuffle of the matrices, with the stochastic growth rate equal to the average log change in projected population size in the latter portion of the shuffled set. Since we did not change any of the defaults, R shuffled the matrices 10,000 times, and the resulting mean log stochastic growth rate and its associated variance, standard deviation, and standard error are calculated over these 10,000 times in the projection.
Users will notice differences between ahistorical and historical \(\text{log} \lambda _{S}\) values. Ahistorical population growth rate estimates are often higher than those for historical MPMs. The reasons are not yet clear, but they may have to do with the life histories that have been used in analysis so far - population growth in long-lived herbaceous perennial plants is typically driven by survival transitions in adults, and the impact of fecundity on growth rate appears even lower when individual history is incorporated into analysis. This may also be due to long-term trade-offs captured within the historical models but not within ahistorical models. Of note is the growth trade-off - we have found that large individuals growing to large size in time t from small size in time t-1 have lower survival probability to time t+1 (Shefferson et al. 2014). Finally, the data are cut more finely to determine elements in the historical case, leading to a greater influence of artificial zeros (some zeros are artificial in the sense that they are zero simply because the dataset is too small to yield individuals moving through some transitions).
It may be interesting in this case to compare our estimates of the population growth rate to the deterministic case. To compare them, we must first estimate the deterministic population growth rate \(\lambda\) for the temporal mean matrices. Then, we need either to take the natural logarithm of \(\lambda\), or to raise the natural number \(e\) to the power of \(a\) given in the slambda3() output. Let’s do the latter. We will put our results together into a data frame using the cbind.data.frame() function, as below.
cyp2rp_mean <- lmean(cypmatrix2rp)
cyp3rp_mean <- lmean(cypmatrix3rp)
cyp2rp_mean_lam <- lambda3(cyp2rp_mean)
cyp3rp_mean_lam <- lambda3(cyp3rp_mean)
cypmatrix2rp_slam$expa <- exp(cypmatrix2rp_slam$a)
cypmatrix3rp_slam$expa <- exp(cypmatrix3rp_slam$a)
lambda_comparison <- cbind.data.frame(pop = cyp2rp_mean_lam$pop,
patch = cyp2rp_mean_lam$patch, lambda_ah = cyp2rp_mean_lam$lambda,
lambda_h = cyp3rp_mean_lam$lambda, expa_ah = cypmatrix2rp_slam$expa,
expa_h = cypmatrix3rp_slam$expa)
lambda_comparison
> pop patch lambda_ah lambda_h expa_ah expa_h
> 1 1 A 0.9835717 0.8510445 0.9670638 0.8311838
> 2 1 B 1.1051470 0.9481901 1.1021705 0.9304027
> 3 1 C 1.0717513 0.9671030 1.0686343 0.9459268
> 4 1 0 1.0450267 0.8946030 1.0431169 0.8820991Temporal variation in fitness leads to lower long-term fitness, resulting in stochastic population growth rate being lower than deterministic growth rate. There also appears to be a general trend of historical matrices yielding lower deterministic and stochastic population growth rates.
10.1.2 Long-run average stage distribution and reproductive value
Package lefko3 also handles the estimation of stochastic long-run stage distribution and long-run reproductive value vectors, which are the stochastic equivalents of the deterministic stable stage equilibrium and asymptotic reproductive value vector. It handles this through the projection of shuffled annual matrices, typically 10,000 occasions forward though the exact number can be set as needed. According to the stochastic strong and weak ergodic theorems, this random shuffling should eventually yield a roughly stationary distribution of stage proportions and stage reproductive values. Thus, the stochastic stable structure is estimated as the arithmetic mean vector of the predicted stage proportion vectors across the final portion of such a projection (in a 10,000 time step projection, this is typically the final 1000 or so time steps).
The stochastic long-run reproductive value is more complicated. Imagine a vector, \(\mathbf{x}(t)\), that includes the expected number of offspring produced by each stage in occasion t+1. This is referred to as the undiscounted reproductive value vector because it is not standardized (Caswell 2001). Vector \(\mathbf{x}(t)\) is related to other occasions in this projection, as in the following.
\[\begin{equation} \mathbf{x}^\top(t) = \mathbf{x}^\top(t+1)\mathbf{A}_t \tag{10.3} \end{equation}\]
Standardizing leads to the discounted reproductive value vector, below.
\[\begin{equation} \mathbf{v}(t) = \frac{\mathbf{x}(t)}{\lVert \mathbf{x}(t) \rVert} \tag{10.4} \end{equation}\]
This reproductive value vector can then be projected as well, as follows.
\[\begin{equation} \mathbf{v}(t) = \frac{\mathbf{v}^\top(t+1)\mathbf{A}_t}{\lVert \mathbf{v}^\top(t+1)\mathbf{A}_t \rVert} \tag{10.5} \end{equation}\]
The reproductive value vector is projected backwards in time. Under the default 10,000 time steps, package lefko3 takes its average in the final 1000 steps of the backward projection (smaller numbers of steps are used in cases where the projection is limited to less than 2000 steps).
Now let’s take a look at the long-run stage distributions at the population level, comparing the deterministic to the stochastic, and the ahistorical to the historical. We will focus only on the population-level MPMs (note that we need to create the mean matrices for the deterministic analysis of the population-level MPMs, and do so within the first two lines). We will first create the stable stage vectors, and then put them all into a common data frame, as below.
cyp2r_mean <- lmean(cypmatrix2r)
cyp3r_mean <- lmean(cypmatrix3r)
tm2ss_r <- stablestage3(cyp2r_mean)
tm3ss_r <- stablestage3(cyp3r_mean)
tm2ss_rs <- stablestage3(cypmatrix2r, stochastic = TRUE, seed = 42)
tm3ss_rs <- stablestage3(cypmatrix3r, stochastic = TRUE, seed = 42)
ss_put_together <- cbind.data.frame(tm2ss_r$ss_prop, tm3ss_r$ahist$ss_prop,
tm2ss_rs$ss_prop, tm3ss_rs$ahist$ss_prop)
names(ss_put_together) <- c("det ahist", "det hist", "sto ahist", "sto hist")
rownames(ss_put_together) <- tm2ss_r$stage
ss_put_together
> det ahist det hist sto ahist sto hist
> SD 4.709506e-01 4.731057e-01 4.568960e-01 4.565872e-01
> P1 4.796543e-01 4.740135e-01 4.696325e-01 4.584031e-01
> P2 4.432261e-02 4.688477e-02 6.502990e-02 7.295521e-02
> P3 4.095645e-03 4.637381e-03 6.863520e-03 9.297594e-03
> SL 1.983961e-04 2.412744e-04 3.354917e-04 5.336241e-04
> D 4.309986e-05 8.679096e-05 9.244503e-05 2.547176e-04
> XSm 2.759814e-04 4.812309e-04 4.249543e-04 9.095035e-04
> Sm 3.049081e-04 4.179082e-04 4.652088e-04 7.679929e-04
> Md 9.705559e-05 1.126409e-04 1.714340e-04 2.549410e-04
> Lg 4.938104e-05 1.777762e-05 7.269498e-05 3.391366e-05
> XLg 8.078062e-06 1.034075e-06 1.583885e-05 2.185849e-06Now let’s compare the stable stage distributions of the mean MPMs against the long-run average stage distributions developed with stochastic analysis (figure 10.1).
ss_put_together <- cbind.data.frame(tm2ss_r$ss_prop, tm3ss_r$ahist$ss_prop,
tm2ss_rs$ss_prop, tm3ss_rs$ahist$ss_prop)
names(ss_put_together) <- c("det ahist", "det hist", "sto ahist", "sto hist")
rownames(ss_put_together) <- tm2ss_r$stage
barplot(t(ss_put_together), beside=T, ylab = "Proportion", xlab = "Stage",
ylim = c(0, 0.95), col = c("black", "orangered", "grey", "darkred"),
bty = "n")
legend("topright", c("det ahist", "det hist", "sto ahist", "sto hist"),
col = c("black", "orangered", "grey", "darkred"), pch = 15, cex = 0.9,
bty = "n")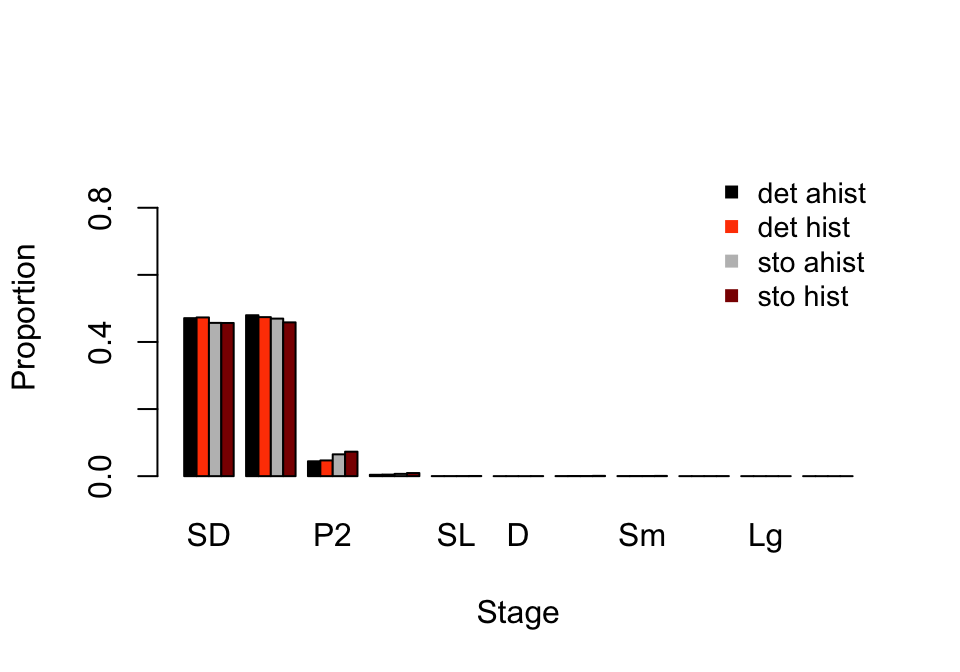
Figure 10.1: Ahistorical vs. historically-corrected stable and long-run mean stage distribution
Overall, these are similar patterns. However, deterministic analyses suggest a greater share of the population should be composed of dormant seeds and 1st year protocorms, and a lower share should be composed of 2nd year protocorms protocorms.
Let’s look at stochastic vs. deterministic reproductive values from ahistorical and historical approaches. First let’s calculate the reproductive values under each scenario.
tm2rv_r <- repvalue3(cyp2r_mean)
tm3rv_r <- repvalue3(cyp3r_mean)
tm2rv_rs <- repvalue3(cypmatrix2r, stochastic = TRUE, seed = 42)
tm3rv_rs <- repvalue3(cypmatrix3r, stochastic = TRUE, seed = 42)
tm2rv_rplot <- as.matrix(tm2rv_r$rep_value)
rownames(tm2rv_rplot) <- tm2rv_r$stage
tm2rv_rsplot <- as.matrix(tm2rv_rs$rep_value)
rownames(tm2rv_rsplot) <- tm2rv_rs$stage
tm3rv_rplot <- as.matrix(tm3rv_r$ahist$rep_value)
rownames(tm3rv_rplot) <- tm3rv_r$ahist$stage
tm3rv_rsplot <- as.matrix(tm3rv_rs$ahist$rep_value)
rownames(tm3rv_rsplot) <- tm3rv_rs$ahist$stageNow let’s compare them graphically (figure 10.2).
par(mfrow=c(2,2))
barplot(t(tm2rv_rplot), ylab = "Rep value", xlab = "", col = "black", bty = "n")
title("a)", adj = 0)
legend("topleft", c("det ahist", "det hist", "sto ahist", "sto hist"), cex =0.8,
col = c("black", "orangered", "grey", "darkred"), pch = 15, bty = "n")
barplot(t(tm3rv_rplot), ylab = "", xlab = "", col = "orangered", bty = "n")
title("b)", adj = 0)
barplot(t(tm2rv_rsplot), ylab = "Rep value", xlab = "Stage", col = "grey",
bty = "n")
title("c)", adj = 0)
barplot(t(tm3rv_rsplot), ylab = "", xlab = "Stage", col = "darkred", bty = "n")
title("d)", adj = 0)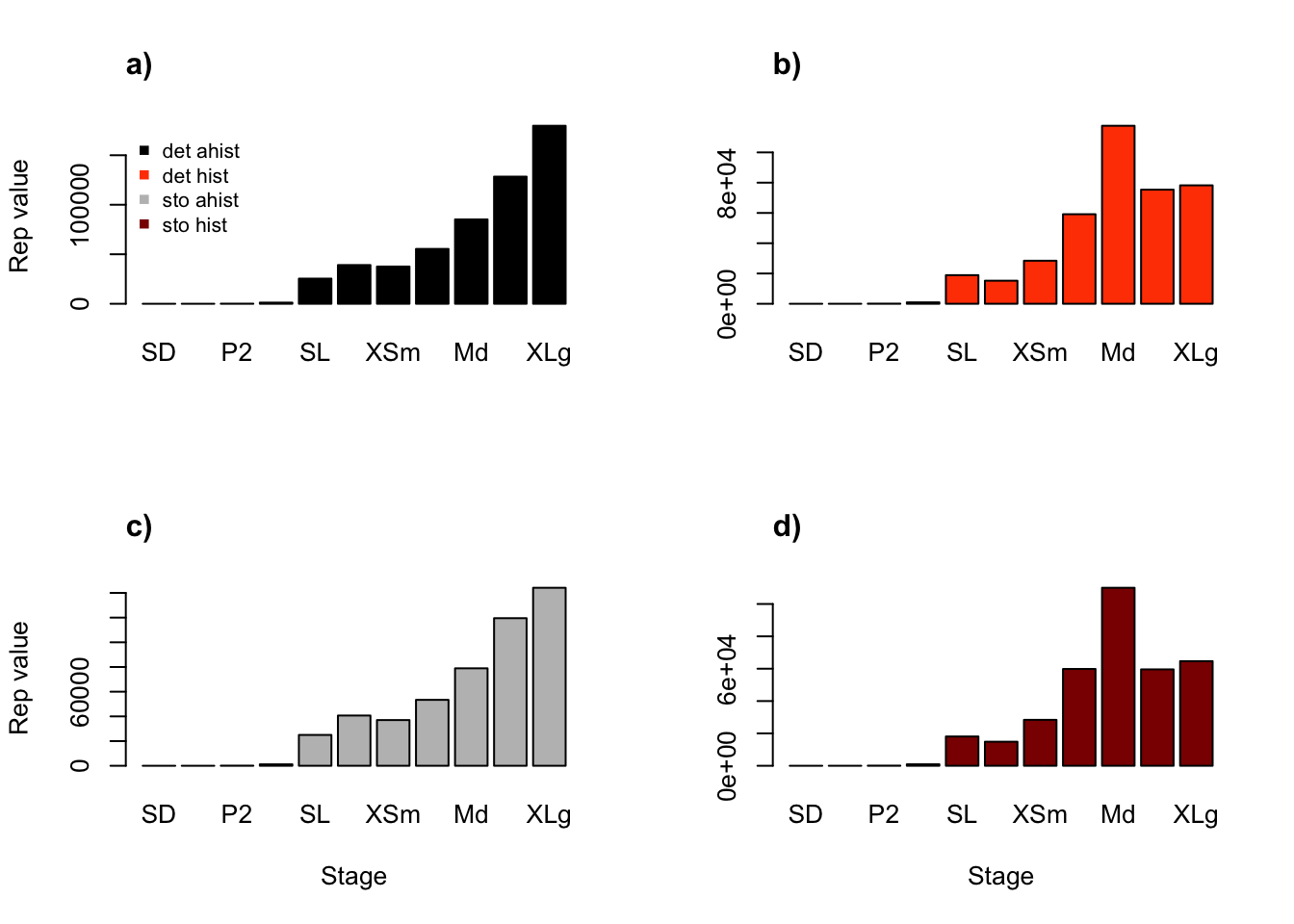
Figure 10.2: Ahistorical (a, c) vs. historically-corrected (b, d) deterministic (a, b) and stochastic (c, d) reproductive values
We see some big differences here, particularly between ahistorical and historical analyses. Indeed, in the ahistorical case, reproductive value increases with size, reaching its peak in the largest adults. In contrast, in the historical case, the greatest reproductive values are associated with medium adults. So, history appears to have large effects here, while temporal stochasticity does not seem to have much influence.
10.1.3 Stochastic sensitivity analysis
Package lefko3 contains functions allowing users to conduct deterministic and stochastic sensitivity and elasticity analyses. Sensitivity and elasticity analysis are forms of perturbation analysis. We urge readers to consult Caswell (2001) and Caswell (2019) to become fully acquainted with the topic. Here, we discuss just the most important aspects to understand these analyses as conducted using lefko3.
Stochastic sensitivity analysis assesses the impact of small, absolute changes in matrix elements on the log stochastic growth rate, \(a = \text{log} \lambda _{S}\) (Caswell 2001). The stochastic sensitivity of \(a\) to an element \(a _{kj}\) is as follows.
\[\begin{equation} \frac{\partial \text{log} \lambda _S}{\partial a _{kj}} = \lim_{T \to \infty} \frac{1}{T} \sum_{t=0}^{T-1} \frac{\mathbf{v}(t+1) \mathbf{w}^\top(t)}{\mathbf{v}^\top(t+1) \mathbf{w}(t+1)} \tag{10.6} \end{equation}\]
Here, \(t\) refers to a specific occasion and \(T\) refers to the number of occasions projected. Stochastic sensitivities for hMPMs may be converted to historically-corrected format as in the deterministic case.
Let’s now try a stochastic sensitivity analysis. We’ll start off using the ahistorical MPM. We will then assess the highest sensitivity value of biologically possible transitions.
set.seed(42)
tm2sens_rs <- sensitivity3(cypmatrix2r, stochastic = TRUE)
> Running stochastic analysis...
# The highest stochastic sensitivity value
max(tm2sens_rs$ah_sensmats[[1]][which(cyp2r_mean$A[[1]] > 0)])
> [1] 1.066749
# This value is associated with element
intersect(which(tm2sens_rs$ah_sensmats[[1]] ==
max(tm2sens_rs$ah_sensmats[[1]][which(cyp2r_mean$A[[1]] > 0)])),
which(cyp2r_mean$A[[1]] > 0))
> [1] 38
The highest sensitivity value is associated with element 38. Since there are 11 stages, and the element number refers to the position of the element within a vectorized form of the matrix, we can infer that \(log \lambda\) is most sensitive to the transition from 3rd year protocorm to seedling. Check this by typing ceiling(38/11) to get the column number and 38 %% 11 to get the row number for element 38.
# From stage
cypmatrix2r$ahstages[ceiling(38/dim(cypmatrix2r$ahstages)[1]),"stage"]
> [1] "P3"
# To stage
cypmatrix2r$ahstages[38 %% dim(cypmatrix2r$ahstages)[1],"stage"]
> [1] "SL"
Let’s compare this to the historical case. Note that the historical sensitivity matrices will be output in sparse format by default, so we need to use as.matrix() in some instances to make the code work properly.
set.seed(42)
tm3sens_rs <- sensitivity3(cypmatrix3r, stochastic = TRUE)
> Running stochastic analysis...
# The highest stochastic sensitivity value
max(tm3sens_rs$h_sensmats[[1]][which(cyp3r_mean$A[[1]] > 0)])
> [1] 1.576569
# This value is associated with element
intersect(which(as.matrix(tm3sens_rs$h_sensmats[[1]]) ==
max(tm3sens_rs$h_sensmats[[1]][which(cyp3r_mean$A[[1]] > 0)])),
which(cyp3r_mean$A[[1]] > 0))
> [1] 3063
Here we find that \(log \lambda\) is most sensitive to element 3063. We can use the same trick as with the ahistorical case to determine which transition this is, but we need to use the hstages portion of the historical MPM rather than the ahstages element. The hstages element outlines the 121 stage-pairs corresponding to the rows and column in these matrices. So, let’s figure this out, as below.
# From stage in t-1:
cypmatrix3r$hstages[ceiling(3063/dim(cypmatrix3r$hstages)[1]), "stage_1"]
> [1] "P2"
# From stage in t:
cypmatrix3r$hstages[ceiling(3063/dim(cypmatrix3r$hstages)[1]), "stage_2"]
> [1] "P3"
# To stage in t:
cypmatrix3r$hstages[3063 %% dim(cypmatrix3r$hstages)[1],"stage_1"]
> [1] "P3"
# To stage in t+1:
cypmatrix3r$hstages[3063 %% dim(cypmatrix3r$hstages)[1],"stage_2"]
> [1] "SL"This transition corresponds is from the 26th stage pair (2nd year and 3rd year protocorms in times t-1 and t, respectively), to the 38th stage pair (3rd year protocorm and seedling in times t and t+1, respectively). This is similar to our results from the deterministic sensitivity analysis in the last chapter (chapter 9).
10.1.4 Stochastic elasticity analysis
Elasticity analyses assess the impacts of small, proportional changes in matrix elements on population growth rate. In stochastic elasticity analysis, the population growth rate used is the log stochastic growth rate, \(a = \text{log} \lambda _{S}\) (Caswell 2001). The stochastic elasticity of \(a = \text{log} \lambda _{S}\) to changes in an element is given as follows.
\[\begin{equation} \frac{\partial \text{log} \lambda _S}{\partial \text{log} a _{kj}} = \lim_{T \to \infty} \frac{1}{T} \sum_{t=0}^{T-1} \frac{\bigl(\mathbf{v}(t+1) \mathbf{w}^\top(t) \bigr) \circ \mathbf{A_t}}{\mathbf{v}^\top(t+1) \mathbf{w}(t+1)} \tag{10.7} \end{equation}\]
Here, \(\mathbf{A_t}\) refers to the \(\mathbf{A}\) matrix corresponding to occasion t. Stochastic elasticity values for hMPMs may be converted to historically-corrected format as in the deterministic case, and may also be summed as before. Elements estimated to be exactly zero must also have elasticity values equal to zero, making their interpretation even more different than sensitivity values.
Let’s assess the elasticity of \(a = \text{log} \lambda _{S}\) to changes in matrix elements, comparing the ahistorical to the historically-corrected case in stochastic analyses. This time, we will use the matrix_interp() function to help interpret the results.
set.seed(42)
tm2elas_rs <- elasticity3(cypmatrix2r, stochastic = TRUE)
> Running stochastic analysis...
set.seed(42)
tm3elas_rs <- elasticity3(cypmatrix3r, stochastic = TRUE)
> Running stochastic analysis...
tm2elas_rs_mi <- matrix_interp(tm2elas_rs)
tm3elas_rs_mi_ah <- matrix_interp(tm3elas_rs)
tm3elas_rs_mi_h <- matrix_interp(tm3elas_rs, part = 2)
tm2elas_rs_mi[c(1:10),]
> index from_stage to_stage column row value
> 1 121 XLg XLg 11 11 0.28381987
> 2 73 XSm XSm 7 7 0.09306550
> 3 85 Sm Sm 8 8 0.07705852
> 4 14 P1 P2 2 3 0.05334194
> 5 26 P2 P3 3 4 0.05333767
> 6 38 P3 SL 4 5 0.05333747
> 7 109 Lg Lg 10 10 0.04733188
> 8 51 SL XSm 5 7 0.03843668
> 9 74 XSm Sm 7 8 0.03607814
> 10 86 Sm Md 8 9 0.03437504
tm3elas_rs_mi_ah[c(1:10),]
> index from_stage to_stage column row value
> 1 73 XSm XSm 7 7 0.17518251
> 2 85 Sm Sm 8 8 0.16986809
> 3 74 XSm Sm 7 8 0.11437259
> 4 15 P1 P3 2 4 0.07882891
> 5 27 P2 SL 3 5 0.07882846
> 6 80 Sm P2 8 3 0.05843126
> 7 40 P3 XSm 4 7 0.05658617
> 8 84 Sm XSm 8 7 0.05401023
> 9 51 SL XSm 5 7 0.05233336
> 10 79 Sm P1 8 2 0.04547141
tm3elas_rs_mi_h[c(1:10),]
> index from_stage to_stage column row value
> 1 8785 st2: XSm st1: XSm st2: XSm st1: XSm 73 73 0.14878660
> 2 10249 st2: Sm st1: Sm st2: Sm st1: Sm 85 85 0.13651363
> 3 1599 st2: P2 st1: P1 st2: P3 st1: P2 14 26 0.07882891
> 4 3063 st2: P3 st1: P2 st2: SL st1: P3 26 38 0.07882846
> 5 9452 st2: P1 st1: Sm st2: P2 st1: P1 79 14 0.05843126
> 6 8918 st2: Sm st1: XSm st2: Sm st1: Sm 74 85 0.05826425
> 7 4528 st2: SL st1: P3 st2: XSm st1: SL 38 51 0.05658617
> 8 8786 st2: XSm st1: XSm st2: Sm st1: XSm 73 74 0.05610833
> 9 6123 st2: XSm st1: SL st2: XSm st1: XSm 51 73 0.04330237
> 10 10243 st2: Sm st1: Sm st2: P1 st1: Sm 85 79 0.03949859
# Max ahistorical stoch elasticity occurs in element
which(tm2elas_rs$ah_elasmats[[1]] == max(tm2elas_rs$ah_elasmats[[1]]))
> [1] 121
# Max historically-corrected stoch elasticity occurs in element
which(as.matrix(tm3elas_rs$ah_elasmats[[1]]) == max(tm3elas_rs$ah_elasmats[[1]]))
> [1] 73
# Max historical stoch elasticity occurs in element
which(as.matrix(tm3elas_rs$h_elasmats[[1]]) == max(tm3elas_rs$h_elasmats[[1]]))
> [1] 8785We see some disagreement between historical and ahistorical elasticity analyses. Particularly, the ahistorical analysis suggests that \(\text{log} \lambda _{S}\) is most elastic to the stasis transition of Extra-Large Adults, with stasis of Extra-Small Adults second and stasis of Small Adults third. Historical analysis suggests that \(\text{log} \lambda _{S}\) is most elastic to the ahistorical stasis transition of Extra-Small Adults, with Small Adults second. Stasis of Extra-Large Adults falls out as effectively zero in historical analysis. These results are quite different from sensitivity analysis, where the ahistorical and historical stochastic sensitivity analyses suggested that population growth rate was most sensitivity to the transition from 3rd year protocorm to seedling (with 2nd year protocorm in time t-1 in the historical case).
Let’s compare the elasticity of population growth to life history stages (figure 10.3).
elas_put_together <- cbind.data.frame(colSums(tm2elas_rs$ah_elasmats[[1]]),
colSums(as.matrix(tm3elas_rs$ah_elasmats[[1]])))
names(elas_put_together) <- c("sto ahist", "sto hist")
rownames(elas_put_together) <- tm2elas_rs$ahstages$stage
barplot(t(elas_put_together), beside=T, ylab = "Elasticity", xlab = "Stage",
col = c("grey", "darkred"), ylim = c(0, 0.50), bty = "n")
legend("topright", c("sto ahist", "sto hist"), col = c("grey", "darkred"),
pch = 15, bty = "n")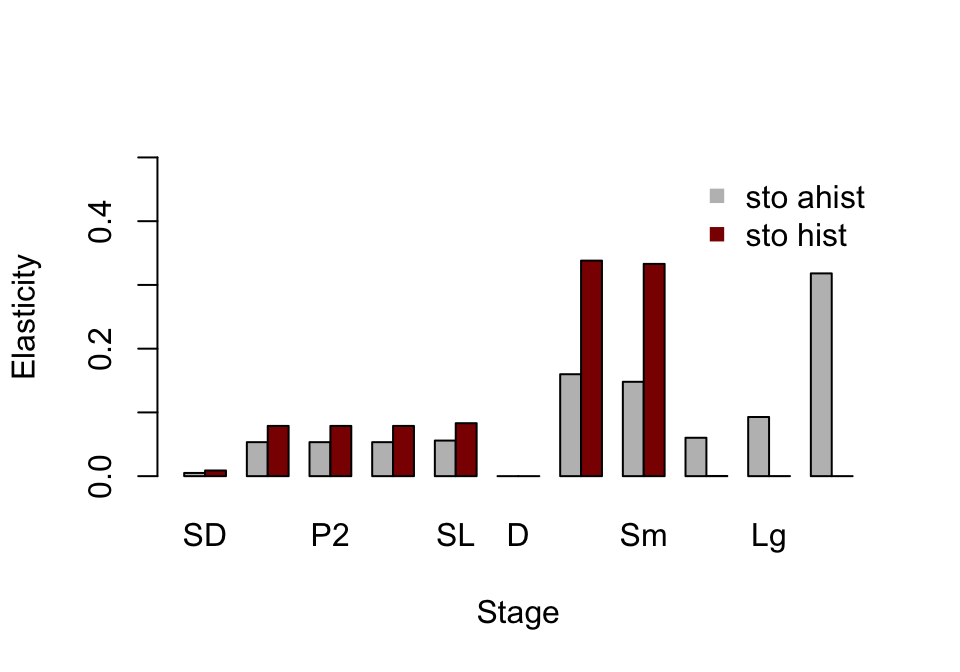
Figure 10.3: Ahistorical vs. historically-corrected stochastic elasticity to stage
Elasticity patterns in these plots show the rather large differences in impact of the adult stages that we alluded to with the matrix_interp() function output. The ahistorical analysis suggests that \(\text{log} \lambda _{S}\) is most elastic in response to changes in transitions from the Extra-Large Adult stage, followed by Extra-Small and Small Adults. The historical analysis suggests that \(\text{log} \lambda _{S}\) is most elastic in response to changes in Extra-Small and Small Adults, followed by Seedlings and the various protocorm stages.
Finally, let’s look at the elasticity sums of different transition types (figure 10.4).
tm2elas_rs_sums <- summary(tm2elas_rs)
tm3elas_rs_sums <- summary(tm3elas_rs)
elas_sums_together <- cbind.data.frame(tm2elas_rs_sums$ahist[,2],
tm3elas_rs_sums$ahist[,2])
names(elas_sums_together) <- c("sto ahist", "sto hist")
rownames(elas_sums_together) <- tm2elas_rs_sums$ahist$category
barplot(t(elas_sums_together), beside=T, ylab = "Elasticity",
xlab = "Transition", col = c("grey", "darkred"), ylim = c(0, 0.60), bty = "n")
legend("topright", c("sto ahist", "sto hist"), col = c("grey", "darkred"),
pch = 15, bty = "n")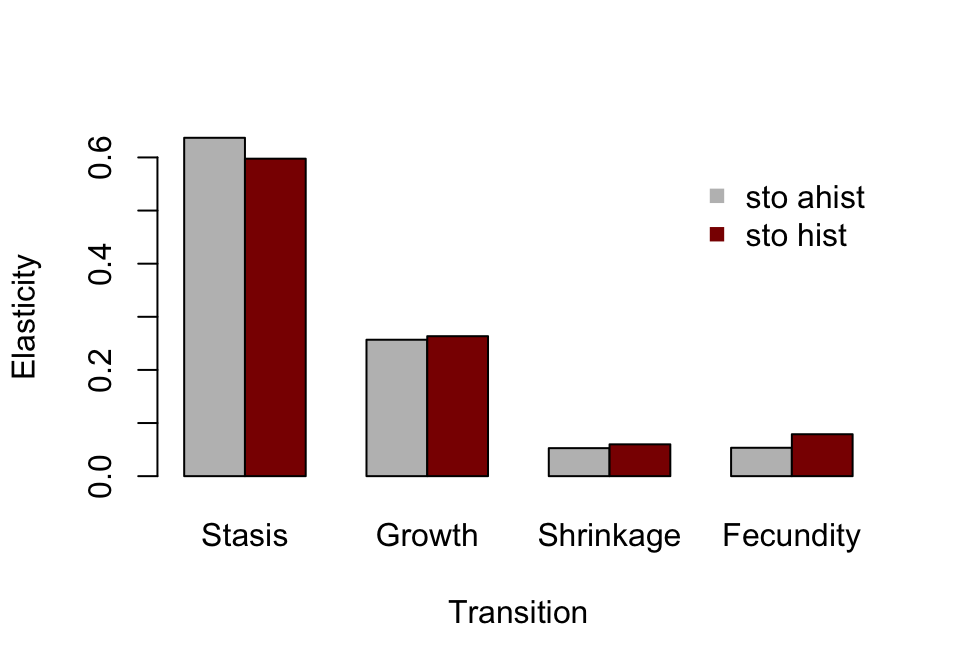
Figure 10.4: Ahistorical vs. historically-corrected elasticity of a to transitions
Both ahistorical and historical analyses show reasonably similar values for transition types, and suggest that \(\text{log} \lambda _{S}\) is most elastic in response to stasis transitions. In both analyses, shrinkage has the least influence (figures 10.4 and 10.5).
elas_hist2plot <- as.matrix(tm3elas_rs_sums$hist[,2])
rownames(elas_hist2plot) <- tm3elas_rs_sums$hist$category
par(mar = c(7, 4, 2, 2) + 0.2)
barplot(t(elas_hist2plot), ylab = "Elasticity", xlab = "", xaxt = "n",
col = c("orangered", "darkred"), bty = "n")
text(cex=0.6, x=seq(from = 0, to = 1.1*length(tm3elas_rs_sums$hist$category),
by = 1.15), y=-0.088, tm3elas_rs_sums$hist$category, xpd=TRUE, srt=45)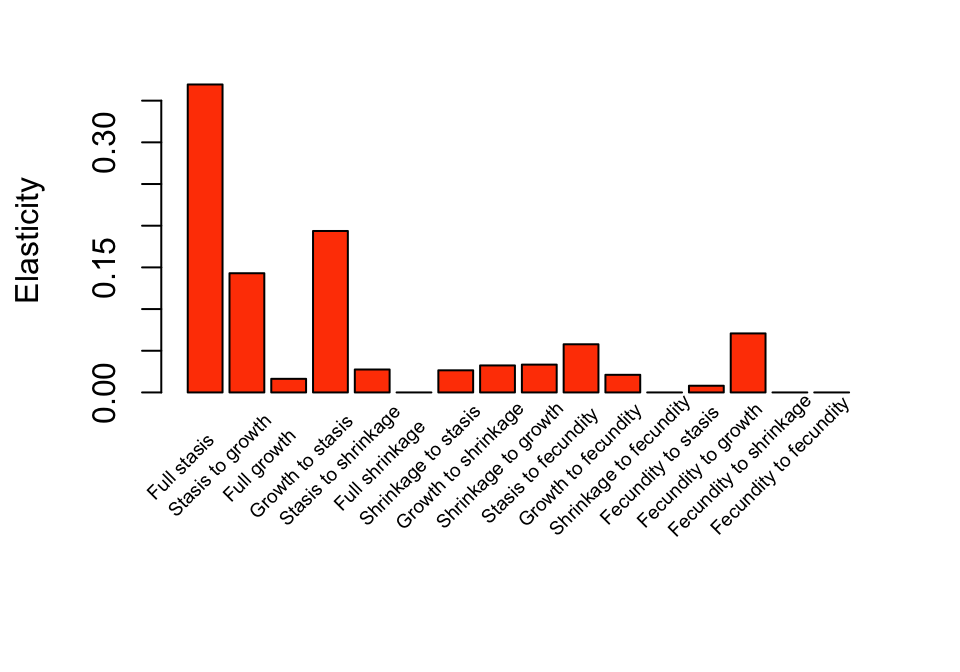
Figure 10.5: Elasticity of a to historical transitions
We can see that full stasis across occasions t-1, t, and t+1 is associated with the greatest summed elasticity, followed by growth to stasis and stasis to growth. Transitions associated with fecundity are typically associated with the lowest summed elasticity values, except for fecundity to growth.
10.2 The discrete-state Markovian sequence
In a discrete state Markovian sequence, the probability of choosing a specific matrix for the next time step depends on the current matrix. Such approaches might be useful when occasional random events make long-term changes to population dynamics, as might happen with fire and its impacts on tree populations, or when there is some degree of periodicity to population dynamics, leading to patterns that can be captured by specific orders of matrices.
Discrete-state Markovian sequences require the creation of state transition matrices. In these matrices, each row and column represents a specific matrix or time. Entries in each column describe the probability of choosing each matrix in the next time, assuming that the current matrix is the one represented by that column. For example, the following state transition matrix describes the probabilities of choosing each of five matrices, depending on which matrix is currently chosen.
\[\begin{equation} \left[\begin{array} {ccccc} 0.20 & 0.1 & 0.1 & 0.5 & 0.0 \\ 0.20 & 0.1 & 0.2 & 0.4 & 0.0 \\ 0.20 & 0.6 & 0.4 & 0.05 & 0.0 \\ 0.20 & 0.1 & 0.2 & 0.05 & 0.5 \\ 0.20 & 0.1 & 0.1 & 0.0 & 0.5 \\ \end{array}\right] \tag{10.8} \end{equation}\]
In the matrix above, we see that each matrix, or environmental state, can be chosen next with equal probability if the current matrix is the first matrix (this is shown by the equal probabilities in the first column). However, the probabilities differ greatly if the current matrix is any of the others. For example, matrix 2 has a 60% of being followed by matrix 3, while matrix 4 has a 50% chance of being followed by matrix 1. For the choice of matrix to be the same as in an iid analysis, all of the columns would need to be the same (though the elements within each column may differ).
The functions that we have described above can handle both the iid sequence scenario, and the discrete-state Markovian sequence scenario. Let’s see how to set up the latter. We will start off by looking at cypmatrix2r, which is our ahistorical Cypripedium MPM without patch-level designations.
summary(cypmatrix2r)
>
> This ahistorical lefkoMat object contains 5 matrices.
>
> Each matrix is square with 11 rows and columns, and a total of 121 elements.
> A total of 120 survival transitions were estimated, with 24 per matrix.
> A total of 40 fecundity transitions were estimated, with 8 per matrix.
> This lefkoMat object covers 1 population, 1 patch, and 5 time steps.
>
> The dataset contains a total of 74 unique individuals and 320 unique transitions.
>
> Survival probability sum check (each matrix represented by column in order):
> [,1] [,2] [,3] [,4] [,5]
> Min. 0.000 0.050 0.050 0.000 0.050
> 1st Qu. 0.100 0.140 0.140 0.100 0.140
> Median 0.689 0.870 0.864 0.610 0.882
> Mean 0.552 0.629 0.629 0.528 0.627
> 3rd Qu. 1.000 1.000 1.000 0.960 1.000
> Max. 1.000 1.000 1.000 1.000 1.000We see above that we have five matrices. Let’s input the state transition matrix given in (10.8), as below.
state_mat <- matrix(c(0.2, 0.2, 0.2, 0.2, 0.2, 0.1, 0.1, 0.6, 0.1, 0.1, 0.1,
0.2, 0.4, 0.2, 0.1, 0.5, 0.4, 0.05, 0.05, 0, 0, 0, 0, 0.5, 0.5), ncol = 5)
state_mat
> [,1] [,2] [,3] [,4] [,5]
> [1,] 0.2 0.1 0.1 0.50 0.0
> [2,] 0.2 0.1 0.2 0.40 0.0
> [3,] 0.2 0.6 0.4 0.05 0.0
> [4,] 0.2 0.1 0.2 0.05 0.5
> [5,] 0.2 0.1 0.1 0.00 0.5Now let’s estimate the stochastic population growth rate.
set.seed(42)
slambda3(cypmatrix2r, tweights = state_mat)
> pop patch a var sd se
> 1 1 1 0.07585393 0.7130141 0.8444016 0.008444016Here we find that \(log \lambda _{S} = a = 0.076\). We can take this further to explore the long-run stage distribution or reproductive value vector.
set.seed(42)
stablestage3(cypmatrix2r, stochastic = TRUE, tweights = state_mat)
> matrix_set poppatch stage_id stage ss_prop
> 1 1 1 1 1 SD 4.598135e-01
> 2 1 1 1 2 P1 4.717131e-01
> 3 1 1 1 3 P2 6.073521e-02
> 4 1 1 1 4 P3 6.301095e-03
> 5 1 1 1 5 SL 3.089116e-04
> 6 1 1 1 6 D 8.699419e-05
> 7 1 1 1 7 XSm 3.751295e-04
> 8 1 1 1 8 Sm 4.160132e-04
> 9 1 1 1 9 Md 1.605221e-04
> 10 1 1 1 10 Lg 6.853425e-05
> 11 1 1 1 11 XLg 2.104869e-05
repvalue3(cypmatrix2r, stochastic = TRUE, tweights = state_mat)
> matrix_set poppatch stage_id stage rep_value
> 1 1 1 1 1 SD 1.000000e+00
> 2 1 1 1 2 P1 9.995122e+00
> 3 1 1 1 3 P2 1.073805e+02
> 4 1 1 1 4 P3 1.150927e+03
> 5 1 1 1 5 SL 2.449901e+04
> 6 1 1 1 6 D 3.939705e+04
> 7 1 1 1 7 XSm 3.657325e+04
> 8 1 1 1 8 Sm 5.429431e+04
> 9 1 1 1 9 Md 8.246725e+04
> 10 1 1 1 10 Lg 1.337378e+05
> 11 1 1 1 11 XLg 1.155669e+05All of these analyses utilize the discrete-state Markovian matrix that we created earlier. Even sensitivity and elasticity analyses are possible. For example, here we conduct a stochastic sensitivity analysis assuming a first-order discrete Markovian state sequence.
dsms_1 <- sensitivity3(cypmatrix2r, stochastic = TRUE, tweights = state_mat)
> Running stochastic analysis with tweights option...
matrix_interp(dsms_1)
> index from_stage to_stage column row value
> 1 22 P1 XLg 2 11 3.248722e+03
> 2 11 SD XLg 1 11 3.191755e+03
> 3 21 P1 Lg 2 10 1.122446e+03
> 4 10 SD Lg 1 10 1.102763e+03
> 5 20 P1 Md 2 9 4.109622e+02
> 6 9 SD Md 1 9 4.037560e+02
> 7 33 P2 XLg 3 11 2.899210e+02
> 8 19 P1 Sm 2 8 2.632190e+02
> 9 8 SD Sm 1 8 2.586035e+02
> 10 18 P1 XSm 2 7 2.263288e+02
> 11 7 SD XSm 1 7 2.223601e+02
> 12 16 P1 SL 2 5 1.339261e+02
> 13 5 SD SL 1 5 1.315778e+02
> 14 32 P2 Lg 3 10 1.001691e+02
> 15 31 P2 Md 3 9 3.667410e+01
> 16 44 P3 XLg 4 11 2.587326e+01
> 17 30 P2 Sm 3 8 2.348927e+01
> 18 29 P2 XSm 3 7 2.019744e+01
> 19 27 P2 SL 3 5 1.195143e+01
> 20 43 P3 Lg 4 10 8.939389e+00
> 21 15 P1 P3 2 4 5.975754e+00
> 22 4 SD P3 1 4 5.870971e+00
> 23 42 P3 Md 4 9 3.272762e+00
> 24 41 P3 Sm 4 8 2.096137e+00
> 25 77 XSm XLg 7 11 2.048337e+00
> 26 40 P3 XSm 4 7 1.802413e+00
> 27 88 Sm XLg 8 11 1.630579e+00
> 28 55 SL XLg 5 11 1.208444e+00
> 29 38 P3 SL 4 5 1.066534e+00
> 30 76 XSm Lg 7 10 7.077164e-01
> 31 87 Sm Lg 8 10 5.633939e-01
> 32 14 P1 P2 2 3 5.333115e-01
> 33 26 P2 P3 3 4 5.332689e-01
> 34 3 SD P2 1 3 5.239600e-01
> 35 99 Md XLg 9 11 4.248392e-01
> 36 54 SL Lg 5 10 4.175657e-01
> 37 121 XLg XLg 11 11 2.839532e-01
> 38 75 XSm Md 7 9 2.590777e-01
> 39 110 Lg XLg 10 11 2.397314e-01
> 40 86 Sm Md 8 9 2.062556e-01
> 41 74 XSm Sm 7 8 1.659371e-01
> 42 53 SL Md 5 9 1.528570e-01
> 43 98 Md Lg 9 10 1.468247e-01
> 44 73 XSm XSm 7 7 1.426916e-01
> 45 85 Sm Sm 8 8 1.321069e-01
> 46 84 Sm XSm 8 7 1.135965e-01
> 47 66 D XLg 6 11 1.123535e-01
> 48 120 XLg Lg 11 10 9.815223e-02
> 49 52 SL Sm 5 8 9.790357e-02
> 50 71 XSm SL 7 5 8.443291e-02
> 51 51 SL XSm 5 7 8.418657e-02
> 52 109 Lg Lg 10 10 8.286982e-02
> 53 17 P1 D 2 6 7.244662e-02
> 54 6 SD D 1 6 7.108606e-02
> 55 82 Sm SL 8 5 6.721781e-02
> 56 97 Md Md 9 9 5.375489e-02
> 57 49 SL SL 5 5 4.981475e-02
> 58 13 P1 P1 2 2 4.763486e-02
> 59 25 P2 P2 3 3 4.759201e-02
> 60 37 P3 P3 4 4 4.758843e-02
> 61 2 SD P1 1 2 4.679960e-02
> 62 65 D Lg 6 10 3.886064e-02
> 63 119 XLg Md 11 9 3.593482e-02
> 64 96 Md Sm 9 8 3.443250e-02
> 65 108 Lg Md 10 9 3.033746e-02
> 66 95 Md XSm 9 7 2.960473e-02
> 67 118 XLg Sm 11 8 2.301840e-02
> 68 117 XLg XSm 11 7 1.978980e-02
> 69 107 Lg Sm 10 8 1.943339e-02
> 70 93 Md SL 9 5 1.751863e-02
> 71 106 Lg XSm 10 7 1.670810e-02
> 72 64 D Md 6 9 1.422238e-02
> 73 115 XLg SL 11 5 1.171091e-02
> 74 104 Lg SL 10 5 9.887189e-03
> 75 63 D Sm 6 8 9.111205e-03
> 76 62 D XSm 6 7 7.832989e-03
> 77 28 P2 D 3 6 6.946818e-03
> 78 60 D SL 6 5 4.635346e-03
> 79 12 P1 SD 2 1 4.623829e-03
> 80 1 SD SD 1 1 4.542752e-03
> 81 24 P2 P1 3 2 4.250858e-03
> 82 36 P3 P2 4 3 4.247053e-03
> 83 70 XSm P3 7 4 3.767423e-03
> 84 81 Sm P3 8 4 2.999303e-03
> 85 48 SL P3 5 4 2.222778e-03
> 86 92 Md P3 9 4 7.817502e-04
> 87 39 P3 D 4 6 6.748169e-04
> 88 114 XLg P3 11 4 5.226117e-04
> 89 103 Lg P3 10 4 4.412369e-04
> 90 23 P2 SD 3 1 4.126224e-04
> 91 35 P3 P1 4 2 3.793406e-04
> 92 69 XSm P2 7 3 3.362256e-04
> 93 80 Sm P2 8 3 2.676751e-04
> 94 59 D P3 6 4 2.068970e-04
> 95 47 SL P2 5 3 1.983729e-04
> 96 91 Md P2 9 3 6.976867e-05
> 97 113 XLg P2 11 3 4.664174e-05
> 98 102 Lg P2 10 3 3.937933e-05
> 99 72 XSm D 7 6 3.908433e-05
> 100 83 Sm D 8 6 3.691910e-05
> 101 34 P3 SD 4 1 3.682185e-05
> 102 50 SL D 5 6 3.384654e-05
> 103 68 XSm P1 7 2 3.003116e-05
> 104 79 Sm P1 8 2 2.390842e-05
> 105 94 Md D 9 6 2.038710e-05
> 106 116 XLg D 11 6 2.014642e-05
> 107 58 D P2 6 3 1.846512e-05
> 108 46 SL P1 5 2 1.771840e-05
> 109 105 Lg D 10 6 1.689389e-05
> 110 61 D D 6 6 1.465154e-05
> 111 90 Md P1 9 2 6.231708e-06
> 112 112 XLg P1 11 2 4.166043e-06
> 113 101 Lg P1 10 2 3.517365e-06
> 114 67 XSm SD 7 1 2.915065e-06
> 115 78 Sm SD 8 1 2.320744e-06
> 116 45 SL SD 5 1 1.719884e-06
> 117 57 D P1 6 2 1.649307e-06
> 118 89 Md SD 9 1 6.049025e-07
> 119 111 XLg SD 11 1 4.043923e-07
> 120 100 Lg SD 10 1 3.414221e-07
> 121 56 D SD 6 1 1.600960e-07
Function matrix_interp() shows us the elements of the sensitivity matrix in order from greatest magnitude to smallest magnitude. Many of the top elements are biologically impossible, but scrolling through the output, we find that the \(log \lambda _{S} = a\) is greatest among biologically plausible elements in the survival transition from seedling (SL) to extra-large adult (XLg), which is the 28th element in the matrix_interp() output.
An alternative, more general approach to conducting discrete-state Markovian sequence-based analyses is to utilize the general projection functions. One way to use these functions is to use the discrete state transition matrix that we made as input into the tweights argument in functions projection3() and f_projection3(), provided we set stochastic = TRUE. However, we can use a more general approach in which we have more control over the sequence of matrices, as well.
Let’s try the latter approach to create a stochastic simulation using state transition matrix state_mat. Perhaps we wish to simulate 100 years forward. We can first use the markov_run() function to create a sequence of times / matrices, as below.
set.seed(42)
cyp_state_seq <- markov_run(c(2004, 2005, 2006, 2007, 2008), mat = state_mat,
times = 100)
cyp_state_seq
> [1] 2004 2008 2008 2007 2005 2004 2006 2007 2004 2007 2005 2006 2007 2006 2006
> [16] 2005 2008 2008 2007 2004 2006 2008 2007 2007 2006 2006 2005 2006 2008 2007
> [31] 2005 2005 2007 2004 2007 2004 2008 2007 2004 2008 2008 2007 2004 2004 2008
> [46] 2007 2007 2005 2004 2008 2008 2007 2004 2005 2005 2006 2007 2005 2006 2006
> [61] 2005 2004 2008 2008 2008 2008 2007 2004 2008 2008 2007 2004 2004 2005 2006
> [76] 2006 2007 2004 2005 2006 2006 2005 2006 2006 2007 2005 2006 2006 2006 2006
> [91] 2006 2007 2004 2005 2008 2008 2008 2007 2005 2005
The first argument in the function is a vector of the years corresponding to the matrices (these can be viewed in the labels object of cypmatrix2r). The second argument is the state matrix. The final argument is the number of time steps to project. The result is a vector of years, which can be used as input into the year argument of function projection3(), as below. Note also that although this is a stochastic simulation, we deliberately leave the stochastic argument to the default, which is FALSE.
cyp_disc_proj1 <- projection3(mpm = cypmatrix2r, times = 100,
year = cyp_state_seq, growthonly = FALSE)
summary(cyp_disc_proj1)
>
> The input lefkoProj object covers 1 population-patches.
> It is a single projection including 100 projected steps per replicate, and 1 replicates, respectively.
> The number of replicates with population size above the threshold size of 1 is as in
> the following matrix, with pop-patches given by column and milepost times given by row:
> $milepost_sums
> 1 1
> 0 1
> 0.25 1
> 0.5 1
> 0.75 1
> 1 1
>
> $extinction_times
> [1] NA
We can look further into the resulting object to get the proper information. For example, using the growthonly = FALSE argument provides stage structure and reproductive value information for each time step, in addition to more general information about population size at each step.
cyp_disc_proj1
> $projection
> $projection[[1]]
> $projection[[1]][[1]]
> [,1] [,2] [,3] [,4] [,5] [,6]
> [1,] 1 9.884009e+03 4086.6829112 3988.5419295 1665.8529124 1.075062e+04
> [2,] 1 9.884029e+03 4284.3630826 4070.2755877 1745.6237510 1.078394e+04
> [3,] 1 1.000000e-01 988.4028571 428.4363083 407.0275588 1.745624e+02
> [4,] 1 1.000000e-01 0.0100000 98.8402857 42.8436308 4.070276e+01
> [5,] 1 1.000000e-01 0.0100000 0.0010000 4.9420643 2.389285e+00
> [6,] 1 7.391304e-02 0.0000000 0.0000000 0.2661808 4.037317e-01
> [7,] 1 1.358696e+00 0.7829767 0.4556765 0.7529154 2.945267e+00
> [8,] 1 1.595756e+00 1.7031782 1.4575460 1.0108652 2.144727e+00
> [9,] 1 7.095238e-01 0.7198788 0.7402830 1.0723051 6.569850e-01
> [10,] 1 7.149068e-01 0.9861558 1.2663124 0.2110521 2.462274e-01
> [11,] 1 1.142857e+00 1.1428571 1.1428571 0.4221041 2.110521e-01
> [,7] [,8] [,9] [,10] [,11]
> [1,] 4033.9675055 7838.5698198 1983.7034612 4756.3671016 1415.1199435
> [2,] 4248.9799116 7919.2491699 2140.4748576 4796.0411708 1510.2472856
> [3,] 1078.3937365 424.8979912 791.9249170 214.0474858 479.6041171
> [4,] 17.4562375 107.8393737 42.4897991 79.1924917 21.4047486
> [5,] 2.1546020 0.9805420 5.4409958 2.3965397 4.0794516
> [6,] 0.2007724 0.2909579 1.2684125 0.2769215 1.7958414
> [7,] 3.5477683 3.2195978 2.5604972 4.7305973 3.5745129
> [8,] 2.6186209 3.2519262 2.3071000 3.5158265 3.0351337
> [9,] 0.6554239 0.7435196 1.5027551 1.0196519 1.5952758
> [10,] 0.3344550 0.8474792 0.2382325 0.3977343 0.1585962
> [11,] 0.2462274 0.0000000 0.2824931 0.3165263 0.1325781
> [,12] [,13] [,14] [,15] [,16]
> [1,] 1.172107e+04 8809.2842778 2316.2342721 11624.483812 1.242907e+04
> [2,] 1.174937e+04 9043.7057208 2492.4199577 11670.808497 1.266156e+04
> [3,] 1.510247e+02 1174.9374547 904.3705721 249.241996 1.167081e+03
> [4,] 4.796041e+01 15.1024729 117.4937455 90.437057 2.492420e+01
> [5,] 1.274210e+00 2.4617311 0.8782102 5.918598 4.817783e+00
> [6,] 6.715540e-01 0.6082888 2.0675720 0.400520 5.337457e-01
> [7,] 4.878131e+00 4.4591268 4.1527872 4.672510 5.737753e+00
> [8,] 5.474599e+00 5.2361778 3.6046796 4.803712 5.949460e+00
> [9,] 1.013134e+00 1.2803040 2.1854554 1.560597 1.439731e+00
> [10,] 9.272176e-02 0.6771072 0.3156141 1.051158 1.580388e+00
> [11,] 6.628905e-02 0.0000000 0.2257024 0.000000 0.000000e+00
> [,17] [,18] [,19] [,20] [,21]
> [1,] 1.935399e+04 4827.822092 5349.415777 4150.8771550 1.238597e+04
> [2,] 1.960257e+04 5214.901890 5445.972218 4257.8654705 1.246899e+04
> [3,] 1.266156e+03 1960.257125 521.490189 544.5972218 4.257865e+02
> [4,] 1.167081e+02 126.615559 196.025712 52.1490189 5.445972e+01
> [5,] 1.487099e+00 5.909759 6.626266 10.1325989 3.114081e+00
> [6,] 1.012542e+00 0.000000 0.000000 2.9707713 5.922416e-01
> [7,] 7.247763e+00 4.763380 4.506058 6.5287368 1.046116e+01
> [8,] 6.810411e+00 8.516369 9.515687 6.3101441 8.810452e+00
> [9,] 1.870775e+00 2.204306 2.655156 4.2326657 2.796751e+00
> [10,] 2.633981e-01 1.131704 2.183744 0.3639573 9.151003e-01
> [11,] 0.000000e+00 0.000000 0.000000 0.7279146 7.799085e-01
> [,22] [,23] [,24] [,25] [,26]
> [1,] 2.615162e+04 9654.390530 6317.9931292 2435.9747299 2.196498e+04
> [2,] 2.639934e+04 10177.422917 6511.0809398 2562.3345925 2.201370e+04
> [3,] 1.246899e+03 2639.933872 1017.7422917 651.1080940 2.562335e+02
> [4,] 4.257865e+01 124.689871 263.9933872 101.7742292 6.511081e+01
> [5,] 2.878690e+00 2.272867 6.3481369 13.5170762 5.764565e+00
> [6,] 9.789391e-01 0.000000 2.8905940 4.0156856 7.669965e-01
> [7,] 8.657651e+00 5.986343 6.6523542 8.1753258 1.325102e+01
> [8,] 9.720188e+00 11.459366 6.9412025 6.9029686 1.196054e+01
> [9,] 2.697447e+00 3.166637 5.5385612 4.2923847 3.046329e+00
> [10,] 2.658385e+00 3.904522 0.6507537 1.0719903 2.277171e+00
> [11,] 0.000000e+00 0.000000 1.3015075 0.2169179 0.000000e+00
> [,27] [,28] [,29] [,30] [,31]
> [1,] 27431.662130 4.287586e+04 26747.452311 10896.412084 7658.8304536
> [2,] 27870.961682 4.342449e+04 27604.969426 11431.361130 7876.7586952
> [3,] 2201.369713 2.787096e+03 4342.448899 2760.496943 1143.1361130
> [4,] 25.623346 2.201370e+02 278.709617 434.244890 276.0496943
> [5,] 3.543769 1.458356e+00 11.079766 14.489469 22.4367180
> [6,] 1.328948 1.714263e+00 1.567947 0.000000 6.1937900
> [7,] 11.707835 1.236486e+01 10.912481 10.177075 13.2267546
> [8,] 12.973028 1.411152e+01 13.538214 17.748744 12.4148630
> [9,] 3.285191 4.171859e+00 3.984145 4.580840 7.7813148
> [10,] 3.501617 5.836029e-01 2.092441 3.884842 0.6474737
> [11,] 0.000000 0.000000e+00 0.000000 0.000000 1.2949475
> [,32] [,33] [,34] [,35] [,36]
> [1,] 6.094007e+04 5.905812e+04 9.918556e+03 1.704734e+04 7173.5524509
> [2,] 6.109324e+04 6.027692e+04 1.109972e+04 1.724571e+04 7514.4992851
> [3,] 7.876759e+02 6.109324e+03 6.027692e+03 1.109972e+03 1724.5712833
> [4,] 1.143136e+02 7.876759e+01 6.109324e+02 6.027692e+02 110.9971838
> [5,] 1.492432e+01 6.461897e+00 4.261474e+00 3.075970e+01 31.6764432
> [6,] 2.975676e+00 3.619220e+00 1.017399e+01 9.825405e-01 10.6343871
> [7,] 2.169432e+01 2.585696e+01 1.961540e+01 1.872821e+01 21.2675925
> [8,] 2.225666e+01 2.409606e+01 1.596040e+01 1.879062e+01 18.1182610
> [9,] 4.701718e+00 4.115987e+00 8.769275e+00 6.350826e+00 8.6483760
> [10,] 7.553860e-01 4.496345e-01 1.281346e+00 2.461969e+00 0.7378416
> [11,] 6.474737e-01 3.237369e-01 1.498782e-01 3.329276e-01 0.8206562
> [,37] [,38] [,39] [,40] [,41]
> [1,] 2.182968e+04 1.612115e+04 1.241389e+04 35062.372579 21362.736320
> [2,] 2.197315e+04 1.655774e+04 1.273631e+04 35310.650322 22063.983771
> [3,] 7.514499e+02 2.197315e+03 1.655774e+03 1273.631017 3531.065032
> [4,] 1.724571e+02 7.514499e+01 2.197315e+02 165.577448 127.363102
> [5,] 7.133681e+00 8.979540e+00 4.206227e+00 11.196888 8.838717
> [6,] 1.888744e+00 0.000000e+00 9.214670e+00 1.016200 0.000000
> [7,] 3.286072e+01 1.965268e+01 2.042823e+01 20.166405 14.622966
> [8,] 2.444230e+01 3.355832e+01 1.969364e+01 23.560959 28.228303
> [9,] 6.584466e+00 7.813914e+00 1.373186e+01 8.901090 9.447695
> [10,] 2.211139e+00 5.295038e+00 8.825064e-01 2.765659 6.376871
> [11,] 9.260621e-01 9.260621e-01 1.765013e+00 1.891085 1.891085
> [,42] [,43] [,44] [,45] [,46]
> [1,] 26036.533884 16274.972440 49121.149010 51540.986111 26026.967144
> [2,] 26463.788611 16795.703118 49446.648459 52523.409091 27057.786866
> [3,] 2206.398377 2646.378861 1679.570312 4944.664846 5252.340909
> [4,] 353.106503 220.639838 264.637886 167.957031 494.466485
> [5,] 6.810091 17.995830 11.931783 13.828483 9.089276
> [6,] 0.000000 6.474005 1.237494 1.358465 0.000000
> [7,] 11.025019 15.865289 22.892449 26.330522 18.560175
> [8,] 27.629903 17.320138 23.814180 25.609260 33.284829
> [9,] 10.406748 14.551386 8.954846 7.998874 9.012010
> [10,] 10.399283 1.733214 3.135342 3.682432 7.188578
> [11,] 1.891085 3.466428 3.714030 4.161936 4.161936
> [,47] [,48] [,49] [,50] [,51]
> [1,] 14729.604770 6202.3858030 8.532644e+04 2.978942e+04 2.204870e+04
> [2,] 15250.144112 6496.9778984 8.545049e+04 3.149595e+04 2.264449e+04
> [3,] 2705.778687 1525.0144112 6.496978e+02 8.545049e+03 3.149595e+03
> [4,] 525.234091 270.5778687 1.525014e+02 6.496978e+01 8.545049e+02
> [5,] 25.177788 27.5205939 1.490492e+01 8.370318e+00 3.667005e+00
> [6,] 8.978713 12.9922946 4.670276e+00 1.931801e+00 0.000000e+00
> [7,] 20.295688 25.5738147 3.399798e+01 3.883187e+01 2.349129e+01
> [8,] 20.128019 20.8250871 3.941941e+01 3.693974e+01 4.473760e+01
> [9,] 14.692064 11.7543985 8.363070e+00 1.001967e+01 1.186060e+01
> [10,] 1.198096 3.1925871 7.317806e-01 2.732640e+00 7.410483e+00
> [11,] 2.396193 0.3993654 1.996827e-01 3.042228e-01 3.042228e-01
> [,52] [,53] [,54] [,55] [,56]
> [1,] 3.034113e+04 21401.481619 66041.845799 1.681186e+05 1.382967e+05
> [2,] 3.078211e+04 22008.304293 66469.875432 1.694395e+05 1.416590e+05
> [3,] 2.264449e+03 3078.210774 2200.830429 6.646988e+03 1.694395e+04
> [4,] 3.149595e+02 226.444917 307.821077 2.200830e+02 6.646988e+02
> [5,] 4.290859e+01 17.893405 12.216916 1.600190e+01 1.180425e+01
> [6,] 0.000000e+00 13.759651 1.869201 5.210816e+00 5.720731e+00
> [7,] 1.435781e+01 30.466248 35.529165 3.795947e+01 4.126493e+01
> [8,] 4.067405e+01 29.964579 37.197505 3.903873e+01 4.280230e+01
> [9,] 1.415870e+01 20.124927 13.353764 1.097833e+01 9.313701e+00
> [10,] 1.300726e+01 2.167876 4.575899 3.085374e+00 1.675591e+00
> [11,] 3.042228e-01 4.335753 4.645449 2.322725e+00 1.161362e+00
> [,57] [,58] [,59] [,60] [,61]
> [1,] 86052.540666 21345.656415 1.458034e+05 1.120823e+05 1.457290e+05
> [2,] 88818.473714 23066.707228 1.462303e+05 1.149983e+05 1.479706e+05
> [3,] 14165.902484 8881.847371 2.306671e+03 1.462303e+04 1.149983e+04
> [4,] 1694.394600 1416.590248 8.881847e+02 2.306671e+02 1.462303e+03
> [5,] 33.825150 86.410988 7.515006e+01 4.816674e+01 1.394169e+01
> [6,] 4.755811 18.984284 9.746438e+00 7.169835e+00 8.869552e+00
> [7,] 37.538980 37.733762 7.028894e+01 8.123277e+01 7.878372e+01
> [8,] 42.964140 32.546923 6.452851e+01 7.982597e+01 8.559553e+01
> [9,] 10.770913 18.574885 1.204589e+01 1.571851e+01 1.954796e+01
> [10,] 7.042350 2.758995 1.633558e+00 8.925604e+00 1.658514e+01
> [11,] 0.000000 2.347450 1.173725e+00 0.000000e+00 0.000000e+00
> [,62] [,63] [,64] [,65] [,66]
> [1,] 248112.02563 7.400904e+04 5.475217e+04 7.803476e+04 1.086920e+05
> [2,] 251026.60499 7.897128e+04 5.623235e+04 7.912980e+04 1.102527e+05
> [3,] 14797.06135 2.510266e+04 7.897128e+03 5.623235e+03 7.912980e+03
> [4,] 1149.98343 1.479706e+03 2.510266e+03 7.897128e+02 5.623235e+02
> [5,] 73.81225 6.118978e+01 7.704480e+01 1.293655e+02 4.595392e+01
> [6,] 10.86959 5.649030e+00 0.000000e+00 0.000000e+00 0.000000e+00
> [7,] 78.25911 1.070374e+02 7.640395e+01 6.625727e+01 7.893774e+01
> [8,] 89.20795 9.233849e+01 1.293084e+02 1.423211e+02 1.626560e+02
> [9,] 23.32096 2.459126e+01 2.930680e+01 3.719286e+01 4.463830e+01
> [10,] 2.76419 7.314203e+00 1.889369e+01 3.382677e+01 5.149681e+01
> [11,] 0.00000 3.948843e-01 3.948843e-01 3.948843e-01 3.948843e-01
> [,67] [,68] [,69] [,70] [,71]
> [1,] 1.439782e+05 102754.34186 315549.29959 152840.94538 169797.16879
> [2,] 1.461520e+05 105633.90601 317604.38643 159151.93138 172853.98769
> [3,] 1.102527e+04 14615.20467 10563.39060 31760.43864 15915.19314
> [4,] 7.912980e+02 1102.52673 1461.52047 1056.33906 3176.04386
> [5,] 3.041387e+01 41.08559 57.18062 75.93505 56.61371
> [6,] 0.000000e+00 34.80049 4.94268 0.00000 0.00000
> [7,] 5.956547e+01 84.92173 98.00281 72.50432 65.03404
> [8,] 1.552455e+02 95.45045 124.13371 144.28848 149.90962
> [9,] 5.261472e+01 84.04250 51.24504 53.03774 56.75342
> [10,] 7.222439e+01 12.03740 18.97501 39.08826 60.83525
> [11,] 3.948843e-01 24.07480 25.79442 25.79442 25.79442
> [,72] [,73] [,74] [,75] [,76]
> [1,] 94261.73737 2.823967e+05 3.003045e+05 746948.99316 489634.44244
> [2,] 97657.68074 2.842819e+05 3.059524e+05 752955.08253 504573.42230
> [3,] 17285.39877 9.765768e+03 2.842819e+04 30595.24024 75295.50825
> [4,] 1591.51931 1.728540e+03 9.765768e+02 2842.81925 3059.52402
> [5,] 161.63288 8.765761e+01 9.080987e+01 53.36933 144.80943
> [6,] 38.92188 8.953841e+00 9.589501e+00 27.11025 19.44700
> [7,] 92.79532 1.591982e+02 1.800153e+02 194.97366 171.51360
> [8,] 99.56234 1.446912e+02 1.600882e+02 175.02298 188.30030
> [9,] 80.79096 5.035857e+01 4.681684e+01 43.76106 47.75880
> [10,] 10.13921 1.790751e+01 2.219038e+01 15.84094 45.81049
> [11,] 20.27842 2.172687e+01 2.428509e+01 12.14254 0.00000
> [,77] [,78] [,79] [,80] [,81]
> [1,] 476062.64318 133678.93602 342907.74936 965868.16222 666150.27822
> [2,] 485855.33203 143200.18889 345581.32808 972726.31721 685467.64147
> [3,] 50457.34223 48585.53320 14320.01889 34558.13281 97272.63172
> [4,] 7529.55083 5045.73422 4858.55332 1432.00189 3455.81328
> [5,] 160.21667 384.48837 271.51113 256.50322 84.42526
> [6,] 20.92226 92.14452 19.65786 54.80749 32.98969
> [7,] 189.58172 182.98899 335.60015 391.37662 384.00104
> [8,] 206.86464 162.92882 245.64868 296.90720 374.92664
> [9,] 49.94446 99.54417 69.51794 63.13923 78.84142
> [10,] 65.06519 17.81828 28.09234 16.79899 57.92452
> [11,] 0.00000 21.68840 24.23387 12.11693 0.00000
> [,82] [,83] [,84] [,85] [,86]
> [1,] 767072.03549 1.204627e+06 763860.92232 965850.45544 278391.81775
> [2,] 780395.04106 1.219969e+06 787953.46912 981127.67389 297708.82686
> [3,] 68546.76415 7.803950e+04 121996.87808 78795.34691 98112.76739
> [4,] 9727.26317 6.854676e+03 7803.95041 12199.68781 7879.53469
> [5,] 177.01193 4.952138e+02 367.49451 408.57225 630.41300
> [6,] 41.65852 5.255404e+01 45.92604 55.71236 243.50211
> [7,] 321.73350 3.783398e+02 487.03854 508.38930 482.96999
> [8,] 372.66940 4.133344e+02 501.41123 550.44453 419.28634
> [9,] 94.15374 1.166798e+02 114.98097 128.95313 242.29753
> [10,] 94.45702 1.574284e+01 59.32461 109.24185 36.77776
> [11,] 0.00000 0.000000e+00 0.00000 0.00000 36.41395
> [,87] [,88] [,89] [,90] [,91]
> [1,] 1.963179e+06 1.431256e+06 1.646752e+06 2045688.3422 2.403000e+06
> [2,] 1.968746e+06 1.470519e+06 1.675377e+06 2078623.3728 2.443914e+06
> [3,] 2.977088e+04 1.968746e+05 1.470519e+05 167537.6644 2.078623e+05
> [4,] 9.811277e+03 2.977088e+03 1.968746e+04 14705.1922 1.675377e+04
> [5,] 4.254974e+02 5.118387e+02 1.744463e+02 993.0955 7.849144e+02
> [6,] 9.589948e+01 8.585065e+01 8.910127e+01 94.5320 9.135007e+01
> [7,] 6.982183e+02 7.225101e+02 7.669595e+02 684.2949 9.295149e+02
> [8,] 7.726558e+02 8.019114e+02 8.507880e+02 822.1506 9.702683e+02
> [9,] 1.571349e+02 1.874256e+02 2.052429e+02 220.6129 2.205045e+02
> [10,] 2.433660e+01 1.172368e+02 1.974627e+02 283.2888 3.687014e+02
> [11,] 1.820697e+01 0.000000e+00 0.000000e+00 0.0000 0.000000e+00
> [,92] [,93] [,94] [,95] [,96]
> [1,] 2889224.1504 834225.2976 2181902.9867 5559379.3930 1251017.9753
> [2,] 2937284.1512 892009.7806 2198587.4926 5603017.4528 1362205.5631
> [3,] 244391.3807 293728.4151 89200.9781 219858.7493 560301.7453
> [4,] 20786.2337 24439.1381 29372.8415 8920.0978 21985.8749
> [5,] 876.9340 1083.1584 1276.1148 1532.4478 522.6273
> [6,] 107.8076 488.9337 74.9714 238.2696 0.0000
> [7,] 1004.5573 966.1313 1343.7895 1710.6774 1483.1639
> [8,] 1077.6302 876.8741 1181.0269 1389.2317 2240.7916
> [9,] 248.0603 556.9062 385.1151 339.9076 418.3697
> [10,] 465.0736 113.4481 162.5238 112.7030 279.3994
> [11,] 0.0000 155.0245 171.2314 85.6157 85.6157
> [,97] [,98] [,99] [,100] [,101]
> [1,] 1321680.3526 1794550.7645 1258517.0494 9766837.8045 8.753171e+06
> [2,] 1346700.7121 1820984.3716 1294408.0647 9792008.1455 8.948508e+06
> [3,] 136220.5563 134670.0712 182098.4372 129440.8065 9.792008e+05
> [4,] 56030.1745 13622.0556 13467.0071 18209.8437 1.294408e+04
> [5,] 1125.4251 2857.7800 823.9918 714.5499 9.462197e+02
> [6,] 0.0000 0.0000 856.3637 274.7066 3.274071e+02
> [7,] 963.8626 922.4809 1832.5532 2047.1176 2.368881e+03
> [8,] 2281.9753 2264.8193 1760.3481 2859.3693 2.771770e+03
> [9,] 577.3999 701.5176 1117.5454 693.2819 5.971625e+02
> [10,] 515.8031 794.3869 132.3978 154.4641 9.194293e+01
> [11,] 85.6157 85.6157 264.7956 132.3978 6.619891e+01
>
>
>
> $stage_dist
> $stage_dist[[1]]
> $stage_dist[[1]][[1]]
> [,1] [,2] [,3] [,4] [,5]
> [1,] 0.09090909 4.998504e-01 4.363875e-01 4.642613e-01 4.304501e-01
> [2,] 0.09090909 4.998514e-01 4.574963e-01 4.737750e-01 4.510626e-01
> [3,] 0.09090909 5.057163e-06 1.055444e-01 4.986945e-02 1.051744e-01
> [4,] 0.09090909 5.057163e-06 1.067828e-06 1.150489e-02 1.107063e-02
> [5,] 0.09090909 5.057163e-06 1.067828e-06 1.163987e-07 1.277011e-03
> [6,] 0.09090909 3.737903e-06 0.000000e+00 0.000000e+00 6.878012e-05
> [7,] 0.09090909 6.871145e-05 8.360844e-05 5.304017e-05 1.945505e-04
> [8,] 0.09090909 8.069997e-05 1.818701e-04 1.696565e-04 2.612038e-04
> [9,] 0.09090909 3.588178e-05 7.687068e-05 8.616802e-05 2.770796e-04
> [10,] 0.09090909 3.615400e-05 1.053045e-04 1.473972e-04 5.453506e-05
> [11,] 0.09090909 5.779615e-05 1.220375e-04 1.330271e-04 1.090701e-04
> [,6] [,7] [,8] [,9] [,10]
> [1,] 4.940810e-01 4.296686e-01 4.808971e-01 3.989594e-01 4.824733e-01
> [2,] 4.956122e-01 4.525702e-01 4.858468e-01 4.304890e-01 4.864977e-01
> [3,] 8.022603e-03 1.148626e-01 2.606754e-02 1.592707e-01 2.171241e-02
> [4,] 1.870632e-03 1.859310e-03 6.615957e-03 8.545484e-03 8.033076e-03
> [5,] 1.098076e-04 2.294924e-04 6.015635e-05 1.094285e-03 2.430986e-04
> [6,] 1.855485e-05 2.138481e-05 1.785030e-05 2.551012e-04 2.809018e-05
> [7,] 1.353597e-04 3.778822e-04 1.975227e-04 5.149633e-04 4.798592e-04
> [8,] 9.856818e-05 2.789163e-04 1.995060e-04 4.640004e-04 3.566361e-04
> [9,] 3.019396e-05 6.981094e-05 4.561500e-05 3.022318e-04 1.034308e-04
> [10,] 1.131621e-05 3.562369e-05 5.199294e-05 4.791296e-05 4.034511e-05
> [11,] 9.699610e-06 2.622634e-05 0.000000e+00 5.681457e-05 3.210758e-05
> [,11] [,12] [,13] [,14] [,15]
> [1,] 4.112827e-01 4.949170e-01 4.622415e-01 3.963475e-01 4.914513e-01
> [2,] 4.389300e-01 4.961121e-01 4.745421e-01 4.264959e-01 4.934098e-01
> [3,] 1.393895e-01 6.376952e-03 6.165142e-02 1.547533e-01 1.053727e-02
> [4,] 6.220959e-03 2.025107e-03 7.924582e-04 2.010520e-02 3.823431e-03
> [5,] 1.185629e-03 5.380295e-05 1.291722e-04 1.502769e-04 2.502221e-04
> [6,] 5.219335e-04 2.835607e-05 3.191818e-05 3.537971e-04 1.693289e-05
> [7,] 1.038877e-03 2.059769e-04 2.339797e-04 7.106132e-04 1.975409e-04
> [8,] 8.821146e-04 2.311625e-04 2.747532e-04 6.168226e-04 2.030878e-04
> [9,] 4.636422e-04 4.277914e-05 6.718022e-05 3.739690e-04 6.597774e-05
> [10,] 4.609354e-05 3.915135e-06 3.552922e-05 5.400700e-05 4.444009e-05
> [11,] 3.853177e-05 2.799026e-06 0.000000e+00 3.862156e-05 0.000000e+00
> [,16] [,17] [,18] [,19] [,20]
> [1,] 4.725398e-01 4.795563e-01 3.972822e-01 0.4636188760 4.593327e-01
> [2,] 4.813788e-01 4.857157e-01 4.291351e-01 0.4719871522 4.711719e-01
> [3,] 4.437117e-02 3.137301e-02 1.613099e-01 0.0451960934 6.026468e-02
> [4,] 9.475914e-04 2.891812e-03 1.041921e-02 0.0169889992 5.770768e-03
> [5,] 1.831669e-04 3.684758e-05 4.863150e-04 0.0005742799 1.121265e-03
> [6,] 2.029244e-05 2.508893e-05 0.000000e+00 0.0000000000 3.287431e-04
> [7,] 2.181433e-04 1.795862e-04 3.919793e-04 0.0003905274 7.224647e-04
> [8,] 2.261921e-04 1.687495e-04 7.008133e-04 0.0008246979 6.982754e-04
> [9,] 5.473703e-05 4.635438e-05 1.813927e-04 0.0002301149 4.683833e-04
> [10,] 6.008467e-05 6.526520e-06 9.312812e-05 0.0001892590 4.027522e-05
> [11,] 0.000000e+00 0.000000e+00 0.000000e+00 0.0000000000 8.055043e-05
> [,21] [,22] [,23] [,24] [,25]
> [1,] 4.883543e-01 4.854757e-01 0.4267468369 0.4467812581 4.207658e-01
> [2,] 4.916275e-01 4.900744e-01 0.4498661022 0.4604355963 4.425919e-01
> [3,] 1.678792e-02 2.314729e-02 0.1166913049 0.0719703507 1.124659e-01
> [4,] 2.147239e-03 7.904254e-04 0.0055115865 0.0186684751 1.757946e-02
> [5,] 1.227820e-04 5.343968e-05 0.0001004661 0.0004489129 2.334804e-03
> [6,] 2.335091e-05 1.817292e-05 0.0000000000 0.0002044104 6.936292e-04
> [7,] 4.124628e-04 1.607197e-04 0.0002646105 0.0004704258 1.412124e-03
> [8,] 3.473787e-04 1.804445e-04 0.0005065310 0.0004908519 1.192349e-03
> [9,] 1.102704e-04 5.007510e-05 0.0001399728 0.0003916632 7.414234e-04
> [10,] 3.608059e-05 4.934996e-05 0.0001725891 0.0000460185 1.851648e-04
> [11,] 3.075025e-05 0.000000e+00 0.0000000000 0.0000920370 3.746822e-05
> [,26] [,27] [,28] [,29] [,30]
> [1,] 4.954087e-01 4.765258e-01 4.799071e-01 4.532179e-01 0.4260838911
> [2,] 4.965075e-01 4.841570e-01 4.860480e-01 4.677480e-01 0.4470020768
> [3,] 5.779213e-03 3.824083e-02 3.119582e-02 7.357993e-02 0.1079440893
> [4,] 1.468541e-03 4.451128e-04 2.463981e-03 4.722551e-03 0.0169803373
> [5,] 1.300168e-04 6.156015e-05 1.632330e-05 1.877393e-04 0.0005665837
> [6,] 1.729921e-05 2.308566e-05 1.918765e-05 2.656782e-05 0.0000000000
> [7,] 2.988699e-04 2.033812e-04 1.383992e-04 1.849048e-04 0.0003979556
> [8,] 2.697637e-04 2.253594e-04 1.579495e-04 2.293961e-04 0.0006940316
> [9,] 6.870837e-05 5.706830e-05 4.669539e-05 6.750871e-05 0.0001791252
> [10,] 5.136041e-05 6.082792e-05 6.532236e-06 3.545503e-05 0.0001519095
> [11,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.0000000000
> [,31] [,32] [,33] [,34] [,35]
> [1,] 4.500225e-01 4.954346e-01 4.702527e-01 3.578496e-01 4.724323e-01
> [2,] 4.628277e-01 4.966799e-01 4.799574e-01 4.004645e-01 4.779297e-01
> [3,] 6.716913e-02 6.403699e-03 4.864575e-02 2.174719e-01 3.076060e-02
> [4,] 1.622031e-02 9.293543e-04 6.271902e-04 2.204171e-02 1.670452e-02
> [5,] 1.318351e-03 1.213327e-04 5.145312e-05 1.537489e-04 8.524422e-04
> [6,] 3.639387e-04 2.419184e-05 2.881819e-05 3.670653e-04 2.722910e-05
> [7,] 7.771862e-04 1.763719e-04 2.058871e-04 7.077000e-04 5.190140e-04
> [8,] 7.294806e-04 1.809437e-04 1.918658e-04 5.758321e-04 5.207438e-04
> [9,] 4.572196e-04 3.822434e-05 3.277372e-05 3.163849e-04 1.760002e-04
> [10,] 3.804468e-05 6.141187e-06 3.580234e-06 4.622942e-05 6.822843e-05
> [11,] 7.608937e-05 5.263875e-06 2.577768e-06 5.407424e-06 9.226409e-06
> [,36] [,37] [,38] [,39] [,40]
> [1,] 4.317380e-01 4.872394e-01 4.602416e-01 4.581510e-01 4.877786e-01
> [2,] 4.522577e-01 4.904416e-01 4.727059e-01 4.700504e-01 4.912326e-01
> [3,] 1.037928e-01 1.677239e-02 6.273100e-02 6.110855e-02 1.771842e-02
> [4,] 6.680330e-03 3.849250e-03 2.145309e-03 8.109484e-03 2.303471e-03
> [5,] 1.906437e-03 1.592240e-04 2.563563e-04 1.552364e-04 1.557682e-04
> [6,] 6.400272e-04 4.215683e-05 0.000000e+00 3.400796e-04 1.413711e-05
> [7,] 1.279983e-03 7.334525e-04 5.610630e-04 7.539310e-04 2.805498e-04
> [8,] 1.090442e-03 5.455530e-04 9.580540e-04 7.268200e-04 3.277740e-04
> [9,] 5.204998e-04 1.469655e-04 2.230789e-04 5.067925e-04 1.238297e-04
> [10,] 4.440676e-05 4.935271e-05 1.511677e-04 3.257007e-05 3.847514e-05
> [11,] 4.939093e-05 2.066974e-05 2.643808e-05 6.514014e-05 2.630829e-05
> [,41] [,42] [,43] [,44] [,45]
> [1,] 4.530365e-01 4.722925e-01 4.518930e-01 4.883416e-01 4.717279e-01
> [2,] 4.679078e-01 4.800427e-01 4.663517e-01 4.915776e-01 4.807195e-01
> [3,] 7.488280e-02 4.002320e-02 7.347970e-02 1.669757e-02 4.525595e-02
> [4,] 2.700971e-03 6.405213e-03 6.126315e-03 2.630917e-03 1.537224e-03
> [5,] 1.874414e-04 1.235324e-04 4.996746e-04 1.186207e-04 1.265649e-04
> [6,] 0.000000e+00 0.000000e+00 1.797581e-04 1.230264e-05 1.243333e-05
> [7,] 3.101072e-04 1.999895e-04 4.405177e-04 2.275870e-04 2.409896e-04
> [8,] 5.986337e-04 5.011955e-04 4.809132e-04 2.367505e-04 2.343883e-04
> [9,] 2.003559e-04 1.887743e-04 4.040357e-04 8.902527e-05 7.320955e-05
> [10,] 1.352334e-04 1.886389e-04 4.812464e-05 3.117023e-05 3.370339e-05
> [11,] 4.010397e-05 3.430354e-05 9.624928e-05 3.692330e-05 3.809204e-05
> [,46] [,47] [,48] [,49] [,50]
> [1,] 4.417875e-01 4.422823e-01 4.249020e-01 4.970045e-01 4.255965e-01
> [2,] 4.592849e-01 4.579124e-01 4.450834e-01 4.977271e-01 4.499774e-01
> [3,] 8.915441e-02 8.124576e-02 1.044730e-01 3.784322e-03 1.220817e-01
> [4,] 8.393184e-03 1.577108e-02 1.853627e-02 8.882816e-04 9.282123e-04
> [5,] 1.542834e-04 7.560074e-04 1.885332e-03 8.681734e-05 1.195853e-04
> [6,] 0.000000e+00 2.696016e-04 8.900530e-04 2.720315e-05 2.759932e-05
> [7,] 3.150445e-04 6.094137e-04 1.751965e-03 1.980295e-04 5.547844e-04
> [8,] 5.649841e-04 6.043792e-04 1.426648e-03 2.296079e-04 5.277518e-04
> [9,] 1.529719e-04 4.411551e-04 8.052494e-04 4.871273e-05 1.431493e-04
> [10,] 1.220205e-04 3.597495e-05 2.187121e-04 4.262433e-06 3.904077e-05
> [11,] 7.064562e-05 7.194990e-05 2.735902e-05 1.163100e-06 4.346380e-06
> [,51] [,52] [,53] [,54] [,55]
> [1,] 4.519217e-01 4.753573e-01 4.569729e-01 4.887291e-01 4.879513e-01
> [2,] 4.641333e-01 4.822661e-01 4.699300e-01 4.918966e-01 4.917849e-01
> [3,] 6.455574e-02 3.547733e-02 6.572717e-02 1.628679e-02 1.929237e-02
> [4,] 1.751438e-02 4.934499e-03 4.835141e-03 2.277967e-03 6.387740e-04
> [5,] 7.516084e-05 6.722528e-04 3.820671e-04 9.040877e-05 4.644428e-05
> [6,] 0.000000e+00 0.000000e+00 2.938015e-04 1.383264e-05 1.512399e-05
> [7,] 4.814898e-04 2.249451e-04 6.505274e-04 2.629263e-04 1.101744e-04
> [8,] 9.169652e-04 6.372440e-04 6.398155e-04 2.752725e-04 1.133069e-04
> [9,] 2.431011e-04 2.218256e-04 4.297154e-04 9.882178e-05 3.186374e-05
> [10,] 1.518891e-04 2.037859e-04 4.628935e-05 3.386300e-05 8.955061e-06
> [11,] 6.235509e-06 4.766286e-06 9.257870e-05 3.437769e-05 6.741529e-06
> [,56] [,57] [,58] [,59] [,60]
> [1,] 4.645846e-01 4.508480e-01 3.887378e-01 4.934741e-01 4.628145e-01
> [2,] 4.758800e-01 4.653393e-01 4.200809e-01 4.949190e-01 4.748557e-01
> [3,] 5.692037e-02 7.421824e-02 1.617524e-01 7.806965e-03 6.038200e-02
> [4,] 2.232945e-03 8.877301e-03 2.579833e-02 3.006076e-03 9.524795e-04
> [5,] 3.965441e-05 1.772173e-04 1.573679e-03 2.543466e-04 1.988920e-04
> [6,] 1.921784e-05 2.491673e-05 3.457336e-04 3.298698e-05 2.960596e-05
> [7,] 1.386227e-04 1.966749e-04 6.871909e-04 2.378941e-04 3.354296e-04
> [8,] 1.437872e-04 2.250985e-04 5.927304e-04 2.183978e-04 3.296205e-04
> [9,] 3.128783e-05 5.643115e-05 3.382778e-04 4.076950e-05 6.490550e-05
> [10,] 5.628871e-06 3.689640e-05 5.024563e-05 5.528803e-06 3.685595e-05
> [11,] 3.901404e-06 0.000000e+00 4.275074e-05 3.972492e-06 0.000000e+00
> [,61] [,62] [,63] [,64] [,65]
> [1,] 4.748650e-01 4.814307e-01 4.114786e-01 4.498086e-01 4.758598e-01
> [2,] 4.821695e-01 4.870861e-01 4.390679e-01 4.619688e-01 4.825374e-01
> [3,] 3.747278e-02 2.871187e-02 1.395668e-01 6.487772e-02 3.429076e-02
> [4,] 4.764987e-03 2.231401e-03 8.226933e-03 2.062273e-02 4.815708e-03
> [5,] 4.542968e-05 1.432235e-04 3.402056e-04 6.329505e-04 7.888775e-04
> [6,] 2.890187e-05 2.109109e-05 3.140772e-05 0.000000e+00 0.000000e+00
> [7,] 2.567206e-04 1.518521e-04 5.951113e-04 6.276857e-04 4.040401e-04
> [8,] 2.789172e-04 1.730970e-04 5.133875e-04 1.062315e-03 8.678808e-04
> [9,] 6.369798e-05 4.525144e-05 1.367235e-04 2.407658e-04 2.268039e-04
> [10,] 5.404349e-05 5.363569e-06 4.066582e-05 1.552184e-04 2.062773e-04
> [11,] 0.000000e+00 0.000000e+00 2.195495e-06 3.244115e-06 2.408024e-06
> [,66] [,67] [,68] [,69] [,70]
> [1,] 4.771293e-01 4.762487e-01 4.577390e-01 4.888002e-01 4.427345e-01
> [2,] 4.839803e-01 4.834393e-01 4.705666e-01 4.919836e-01 4.610156e-01
> [3,] 3.473591e-02 3.646919e-02 6.510624e-02 1.636317e-02 9.200049e-02
> [4,] 2.468453e-03 2.617442e-03 4.911417e-03 2.263962e-03 3.059898e-03
> [5,] 2.017257e-04 1.006025e-04 1.830237e-04 8.857537e-05 2.199611e-04
> [6,] 0.000000e+00 0.000000e+00 1.550255e-04 7.656436e-06 0.000000e+00
> [7,] 3.465160e-04 1.970297e-04 3.783002e-04 1.518108e-04 2.100233e-04
> [8,] 7.140173e-04 5.135184e-04 4.252024e-04 1.922888e-04 4.179606e-04
> [9,] 1.959504e-04 1.740381e-04 3.743835e-04 7.938089e-05 1.536345e-04
> [10,] 2.260575e-04 2.389026e-04 5.362291e-05 2.939316e-05 1.132270e-04
> [11,] 1.733439e-06 1.306192e-06 1.072458e-04 3.995673e-05 7.471874e-05
> [,71] [,72] [,73] [,74] [,75]
> [1,] 4.688492e-01 4.461029e-01 4.880155e-01 4.720318e-01 4.869720e-01
> [2,] 4.772898e-01 4.621745e-01 4.912734e-01 4.809095e-01 4.908877e-01
> [3,] 4.394552e-02 8.180483e-02 1.687642e-02 4.468468e-02 1.994651e-02
> [4,] 8.769790e-03 7.532020e-03 2.987125e-03 1.535026e-03 1.853371e-03
> [5,] 1.563235e-04 7.649433e-04 1.514829e-04 1.427390e-04 3.479404e-05
> [6,] 0.000000e+00 1.842016e-04 1.547331e-05 1.507320e-05 1.767448e-05
> [7,] 1.795740e-04 4.391629e-04 2.751136e-04 2.829560e-04 1.271127e-04
> [8,] 4.139351e-04 4.711885e-04 2.500438e-04 2.516337e-04 1.141059e-04
> [9,] 1.567093e-04 3.823511e-04 8.702566e-05 7.358877e-05 2.852994e-05
> [10,] 1.679802e-04 4.798479e-05 3.094633e-05 3.487982e-05 1.032747e-05
> [11,] 7.122436e-05 9.596958e-05 3.754665e-05 3.817237e-05 7.916310e-06
> [,76] [,77] [,78] [,79] [,80]
> [1,] 4.562461e-01 4.664549e-01 4.032888e-01 4.838806e-01 4.888798e-01
> [2,] 4.701664e-01 4.760499e-01 4.320129e-01 4.876533e-01 4.923511e-01
> [3,] 7.016108e-02 4.943902e-02 1.465751e-01 2.020712e-02 1.749180e-02
> [4,] 2.850894e-03 7.377591e-03 1.522220e-02 6.855954e-03 7.248161e-04
> [5,] 1.349348e-04 1.569832e-04 1.159942e-03 3.831321e-04 1.298306e-04
> [6,] 1.812090e-05 2.050001e-05 2.779858e-04 2.773941e-05 2.774113e-05
> [7,] 1.598180e-04 1.857556e-04 5.520496e-04 4.735688e-04 1.980975e-04
> [8,] 1.754600e-04 2.026897e-04 4.915312e-04 3.466373e-04 1.502813e-04
> [9,] 4.450211e-05 4.893649e-05 3.003094e-04 9.809747e-05 3.195829e-05
> [10,] 4.268666e-05 6.375206e-05 5.375502e-05 3.964138e-05 8.502906e-06
> [11,] 0.000000e+00 0.000000e+00 6.543056e-05 3.419666e-05 6.133056e-06
> [,81] [,82] [,83] [,84] [,85]
> [1,] 4.583520e-01 4.715096e-01 4.797473e-01 4.538170e-01 4.735177e-01
> [2,] 4.716436e-01 4.796991e-01 4.858571e-01 4.681306e-01 4.810075e-01
> [3,] 6.692951e-02 4.213484e-02 3.107952e-02 7.247950e-02 3.863020e-02
> [4,] 2.377810e-03 5.979228e-03 2.729900e-03 4.636401e-03 5.981018e-03
> [5,] 5.808973e-05 1.088070e-04 1.972207e-04 2.183320e-04 2.003066e-04
> [6,] 2.269892e-05 2.560697e-05 2.092984e-05 2.728510e-05 2.731353e-05
> [7,] 2.642161e-04 1.977656e-04 1.506752e-04 2.893542e-04 2.492429e-04
> [8,] 2.579724e-04 2.290752e-04 1.646119e-04 2.978932e-04 2.698609e-04
> [9,] 5.424770e-05 5.787513e-05 4.646815e-05 6.831129e-05 6.322055e-05
> [10,] 3.985560e-05 5.806155e-05 6.269643e-06 3.524532e-05 5.355690e-05
> [11,] 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
> [,86] [,87] [,88] [,89] [,90]
> [1,] 4.068958e-01 4.940431e-01 4.610925e-01 4.716929e-01 4.746759e-01
> [2,] 4.351294e-01 4.954443e-01 4.737416e-01 4.798923e-01 4.823181e-01
> [3,] 1.434010e-01 7.491982e-03 6.342502e-02 4.212132e-02 3.887498e-02
> [4,] 1.151668e-02 2.469054e-03 9.590970e-04 5.639247e-03 3.412153e-03
> [5,] 9.214078e-04 1.070784e-04 1.648937e-04 4.996814e-05 2.304352e-04
> [6,] 3.559012e-04 2.413355e-05 2.765759e-05 2.552203e-05 2.193495e-05
> [7,] 7.059060e-04 1.757099e-04 2.327634e-04 2.196867e-04 1.587819e-04
> [8,] 6.128263e-04 1.944425e-04 2.583433e-04 2.436984e-04 1.907696e-04
> [9,] 3.541406e-04 3.954374e-05 6.038092e-05 5.878945e-05 5.119041e-05
> [10,] 5.375415e-05 6.124420e-06 3.776893e-05 5.656090e-05 6.573356e-05
> [11,] 5.322240e-05 4.581870e-06 0.000000e+00 0.000000e+00 0.000000e+00
> [,91] [,92] [,93] [,94] [,95]
> [1,] 4.735073e-01 4.739956e-01 4.072087e-01 4.844734e-01 4.878110e-01
> [2,] 4.815693e-01 4.818802e-01 4.354149e-01 4.881780e-01 4.916401e-01
> [3,] 4.095894e-02 4.009396e-02 1.433771e-01 1.980633e-02 1.929163e-02
> [4,] 3.301303e-03 3.410114e-03 1.192943e-02 6.521995e-03 7.826992e-04
> [5,] 1.546661e-04 1.438666e-04 5.287199e-04 2.833507e-04 1.344655e-04
> [6,] 1.800038e-05 1.768652e-05 2.386622e-04 1.664677e-05 2.090710e-05
> [7,] 1.831594e-04 1.648040e-04 4.715957e-04 2.983773e-04 1.501044e-04
> [8,] 1.911898e-04 1.767921e-04 4.280268e-04 2.622372e-04 1.218989e-04
> [9,] 4.345007e-05 4.069587e-05 2.718415e-04 8.551159e-05 2.982540e-05
> [10,] 7.265202e-05 7.629828e-05 5.537720e-05 3.608706e-05 9.889192e-06
> [11,] 0.000000e+00 0.000000e+00 7.567181e-05 3.802051e-05 7.512400e-06
> [,96] [,97] [,98] [,99] [,100]
> [1,] 3.908770e-01 4.611293e-01 4.758247e-01 4.567658e-01 4.954423e-01
> [2,] 4.256173e-01 4.698588e-01 4.828335e-01 4.697921e-01 4.967191e-01
> [3,] 1.750647e-01 4.752684e-02 3.570773e-02 6.609075e-02 6.566142e-03
> [4,] 6.869424e-03 1.954872e-02 3.611884e-03 4.887712e-03 9.237305e-04
> [5,] 1.632934e-04 3.926566e-04 7.577396e-04 2.990593e-04 3.624697e-05
> [6,] 0.000000e+00 0.000000e+00 0.000000e+00 3.108084e-04 1.393504e-05
> [7,] 4.634104e-04 3.362880e-04 2.445956e-04 6.651063e-04 1.038441e-04
> [8,] 7.001290e-04 7.961725e-04 6.005163e-04 6.389002e-04 1.450472e-04
> [9,] 1.307184e-04 2.014526e-04 1.860072e-04 4.056016e-04 3.516810e-05
> [10,] 8.729756e-05 1.799618e-04 2.106315e-04 4.805243e-05 7.835500e-06
> [11,] 2.675038e-05 2.987099e-05 2.270098e-05 9.610486e-05 6.716143e-06
> [,101]
> [1,] 4.680591e-01
> [2,] 4.785044e-01
> [3,] 5.236090e-02
> [4,] 6.921601e-04
> [5,] 5.059730e-05
> [6,] 1.750747e-05
> [7,] 1.266714e-04
> [8,] 1.482151e-04
> [9,] 3.193213e-05
> [10,] 4.916473e-06
> [11,] 3.539861e-06
>
>
>
> $rep_value
> $rep_value[[1]]
> $rep_value[[1]][[1]]
> [,1] [,2] [,3] [,4] [,5]
> [1,] 2.059315e-06 2.051850e-06 2.027621e-06 2.217066e-06 1.750944e-06
> [2,] 2.218361e-05 1.901258e-05 2.219280e-05 2.115301e-05 1.236259e-05
> [3,] 2.772467e-04 2.224923e-04 2.206705e-04 2.509379e-04 1.313160e-04
> [4,] 2.961903e-03 2.780667e-03 2.582367e-03 2.495159e-03 1.557799e-03
> [5,] 6.001986e-02 5.941328e-02 6.454790e-02 5.839855e-02 3.097945e-02
> [6,] 0.000000e+00 8.648707e-02 9.402328e-02 1.508451e-01 6.941306e-02
> [7,] 9.717249e-02 8.090373e-02 8.852219e-02 9.160972e-02 4.396778e-02
> [8,] 1.348577e-01 1.160527e-01 1.201474e-01 1.308204e-01 8.122502e-02
> [9,] 2.123911e-01 2.445035e-01 2.150608e-01 1.548799e-01 1.458578e-01
> [10,] 2.865765e-01 3.612713e-01 3.890357e-01 4.106768e-01 1.675490e-01
> [11,] 2.057190e-01 4.834425e-02 2.583546e-02 0.000000e+00 4.593047e-01
> [,6] [,7] [,8] [,9] [,10]
> [1,] 2.008976e-06 2.078936e-06 3.676328e-06 2.664671e-06 2.426636e-06
> [2,] 2.111449e-05 2.173421e-05 3.736412e-05 2.628562e-05 2.548023e-05
> [3,] 1.604270e-04 2.459080e-04 4.213701e-04 2.888180e-04 2.704995e-04
> [4,] 1.704063e-03 1.868399e-03 4.767519e-03 3.257115e-03 2.972161e-03
> [5,] 4.043055e-02 3.969243e-02 7.244683e-02 7.370414e-02 6.703650e-02
> [6,] 0.000000e+00 6.463830e-02 1.695284e-01 0.000000e+00 1.620030e-01
> [7,] 6.386993e-02 6.103279e-02 1.089890e-01 1.163968e-01 1.024839e-01
> [8,] 9.007604e-02 1.003615e-01 1.579728e-01 1.359868e-01 1.365464e-01
> [9,] 1.319516e-01 1.419734e-01 1.958992e-01 1.902195e-01 1.556821e-01
> [10,] 2.082661e-01 2.289298e-01 2.899339e-01 2.767305e-01 3.729775e-01
> [11,] 4.635182e-01 3.612336e-01 0.000000e+00 2.033874e-01 0.000000e+00
> [,11] [,12] [,13] [,14] [,15]
> [1,] 1.274378e-06 1.305512e-06 2.243114e-06 1.343700e-06 1.340560e-06
> [2,] 1.470972e-05 1.345320e-05 2.014789e-05 1.377954e-05 1.520615e-05
> [3,] 1.651604e-04 1.673410e-04 2.261145e-04 1.334247e-04 1.669358e-04
> [4,] 1.753352e-03 1.878901e-03 2.812584e-03 1.497391e-03 1.616407e-03
> [5,] 3.853054e-02 3.989304e-02 6.315925e-02 3.725136e-02 3.628104e-02
> [6,] 8.844813e-02 6.514867e-02 1.892245e-01 6.040838e-02 5.839648e-02
> [7,] 5.394898e-02 6.013681e-02 9.714276e-02 5.856254e-02 5.850613e-02
> [8,] 9.100378e-02 1.006205e-01 1.342102e-01 9.804670e-02 1.025376e-01
> [9,] 1.421280e-01 1.282286e-01 1.596285e-01 1.448056e-01 1.581389e-01
> [10,] 1.726294e-01 2.603243e-01 3.535737e-01 2.569575e-01 2.492476e-01
> [11,] 4.113767e-01 3.435870e-01 0.000000e+00 3.423220e-01 3.350924e-01
> [,16] [,17] [,18] [,19] [,20]
> [1,] 1.808144e-06 2.468391e-06 3.355312e-06 3.816599e-06 2.034643e-06
> [2,] 1.326327e-05 2.514388e-05 2.661528e-05 3.740476e-05 2.268833e-05
> [3,] 1.668551e-04 1.989229e-04 2.984551e-04 3.209246e-04 2.383105e-04
> [4,] 1.831765e-03 2.502497e-03 2.361194e-03 3.598745e-03 2.044652e-03
> [5,] 3.547326e-02 5.494571e-02 5.940875e-02 5.694212e-02 4.585613e-02
> [6,] 7.497130e-02 7.959694e-02 8.590985e-02 1.409469e-01 0.000000e+00
> [7,] 5.006043e-02 7.491888e-02 8.149650e-02 8.679810e-02 7.044335e-02
> [8,] 9.211225e-02 1.124422e-01 1.161211e-01 1.315747e-01 9.558358e-02
> [9,] 1.792275e-01 2.492917e-01 2.235535e-01 1.633511e-01 1.349824e-01
> [10,] 2.169784e-01 3.585131e-01 3.880880e-01 4.164263e-01 1.989538e-01
> [11,] 3.491632e-01 6.756248e-02 4.273270e-02 0.000000e+00 4.518731e-01
> [,21] [,22] [,23] [,24] [,25]
> [1,] 2.101763e-06 3.168483e-06 2.937919e-06 2.209581e-06 1.530165e-06
> [2,] 2.177654e-05 3.493093e-05 2.924331e-05 2.256939e-05 1.343077e-05
> [3,] 2.615799e-04 3.881854e-04 3.483040e-04 2.422449e-04 1.496900e-04
> [4,] 2.747547e-03 4.662885e-03 3.870683e-03 2.885271e-03 1.606673e-03
> [5,] 4.714671e-02 9.795474e-02 9.298932e-02 6.412770e-02 3.827273e-02
> [6,] 7.712836e-02 1.454073e-01 2.564604e-01 1.862181e-01 6.208873e-02
> [7,] 7.104684e-02 1.332741e-01 1.369869e-01 9.841241e-02 5.978865e-02
> [8,] 1.033662e-01 1.459154e-01 1.583254e-01 1.350986e-01 9.873138e-02
> [9,] 1.480818e-01 2.035635e-01 1.634177e-01 1.602837e-01 1.448951e-01
> [10,] 2.083075e-01 2.284531e-01 1.875692e-01 3.527071e-01 2.486465e-01
> [11,] 3.418896e-01 4.034263e-02 0.000000e+00 0.000000e+00 3.458056e-01
> [,26] [,27] [,28] [,29] [,30]
> [1,] 1.516846e-06 1.265738e-06 1.289968e-06 2.061224e-06 2.846647e-06
> [2,] 1.782556e-05 1.400172e-05 1.318527e-05 2.053500e-05 2.082839e-05
> [3,] 1.671119e-04 1.764440e-04 1.572726e-04 2.267512e-04 2.301912e-04
> [4,] 1.862513e-03 1.654136e-03 1.981886e-03 2.704664e-03 2.541813e-03
> [5,] 3.998195e-02 3.687169e-02 3.715976e-02 6.816620e-02 6.063696e-02
> [6,] 6.451272e-02 8.337459e-02 6.041553e-02 9.919680e-02 1.576808e-01
> [7,] 6.283510e-02 5.171157e-02 5.745170e-02 9.351648e-02 9.535599e-02
> [8,] 1.060909e-01 8.814817e-02 9.364950e-02 1.246623e-01 1.375978e-01
> [9,] 1.544419e-01 1.442907e-01 1.390401e-01 2.158237e-01 1.615744e-01
> [10,] 2.368436e-01 1.771837e-01 2.640043e-01 3.692804e-01 3.843585e-01
> [11,] 3.332448e-01 4.165737e-01 3.461255e-01 2.640016e-02 0.000000e+00
> [,31] [,32] [,33] [,34] [,35]
> [1,] 1.620867e-06 2.486186e-06 5.004598e-06 3.063133e-06 3.954415e-06
> [2,] 1.725955e-05 1.839995e-05 4.717484e-05 3.671238e-05 3.126922e-05
> [3,] 1.357726e-04 2.171080e-04 3.787658e-04 3.691612e-04 4.126847e-04
> [4,] 1.500532e-03 1.707884e-03 4.469201e-03 2.963987e-03 4.149749e-03
> [5,] 3.313829e-02 3.775039e-02 7.031412e-02 6.994641e-02 6.663649e-02
> [6,] 7.780786e-02 7.834957e-02 1.485941e-01 0.000000e+00 1.531627e-01
> [7,] 4.700157e-02 5.424452e-02 1.068201e-01 1.080342e-01 1.024489e-01
> [8,] 8.835202e-02 9.787455e-02 1.612838e-01 1.431874e-01 1.568172e-01
> [9,] 1.611787e-01 1.750446e-01 1.988002e-01 1.996399e-01 1.971658e-01
> [10,] 1.835494e-01 1.945005e-01 3.092875e-01 2.408074e-01 3.191713e-01
> [11,] 4.073170e-01 3.602900e-01 0.000000e+00 2.350118e-01 0.000000e+00
> [,36] [,37] [,38] [,39] [,40]
> [1,] 2.910862e-06 3.025012e-06 2.945838e-06 2.750312e-06 3.104949e-06
> [2,] 2.748032e-05 3.042756e-05 3.254514e-05 1.910406e-05 2.826744e-05
> [3,] 2.357123e-04 3.101011e-04 3.510653e-04 2.353665e-04 2.136036e-04
> [4,] 3.110882e-03 2.659891e-03 3.577867e-03 2.538905e-03 2.631647e-03
> [5,] 6.256293e-02 7.020939e-02 6.137828e-02 5.175029e-02 5.677531e-02
> [6,] 0.000000e+00 1.012684e-01 1.580814e-01 0.000000e+00 8.249135e-02
> [7,] 9.758533e-02 9.649929e-02 9.623542e-02 8.346248e-02 7.734809e-02
> [8,] 1.325433e-01 1.311161e-01 1.511832e-01 1.220169e-01 1.130407e-01
> [9,] 1.987376e-01 2.310308e-01 1.945966e-01 1.976276e-01 2.480793e-01
> [10,] 2.487840e-01 3.284216e-01 3.345607e-01 2.595110e-01 3.384413e-01
> [11,] 2.564099e-01 3.845096e-02 0.000000e+00 2.828356e-01 8.094724e-02
> [,41] [,42] [,43] [,44] [,45]
> [1,] 3.907917e-06 4.540104e-06 2.676826e-06 3.160125e-06 3.504378e-06
> [2,] 3.426237e-05 4.500283e-05 2.873145e-05 3.337552e-05 3.390024e-05
> [3,] 3.403866e-04 4.264030e-04 3.060212e-04 3.853681e-04 3.876451e-04
> [4,] 2.572140e-03 4.236189e-03 2.899560e-03 4.104590e-03 4.475916e-03
> [5,] 6.337876e-02 6.402173e-02 5.761255e-02 7.778221e-02 9.534676e-02
> [6,] 9.175750e-02 1.286467e-01 0.000000e+00 0.000000e+00 1.411743e-01
> [7,] 8.686660e-02 9.641896e-02 8.456163e-02 1.139379e-01 1.298155e-01
> [8,] 1.201109e-01 1.438198e-01 1.139248e-01 1.404321e-01 1.446620e-01
> [9,] 2.253482e-01 1.764972e-01 1.497511e-01 1.859043e-01 2.074678e-01
> [10,] 3.598264e-01 3.858834e-01 1.778794e-01 1.974424e-01 2.319867e-01
> [11,] 4.976097e-02 0.000000e+00 4.130335e-01 2.799746e-01 4.464605e-02
> [,46] [,47] [,48] [,49] [,50]
> [1,] 3.460116e-06 2.599314e-06 1.426472e-06 2.337370e-06 2.171729e-06
> [2,] 3.326277e-05 2.704777e-05 1.654245e-05 1.802082e-05 2.264751e-05
> [3,] 3.485511e-04 2.800057e-04 1.840111e-04 2.306677e-04 1.880044e-04
> [4,] 3.985639e-03 2.934101e-03 1.904932e-03 2.565849e-03 2.406469e-03
> [5,] 9.203980e-02 6.710215e-02 3.992248e-02 5.312470e-02 5.353706e-02
> [6,] 2.451617e-01 1.678071e-01 9.154106e-02 0.000000e+00 7.738737e-02
> [7,] 1.356962e-01 1.039635e-01 5.589774e-02 8.794513e-02 7.304371e-02
> [8,] 1.609083e-01 1.437706e-01 9.796596e-02 1.276448e-01 1.120088e-01
> [9,] 1.692056e-01 1.667527e-01 1.672888e-01 2.098104e-01 2.508692e-01
> [10,] 1.926175e-01 3.473602e-01 1.950482e-01 2.890703e-01 3.771586e-01
> [11,] 0.000000e+00 0.000000e+00 3.502288e-01 2.295878e-01 5.337596e-02
> [,51] [,52] [,53] [,54] [,55]
> [1,] 2.392395e-06 2.569001e-06 1.453424e-06 1.391475e-06 1.358196e-06
> [2,] 2.379788e-05 2.584491e-05 1.422696e-05 1.473923e-05 1.440917e-05
> [3,] 2.681312e-04 2.775309e-04 1.548249e-04 1.551725e-04 1.641389e-04
> [4,] 2.225844e-03 3.126946e-03 1.662559e-03 1.688665e-03 1.728031e-03
> [5,] 5.698191e-02 5.191558e-02 3.746416e-02 3.626685e-02 3.761059e-02
> [6,] 8.236499e-02 1.386206e-01 0.000000e+00 8.014041e-02 8.479275e-02
> [7,] 7.822295e-02 8.013751e-02 5.789798e-02 5.093639e-02 5.276133e-02
> [8,] 1.139521e-01 1.225816e-01 8.595431e-02 8.776771e-02 8.924588e-02
> [9,] 2.217099e-01 1.562646e-01 1.250760e-01 1.486623e-01 1.419486e-01
> [10,] 4.137923e-01 4.470472e-01 1.912256e-01 1.694011e-01 1.727867e-01
> [11,] 3.045566e-02 0.000000e+00 5.005489e-01 4.249652e-01 4.189462e-01
> [,56] [,57] [,58] [,59] [,60]
> [1,] 1.286548e-06 2.019161e-06 1.306636e-06 1.479348e-06 1.664153e-06
> [2,] 1.464904e-05 2.069878e-05 1.202609e-05 1.393663e-05 1.669547e-05
> [3,] 1.663317e-04 2.540754e-04 1.339972e-04 1.391633e-04 1.698266e-04
> [4,] 1.894731e-03 2.884886e-03 1.644802e-03 1.550587e-03 1.695793e-03
> [5,] 3.989491e-02 6.572505e-02 3.735164e-02 3.806660e-02 3.778977e-02
> [6,] 6.520931e-02 1.627918e-01 8.576573e-02 6.173255e-02 6.084090e-02
> [7,] 5.993091e-02 1.012346e-01 5.245781e-02 5.979859e-02 6.041535e-02
> [8,] 9.788019e-02 1.368313e-01 9.040758e-02 9.924627e-02 1.048443e-01
> [9,] 1.263405e-01 1.586002e-01 1.484142e-01 1.469681e-01 1.587256e-01
> [10,] 2.634014e-01 3.716555e-01 1.779349e-01 2.491582e-01 2.347664e-01
> [11,] 3.452658e-01 0.000000e+00 4.058761e-01 3.433245e-01 3.407337e-01
> [,61] [,62] [,63] [,64] [,65]
> [1,] 1.721162e-06 2.399155e-06 2.001791e-06 2.493112e-06 2.722469e-06
> [2,] 1.691210e-05 2.397893e-05 2.432769e-05 2.055113e-05 2.640733e-05
> [3,] 1.834830e-04 2.544756e-04 2.591549e-04 2.739962e-04 2.356334e-04
> [4,] 1.866393e-03 2.760861e-03 2.750272e-03 2.918791e-03 3.141561e-03
> [5,] 3.727349e-02 5.616707e-02 5.967660e-02 6.195114e-02 6.693203e-02
> [6,] 8.622074e-02 0.000000e+00 8.648869e-02 9.014655e-02 9.753921e-02
> [7,] 5.248706e-02 8.797024e-02 8.132332e-02 8.433192e-02 9.112924e-02
> [8,] 9.561811e-02 1.297360e-01 1.180308e-01 1.192064e-01 1.237431e-01
> [9,] 1.674532e-01 2.008733e-01 2.568210e-01 2.543047e-01 2.465310e-01
> [10,] 1.881333e-01 2.429016e-01 2.902277e-01 2.980702e-01 3.053465e-01
> [11,] 3.707455e-01 2.793100e-01 1.043962e-01 8.877327e-02 6.537262e-02
> [,66] [,67] [,68] [,69] [,70]
> [1,] 2.812595e-06 2.613579e-06 2.317848e-06 2.138089e-06 2.187933e-06
> [2,] 2.940562e-05 2.947167e-05 1.756587e-05 2.236257e-05 2.371242e-05
> [3,] 3.070531e-04 3.299855e-04 2.189887e-04 1.824382e-04 2.663186e-04
> [4,] 2.739843e-03 3.445705e-03 2.451951e-03 2.274405e-03 2.172679e-03
> [5,] 7.305743e-02 6.149223e-02 5.120648e-02 5.093167e-02 5.417234e-02
> [6,] 1.053473e-01 1.720754e-01 0.000000e+00 7.351950e-02 7.850493e-02
> [7,] 1.004537e-01 9.711795e-02 8.605588e-02 6.951038e-02 7.428522e-02
> [8,] 1.350155e-01 1.533880e-01 1.259867e-01 1.095171e-01 1.096720e-01
> [9,] 2.325363e-01 1.989939e-01 2.109416e-01 2.515804e-01 2.187208e-01
> [10,] 3.147710e-01 3.131248e-01 2.975249e-01 3.919142e-01 4.343600e-01
> [11,] 3.573970e-02 0.000000e+00 2.255936e-01 5.054541e-02 2.781972e-02
> [,71] [,72] [,73] [,74] [,75]
> [1,] 2.155792e-06 1.029489e-06 1.083601e-06 1.357995e-06 1.368084e-06
> [2,] 2.333465e-05 1.154175e-05 1.080575e-05 1.030384e-05 1.422819e-05
> [3,] 2.715880e-04 1.338445e-04 1.308635e-04 1.135842e-04 1.162613e-04
> [4,] 3.050256e-03 1.557793e-03 1.517565e-03 1.375567e-03 1.281605e-03
> [5,] 4.976917e-02 3.499173e-02 3.532537e-02 3.190367e-02 3.104187e-02
> [6,] 1.487846e-01 0.000000e+00 0.000000e+00 7.760788e-02 5.017893e-02
> [7,] 7.605328e-02 5.537947e-02 5.560670e-02 4.511402e-02 4.865449e-02
> [8,] 1.130176e-01 7.559645e-02 8.229166e-02 8.266493e-02 8.756730e-02
> [9,] 1.434007e-01 1.068246e-01 1.205565e-01 1.401394e-01 1.293272e-01
> [10,] 4.656272e-01 2.006432e-01 1.986285e-01 1.767255e-01 2.823956e-01
> [11,] 0.000000e+00 5.248603e-01 5.059309e-01 4.443438e-01 3.694212e-01
> [,76] [,77] [,78] [,79] [,80]
> [1,] 1.487517e-06 2.397556e-06 1.346815e-06 1.283611e-06 1.328416e-06
> [2,] 1.554183e-05 2.657147e-05 1.356156e-05 1.330778e-05 1.375355e-05
> [3,] 1.740126e-04 2.976631e-04 1.622402e-04 1.443409e-04 1.536072e-04
> [4,] 1.421890e-03 3.332757e-03 1.817473e-03 1.726785e-03 1.666078e-03
> [5,] 3.134838e-02 5.446517e-02 4.069833e-02 3.868814e-02 3.986339e-02
> [6,] 5.102520e-02 1.411904e-01 0.000000e+00 8.758659e-02 6.465866e-02
> [7,] 4.828244e-02 8.362069e-02 6.278815e-02 5.422218e-02 6.200584e-02
> [8,] 8.754350e-02 1.259349e-01 9.049922e-02 9.175761e-02 1.010982e-01
> [9,] 1.226264e-01 1.605981e-01 1.291303e-01 1.480872e-01 1.454563e-01
> [10,] 2.815133e-01 4.305313e-01 1.958362e-01 1.773333e-01 2.502290e-01
> [11,] 3.760479e-01 0.000000e+00 4.790531e-01 4.004394e-01 3.348539e-01
> [,81] [,82] [,83] [,84] [,85]
> [1,] 1.522155e-06 1.324407e-06 1.335951e-06 1.364469e-06 1.985645e-06
> [2,] 1.459032e-05 1.383816e-05 1.399321e-05 1.511258e-05 2.244330e-05
> [3,] 1.636661e-04 1.427989e-04 1.573760e-04 1.697279e-04 2.661717e-04
> [4,] 1.827913e-03 1.601839e-03 1.623996e-03 1.908862e-03 2.989347e-03
> [5,] 3.965240e-02 3.578043e-02 3.643417e-02 3.939589e-02 6.723999e-02
> [6,] 6.394878e-02 8.253800e-02 5.905957e-02 6.442785e-02 1.653248e-01
> [7,] 6.241303e-02 5.029166e-02 5.596915e-02 5.911695e-02 1.026350e-01
> [8,] 1.060038e-01 8.718119e-02 9.386723e-02 9.667158e-02 1.351524e-01
> [9,] 1.544509e-01 1.424892e-01 1.321977e-01 1.253273e-01 1.545217e-01
> [10,] 2.373486e-01 1.754391e-01 2.678862e-01 2.631384e-01 3.718462e-01
> [11,] 3.341748e-01 4.245206e-01 3.527893e-01 3.498269e-01 0.000000e+00
> [,86] [,87] [,88] [,89] [,90]
> [1,] 1.052173e-06 9.324404e-07 9.735343e-07 1.288946e-06 1.414766e-06
> [2,] 1.191530e-05 1.043595e-05 9.933084e-06 1.002445e-05 1.436184e-05
> [3,] 1.441900e-04 1.266292e-04 1.198887e-04 1.128016e-04 1.204980e-04
> [4,] 1.710055e-03 1.532371e-03 1.454721e-03 1.361474e-03 1.355922e-03
> [5,] 3.841091e-02 3.634703e-02 3.520787e-02 3.304007e-02 3.273096e-02
> [6,] 8.904763e-02 5.890574e-02 5.703105e-02 5.350949e-02 5.295942e-02
> [7,] 5.359253e-02 5.608549e-02 5.470046e-02 5.179869e-02 5.132157e-02
> [8,] 8.961048e-02 9.463488e-02 9.361251e-02 9.069864e-02 9.031865e-02
> [9,] 1.393932e-01 1.322890e-01 1.332280e-01 1.336516e-01 1.336021e-01
> [10,] 1.760052e-01 2.803653e-01 2.811850e-01 2.768928e-01 2.736742e-01
> [11,] 4.120729e-01 3.397022e-01 3.434497e-01 3.589231e-01 3.639009e-01
> [,91] [,92] [,93] [,94] [,95]
> [1,] 1.744392e-06 3.072710e-06 1.776077e-06 1.291221e-06 7.093269e-07
> [2,] 1.570672e-05 3.192549e-05 1.878627e-05 1.796370e-05 1.662488e-05
> [3,] 1.736115e-04 3.095947e-04 2.099523e-04 2.009354e-04 2.391829e-04
> [4,] 1.456626e-03 3.422051e-03 2.035995e-03 2.245621e-03 2.675413e-03
> [5,] 3.278182e-02 5.742303e-02 4.500901e-02 4.355344e-02 5.979996e-02
> [6,] 5.332957e-02 1.456564e-01 0.000000e+00 9.240591e-02 8.626128e-02
> [7,] 5.080157e-02 8.897199e-02 7.057137e-02 6.042626e-02 8.160649e-02
> [8,] 9.045503e-02 1.374093e-01 1.041303e-01 1.022850e-01 1.230366e-01
> [9,] 1.292387e-01 1.749138e-01 1.555660e-01 1.835182e-01 2.655104e-01
> [10,] 2.653863e-01 3.918589e-01 2.167937e-01 2.258656e-01 3.717880e-01
> [11,] 3.763594e-01 0.000000e+00 4.056632e-01 2.894799e-01 9.065383e-03
> [,96] [,97] [,98] [,99] [,100]
> [1,] 2.415836e-09 1.359686e-08 1.475451e-07 6.893658e-07 4.537576e-06
> [2,] 7.870103e-06 1.564892e-08 2.499070e-08 2.825270e-07 2.520876e-06
> [3,] 1.845011e-04 8.641543e-05 1.646126e-07 1.412635e-07 2.520876e-06
> [4,] 2.654427e-03 2.025862e-03 9.090129e-04 9.304964e-07 1.260438e-06
> [5,] 5.938290e-02 5.829237e-02 4.262051e-02 1.027665e-02 1.660490e-05
> [6,] 8.583516e-02 8.425427e-02 1.570422e-01 6.281098e-02 2.520876e-05
> [7,] 8.104068e-02 8.038072e-02 7.266740e-02 1.553947e-02 5.502085e-03
> [8,] 1.202171e-01 1.173624e-01 1.152289e-01 6.272751e-02 5.604373e-02
> [9,] 2.476915e-01 2.151839e-01 1.465831e-01 1.478680e-01 1.820884e-01
> [10,] 4.027658e-01 4.422090e-01 4.649486e-01 1.879607e-01 1.890909e-01
> [11,] 2.200174e-04 2.050267e-04 0.000000e+00 5.128147e-01 5.672222e-01
> [,101]
> [1,] 0.09090909
> [2,] 0.09090909
> [3,] 0.09090909
> [4,] 0.09090909
> [5,] 0.09090909
> [6,] 0.09090909
> [7,] 0.09090909
> [8,] 0.09090909
> [9,] 0.09090909
> [10,] 0.09090909
> [11,] 0.09090909
>
>
>
> $pop_size
> $pop_size[[1]]
> [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
> [1,] 11 19773.93 9364.804 8591.158 3870.025 21758.82 9388.555 16299.89
> [,9] [,10] [,11] [,12] [,13] [,14] [,15] [,16]
> [1,] 4972.194 9858.302 3440.747 23682.9 19057.75 5843.949 23653.38 26302.69
> [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
> [1,] 40358.12 12152.12 11538.39 9036.756 25362.67 53868.03 22623.23 14141.13
> [,25] [,26] [,27] [,28] [,29] [,30] [,31] [,32]
> [1,] 5789.384 44337.09 57565.96 89341.98 59016.76 25573.4 17018.77 123003.3
> [,33] [,34] [,35] [,36] [,37] [,38] [,39] [,40]
> [1,] 125588 27717.11 36084.2 16615.52 44802.79 35027.58 27095.63 71881.73
> [,41] [,42] [,43] [,44] [,45] [,46] [,47] [,48]
> [1,] 47154.55 55127.99 36015.1 100587.7 109260 58912.86 33303.63 14597.21
> [,49] [,50] [,51] [,52] [,53] [,54] [,55] [,56]
> [1,] 171681.4 69994.52 48788.77 63828.06 46833.15 135129.8 344539.8 297678.1
> [,57] [,58] [,59] [,60] [,61] [,62] [,63] [,64]
> [1,] 190868.2 54910.16 295463.2 242175.4 306885 515363.9 179861.2 121723.3
> [,65] [,66] [,67] [,68] [,69] [,70] [,71] [,72]
> [1,] 163986.9 227804 302317.3 224482.4 645558.9 345220.3 362157.3 211300.5
> [,73] [,74] [,75] [,76] [,77] [,78] [,79] [,80] [,81]
> [1,] 578663.4 636195.4 1533864 1073181 1020597 331472 708661.9 1975676 1453359
> [,82] [,83] [,84] [,85] [,86] [,87] [,88] [,89] [,90]
> [1,] 1626843 2510962 1683191 2039734 684184.6 3973699 3104053 3491152 4309653
> [,91] [,92] [,93] [,94] [,95] [,96] [,97] [,98] [,99]
> [1,] 5074895 6095466 2048643 4503659 11396585 3200541 2866182 3771454 2755279
> [,100] [,101]
> [1,] 19713372 18700993
>
>
> $labels
> pop patch
> 1 1 1
>
> $ahstages
> stage_id stage original_size original_size_b original_size_c min_age max_age
> 1 1 SD 0.0 NA NA 0 NA
> 2 2 P1 0.0 NA NA 0 NA
> 3 3 P2 0.0 NA NA 0 NA
> 4 4 P3 0.0 NA NA 0 NA
> 5 5 SL 0.0 NA NA 0 NA
> 6 6 D 0.0 NA NA 0 NA
> 7 7 XSm 1.0 NA NA 0 NA
> 8 8 Sm 3.0 NA NA 0 NA
> 9 9 Md 6.0 NA NA 0 NA
> 10 10 Lg 11.0 NA NA 0 NA
> 11 11 XLg 19.5 NA NA 0 NA
> repstatus obsstatus propstatus immstatus matstatus entrystage indataset
> 1 0 0 1 0 0 1 0
> 2 0 0 0 1 0 1 0
> 3 0 0 0 1 0 0 0
> 4 0 0 0 1 0 0 0
> 5 0 0 0 1 0 0 0
> 6 0 0 0 0 1 0 1
> 7 1 1 0 0 1 0 1
> 8 1 1 0 0 1 0 1
> 9 1 1 0 0 1 0 1
> 10 1 1 0 0 1 0 1
> 11 1 1 0 0 1 0 1
> binhalfwidth_raw sizebin_min sizebin_max sizebin_center sizebin_width
> 1 0.0 0.0 0.0 0.0 0
> 2 0.0 0.0 0.0 0.0 0
> 3 0.0 0.0 0.0 0.0 0
> 4 0.0 0.0 0.0 0.0 0
> 5 0.0 0.0 0.0 0.0 0
> 6 0.5 -0.5 0.5 0.0 1
> 7 0.5 0.5 1.5 1.0 1
> 8 1.5 1.5 4.5 3.0 3
> 9 1.5 4.5 7.5 6.0 3
> 10 3.5 7.5 14.5 11.0 7
> 11 5.0 14.5 24.5 19.5 10
> binhalfwidthb_raw sizebinb_min sizebinb_max sizebinb_center sizebinb_width
> 1 NA NA NA NA NA
> 2 NA NA NA NA NA
> 3 NA NA NA NA NA
> 4 NA NA NA NA NA
> 5 NA NA NA NA NA
> 6 NA NA NA NA NA
> 7 NA NA NA NA NA
> 8 NA NA NA NA NA
> 9 NA NA NA NA NA
> 10 NA NA NA NA NA
> 11 NA NA NA NA NA
> binhalfwidthc_raw sizebinc_min sizebinc_max sizebinc_center sizebinc_width
> 1 NA NA NA NA NA
> 2 NA NA NA NA NA
> 3 NA NA NA NA NA
> 4 NA NA NA NA NA
> 5 NA NA NA NA NA
> 6 NA NA NA NA NA
> 7 NA NA NA NA NA
> 8 NA NA NA NA NA
> 9 NA NA NA NA NA
> 10 NA NA NA NA NA
> 11 NA NA NA NA NA
> group comments alive almostborn
> 1 0 Dormant seed 1 0
> 2 0 1st yr protocorm 1 0
> 3 0 2nd yr protocorm 1 0
> 4 0 3rd yr protocorm 1 0
> 5 0 Seedling 1 0
> 6 0 Dormant adult 1 0
> 7 0 Extra small adult (1 shoot) 1 0
> 8 0 Small adult (2-4 shoots) 1 0
> 9 0 Medium adult (5-7 shoots) 1 0
> 10 0 Large adult (8-14 shoots) 1 0
> 11 0 Extra large adult (>14 shoots) 1 0
>
> $hstages
> X1
> 1 NA
>
> $agestages
> X1
> 1 NA
>
> $control
> [1] 1 100
>
> attr(,"class")
> [1] "lefkoProj"
Of course, we can use the same approach with function-based projection, using function f_projection3().
10.3 Points to remember
- Stochastic analysis typically refers to matrix projection in which matrices are shuffled randomly a large number of times. The properties of the projection in the long-term have a tendency to be approximately stationary. These analyses assess the impacts of random environmental shifts across time on population dynamics. Although stochasticity may also be demographic or spatial, we concern ourselves only with temporal stochasticity in this chapter because of its dominance in the literature.
- Package
lefko3can conduct all major stochastic analyses even for large numbers of massive matrices, such as historical IPMs and age-by-stage MPMs. This includes even sensitivity and elasticity analyses. - In most cases, stochastic analysis in
lefko3is handled with the same functions as deterministic analysis, but using the optionstochastic = TRUE. - Package
lefko3can also be used to set up discrete-state Markovian stochastic sequences. All functions developed to handle stochastic analysis can handle this type of stochasticity as well, provided that a state transition matrix is provided using thetweightsoption.