Chapter 15 Further Issues II: Importing IPMs and Function-based MPMs
More and more of our imports come from overseas.
It is relatively common for population ecologists running matrix projection analyses to find themselves wanting to build IPMs and function-based MPMs (fbMPMs) published by other authors. For example, users might find themselves reading an interesting paper utilizing IPMs, such as Childs et al. (2003) or Dahlgren & Ehrlén (2011), and wanting to replicate the analyses. Fortunately, lefko3 includes tools to make this relatively easy.
The strategy used in lefko3 is to take all of the characteristics of an IPM or a fbMPM and input those characteristics as data in a vrm_input object. This S3 object is essentially a list that contains up to 13 elements, most of which are structured data frames that need to be edited manually. The function that creates these objects is vrm_import().
To use function vrm_import(), users should first determine the monitoring occasions or years for which information will be entered, the number of patches to be covered, whether there are any stage groups, which vital rate models should be developed, whether information is provided for interactions between independent terms, whether any independent factors are categorical, and the distributions and associated parameters assumed for size and fecundity. Although a stageframe is not required to create vrm_input objects, a stageframe will be required to create the IPMs, fbMPMs, or projections resulting from them, so users should pay serious attention to creating realistic stageframes.
Let’s consider this process using the simplest vrm_input object, which includes only terms for main effects, three years, and a single patch, with Gaussian primary size and fecundity. Let’s say that our monitoring occurred over the years 2020, 2021, and 2022. This yields only two years at time t, since 2022 is the final year of data and so is the ultimate year in time t+1. So we will include only those two years in the input options.
vrm_example <- vrm_import(years = c(2020, 2021))
vrm_example
> $vrm_frame
> main_effect_1 main_1_defined surv obs sizea sizeb sizec
> 1 intercept y-intercept 0 0 0 0 0
> 2 size2 sizea in time t 0 0 0 0 0
> 3 size1 sizea in time t-1 0 0 0 0 0
> 4 sizeb2 sizeb in time t 0 0 0 0 0
> 5 sizeb1 sizeb in time t-1 0 0 0 0 0
> 6 sizec2 sizec in time t 0 0 0 0 0
> 7 sizec1 sizec in time t-1 0 0 0 0 0
> 8 repst2 reproductive status in time t 0 0 0 0 0
> 9 repst1 reproductive status in time t-1 0 0 0 0 0
> 10 age age in time t 0 0 0 0 0
> 11 density density in time t 0 0 0 0 0
> 12 indcova2 individual covariate a in time t 0 0 0 0 0
> 13 indcova1 individual covariate a in time t-1 0 0 0 0 0
> 14 indcovb2 individual covariate b in time t 0 0 0 0 0
> 15 indcovb1 individual covariate b in time t-1 0 0 0 0 0
> 16 indcovc2 individual covariate c in time t 0 0 0 0 0
> 17 indcovc1 individual covariate c in time t-1 0 0 0 0 0
> 18 annucova2 annual covariate a in time t 0 0 0 0 0
> 19 annucova1 annual covariate a in time t-1 0 0 0 0 0
> 20 annucovb2 annual covariate b in time t 0 0 0 0 0
> 21 annucovb1 annual covariate b in time t-1 0 0 0 0 0
> 22 annucovc2 annual covariate c in time t 0 0 0 0 0
> 23 annucovc1 annual covariate c in time t-1 0 0 0 0 0
> repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst
> 1 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0
> 4 0 0 0 0 0 0 0 0 0
> 5 0 0 0 0 0 0 0 0 0
> 6 0 0 0 0 0 0 0 0 0
> 7 0 0 0 0 0 0 0 0 0
> 8 0 0 0 0 0 0 0 0 0
> 9 0 0 0 0 0 0 0 0 0
> 10 0 0 0 0 0 0 0 0 0
> 11 0 0 0 0 0 0 0 0 0
> 12 0 0 0 0 0 0 0 0 0
> 13 0 0 0 0 0 0 0 0 0
> 14 0 0 0 0 0 0 0 0 0
> 15 0 0 0 0 0 0 0 0 0
> 16 0 0 0 0 0 0 0 0 0
> 17 0 0 0 0 0 0 0 0 0
> 18 0 0 0 0 0 0 0 0 0
> 19 0 0 0 0 0 0 0 0 0
> 20 0 0 0 0 0 0 0 0 0
> 21 0 0 0 0 0 0 0 0 0
> 22 0 0 0 0 0 0 0 0 0
> 23 0 0 0 0 0 0 0 0 0
>
> $year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 2020 0 0 0 0 0 0 0 0 0 0 0 0
> 2 2021 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst
> 1 0 0
> 2 0 0
>
> $patch_frame
> patches surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst
> 1 0 0
>
> $group2_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst
> 1 0 0
>
> $group1_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst
> 1 0 0
>
> $dist_frame
> response dist
> 1 surv binom
> 2 obs constant
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec gaussian
> 8 jsurv constant
> 9 jobs constant
> 10 jsizea constant
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constant
>
> $st_frame
> surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb
> 1 1 1 1 1 1 1 1 1 1 1
> jsizec jrepst jmatst
> 1 1 1
>
> attr(,"class")
> [1] "vrm_input"
Our example vrm_input objects is a list holding only 7 elements. The first, vrm_frame, is a data frame holding the main effects factors that we can set for each of up to 14 vital rate models. The 14 vital rate models are the same as those listed in chapter 5 on function-based MPMs: survival (surv), observation status (obs), primary size (sizea), secondary size (sizeb), tertiary size (sizec), reproductive status (repst), fecundity (fec), juvenile survival (jsurv), juvenile observation status (jobs), juvenile primary size (jsizea), juvenile secondary size (jsizeb), juvenile tertiary size (jsizec), juvenile reproductive status (jrepst), and juvenile maturity status (jmatst). We see rows in which we can alter the coefficients to be used in linear models of vital rates, including the y-intercept (intercept), primary size in time t (size2), tertiary size in time t-1 (sizec1), spatial density (density), etc. The general strategy is for users to change the coefficients that they have explicit values for, and to leave the rest as 0.
Object year_frame allows us to set specific coefficients for each year associated with each vital rate model. This is particularly useful as the IPM in question used a mixed modeling approach with year as a random term, although it serves the same function with year as a fixed categorical term. Object patch_frame functions in the same way, except for patches or subpopulations (we do not currently offer a top-level population category, but the patch level can be used for populations if the latter are not to be subdivided). Objects group2_frame and group1_frame provide coefficients associated with different life history stage groups in times t and t-1, respectively, if such information is provided and stages are grouped in a way that is incorporated into linear modeling.
Object dist_frame gives the distribution of each vital rate model’s response term. Any vital rate that uses a linear model for estimation needs to be set to binom (for binomial distribution), gaussian (for the Gaussian distribution), gamma (for the gamma distribution), poisson (for the Poisson distribution), or negbin (for the negative binomial distribution). Unused vital rates should be set to constant. Object st_frame allows the user to set \(\sigma\) if the distribution is Gaussian, or \(\theta\) if the distribution is negative binomial (all other cases should be left as 1).
Let’s now take a look at some examples.
15.1 Generating standard ahistorical IPMs and function-based MPMs
Let’s start off by recreating the ahistorical IPM set up in Chapter 7. This example will focus on Lathyrus vernus (section 1.8.2). To remind ourselves of this plant and its dataset, let’s take a look at a data summary. Note that in a real example from the literature, we might not have the original dataset to work with, but would need to infer certain characteristics about the dataset from the publication.
data(lathyrus)
summary(lathyrus)
> SUBPLOT GENET Volume88 lnVol88
> Min. :1.000 Min. : 1.0 Min. : 3.4 Min. :1.200
> 1st Qu.:2.000 1st Qu.: 48.0 1st Qu.: 63.0 1st Qu.:4.100
> Median :3.000 Median : 97.0 Median : 732.5 Median :6.600
> Mean :3.223 Mean :110.2 Mean : 749.4 Mean :5.538
> 3rd Qu.:4.000 3rd Qu.:167.5 3rd Qu.:1025.5 3rd Qu.:6.900
> Max. :6.000 Max. :284.0 Max. :7032.0 Max. :8.900
> NA's :404 NA's :404
> FCODE88 Flow88 Intactseed88 Dead1988 Dormant1988
> Min. :0.0000 Min. : 1.00 Min. : 0 Mode:logical Mode:logical
> 1st Qu.:0.0000 1st Qu.: 4.00 1st Qu.: 0 NA's:1119 NA's:1119
> Median :0.0000 Median : 8.00 Median : 0
> Mean :0.3399 Mean :11.86 Mean : 3
> 3rd Qu.:1.0000 3rd Qu.:15.00 3rd Qu.: 4
> Max. :1.0000 Max. :66.00 Max. :34
> NA's :404 NA's :910 NA's :875
> Missing1988 Seedling1988 Volume89 lnVol89
> Mode:logical Min. :1.000 Min. : 1.8 Min. :0.600
> NA's:1119 1st Qu.:2.000 1st Qu.: 15.6 1st Qu.:2.700
> Median :2.000 Median : 118.8 Median :4.800
> Mean :2.144 Mean : 573.3 Mean :4.855
> 3rd Qu.:3.000 3rd Qu.: 968.8 3rd Qu.:6.900
> Max. :3.000 Max. :6539.4 Max. :8.800
> NA's :1022 NA's :294 NA's :294
> FCODE89 Flow89 Intactseed89 Dead1989
> Min. :0.0000 Min. : 1.00 Min. : 0.000 Min. :1
> 1st Qu.:0.0000 1st Qu.: 5.00 1st Qu.: 0.000 1st Qu.:1
> Median :0.0000 Median :11.00 Median : 5.000 Median :1
> Mean :0.2667 Mean :14.88 Mean : 8.273 Mean :1
> 3rd Qu.:1.0000 3rd Qu.:20.00 3rd Qu.:13.000 3rd Qu.:1
> Max. :1.0000 Max. :97.00 Max. :66.000 Max. :1
> NA's :294 NA's :906 NA's :899 NA's :1077
> Dormant1989 Missing1989 Seedling1989 Volume90 lnVol90
> Min. :1 Min. :1 Min. :1.000 Min. : 2.1 Min. :0.700
> 1st Qu.:1 1st Qu.:1 1st Qu.:2.000 1st Qu.: 12.6 1st Qu.:2.500
> Median :1 Median :1 Median :2.000 Median : 61.0 Median :4.100
> Mean :1 Mean :1 Mean :2.136 Mean : 244.1 Mean :4.207
> 3rd Qu.:1 3rd Qu.:1 3rd Qu.:2.000 3rd Qu.: 295.2 3rd Qu.:5.700
> Max. :1 Max. :1 Max. :3.000 Max. :4242.8 Max. :8.400
> NA's :1046 NA's :1112 NA's :1001 NA's :245 NA's :245
> FCODE90 Flow90 Intactseed90 Dead1990
> Min. :0.0000 Min. : 1.000 Min. : 0.000 Min. :1
> 1st Qu.:0.0000 1st Qu.: 3.000 1st Qu.: 0.000 1st Qu.:1
> Median :0.0000 Median : 6.000 Median : 0.000 Median :1
> Mean :0.1581 Mean : 8.104 Mean : 2.514 Mean :1
> 3rd Qu.:0.0000 3rd Qu.:10.750 3rd Qu.: 1.000 3rd Qu.:1
> Max. :1.0000 Max. :54.000 Max. :37.000 Max. :1
> NA's :246 NA's :985 NA's :981 NA's :1007
> Dormant1990 Missing1990 Seedling1990 Volume91 lnVol91
> Min. :1 Min. :1 Min. :1.000 Min. : 4.0 Min. :1.400
> 1st Qu.:1 1st Qu.:1 1st Qu.:2.000 1st Qu.: 12.0 1st Qu.:2.500
> Median :1 Median :1 Median :2.000 Median : 118.5 Median :4.800
> Mean :1 Mean :1 Mean :2.186 Mean : 418.7 Mean :4.642
> 3rd Qu.:1 3rd Qu.:1 3rd Qu.:2.000 3rd Qu.: 689.7 3rd Qu.:6.500
> Max. :1 Max. :1 Max. :3.000 Max. :6645.8 Max. :8.800
> NA's :1054 NA's :1105 NA's :1049 NA's :305 NA's :305
> FCODE91 Flow91 Intactseed91 Dead1991 Dormant1991
> Min. :0.0000 Min. : 1.00 Min. : 0.000 Min. :1 Min. :1
> 1st Qu.:0.0000 1st Qu.: 4.00 1st Qu.: 0.000 1st Qu.:1 1st Qu.:1
> Median :0.0000 Median : 8.00 Median : 3.500 Median :1 Median :1
> Mean :0.2525 Mean :11.12 Mean : 5.805 Mean :1 Mean :1
> 3rd Qu.:1.0000 3rd Qu.:15.00 3rd Qu.:10.000 3rd Qu.:1 3rd Qu.:1
> Max. :1.0000 Max. :48.00 Max. :48.000 Max. :1 Max. :1
> NA's :307 NA's :954 NA's :919 NA's :925 NA's :1034
> Missing1991 Seedling1991
> Min. :1 Min. :1.000
> 1st Qu.:1 1st Qu.:2.000
> Median :1 Median :2.000
> Mean :1 Mean :1.973
> 3rd Qu.:1 3rd Qu.:2.000
> Max. :1 Max. :3.000
> NA's :1095 NA's :1082
The data were collected over four years - 1988 through 1991. Size is given in two formats - either by the total leaf volume (Volume), or by the natural logarithm of the total leaf volume (lnVol). Let’s use the total volume for this example. We also need to note the minimum and maximum size, and whether an unobservable size class is included. The minimum leaf volume appears to be be 1.8, while the maximum appears to be 7032.0, and the literature on this plant shows that it can experience vegetative dormancy, during which there would be no aboveground tissue and hence leaf volume would be 0.
As before, we need to create a stageframe describing the life history and the actual stages that will compose the discretized IPM. We do so below, utilizing the information that we have gleaned from the publication, and then show four key variables within that output. Note that this stageframe covers a complex IPM, involving 100 size-classified stages and three stages that do not fit in the size gradient (dormant seed, seedling, and vegetative dormancy).
sizevector <- c(0, 100, 0, 1, 7100)
stagevector <- c("Sd", "Sdl", "Dorm", "ipm", "ipm")
repvector <- c(0, 0, 0, 1, 1)
obsvector <- c(0, 1, 0, 1, 1)
matvector <- c(0, 0, 1, 1, 1)
immvector <- c(1, 1, 0, 0, 0)
propvector <- c(1, 0, 0, 0, 0)
indataset <- c(0, 1, 1, 1, 1)
binvec <- c(0, 100, 0.5, 1, 1)
comments <- c("Dormant seed", "Seedling", "Dormant", "ipm adult stage",
"ipm adult stage")
lathframeipm <- sf_create(sizes = sizevector, stagenames = stagevector,
repstatus = repvector, obsstatus = obsvector, propstatus = propvector,
immstatus = immvector, matstatus = matvector, comments = comments,
indataset = indataset, binhalfwidth = binvec, ipmbins = 100, roundsize = 3)
lathframeipm[,c("stage", "size", "sizebin_min", "sizebin_max", "comments")]
> stage size sizebin_min sizebin_max comments
> 1 Sd 0.000 0.00 0.00 Dormant seed
> 2 Sdl 100.000 0.00 200.00 Seedling
> 3 Dorm 0.000 -0.50 0.50 Dormant
> 4 sza_36.495_0 36.495 1.00 71.99 ipm adult stage
> 5 sza_107.48_0 107.485 71.99 142.98 ipm adult stage
> 6 sza_178.47_0 178.475 142.98 213.97 ipm adult stage
> 7 sza_249.46_0 249.465 213.97 284.96 ipm adult stage
> 8 sza_320.45_0 320.455 284.96 355.95 ipm adult stage
> 9 sza_391.44_0 391.445 355.95 426.94 ipm adult stage
> 10 sza_462.43_0 462.435 426.94 497.93 ipm adult stage
> 11 sza_533.42_0 533.425 497.93 568.92 ipm adult stage
> 12 sza_604.41_0 604.415 568.92 639.91 ipm adult stage
> 13 sza_675.40_0 675.405 639.91 710.90 ipm adult stage
> 14 sza_746.39_0 746.395 710.90 781.89 ipm adult stage
> 15 sza_817.38_0 817.385 781.89 852.88 ipm adult stage
> 16 sza_888.37_0 888.375 852.88 923.87 ipm adult stage
> 17 sza_959.36_0 959.365 923.87 994.86 ipm adult stage
> 18 sza_1030.3_0 1030.355 994.86 1065.85 ipm adult stage
> 19 sza_1101.3_0 1101.345 1065.85 1136.84 ipm adult stage
> 20 sza_1172.3_0 1172.335 1136.84 1207.83 ipm adult stage
> 21 sza_1243.3_0 1243.325 1207.83 1278.82 ipm adult stage
> 22 sza_1314.3_0 1314.315 1278.82 1349.81 ipm adult stage
> 23 sza_1385.3_0 1385.305 1349.81 1420.80 ipm adult stage
> 24 sza_1456.2_0 1456.295 1420.80 1491.79 ipm adult stage
> 25 sza_1527.2_0 1527.285 1491.79 1562.78 ipm adult stage
> 26 sza_1598.2_0 1598.275 1562.78 1633.77 ipm adult stage
> 27 sza_1669.2_0 1669.265 1633.77 1704.76 ipm adult stage
> 28 sza_1740.2_0 1740.255 1704.76 1775.75 ipm adult stage
> 29 sza_1811.2_0 1811.245 1775.75 1846.74 ipm adult stage
> 30 sza_1882.2_0 1882.235 1846.74 1917.73 ipm adult stage
> 31 sza_1953.2_0 1953.225 1917.73 1988.72 ipm adult stage
> 32 sza_2024.2_0 2024.215 1988.72 2059.71 ipm adult stage
> 33 sza_2095.2_0 2095.205 2059.71 2130.70 ipm adult stage
> 34 sza_2166.1_0 2166.195 2130.70 2201.69 ipm adult stage
> 35 sza_2237.1_0 2237.185 2201.69 2272.68 ipm adult stage
> 36 sza_2308.1_0 2308.175 2272.68 2343.67 ipm adult stage
> 37 sza_2379.1_0 2379.165 2343.67 2414.66 ipm adult stage
> 38 sza_2450.1_0 2450.155 2414.66 2485.65 ipm adult stage
> 39 sza_2521.1_0 2521.145 2485.65 2556.64 ipm adult stage
> 40 sza_2592.1_0 2592.135 2556.64 2627.63 ipm adult stage
> 41 sza_2663.1_0 2663.125 2627.63 2698.62 ipm adult stage
> 42 sza_2734.1_0 2734.115 2698.62 2769.61 ipm adult stage
> 43 sza_2805.1_0 2805.105 2769.61 2840.60 ipm adult stage
> 44 sza_2876.0_0 2876.095 2840.60 2911.59 ipm adult stage
> 45 sza_2947.0_0 2947.085 2911.59 2982.58 ipm adult stage
> 46 sza_3018.0_0 3018.075 2982.58 3053.57 ipm adult stage
> 47 sza_3089.0_0 3089.065 3053.57 3124.56 ipm adult stage
> 48 sza_3160.0_0 3160.055 3124.56 3195.55 ipm adult stage
> 49 sza_3231.0_0 3231.045 3195.55 3266.54 ipm adult stage
> 50 sza_3302.0_0 3302.035 3266.54 3337.53 ipm adult stage
> 51 sza_3373.0_0 3373.025 3337.53 3408.52 ipm adult stage
> 52 sza_3444.0_0 3444.015 3408.52 3479.51 ipm adult stage
> 53 sza_3515.0_0 3515.005 3479.51 3550.50 ipm adult stage
> 54 sza_3585.9_0 3585.995 3550.50 3621.49 ipm adult stage
> 55 sza_3656.9_0 3656.985 3621.49 3692.48 ipm adult stage
> 56 sza_3727.9_0 3727.975 3692.48 3763.47 ipm adult stage
> 57 sza_3798.9_0 3798.965 3763.47 3834.46 ipm adult stage
> 58 sza_3869.9_0 3869.955 3834.46 3905.45 ipm adult stage
> 59 sza_3940.9_0 3940.945 3905.45 3976.44 ipm adult stage
> 60 sza_4011.9_0 4011.935 3976.44 4047.43 ipm adult stage
> 61 sza_4082.9_0 4082.925 4047.43 4118.42 ipm adult stage
> 62 sza_4153.9_0 4153.915 4118.42 4189.41 ipm adult stage
> 63 sza_4224.9_0 4224.905 4189.41 4260.40 ipm adult stage
> 64 sza_4295.8_0 4295.895 4260.40 4331.39 ipm adult stage
> 65 sza_4366.8_0 4366.885 4331.39 4402.38 ipm adult stage
> 66 sza_4437.8_0 4437.875 4402.38 4473.37 ipm adult stage
> 67 sza_4508.8_0 4508.865 4473.37 4544.36 ipm adult stage
> 68 sza_4579.8_0 4579.855 4544.36 4615.35 ipm adult stage
> 69 sza_4650.8_0 4650.845 4615.35 4686.34 ipm adult stage
> 70 sza_4721.8_0 4721.835 4686.34 4757.33 ipm adult stage
> 71 sza_4792.8_0 4792.825 4757.33 4828.32 ipm adult stage
> 72 sza_4863.8_0 4863.815 4828.32 4899.31 ipm adult stage
> 73 sza_4934.8_0 4934.805 4899.31 4970.30 ipm adult stage
> 74 sza_5005.7_0 5005.795 4970.30 5041.29 ipm adult stage
> 75 sza_5076.7_0 5076.785 5041.29 5112.28 ipm adult stage
> 76 sza_5147.7_0 5147.775 5112.28 5183.27 ipm adult stage
> 77 sza_5218.7_0 5218.765 5183.27 5254.26 ipm adult stage
> 78 sza_5289.7_0 5289.755 5254.26 5325.25 ipm adult stage
> 79 sza_5360.7_0 5360.745 5325.25 5396.24 ipm adult stage
> 80 sza_5431.7_0 5431.735 5396.24 5467.23 ipm adult stage
> 81 sza_5502.7_0 5502.725 5467.23 5538.22 ipm adult stage
> 82 sza_5573.7_0 5573.715 5538.22 5609.21 ipm adult stage
> 83 sza_5644.7_0 5644.705 5609.21 5680.20 ipm adult stage
> 84 sza_5715.6_0 5715.695 5680.20 5751.19 ipm adult stage
> 85 sza_5786.6_0 5786.685 5751.19 5822.18 ipm adult stage
> 86 sza_5857.6_0 5857.675 5822.18 5893.17 ipm adult stage
> 87 sza_5928.6_0 5928.665 5893.17 5964.16 ipm adult stage
> 88 sza_5999.6_0 5999.655 5964.16 6035.15 ipm adult stage
> 89 sza_6070.6_0 6070.645 6035.15 6106.14 ipm adult stage
> 90 sza_6141.6_0 6141.635 6106.14 6177.13 ipm adult stage
> 91 sza_6212.6_0 6212.625 6177.13 6248.12 ipm adult stage
> 92 sza_6283.6_0 6283.615 6248.12 6319.11 ipm adult stage
> 93 sza_6354.6_0 6354.605 6319.11 6390.10 ipm adult stage
> 94 sza_6425.5_0 6425.595 6390.10 6461.09 ipm adult stage
> 95 sza_6496.5_0 6496.585 6461.09 6532.08 ipm adult stage
> 96 sza_6567.5_0 6567.575 6532.08 6603.07 ipm adult stage
> 97 sza_6638.5_0 6638.565 6603.07 6674.06 ipm adult stage
> 98 sza_6709.5_0 6709.555 6674.06 6745.05 ipm adult stage
> 99 sza_6780.5_0 6780.545 6745.05 6816.04 ipm adult stage
> 100 sza_6851.5_0 6851.535 6816.04 6887.03 ipm adult stage
> 101 sza_6922.5_0 6922.525 6887.03 6958.02 ipm adult stage
> 102 sza_6993.5_0 6993.515 6958.02 7029.01 ipm adult stage
> 103 sza_7064.5_0 7064.505 7029.01 7100.00 ipm adult stage15.1.1 Incorporating vital rate functions used in IPMs and fbMPMs
To be useful, publications involving IPMs need to show the parameterizations of their kernels, which are generally composed of vital rate models. These parameterizations vary in complexity, as different authors have different preferences for developing vital rate models. Some choose approaches involving splines or general additive modeling - these approaches produce potentially complex patterns and are difficult to characterize except via saved data structures describing the localized relationships between independent terms and response (for an excellent example of a well-done non-linear IPM, see Garcia et al. 2011). Other approaches utilize linear modeling, and may involve generalized linear modeling (GLM) or generalized linear mixed modeling (GLMM) (e.g., Dahlgren & Ehrlén 2011; Shefferson et al. 2014). Package lefko3 is currently set up to allow imports of GLM and GLMM models. We anticipate developing methods to import spline-based kernels in the near future.
Let’s assume that our IPM is composed of a kernel that is itself composed of four vital rates: survival probability, sprouting probability, size transition, and fecundity. The kernel for a typical sprouting individual would be given as the following.
\[\begin{equation} K(x_j, x_i) = s(x_i, t) r(x_j, t+1) g(x_j, x_i) + f(x_i, t) \tag{15.1} \end{equation}\]
Here, \(s(x_i, t)\) is the survival of an individual of discretized size \(x_i\) at time t to time t+1, \(r(x_j, t+1)\) is the sprouting probability of an individual in discretized size \(x_j\) at time t+1 that has survived from time t, \(g(x_j, x_i)\) is the probability of size transition from discretized size \(x_i\) at time t to discretized size \(x_j\) in time t+1 assuming survival and sprouting, and \(f(x_i, t)\) is the average offspring production in time t+1 of an individual in discretized size \(x_i\) at time t. For a vegetatively dormant individual, the kernel differs because a lack of sprouting prevents any size transition or offspring production from occurring, as in the following.
\[\begin{equation} K(x_j, x_i) = s(x_i, t) (1 - r(x_j, t+1)) \tag{15.2} \end{equation}\]
Next we need to scour the publication to find the definitions of the vital rate models defining the kernels. In our case, this means finding the slope coefficients and response distributions for all vital rate models used, including survival probability, sprouting probability, size transition, fecundity, etc. The probability distributions, as shown in our IPM chapter (chapter 7), should be binomial for vital rates such as survival, observation status (sprouting), reproductive status, and maturity status. They could be Gaussian, gamma, Poisson, or negative binomial for size and fecundity, or might be zero-truncated or zero-inflated versions of the Poisson or negative binomial. We also need to know whether juvenile vital rate models will be used, and what those distributions correspond to.
Chapter 7 provides model summaries (just preceding section 7.2.4). For this example, following the model summaries in the IPM chapter, we see that we need survival, observation status, size transition, and fecundity, and that we will also use juvenile survival, juvenile observation status, and juvenile size transition to model the seedling class. The modeling approach is the generalized linear mixed model, with year as a random categorical factor.
Let’s start off by building a skeleton vrm_input object. Note that we input only the years capable of being transitioned from in the dataset, which means the three years 1988, 1989, and 1990. We will make this object a bit bigger than before, because we will allow fecundity to be zero-inflated (setting zi = TRUE will add seven new columns governing the zero-inflation binomial model for all parameters capable of being zero-inflated). We will also set use.juv = TRUE to change some defaults to allow the use of juvenile transitions. Here is the code to produce our skeleton object.
lath_vrm <- vrm_import(years = c(1988:1990), zi = TRUE, dist.fec = "negbin",
use.juv = TRUE)
lath_vrm
> $vrm_frame
> main_effect_1 main_1_defined surv obs sizea sizeb sizec
> 1 intercept y-intercept 0 0 0 0 0
> 2 size2 sizea in time t 0 0 0 0 0
> 3 size1 sizea in time t-1 0 0 0 0 0
> 4 sizeb2 sizeb in time t 0 0 0 0 0
> 5 sizeb1 sizeb in time t-1 0 0 0 0 0
> 6 sizec2 sizec in time t 0 0 0 0 0
> 7 sizec1 sizec in time t-1 0 0 0 0 0
> 8 repst2 reproductive status in time t 0 0 0 0 0
> 9 repst1 reproductive status in time t-1 0 0 0 0 0
> 10 age age in time t 0 0 0 0 0
> 11 density density in time t 0 0 0 0 0
> 12 indcova2 individual covariate a in time t 0 0 0 0 0
> 13 indcova1 individual covariate a in time t-1 0 0 0 0 0
> 14 indcovb2 individual covariate b in time t 0 0 0 0 0
> 15 indcovb1 individual covariate b in time t-1 0 0 0 0 0
> 16 indcovc2 individual covariate c in time t 0 0 0 0 0
> 17 indcovc1 individual covariate c in time t-1 0 0 0 0 0
> 18 annucova2 annual covariate a in time t 0 0 0 0 0
> 19 annucova1 annual covariate a in time t-1 0 0 0 0 0
> 20 annucovb2 annual covariate b in time t 0 0 0 0 0
> 21 annucovb1 annual covariate b in time t-1 0 0 0 0 0
> 22 annucovc2 annual covariate c in time t 0 0 0 0 0
> 23 annucovc1 annual covariate c in time t-1 0 0 0 0 0
> repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi sizeb_zi
> 1 0 0 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0 0 0
> 4 0 0 0 0 0 0 0 0 0 0 0
> 5 0 0 0 0 0 0 0 0 0 0 0
> 6 0 0 0 0 0 0 0 0 0 0 0
> 7 0 0 0 0 0 0 0 0 0 0 0
> 8 0 0 0 0 0 0 0 0 0 0 0
> 9 0 0 0 0 0 0 0 0 0 0 0
> 10 0 0 0 0 0 0 0 0 0 0 0
> 11 0 0 0 0 0 0 0 0 0 0 0
> 12 0 0 0 0 0 0 0 0 0 0 0
> 13 0 0 0 0 0 0 0 0 0 0 0
> 14 0 0 0 0 0 0 0 0 0 0 0
> 15 0 0 0 0 0 0 0 0 0 0 0
> 16 0 0 0 0 0 0 0 0 0 0 0
> 17 0 0 0 0 0 0 0 0 0 0 0
> 18 0 0 0 0 0 0 0 0 0 0 0
> 19 0 0 0 0 0 0 0 0 0 0 0
> 20 0 0 0 0 0 0 0 0 0 0 0
> 21 0 0 0 0 0 0 0 0 0 0 0
> 22 0 0 0 0 0 0 0 0 0 0 0
> 23 0 0 0 0 0 0 0 0 0 0 0
> sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0
> 2 0 0 0 0 0
> 3 0 0 0 0 0
> 4 0 0 0 0 0
> 5 0 0 0 0 0
> 6 0 0 0 0 0
> 7 0 0 0 0 0
> 8 0 0 0 0 0
> 9 0 0 0 0 0
> 10 0 0 0 0 0
> 11 0 0 0 0 0
> 12 0 0 0 0 0
> 13 0 0 0 0 0
> 14 0 0 0 0 0
> 15 0 0 0 0 0
> 16 0 0 0 0 0
> 17 0 0 0 0 0
> 18 0 0 0 0 0
> 19 0 0 0 0 0
> 20 0 0 0 0 0
> 21 0 0 0 0 0
> 22 0 0 0 0 0
> 23 0 0 0 0 0
>
> $year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1988 0 0 0 0 0 0 0 0 0 0 0 0
> 2 1989 0 0 0 0 0 0 0 0 0 0 0 0
> 3 1990 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0
>
> $patch_frame
> patches surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group2_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group1_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $dist_frame
> response dist
> 1 surv binom
> 2 obs constant
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec negbin
> 8 jsurv binom
> 9 jobs constant
> 10 jsizea gaussian
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constant
>
> $st_frame
> surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb
> 1 1 1 1 1 1 1 1 1 1 1
> jsizec jrepst jmatst
> 1 1 1
>
> attr(,"class")
> [1] "vrm_input"
Now that we have our skeleton vrm_input object, let’s take a look at the vital rate models. In a typical publication, the authors might present equations showing the linear relationships among terms. Alternatively, they may present some of the output from modeling, giving us the slope coefficients. Since chapter 7 includes the latter, let’s instead assume that we have a paper that presents the vital rate models as equations. Below, we see how the survival and sprouting models might be presented, using the real estimated terms.
\[\begin{equation} logit(s(x_i, t)) = 2.32571 + 0.00109 size(t) + year(t) + indiv(i) \tag{15.3} \end{equation}\]
\[\begin{equation} logit(r(x_j, t+1)) = 2.230 + year(t) + indiv(i) \tag{15.4} \end{equation}\]
In these models, we see that both are binomial models using the logit link. Both have y-intercepts (2.32571 in the case of survival, and 2.230 in the case of sprouting). The survival model involves a relationship with size in time t, and that relationship is linear with a slope of 0.00109. Both equations include categorical values for year in time t and individual, because both survival and sprouting probabilities were estimated as mixed models with year in time t and individual as random terms. Let’s input all of the main terms into our skeleton vrm_input object, particularly getting the y-intercepts and slope coefficients into the appropriate parts of the vrm_frame. Let’s also change the distribution of the sprouting model from constant (the current setting) to binom.
int.elem <- which(lath_vrm$vrm_frame$main_effect_1 == "intercept")
size2.elem <- which(lath_vrm$vrm_frame$main_effect_1 == "size2")
lath_vrm$vrm_frame$surv[int.elem] <- 2.32571
lath_vrm$vrm_frame$surv[size2.elem] <- 0.00109
lath_vrm$vrm_frame$obs[int.elem] <- 2.230
lath_vrm$dist_frame$dist[2] <- "binom"
lath_vrm$vrm_frame
> main_effect_1 main_1_defined surv obs sizea sizeb
> 1 intercept y-intercept 2.32571 2.23 0 0
> 2 size2 sizea in time t 0.00109 0.00 0 0
> 3 size1 sizea in time t-1 0.00000 0.00 0 0
> 4 sizeb2 sizeb in time t 0.00000 0.00 0 0
> 5 sizeb1 sizeb in time t-1 0.00000 0.00 0 0
> 6 sizec2 sizec in time t 0.00000 0.00 0 0
> 7 sizec1 sizec in time t-1 0.00000 0.00 0 0
> 8 repst2 reproductive status in time t 0.00000 0.00 0 0
> 9 repst1 reproductive status in time t-1 0.00000 0.00 0 0
> 10 age age in time t 0.00000 0.00 0 0
> 11 density density in time t 0.00000 0.00 0 0
> 12 indcova2 individual covariate a in time t 0.00000 0.00 0 0
> 13 indcova1 individual covariate a in time t-1 0.00000 0.00 0 0
> 14 indcovb2 individual covariate b in time t 0.00000 0.00 0 0
> 15 indcovb1 individual covariate b in time t-1 0.00000 0.00 0 0
> 16 indcovc2 individual covariate c in time t 0.00000 0.00 0 0
> 17 indcovc1 individual covariate c in time t-1 0.00000 0.00 0 0
> 18 annucova2 annual covariate a in time t 0.00000 0.00 0 0
> 19 annucova1 annual covariate a in time t-1 0.00000 0.00 0 0
> 20 annucovb2 annual covariate b in time t 0.00000 0.00 0 0
> 21 annucovb1 annual covariate b in time t-1 0.00000 0.00 0 0
> 22 annucovc2 annual covariate c in time t 0.00000 0.00 0 0
> 23 annucovc1 annual covariate c in time t-1 0.00000 0.00 0 0
> sizec repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi
> 1 0 0 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0 0 0
> 4 0 0 0 0 0 0 0 0 0 0 0
> 5 0 0 0 0 0 0 0 0 0 0 0
> 6 0 0 0 0 0 0 0 0 0 0 0
> 7 0 0 0 0 0 0 0 0 0 0 0
> 8 0 0 0 0 0 0 0 0 0 0 0
> 9 0 0 0 0 0 0 0 0 0 0 0
> 10 0 0 0 0 0 0 0 0 0 0 0
> 11 0 0 0 0 0 0 0 0 0 0 0
> 12 0 0 0 0 0 0 0 0 0 0 0
> 13 0 0 0 0 0 0 0 0 0 0 0
> 14 0 0 0 0 0 0 0 0 0 0 0
> 15 0 0 0 0 0 0 0 0 0 0 0
> 16 0 0 0 0 0 0 0 0 0 0 0
> 17 0 0 0 0 0 0 0 0 0 0 0
> 18 0 0 0 0 0 0 0 0 0 0 0
> 19 0 0 0 0 0 0 0 0 0 0 0
> 20 0 0 0 0 0 0 0 0 0 0 0
> 21 0 0 0 0 0 0 0 0 0 0 0
> 22 0 0 0 0 0 0 0 0 0 0 0
> 23 0 0 0 0 0 0 0 0 0 0 0
> sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0
> 2 0 0 0 0 0 0
> 3 0 0 0 0 0 0
> 4 0 0 0 0 0 0
> 5 0 0 0 0 0 0
> 6 0 0 0 0 0 0
> 7 0 0 0 0 0 0
> 8 0 0 0 0 0 0
> 9 0 0 0 0 0 0
> 10 0 0 0 0 0 0
> 11 0 0 0 0 0 0
> 12 0 0 0 0 0 0
> 13 0 0 0 0 0 0
> 14 0 0 0 0 0 0
> 15 0 0 0 0 0 0
> 16 0 0 0 0 0 0
> 17 0 0 0 0 0 0
> 18 0 0 0 0 0 0
> 19 0 0 0 0 0 0
> 20 0 0 0 0 0 0
> 21 0 0 0 0 0 0
> 22 0 0 0 0 0 0
> 23 0 0 0 0 0 0
lath_vrm$dist_frame
> response dist
> 1 surv binom
> 2 obs binom
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec negbin
> 8 jsurv binom
> 9 jobs constant
> 10 jsizea gaussian
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constantWe have added the fixed main effects to our survival and sprouting models. Next, we will add the appropriate year terms. Year is a random term in both cases, meaning that the average effect of year has actually already been absorbed by the y-intercept and the mean of the year terms should be approximately zero. So, if we cannot find these terms in the paper, then we can simply assume it is 0, or we can produce random numbers if we have information on the variance of the year term in the model. In our case, we see in the output for the survival and sprouting models in the IPM chapter that the standard deviation of the year term is 0, meaning that these coefficients were inestimable under the mixed structure used. So, we will skip adding these terms here. Because we are not interested in predicting individual survival probabilities, we will also not incorporate any individual terms.
Let’s move on to size. Our size model has a Gaussian response and so uses the identity link. Thus, our predicted size in time t+1 is given by the equation below.
\[\begin{equation} E(size(x_j, t+1)) = 164.0695 + 0.6211 size(z_i, t) + year(t) + indiv(i) \tag{15.5} \end{equation}\]
The probability of becoming size j in time t+1 assuming a Gaussian distribution is the following.
\[\begin{equation} g(x_j, x_i) = \frac{1}{\sqrt{2 \pi} \sigma(x_j)} e^{-E(size(x_j, t+1))} \tag{15.6} \end{equation}\]
Our size model includes year terms, which are 96.3244, -240.8036, and 144.4792 for years 1988, 1989, and 1990. We also see that \(\sigma = 503.6167\), which is shown as the standard deviation of the residual component in the random effects section of the model summary output. We will add these terms below. Note that primary size is set to the Gaussian distribution by default.
lath_vrm$vrm_frame$sizea[int.elem] <- 164.0695
lath_vrm$vrm_frame$sizea[size2.elem] <- 0.6211
lath_vrm$year_frame$sizea <- c(96.3244, -240.8036, 144.4792)
lath_vrm$st_frame[3] <- 503.6167
lath_vrm$vrm_frame
> main_effect_1 main_1_defined surv obs sizea sizeb
> 1 intercept y-intercept 2.32571 2.23 164.0695 0
> 2 size2 sizea in time t 0.00109 0.00 0.6211 0
> 3 size1 sizea in time t-1 0.00000 0.00 0.0000 0
> 4 sizeb2 sizeb in time t 0.00000 0.00 0.0000 0
> 5 sizeb1 sizeb in time t-1 0.00000 0.00 0.0000 0
> 6 sizec2 sizec in time t 0.00000 0.00 0.0000 0
> 7 sizec1 sizec in time t-1 0.00000 0.00 0.0000 0
> 8 repst2 reproductive status in time t 0.00000 0.00 0.0000 0
> 9 repst1 reproductive status in time t-1 0.00000 0.00 0.0000 0
> 10 age age in time t 0.00000 0.00 0.0000 0
> 11 density density in time t 0.00000 0.00 0.0000 0
> 12 indcova2 individual covariate a in time t 0.00000 0.00 0.0000 0
> 13 indcova1 individual covariate a in time t-1 0.00000 0.00 0.0000 0
> 14 indcovb2 individual covariate b in time t 0.00000 0.00 0.0000 0
> 15 indcovb1 individual covariate b in time t-1 0.00000 0.00 0.0000 0
> 16 indcovc2 individual covariate c in time t 0.00000 0.00 0.0000 0
> 17 indcovc1 individual covariate c in time t-1 0.00000 0.00 0.0000 0
> 18 annucova2 annual covariate a in time t 0.00000 0.00 0.0000 0
> 19 annucova1 annual covariate a in time t-1 0.00000 0.00 0.0000 0
> 20 annucovb2 annual covariate b in time t 0.00000 0.00 0.0000 0
> 21 annucovb1 annual covariate b in time t-1 0.00000 0.00 0.0000 0
> 22 annucovc2 annual covariate c in time t 0.00000 0.00 0.0000 0
> 23 annucovc1 annual covariate c in time t-1 0.00000 0.00 0.0000 0
> sizec repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi
> 1 0 0 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0 0 0
> 4 0 0 0 0 0 0 0 0 0 0 0
> 5 0 0 0 0 0 0 0 0 0 0 0
> 6 0 0 0 0 0 0 0 0 0 0 0
> 7 0 0 0 0 0 0 0 0 0 0 0
> 8 0 0 0 0 0 0 0 0 0 0 0
> 9 0 0 0 0 0 0 0 0 0 0 0
> 10 0 0 0 0 0 0 0 0 0 0 0
> 11 0 0 0 0 0 0 0 0 0 0 0
> 12 0 0 0 0 0 0 0 0 0 0 0
> 13 0 0 0 0 0 0 0 0 0 0 0
> 14 0 0 0 0 0 0 0 0 0 0 0
> 15 0 0 0 0 0 0 0 0 0 0 0
> 16 0 0 0 0 0 0 0 0 0 0 0
> 17 0 0 0 0 0 0 0 0 0 0 0
> 18 0 0 0 0 0 0 0 0 0 0 0
> 19 0 0 0 0 0 0 0 0 0 0 0
> 20 0 0 0 0 0 0 0 0 0 0 0
> 21 0 0 0 0 0 0 0 0 0 0 0
> 22 0 0 0 0 0 0 0 0 0 0 0
> 23 0 0 0 0 0 0 0 0 0 0 0
> sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0
> 2 0 0 0 0 0 0
> 3 0 0 0 0 0 0
> 4 0 0 0 0 0 0
> 5 0 0 0 0 0 0
> 6 0 0 0 0 0 0
> 7 0 0 0 0 0 0
> 8 0 0 0 0 0 0
> 9 0 0 0 0 0 0
> 10 0 0 0 0 0 0
> 11 0 0 0 0 0 0
> 12 0 0 0 0 0 0
> 13 0 0 0 0 0 0
> 14 0 0 0 0 0 0
> 15 0 0 0 0 0 0
> 16 0 0 0 0 0 0
> 17 0 0 0 0 0 0
> 18 0 0 0 0 0 0
> 19 0 0 0 0 0 0
> 20 0 0 0 0 0 0
> 21 0 0 0 0 0 0
> 22 0 0 0 0 0 0
> 23 0 0 0 0 0 0
lath_vrm$year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb
> 1 1988 0 0 96.3244 0 0 0 0 0 0 0 0
> 2 1989 0 0 -240.8036 0 0 0 0 0 0 0 0
> 3 1990 0 0 144.4792 0 0 0 0 0 0 0 0
> jsizec jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi
> 1 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0
> jsizec_zi
> 1 0
> 2 0
> 3 0
lath_vrm$st_frame
> surv obs sizea sizeb sizec repst fec jsurv
> 1.0000 1.0000 503.6167 1.0000 1.0000 1.0000 1.0000 1.0000
> jobs jsizea jsizeb jsizec jrepst jmatst
> 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000The next model to add is the fecundity model. This will be a zero-inflated negative binomial mixed model. Zero-inflation models are actually composed of two linear models - a binomial model governing the occurrence of excess zeros, and a second conditional model with the target distribution covering all non-zeros and a smattering of regular zeros (in this case, a negative binomial with a log link). So, we will need to parameterize both. Here are the two models, as shown in the model output summary in chapter 7.
\[\begin{equation} logit(f(x_i) = 0) = 6.252765 - 0.007313 size(t) + year(t) + indiv(i) \tag{15.7} \end{equation}\]
\[\begin{equation} log(f(x_i) \geq 0) = 1.517 + year(t) + indiv(i) \tag{15.8} \end{equation}\]
The dispersion parameter for the negative binomial is \(\theta\), and we see in the IPM chapter that this is given as 0.2342114. The year terms for the zero-inflation binomial model are \(3.741475 \times 10^{-7}\), \(-7.804715 \times 10^{-8}\), and \(-2.533755 \times 10^{-7}\) for 1988, 1989, and 1990, respectively. The year terms for the conditional model are -0.41749627, 0.51421684, and -0.07964038, respectively. Let’s incorporate all of these values.
lath_vrm$vrm_frame$fec[int.elem] <- 1.517
lath_vrm$vrm_frame$fec_zi[int.elem] <- 6.252765
lath_vrm$vrm_frame$fec_zi[size2.elem] <- -0.007313
lath_vrm$year_frame$fec <- c(-0.41749627, 0.51421684, -0.07964038)
lath_vrm$year_frame$fec_zi <- c(3.741475e-07, -7.804715e-08, -2.533755e-07)
lath_vrm$st_frame[7] <- 0.2342114
lath_vrm
> $vrm_frame
> main_effect_1 main_1_defined surv obs sizea sizeb
> 1 intercept y-intercept 2.32571 2.23 164.0695 0
> 2 size2 sizea in time t 0.00109 0.00 0.6211 0
> 3 size1 sizea in time t-1 0.00000 0.00 0.0000 0
> 4 sizeb2 sizeb in time t 0.00000 0.00 0.0000 0
> 5 sizeb1 sizeb in time t-1 0.00000 0.00 0.0000 0
> 6 sizec2 sizec in time t 0.00000 0.00 0.0000 0
> 7 sizec1 sizec in time t-1 0.00000 0.00 0.0000 0
> 8 repst2 reproductive status in time t 0.00000 0.00 0.0000 0
> 9 repst1 reproductive status in time t-1 0.00000 0.00 0.0000 0
> 10 age age in time t 0.00000 0.00 0.0000 0
> 11 density density in time t 0.00000 0.00 0.0000 0
> 12 indcova2 individual covariate a in time t 0.00000 0.00 0.0000 0
> 13 indcova1 individual covariate a in time t-1 0.00000 0.00 0.0000 0
> 14 indcovb2 individual covariate b in time t 0.00000 0.00 0.0000 0
> 15 indcovb1 individual covariate b in time t-1 0.00000 0.00 0.0000 0
> 16 indcovc2 individual covariate c in time t 0.00000 0.00 0.0000 0
> 17 indcovc1 individual covariate c in time t-1 0.00000 0.00 0.0000 0
> 18 annucova2 annual covariate a in time t 0.00000 0.00 0.0000 0
> 19 annucova1 annual covariate a in time t-1 0.00000 0.00 0.0000 0
> 20 annucovb2 annual covariate b in time t 0.00000 0.00 0.0000 0
> 21 annucovb1 annual covariate b in time t-1 0.00000 0.00 0.0000 0
> 22 annucovc2 annual covariate c in time t 0.00000 0.00 0.0000 0
> 23 annucovc1 annual covariate c in time t-1 0.00000 0.00 0.0000 0
> sizec repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi
> 1 0 0 1.517 0 0 0 0 0 0 0 0
> 2 0 0 0.000 0 0 0 0 0 0 0 0
> 3 0 0 0.000 0 0 0 0 0 0 0 0
> 4 0 0 0.000 0 0 0 0 0 0 0 0
> 5 0 0 0.000 0 0 0 0 0 0 0 0
> 6 0 0 0.000 0 0 0 0 0 0 0 0
> 7 0 0 0.000 0 0 0 0 0 0 0 0
> 8 0 0 0.000 0 0 0 0 0 0 0 0
> 9 0 0 0.000 0 0 0 0 0 0 0 0
> 10 0 0 0.000 0 0 0 0 0 0 0 0
> 11 0 0 0.000 0 0 0 0 0 0 0 0
> 12 0 0 0.000 0 0 0 0 0 0 0 0
> 13 0 0 0.000 0 0 0 0 0 0 0 0
> 14 0 0 0.000 0 0 0 0 0 0 0 0
> 15 0 0 0.000 0 0 0 0 0 0 0 0
> 16 0 0 0.000 0 0 0 0 0 0 0 0
> 17 0 0 0.000 0 0 0 0 0 0 0 0
> 18 0 0 0.000 0 0 0 0 0 0 0 0
> 19 0 0 0.000 0 0 0 0 0 0 0 0
> 20 0 0 0.000 0 0 0 0 0 0 0 0
> 21 0 0 0.000 0 0 0 0 0 0 0 0
> 22 0 0 0.000 0 0 0 0 0 0 0 0
> 23 0 0 0.000 0 0 0 0 0 0 0 0
> sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 6.252765 0 0 0
> 2 0 0 -0.007313 0 0 0
> 3 0 0 0.000000 0 0 0
> 4 0 0 0.000000 0 0 0
> 5 0 0 0.000000 0 0 0
> 6 0 0 0.000000 0 0 0
> 7 0 0 0.000000 0 0 0
> 8 0 0 0.000000 0 0 0
> 9 0 0 0.000000 0 0 0
> 10 0 0 0.000000 0 0 0
> 11 0 0 0.000000 0 0 0
> 12 0 0 0.000000 0 0 0
> 13 0 0 0.000000 0 0 0
> 14 0 0 0.000000 0 0 0
> 15 0 0 0.000000 0 0 0
> 16 0 0 0.000000 0 0 0
> 17 0 0 0.000000 0 0 0
> 18 0 0 0.000000 0 0 0
> 19 0 0 0.000000 0 0 0
> 20 0 0 0.000000 0 0 0
> 21 0 0 0.000000 0 0 0
> 22 0 0 0.000000 0 0 0
> 23 0 0 0.000000 0 0 0
>
> $year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs jsizea
> 1 1988 0 0 96.3244 0 0 0 -0.41749627 0 0 0
> 2 1989 0 0 -240.8036 0 0 0 0.51421684 0 0 0
> 3 1990 0 0 144.4792 0 0 0 -0.07964038 0 0 0
> jsizeb jsizec jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi
> 1 0 0 0 0 0 0 0 3.741475e-07
> 2 0 0 0 0 0 0 0 -7.804715e-08
> 3 0 0 0 0 0 0 0 -2.533755e-07
> jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0
> 2 0 0 0
> 3 0 0 0
>
> $patch_frame
> patches surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group2_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group1_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $dist_frame
> response dist
> 1 surv binom
> 2 obs binom
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec negbin
> 8 jsurv binom
> 9 jobs constant
> 10 jsizea gaussian
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constant
>
> $st_frame
> surv obs sizea sizeb sizec repst
> 1.0000000 1.0000000 503.6167000 1.0000000 1.0000000 1.0000000
> fec jsurv jobs jsizea jsizeb jsizec
> 0.2342114 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000
> jrepst jmatst
> 1.0000000 1.0000000
>
> attr(,"class")
> [1] "vrm_input"Next we will need to input the associated parameters for any other model included in the IPM. Particularly, we know that vital rate models were also estimated for seedlings, and that these models were incorporated as juvenile vital rate models. The juvenile vital rates include survival, sprouting, and size transition. The equations for these models are as follows.
\[\begin{equation} logit(s_{juv}(x_i, t)) = 1.03 + year(t) + indiv(i) \tag{15.9} \end{equation}\]
\[\begin{equation} logit(r_{juv}(x_j, t+1)) = 10.390 + year(t) + indiv(i) \tag{15.10} \end{equation}\]
\[\begin{equation} E_{juv}(size(x_j, t+1)) = 3.0559 + 0.8482 size(t) + year(t) + indiv(i) \tag{15.11} \end{equation}\]
Together with the residual \(\sigma\) for the size model and year terms for sprouting and size, let’s add all of these terms to our vrm_input object.
lath_vrm$vrm_frame$jsurv[int.elem] <- 1.03
lath_vrm$vrm_frame$jobs[int.elem] <- 10.390
lath_vrm$vrm_frame$jsizea[int.elem] <- 3.0559
lath_vrm$vrm_frame$jsizea[size2.elem] <- 0.8482
lath_vrm$st_frame[10] <- 5.831
lath_vrm$year_frame$jobs <- c(-0.7459843, 0.6118826, -0.9468618)
lath_vrm$year_frame$jsizea <- c(0.5937962, 1.4551236, -2.0489198)
lath_vrm$dist_frame$dist[9] <- "binom"
lath_vrm
> $vrm_frame
> main_effect_1 main_1_defined surv obs sizea sizeb
> 1 intercept y-intercept 2.32571 2.23 164.0695 0
> 2 size2 sizea in time t 0.00109 0.00 0.6211 0
> 3 size1 sizea in time t-1 0.00000 0.00 0.0000 0
> 4 sizeb2 sizeb in time t 0.00000 0.00 0.0000 0
> 5 sizeb1 sizeb in time t-1 0.00000 0.00 0.0000 0
> 6 sizec2 sizec in time t 0.00000 0.00 0.0000 0
> 7 sizec1 sizec in time t-1 0.00000 0.00 0.0000 0
> 8 repst2 reproductive status in time t 0.00000 0.00 0.0000 0
> 9 repst1 reproductive status in time t-1 0.00000 0.00 0.0000 0
> 10 age age in time t 0.00000 0.00 0.0000 0
> 11 density density in time t 0.00000 0.00 0.0000 0
> 12 indcova2 individual covariate a in time t 0.00000 0.00 0.0000 0
> 13 indcova1 individual covariate a in time t-1 0.00000 0.00 0.0000 0
> 14 indcovb2 individual covariate b in time t 0.00000 0.00 0.0000 0
> 15 indcovb1 individual covariate b in time t-1 0.00000 0.00 0.0000 0
> 16 indcovc2 individual covariate c in time t 0.00000 0.00 0.0000 0
> 17 indcovc1 individual covariate c in time t-1 0.00000 0.00 0.0000 0
> 18 annucova2 annual covariate a in time t 0.00000 0.00 0.0000 0
> 19 annucova1 annual covariate a in time t-1 0.00000 0.00 0.0000 0
> 20 annucovb2 annual covariate b in time t 0.00000 0.00 0.0000 0
> 21 annucovb1 annual covariate b in time t-1 0.00000 0.00 0.0000 0
> 22 annucovc2 annual covariate c in time t 0.00000 0.00 0.0000 0
> 23 annucovc1 annual covariate c in time t-1 0.00000 0.00 0.0000 0
> sizec repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi
> 1 0 0 1.517 1.03 10.39 3.0559 0 0 0 0 0
> 2 0 0 0.000 0.00 0.00 0.8482 0 0 0 0 0
> 3 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 4 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 5 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 6 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 7 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 8 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 9 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 10 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 11 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 12 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 13 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 14 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 15 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 16 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 17 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 18 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 19 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 20 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 21 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 22 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 23 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 6.252765 0 0 0
> 2 0 0 -0.007313 0 0 0
> 3 0 0 0.000000 0 0 0
> 4 0 0 0.000000 0 0 0
> 5 0 0 0.000000 0 0 0
> 6 0 0 0.000000 0 0 0
> 7 0 0 0.000000 0 0 0
> 8 0 0 0.000000 0 0 0
> 9 0 0 0.000000 0 0 0
> 10 0 0 0.000000 0 0 0
> 11 0 0 0.000000 0 0 0
> 12 0 0 0.000000 0 0 0
> 13 0 0 0.000000 0 0 0
> 14 0 0 0.000000 0 0 0
> 15 0 0 0.000000 0 0 0
> 16 0 0 0.000000 0 0 0
> 17 0 0 0.000000 0 0 0
> 18 0 0 0.000000 0 0 0
> 19 0 0 0.000000 0 0 0
> 20 0 0 0.000000 0 0 0
> 21 0 0 0.000000 0 0 0
> 22 0 0 0.000000 0 0 0
> 23 0 0 0.000000 0 0 0
>
> $year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs
> 1 1988 0 0 96.3244 0 0 0 -0.41749627 0 -0.7459843
> 2 1989 0 0 -240.8036 0 0 0 0.51421684 0 0.6118826
> 3 1990 0 0 144.4792 0 0 0 -0.07964038 0 -0.9468618
> jsizea jsizeb jsizec jrepst jmatst sizea_zi sizeb_zi sizec_zi
> 1 0.5937962 0 0 0 0 0 0 0
> 2 1.4551236 0 0 0 0 0 0 0
> 3 -2.0489198 0 0 0 0 0 0 0
> fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 3.741475e-07 0 0 0
> 2 -7.804715e-08 0 0 0
> 3 -2.533755e-07 0 0 0
>
> $patch_frame
> patches surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group2_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group1_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $dist_frame
> response dist
> 1 surv binom
> 2 obs binom
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec negbin
> 8 jsurv binom
> 9 jobs binom
> 10 jsizea gaussian
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constant
>
> $st_frame
> surv obs sizea sizeb sizec repst
> 1.0000000 1.0000000 503.6167000 1.0000000 1.0000000 1.0000000
> fec jsurv jobs jsizea jsizeb jsizec
> 0.2342114 1.0000000 1.0000000 5.8310000 1.0000000 1.0000000
> jrepst jmatst
> 1.0000000 1.0000000
>
> attr(,"class")
> [1] "vrm_input"Voilà!
15.1.2 Fitting vital rate models to matrix estimation functions
At this point, we have created all of our main IPM vital rate model inputs. However, there are still a few missing pieces that we need to fit in order to create the IPM properly. Our next step is to include instructions that tell lefko3 how the vital rate models fit together. Let’s see how this works.
By default, elements in survival-transition matrices created by functions flefko2(), flefko3(), aflefko2(), and fleslie() are estimated via the following two kernels, the first for adults and the second for juveniles.
\[\begin{equation} e_{j, i} = surv_{kernel} obs_{kernel} sizea_{kernel} sizeb_{kernel} sizec_{kernel} repr_{kernel} \tag{15.12} \end{equation}\]
\[\begin{equation} e_{j, i} = jsurv_{kernel} jobs_{kernel} jsizea_{kernel} jsizeb_{kernel} jsizec_{kernel} jrepr_{kernel} jmatst_{kernel} \tag{15.13} \end{equation}\]
Here, \(e_{j, i}\) refers to the element at the jth row and the ith column. The terms to the right of the equal sign refer to the values developed by kernels representing different vital rates. So, \(surv_{kernel}\) is the kernel developing the probability of survival, \(obs_{kernel}\) is the kernel developing the probability of observation (or sprouting), \(sizea_{kernel}\) is the probability of size transition in the primary size variable, \(sizeb_{kernel}\) is the probability of size transition in the secondary size variable, \(sizec_{kernel}\) is the probability of size transition in the tertiary size variable, and \(repr_{kernel}\) is the probability of becoming reproductive or its complement. The juvenile kernel is composed of similar vital rate kernels, but also includes \(jmatst_{kernel}\), which is the probability of becoming mature.
Package lefko3 uses the vital rate kernels above to produce values in essentially all cases, and so vital rate kernel values can shift to a constant value of \(1\) if a vital rate is not used. There are also circumstances in which vital rates may be fixed to 0 or even other constants, though these are relatively rare (this may occur is a juvenile size class is not utilized, because then juvenile vital rates should generally equal zero during matrix creation). The key is to fix unused vital rates to constant values of \(1\). We do this by changing the y-intercepts of unused vital rate models to exactly 1, and changing the distribution listed for the vital rate in dist_frame to constant. Note that we do not need to bother doing this with zero-inflation components of unused vital rates. In our case, all unused vital rate models are already set to constant, so we will just change the intercepts to 1.
lath_vrm$vrm_frame$sizeb[1] <- 1
lath_vrm$vrm_frame$sizec[1] <- 1
lath_vrm$vrm_frame$repst[1] <- 1
lath_vrm$vrm_frame$jsizeb[1] <- 1
lath_vrm$vrm_frame$jsizec[1] <- 1
lath_vrm$vrm_frame$jrepst[1] <- 1
lath_vrm$vrm_frame$jmatst[1] <- 1
lath_vrm
> $vrm_frame
> main_effect_1 main_1_defined surv obs sizea sizeb
> 1 intercept y-intercept 2.32571 2.23 164.0695 1
> 2 size2 sizea in time t 0.00109 0.00 0.6211 0
> 3 size1 sizea in time t-1 0.00000 0.00 0.0000 0
> 4 sizeb2 sizeb in time t 0.00000 0.00 0.0000 0
> 5 sizeb1 sizeb in time t-1 0.00000 0.00 0.0000 0
> 6 sizec2 sizec in time t 0.00000 0.00 0.0000 0
> 7 sizec1 sizec in time t-1 0.00000 0.00 0.0000 0
> 8 repst2 reproductive status in time t 0.00000 0.00 0.0000 0
> 9 repst1 reproductive status in time t-1 0.00000 0.00 0.0000 0
> 10 age age in time t 0.00000 0.00 0.0000 0
> 11 density density in time t 0.00000 0.00 0.0000 0
> 12 indcova2 individual covariate a in time t 0.00000 0.00 0.0000 0
> 13 indcova1 individual covariate a in time t-1 0.00000 0.00 0.0000 0
> 14 indcovb2 individual covariate b in time t 0.00000 0.00 0.0000 0
> 15 indcovb1 individual covariate b in time t-1 0.00000 0.00 0.0000 0
> 16 indcovc2 individual covariate c in time t 0.00000 0.00 0.0000 0
> 17 indcovc1 individual covariate c in time t-1 0.00000 0.00 0.0000 0
> 18 annucova2 annual covariate a in time t 0.00000 0.00 0.0000 0
> 19 annucova1 annual covariate a in time t-1 0.00000 0.00 0.0000 0
> 20 annucovb2 annual covariate b in time t 0.00000 0.00 0.0000 0
> 21 annucovb1 annual covariate b in time t-1 0.00000 0.00 0.0000 0
> 22 annucovc2 annual covariate c in time t 0.00000 0.00 0.0000 0
> 23 annucovc1 annual covariate c in time t-1 0.00000 0.00 0.0000 0
> sizec repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi
> 1 1 1 1.517 1.03 10.39 3.0559 1 1 1 1 0
> 2 0 0 0.000 0.00 0.00 0.8482 0 0 0 0 0
> 3 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 4 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 5 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 6 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 7 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 8 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 9 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 10 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 11 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 12 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 13 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 14 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 15 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 16 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 17 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 18 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 19 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 20 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 21 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 22 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 23 0 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 6.252765 0 0 0
> 2 0 0 -0.007313 0 0 0
> 3 0 0 0.000000 0 0 0
> 4 0 0 0.000000 0 0 0
> 5 0 0 0.000000 0 0 0
> 6 0 0 0.000000 0 0 0
> 7 0 0 0.000000 0 0 0
> 8 0 0 0.000000 0 0 0
> 9 0 0 0.000000 0 0 0
> 10 0 0 0.000000 0 0 0
> 11 0 0 0.000000 0 0 0
> 12 0 0 0.000000 0 0 0
> 13 0 0 0.000000 0 0 0
> 14 0 0 0.000000 0 0 0
> 15 0 0 0.000000 0 0 0
> 16 0 0 0.000000 0 0 0
> 17 0 0 0.000000 0 0 0
> 18 0 0 0.000000 0 0 0
> 19 0 0 0.000000 0 0 0
> 20 0 0 0.000000 0 0 0
> 21 0 0 0.000000 0 0 0
> 22 0 0 0.000000 0 0 0
> 23 0 0 0.000000 0 0 0
>
> $year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs
> 1 1988 0 0 96.3244 0 0 0 -0.41749627 0 -0.7459843
> 2 1989 0 0 -240.8036 0 0 0 0.51421684 0 0.6118826
> 3 1990 0 0 144.4792 0 0 0 -0.07964038 0 -0.9468618
> jsizea jsizeb jsizec jrepst jmatst sizea_zi sizeb_zi sizec_zi
> 1 0.5937962 0 0 0 0 0 0 0
> 2 1.4551236 0 0 0 0 0 0 0
> 3 -2.0489198 0 0 0 0 0 0 0
> fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 3.741475e-07 0 0 0
> 2 -7.804715e-08 0 0 0
> 3 -2.533755e-07 0 0 0
>
> $patch_frame
> patches surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group2_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group1_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $dist_frame
> response dist
> 1 surv binom
> 2 obs binom
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec negbin
> 8 jsurv binom
> 9 jobs binom
> 10 jsizea gaussian
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constant
>
> $st_frame
> surv obs sizea sizeb sizec repst
> 1.0000000 1.0000000 503.6167000 1.0000000 1.0000000 1.0000000
> fec jsurv jobs jsizea jsizeb jsizec
> 0.2342114 1.0000000 1.0000000 5.8310000 1.0000000 1.0000000
> jrepst jmatst
> 1.0000000 1.0000000
>
> attr(,"class")
> [1] "vrm_input"Next, we will add supplemental information not covered by IPM vital rate models. Let’s add that portion now.
lathsupp2 <- supplemental(stage3 = c("Sd", "Sdl", "Sd", "Sdl"),
stage2 = c("Sd", "Sd", "rep", "rep"),
givenrate = c(0.345, 0.054, NA, NA),
multiplier = c(NA, NA, 0.345, 0.054),
type = c(1, 1, 3, 3), stageframe = lathframeipm, historical = FALSE)
lathsupp2
> stage3 stage2 stage1 age2 eststage3 eststage2 eststage1 estage2 givenrate
> 1 Sd Sd <NA> NA <NA> <NA> <NA> NA 0.345
> 2 Sdl Sd <NA> NA <NA> <NA> <NA> NA 0.054
> 3 Sd rep <NA> NA <NA> <NA> <NA> NA NA
> 4 Sdl rep <NA> NA <NA> <NA> <NA> NA NA
> multiplier convtype convtype_t12
> 1 NA 1 1
> 2 NA 1 1
> 3 0.345 3 1
> 4 0.054 3 1
Finally, let’s build our IPM using the flefko2() function.
lathmat2_importipm <- flefko2(stageframe = lathframeipm, modelsuite = lath_vrm,
supplement = lathsupp2, reduce = FALSE)
summary(lathmat2_importipm)
>
> This ahistorical lefkoMat object contains 3 matrices.
>
> Each matrix is square with 103 rows and columns, and a total of 10609 elements.
> A total of 26926 survival transitions were estimated, with 8975.333 per matrix.
> A total of 600 fecundity transitions were estimated, with 200 per matrix.
> This lefkoMat object covers 1 population, 1 patch, and 3 time steps.
>
> The dataset contains a total of 0 unique individuals and 0 unique transitions.
>
> Survival probability sum check (each matrix represented by column in order):
> [,1] [,2] [,3]
> Min. 0.000 0.000 0.000
> 1st Qu. 0.979 0.956 0.980
> Median 0.998 0.998 0.998
> Mean 0.951 0.922 0.954
> 3rd Qu. 1.000 1.000 1.000
> Max. 1.000 1.000 1.000Users exploring the output and comparing against the original published IPM will notice that the element values are almost the same, but differ by tiny amounts (often on the order of 10-5 or smaller). These small differences occur because of the rounding that happens when authors publish their models, and are not a cause of concern nor will they cause dramatic differences in inference.
15.2 Importing complex IPMs and fbMPMs
Users may wish to import more complex structures using further terms or interactions. The approach above works in these cases, as well. For example, suppose that we wished to import the historical IPM for Lathyrus shown in the IPM chapter (chapter 7). That IPM involves models with historical size and some two-way interactions. We can also produce imported IPMs for this more complicated case, but need to expand the vrm_input object by noting interactions = TRUE in the input to that function, as below.
lath3_vrm <- vrm_import(years = c(1988:1990), interactions = TRUE, zi = TRUE,
dist.fec = "negbin", use.juv = TRUE)
lath3_vrm
> $vrm_frame
> main_effect_1 main_1_defined main_effect_2
> 1 intercept y-intercept
> 2 size2 sizea in time t
> 3 size1 sizea in time t-1
> 4 sizeb2 sizeb in time t
> 5 sizeb1 sizeb in time t-1
> 6 sizec2 sizec in time t
> 7 sizec1 sizec in time t-1
> 8 repst2 reproductive status in time t
> 9 repst1 reproductive status in time t-1
> 10 age age in time t
> 11 density density in time t
> 12 indcova2 individual covariate a in time t
> 13 indcova1 individual covariate a in time t-1
> 14 indcovb2 individual covariate b in time t
> 15 indcovb1 individual covariate b in time t-1
> 16 indcovc2 individual covariate c in time t
> 17 indcovc1 individual covariate c in time t-1
> 18 annucova2 annual covariate a in time t
> 19 annucova1 annual covariate a in time t-1
> 20 annucovb2 annual covariate b in time t
> 21 annucovb1 annual covariate b in time t-1
> 22 annucovc2 annual covariate c in time t
> 23 annucovc1 annual covariate c in time t-1
> 24 repst1 reproductive status in time t-1 repst2
> 25 size1 sizea in time t-1 size2
> 26 size1 sizea in time t-1 repst1
> 27 size2 sizea in time t repst2
> 28 size2 sizea in time t repst1
> 29 size1 sizea in time t-1 repst2
> 30 age age in time t size1
> 31 age age in time t size2
> 32 age age in time t repst1
> 33 age age in time t repst2
> 34 indcova2 individual covariate a in time t size2
> 35 indcovb2 individual covariate b in time t size2
> 36 indcovc2 individual covariate c in time t size2
> 37 indcova2 individual covariate a in time t repst2
> 38 indcovb2 individual covariate b in time t repst2
> 39 indcovc2 individual covariate c in time t repst2
> 40 indcova1 individual covariate a in time t-1 size1
> 41 indcovb1 individual covariate b in time t-1 size1
> 42 indcovc1 individual covariate c in time t-1 size1
> 43 indcova1 individual covariate a in time t-1 repst1
> 44 indcovb1 individual covariate b in time t-1 repst1
> 45 indcovc1 individual covariate c in time t-1 repst1
> 46 indcova2 individual covariate a in time t indcovb2
> 47 indcova2 individual covariate a in time t indcovc2
> 48 indcovb2 individual covariate b in time t indcovc2
> 49 indcova1 individual covariate a in time t-1 indcovb1
> 50 indcova1 individual covariate a in time t-1 indcovc1
> 51 indcovb1 individual covariate b in time t-1 indcovc1
> 52 indcova2 individual covariate a in time t indcovb1
> 53 indcova1 individual covariate a in time t-1 indcovb2
> 54 indcova2 individual covariate a in time t indcovc1
> 55 indcova1 individual covariate a in time t-1 indcovc2
> 56 indcovb2 individual covariate b in time t indcovc1
> 57 indcovb1 individual covariate b in time t-1 indcovc2
> 58 sizeb2 sizeb in time t sizeb1
> 59 sizec2 sizec in time t sizec1
> 60 size1 sizea in time t-1 sizeb1
> 61 size1 sizea in time t-1 sizec1
> 62 sizeb1 sizeb in time t-1 sizec1
> 63 size2 sizea in time t sizeb2
> 64 size2 sizea in time t sizec2
> 65 sizeb2 sizeb in time t sizec2
> 66 size1 sizea in time t-1 sizeb2
> 67 size1 sizea in time t-1 sizec2
> 68 sizeb1 sizeb in time t-1 sizec2
> 69 size2 sizea in time t sizeb1
> 70 size2 sizea in time t sizec1
> 71 sizeb2 sizeb in time t sizec1
> 72 density density in time t size2
> 73 density density in time t sizeb2
> 74 density density in time t sizec2
> 75 density density in time t size1
> 76 density density in time t sizeb1
> 77 density density in time t sizec1
> 78 density density in time t repst2
> 79 density density in time t repst1
> 80 sizeb2 sizeb in time t repst2
> 81 sizec2 sizec in time t repst2
> 82 sizeb1 sizeb in time t-1 repst1
> 83 sizeb2 sizeb in time t repst1
> 84 sizeb1 sizeb in time t-1 repst2
> 85 sizec1 sizec in time t-1 repst1
> 86 sizec2 sizec in time t repst1
> 87 sizec1 sizec in time t-1 repst2
> 88 sizeb2 sizeb in time t age
> 89 sizec2 sizec in time t age
> 90 density density in time t age
> 91 sizeb1 sizeb in time t-1 age
> 92 sizec1 sizec in time t-1 age
> 93 indcova2 individual covariate a in time t sizeb2
> 94 indcova2 individual covariate a in time t sizec2
> 95 indcova2 individual covariate a in time t density
> 96 indcova1 individual covariate a in time t-1 sizeb1
> 97 indcova1 individual covariate a in time t-1 sizec1
> 98 indcova1 individual covariate a in time t-1 sizeb2
> 99 indcova1 individual covariate a in time t-1 sizec2
> 100 indcova2 individual covariate a in time t sizeb1
> 101 indcova2 individual covariate a in time t sizec1
> 102 indcova1 individual covariate a in time t-1 density
> 103 indcovb2 individual covariate b in time t sizeb2
> 104 indcovb2 individual covariate b in time t sizec2
> 105 indcovb2 individual covariate b in time t density
> 106 indcovb1 individual covariate b in time t-1 sizeb1
> 107 indcovb1 individual covariate b in time t-1 sizec1
> 108 indcovb1 individual covariate b in time t-1 sizeb2
> 109 indcovb1 individual covariate b in time t-1 sizec2
> 110 indcovb2 individual covariate b in time t sizeb1
> 111 indcovb2 individual covariate b in time t sizec1
> 112 indcovb1 individual covariate b in time t-1 density
> 113 indcovc2 individual covariate c in time t sizeb2
> 114 indcovc2 individual covariate c in time t sizec2
> 115 indcovc2 individual covariate c in time t density
> 116 indcovc1 individual covariate c in time t-1 sizeb1
> 117 indcovc1 individual covariate c in time t-1 sizec1
> 118 indcovc1 individual covariate c in time t-1 sizeb2
> 119 indcovc1 individual covariate c in time t-1 sizec2
> 120 indcovc2 individual covariate c in time t sizeb1
> 121 indcovc2 individual covariate c in time t sizec1
> 122 indcovc1 individual covariate c in time t-1 density
> 123 indcova2 individual covariate a in time t size1
> 124 indcovb2 individual covariate b in time t size1
> 125 indcovc2 individual covariate c in time t size1
> 126 indcova1 individual covariate a in time t-1 size2
> 127 indcovb1 individual covariate b in time t-1 size2
> 128 indcovc1 individual covariate c in time t-1 size2
> 129 indcova2 individual covariate a in time t repst1
> 130 indcovb2 individual covariate b in time t repst1
> 131 indcovc2 individual covariate c in time t repst1
> 132 indcova1 individual covariate a in time t-1 repst2
> 133 indcovb1 individual covariate b in time t-1 repst2
> 134 indcovc1 individual covariate c in time t-1 repst2
> 135 age age in time t indcova2
> 136 age age in time t indcova1
> 137 age age in time t indcovb2
> 138 age age in time t indcovb1
> 139 age age in time t indcovc2
> 140 age age in time t indcovc1
> 141 annucova2 annual covariate a in time t size2
> 142 annucova2 annual covariate a in time t size1
> 143 annucova2 annual covariate a in time t sizeb2
> 144 annucova2 annual covariate a in time t sizeb1
> 145 annucova2 annual covariate a in time t sizec2
> 146 annucova2 annual covariate a in time t sizec1
> 147 annucova2 annual covariate a in time t repst2
> 148 annucova2 annual covariate a in time t repst1
> 149 annucova2 annual covariate a in time t age
> 150 annucova2 annual covariate a in time t density
> 151 annucova1 annual covariate a in time t-1 size2
> 152 annucova1 annual covariate a in time t-1 size1
> 153 annucova1 annual covariate a in time t-1 sizeb2
> 154 annucova1 annual covariate a in time t-1 sizeb1
> 155 annucova1 annual covariate a in time t-1 sizec2
> 156 annucova1 annual covariate a in time t-1 sizec1
> 157 annucova1 annual covariate a in time t-1 repst2
> 158 annucova1 annual covariate a in time t-1 repst1
> 159 annucova1 annual covariate a in time t-1 age
> 160 annucova1 annual covariate a in time t-1 density
> 161 annucovb2 annual covariate b in time t size2
> 162 annucovb2 annual covariate b in time t size1
> 163 annucovb2 annual covariate b in time t sizeb2
> 164 annucovb2 annual covariate b in time t sizeb1
> 165 annucovb2 annual covariate b in time t sizec2
> 166 annucovb2 annual covariate b in time t sizec1
> 167 annucovb2 annual covariate b in time t repst2
> 168 annucovb2 annual covariate b in time t repst1
> 169 annucovb2 annual covariate b in time t age
> 170 annucovb2 annual covariate b in time t density
> 171 annucovb1 annual covariate b in time t-1 size2
> 172 annucovb1 annual covariate b in time t-1 size1
> 173 annucovb1 annual covariate b in time t-1 sizeb2
> 174 annucovb1 annual covariate b in time t-1 sizeb1
> 175 annucovb1 annual covariate b in time t-1 sizec2
> 176 annucovb1 annual covariate b in time t-1 sizec1
> 177 annucovb1 annual covariate b in time t-1 repst2
> 178 annucovb1 annual covariate b in time t-1 repst1
> 179 annucovb1 annual covariate b in time t-1 age
> 180 annucovb1 annual covariate b in time t-1 density
> 181 annucovc2 annual covariate c in time t size2
> 182 annucovc2 annual covariate c in time t size1
> 183 annucovc2 annual covariate c in time t sizeb2
> 184 annucovc2 annual covariate c in time t sizeb1
> 185 annucovc2 annual covariate c in time t sizec2
> 186 annucovc2 annual covariate c in time t sizec1
> 187 annucovc2 annual covariate c in time t repst2
> 188 annucovc2 annual covariate c in time t repst1
> 189 annucovc2 annual covariate c in time t age
> 190 annucovc2 annual covariate c in time t density
> 191 annucovc1 annual covariate c in time t-1 size2
> 192 annucovc1 annual covariate c in time t-1 size1
> 193 annucovc1 annual covariate c in time t-1 sizeb2
> 194 annucovc1 annual covariate c in time t-1 sizeb1
> 195 annucovc1 annual covariate c in time t-1 sizec2
> 196 annucovc1 annual covariate c in time t-1 sizec1
> 197 annucovc1 annual covariate c in time t-1 repst2
> 198 annucovc1 annual covariate c in time t-1 repst1
> 199 annucovc1 annual covariate c in time t-1 age
> 200 annucovc1 annual covariate c in time t-1 density
> 201 annucova2 annual covariate a in time t annucova1
> 202 annucova2 annual covariate a in time t annucovb2
> 203 annucova2 annual covariate a in time t annucovb1
> 204 annucova2 annual covariate a in time t annucovc2
> 205 annucova2 annual covariate a in time t annucovc1
> 206 annucova1 annual covariate a in time t-1 annucovb2
> 207 annucova1 annual covariate a in time t-1 annucovb1
> 208 annucova1 annual covariate a in time t-1 annucovc2
> 209 annucova1 annual covariate a in time t-1 annucovc1
> 210 annucovb2 annual covariate b in time t annucovb1
> 211 annucovb2 annual covariate b in time t annucovc2
> 212 annucovb2 annual covariate b in time t annucovc1
> 213 annucovb1 annual covariate b in time t-1 annucovc2
> 214 annucovb1 annual covariate b in time t-1 annucovc1
> 215 annucovc2 annual covariate c in time t annucovc1
> 216 indcova2 individual covariate a in time t annucova2
> 217 indcova2 individual covariate a in time t annucova1
> 218 indcova2 individual covariate a in time t annucovb2
> 219 indcova2 individual covariate a in time t annucovb1
> 220 indcova2 individual covariate a in time t annucovc2
> 221 indcova2 individual covariate a in time t annucovc1
> 222 indcova1 individual covariate a in time t-1 annucova2
> 223 indcova1 individual covariate a in time t-1 annucova1
> 224 indcova1 individual covariate a in time t-1 annucovb2
> 225 indcova1 individual covariate a in time t-1 annucovb1
> 226 indcova1 individual covariate a in time t-1 annucovc2
> 227 indcova1 individual covariate a in time t-1 annucovc1
> 228 indcovb2 individual covariate b in time t annucova2
> 229 indcovb2 individual covariate b in time t annucova1
> 230 indcovb2 individual covariate b in time t annucovb2
> 231 indcovb2 individual covariate b in time t annucovb1
> 232 indcovb2 individual covariate b in time t annucovc2
> 233 indcovb2 individual covariate b in time t annucovc1
> 234 indcovb1 individual covariate b in time t-1 annucova2
> 235 indcovb1 individual covariate b in time t-1 annucova1
> 236 indcovb1 individual covariate b in time t-1 annucovb2
> 237 indcovb1 individual covariate b in time t-1 annucovb1
> 238 indcovb1 individual covariate b in time t-1 annucovc2
> 239 indcovb1 individual covariate b in time t-1 annucovc1
> 240 indcovc2 individual covariate c in time t annucova2
> 241 indcovc2 individual covariate c in time t annucova1
> 242 indcovc2 individual covariate c in time t annucovb2
> 243 indcovc2 individual covariate c in time t annucovb1
> 244 indcovc2 individual covariate c in time t annucovc2
> 245 indcovc2 individual covariate c in time t annucovc1
> 246 indcovc1 individual covariate c in time t-1 annucova2
> 247 indcovc1 individual covariate c in time t-1 annucova1
> 248 indcovc1 individual covariate c in time t-1 annucovb2
> 249 indcovc1 individual covariate c in time t-1 annucovb1
> 250 indcovc1 individual covariate c in time t-1 annucovc2
> 251 indcovc1 individual covariate c in time t-1 annucovc1
> 252 indcova2 individual covariate a in time t indcova1
> 253 indcovb2 individual covariate b in time t indcovb1
> 254 indcovc2 individual covariate c in time t indcovc1
> main_2_defined surv obs sizea sizeb sizec repst fec
> 1 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0
> 4 0 0 0 0 0 0 0
> 5 0 0 0 0 0 0 0
> 6 0 0 0 0 0 0 0
> 7 0 0 0 0 0 0 0
> 8 0 0 0 0 0 0 0
> 9 0 0 0 0 0 0 0
> 10 0 0 0 0 0 0 0
> 11 0 0 0 0 0 0 0
> 12 0 0 0 0 0 0 0
> 13 0 0 0 0 0 0 0
> 14 0 0 0 0 0 0 0
> 15 0 0 0 0 0 0 0
> 16 0 0 0 0 0 0 0
> 17 0 0 0 0 0 0 0
> 18 0 0 0 0 0 0 0
> 19 0 0 0 0 0 0 0
> 20 0 0 0 0 0 0 0
> 21 0 0 0 0 0 0 0
> 22 0 0 0 0 0 0 0
> 23 0 0 0 0 0 0 0
> 24 reproductive status in time t 0 0 0 0 0 0 0
> 25 sizea in time t 0 0 0 0 0 0 0
> 26 reproductive status in time t-1 0 0 0 0 0 0 0
> 27 reproductive status in time t 0 0 0 0 0 0 0
> 28 reproductive status in time t-1 0 0 0 0 0 0 0
> 29 reproductive status in time t 0 0 0 0 0 0 0
> 30 sizea in time t-1 0 0 0 0 0 0 0
> 31 sizea in time t 0 0 0 0 0 0 0
> 32 reproductive status in time t-1 0 0 0 0 0 0 0
> 33 reproductive status in time t 0 0 0 0 0 0 0
> 34 sizea in time t 0 0 0 0 0 0 0
> 35 sizea in time t 0 0 0 0 0 0 0
> 36 sizea in time t 0 0 0 0 0 0 0
> 37 reproductive status in time t 0 0 0 0 0 0 0
> 38 reproductive status in time t 0 0 0 0 0 0 0
> 39 reproductive status in time t 0 0 0 0 0 0 0
> 40 sizea in time t-1 0 0 0 0 0 0 0
> 41 sizea in time t-1 0 0 0 0 0 0 0
> 42 sizea in time t-1 0 0 0 0 0 0 0
> 43 reproductive status in time t-1 0 0 0 0 0 0 0
> 44 reproductive status in time t-1 0 0 0 0 0 0 0
> 45 reproductive status in time t-1 0 0 0 0 0 0 0
> 46 individual covariate b in time t 0 0 0 0 0 0 0
> 47 individual covariate c in time t 0 0 0 0 0 0 0
> 48 individual covariate c in time t 0 0 0 0 0 0 0
> 49 individual covariate b in time t-1 0 0 0 0 0 0 0
> 50 individual covariate c in time t-1 0 0 0 0 0 0 0
> 51 individual covariate c in time t-1 0 0 0 0 0 0 0
> 52 individual covariate b in time t-1 0 0 0 0 0 0 0
> 53 individual covariate b in time t 0 0 0 0 0 0 0
> 54 individual covariate c in time t-1 0 0 0 0 0 0 0
> 55 individual covariate c in time t 0 0 0 0 0 0 0
> 56 individual covariate c in time t-1 0 0 0 0 0 0 0
> 57 individual covariate c in time t 0 0 0 0 0 0 0
> 58 sizeb in time t-1 0 0 0 0 0 0 0
> 59 sizec in time t-1 0 0 0 0 0 0 0
> 60 sizeb in time t-1 0 0 0 0 0 0 0
> 61 sizec in time t-1 0 0 0 0 0 0 0
> 62 sizec in time t-1 0 0 0 0 0 0 0
> 63 sizeb in time t 0 0 0 0 0 0 0
> 64 sizec in time t 0 0 0 0 0 0 0
> 65 sizec in time t 0 0 0 0 0 0 0
> 66 sizeb in time t 0 0 0 0 0 0 0
> 67 sizec in time t 0 0 0 0 0 0 0
> 68 sizec in time t 0 0 0 0 0 0 0
> 69 sizeb in time t-1 0 0 0 0 0 0 0
> 70 sizec in time t-1 0 0 0 0 0 0 0
> 71 sizec in time t-1 0 0 0 0 0 0 0
> 72 sizea in time t 0 0 0 0 0 0 0
> 73 sizeb in time t 0 0 0 0 0 0 0
> 74 sizec in time t 0 0 0 0 0 0 0
> 75 sizea in time t-1 0 0 0 0 0 0 0
> 76 sizeb in time t-1 0 0 0 0 0 0 0
> 77 sizec in time t-1 0 0 0 0 0 0 0
> 78 reproductive status in time t 0 0 0 0 0 0 0
> 79 reproductive status in time t-1 0 0 0 0 0 0 0
> 80 reproductive status in time t 0 0 0 0 0 0 0
> 81 reproductive status in time t 0 0 0 0 0 0 0
> 82 reproductive status in time t-1 0 0 0 0 0 0 0
> 83 reproductive status in time t-1 0 0 0 0 0 0 0
> 84 reproductive status in time t 0 0 0 0 0 0 0
> 85 reproductive status in time t-1 0 0 0 0 0 0 0
> 86 reproductive status in time t-1 0 0 0 0 0 0 0
> 87 reproductive status in time t 0 0 0 0 0 0 0
> 88 age in time t 0 0 0 0 0 0 0
> 89 age in time t 0 0 0 0 0 0 0
> 90 age in time t 0 0 0 0 0 0 0
> 91 age in time t 0 0 0 0 0 0 0
> 92 age in time t 0 0 0 0 0 0 0
> 93 sizeb in time t 0 0 0 0 0 0 0
> 94 sizec in time t 0 0 0 0 0 0 0
> 95 density in time t 0 0 0 0 0 0 0
> 96 sizeb in time t-1 0 0 0 0 0 0 0
> 97 sizec in time t-1 0 0 0 0 0 0 0
> 98 sizeb in time t 0 0 0 0 0 0 0
> 99 sizec in time t 0 0 0 0 0 0 0
> 100 sizeb in time t-1 0 0 0 0 0 0 0
> 101 sizec in time t-1 0 0 0 0 0 0 0
> 102 density in time t 0 0 0 0 0 0 0
> 103 sizeb in time t 0 0 0 0 0 0 0
> 104 sizec in time t 0 0 0 0 0 0 0
> 105 density in time t 0 0 0 0 0 0 0
> 106 sizeb in time t-1 0 0 0 0 0 0 0
> 107 sizec in time t-1 0 0 0 0 0 0 0
> 108 sizeb in time t 0 0 0 0 0 0 0
> 109 sizec in time t 0 0 0 0 0 0 0
> 110 sizeb in time t-1 0 0 0 0 0 0 0
> 111 sizec in time t-1 0 0 0 0 0 0 0
> 112 density in time t 0 0 0 0 0 0 0
> 113 sizeb in time t 0 0 0 0 0 0 0
> 114 sizec in time t 0 0 0 0 0 0 0
> 115 density in time t 0 0 0 0 0 0 0
> 116 sizeb in time t-1 0 0 0 0 0 0 0
> 117 sizec in time t-1 0 0 0 0 0 0 0
> 118 sizeb in time t 0 0 0 0 0 0 0
> 119 sizec in time t 0 0 0 0 0 0 0
> 120 sizeb in time t-1 0 0 0 0 0 0 0
> 121 sizec in time t-1 0 0 0 0 0 0 0
> 122 density in time t 0 0 0 0 0 0 0
> 123 sizea in time t-1 0 0 0 0 0 0 0
> 124 sizea in time t-1 0 0 0 0 0 0 0
> 125 sizea in time t-1 0 0 0 0 0 0 0
> 126 sizea in time t 0 0 0 0 0 0 0
> 127 sizea in time t 0 0 0 0 0 0 0
> 128 sizea in time t 0 0 0 0 0 0 0
> 129 reproductive status in time t-1 0 0 0 0 0 0 0
> 130 reproductive status in time t-1 0 0 0 0 0 0 0
> 131 reproductive status in time t-1 0 0 0 0 0 0 0
> 132 reproductive status in time t 0 0 0 0 0 0 0
> 133 reproductive status in time t 0 0 0 0 0 0 0
> 134 reproductive status in time t 0 0 0 0 0 0 0
> 135 individual covariate a in time t 0 0 0 0 0 0 0
> 136 individual covariate a in time t-1 0 0 0 0 0 0 0
> 137 individual covariate b in time t 0 0 0 0 0 0 0
> 138 individual covariate b in time t-1 0 0 0 0 0 0 0
> 139 individual covariate c in time t 0 0 0 0 0 0 0
> 140 individual covariate c in time t-1 0 0 0 0 0 0 0
> 141 sizea in time t 0 0 0 0 0 0 0
> 142 sizea in time t-1 0 0 0 0 0 0 0
> 143 sizeb in time t 0 0 0 0 0 0 0
> 144 sizeb in time t-1 0 0 0 0 0 0 0
> 145 sizec in time t 0 0 0 0 0 0 0
> 146 sizec in time t-1 0 0 0 0 0 0 0
> 147 reproductive status in time t 0 0 0 0 0 0 0
> 148 reproductive status in time t-1 0 0 0 0 0 0 0
> 149 age in time t 0 0 0 0 0 0 0
> 150 density in time t 0 0 0 0 0 0 0
> 151 sizea in time t 0 0 0 0 0 0 0
> 152 sizea in time t-1 0 0 0 0 0 0 0
> 153 sizeb in time t 0 0 0 0 0 0 0
> 154 sizeb in time t-1 0 0 0 0 0 0 0
> 155 sizec in time t 0 0 0 0 0 0 0
> 156 sizec in time t-1 0 0 0 0 0 0 0
> 157 reproductive status in time t 0 0 0 0 0 0 0
> 158 reproductive status in time t-1 0 0 0 0 0 0 0
> 159 age in time t 0 0 0 0 0 0 0
> 160 density in time t 0 0 0 0 0 0 0
> 161 sizea in time t 0 0 0 0 0 0 0
> 162 sizea in time t-1 0 0 0 0 0 0 0
> 163 sizeb in time t 0 0 0 0 0 0 0
> 164 sizeb in time t-1 0 0 0 0 0 0 0
> 165 sizec in time t 0 0 0 0 0 0 0
> 166 sizec in time t-1 0 0 0 0 0 0 0
> 167 reproductive status in time t 0 0 0 0 0 0 0
> 168 reproductive status in time t-1 0 0 0 0 0 0 0
> 169 age in time t 0 0 0 0 0 0 0
> 170 density in time t 0 0 0 0 0 0 0
> 171 sizea in time t 0 0 0 0 0 0 0
> 172 sizea in time t-1 0 0 0 0 0 0 0
> 173 sizeb in time t 0 0 0 0 0 0 0
> 174 sizeb in time t-1 0 0 0 0 0 0 0
> 175 sizec in time t 0 0 0 0 0 0 0
> 176 sizec in time t-1 0 0 0 0 0 0 0
> 177 reproductive status in time t 0 0 0 0 0 0 0
> 178 reproductive status in time t-1 0 0 0 0 0 0 0
> 179 age in time t 0 0 0 0 0 0 0
> 180 density in time t 0 0 0 0 0 0 0
> 181 sizea in time t 0 0 0 0 0 0 0
> 182 sizea in time t-1 0 0 0 0 0 0 0
> 183 sizeb in time t 0 0 0 0 0 0 0
> 184 sizeb in time t-1 0 0 0 0 0 0 0
> 185 sizec in time t 0 0 0 0 0 0 0
> 186 sizec in time t-1 0 0 0 0 0 0 0
> 187 reproductive status in time t 0 0 0 0 0 0 0
> 188 reproductive status in time t-1 0 0 0 0 0 0 0
> 189 age in time t 0 0 0 0 0 0 0
> 190 density in time t 0 0 0 0 0 0 0
> 191 sizea in time t 0 0 0 0 0 0 0
> 192 sizea in time t-1 0 0 0 0 0 0 0
> 193 sizeb in time t 0 0 0 0 0 0 0
> 194 sizeb in time t-1 0 0 0 0 0 0 0
> 195 sizec in time t 0 0 0 0 0 0 0
> 196 sizec in time t-1 0 0 0 0 0 0 0
> 197 reproductive status in time t 0 0 0 0 0 0 0
> 198 reproductive status in time t-1 0 0 0 0 0 0 0
> 199 age in time t 0 0 0 0 0 0 0
> 200 density in time t 0 0 0 0 0 0 0
> 201 annual covariate a in time t-1 0 0 0 0 0 0 0
> 202 annual covariate b in time t 0 0 0 0 0 0 0
> 203 annual covariate b in time t-1 0 0 0 0 0 0 0
> 204 annual covariate c in time t 0 0 0 0 0 0 0
> 205 annual covariate c in time t-1 0 0 0 0 0 0 0
> 206 annual covariate b in time t 0 0 0 0 0 0 0
> 207 annual covariate b in time t-1 0 0 0 0 0 0 0
> 208 annual covariate c in time t 0 0 0 0 0 0 0
> 209 annual covariate c in time t-1 0 0 0 0 0 0 0
> 210 annual covariate b in time t-1 0 0 0 0 0 0 0
> 211 annual covariate c in time t 0 0 0 0 0 0 0
> 212 annual covariate c in time t-1 0 0 0 0 0 0 0
> 213 annual covariate c in time t 0 0 0 0 0 0 0
> 214 annual covariate c in time t-1 0 0 0 0 0 0 0
> 215 annual covariate c in time t-1 0 0 0 0 0 0 0
> 216 annual covariate a in time t 0 0 0 0 0 0 0
> 217 annual covariate a in time t-1 0 0 0 0 0 0 0
> 218 annual covariate b in time t 0 0 0 0 0 0 0
> 219 annual covariate b in time t-1 0 0 0 0 0 0 0
> 220 annual covariate c in time t 0 0 0 0 0 0 0
> 221 annual covariate c in time t-1 0 0 0 0 0 0 0
> 222 annual covariate a in time t 0 0 0 0 0 0 0
> 223 annual covariate a in time t-1 0 0 0 0 0 0 0
> 224 annual covariate b in time t 0 0 0 0 0 0 0
> 225 annual covariate b in time t-1 0 0 0 0 0 0 0
> 226 annual covariate c in time t 0 0 0 0 0 0 0
> 227 annual covariate c in time t-1 0 0 0 0 0 0 0
> 228 annual covariate a in time t 0 0 0 0 0 0 0
> 229 annual covariate a in time t-1 0 0 0 0 0 0 0
> 230 annual covariate b in time t 0 0 0 0 0 0 0
> 231 annual covariate b in time t-1 0 0 0 0 0 0 0
> 232 annual covariate c in time t 0 0 0 0 0 0 0
> 233 annual covariate c in time t-1 0 0 0 0 0 0 0
> 234 annual covariate a in time t 0 0 0 0 0 0 0
> 235 annual covariate a in time t-1 0 0 0 0 0 0 0
> 236 annual covariate b in time t 0 0 0 0 0 0 0
> 237 annual covariate b in time t-1 0 0 0 0 0 0 0
> 238 annual covariate c in time t 0 0 0 0 0 0 0
> 239 annual covariate c in time t-1 0 0 0 0 0 0 0
> 240 annual covariate a in time t 0 0 0 0 0 0 0
> 241 annual covariate a in time t-1 0 0 0 0 0 0 0
> 242 annual covariate b in time t 0 0 0 0 0 0 0
> 243 annual covariate b in time t-1 0 0 0 0 0 0 0
> 244 annual covariate c in time t 0 0 0 0 0 0 0
> 245 annual covariate c in time t-1 0 0 0 0 0 0 0
> 246 annual covariate a in time t 0 0 0 0 0 0 0
> 247 annual covariate a in time t-1 0 0 0 0 0 0 0
> 248 annual covariate b in time t 0 0 0 0 0 0 0
> 249 annual covariate b in time t-1 0 0 0 0 0 0 0
> 250 annual covariate c in time t 0 0 0 0 0 0 0
> 251 annual covariate c in time t-1 0 0 0 0 0 0 0
> 252 individual covariate a in time t-1 0 0 0 0 0 0 0
> 253 individual covariate b in time t-1 0 0 0 0 0 0 0
> 254 individual covariate c in time t-1 0 0 0 0 0 0 0
> jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi sizeb_zi sizec_zi
> 1 0 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0 0
> 4 0 0 0 0 0 0 0 0 0 0
> 5 0 0 0 0 0 0 0 0 0 0
> 6 0 0 0 0 0 0 0 0 0 0
> 7 0 0 0 0 0 0 0 0 0 0
> 8 0 0 0 0 0 0 0 0 0 0
> 9 0 0 0 0 0 0 0 0 0 0
> 10 0 0 0 0 0 0 0 0 0 0
> 11 0 0 0 0 0 0 0 0 0 0
> 12 0 0 0 0 0 0 0 0 0 0
> 13 0 0 0 0 0 0 0 0 0 0
> 14 0 0 0 0 0 0 0 0 0 0
> 15 0 0 0 0 0 0 0 0 0 0
> 16 0 0 0 0 0 0 0 0 0 0
> 17 0 0 0 0 0 0 0 0 0 0
> 18 0 0 0 0 0 0 0 0 0 0
> 19 0 0 0 0 0 0 0 0 0 0
> 20 0 0 0 0 0 0 0 0 0 0
> 21 0 0 0 0 0 0 0 0 0 0
> 22 0 0 0 0 0 0 0 0 0 0
> 23 0 0 0 0 0 0 0 0 0 0
> 24 0 0 0 0 0 0 0 0 0 0
> 25 0 0 0 0 0 0 0 0 0 0
> 26 0 0 0 0 0 0 0 0 0 0
> 27 0 0 0 0 0 0 0 0 0 0
> 28 0 0 0 0 0 0 0 0 0 0
> 29 0 0 0 0 0 0 0 0 0 0
> 30 0 0 0 0 0 0 0 0 0 0
> 31 0 0 0 0 0 0 0 0 0 0
> 32 0 0 0 0 0 0 0 0 0 0
> 33 0 0 0 0 0 0 0 0 0 0
> 34 0 0 0 0 0 0 0 0 0 0
> 35 0 0 0 0 0 0 0 0 0 0
> 36 0 0 0 0 0 0 0 0 0 0
> 37 0 0 0 0 0 0 0 0 0 0
> 38 0 0 0 0 0 0 0 0 0 0
> 39 0 0 0 0 0 0 0 0 0 0
> 40 0 0 0 0 0 0 0 0 0 0
> 41 0 0 0 0 0 0 0 0 0 0
> 42 0 0 0 0 0 0 0 0 0 0
> 43 0 0 0 0 0 0 0 0 0 0
> 44 0 0 0 0 0 0 0 0 0 0
> 45 0 0 0 0 0 0 0 0 0 0
> 46 0 0 0 0 0 0 0 0 0 0
> 47 0 0 0 0 0 0 0 0 0 0
> 48 0 0 0 0 0 0 0 0 0 0
> 49 0 0 0 0 0 0 0 0 0 0
> 50 0 0 0 0 0 0 0 0 0 0
> 51 0 0 0 0 0 0 0 0 0 0
> 52 0 0 0 0 0 0 0 0 0 0
> 53 0 0 0 0 0 0 0 0 0 0
> 54 0 0 0 0 0 0 0 0 0 0
> 55 0 0 0 0 0 0 0 0 0 0
> 56 0 0 0 0 0 0 0 0 0 0
> 57 0 0 0 0 0 0 0 0 0 0
> 58 0 0 0 0 0 0 0 0 0 0
> 59 0 0 0 0 0 0 0 0 0 0
> 60 0 0 0 0 0 0 0 0 0 0
> 61 0 0 0 0 0 0 0 0 0 0
> 62 0 0 0 0 0 0 0 0 0 0
> 63 0 0 0 0 0 0 0 0 0 0
> 64 0 0 0 0 0 0 0 0 0 0
> 65 0 0 0 0 0 0 0 0 0 0
> 66 0 0 0 0 0 0 0 0 0 0
> 67 0 0 0 0 0 0 0 0 0 0
> 68 0 0 0 0 0 0 0 0 0 0
> 69 0 0 0 0 0 0 0 0 0 0
> 70 0 0 0 0 0 0 0 0 0 0
> 71 0 0 0 0 0 0 0 0 0 0
> 72 0 0 0 0 0 0 0 0 0 0
> 73 0 0 0 0 0 0 0 0 0 0
> 74 0 0 0 0 0 0 0 0 0 0
> 75 0 0 0 0 0 0 0 0 0 0
> 76 0 0 0 0 0 0 0 0 0 0
> 77 0 0 0 0 0 0 0 0 0 0
> 78 0 0 0 0 0 0 0 0 0 0
> 79 0 0 0 0 0 0 0 0 0 0
> 80 0 0 0 0 0 0 0 0 0 0
> 81 0 0 0 0 0 0 0 0 0 0
> 82 0 0 0 0 0 0 0 0 0 0
> 83 0 0 0 0 0 0 0 0 0 0
> 84 0 0 0 0 0 0 0 0 0 0
> 85 0 0 0 0 0 0 0 0 0 0
> 86 0 0 0 0 0 0 0 0 0 0
> 87 0 0 0 0 0 0 0 0 0 0
> 88 0 0 0 0 0 0 0 0 0 0
> 89 0 0 0 0 0 0 0 0 0 0
> 90 0 0 0 0 0 0 0 0 0 0
> 91 0 0 0 0 0 0 0 0 0 0
> 92 0 0 0 0 0 0 0 0 0 0
> 93 0 0 0 0 0 0 0 0 0 0
> 94 0 0 0 0 0 0 0 0 0 0
> 95 0 0 0 0 0 0 0 0 0 0
> 96 0 0 0 0 0 0 0 0 0 0
> 97 0 0 0 0 0 0 0 0 0 0
> 98 0 0 0 0 0 0 0 0 0 0
> 99 0 0 0 0 0 0 0 0 0 0
> 100 0 0 0 0 0 0 0 0 0 0
> 101 0 0 0 0 0 0 0 0 0 0
> 102 0 0 0 0 0 0 0 0 0 0
> 103 0 0 0 0 0 0 0 0 0 0
> 104 0 0 0 0 0 0 0 0 0 0
> 105 0 0 0 0 0 0 0 0 0 0
> 106 0 0 0 0 0 0 0 0 0 0
> 107 0 0 0 0 0 0 0 0 0 0
> 108 0 0 0 0 0 0 0 0 0 0
> 109 0 0 0 0 0 0 0 0 0 0
> 110 0 0 0 0 0 0 0 0 0 0
> 111 0 0 0 0 0 0 0 0 0 0
> 112 0 0 0 0 0 0 0 0 0 0
> 113 0 0 0 0 0 0 0 0 0 0
> 114 0 0 0 0 0 0 0 0 0 0
> 115 0 0 0 0 0 0 0 0 0 0
> 116 0 0 0 0 0 0 0 0 0 0
> 117 0 0 0 0 0 0 0 0 0 0
> 118 0 0 0 0 0 0 0 0 0 0
> 119 0 0 0 0 0 0 0 0 0 0
> 120 0 0 0 0 0 0 0 0 0 0
> 121 0 0 0 0 0 0 0 0 0 0
> 122 0 0 0 0 0 0 0 0 0 0
> 123 0 0 0 0 0 0 0 0 0 0
> 124 0 0 0 0 0 0 0 0 0 0
> 125 0 0 0 0 0 0 0 0 0 0
> 126 0 0 0 0 0 0 0 0 0 0
> 127 0 0 0 0 0 0 0 0 0 0
> 128 0 0 0 0 0 0 0 0 0 0
> 129 0 0 0 0 0 0 0 0 0 0
> 130 0 0 0 0 0 0 0 0 0 0
> 131 0 0 0 0 0 0 0 0 0 0
> 132 0 0 0 0 0 0 0 0 0 0
> 133 0 0 0 0 0 0 0 0 0 0
> 134 0 0 0 0 0 0 0 0 0 0
> 135 0 0 0 0 0 0 0 0 0 0
> 136 0 0 0 0 0 0 0 0 0 0
> 137 0 0 0 0 0 0 0 0 0 0
> 138 0 0 0 0 0 0 0 0 0 0
> 139 0 0 0 0 0 0 0 0 0 0
> 140 0 0 0 0 0 0 0 0 0 0
> 141 0 0 0 0 0 0 0 0 0 0
> 142 0 0 0 0 0 0 0 0 0 0
> 143 0 0 0 0 0 0 0 0 0 0
> 144 0 0 0 0 0 0 0 0 0 0
> 145 0 0 0 0 0 0 0 0 0 0
> 146 0 0 0 0 0 0 0 0 0 0
> 147 0 0 0 0 0 0 0 0 0 0
> 148 0 0 0 0 0 0 0 0 0 0
> 149 0 0 0 0 0 0 0 0 0 0
> 150 0 0 0 0 0 0 0 0 0 0
> 151 0 0 0 0 0 0 0 0 0 0
> 152 0 0 0 0 0 0 0 0 0 0
> 153 0 0 0 0 0 0 0 0 0 0
> 154 0 0 0 0 0 0 0 0 0 0
> 155 0 0 0 0 0 0 0 0 0 0
> 156 0 0 0 0 0 0 0 0 0 0
> 157 0 0 0 0 0 0 0 0 0 0
> 158 0 0 0 0 0 0 0 0 0 0
> 159 0 0 0 0 0 0 0 0 0 0
> 160 0 0 0 0 0 0 0 0 0 0
> 161 0 0 0 0 0 0 0 0 0 0
> 162 0 0 0 0 0 0 0 0 0 0
> 163 0 0 0 0 0 0 0 0 0 0
> 164 0 0 0 0 0 0 0 0 0 0
> 165 0 0 0 0 0 0 0 0 0 0
> 166 0 0 0 0 0 0 0 0 0 0
> 167 0 0 0 0 0 0 0 0 0 0
> 168 0 0 0 0 0 0 0 0 0 0
> 169 0 0 0 0 0 0 0 0 0 0
> 170 0 0 0 0 0 0 0 0 0 0
> 171 0 0 0 0 0 0 0 0 0 0
> 172 0 0 0 0 0 0 0 0 0 0
> 173 0 0 0 0 0 0 0 0 0 0
> 174 0 0 0 0 0 0 0 0 0 0
> 175 0 0 0 0 0 0 0 0 0 0
> 176 0 0 0 0 0 0 0 0 0 0
> 177 0 0 0 0 0 0 0 0 0 0
> 178 0 0 0 0 0 0 0 0 0 0
> 179 0 0 0 0 0 0 0 0 0 0
> 180 0 0 0 0 0 0 0 0 0 0
> 181 0 0 0 0 0 0 0 0 0 0
> 182 0 0 0 0 0 0 0 0 0 0
> 183 0 0 0 0 0 0 0 0 0 0
> 184 0 0 0 0 0 0 0 0 0 0
> 185 0 0 0 0 0 0 0 0 0 0
> 186 0 0 0 0 0 0 0 0 0 0
> 187 0 0 0 0 0 0 0 0 0 0
> 188 0 0 0 0 0 0 0 0 0 0
> 189 0 0 0 0 0 0 0 0 0 0
> 190 0 0 0 0 0 0 0 0 0 0
> 191 0 0 0 0 0 0 0 0 0 0
> 192 0 0 0 0 0 0 0 0 0 0
> 193 0 0 0 0 0 0 0 0 0 0
> 194 0 0 0 0 0 0 0 0 0 0
> 195 0 0 0 0 0 0 0 0 0 0
> 196 0 0 0 0 0 0 0 0 0 0
> 197 0 0 0 0 0 0 0 0 0 0
> 198 0 0 0 0 0 0 0 0 0 0
> 199 0 0 0 0 0 0 0 0 0 0
> 200 0 0 0 0 0 0 0 0 0 0
> 201 0 0 0 0 0 0 0 0 0 0
> 202 0 0 0 0 0 0 0 0 0 0
> 203 0 0 0 0 0 0 0 0 0 0
> 204 0 0 0 0 0 0 0 0 0 0
> 205 0 0 0 0 0 0 0 0 0 0
> 206 0 0 0 0 0 0 0 0 0 0
> 207 0 0 0 0 0 0 0 0 0 0
> 208 0 0 0 0 0 0 0 0 0 0
> 209 0 0 0 0 0 0 0 0 0 0
> 210 0 0 0 0 0 0 0 0 0 0
> 211 0 0 0 0 0 0 0 0 0 0
> 212 0 0 0 0 0 0 0 0 0 0
> 213 0 0 0 0 0 0 0 0 0 0
> 214 0 0 0 0 0 0 0 0 0 0
> 215 0 0 0 0 0 0 0 0 0 0
> 216 0 0 0 0 0 0 0 0 0 0
> 217 0 0 0 0 0 0 0 0 0 0
> 218 0 0 0 0 0 0 0 0 0 0
> 219 0 0 0 0 0 0 0 0 0 0
> 220 0 0 0 0 0 0 0 0 0 0
> 221 0 0 0 0 0 0 0 0 0 0
> 222 0 0 0 0 0 0 0 0 0 0
> 223 0 0 0 0 0 0 0 0 0 0
> 224 0 0 0 0 0 0 0 0 0 0
> 225 0 0 0 0 0 0 0 0 0 0
> 226 0 0 0 0 0 0 0 0 0 0
> 227 0 0 0 0 0 0 0 0 0 0
> 228 0 0 0 0 0 0 0 0 0 0
> 229 0 0 0 0 0 0 0 0 0 0
> 230 0 0 0 0 0 0 0 0 0 0
> 231 0 0 0 0 0 0 0 0 0 0
> 232 0 0 0 0 0 0 0 0 0 0
> 233 0 0 0 0 0 0 0 0 0 0
> 234 0 0 0 0 0 0 0 0 0 0
> 235 0 0 0 0 0 0 0 0 0 0
> 236 0 0 0 0 0 0 0 0 0 0
> 237 0 0 0 0 0 0 0 0 0 0
> 238 0 0 0 0 0 0 0 0 0 0
> 239 0 0 0 0 0 0 0 0 0 0
> 240 0 0 0 0 0 0 0 0 0 0
> 241 0 0 0 0 0 0 0 0 0 0
> 242 0 0 0 0 0 0 0 0 0 0
> 243 0 0 0 0 0 0 0 0 0 0
> 244 0 0 0 0 0 0 0 0 0 0
> 245 0 0 0 0 0 0 0 0 0 0
> 246 0 0 0 0 0 0 0 0 0 0
> 247 0 0 0 0 0 0 0 0 0 0
> 248 0 0 0 0 0 0 0 0 0 0
> 249 0 0 0 0 0 0 0 0 0 0
> 250 0 0 0 0 0 0 0 0 0 0
> 251 0 0 0 0 0 0 0 0 0 0
> 252 0 0 0 0 0 0 0 0 0 0
> 253 0 0 0 0 0 0 0 0 0 0
> 254 0 0 0 0 0 0 0 0 0 0
> fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0
> 2 0 0 0 0
> 3 0 0 0 0
> 4 0 0 0 0
> 5 0 0 0 0
> 6 0 0 0 0
> 7 0 0 0 0
> 8 0 0 0 0
> 9 0 0 0 0
> 10 0 0 0 0
> 11 0 0 0 0
> 12 0 0 0 0
> 13 0 0 0 0
> 14 0 0 0 0
> 15 0 0 0 0
> 16 0 0 0 0
> 17 0 0 0 0
> 18 0 0 0 0
> 19 0 0 0 0
> 20 0 0 0 0
> 21 0 0 0 0
> 22 0 0 0 0
> 23 0 0 0 0
> 24 0 0 0 0
> 25 0 0 0 0
> 26 0 0 0 0
> 27 0 0 0 0
> 28 0 0 0 0
> 29 0 0 0 0
> 30 0 0 0 0
> 31 0 0 0 0
> 32 0 0 0 0
> 33 0 0 0 0
> 34 0 0 0 0
> 35 0 0 0 0
> 36 0 0 0 0
> 37 0 0 0 0
> 38 0 0 0 0
> 39 0 0 0 0
> 40 0 0 0 0
> 41 0 0 0 0
> 42 0 0 0 0
> 43 0 0 0 0
> 44 0 0 0 0
> 45 0 0 0 0
> 46 0 0 0 0
> 47 0 0 0 0
> 48 0 0 0 0
> 49 0 0 0 0
> 50 0 0 0 0
> 51 0 0 0 0
> 52 0 0 0 0
> 53 0 0 0 0
> 54 0 0 0 0
> 55 0 0 0 0
> 56 0 0 0 0
> 57 0 0 0 0
> 58 0 0 0 0
> 59 0 0 0 0
> 60 0 0 0 0
> 61 0 0 0 0
> 62 0 0 0 0
> 63 0 0 0 0
> 64 0 0 0 0
> 65 0 0 0 0
> 66 0 0 0 0
> 67 0 0 0 0
> 68 0 0 0 0
> 69 0 0 0 0
> 70 0 0 0 0
> 71 0 0 0 0
> 72 0 0 0 0
> 73 0 0 0 0
> 74 0 0 0 0
> 75 0 0 0 0
> 76 0 0 0 0
> 77 0 0 0 0
> 78 0 0 0 0
> 79 0 0 0 0
> 80 0 0 0 0
> 81 0 0 0 0
> 82 0 0 0 0
> 83 0 0 0 0
> 84 0 0 0 0
> 85 0 0 0 0
> 86 0 0 0 0
> 87 0 0 0 0
> 88 0 0 0 0
> 89 0 0 0 0
> 90 0 0 0 0
> 91 0 0 0 0
> 92 0 0 0 0
> 93 0 0 0 0
> 94 0 0 0 0
> 95 0 0 0 0
> 96 0 0 0 0
> 97 0 0 0 0
> 98 0 0 0 0
> 99 0 0 0 0
> 100 0 0 0 0
> 101 0 0 0 0
> 102 0 0 0 0
> 103 0 0 0 0
> 104 0 0 0 0
> 105 0 0 0 0
> 106 0 0 0 0
> 107 0 0 0 0
> 108 0 0 0 0
> 109 0 0 0 0
> 110 0 0 0 0
> 111 0 0 0 0
> 112 0 0 0 0
> 113 0 0 0 0
> 114 0 0 0 0
> 115 0 0 0 0
> 116 0 0 0 0
> 117 0 0 0 0
> 118 0 0 0 0
> 119 0 0 0 0
> 120 0 0 0 0
> 121 0 0 0 0
> 122 0 0 0 0
> 123 0 0 0 0
> 124 0 0 0 0
> 125 0 0 0 0
> 126 0 0 0 0
> 127 0 0 0 0
> 128 0 0 0 0
> 129 0 0 0 0
> 130 0 0 0 0
> 131 0 0 0 0
> 132 0 0 0 0
> 133 0 0 0 0
> 134 0 0 0 0
> 135 0 0 0 0
> 136 0 0 0 0
> 137 0 0 0 0
> 138 0 0 0 0
> 139 0 0 0 0
> 140 0 0 0 0
> 141 0 0 0 0
> 142 0 0 0 0
> 143 0 0 0 0
> 144 0 0 0 0
> 145 0 0 0 0
> 146 0 0 0 0
> 147 0 0 0 0
> 148 0 0 0 0
> 149 0 0 0 0
> 150 0 0 0 0
> 151 0 0 0 0
> 152 0 0 0 0
> 153 0 0 0 0
> 154 0 0 0 0
> 155 0 0 0 0
> 156 0 0 0 0
> 157 0 0 0 0
> 158 0 0 0 0
> 159 0 0 0 0
> 160 0 0 0 0
> 161 0 0 0 0
> 162 0 0 0 0
> 163 0 0 0 0
> 164 0 0 0 0
> 165 0 0 0 0
> 166 0 0 0 0
> 167 0 0 0 0
> 168 0 0 0 0
> 169 0 0 0 0
> 170 0 0 0 0
> 171 0 0 0 0
> 172 0 0 0 0
> 173 0 0 0 0
> 174 0 0 0 0
> 175 0 0 0 0
> 176 0 0 0 0
> 177 0 0 0 0
> 178 0 0 0 0
> 179 0 0 0 0
> 180 0 0 0 0
> 181 0 0 0 0
> 182 0 0 0 0
> 183 0 0 0 0
> 184 0 0 0 0
> 185 0 0 0 0
> 186 0 0 0 0
> 187 0 0 0 0
> 188 0 0 0 0
> 189 0 0 0 0
> 190 0 0 0 0
> 191 0 0 0 0
> 192 0 0 0 0
> 193 0 0 0 0
> 194 0 0 0 0
> 195 0 0 0 0
> 196 0 0 0 0
> 197 0 0 0 0
> 198 0 0 0 0
> 199 0 0 0 0
> 200 0 0 0 0
> 201 0 0 0 0
> 202 0 0 0 0
> 203 0 0 0 0
> 204 0 0 0 0
> 205 0 0 0 0
> 206 0 0 0 0
> 207 0 0 0 0
> 208 0 0 0 0
> 209 0 0 0 0
> 210 0 0 0 0
> 211 0 0 0 0
> 212 0 0 0 0
> 213 0 0 0 0
> 214 0 0 0 0
> 215 0 0 0 0
> 216 0 0 0 0
> 217 0 0 0 0
> 218 0 0 0 0
> 219 0 0 0 0
> 220 0 0 0 0
> 221 0 0 0 0
> 222 0 0 0 0
> 223 0 0 0 0
> 224 0 0 0 0
> 225 0 0 0 0
> 226 0 0 0 0
> 227 0 0 0 0
> 228 0 0 0 0
> 229 0 0 0 0
> 230 0 0 0 0
> 231 0 0 0 0
> 232 0 0 0 0
> 233 0 0 0 0
> 234 0 0 0 0
> 235 0 0 0 0
> 236 0 0 0 0
> 237 0 0 0 0
> 238 0 0 0 0
> 239 0 0 0 0
> 240 0 0 0 0
> 241 0 0 0 0
> 242 0 0 0 0
> 243 0 0 0 0
> 244 0 0 0 0
> 245 0 0 0 0
> 246 0 0 0 0
> 247 0 0 0 0
> 248 0 0 0 0
> 249 0 0 0 0
> 250 0 0 0 0
> 251 0 0 0 0
> 252 0 0 0 0
> 253 0 0 0 0
> 254 0 0 0 0
>
> $year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1988 0 0 0 0 0 0 0 0 0 0 0 0
> 2 1989 0 0 0 0 0 0 0 0 0 0 0 0
> 3 1990 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0
>
> $patch_frame
> patches surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group2_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group1_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $dist_frame
> response dist
> 1 surv binom
> 2 obs constant
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec negbin
> 8 jsurv binom
> 9 jobs constant
> 10 jsizea gaussian
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constant
>
> $st_frame
> surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb
> 1 1 1 1 1 1 1 1 1 1 1
> jsizec jrepst jmatst
> 1 1 1
>
> attr(,"class")
> [1] "vrm_input"
Our new vrm_input object is bigger. The difference in size is a direct result of an increased number of rows in the vrm_frame element: previously, that data frame held 17 rows, but now it holds 128. The first 17 correspond to the main effects, as before, while the remaining 111 rows correspond to the two-way interactions.
Let’s start off by changing the distributions, as before.
Now let’s take a look at our vital rate models. The equations are as follows.
\[\begin{equation} logit(s(x_i, t)) = 2.060 + 0.0009891 size(t) + 0.001531 size(t-1) - \\ 0.0000004125 size(t) size(t-1) + year(t) + indiv(i) \tag{15.14} \end{equation}\]
\[\begin{equation} logit(r(x_j, t+1)) = 2.230 + year(t) + indiv(i) \tag{15.15} \end{equation}\]
\[\begin{equation} E(size(x_j, t+1)) = 89.98 + 0.5954 size(t) + 0.3119 size(t-1) - \\ 0.00009417 size(t) size(t-1) + year(t) + indiv(i) \tag{15.16} \end{equation}\]
\[\begin{equation} logit(f(x_i) = 0) = 6.252765 - 0.007313 size(t) + year(t) + indiv(i) \tag{15.17} \end{equation}\]
\[\begin{equation} log(f(x_i) > 0) = 1.517 + year(t) + indiv(i) \tag{15.18} \end{equation}\]
\[\begin{equation} logit(s_{juv}(x_i, t)) = 1.03 + year(t) + indiv(i) \tag{15.19} \end{equation}\]
\[\begin{equation} logit(r_{juv}(x_j, t+1)) = 10.390 + year(t) + indiv(i) \tag{15.20} \end{equation}\]
\[\begin{equation} E_{juv}(size(x_j, t+1)) = 3.0559 + 0.8482 size(t) + year(t) + indiv(i) \tag{15.21} \end{equation}\]
Some of these models are the same as in the ahistorical case, but a number are quite different. We will add these coefficients to the vrm_frame as before, but paying special attention to interaction terms. We will also add constant values of 1 for the intercepts of unused vital rate model.
int.elem <- which(lath3_vrm$vrm_frame$main_effect_1 == "intercept")
size2.elem <- which(lath3_vrm$vrm_frame$main_effect_1 == "size2")[1]
size1.elem <- which(lath3_vrm$vrm_frame$main_effect_1 == "size1")[1]
size2.size1.elem <- intersect(which(lath3_vrm$vrm_frame$main_effect_1 == "size1"),
which(lath3_vrm$vrm_frame$main_effect_2 == "size2"))
lath3_vrm$vrm_frame$surv[int.elem] <- 2.060
lath3_vrm$vrm_frame$surv[size2.elem] <- 0.0009891
lath3_vrm$vrm_frame$surv[size1.elem] <- 0.001531
lath3_vrm$vrm_frame$surv[size2.size1.elem] <- -0.0000004125
lath3_vrm$vrm_frame$obs[int.elem] <- 2.230
lath3_vrm$vrm_frame$sizea[int.elem] <- 89.98
lath3_vrm$vrm_frame$sizea[size2.elem] <- 0.5954
lath3_vrm$vrm_frame$sizea[size1.elem] <- 0.3119
lath3_vrm$vrm_frame$sizea[size2.size1.elem] <- -0.00009417
lath3_vrm$vrm_frame$fec[int.elem] <- 1.517
lath3_vrm$vrm_frame$fec_zi[int.elem] <- 6.252765
lath3_vrm$vrm_frame$fec_zi[size2.elem] <- -0.007313
lath3_vrm$vrm_frame$jsurv[int.elem] <- 1.03
lath3_vrm$vrm_frame$jobs[int.elem] <- 10.390
lath3_vrm$vrm_frame$jsizea[int.elem] <- 3.0559
lath3_vrm$vrm_frame$jsizea[size2.elem] <- 0.8482
lath3_vrm$vrm_frame$sizeb[1] <- 1
lath3_vrm$vrm_frame$sizec[1] <- 1
lath3_vrm$vrm_frame$repst[1] <- 1
lath3_vrm$vrm_frame$jsizeb[1] <- 1
lath3_vrm$vrm_frame$jsizec[1] <- 1
lath3_vrm$vrm_frame$jrepst[1] <- 1
lath3_vrm$vrm_frame$jmatst[1] <- 1
lath3_vrm
> $vrm_frame
> main_effect_1 main_1_defined main_effect_2
> 1 intercept y-intercept
> 2 size2 sizea in time t
> 3 size1 sizea in time t-1
> 4 sizeb2 sizeb in time t
> 5 sizeb1 sizeb in time t-1
> 6 sizec2 sizec in time t
> 7 sizec1 sizec in time t-1
> 8 repst2 reproductive status in time t
> 9 repst1 reproductive status in time t-1
> 10 age age in time t
> 11 density density in time t
> 12 indcova2 individual covariate a in time t
> 13 indcova1 individual covariate a in time t-1
> 14 indcovb2 individual covariate b in time t
> 15 indcovb1 individual covariate b in time t-1
> 16 indcovc2 individual covariate c in time t
> 17 indcovc1 individual covariate c in time t-1
> 18 annucova2 annual covariate a in time t
> 19 annucova1 annual covariate a in time t-1
> 20 annucovb2 annual covariate b in time t
> 21 annucovb1 annual covariate b in time t-1
> 22 annucovc2 annual covariate c in time t
> 23 annucovc1 annual covariate c in time t-1
> 24 repst1 reproductive status in time t-1 repst2
> 25 size1 sizea in time t-1 size2
> 26 size1 sizea in time t-1 repst1
> 27 size2 sizea in time t repst2
> 28 size2 sizea in time t repst1
> 29 size1 sizea in time t-1 repst2
> 30 age age in time t size1
> 31 age age in time t size2
> 32 age age in time t repst1
> 33 age age in time t repst2
> 34 indcova2 individual covariate a in time t size2
> 35 indcovb2 individual covariate b in time t size2
> 36 indcovc2 individual covariate c in time t size2
> 37 indcova2 individual covariate a in time t repst2
> 38 indcovb2 individual covariate b in time t repst2
> 39 indcovc2 individual covariate c in time t repst2
> 40 indcova1 individual covariate a in time t-1 size1
> 41 indcovb1 individual covariate b in time t-1 size1
> 42 indcovc1 individual covariate c in time t-1 size1
> 43 indcova1 individual covariate a in time t-1 repst1
> 44 indcovb1 individual covariate b in time t-1 repst1
> 45 indcovc1 individual covariate c in time t-1 repst1
> 46 indcova2 individual covariate a in time t indcovb2
> 47 indcova2 individual covariate a in time t indcovc2
> 48 indcovb2 individual covariate b in time t indcovc2
> 49 indcova1 individual covariate a in time t-1 indcovb1
> 50 indcova1 individual covariate a in time t-1 indcovc1
> 51 indcovb1 individual covariate b in time t-1 indcovc1
> 52 indcova2 individual covariate a in time t indcovb1
> 53 indcova1 individual covariate a in time t-1 indcovb2
> 54 indcova2 individual covariate a in time t indcovc1
> 55 indcova1 individual covariate a in time t-1 indcovc2
> 56 indcovb2 individual covariate b in time t indcovc1
> 57 indcovb1 individual covariate b in time t-1 indcovc2
> 58 sizeb2 sizeb in time t sizeb1
> 59 sizec2 sizec in time t sizec1
> 60 size1 sizea in time t-1 sizeb1
> 61 size1 sizea in time t-1 sizec1
> 62 sizeb1 sizeb in time t-1 sizec1
> 63 size2 sizea in time t sizeb2
> 64 size2 sizea in time t sizec2
> 65 sizeb2 sizeb in time t sizec2
> 66 size1 sizea in time t-1 sizeb2
> 67 size1 sizea in time t-1 sizec2
> 68 sizeb1 sizeb in time t-1 sizec2
> 69 size2 sizea in time t sizeb1
> 70 size2 sizea in time t sizec1
> 71 sizeb2 sizeb in time t sizec1
> 72 density density in time t size2
> 73 density density in time t sizeb2
> 74 density density in time t sizec2
> 75 density density in time t size1
> 76 density density in time t sizeb1
> 77 density density in time t sizec1
> 78 density density in time t repst2
> 79 density density in time t repst1
> 80 sizeb2 sizeb in time t repst2
> 81 sizec2 sizec in time t repst2
> 82 sizeb1 sizeb in time t-1 repst1
> 83 sizeb2 sizeb in time t repst1
> 84 sizeb1 sizeb in time t-1 repst2
> 85 sizec1 sizec in time t-1 repst1
> 86 sizec2 sizec in time t repst1
> 87 sizec1 sizec in time t-1 repst2
> 88 sizeb2 sizeb in time t age
> 89 sizec2 sizec in time t age
> 90 density density in time t age
> 91 sizeb1 sizeb in time t-1 age
> 92 sizec1 sizec in time t-1 age
> 93 indcova2 individual covariate a in time t sizeb2
> 94 indcova2 individual covariate a in time t sizec2
> 95 indcova2 individual covariate a in time t density
> 96 indcova1 individual covariate a in time t-1 sizeb1
> 97 indcova1 individual covariate a in time t-1 sizec1
> 98 indcova1 individual covariate a in time t-1 sizeb2
> 99 indcova1 individual covariate a in time t-1 sizec2
> 100 indcova2 individual covariate a in time t sizeb1
> 101 indcova2 individual covariate a in time t sizec1
> 102 indcova1 individual covariate a in time t-1 density
> 103 indcovb2 individual covariate b in time t sizeb2
> 104 indcovb2 individual covariate b in time t sizec2
> 105 indcovb2 individual covariate b in time t density
> 106 indcovb1 individual covariate b in time t-1 sizeb1
> 107 indcovb1 individual covariate b in time t-1 sizec1
> 108 indcovb1 individual covariate b in time t-1 sizeb2
> 109 indcovb1 individual covariate b in time t-1 sizec2
> 110 indcovb2 individual covariate b in time t sizeb1
> 111 indcovb2 individual covariate b in time t sizec1
> 112 indcovb1 individual covariate b in time t-1 density
> 113 indcovc2 individual covariate c in time t sizeb2
> 114 indcovc2 individual covariate c in time t sizec2
> 115 indcovc2 individual covariate c in time t density
> 116 indcovc1 individual covariate c in time t-1 sizeb1
> 117 indcovc1 individual covariate c in time t-1 sizec1
> 118 indcovc1 individual covariate c in time t-1 sizeb2
> 119 indcovc1 individual covariate c in time t-1 sizec2
> 120 indcovc2 individual covariate c in time t sizeb1
> 121 indcovc2 individual covariate c in time t sizec1
> 122 indcovc1 individual covariate c in time t-1 density
> 123 indcova2 individual covariate a in time t size1
> 124 indcovb2 individual covariate b in time t size1
> 125 indcovc2 individual covariate c in time t size1
> 126 indcova1 individual covariate a in time t-1 size2
> 127 indcovb1 individual covariate b in time t-1 size2
> 128 indcovc1 individual covariate c in time t-1 size2
> 129 indcova2 individual covariate a in time t repst1
> 130 indcovb2 individual covariate b in time t repst1
> 131 indcovc2 individual covariate c in time t repst1
> 132 indcova1 individual covariate a in time t-1 repst2
> 133 indcovb1 individual covariate b in time t-1 repst2
> 134 indcovc1 individual covariate c in time t-1 repst2
> 135 age age in time t indcova2
> 136 age age in time t indcova1
> 137 age age in time t indcovb2
> 138 age age in time t indcovb1
> 139 age age in time t indcovc2
> 140 age age in time t indcovc1
> 141 annucova2 annual covariate a in time t size2
> 142 annucova2 annual covariate a in time t size1
> 143 annucova2 annual covariate a in time t sizeb2
> 144 annucova2 annual covariate a in time t sizeb1
> 145 annucova2 annual covariate a in time t sizec2
> 146 annucova2 annual covariate a in time t sizec1
> 147 annucova2 annual covariate a in time t repst2
> 148 annucova2 annual covariate a in time t repst1
> 149 annucova2 annual covariate a in time t age
> 150 annucova2 annual covariate a in time t density
> 151 annucova1 annual covariate a in time t-1 size2
> 152 annucova1 annual covariate a in time t-1 size1
> 153 annucova1 annual covariate a in time t-1 sizeb2
> 154 annucova1 annual covariate a in time t-1 sizeb1
> 155 annucova1 annual covariate a in time t-1 sizec2
> 156 annucova1 annual covariate a in time t-1 sizec1
> 157 annucova1 annual covariate a in time t-1 repst2
> 158 annucova1 annual covariate a in time t-1 repst1
> 159 annucova1 annual covariate a in time t-1 age
> 160 annucova1 annual covariate a in time t-1 density
> 161 annucovb2 annual covariate b in time t size2
> 162 annucovb2 annual covariate b in time t size1
> 163 annucovb2 annual covariate b in time t sizeb2
> 164 annucovb2 annual covariate b in time t sizeb1
> 165 annucovb2 annual covariate b in time t sizec2
> 166 annucovb2 annual covariate b in time t sizec1
> 167 annucovb2 annual covariate b in time t repst2
> 168 annucovb2 annual covariate b in time t repst1
> 169 annucovb2 annual covariate b in time t age
> 170 annucovb2 annual covariate b in time t density
> 171 annucovb1 annual covariate b in time t-1 size2
> 172 annucovb1 annual covariate b in time t-1 size1
> 173 annucovb1 annual covariate b in time t-1 sizeb2
> 174 annucovb1 annual covariate b in time t-1 sizeb1
> 175 annucovb1 annual covariate b in time t-1 sizec2
> 176 annucovb1 annual covariate b in time t-1 sizec1
> 177 annucovb1 annual covariate b in time t-1 repst2
> 178 annucovb1 annual covariate b in time t-1 repst1
> 179 annucovb1 annual covariate b in time t-1 age
> 180 annucovb1 annual covariate b in time t-1 density
> 181 annucovc2 annual covariate c in time t size2
> 182 annucovc2 annual covariate c in time t size1
> 183 annucovc2 annual covariate c in time t sizeb2
> 184 annucovc2 annual covariate c in time t sizeb1
> 185 annucovc2 annual covariate c in time t sizec2
> 186 annucovc2 annual covariate c in time t sizec1
> 187 annucovc2 annual covariate c in time t repst2
> 188 annucovc2 annual covariate c in time t repst1
> 189 annucovc2 annual covariate c in time t age
> 190 annucovc2 annual covariate c in time t density
> 191 annucovc1 annual covariate c in time t-1 size2
> 192 annucovc1 annual covariate c in time t-1 size1
> 193 annucovc1 annual covariate c in time t-1 sizeb2
> 194 annucovc1 annual covariate c in time t-1 sizeb1
> 195 annucovc1 annual covariate c in time t-1 sizec2
> 196 annucovc1 annual covariate c in time t-1 sizec1
> 197 annucovc1 annual covariate c in time t-1 repst2
> 198 annucovc1 annual covariate c in time t-1 repst1
> 199 annucovc1 annual covariate c in time t-1 age
> 200 annucovc1 annual covariate c in time t-1 density
> 201 annucova2 annual covariate a in time t annucova1
> 202 annucova2 annual covariate a in time t annucovb2
> 203 annucova2 annual covariate a in time t annucovb1
> 204 annucova2 annual covariate a in time t annucovc2
> 205 annucova2 annual covariate a in time t annucovc1
> 206 annucova1 annual covariate a in time t-1 annucovb2
> 207 annucova1 annual covariate a in time t-1 annucovb1
> 208 annucova1 annual covariate a in time t-1 annucovc2
> 209 annucova1 annual covariate a in time t-1 annucovc1
> 210 annucovb2 annual covariate b in time t annucovb1
> 211 annucovb2 annual covariate b in time t annucovc2
> 212 annucovb2 annual covariate b in time t annucovc1
> 213 annucovb1 annual covariate b in time t-1 annucovc2
> 214 annucovb1 annual covariate b in time t-1 annucovc1
> 215 annucovc2 annual covariate c in time t annucovc1
> 216 indcova2 individual covariate a in time t annucova2
> 217 indcova2 individual covariate a in time t annucova1
> 218 indcova2 individual covariate a in time t annucovb2
> 219 indcova2 individual covariate a in time t annucovb1
> 220 indcova2 individual covariate a in time t annucovc2
> 221 indcova2 individual covariate a in time t annucovc1
> 222 indcova1 individual covariate a in time t-1 annucova2
> 223 indcova1 individual covariate a in time t-1 annucova1
> 224 indcova1 individual covariate a in time t-1 annucovb2
> 225 indcova1 individual covariate a in time t-1 annucovb1
> 226 indcova1 individual covariate a in time t-1 annucovc2
> 227 indcova1 individual covariate a in time t-1 annucovc1
> 228 indcovb2 individual covariate b in time t annucova2
> 229 indcovb2 individual covariate b in time t annucova1
> 230 indcovb2 individual covariate b in time t annucovb2
> 231 indcovb2 individual covariate b in time t annucovb1
> 232 indcovb2 individual covariate b in time t annucovc2
> 233 indcovb2 individual covariate b in time t annucovc1
> 234 indcovb1 individual covariate b in time t-1 annucova2
> 235 indcovb1 individual covariate b in time t-1 annucova1
> 236 indcovb1 individual covariate b in time t-1 annucovb2
> 237 indcovb1 individual covariate b in time t-1 annucovb1
> 238 indcovb1 individual covariate b in time t-1 annucovc2
> 239 indcovb1 individual covariate b in time t-1 annucovc1
> 240 indcovc2 individual covariate c in time t annucova2
> 241 indcovc2 individual covariate c in time t annucova1
> 242 indcovc2 individual covariate c in time t annucovb2
> 243 indcovc2 individual covariate c in time t annucovb1
> 244 indcovc2 individual covariate c in time t annucovc2
> 245 indcovc2 individual covariate c in time t annucovc1
> 246 indcovc1 individual covariate c in time t-1 annucova2
> 247 indcovc1 individual covariate c in time t-1 annucova1
> 248 indcovc1 individual covariate c in time t-1 annucovb2
> 249 indcovc1 individual covariate c in time t-1 annucovb1
> 250 indcovc1 individual covariate c in time t-1 annucovc2
> 251 indcovc1 individual covariate c in time t-1 annucovc1
> 252 indcova2 individual covariate a in time t indcova1
> 253 indcovb2 individual covariate b in time t indcovb1
> 254 indcovc2 individual covariate c in time t indcovc1
> main_2_defined surv obs sizea sizeb sizec
> 1 2.060e+00 2.23 8.998e+01 1 1
> 2 9.891e-04 0.00 5.954e-01 0 0
> 3 1.531e-03 0.00 3.119e-01 0 0
> 4 0.000e+00 0.00 0.000e+00 0 0
> 5 0.000e+00 0.00 0.000e+00 0 0
> 6 0.000e+00 0.00 0.000e+00 0 0
> 7 0.000e+00 0.00 0.000e+00 0 0
> 8 0.000e+00 0.00 0.000e+00 0 0
> 9 0.000e+00 0.00 0.000e+00 0 0
> 10 0.000e+00 0.00 0.000e+00 0 0
> 11 0.000e+00 0.00 0.000e+00 0 0
> 12 0.000e+00 0.00 0.000e+00 0 0
> 13 0.000e+00 0.00 0.000e+00 0 0
> 14 0.000e+00 0.00 0.000e+00 0 0
> 15 0.000e+00 0.00 0.000e+00 0 0
> 16 0.000e+00 0.00 0.000e+00 0 0
> 17 0.000e+00 0.00 0.000e+00 0 0
> 18 0.000e+00 0.00 0.000e+00 0 0
> 19 0.000e+00 0.00 0.000e+00 0 0
> 20 0.000e+00 0.00 0.000e+00 0 0
> 21 0.000e+00 0.00 0.000e+00 0 0
> 22 0.000e+00 0.00 0.000e+00 0 0
> 23 0.000e+00 0.00 0.000e+00 0 0
> 24 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 25 sizea in time t -4.125e-07 0.00 -9.417e-05 0 0
> 26 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 27 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 28 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 29 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 30 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 31 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 32 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 33 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 34 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 35 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 36 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 37 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 38 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 39 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 40 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 41 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 42 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 43 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 44 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 45 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 46 individual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 47 individual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 48 individual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 49 individual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 50 individual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 51 individual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 52 individual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 53 individual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 54 individual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 55 individual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 56 individual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 57 individual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 58 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 59 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 60 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 61 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 62 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 63 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 64 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 65 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 66 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 67 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 68 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 69 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 70 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 71 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 72 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 73 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 74 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 75 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 76 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 77 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 78 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 79 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 80 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 81 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 82 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 83 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 84 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 85 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 86 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 87 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 88 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 89 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 90 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 91 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 92 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 93 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 94 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 95 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 96 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 97 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 98 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 99 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 100 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 101 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 102 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 103 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 104 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 105 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 106 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 107 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 108 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 109 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 110 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 111 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 112 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 113 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 114 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 115 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 116 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 117 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 118 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 119 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 120 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 121 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 122 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 123 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 124 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 125 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 126 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 127 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 128 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 129 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 130 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 131 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 132 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 133 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 134 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 135 individual covariate a in time t 0.000e+00 0.00 0.000e+00 0 0
> 136 individual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 137 individual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 138 individual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 139 individual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 140 individual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 141 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 142 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 143 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 144 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 145 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 146 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 147 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 148 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 149 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 150 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 151 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 152 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 153 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 154 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 155 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 156 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 157 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 158 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 159 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 160 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 161 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 162 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 163 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 164 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 165 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 166 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 167 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 168 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 169 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 170 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 171 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 172 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 173 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 174 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 175 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 176 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 177 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 178 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 179 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 180 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 181 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 182 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 183 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 184 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 185 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 186 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 187 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 188 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 189 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 190 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 191 sizea in time t 0.000e+00 0.00 0.000e+00 0 0
> 192 sizea in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 193 sizeb in time t 0.000e+00 0.00 0.000e+00 0 0
> 194 sizeb in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 195 sizec in time t 0.000e+00 0.00 0.000e+00 0 0
> 196 sizec in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 197 reproductive status in time t 0.000e+00 0.00 0.000e+00 0 0
> 198 reproductive status in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 199 age in time t 0.000e+00 0.00 0.000e+00 0 0
> 200 density in time t 0.000e+00 0.00 0.000e+00 0 0
> 201 annual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 202 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 203 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 204 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 205 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 206 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 207 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 208 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 209 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 210 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 211 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 212 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 213 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 214 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 215 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 216 annual covariate a in time t 0.000e+00 0.00 0.000e+00 0 0
> 217 annual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 218 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 219 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 220 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 221 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 222 annual covariate a in time t 0.000e+00 0.00 0.000e+00 0 0
> 223 annual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 224 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 225 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 226 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 227 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 228 annual covariate a in time t 0.000e+00 0.00 0.000e+00 0 0
> 229 annual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 230 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 231 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 232 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 233 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 234 annual covariate a in time t 0.000e+00 0.00 0.000e+00 0 0
> 235 annual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 236 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 237 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 238 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 239 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 240 annual covariate a in time t 0.000e+00 0.00 0.000e+00 0 0
> 241 annual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 242 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 243 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 244 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 245 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 246 annual covariate a in time t 0.000e+00 0.00 0.000e+00 0 0
> 247 annual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 248 annual covariate b in time t 0.000e+00 0.00 0.000e+00 0 0
> 249 annual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 250 annual covariate c in time t 0.000e+00 0.00 0.000e+00 0 0
> 251 annual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 252 individual covariate a in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 253 individual covariate b in time t-1 0.000e+00 0.00 0.000e+00 0 0
> 254 individual covariate c in time t-1 0.000e+00 0.00 0.000e+00 0 0
> repst fec jsurv jobs jsizea jsizeb jsizec jrepst jmatst sizea_zi
> 1 1 1.517 1.03 10.39 3.0559 1 1 1 1 0
> 2 0 0.000 0.00 0.00 0.8482 0 0 0 0 0
> 3 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 4 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 5 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 6 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 7 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 8 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 9 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 10 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 11 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 12 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 13 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 14 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 15 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 16 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 17 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 18 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 19 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 20 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 21 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 22 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 23 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 24 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 25 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 26 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 27 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 28 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 29 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 30 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 31 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 32 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 33 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 34 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 35 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 36 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 37 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 38 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 39 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 40 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 41 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 42 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 43 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 44 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 45 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 46 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 47 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 48 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 49 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 50 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 51 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 52 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 53 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 54 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 55 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 56 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 57 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 58 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 59 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 60 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 61 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 62 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 63 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 64 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 65 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 66 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 67 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 68 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 69 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 70 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 71 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 72 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 73 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 74 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 75 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 76 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 77 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 78 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 79 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 80 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 81 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 82 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 83 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 84 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 85 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 86 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 87 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 88 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 89 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 90 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 91 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 92 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 93 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 94 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 95 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 96 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 97 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 98 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 99 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 100 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 101 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 102 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 103 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 104 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 105 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 106 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 107 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 108 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 109 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 110 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 111 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 112 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 113 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 114 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 115 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 116 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 117 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 118 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 119 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 120 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 121 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 122 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 123 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 124 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 125 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 126 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 127 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 128 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 129 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 130 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 131 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 132 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 133 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 134 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 135 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 136 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 137 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 138 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 139 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 140 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 141 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 142 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 143 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 144 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 145 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 146 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 147 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 148 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 149 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 150 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 151 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 152 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 153 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 154 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 155 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 156 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 157 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 158 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 159 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 160 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 161 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 162 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 163 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 164 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 165 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 166 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 167 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 168 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 169 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 170 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 171 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 172 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 173 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 174 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 175 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 176 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 177 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 178 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 179 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 180 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 181 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 182 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 183 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 184 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 185 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 186 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 187 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 188 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 189 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 190 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 191 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 192 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 193 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 194 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 195 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 196 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 197 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 198 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 199 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 200 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 201 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 202 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 203 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 204 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 205 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 206 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 207 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 208 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 209 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 210 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 211 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 212 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 213 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 214 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 215 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 216 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 217 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 218 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 219 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 220 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 221 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 222 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 223 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 224 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 225 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 226 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 227 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 228 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 229 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 230 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 231 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 232 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 233 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 234 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 235 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 236 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 237 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 238 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 239 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 240 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 241 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 242 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 243 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 244 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 245 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 246 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 247 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 248 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 249 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 250 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 251 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 252 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 253 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> 254 0 0.000 0.00 0.00 0.0000 0 0 0 0 0
> sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 6.252765 0 0 0
> 2 0 0 -0.007313 0 0 0
> 3 0 0 0.000000 0 0 0
> 4 0 0 0.000000 0 0 0
> 5 0 0 0.000000 0 0 0
> 6 0 0 0.000000 0 0 0
> 7 0 0 0.000000 0 0 0
> 8 0 0 0.000000 0 0 0
> 9 0 0 0.000000 0 0 0
> 10 0 0 0.000000 0 0 0
> 11 0 0 0.000000 0 0 0
> 12 0 0 0.000000 0 0 0
> 13 0 0 0.000000 0 0 0
> 14 0 0 0.000000 0 0 0
> 15 0 0 0.000000 0 0 0
> 16 0 0 0.000000 0 0 0
> 17 0 0 0.000000 0 0 0
> 18 0 0 0.000000 0 0 0
> 19 0 0 0.000000 0 0 0
> 20 0 0 0.000000 0 0 0
> 21 0 0 0.000000 0 0 0
> 22 0 0 0.000000 0 0 0
> 23 0 0 0.000000 0 0 0
> 24 0 0 0.000000 0 0 0
> 25 0 0 0.000000 0 0 0
> 26 0 0 0.000000 0 0 0
> 27 0 0 0.000000 0 0 0
> 28 0 0 0.000000 0 0 0
> 29 0 0 0.000000 0 0 0
> 30 0 0 0.000000 0 0 0
> 31 0 0 0.000000 0 0 0
> 32 0 0 0.000000 0 0 0
> 33 0 0 0.000000 0 0 0
> 34 0 0 0.000000 0 0 0
> 35 0 0 0.000000 0 0 0
> 36 0 0 0.000000 0 0 0
> 37 0 0 0.000000 0 0 0
> 38 0 0 0.000000 0 0 0
> 39 0 0 0.000000 0 0 0
> 40 0 0 0.000000 0 0 0
> 41 0 0 0.000000 0 0 0
> 42 0 0 0.000000 0 0 0
> 43 0 0 0.000000 0 0 0
> 44 0 0 0.000000 0 0 0
> 45 0 0 0.000000 0 0 0
> 46 0 0 0.000000 0 0 0
> 47 0 0 0.000000 0 0 0
> 48 0 0 0.000000 0 0 0
> 49 0 0 0.000000 0 0 0
> 50 0 0 0.000000 0 0 0
> 51 0 0 0.000000 0 0 0
> 52 0 0 0.000000 0 0 0
> 53 0 0 0.000000 0 0 0
> 54 0 0 0.000000 0 0 0
> 55 0 0 0.000000 0 0 0
> 56 0 0 0.000000 0 0 0
> 57 0 0 0.000000 0 0 0
> 58 0 0 0.000000 0 0 0
> 59 0 0 0.000000 0 0 0
> 60 0 0 0.000000 0 0 0
> 61 0 0 0.000000 0 0 0
> 62 0 0 0.000000 0 0 0
> 63 0 0 0.000000 0 0 0
> 64 0 0 0.000000 0 0 0
> 65 0 0 0.000000 0 0 0
> 66 0 0 0.000000 0 0 0
> 67 0 0 0.000000 0 0 0
> 68 0 0 0.000000 0 0 0
> 69 0 0 0.000000 0 0 0
> 70 0 0 0.000000 0 0 0
> 71 0 0 0.000000 0 0 0
> 72 0 0 0.000000 0 0 0
> 73 0 0 0.000000 0 0 0
> 74 0 0 0.000000 0 0 0
> 75 0 0 0.000000 0 0 0
> 76 0 0 0.000000 0 0 0
> 77 0 0 0.000000 0 0 0
> 78 0 0 0.000000 0 0 0
> 79 0 0 0.000000 0 0 0
> 80 0 0 0.000000 0 0 0
> 81 0 0 0.000000 0 0 0
> 82 0 0 0.000000 0 0 0
> 83 0 0 0.000000 0 0 0
> 84 0 0 0.000000 0 0 0
> 85 0 0 0.000000 0 0 0
> 86 0 0 0.000000 0 0 0
> 87 0 0 0.000000 0 0 0
> 88 0 0 0.000000 0 0 0
> 89 0 0 0.000000 0 0 0
> 90 0 0 0.000000 0 0 0
> 91 0 0 0.000000 0 0 0
> 92 0 0 0.000000 0 0 0
> 93 0 0 0.000000 0 0 0
> 94 0 0 0.000000 0 0 0
> 95 0 0 0.000000 0 0 0
> 96 0 0 0.000000 0 0 0
> 97 0 0 0.000000 0 0 0
> 98 0 0 0.000000 0 0 0
> 99 0 0 0.000000 0 0 0
> 100 0 0 0.000000 0 0 0
> 101 0 0 0.000000 0 0 0
> 102 0 0 0.000000 0 0 0
> 103 0 0 0.000000 0 0 0
> 104 0 0 0.000000 0 0 0
> 105 0 0 0.000000 0 0 0
> 106 0 0 0.000000 0 0 0
> 107 0 0 0.000000 0 0 0
> 108 0 0 0.000000 0 0 0
> 109 0 0 0.000000 0 0 0
> 110 0 0 0.000000 0 0 0
> 111 0 0 0.000000 0 0 0
> 112 0 0 0.000000 0 0 0
> 113 0 0 0.000000 0 0 0
> 114 0 0 0.000000 0 0 0
> 115 0 0 0.000000 0 0 0
> 116 0 0 0.000000 0 0 0
> 117 0 0 0.000000 0 0 0
> 118 0 0 0.000000 0 0 0
> 119 0 0 0.000000 0 0 0
> 120 0 0 0.000000 0 0 0
> 121 0 0 0.000000 0 0 0
> 122 0 0 0.000000 0 0 0
> 123 0 0 0.000000 0 0 0
> 124 0 0 0.000000 0 0 0
> 125 0 0 0.000000 0 0 0
> 126 0 0 0.000000 0 0 0
> 127 0 0 0.000000 0 0 0
> 128 0 0 0.000000 0 0 0
> 129 0 0 0.000000 0 0 0
> 130 0 0 0.000000 0 0 0
> 131 0 0 0.000000 0 0 0
> 132 0 0 0.000000 0 0 0
> 133 0 0 0.000000 0 0 0
> 134 0 0 0.000000 0 0 0
> 135 0 0 0.000000 0 0 0
> 136 0 0 0.000000 0 0 0
> 137 0 0 0.000000 0 0 0
> 138 0 0 0.000000 0 0 0
> 139 0 0 0.000000 0 0 0
> 140 0 0 0.000000 0 0 0
> 141 0 0 0.000000 0 0 0
> 142 0 0 0.000000 0 0 0
> 143 0 0 0.000000 0 0 0
> 144 0 0 0.000000 0 0 0
> 145 0 0 0.000000 0 0 0
> 146 0 0 0.000000 0 0 0
> 147 0 0 0.000000 0 0 0
> 148 0 0 0.000000 0 0 0
> 149 0 0 0.000000 0 0 0
> 150 0 0 0.000000 0 0 0
> 151 0 0 0.000000 0 0 0
> 152 0 0 0.000000 0 0 0
> 153 0 0 0.000000 0 0 0
> 154 0 0 0.000000 0 0 0
> 155 0 0 0.000000 0 0 0
> 156 0 0 0.000000 0 0 0
> 157 0 0 0.000000 0 0 0
> 158 0 0 0.000000 0 0 0
> 159 0 0 0.000000 0 0 0
> 160 0 0 0.000000 0 0 0
> 161 0 0 0.000000 0 0 0
> 162 0 0 0.000000 0 0 0
> 163 0 0 0.000000 0 0 0
> 164 0 0 0.000000 0 0 0
> 165 0 0 0.000000 0 0 0
> 166 0 0 0.000000 0 0 0
> 167 0 0 0.000000 0 0 0
> 168 0 0 0.000000 0 0 0
> 169 0 0 0.000000 0 0 0
> 170 0 0 0.000000 0 0 0
> 171 0 0 0.000000 0 0 0
> 172 0 0 0.000000 0 0 0
> 173 0 0 0.000000 0 0 0
> 174 0 0 0.000000 0 0 0
> 175 0 0 0.000000 0 0 0
> 176 0 0 0.000000 0 0 0
> 177 0 0 0.000000 0 0 0
> 178 0 0 0.000000 0 0 0
> 179 0 0 0.000000 0 0 0
> 180 0 0 0.000000 0 0 0
> 181 0 0 0.000000 0 0 0
> 182 0 0 0.000000 0 0 0
> 183 0 0 0.000000 0 0 0
> 184 0 0 0.000000 0 0 0
> 185 0 0 0.000000 0 0 0
> 186 0 0 0.000000 0 0 0
> 187 0 0 0.000000 0 0 0
> 188 0 0 0.000000 0 0 0
> 189 0 0 0.000000 0 0 0
> 190 0 0 0.000000 0 0 0
> 191 0 0 0.000000 0 0 0
> 192 0 0 0.000000 0 0 0
> 193 0 0 0.000000 0 0 0
> 194 0 0 0.000000 0 0 0
> 195 0 0 0.000000 0 0 0
> 196 0 0 0.000000 0 0 0
> 197 0 0 0.000000 0 0 0
> 198 0 0 0.000000 0 0 0
> 199 0 0 0.000000 0 0 0
> 200 0 0 0.000000 0 0 0
> 201 0 0 0.000000 0 0 0
> 202 0 0 0.000000 0 0 0
> 203 0 0 0.000000 0 0 0
> 204 0 0 0.000000 0 0 0
> 205 0 0 0.000000 0 0 0
> 206 0 0 0.000000 0 0 0
> 207 0 0 0.000000 0 0 0
> 208 0 0 0.000000 0 0 0
> 209 0 0 0.000000 0 0 0
> 210 0 0 0.000000 0 0 0
> 211 0 0 0.000000 0 0 0
> 212 0 0 0.000000 0 0 0
> 213 0 0 0.000000 0 0 0
> 214 0 0 0.000000 0 0 0
> 215 0 0 0.000000 0 0 0
> 216 0 0 0.000000 0 0 0
> 217 0 0 0.000000 0 0 0
> 218 0 0 0.000000 0 0 0
> 219 0 0 0.000000 0 0 0
> 220 0 0 0.000000 0 0 0
> 221 0 0 0.000000 0 0 0
> 222 0 0 0.000000 0 0 0
> 223 0 0 0.000000 0 0 0
> 224 0 0 0.000000 0 0 0
> 225 0 0 0.000000 0 0 0
> 226 0 0 0.000000 0 0 0
> 227 0 0 0.000000 0 0 0
> 228 0 0 0.000000 0 0 0
> 229 0 0 0.000000 0 0 0
> 230 0 0 0.000000 0 0 0
> 231 0 0 0.000000 0 0 0
> 232 0 0 0.000000 0 0 0
> 233 0 0 0.000000 0 0 0
> 234 0 0 0.000000 0 0 0
> 235 0 0 0.000000 0 0 0
> 236 0 0 0.000000 0 0 0
> 237 0 0 0.000000 0 0 0
> 238 0 0 0.000000 0 0 0
> 239 0 0 0.000000 0 0 0
> 240 0 0 0.000000 0 0 0
> 241 0 0 0.000000 0 0 0
> 242 0 0 0.000000 0 0 0
> 243 0 0 0.000000 0 0 0
> 244 0 0 0.000000 0 0 0
> 245 0 0 0.000000 0 0 0
> 246 0 0 0.000000 0 0 0
> 247 0 0 0.000000 0 0 0
> 248 0 0 0.000000 0 0 0
> 249 0 0 0.000000 0 0 0
> 250 0 0 0.000000 0 0 0
> 251 0 0 0.000000 0 0 0
> 252 0 0 0.000000 0 0 0
> 253 0 0 0.000000 0 0 0
> 254 0 0 0.000000 0 0 0
>
> $year_frame
> years surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1988 0 0 0 0 0 0 0 0 0 0 0 0
> 2 1989 0 0 0 0 0 0 0 0 0 0 0 0
> 3 1990 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
> 2 0 0 0 0 0 0 0 0 0
> 3 0 0 0 0 0 0 0 0 0
>
> $patch_frame
> patches surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 1 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group2_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $group1_frame
> groups surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb jsizec
> 1 0 0 0 0 0 0 0 0 0 0 0 0 0
> jrepst jmatst sizea_zi sizeb_zi sizec_zi fec_zi jsizea_zi jsizeb_zi jsizec_zi
> 1 0 0 0 0 0 0 0 0 0
>
> $dist_frame
> response dist
> 1 surv binom
> 2 obs binom
> 3 sizea gaussian
> 4 sizeb constant
> 5 sizec constant
> 6 repst constant
> 7 fec negbin
> 8 jsurv binom
> 9 jobs binom
> 10 jsizea gaussian
> 11 jsizeb constant
> 12 jsizec constant
> 13 jrepst constant
> 14 jmatst constant
>
> $st_frame
> surv obs sizea sizeb sizec repst fec jsurv jobs jsizea jsizeb
> 1 1 1 1 1 1 1 1 1 1 1
> jsizec jrepst jmatst
> 1 1 1
>
> attr(,"class")
> [1] "vrm_input"Now we will add the appropriate year terms and the values of \(\sigma\) and \(\theta\), and the year coefficients.
lath3_vrm$st_frame[3] <- 480.4092
lath3_vrm$st_frame[7] <- 0.2342114
lath3_vrm$st_frame[10] <- 5.831241
lath3_vrm$year_frame$sizea <- c(193.44474, -277.14757, 83.70283)
lath3_vrm$year_frame$fec <- c(-0.41749627, 0.51421684, -0.07964038)
lath3_vrm$year_frame$fec_zi <- c(3.741475e-07, -7.804715e-08, -2.533755e-07)
lath3_vrm$year_frame$sizea <- c(193.44474, -277.14757, 83.70283)
lath3_vrm$year_frame$jobs <- c(-0.7459843, 0.6118826, -0.9468618)
lath_vrm$year_frame$jsizea <- c(0.5937962, 1.4551236, -2.0489198)As before, we still need to supply supplemental information. We’ll do that as below.
lathsupp3 <- supplemental(stage3 = c("Sd","Sd","Sdl","Sdl","npr","Sd","Sdl"),
stage2 = c("Sd", "Sd", "Sd", "Sd", "Sdl", "rep", "rep"),
stage1 = c("Sd", "rep", "Sd", "rep", "Sd", "mat", "mat"),
eststage3 = c(NA, NA, NA, NA, "npr", NA, NA),
eststage2 = c(NA, NA, NA, NA, "Sdl", NA, NA),
eststage1 = c(NA, NA, NA, NA, "Sdl", NA, NA),
givenrate = c(0.345, 0.345, 0.054, 0.054, NA, NA, NA),
multiplier = c(NA, NA, NA, NA, NA, 0.345, 0.054),
type = c(1, 1, 1, 1, 1, 3, 3), type_t12 = c(1, 2, 1, 2, 1, 1, 1),
stageframe = lathframeipm, historical = TRUE)Finally we can produce our historical IPMs. Because they will be huge, we will create them in sparse format (standard matrix format will lead to an object around 7 gigabytes in size).
lathmat3_importipm <- flefko3(stageframe = lathframeipm, modelsuite = lath3_vrm,
supplement = lathsupp3, reduce = FALSE, sparse_output = TRUE)
summary(lathmat3_importipm)
>
> This historical lefkoMat object contains 3 matrices.
>
> Each matrix is square with 10609 rows and columns, and a total of 112550881 elements.
> A total of 2684746 survival transitions were estimated, with 894915.333 per matrix.
> A total of 60600 fecundity transitions were estimated, with 20200 per matrix.
> This lefkoMat object covers 1 population, 1 patch, and 3 time steps.
>
> The dataset contains a total of 0 unique individuals and 0 unique transitions.
>
> Survival probability sum check (each matrix represented by column in order):
> [,1] [,2] [,3]
> Min. 0.000 0.000 0.000
> 1st Qu. 0.989 0.981 0.988
> Median 0.997 0.996 0.997
> Mean 0.955 0.945 0.954
> 3rd Qu. 0.999 0.998 0.999
> Max. 1.000 1.000 1.000
As before, we can use this IPM in any way that might use a normal fbMPM in lefko3. The general approach shown above can also be used to develop age-based (Leslie) or age-by-stage function-based MPMs.
15.3 Running projections from imported IPMs and fbMPMs
The vrm_input approach can also be used to run custom function-based projections.
lath_proj <- f_projection3(format = 3, stageframe = lathframeipm,
supplement = lathsupp2, modelsuite = lath_vrm, nreps = 10, times = 10,
stochastic = TRUE)
> Warning: Option patch not set, so will set to first patch/population.
summary(lath_proj)
>
> The input lefkoProj object covers 1 population-patches.
> It is a single projection including 10 projected steps per replicate, and 10 replicates, respectively.
> The number of replicates with population size above the threshold size of 1 is as in
> the following matrix, with pop-patches given by column and milepost times given by row:
> $milepost_sums
> 1 1
> 0 10
> 0.25 10
> 0.5 10
> 0.75 10
> 1 10
>
> $extinction_times
> [1] NALet’s take a look at what our projection replicates look like (figure 15.1).
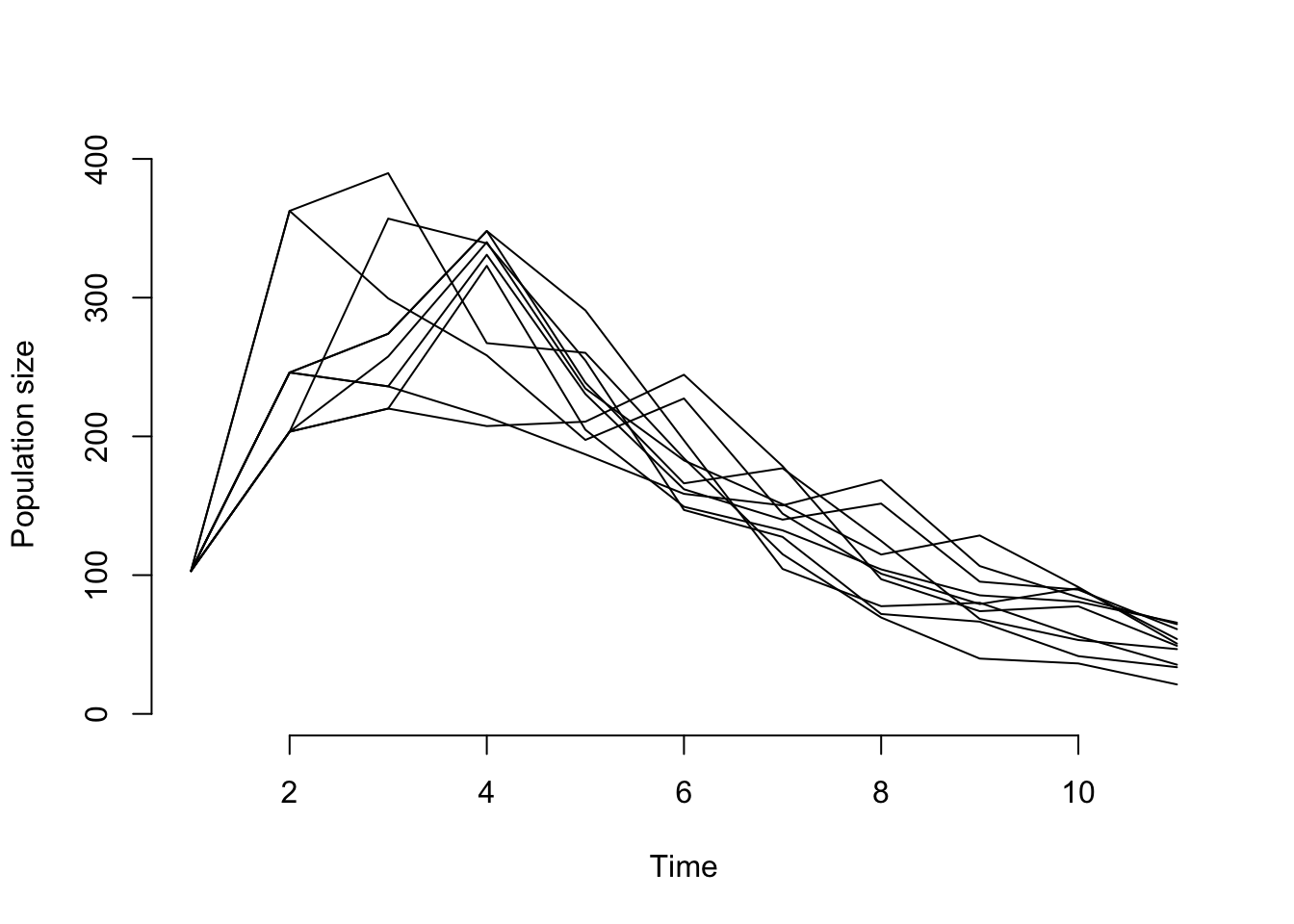
Figure 15.1: Replicated projection resulting from imported Lathyrus IPM
15.4 Points to remember
- Users may import IPMs and fbMPMs into
lefko3if they are presented as kernels of linear models, with functionvrm_import(). - Imported IPMs and fbMPMs may also be loaded into projections, including function-based projections that create new matrices at each time step with function
f_projection3().
References
Childs, D.Z., Rees, M., Rose, K.E., Grubb, P.J. & Ellner, S.P. (2003). Evolution of complex flowering strategies: An age- and size-structured integral projection model. Proceedings Of The Royal Society Of London Series B-Biological Sciences, 270, 1829–1838.
Dahlgren, J.P. & Ehrlén, J. (2011). Incorporating environmental change over succession in an integral projection model of population dynamics of a forest herb. Oikos, 120, 1183–1190.
Garcia, M.B., Dahlgren, J.P. & Ehrlén, J. (2011). No evidence of senescence in a 300-year-old mountain herb. Journal of Ecology, 99, 1424–1430.
Shefferson, R.P., Warren II, R.J. & Pulliam, H.R. (2014). Life history costs make perfect sprouting maladaptive in two herbaceous perennials. Journal of Ecology, 102, 1318–1328.