12 Análisis de componentes principales
Los contenidos de este material se basa principalemente en Schumacker (2015). Las referencias o extensiones necesarias se citarán conforme se desarrolla el material.
12.1 Planteamiento2
Se aplica a tablas de datos donde las filas son considerados como individuos y las columnas como datos cuantitativos.
Más formalmente, se dispone de los valores de \(p\) variables y \(n\) elementos dispuestos en una matriz \(\mathbf{X}\) de dimensión \(n\times p\).
Siempre (casi) se usa la matriz centrada y/o estandarizada, los paquetes suelen hacer este trabajo por nosostros. Supongamos que \(\mathbf{X}\) ha sido centrada, su matriz de varianza covarianza viene dada por \(\frac{1}{n}\mathbf{X'X}\).
¿Cómo encontrar un espacio de dimensión más reducida que represente adeucadamente los datos?
12.2 Notación
Se desea encontrar un subespacio de dimensión menor que \(p\) tal que al proyectar sobre él los puntos conserven su estructura con la menor distorsión posible.
Consideremos primero un subespacio de dimensión uno (una recta) obtenida por un conjunto de \(p=2\) variables.
La siguiente figura indica el diagrama de dispersión y una recta que, intuitivamente, proporciona un buen resumen de los datos, ya que las proyecciones de los puntos sobre ella indican aproximadamente la situación de los puntos en el plano.
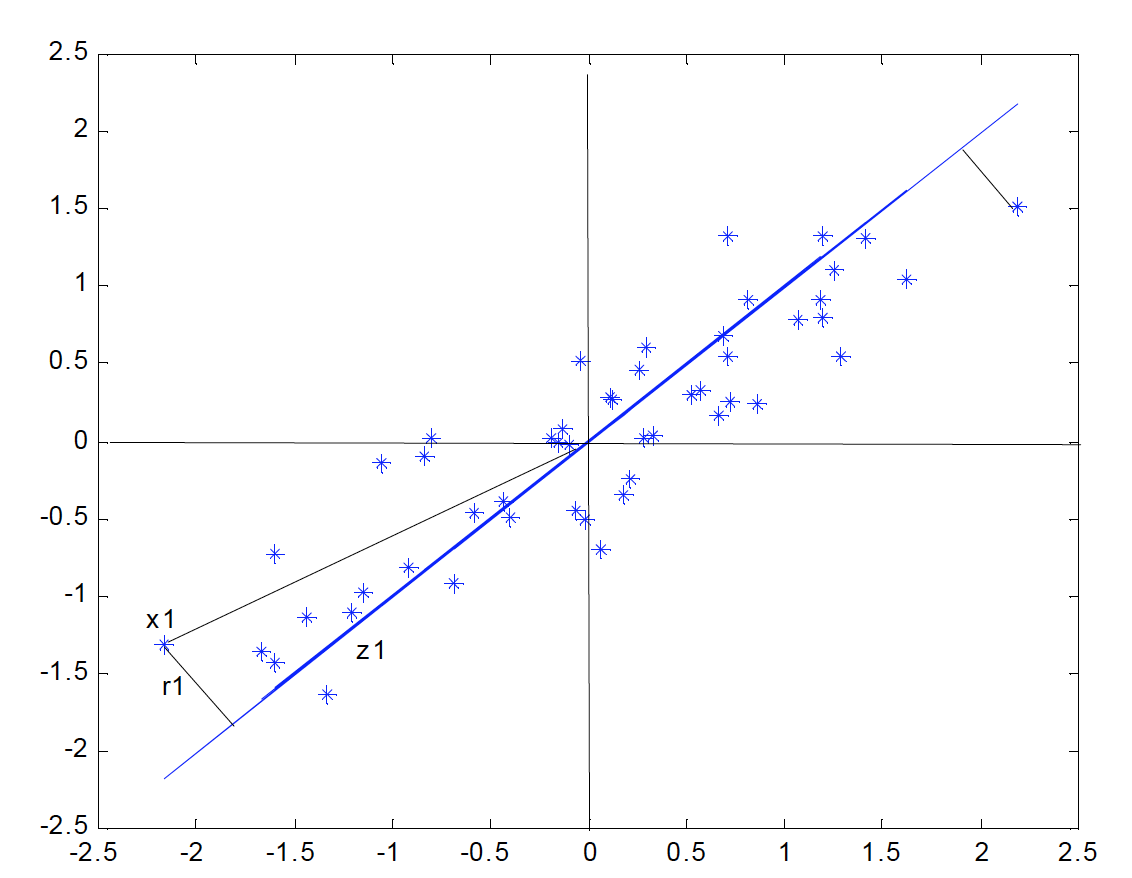
Si consideramos un punto \(\mathbf{x_i}\) y una dirección \(\mathbf{a_1} = (a_{11}, \ldots, a_{1p})'\), definida por un vector \(\mathbf{a_1}\) de norma unidad, la proyección del punto \(\mathbf{x_i}\) sobre esta dirección es el escalar:
\[ z_i= a_{11}x_{i1}+\ldots+a_{1p}x_{ip} = \mathbf{a_1^{'}x_i} \]
y el vector que representa esta proyección será \(z_i\mathbf{a_1}\). Llamando \(r_i\) a la distancia entre el punto \(x_i\), y su proyección sobre la dirección \(\mathbf{a_1}\), este criterio implica:
\[ min\sum_{i = 1}^{n} r^2_i = \sum_{i = 1}^{n} |\mathbf{x_i}-z_i\mathbf{a_1}|^2 \]
donde \(|\cdot|\) es la norma euclideana o módulo del vector.
Notemos que al proyectar cada punto sobre la recta se forma un triángulo rectángulo donde la hipotenusa es la distancia al origen del punto al origen, \((\mathbf{x_i'x_i})^{1/2}\), y los catetos la proyeccion del punto sobre la recta \((z_i)\) y la distancia entre el punto y su proyección \((r_i)\). Por el teorema de Pitágoras, podemos escribir:
\[ (\mathbf{x_i'x_i}) = z_i^2+r_i^2 \]
y sumando esta expresión para todos los puntos, se obtiene:
\[ \sum_{i=1}^{n}(\mathbf{x_i'x_i}) = \sum_{i=1}^{n}z_i^2+\sum_{i=1}^{n}r_i^2 \]
Como el primer miembro es constante, minimizar \(\sum_{i=1}^{n}r_i^2\), la suma de las distancias a la recta de todos los puntos, es equivalente a maximizar \(\sum_{i=1}^{n}z_i^2\), la suma al cuadrado de los valores de las proyecciones. Como las proyecciones \(z_i\) son variables de media cero, maximizar la suma de sus cuadrados equivale a maximizar su varianza.
¿Cómo es eso posible?
12.3 Cálculo del primer componente
El primer componente principal será la combinación lineal de las variables originales que tenga varianza máxima. Los valores de este primer componente en los \(n\) individuos se representarán por un vector \(\mathbf{z_1}\), dado por
\[ \mathbf{z_1} = \mathbf{Xa_1} \]
Como las variables originales tienen media cero también \(\mathbf{z_1}\) tendrá media nula. Su varianza será:
\[ Var(\mathbf{z_1}) = \frac{1}{n}\mathbf{z_1^{'}z_1} = \frac{1}{n}\mathbf{a_1^{'}X'Xa_1} = \mathbf{a_1^{'}Sa_1} \]
donde \(S\) es la matriz de varianzas y covarianzas de las observaciones. Para que la maximización de la ecuación anterior tenga solución debemos imponer una restricción al módulo del vector \(\mathbf{a_1}\), y, sin pérdida de generalidad, impondremos que \(\mathbf{a_1^{'}a_1}=1\). Usamos para ello el multiplicador de Lagrange
\[ M = \mathbf{a_1^{'}Sa_1}- \lambda(\mathbf{a_1^{'}a_1}-1) \]
Se maximiza derivando respecto a los componentes de \(\mathbf{a_1}\) e igualando a cero. Entonces
\[ \frac{\partial M}{\partial\mathbf{a_1}} = 2\mathbf{Sa_1}-2\lambda\mathbf{a_1} = 0 \]
cuya solución es:
\[ \mathbf{Sa_1} = \lambda\mathbf{a_1} \]
que implica que \(\mathbf{a_1}\) es un vector propio de la matriz \(\mathbf{S}\), y \(\lambda\) su correspondiente valor propio. Para determinar qué valor propio de \(\mathbf{S}\) es la solución de la ecuación tendremos en cuenta que, multiplicando por la izquierda por \(\mathbf{a'_{1}}\) esta ecuación,
\[ \mathbf{a_1^{'}Sa_1} = \lambda \mathbf{a_1^{'}a_1} = \lambda \]
y concluimos, que \(\lambda\) es la varianza de \(\mathbf{z_1}\). Como esta es la cantidad que queremos maximizar, \(\lambda\) será el mayor valor propio de la matriz \(\mathbf{S}\). Su vector asociado, \(\mathbf{a1}\), define los coeficientes de cada variable en el primer componente principal.
12.4 En R
El siguiente conjunto de datos corresponde a calificaciones de 20 estudiantes en 5 materias Ciencias Natuales (CNa), Matemáticas (Mat), Francés (Fra), Latín (Lat) y Literatura (Lit)
CNa <- c(7,5,5,6,7,4,5,5,6,6,6,5,6,8,6,4,6,6,6,7)
Mat <- c(7,5,6,8,6,4,5,6,5,5,7,5,6,7,7,3,4,6,5,7)
Fra <- c(5,6,5,5,6,6,5,5,7,6,5,4,6,8,5,4,7,7,4,6)
Lat <- c(5,6,7,6,7,7,5,5,6,6,6,5,6,8,6,4,8,7,4,7)
Lit <- c(6,5,5,6,6,6,6,5,6,6,5,4,5,8,6,4,7,7,4,6)
Notas <- cbind(CNa,Mat,Fra,Lat,Lit)
Notas## CNa Mat Fra Lat Lit
## [1,] 7 7 5 5 6
## [2,] 5 5 6 6 5
## [3,] 5 6 5 7 5
## [4,] 6 8 5 6 6
## [5,] 7 6 6 7 6
## [6,] 4 4 6 7 6
## [7,] 5 5 5 5 6
## [8,] 5 6 5 5 5
## [9,] 6 5 7 6 6
## [10,] 6 5 6 6 6
## [11,] 6 7 5 6 5
## [12,] 5 5 4 5 4
## [13,] 6 6 6 6 5
## [14,] 8 7 8 8 8
## [15,] 6 7 5 6 6
## [16,] 4 3 4 4 4
## [17,] 6 4 7 8 7
## [18,] 6 6 7 7 7
## [19,] 6 5 4 4 4
## [20,] 7 7 6 7 6Es pertiente empezar por un análisis explotario para tener una mejor perspectiva de los datos:
## CNa Mat Fra Lat Lit
## Min. :4.0 Min. :3.0 Min. :4.0 Min. :4.00 Min. :4.00
## 1st Qu.:5.0 1st Qu.:5.0 1st Qu.:5.0 1st Qu.:5.00 1st Qu.:5.00
## Median :6.0 Median :6.0 Median :5.5 Median :6.00 Median :6.00
## Mean :5.8 Mean :5.7 Mean :5.6 Mean :6.05 Mean :5.65
## 3rd Qu.:6.0 3rd Qu.:7.0 3rd Qu.:6.0 3rd Qu.:7.00 3rd Qu.:6.00
## Max. :8.0 Max. :8.0 Max. :8.0 Max. :8.00 Max. :8.00Ahora algo gráfico:
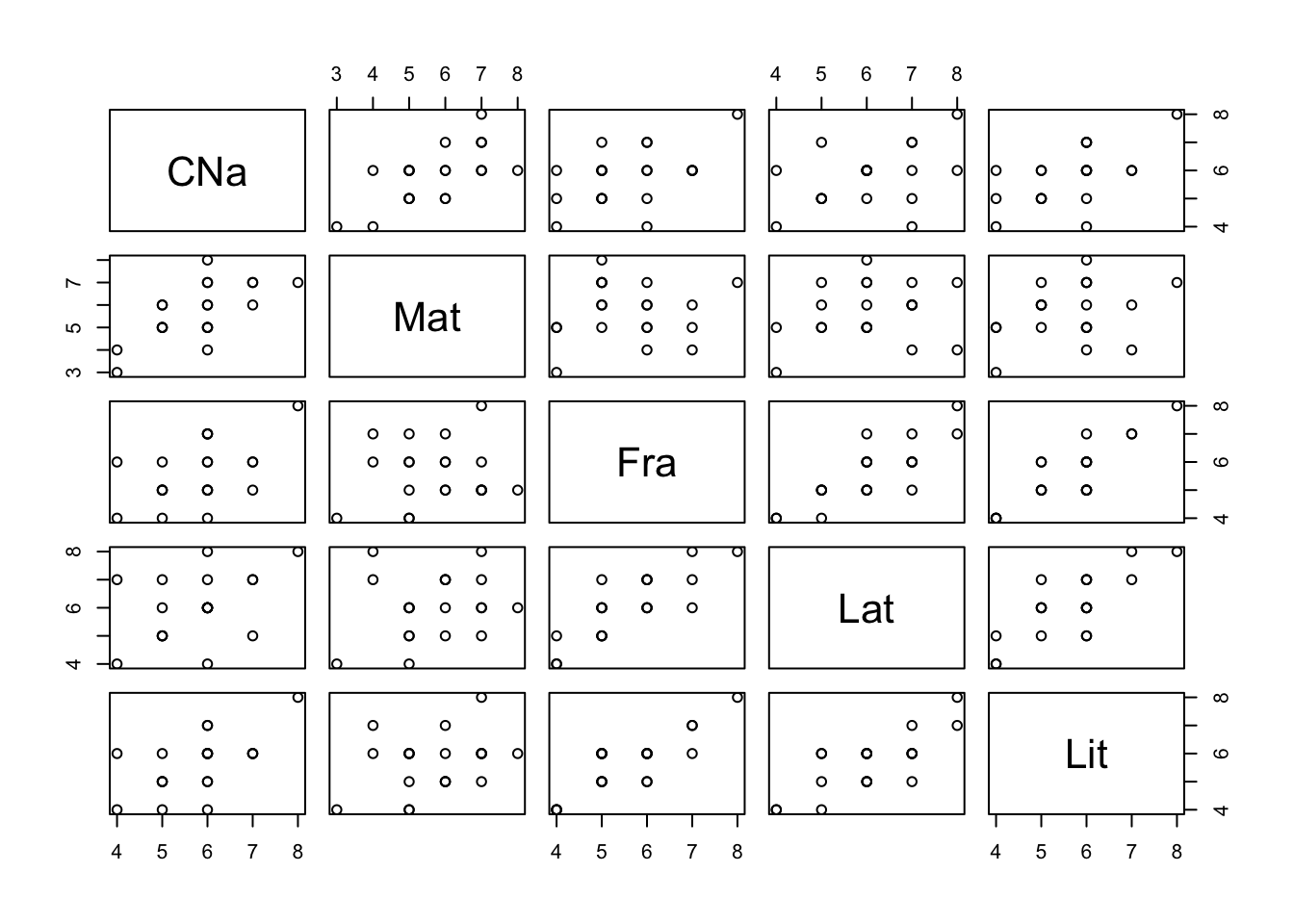
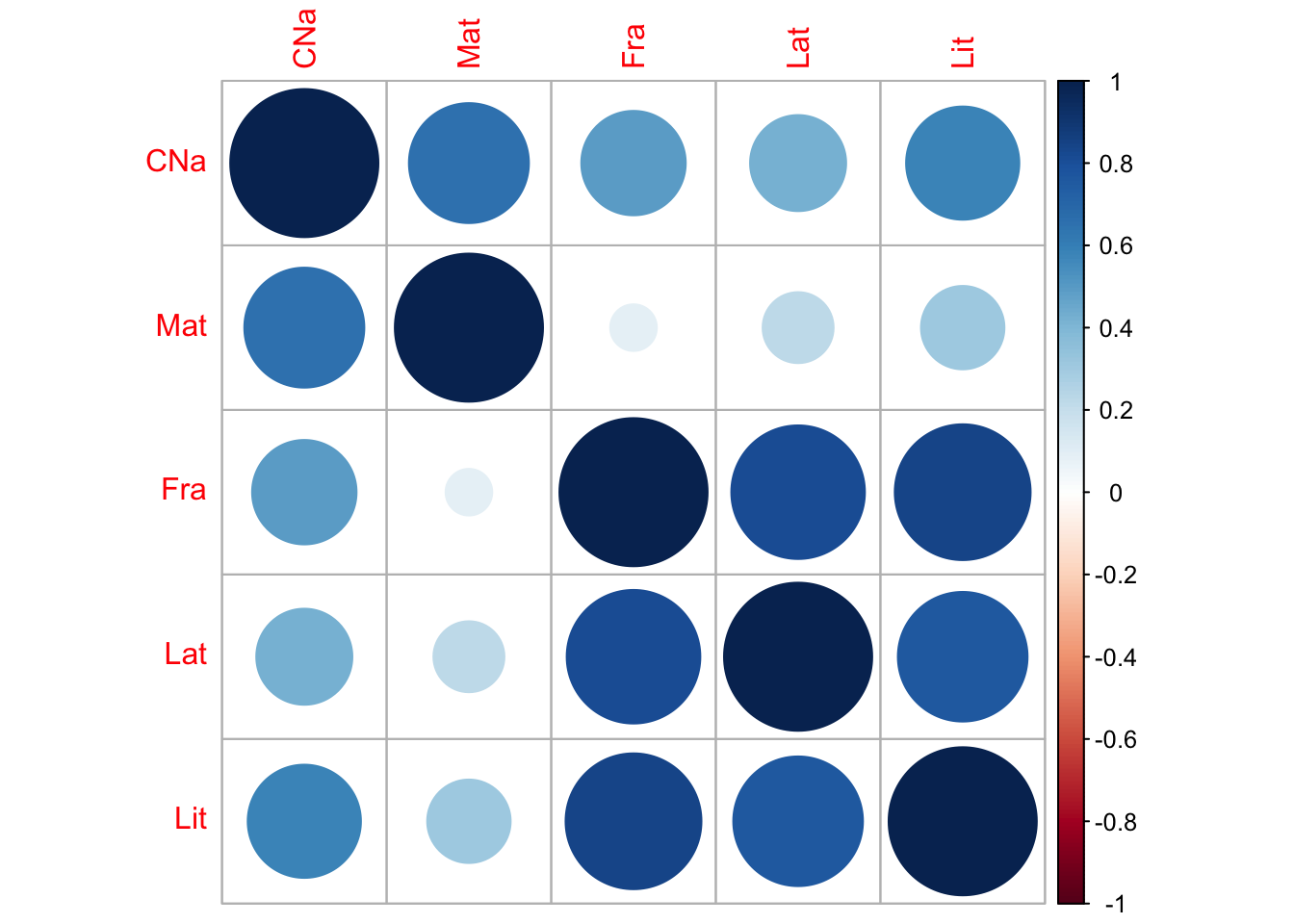
Como habíamos visto, los valores propios corresponden la varianzas explicadas de cada componente y los vectores propios son sus direcciones o pesos (loadings). Es decir:
fc <- function(x) return((x-mean(x)))
Notasc <- apply(Notas,2,fc) #Datos centrados
S <- cov(Notas*19/20) # Matriz de covarianza
VarLoad <- eigen(S) # valores y vectores propios
VarLoad## eigen() decomposition
## $values
## [1] 3.4101493 1.4993717 0.3696656 0.1987624 0.1128010
##
## $vectors
## [,1] [,2] [,3] [,4] [,5]
## [1,] -0.3953452 0.3310292 0.6615512 -0.47595392 0.2644611
## [2,] -0.3488288 0.7977236 -0.3708461 0.17998543 -0.2683914
## [3,] -0.4822572 -0.3715412 0.2152088 0.01712248 -0.7633984
## [4,] -0.5040057 -0.2987146 -0.5998378 -0.46491466 0.2842478
## [5,] -0.4852081 -0.1636565 0.1367586 0.72431643 0.4409676Ahora podemos calcular los puntajes de los componetes por individuo:
## [,1] [,2] [,3] [,4] [,5]
## [1,] -0.27915411 1.91357104 0.86033137 0.39423402 0.282362039
## [2,] 0.70813894 -0.85053394 -0.24246638 -0.18593762 -0.629895638
## [3,] 0.33756163 0.02001625 -1.42835911 -0.48798933 0.149359151
## [4,] -0.73664347 2.08155078 -0.77190377 0.58525870 0.033757315
## [5,] -1.42059398 0.14687700 0.24671081 -0.69845826 0.355850690
## [6,] 0.46309908 -2.44165783 -0.99625060 0.36943263 0.099250083
## [7,] 1.20919379 -0.34393456 0.27892119 0.98617099 0.290222569
## [8,] 1.34557309 0.61744548 -0.22868359 0.44183999 -0.419136475
## [9,] -0.65467152 -1.05470241 0.77105231 0.07954737 -0.687865235
## [10,] -0.17241431 -0.68316118 0.55584349 0.06242489 0.075533142
## [11,] 0.09739341 1.44748367 -0.53781626 -0.31904316 -0.138818927
## [12,] 2.66186718 0.35491959 -0.20980490 -0.47958435 0.171685659
## [13,] -0.03603501 0.27821886 0.04823871 -0.48190611 -0.633825902
## [14,] -4.60370426 -0.09348019 0.64151305 0.02353642 -0.008693228
## [15,] -0.38781468 1.28382720 -0.40105762 0.40527327 0.302148716
## [16,] 4.25887565 -1.27284218 0.47017392 0.10131336 0.159759512
## [17,] -1.79906227 -2.61351169 0.07898156 -0.30595095 0.589989436
## [18,] -1.99271412 -0.71934991 -0.06287296 0.51893457 -0.231041180
## [19,] 2.77052775 0.98466343 1.05158410 -0.49062361 0.151898983
## [20,] -1.76942278 0.94460058 -0.12413533 -0.51847283 0.087459289El porcentaje de la varianza explicada por cada componente es:
## [1] 0.60996276 0.26818793 0.06612094 0.03555201 0.02017636Verifiquemos nuestros resultados usando la función princomp de R:
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 1.8946321 1.2562985 0.62379622 0.45740967 0.34458364
## Proportion of Variance 0.6099628 0.2681879 0.06612094 0.03555201 0.02017636
## Cumulative Proportion 0.6099628 0.8781507 0.94427162 0.97982364 1.00000000##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## CNa 0.395 0.331 0.662 0.476 0.264
## Mat 0.349 0.798 -0.371 -0.180 -0.268
## Fra 0.482 -0.372 0.215 -0.763
## Lat 0.504 -0.299 -0.600 0.465 0.284
## Lit 0.485 -0.164 0.137 -0.724 0.441
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## SS loadings 1.0 1.0 1.0 1.0 1.0
## Proportion Var 0.2 0.2 0.2 0.2 0.2
## Cumulative Var 0.2 0.4 0.6 0.8 1.0## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## 1.8946321 1.2562985 0.6237962 0.4574097 0.3445836## List of 7
## $ sdev : Named num [1:5] 1.895 1.256 0.624 0.457 0.345
## ..- attr(*, "names")= chr [1:5] "Comp.1" "Comp.2" "Comp.3" "Comp.4" ...
## $ loadings: 'loadings' num [1:5, 1:5] 0.395 0.349 0.482 0.504 0.485 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : chr [1:5] "CNa" "Mat" "Fra" "Lat" ...
## .. ..$ : chr [1:5] "Comp.1" "Comp.2" "Comp.3" "Comp.4" ...
## $ center : Named num [1:5] 5.8 5.7 5.6 6.05 5.65
## ..- attr(*, "names")= chr [1:5] "CNa" "Mat" "Fra" "Lat" ...
## $ scale : Named num [1:5] 1 1 1 1 1
## ..- attr(*, "names")= chr [1:5] "CNa" "Mat" "Fra" "Lat" ...
## $ n.obs : int 20
## $ scores : num [1:20, 1:5] 0.279 -0.708 -0.338 0.737 1.421 ...
## ..- attr(*, "dimnames")=List of 2
## .. ..$ : NULL
## .. ..$ : chr [1:5] "Comp.1" "Comp.2" "Comp.3" "Comp.4" ...
## $ call : language princomp(x = Notas, cor = FALSE)
## - attr(*, "class")= chr "princomp"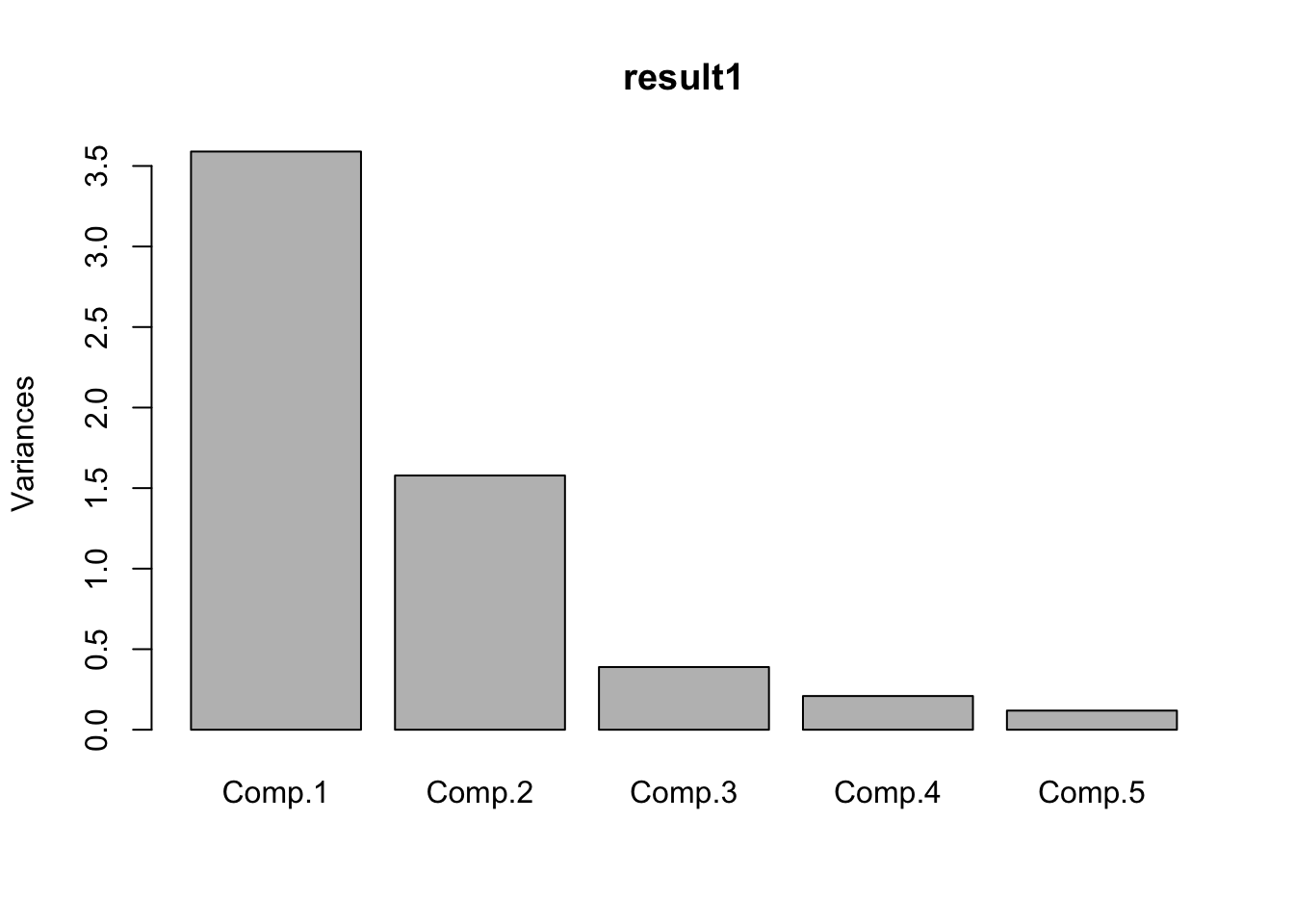
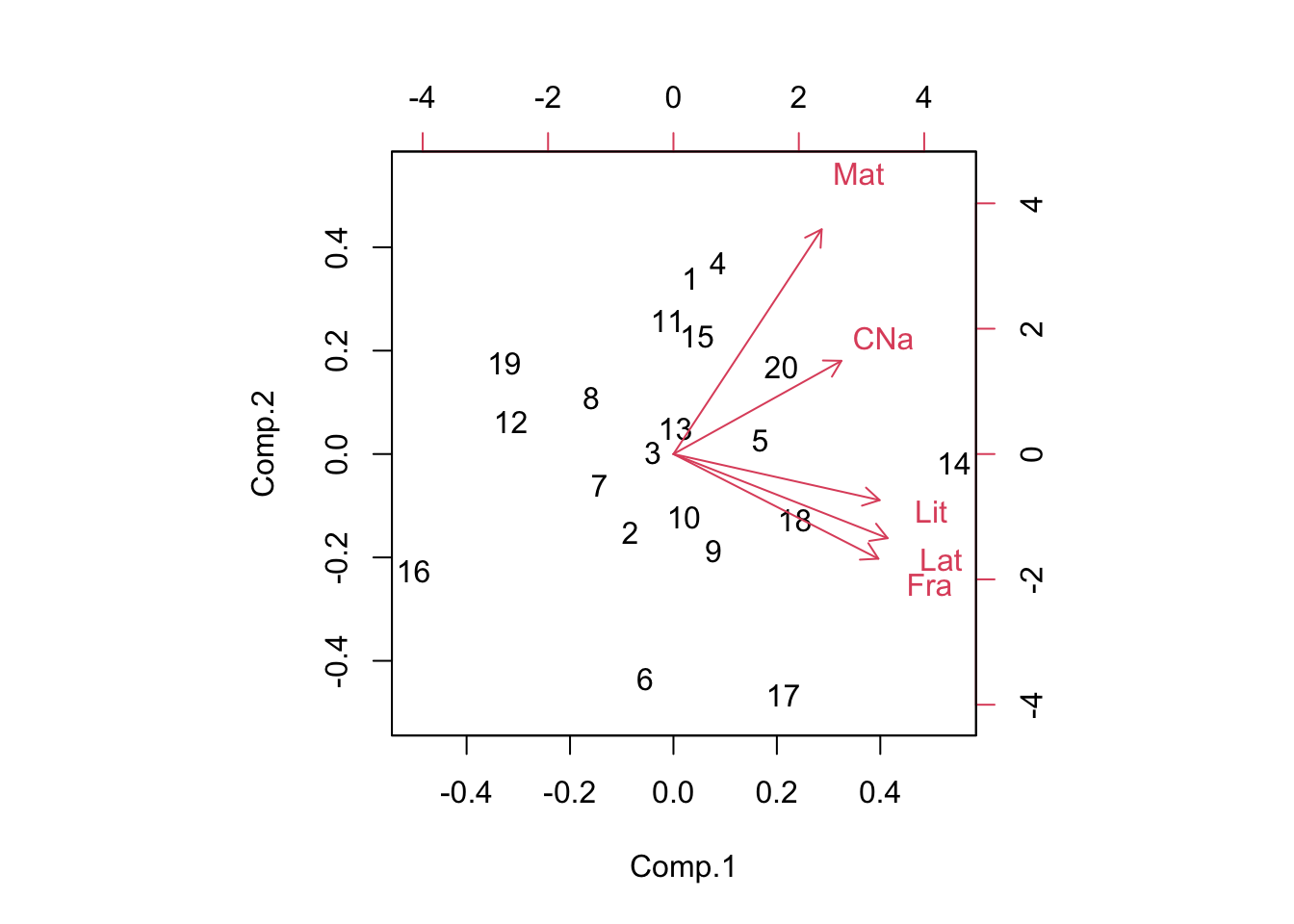
12.4.1 FactoMineR
En este paquete tenemos la función PCA que nos brinda la misma información anterior además de otros temas interesantes:
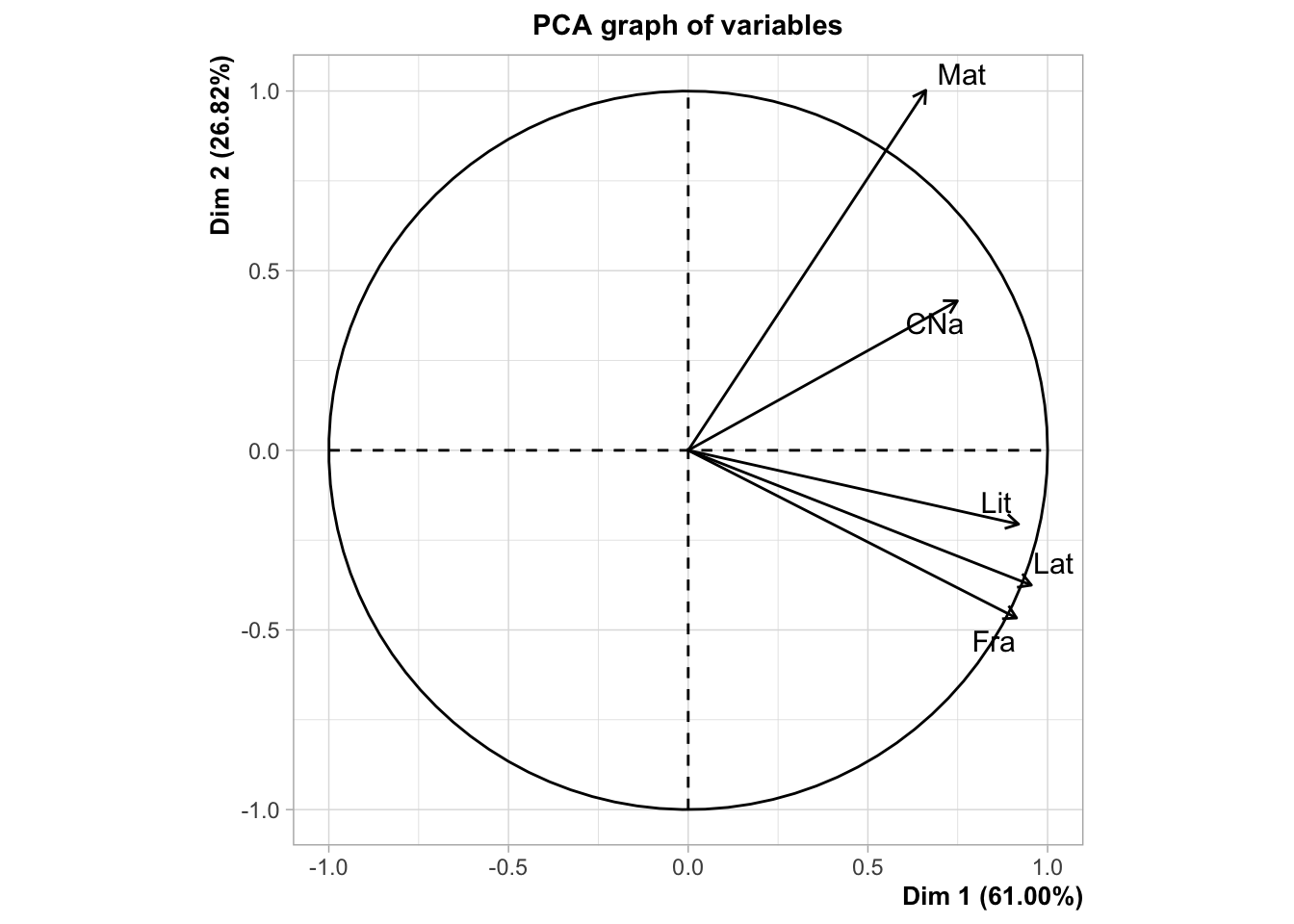
##
## Call:
## PCA(X = Notas, scale.unit = FALSE, graph = FALSE)
##
##
## Eigenvalues
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## Variance 3.590 1.578 0.389 0.209 0.119
## % of var. 60.996 26.819 6.612 3.555 2.018
## Cumulative % of var. 60.996 87.815 94.427 97.982 100.000
##
## Individuals (the 10 first)
## Dist Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr
## 1 | 2.171 | 0.279 0.109 0.017 | 1.914 11.600 0.777 | 0.860 9.511
## 2 | 1.310 | -0.708 0.698 0.292 | -0.851 2.292 0.422 | -0.242 0.755
## 3 | 1.554 | -0.338 0.159 0.047 | 0.020 0.001 0.000 | -1.428 26.216
## 4 | 2.411 | 0.737 0.756 0.093 | 2.082 13.726 0.745 | -0.772 7.656
## 5 | 1.648 | 1.421 2.811 0.743 | 0.147 0.068 0.008 | 0.247 0.782
## 6 | 2.705 | -0.463 0.299 0.029 | -2.442 18.887 0.815 | -0.996 12.753
## 7 | 1.648 | -1.209 2.037 0.539 | -0.344 0.375 0.044 | 0.279 1.000
## 8 | 1.617 | -1.346 2.522 0.692 | 0.617 1.208 0.146 | -0.229 0.672
## 9 | 1.617 | 0.655 0.597 0.164 | -1.055 3.524 0.425 | 0.771 7.639
## 10 | 0.903 | 0.172 0.041 0.036 | -0.683 1.479 0.573 | 0.556 3.970
## cos2
## 1 0.157 |
## 2 0.034 |
## 3 0.845 |
## 4 0.102 |
## 5 0.022 |
## 6 0.136 |
## 7 0.029 |
## 8 0.020 |
## 9 0.227 |
## 10 0.379 |
##
## Variables
## Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr cos2
## CNa | 0.749 15.630 0.584 | 0.416 10.958 0.180 | 0.413 43.765 0.177 |
## Mat | 0.661 12.168 0.289 | 1.002 63.636 0.665 | -0.231 13.753 0.035 |
## Fra | 0.914 23.257 0.732 | -0.467 13.804 0.191 | 0.134 4.631 0.016 |
## Lat | 0.955 25.402 0.731 | -0.375 8.923 0.113 | -0.374 35.981 0.112 |
## Lit | 0.919 23.543 0.822 | -0.206 2.678 0.041 | 0.085 1.870 0.007 |## [1] 4.57672## $coord
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## CNa 0.7490336 0.4158715 0.41267316 0.217705924 -0.09112898
## Mat 0.6609022 1.0021789 -0.23133242 -0.082327077 0.09248328
## Fra 0.9137000 -0.4667667 0.13424645 -0.007831989 0.26305459
## Lat 0.9549054 -0.3752747 -0.37417653 0.212656462 -0.09794715
## Lit 0.9192908 -0.2056014 0.08530952 -0.331309338 -0.15195023
##
## $cor
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## CNa 0.7644793 0.4244471 0.42118278 0.22219518 -0.09300813
## Mat 0.5378346 0.8155617 -0.18825566 -0.06699682 0.07526183
## Fra 0.8557585 -0.4371671 0.12573332 -0.00733533 0.24637320
## Lat 0.8549488 -0.3359921 -0.33500884 0.19039621 -0.08769433
## Lit 0.9069054 -0.2028314 0.08416016 -0.32684569 -0.14990305
##
## $cos2
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## CNa 0.5844285 0.18015533 0.177394933 4.937070e-02 0.008650511
## Mat 0.2892661 0.66514083 0.035440192 4.488575e-03 0.005664343
## Fra 0.7323225 0.19111504 0.015808868 5.380707e-05 0.060699751
## Lat 0.7309374 0.11289068 0.112230921 3.625072e-02 0.007690295
## Lit 0.8224775 0.04114056 0.007082933 1.068281e-01 0.022470923
##
## $contrib
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## CNa 15.62978 10.958035 43.765004 22.65321318 6.993969
## Mat 12.16815 63.636291 13.752686 3.23947557 7.203394
## Fra 23.25720 13.804288 4.631484 0.02931794 58.277708
## Lat 25.40218 8.923042 35.980534 21.61456435 8.079682
## Lit 23.54269 2.678344 1.870292 52.46342895 19.44524612.5 Ejemplo
12.5.1 Paso 1: recopilación de datos
Trabajemos los datos de los resultados de las competencias de heptatlón en Seúl 1988
Las variables son
- hurdles: vallas 100m
- highjump: salto alto
- shot: tiro
- run200m: velocidad 200m
- longjump: salto largo
- javelin: lanzamiento de javalina
- run800m: velocidad 800m
- score: puntaje
12.5.2 Paso 2: Explorar y preparar los datos
Resumimos la variable score:
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4566 5746 6137 6091 6351 7291Ahora las variables que generaron el score
## hurdles highjump shot run200m longjump
## hurdles 1.000000000 -0.811402536 -0.6513347 0.7737205 -0.91213362
## highjump -0.811402536 1.000000000 0.4407861 -0.4876637 0.78244227
## shot -0.651334688 0.440786140 1.0000000 -0.6826704 0.74307300
## run200m 0.773720543 -0.487663685 -0.6826704 1.0000000 -0.81720530
## longjump -0.912133617 0.782442273 0.7430730 -0.8172053 1.00000000
## javelin -0.007762549 0.002153016 0.2689888 -0.3330427 0.06710841
## run800m 0.779257110 -0.591162823 -0.4196196 0.6168101 -0.69951116
## javelin run800m
## hurdles -0.007762549 0.77925711
## highjump 0.002153016 -0.59116282
## shot 0.268988837 -0.41961957
## run200m -0.333042722 0.61681006
## longjump 0.067108409 -0.69951116
## javelin 1.000000000 0.02004909
## run800m 0.020049088 1.00000000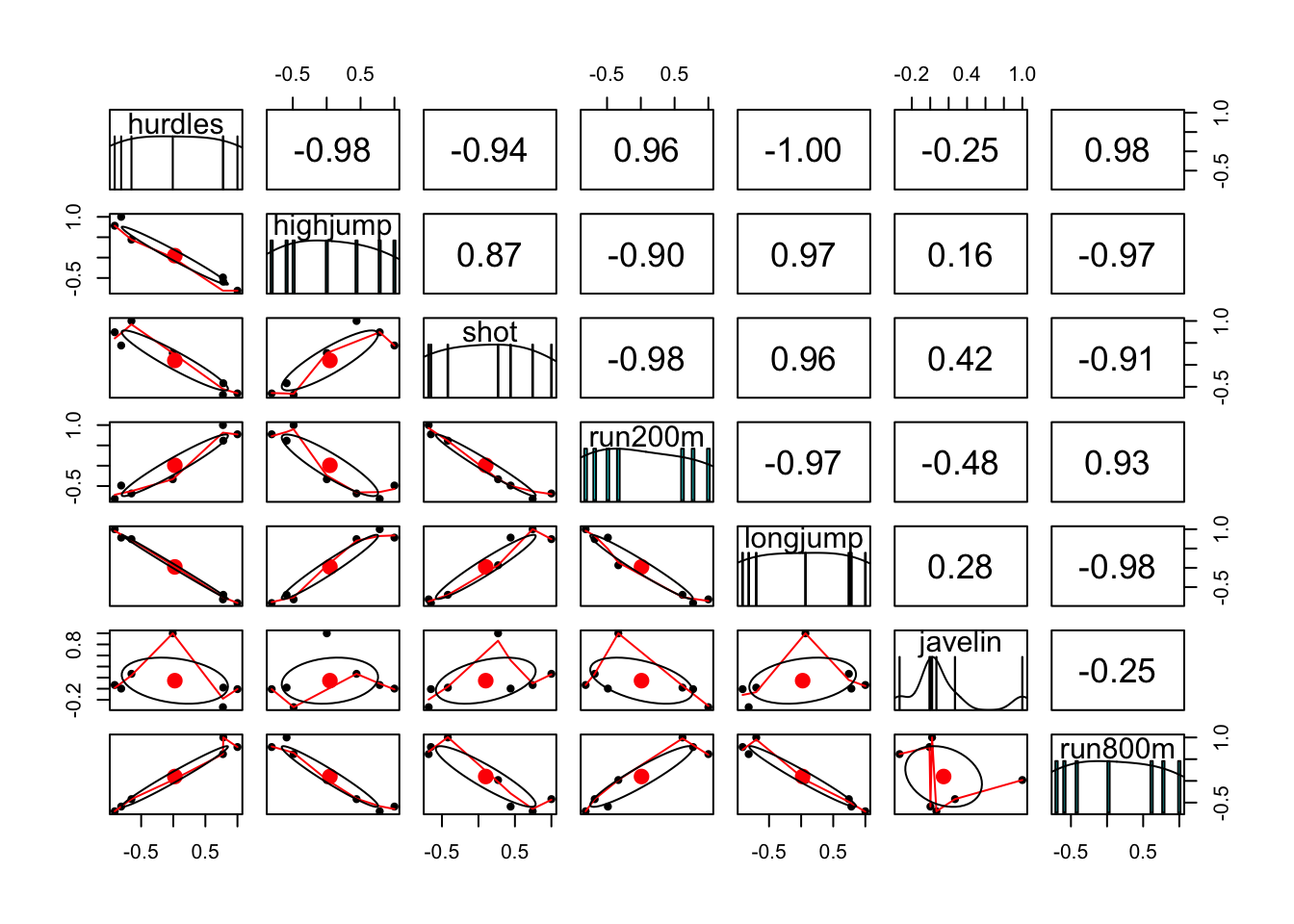
## hurdles highjump shot run200m longjump javelin run800m
## Joyner-Kersee (USA) 12.69 1.86 15.80 22.56 7.27 45.66 128.51
## John (GDR) 12.85 1.80 16.23 23.65 6.71 42.56 126.12
## Behmer (GDR) 13.20 1.83 14.20 23.10 6.68 44.54 124.20
## Sablovskaite (URS) 13.61 1.80 15.23 23.92 6.25 42.78 132.24
## Choubenkova (URS) 13.51 1.74 14.76 23.93 6.32 47.46 127.90
## Schulz (GDR) 13.75 1.83 13.50 24.65 6.33 42.82 125.79
## Fleming (AUS) 13.38 1.80 12.88 23.59 6.37 40.28 132.54
## Greiner (USA) 13.55 1.80 14.13 24.48 6.47 38.00 133.65
## Lajbnerova (CZE) 13.63 1.83 14.28 24.86 6.11 42.20 136.05
## Bouraga (URS) 13.25 1.77 12.62 23.59 6.28 39.06 134.74
## Wijnsma (HOL) 13.75 1.86 13.01 25.03 6.34 37.86 131.49
## Dimitrova (BUL) 13.24 1.80 12.88 23.59 6.37 40.28 132.54
## Scheider (SWI) 13.85 1.86 11.58 24.87 6.05 47.50 134.93
## Braun (FRG) 13.71 1.83 13.16 24.78 6.12 44.58 142.82
## Ruotsalainen (FIN) 13.79 1.80 12.32 24.61 6.08 45.44 137.06
## Yuping (CHN) 13.93 1.86 14.21 25.00 6.40 38.60 146.67
## Hagger (GB) 13.47 1.80 12.75 25.47 6.34 35.76 138.48
## Brown (USA) 14.07 1.83 12.69 24.83 6.13 44.34 146.43
## Mulliner (GB) 14.39 1.71 12.68 24.92 6.10 37.76 138.02
## Hautenauve (BEL) 14.04 1.77 11.81 25.61 5.99 35.68 133.90
## Kytola (FIN) 14.31 1.77 11.66 25.69 5.75 39.48 133.35
## Geremias (BRA) 14.23 1.71 12.95 25.50 5.50 39.64 144.02
## Hui-Ing (TAI) 14.85 1.68 10.00 25.23 5.47 39.14 137.30
## Jeong-Mi (KOR) 14.53 1.71 10.83 26.61 5.50 39.26 139.17
## Launa (PNG) 16.42 1.50 11.78 26.16 4.88 46.38 163.43El sentido de los datos podría ser un problema. Podemos hacer que estos apunten a un mismo sentido:
heptathlon$hurdles <- with(heptathlon, max(hurdles)-hurdles)
heptathlon$run200m <- with(heptathlon, max(run200m)-run200m)
heptathlon$run800m <- with(heptathlon, max(run800m)-run800m)
score <- which(colnames(heptathlon) == "score")
pairs.panels(heptathlon[,-score])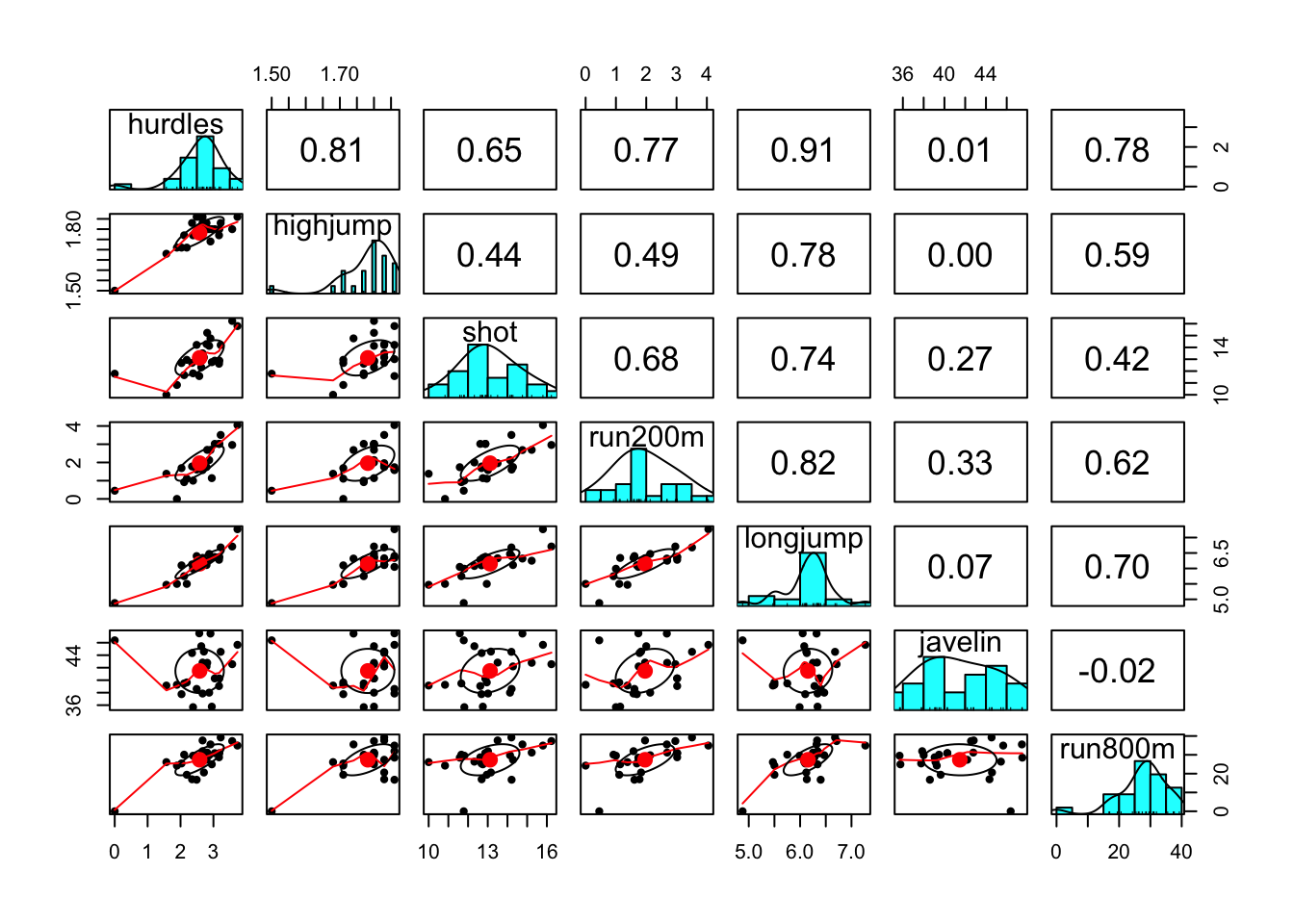
12.5.3 Paso 3: entrenar un modelo en los datos
Ajustamos un PCA:
## [,1]
## Joyner-Kersee (USA) -4.121447626
## John (GDR) -2.882185935
## Behmer (GDR) -2.649633766
## Sablovskaite (URS) -1.343351210
## Choubenkova (URS) -1.359025696
## Schulz (GDR) -1.043847471
## Fleming (AUS) -1.100385639
## Greiner (USA) -0.923173639
## Lajbnerova (CZE) -0.530250689
## Bouraga (URS) -0.759819024
## Wijnsma (HOL) -0.556268302
## Dimitrova (BUL) -1.186453832
## Scheider (SWI) 0.015461226
## Braun (FRG) 0.003774223
## Ruotsalainen (FIN) 0.090747709
## Yuping (CHN) -0.137225440
## Hagger (GB) 0.171128651
## Brown (USA) 0.519252646
## Mulliner (GB) 1.125481833
## Hautenauve (BEL) 1.085697646
## Kytola (FIN) 1.447055499
## Geremias (BRA) 2.014029620
## Hui-Ing (TAI) 2.880298635
## Jeong-Mi (KOR) 2.970118607
## Launa (PNG) 6.270021972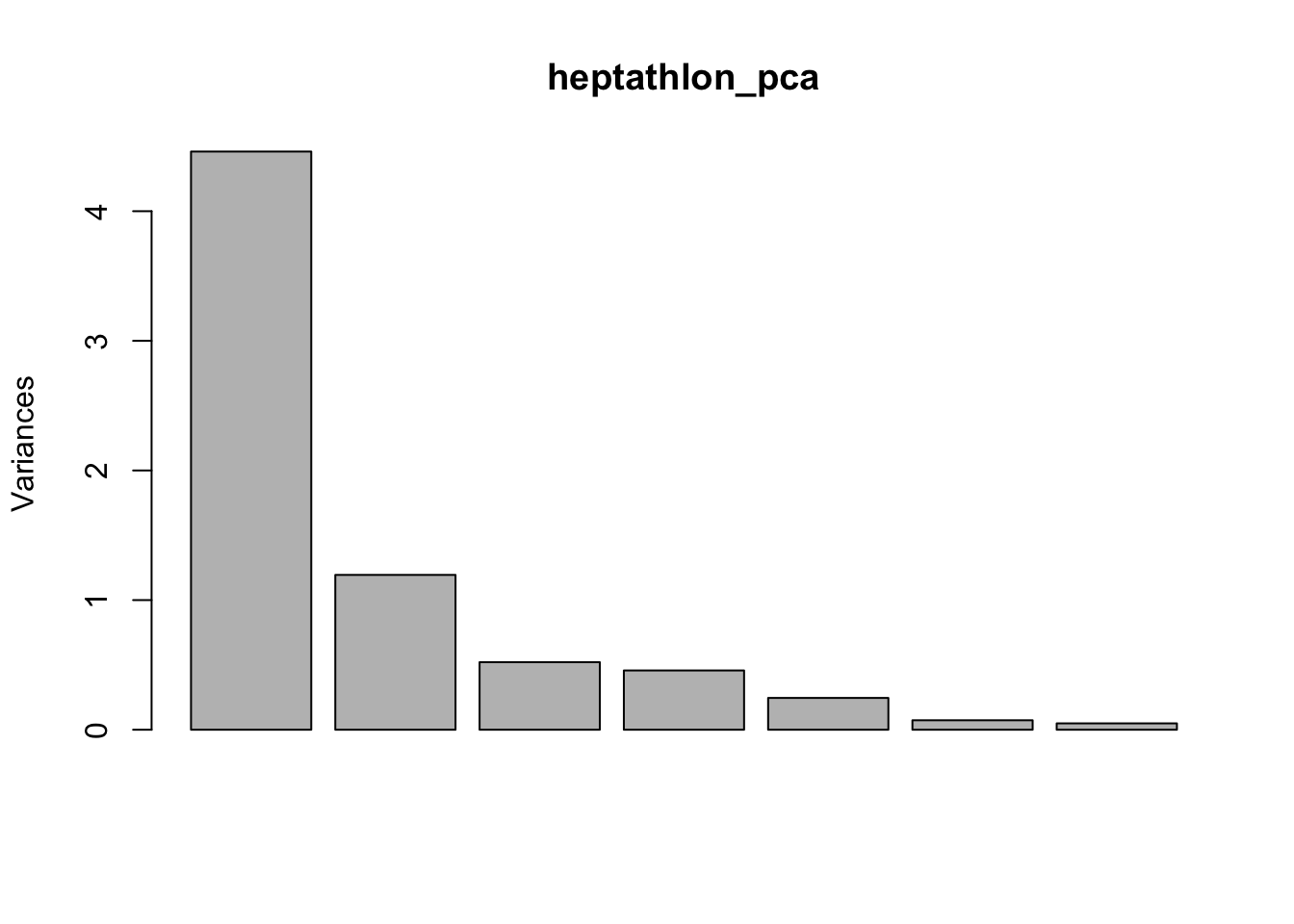
12.5.4 Paso 4: evaluar el rendimiento del modelo
Obtenemos la correlación entre el primer componente y los puntajes oficiales:
## [1] -0.9910978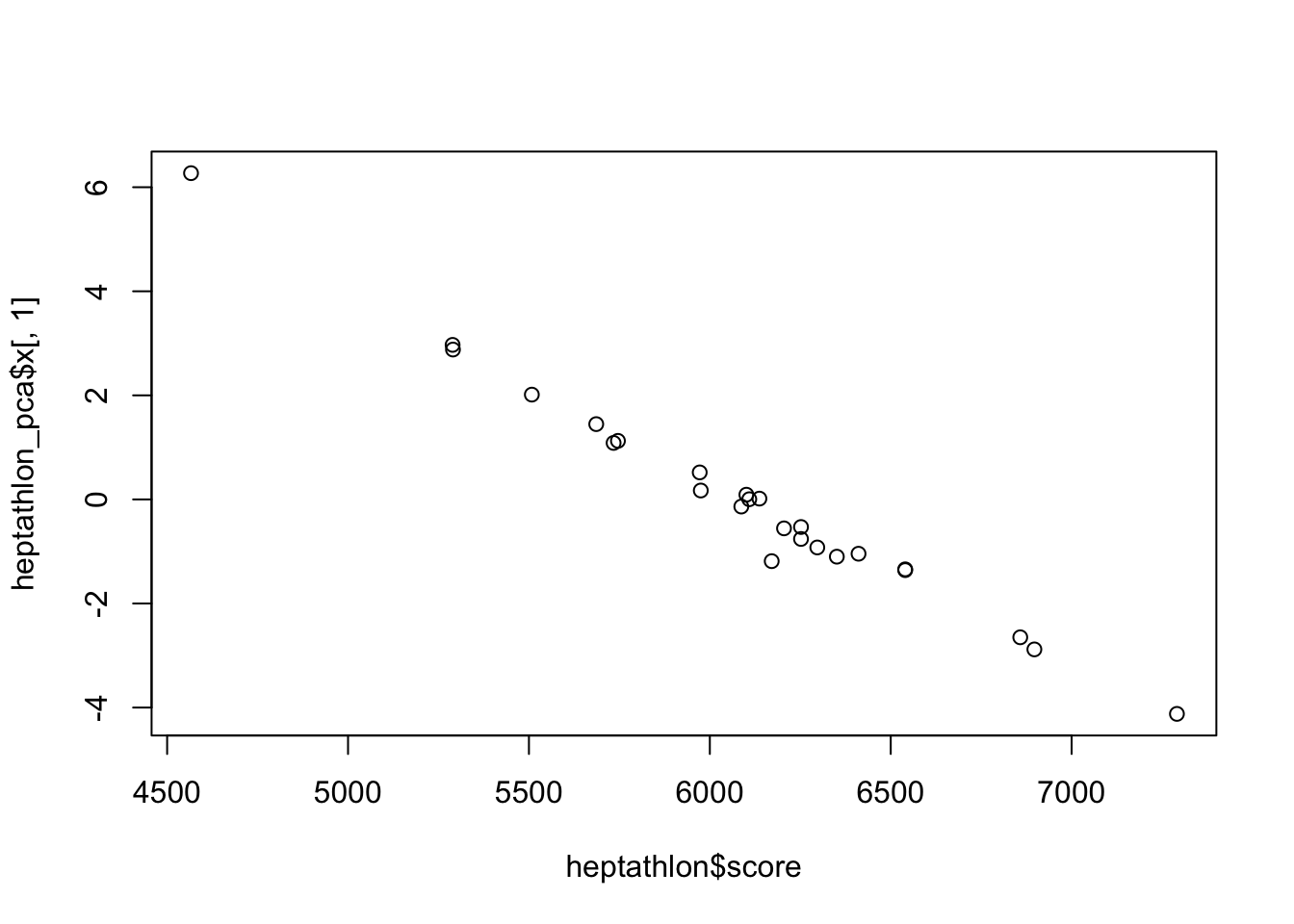
12.5.5 Paso 5: mejorando el ajuste
Una de las alternativas más usadas es probar con diferentes rotaciones de los ejes.
Bonus
dm <- dist(heptathlon[,-8])
par(mfrow = c(1,3))
plot(cs <- hclust(dm, method = "single"))
plot(cc <- hclust(dm, method = "complete"))
plot(ca <- hclust(dm, method = "average"))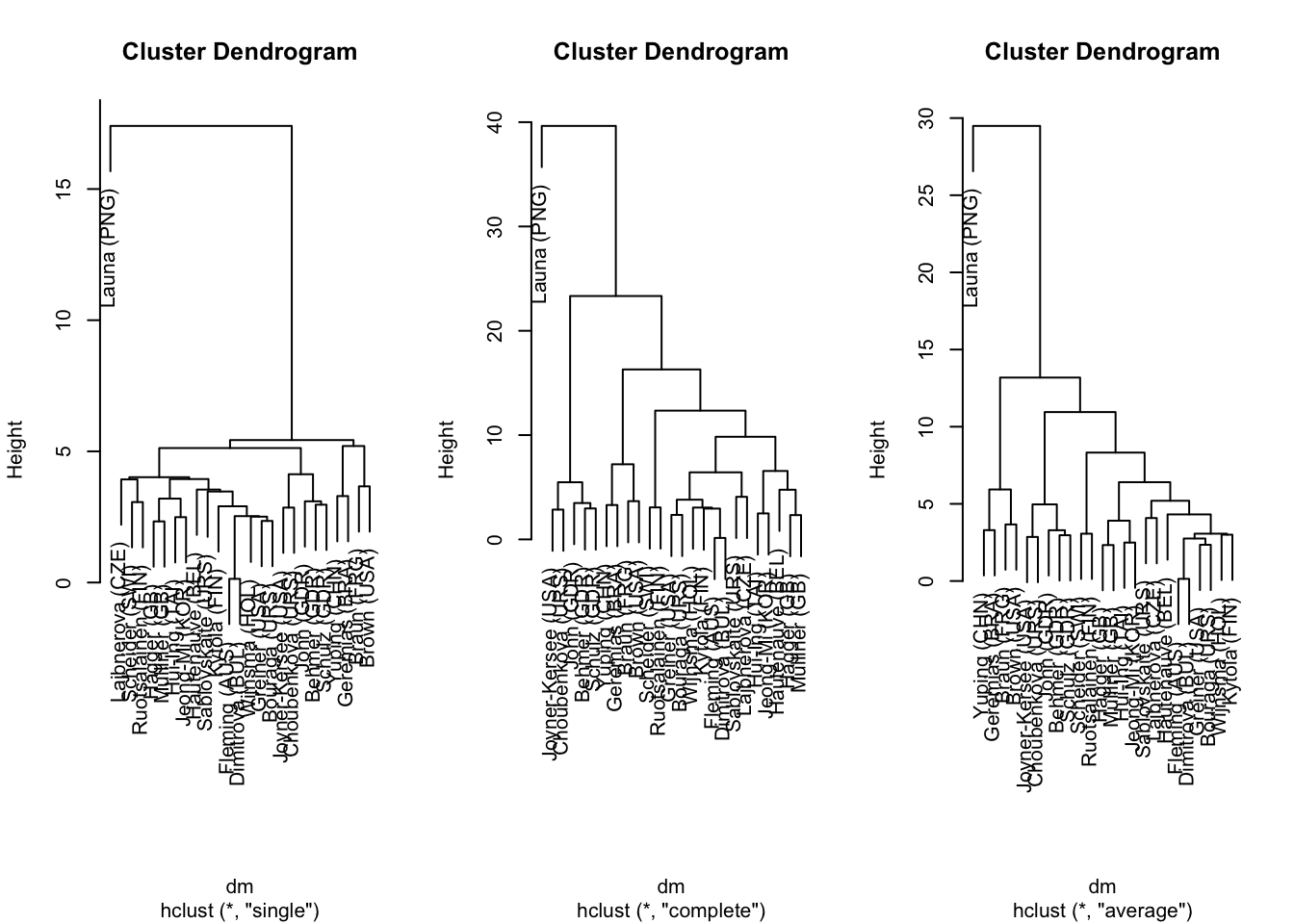
12.6 ACP: Datos de rating de marca del consumidor
Estos datos son comunes en investigación de mercado, se refieren a encuestas de percepción de marca.
Las preguntas suelen ser realizadas usando escalas de Likert como: En la escala del 1 al 10, donde 1 es menos y 10 es más, cuán [adjetivo] es la [marca]?
- ¿Cuán de moda es la marca Metal?
12.6.1 Datos
Tenemos 10 marcas (de la a a la j) con 9 adjetivos para \(N=100\) clientes. Veamos los datos:
uu <- "https://raw.githubusercontent.com/vmoprojs/DataLectures/master/IQl8nc.csv"
brand.ratings <- read.csv(uu)
head(brand.ratings)## perform leader latest fun serious bargain value trendy rebuy brand
## 1 2 4 8 8 2 9 7 4 6 a
## 2 1 1 4 7 1 1 1 2 2 a
## 3 2 3 5 9 2 9 5 1 6 a
## 4 1 6 10 8 3 4 5 2 1 a
## 5 1 1 5 8 1 9 9 1 1 a
## 6 2 8 9 5 3 8 7 1 2 aAhora una inspección de los datos:
## perform leader latest fun
## Min. : 1.000 Min. : 1.000 Min. : 1.000 Min. : 1.000
## 1st Qu.: 1.000 1st Qu.: 2.000 1st Qu.: 4.000 1st Qu.: 4.000
## Median : 4.000 Median : 4.000 Median : 7.000 Median : 6.000
## Mean : 4.488 Mean : 4.417 Mean : 6.195 Mean : 6.068
## 3rd Qu.: 7.000 3rd Qu.: 6.000 3rd Qu.: 9.000 3rd Qu.: 8.000
## Max. :10.000 Max. :10.000 Max. :10.000 Max. :10.000
## serious bargain value trendy
## Min. : 1.000 Min. : 1.000 Min. : 1.000 Min. : 1.00
## 1st Qu.: 2.000 1st Qu.: 2.000 1st Qu.: 2.000 1st Qu.: 3.00
## Median : 4.000 Median : 4.000 Median : 4.000 Median : 5.00
## Mean : 4.323 Mean : 4.259 Mean : 4.337 Mean : 5.22
## 3rd Qu.: 6.000 3rd Qu.: 6.000 3rd Qu.: 6.000 3rd Qu.: 7.00
## Max. :10.000 Max. :10.000 Max. :10.000 Max. :10.00
## rebuy brand
## Min. : 1.000 Length:1000
## 1st Qu.: 1.000 Class :character
## Median : 3.000 Mode :character
## Mean : 3.727
## 3rd Qu.: 5.000
## Max. :10.000## 'data.frame': 1000 obs. of 10 variables:
## $ perform: int 2 1 2 1 1 2 1 2 2 3 ...
## $ leader : int 4 1 3 6 1 8 1 1 1 1 ...
## $ latest : int 8 4 5 10 5 9 5 7 8 9 ...
## $ fun : int 8 7 9 8 8 5 7 5 10 8 ...
## $ serious: int 2 1 2 3 1 3 1 2 1 1 ...
## $ bargain: int 9 1 9 4 9 8 5 8 7 3 ...
## $ value : int 7 1 5 5 9 7 1 7 7 3 ...
## $ trendy : int 4 2 1 2 1 1 1 7 5 4 ...
## $ rebuy : int 6 2 6 1 1 2 1 1 1 1 ...
## $ brand : chr "a" "a" "a" "a" ...12.6.2 Reescalando los datos
brand.sc <- brand.ratings
brand.sc [ , 1:9] <- data.frame(scale(brand.ratings [ , 1:9]))
summary(brand.sc)## perform leader latest fun
## Min. :-1.0888 Min. :-1.3100 Min. :-1.6878 Min. :-1.84677
## 1st Qu.:-1.0888 1st Qu.:-0.9266 1st Qu.:-0.7131 1st Qu.:-0.75358
## Median :-0.1523 Median :-0.1599 Median : 0.2615 Median :-0.02478
## Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.00000
## 3rd Qu.: 0.7842 3rd Qu.: 0.6069 3rd Qu.: 0.9113 3rd Qu.: 0.70402
## Max. : 1.7206 Max. : 2.1404 Max. : 1.2362 Max. : 1.43281
## serious bargain value trendy
## Min. :-1.1961 Min. :-1.22196 Min. :-1.3912 Min. :-1.53897
## 1st Qu.:-0.8362 1st Qu.:-0.84701 1st Qu.:-0.9743 1st Qu.:-0.80960
## Median :-0.1163 Median :-0.09711 Median :-0.1405 Median :-0.08023
## Mean : 0.0000 Mean : 0.00000 Mean : 0.0000 Mean : 0.00000
## 3rd Qu.: 0.6036 3rd Qu.: 0.65279 3rd Qu.: 0.6933 3rd Qu.: 0.64914
## Max. : 2.0434 Max. : 2.15258 Max. : 2.3610 Max. : 1.74319
## rebuy brand
## Min. :-1.0717 Length:1000
## 1st Qu.:-1.0717 Class :character
## Median :-0.2857 Mode :character
## Mean : 0.0000
## 3rd Qu.: 0.5003
## Max. : 2.4652Exploremos las correlaciones por parejas:
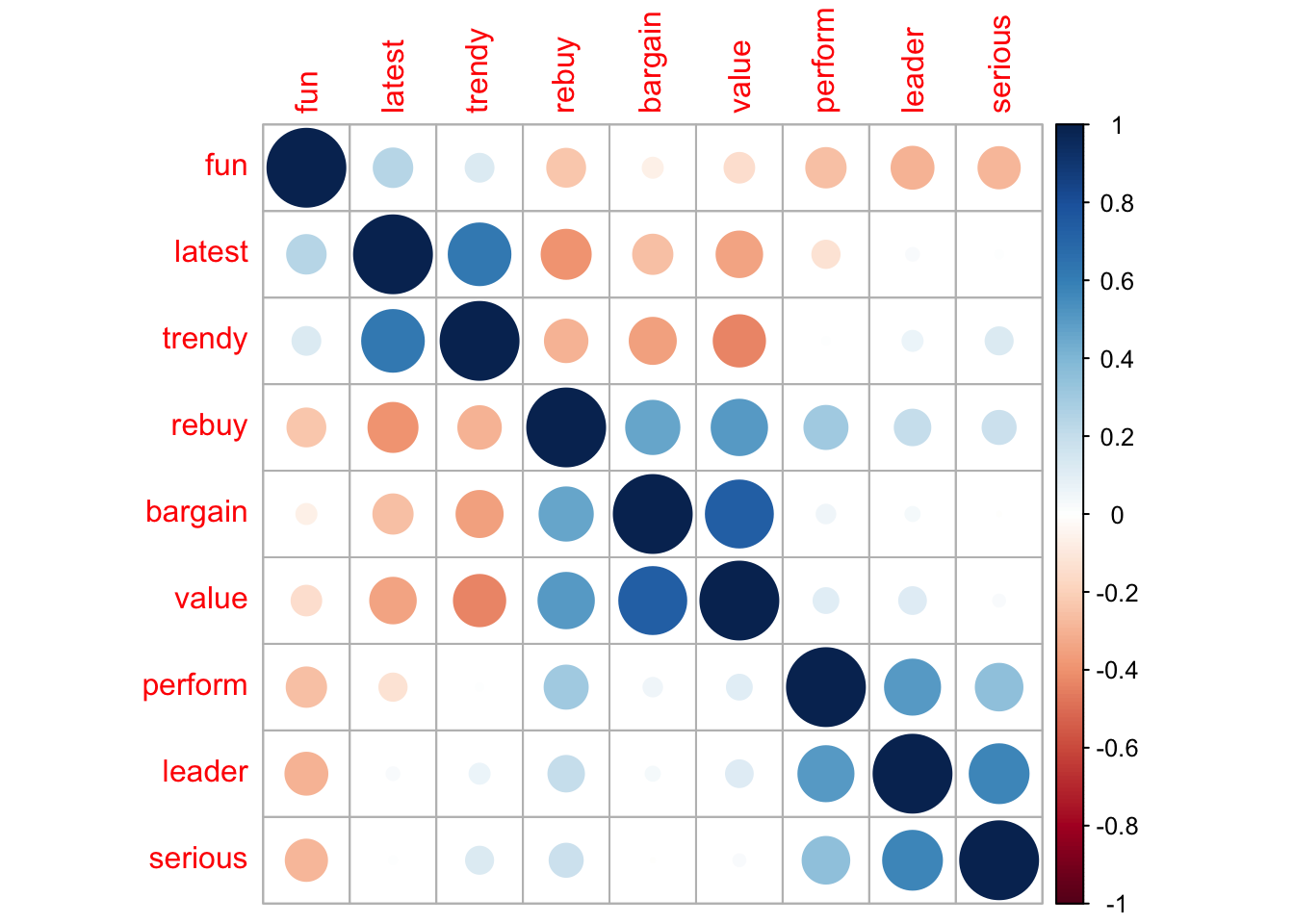
El argumento order="hclust" reordena las filas y las columnas de acuerdo a la similaridad de las variables.
12.6.3 Media de los ratings por marca
## brand perform leader latest fun serious
## 1 a -0.88591874 -0.5279035 0.4109732 0.6566458 -0.91894067
## 2 b 0.93087022 1.0707584 0.7261069 -0.9722147 1.18314061
## 3 c 0.64992347 1.1627677 -0.1023372 -0.8446753 1.22273461
## 4 d -0.67989112 -0.5930767 0.3524948 0.1865719 -0.69217505
## 5 e -0.56439079 0.1928362 0.4564564 0.2958914 0.04211361
## 6 f -0.05868665 0.2695106 -1.2621589 -0.2179102 0.58923066
## 7 g 0.91838369 -0.1675336 -1.2849005 -0.5167168 -0.53379906
## 8 h -0.01498383 -0.2978802 0.5019396 0.7149495 -0.14145855
## 9 i 0.33463879 -0.3208825 0.3557436 0.4124989 -0.14865746
## 10 j -0.62994504 -0.7885965 -0.1543180 0.2849595 -0.60218870
## bargain value trendy rebuy
## 1 0.21409609 0.18469264 -0.52514473 -0.59616642
## 2 0.04161938 0.15133957 0.74030819 0.23697320
## 3 -0.60704302 -0.44067747 0.02552787 -0.13243776
## 4 -0.88075605 -0.93263529 0.73666135 -0.49398892
## 5 0.55155051 0.41816415 0.13857986 0.03654811
## 6 0.87400696 1.02268859 -0.81324496 1.35699580
## 7 0.89650392 1.25616009 -1.27639344 1.36092571
## 8 -0.73827529 -0.78254646 0.86430070 -0.60402622
## 9 -0.25459062 -0.80339213 0.59078782 -0.20317603
## 10 -0.09711188 -0.07379367 -0.48138267 -0.96164748rownames(brand.mean) <- brand.mean [ , 1] # la marca como nombre de filas
brand.mean <- brand.mean [ , -1] # eliminamos la columna de marca
brand.mean## perform leader latest fun serious bargain
## a -0.88591874 -0.5279035 0.4109732 0.6566458 -0.91894067 0.21409609
## b 0.93087022 1.0707584 0.7261069 -0.9722147 1.18314061 0.04161938
## c 0.64992347 1.1627677 -0.1023372 -0.8446753 1.22273461 -0.60704302
## d -0.67989112 -0.5930767 0.3524948 0.1865719 -0.69217505 -0.88075605
## e -0.56439079 0.1928362 0.4564564 0.2958914 0.04211361 0.55155051
## f -0.05868665 0.2695106 -1.2621589 -0.2179102 0.58923066 0.87400696
## g 0.91838369 -0.1675336 -1.2849005 -0.5167168 -0.53379906 0.89650392
## h -0.01498383 -0.2978802 0.5019396 0.7149495 -0.14145855 -0.73827529
## i 0.33463879 -0.3208825 0.3557436 0.4124989 -0.14865746 -0.25459062
## j -0.62994504 -0.7885965 -0.1543180 0.2849595 -0.60218870 -0.09711188
## value trendy rebuy
## a 0.18469264 -0.52514473 -0.59616642
## b 0.15133957 0.74030819 0.23697320
## c -0.44067747 0.02552787 -0.13243776
## d -0.93263529 0.73666135 -0.49398892
## e 0.41816415 0.13857986 0.03654811
## f 1.02268859 -0.81324496 1.35699580
## g 1.25616009 -1.27639344 1.36092571
## h -0.78254646 0.86430070 -0.60402622
## i -0.80339213 0.59078782 -0.20317603
## j -0.07379367 -0.48138267 -0.96164748Un heatmap es una forma útil de explorar estos datos porque se grafican colores de acuerdo a la intensidad del valor:
library(gplots)
library(RColorBrewer)
heatmap.2(as.matrix(brand.mean),
col=brewer.pal(9, "GnBu") , trace="none" , key=FALSE , dend="none",
main="\n\n\n\n\nAtributos de la marca")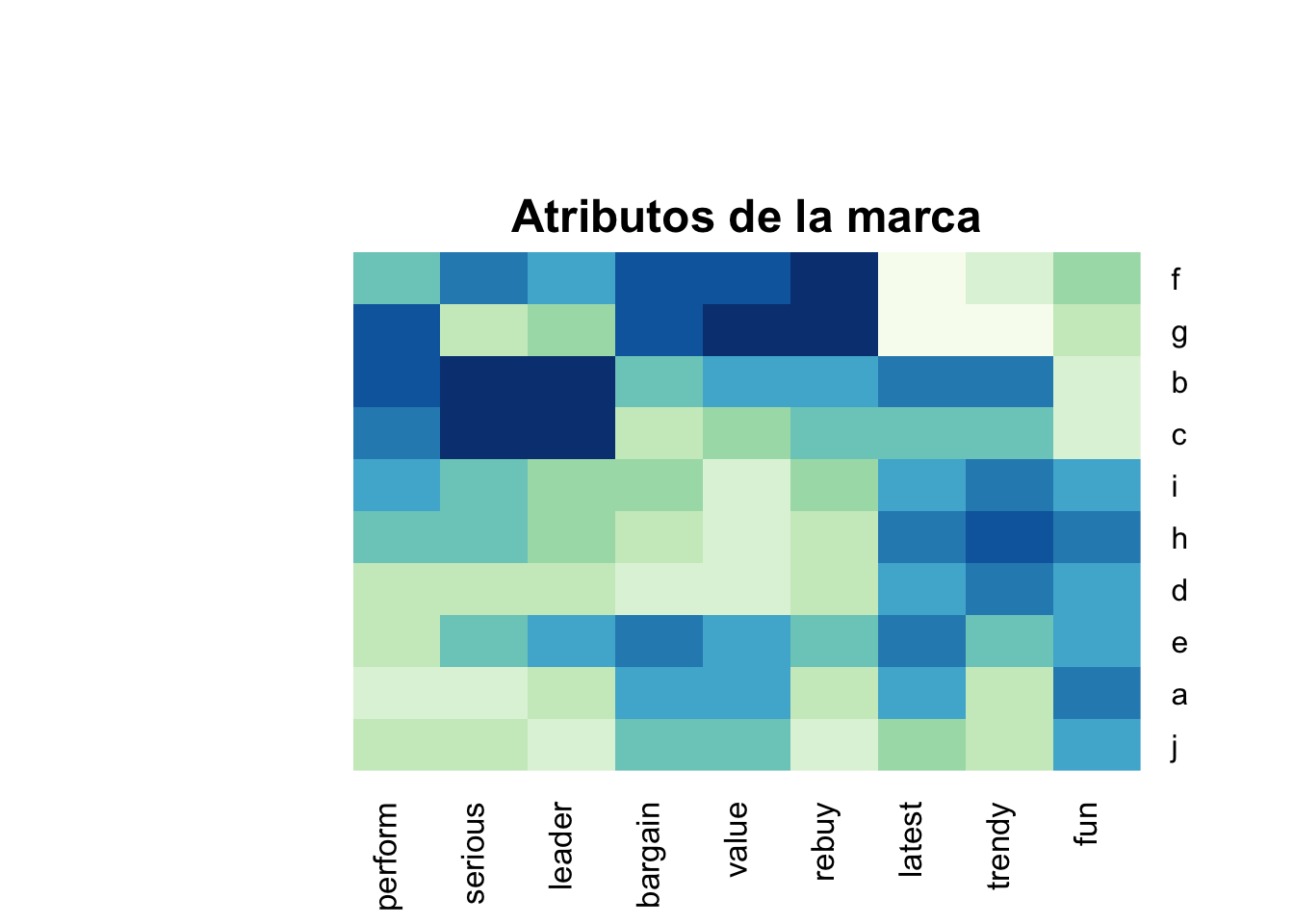
Las marcas f y g son similares, con altas calificaciones para recompra y valor, pero bajas calificaciones para lo último y divertido. Otros grupos de marcas similares son b/c, i/h/d, y a/j.
12.7 Análisis de componentes principales y mapas perceptuales
## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 1.726 1.4479 1.0389 0.8528 0.79846 0.73133 0.62458
## Proportion of Variance 0.331 0.2329 0.1199 0.0808 0.07084 0.05943 0.04334
## Cumulative Proportion 0.331 0.5640 0.6839 0.7647 0.83554 0.89497 0.93831
## PC8 PC9
## Standard deviation 0.55861 0.49310
## Proportion of Variance 0.03467 0.02702
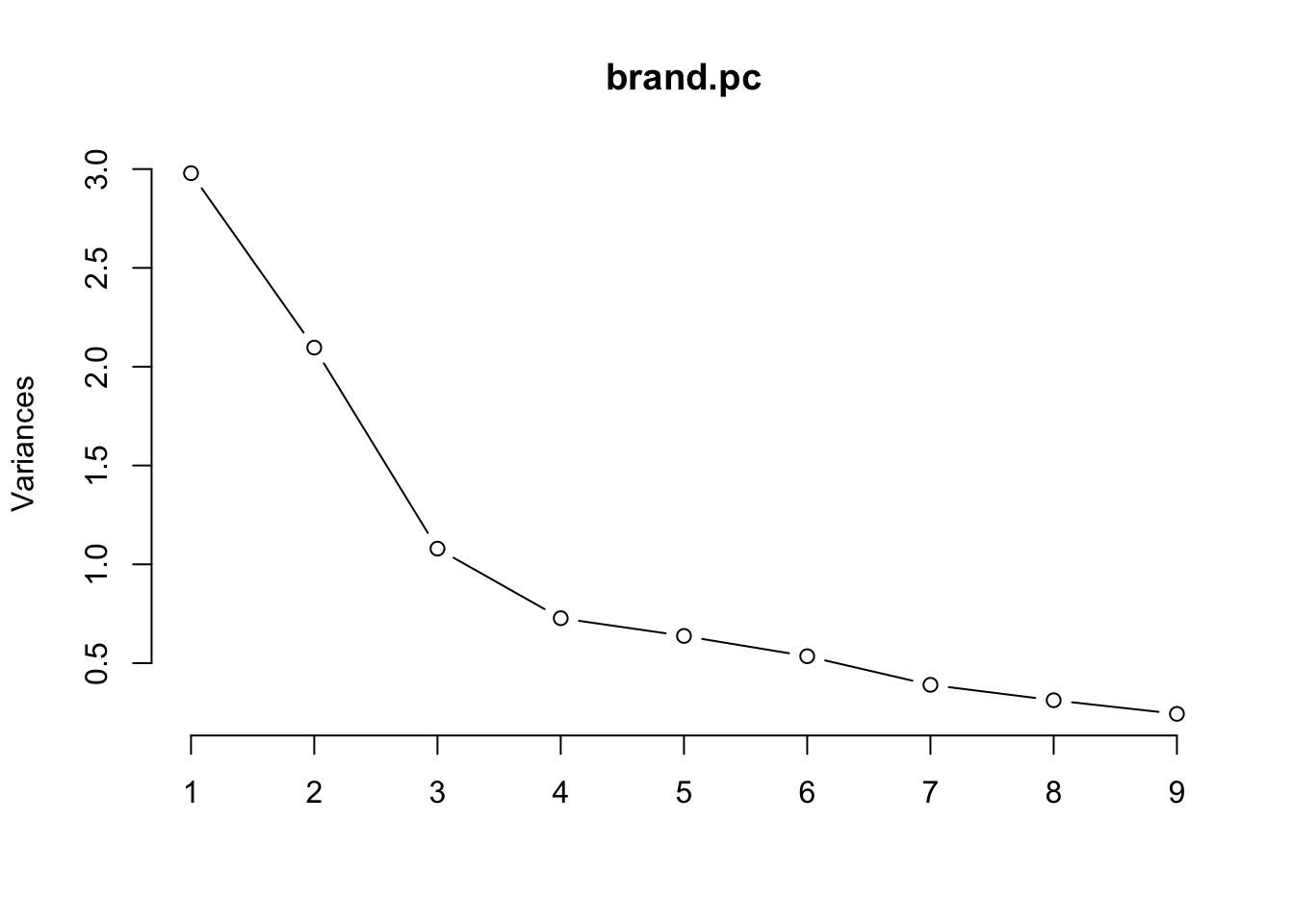
## Cumulative Proportion 0.97298 1.00000Un gráfico scree de una solución de PCA muestra la variación sucesiva contabilizada por cada componente. Para los datos de calificación de marca, la proporción se nivela en gran medida después del tercer componente:
Un biplot de un intento inicial de análisis de componentes principales para calificaciones de marcas de consumo: Aunque vemos agrupaciones de adjetivos en las flechas de los loadings en rojo, y obtenemos una idea de las áreas donde las clasificaciones se agrupan (como áreas densas de puntos de observación), el gráfico sería más útil si los datos se agregaran primero por marca
## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 2.1345 1.7349 0.7690 0.61498 0.50983 0.36662 0.21506
## Proportion of Variance 0.5062 0.3345 0.0657 0.04202 0.02888 0.01493 0.00514
## Cumulative Proportion 0.5062 0.8407 0.9064 0.94842 0.97730 0.99223 0.99737
## PC8 PC9
## Standard deviation 0.14588 0.04867
## Proportion of Variance 0.00236 0.00026
## Cumulative Proportion 0.99974 1.0000012.7.1 Mapas perceptuales de las marcas
Un biplot de la solución PCA para las calificaciones medias da un mapa perceptual interpretable:

Las posiciones variables en los componentes son consistentes con PCA en el conjunto completo de observaciones, y seguimos adelante para interpretar el gráfico.
¿Qué nos dice el mapa?
Primero, interpretamos los grupos de adjetivos y las relaciones, y vemos cuatro áreas con conjuntos bien diferenciados de adjetivos y marcas que se encuentran cerca.
Las marcas f y g son altas en valor, por ejemplo, mientras que a y j son relativamente altas en diversión, que es opuesta en dirección a los adjetivos de liderazgo (líder y serio).
Con este mapa, uno podría formular preguntas y luego consultar los datos subyacentes para responderlas.
Por ejemplo, suponga que usted es el gerente de la marca e. ¿Qué te dice el mapa? Por un lado, su marca está en el centro y, por lo tanto, parece no estar bien diferenciada en ninguna de las dimensiones. Eso podría ser bueno o malo, dependiendo de sus objetivos estratégicos.
Si su objetivo es ser una marca segura que atraiga a muchos consumidores, entonces podría ser deseable una posición relativamente indiferenciada como e. Por otro lado, si desea que su marca tenga una percepción fuerte y diferenciada, este hallazgo no sería deseado (pero es importante saberlo).
¿Qué debe hacer con respecto a la posición de su marca e?
Nuevamente, depende de los objetivos estratégicos. Si desea aumentar la diferenciación, una posibilidad sería tomar medidas para cambiar su marca en alguna dirección en el mapa. Supongamos que desea moverse en la dirección de la marca c. Puede observar las diferencias específicas de c en los datos:
## perform leader latest fun serious bargain value
## c 1.214314 0.9699315 -0.5587936 -1.140567 1.180621 -1.158594 -0.8588416
## trendy rebuy
## c -0.113052 -0.1689859Esto muestra que e es relativamente más fuerte que c en value y fun, lo que sugiere reducir los mensajes u otros atributos que los refuercen (suponiendo, por supuesto, que realmente desea avanzar en la dirección de c). Del mismo modo, c es más fuerte en perform y serious, por lo que podrían ser aspectos del producto o mensaje para que e se fortalezca.
Otra opción sería no seguir a otra marca, sino apuntar a un espacio diferenciado donde ninguna marca esté posicionada. En el biplot hay una gran brecha entre el grupo b y c en la parte inferior del gráfico, frente a f y g en la parte superior derecha. Esta área podría describirse como el área de value leader o similar.
¿Cómo descubrimos cómo posicionarnos allí? Supongamos que la brecha refleja aproximadamente el promedio de esas cuatro marcas. Podemos encontrar ese promedio en las filas de las marcas, y luego tomar la diferencia de e de ese promedio:
## perform leader latest fun serious bargain value
## e 1.174513 0.3910396 -0.9372789 -0.9337707 0.5732131 -0.2502787 0.07921355
## trendy rebuy
## e -0.4695304 0.6690661Esto sugiere que la marca e podría apuntar a la brecha al aumentar su énfasis en el rendimiento (performance) al tiempo que reduce el énfasis en latest y fun.
12.7.2 Precauciones
- Se debe elegir el nivel y el tipo de agregación cuidadosamente.
- Las relaciones son estrictamente relativas a la categoría del producto y las marcas y adjetivos que se prueban. En una categoría de producto diferente, o con diferentes marcas, los adjetivos como fun y lider podrían tener una relación muy diferente. A veces, simplemente agregar o soltar una marca puede cambiar el mapa resultante significativamente porque las posiciones son relativas. En otras palabras, si una nueva marca ingresa al mercado (o el análisis de uno), las otras posiciones pueden cambiar sustancialmente. También hay que confiar en que se han evaluado todas las percepciones clave (adjetivos, en este ejemplo).
Teoría obtenida de Peña, D. Análisis de datos multivariantes (2002). Referencias de
FactoMineRvienen de Husson, F. Exploratory multivariate analysis by example using R (2017)↩︎