Chapter 3 Tema
Existem inúmeras distribuições teóricas que podem ser usadas para modelar dados ecológicos. Neste tema pretende-se que apresentem exemplos de dados univariados discretos e as possíeis distribuições teóricas que poderiam ser usadas para os modelar.
3.1 Membros do grupo
Este grupo é composto pelos seguintes elementos:
- Catarina Nobre, 46792
- Danyal Habibo, 46487
- Gonçalo Mota, 52513
- Márcia Branquinho, 52638
- Margarida Paim, 52573
- Maria Zacarias, 50807
- Miguel Jorge, 50868
3.2 Introdução Teórica
O objectivo principal com o desenvolvimento deste trabalho será explorar as características destas famílias de distribuição de dados, aplicando exemplos práticos e analisando de forma sucinta um conjunto específico de dados estatísticos recolhidos para o efeito.
É possível separar os dados em qualitativos, quando se referem a classificações descritivas por categorias, ou quantitativos, que podem ser discretos (valor exato) ou contínuos (qualquer valor entre dois limites). Os dados quantitativos discretos são referentes a uma variável aleatória discreta que assume valores dentro de um conjunto de números especificados. É, portanto, a tipologia dos dados em estudo que determina a variável a considerar, definindo se esta será discreta ou contínua. No seguimento desta ideia, determina-se igualmente o tipo de tratamento a aplicar na exploração da nossa variável.
Na medição de dados discretos podem ser usados vários tipos de escalas: nominais, ordinais, intervaladas e de razão. No caso da escala nominal, por exemplo, as observações são agrupadas consoante critérios categóricos (ex: cor, espécie, sexo), formando conjuntos distintos.
No caso das variáveis aleatórias discretas, a respectiva função de distribuição de probabilidades denomina-se “função massa de probabilidade”. Esta associa cada valor (discreto) possível da variável à sua probabilidade de ocorrência, sendo que este valor de probabilidade será diferente de zero e a soma de todas as probabilidades deverá ser 1. A variável que está a ser medida só pode assumir valores inteiros pelo que não faz sentido usar casas decimais nestes tipo de dados.
A nível gráfico, este tipo de distribuição é construído representando os resultados possíveis (valores tomados pela variável aleatória discreta) no eixo do x, e as respectivas probabilidades de ocorrência no eixo do y.
Verificamos que uma distribuição de dados discretos descreve a probabilidade de ocorrência de acontecimentos únicos e distintos. Entre as várias famílias representativas desta distribuição de dados destacam-se as seguintes:
- Binomial
- Bernoulli
- Binomial negativa
- Poisson
- Hipergeométrica
3.3 Famílias Discretas:
3.3.1 1. Distribuição Bernoulli
A prova de Bernoulli é experiência aleatória em que o desfecho é do tipo sucesso ou insucesso e que pode ser repetida inúmeras vezes, sempre nas mesmas condições, isto é, mantendo-se constante a probabilidade de sucesso. Desta forma, sendo X a nossa variável aleatória, esta apenas poderá tomar 2 valores.
3.3.2 2. Distribuição Binomial
Na distribuição binomial estamos interessados no número de sucessos entre n observações. Desta forma, verificamos que a Binomial corresponde a um conjunto de n provas de Bernoulli da qual resulta uma sucessão de sucessos e insucessos, representados por 1 e 0 respectivamente.
Assim, os parâmetros da binomial são p, que corresponde à probabilidade de sucesso e n, que corresponde ao número de provas a repetir.
Para calcularmos a função binomial multiplicamos a probabilidade de sucesso de cada uma das tentativas, a probabilidade de insucesso das restantes tentativas e as combinações que nos oferecem o número de maneiras possiveis de obter k sucessos em n repetições uma vez que estes podem ocorrer a qualquer altura da experiência. Por fim, podemos verificar que, quanto maior a nossa probabilidade, maior o número de sucessos.
A binomial apresenta dois pressupostos fundamentais, a independência das experiências e o facto da probabilidade de sucesso ser constante para as diferentes provas.
Para aplicar a distribuição binomial no R podemos ter quatro diferentes tipos de funções.
3.3.2.1 2.1 Função dbinom
A função dbinom apresenta a probabilidade da função.
3.3.2.2 2.2 Função pbinom
A função pbinom apresenta a probabilidade da distribuição.
3.3.2.3 2.3 Função qbinom
A função qbinom fornece os quantis da distribuição binomial.
3.3.2.4 2.4 Função rbinom
A função rbinom permite simular a nossa distribuição através de valores aleatórios.
3.3.3 3. Distribuição Binomial Negativa
A distribuição Binomial Negativa consiste em considerar a variável aleatória que representa o número de provas de Bernoulli necessárias para obter k sucessos. Está, portanto, associada a fenómenos de sucesso/insucesso e tem como pressupostos a independência das provas e uma probabilidade de sucesso constante para estas.
No R, a distribuição Binomial Negativa encontra-se representada pelas funções:
3.3.3.1 3.1 Função dnbinom
A função dnbinom calcula a probabilidade de x insucessos antes de obtermos k sucessos.
3.3.3.2 3.2 Função pnbinom
A função pnbinom calcula a probabilidade cumulativa menor ou igual a x insucessos antes de k sucessos.
3.3.3.3 3.3 Função qnbinom
A função qnbinom devolve-nos os quantis.
3.3.3.4 3.4 Função rnbinom
A função rnbinom permite-nos simular a distribuição com valores aleatórios.
3.3.4 4. Distribuição Poisson
A distribuição de Poisson é uma distribuição de probabilidade de variáveis aleatórias discretas, que expressa a probabilidade de uma série de eventos ocorrer num certo período de tempo, se estes eventos ocorrerem independentemente uns dos outros.
A probabilidade de eventos que seguem uma distribuição de Poisson pode ser calculada através da seguinte função de probabilidade
P(X=k)=(e^-k*lambda^k)/x!
, onde λ é a média de ocorrências num determinado intervalo de tempo, área ou volume, ou então a taxa média de ocorrência por unidade de medida, e onde X é a variável aleatória que representa a contagem do número de eventos que ocorrem no intervalo definido.
Quando queremos aplicar esta distribuição no R, temos várias opções. Podemos utilizar as funções ppois, dpois e qpois.
3.3.4.1 4.1 Função dpois
Assim como em dbinom, a função dpois retorna a probabilidade associada a um valor de X.
3.3.4.2 4.2 Função ppois
A função ppois retorna o valor da probabilidade acumulada avaliada num valor de X qualquer.
3.3.4.3 4.3 Função qpois
Quando estamos interessados em descobrir os quantis da distribuição Poisson, utilizamos a função qpois.
3.3.4.4 4.4 Função rpois
A função rpois permite simular a nossa distribuição através de valores aleatórios.
3.3.5 5. Distribuição Hipergeométrica
A distribuição hipergeomérica contrasta com a distribuição binomial dado tratar-se de uma função estatística discreta que descreve a probabilidade de obter k sucessos em n extrações sem reposição, enquanto que na Binomial há reposição após cada extração.
Para poder ser aplicada é necessário que:
A propriedade/classe de interesse a ser estudada seja binária, isto é, poder apenas receber dois valores: 1 ou 0, verdadeiro ou falso (sucesso ou insucesso);
Se trate de uma amostra pequena (mesmo que a população seja grande);
As extrações não sejam substituídas, ou seja, que os elementos extraídos da amostra um por um não sejam novamente incorporados na população (sem reposição);
As probabilidades não sejam constantes, dado que, não havendo reposição, a população diminui à medida que são extraídos indivíduos. Consequentemente, a probabilidade de obter um sucesso varia após cada extração, não podendo por isso ser constante.
3.3.5.1 5.1 Função phyper
A função phyper dá-nos a probabilidade acumulada.
3.3.5.2 5.2 Função dhyper
A função dhyper dá-nos a probabilidade de termos um certo valor de X.
3.3.5.3 5.3 Função qhyper
Quando estamos interessados em descobrir os quantis da distribuição Hipergeométrica, utilizamos a função qhyper.
3.3.5.4 5.4 Função rhyper
A função rhyper permite simular a nossa distribuição através de valores aleatórios.
3.4 Exemplo em R
Escolhemos utilizar os dados do primeiro trabalho do nosso colega Gonçalo cuja pergunta ecológica era: “De que depende a velocidade de nado de um peixe de aquário?”. Muito sucintamente, para esta experiência o Gonçalo utilizou ciclídeos de três espécies diferentes, 32 machos e 38 fêmeas, perfazendo uma amostra de 70 indivíduos. Num aquário de dimensões consideráveis, ele mediu individualmente o tempo médio que cada um dos peixes demorou a percorrer um percurso de 80 cm, recorrendo a reforço positivo de comida no ponto de chegada a que os mesmo tinham de se dirigir. Após a recolha dos dados verificou posteriormente se as suas variáveis sexo, espécie e tamanho dos indivíduos eram explicativas para a questão levantada.
3.4.1 1. Distribuição Bernoulli
Como vimos anteriormente, aplicamos a distribuição Bernoulli quando pretendemos realizar uma única experiência com dois desfechos possíveis. Desta forma, podemos calcular a probabilidade de um peixe ser macho (sucesso) e fêmea (insucesso).
Qual a probabilidade de observarmos um macho?
## [1] 0.457Qual a probabilidade de observarmos uma fêmea?
## [1] 0.543#Distribuição da função
FX <- dbinom(1, 1, 0.457)
RX <- dbinom(0, 1, 0.457)
dados <- c(FX, RX)
barplot (dados, col="light blue", ylim = c(0,1), ylab="Probabilidade", xlab="Sexo do Peixe", names.arg=c("Macho","Fêmea"), main="Aplicação da distribuição de Bernoulli no sexo dos peixes")
Podemos observar que a probabilidade de ser macho é inferior à probabilidade de ser fêmea pelo que concluimos que há menos machos na população do que fêmeas.
3.4.2 2. Distribuição Binomial
3.4.2.1 Função dbinom
Qual a probabilidade de em 70 peixes observarmos 40 machos?
## [1] 0.015266623.4.2.2 Função choose
## [1] 5.534774e+19## [1] 0.01526662Como vimos anteriormente, a função choose oferece-nos as combinações possiveis dos 40 machos na população dos 70 peixes. Se multiplicarmos o número de combinações obtidas com a função choose pela probabilidade de ser macho (sucesso) de cada um dos peixes e a probabilidade de ser fêmea (insucesso) dos restantes, obtemos a mesma probabilidade calculada pela função dbinom.
yes <- 0:70
gx <- dbinom(yes,70,0.457)
plot(yes, gx, pch=19, ylab="Probabilidade P(X=x)", xlab="Nº Observações - Provas de Bernoulli", main="Gráfico da função probabilidade")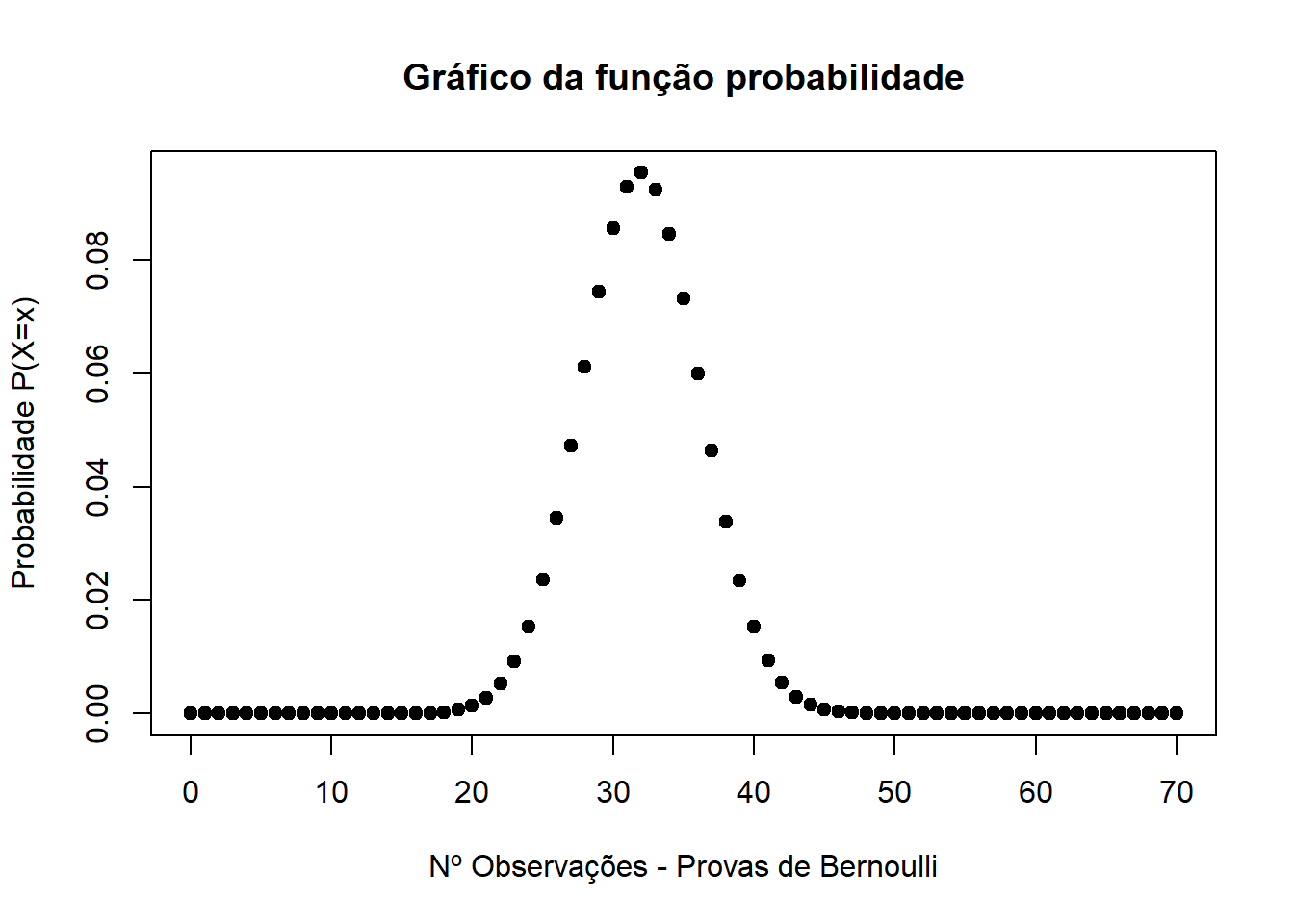
Como podemos observar no gráfico, números muito altos ou muito baixos de sucessos são resultados improváveis.
Qual a probabilidade de, em 70 ensaios, ter no máximo 20 machos?
## [1] 0.002521982Qual a probabilidade de, em 70 ensaios, ter mais de 20 machos?
## [1] 0.997478Isto acontece porque se lower.tail for interpretado como TRUE, calcula as probabilidades dos valores acumulados à esquerda P ( X ≤ 20) e se for interpretado como FALSE, retorna as probabilidades dos valores acumulados à direita P( X > 20).
Se calcularmos as probabilidades separadas utilizando o dbinom e as somarmos, devemos encontrar o mesmo resultado obtido com o pbinom.
hgx <- pbinom(yes,70,0.457)
plot(yes, hgx, pch=19, ylab="Probabilidade P(X<=x)", xlab="Nº Observações - Provas de Bernoulli ", main="Gráfico da função distribuição")
abline (v=20, col="Blue")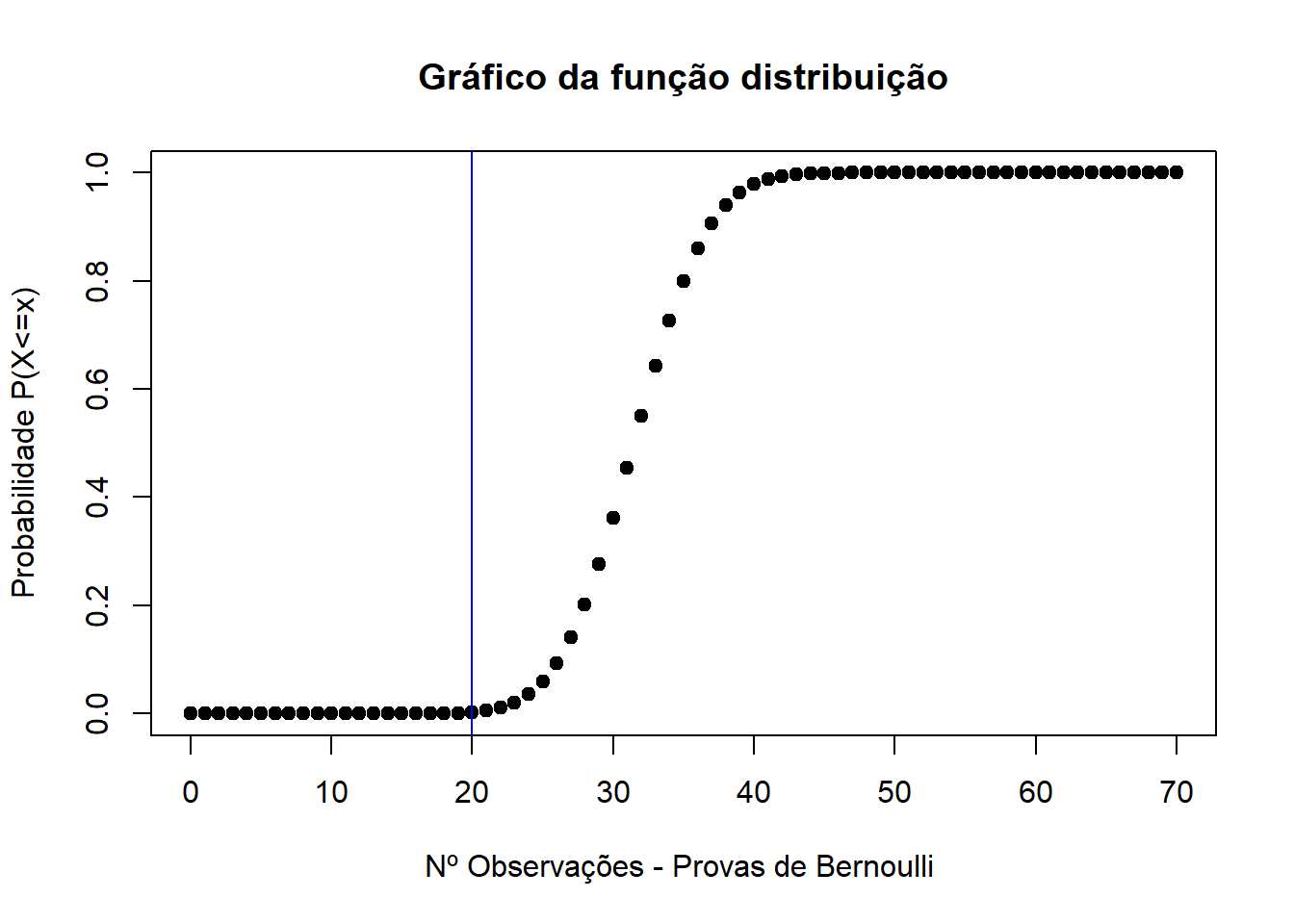
Pegando agora no exemplo anterior, verificamos que a probabilidade de obter machos em 20 peixes é menor do que a probabilidade de obter machos nos restantes 50. Estes valores fazem sentido porque, em média, a nossa variável aleatória tem valor médio 70*0.457=31.99 que é bem superior a 20.
3.4.3 3. Distribuição Binomial Negativa
3.4.3.1 Função dnbinom
Sabendo que a nossa amostra de peixes é 70, e a probabilidade de ser fêmea é de 0,543, qual a probabilidade de encontrarmos a 2ª fêmea no 8º peixe observado, fazemos:
## [1] 0.005048609#x - número de provas de Bernoulli feitas
#n - número de sucesso
#p - probabilidade de ser femêa (sucesso)Para representarmos graficamente:
dados<-2:30 #Pois obter 2 fêmeas após 1 observação não seria lógico!
bnexemplo1<-dnbinom(dados, 2, 0.543)
bnexemplo1## [1] 1.847368e-01 1.125663e-01 6.430348e-02 3.526403e-02 1.880160e-02
## [6] 9.819809e-03 5.048609e-03 2.563572e-03 1.288707e-03 6.424793e-04
## [11] 3.180808e-04 1.565447e-04 7.665098e-05 3.736480e-05 1.814294e-05
## [16] 8.779051e-06 4.234917e-06 2.037218e-06 9.775589e-07 4.680180e-07
## [21] 2.236062e-07 1.066310e-07 5.076080e-08 2.412559e-08 1.144945e-08
## [26] 5.426191e-09 2.568333e-09 1.214201e-09 5.733864e-10plot(bnexemplo1,ylab="Probabilidade",xlab="Nº Observações - Provas de Bernoulli ",main="Probabilidade de encontrar a 2ª fêmea ao xº ensaio",col="blue", pch=16)
abline(v=8,lty=2,col="blue")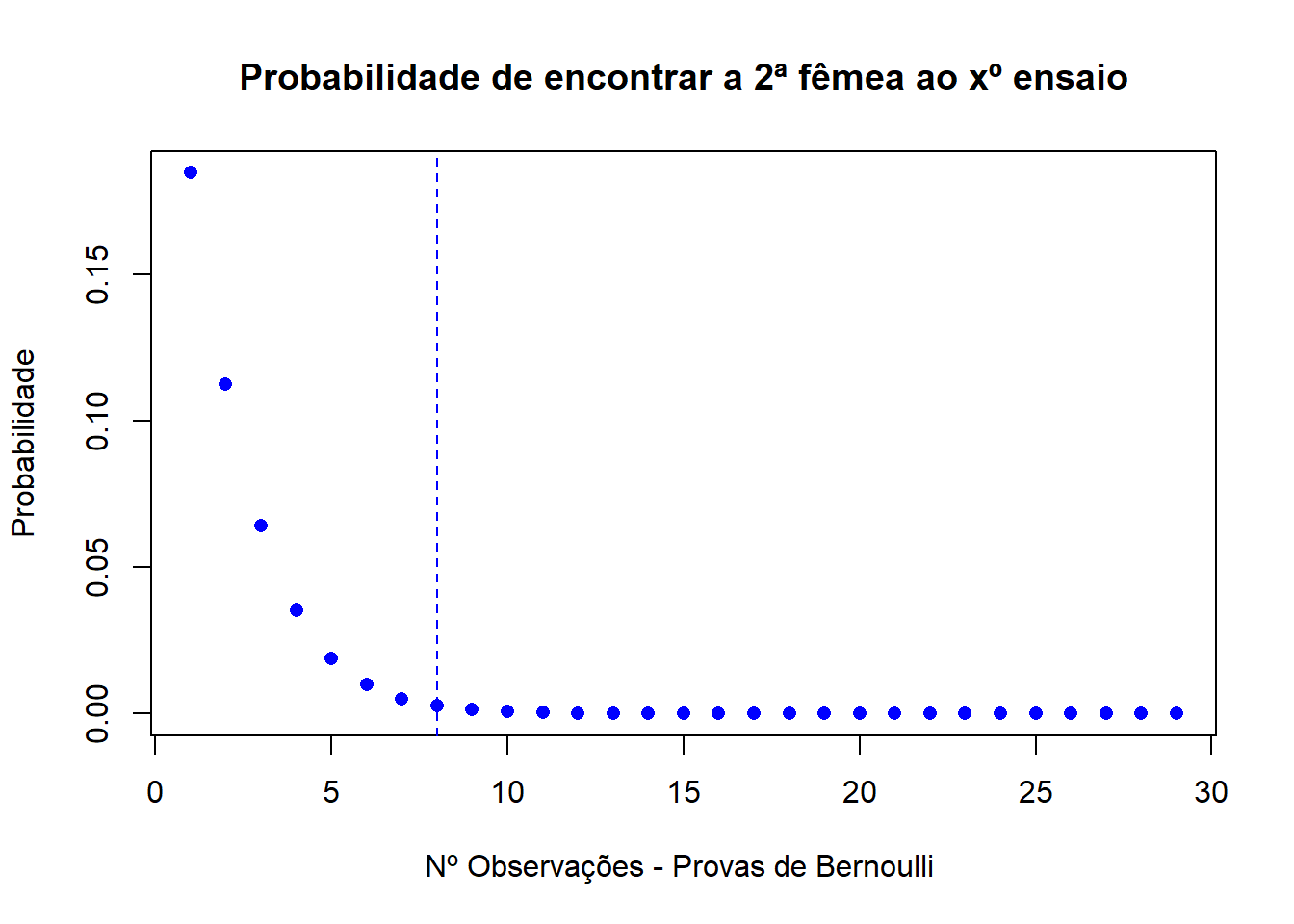
Como podemos observar, a probabilidade de encontrarmos a 2ª fêmea ao x ensaio vai diminuindo conforme x (o número de provas de Bernoulli efetuadas) aumenta, devido ao facto de a probabilidade de o invidíduo ser fêmea ser de 0.543.
3.4.3.2 Função pnbinom
No mesmo contexto ecológico, queremos saber a probabilidade de observarmos, no máximo, 6 peixes até encontrarmos a 2ª fêmea. Para calcular, fazemos:
## [1] 0.9800131Para representarmos graficamente:
## [1] 0.7490777 0.8616440 0.9259475 0.9612115 0.9800131 0.9898329 0.9948815
## [8] 0.9974451 0.9987338 0.9993763 0.9996944 0.9998509 0.9999276 0.9999649
## [15] 0.9999831 0.9999919 0.9999961 0.9999981 0.9999991 0.9999996 0.9999998
## [22] 0.9999999 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000
## [29] 1.0000000plot(bnexemplo2,ylab="Probabilidade",xlab="Número de observações - Provas de Bernoulli",main="Probabilidade de encontrar a 2ª fêmea, no máximo, ao xº ensaio",col="blue", pch=16)
abline(v=6,lty=2,col="red")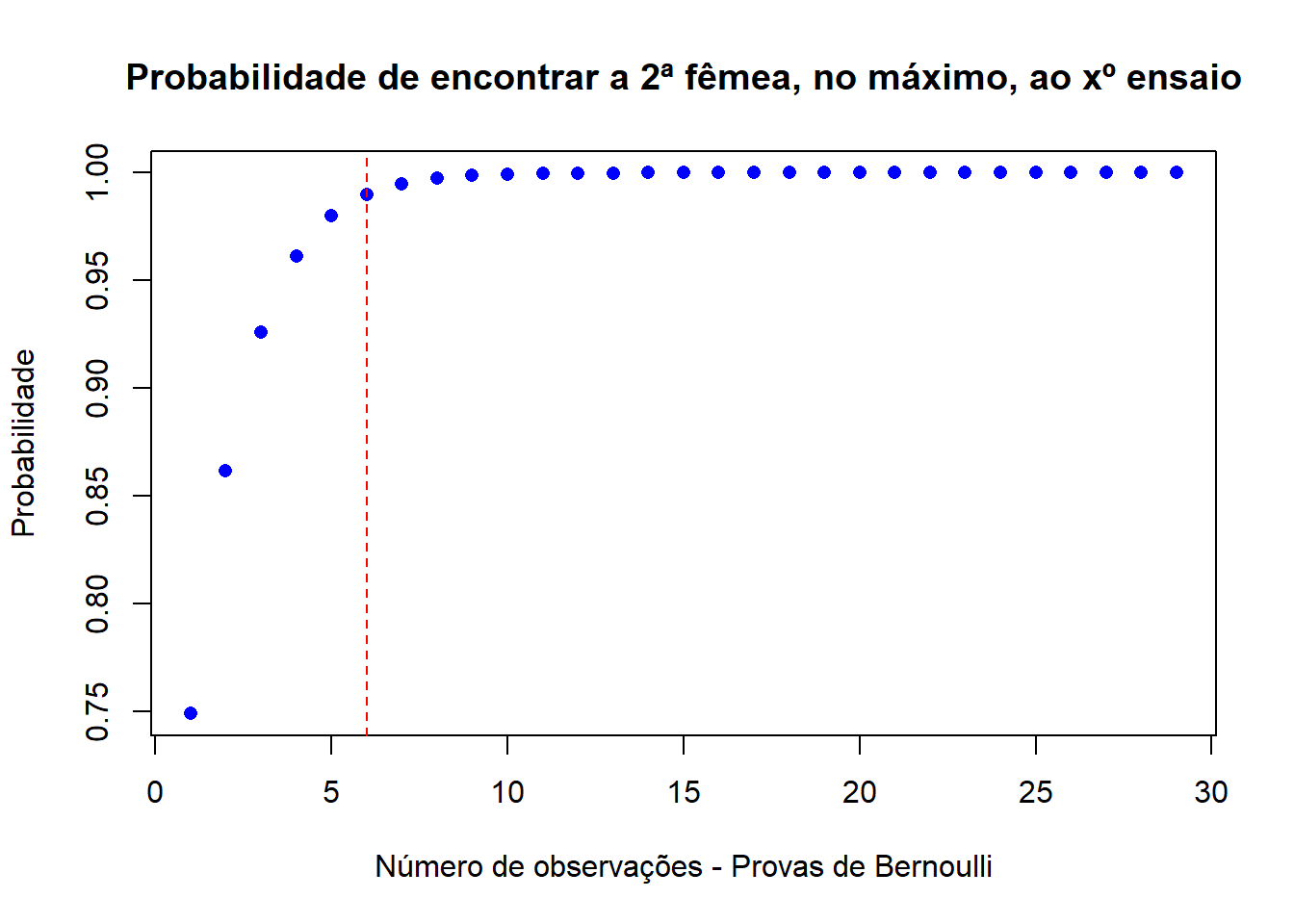
Aqui, podemos observar que a probabilidade de a 2ª fêmea ser encontrada no máximo ao xº ensaio vai aumentando conforme o número de ensaios que sejam feitos, devido ao facto de estar a ser calculada a probabilidade cumulativa.
3.4.4 4. Distribuição Poisson
Um peixe da espécie Labidochromis caerueleus demora, em média, 2.67 segundos a atravessar o aquário (uma piscina). Se ele estiver sempre a nadar de uma ponta do aquário para a outra, num minuto ele fará um número médio de 22 piscinas (λ=22).
3.4.4.1 Função ppois
Qual a probabilidade de um peixe fazer 24 piscinas ou menos?
## [1] 0.7117195Se quisermos uma representação gráfica da função massa de probabilidade fazemos o seguinte:
k <- 0:30
plot(k, ppois(k, lambda=22),
type='h',
main='Distribuição Poisson (lambda = 22)',
ylab='Probabilidade',
xlab ='k (número de piscinas)',
lwd=3)
abline(v=24, col="Dark orange")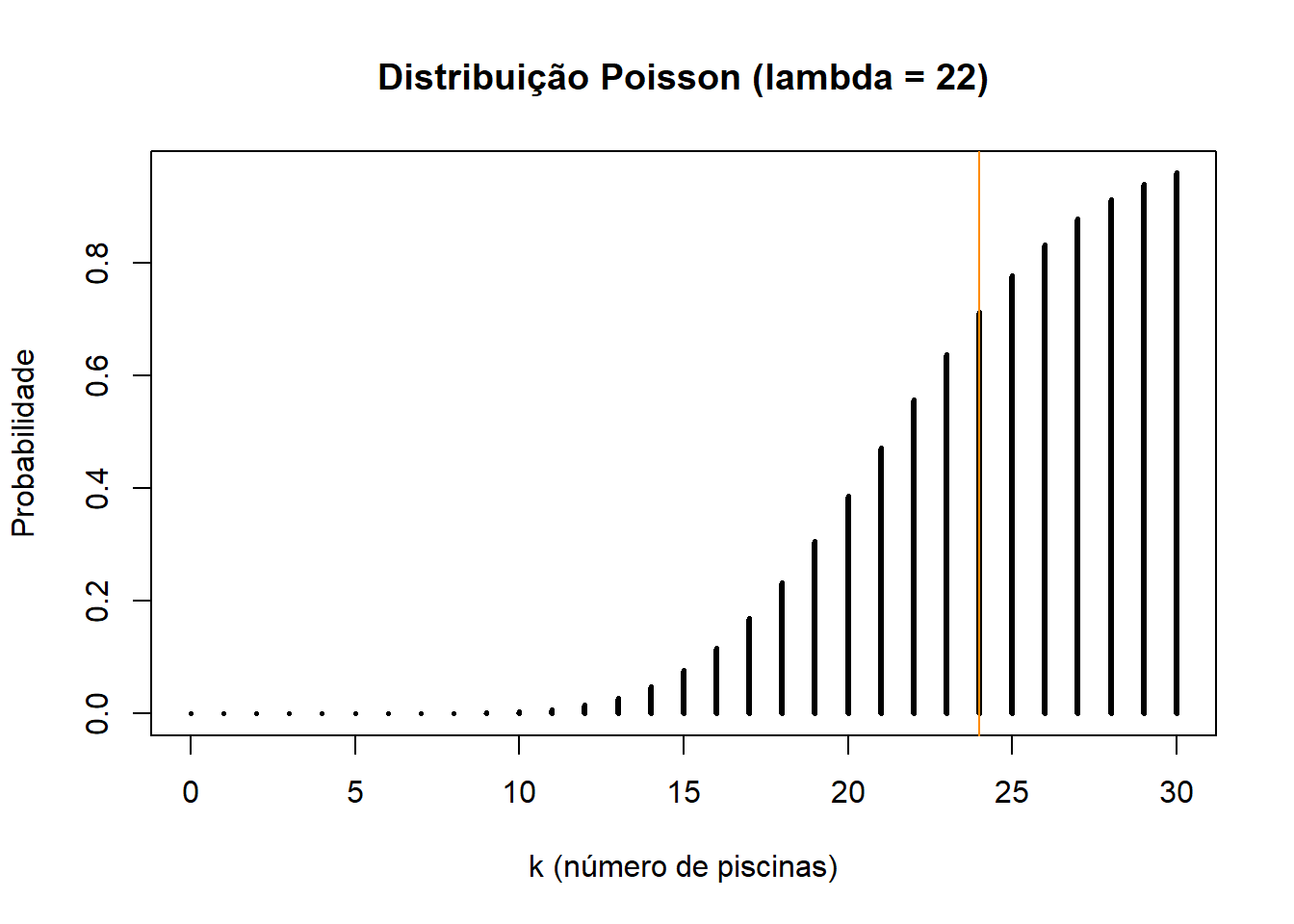
No gráfico, podemos observar a probabilidade cumulativa do peixe fazer no máximo 24 piscinas.
Qual a probabilidade de um peixe fazer 24 piscinas ou mais?
## [1] 0.28828053.4.4.2 Função dpois
Qual a probabilidade de o peixe fazer 5 piscinas?
## [1] 1.197991e-05E de fazer 24 piscinas?
## [1] 0.07429508Se quisermos ver os resultados de forma gráfica, fazemos da seguinte forma:
k <- 0:30
plot(k, dpois(k, lambda=22),
type='h',
main='Distribuição Poisson (lambda = 22)',
ylab='Probabilidade',
xlab ='k (número de piscinas)',
lwd=3)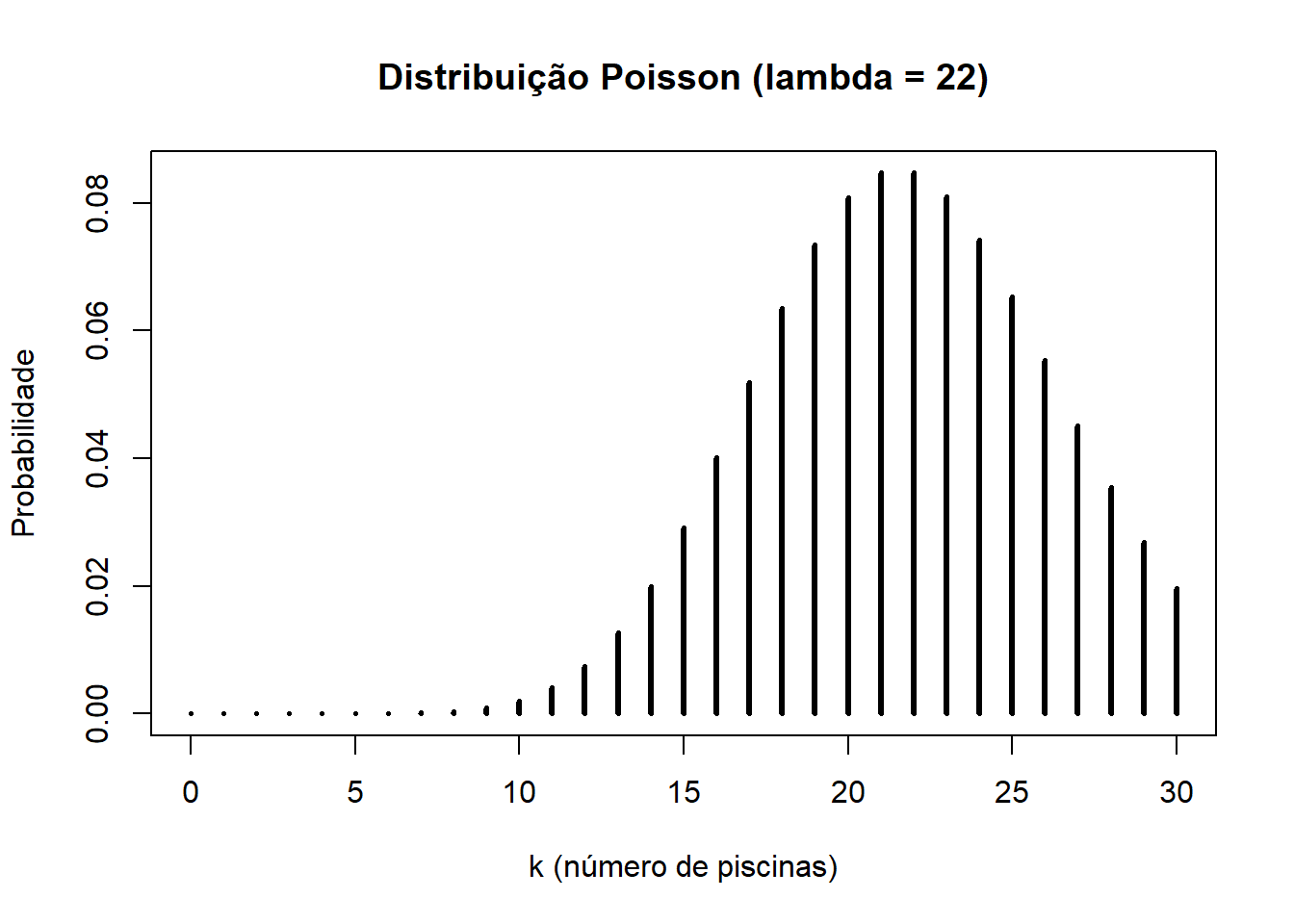
Neste gráfico podemos observar as respetivas probabilidades para os possíveis números de piscinas percorridas pelos peixes.
3.4.4.3 Função qpois
Qual o número de piscinas que um peixe faz, em 8% dos casos (quantil de 0.08 da Poisson)?
## [1] 163.4.5 5. Distribuição hipergeométrica
Como dito mais em cima, a distribuição hipergeométrica é muitas vezes utilizada para detetar a probabilidade de encontrar elementos defeituosos ou não conformantes com a classe de interesse. No caso dos dados que estamos a analisar, o ser macho ou fêmea não é considerado um defeito. Ainda assim, podemos aplicar o modelo por tratar-se de uma variável binária.
Esta função tem como argumentos (x,m,n,k), onde:
- x é o número de machos extraídos (5)
- m é o número total de indivíduos machos (32)
- n é o número total de indivíduos fêmeas (38)
- k é o número de indivíduos extraídos (10)
3.4.5.1 Função dhyper
Qual a probabilidade de extraindo 10 individuos, 5 deles serem machos?
## [1] 0.25479693.4.5.2 Função phyper
Qual a probabilidade de extraindo 10 indivíduos, pelos menos 5 serem machos?
## [1] 0.73832Qual a probabilidade de extraindo 10 indivíduos, mais de 5 serem machos?
## [1] 0.261683.5 Exemplos reais de aplicação
The impact of grain quantity on the biology of Sitophilus zeamais Motschulsky (Coleoptera: Curculionidae): oviposition, distribution of eggs, adult emergence, body weight and sex ratio Gorgulho-do-milho
O Gogulho-do-milho é uma das maiores pragas da planta do milho nas regiões tropicais e sub-tropicais. Neste estudo é analisada a relação entre a quantidade de grãos disponíveis e a postura de ovos, peso dos indivíduos adultos e rácio entre sexos. A análise estatística dos dados, nomeadamente a nível da agregação dos ovos, foi feita com recurso a uma distribuição poisson e binomial negativa. Isto permitiu verificar que há uma tendência para um aumento da postura de ovos de acordo com o aumento da disponibilidade dos grãos de milho e que há um decréscimo na frequência de grãos infestados com o aumento do número de ovos. Em suma, a maneira como as fêmeas põem os ovos de forma mais ou menos espaçada influencia o fitness da espécie sendo mais vantajoso aglomerar os ovos, apesar de haver uma maior competição, uma vez que distribuí-los aleatoriamente poderia levar a eventuais perdas de qualidade e quantidade.
Determination of manatee population trends along the atlantic coast of Florida using a bayesian approach with temperature-adjusted aerial survey data
Este estudo usa um modelo estocástico para estimar a população de manatins da Flórida ao longo da costa atlântica do estado. Para isto, foi feita uma contagem aérea dos indivíduos observados na população sendo que estas observações seguem uma distribuição binomial onde a região e a temperatura do ar afetam a probabilidade média de observar um indivíduo. De forma geral, verificou-se um aumento populacional na década de 80 seguido de um período de estabilização nos anos 90, após o qual houve um crescimento populacional contínuo de 3%-4% por ano. Os resultados sugerem que a análise de contagens de amostragens aéreas de longa duração permite estimar o tamanho da população e fazer estimativas com elevado grau de certeza relativamente ao crescimento populacional num futuro próximo.
3.6 Recursos adicionais
RPubs: https://rpubs.com/EstatBasica/Cap6
Common Probability Distribuction: https://medium.com/@srowen/common-probability-distributions-347e6b945ce4
3.7 Considerações finais
O nosso grupo tentou abordar todos os exemplos de famílias de distribuição que o professor mencionou na aula porém, decidimos não colocar informações sobre a Distribuição Multinomial porque a função não está vetorizada atualmente no RStudio.
3.8 Referências
ANTUNES, Marília. Bioestatística: Notas de aula: Variáveis aleatórias. 1. ed. Departamento de Estatística e Investigação Operacional, FCUL: [s.n.], 2019. p. 68-95.
BOOKDOWN. Capítulo 5 Distribuicoes de Probabilidade. Disponível em: https://bookdown.org/matheusogonzaga/apostila_r2/distribuicoes-de-probabilidade.html. Acesso em: 15 nov. 2020.
CRAN R PROJECT. Tópicos de Estatística utilizando R. Disponível em: https://cran.r-project.org/doc/contrib/Itano-descriptive-stats.pdf. Acesso em: 18 nov. 2020.
DANHO, M.; GASPAR, C.; HAUBRUGE, E.. The impact of grain quantity on the biology of Sitophilus zeamais Motschulsky (Coleoptera: Curculionidae): oviposition, distribution of eggs, adult emergence, body weight and sex ratio. Journal of Stored Products Research, Journal of Stored Products Research, v. 38, n. 3, p. 191-318, jul./2002.
CRAIG, Bruce A.; REYNOLD, John E.. Determination of manatee population trends along the atlantic coast of Florida using a bayesion approach with temperature-adjusted aerial survey data. MARINE MAMMAL SCIENCE, Society for Marine Mammalogy , v. 20, n. 3, p. 386-400, jul./2004.
MEDIUM. Common Probability Distributions: The Data Scientist’s Crib Sheet. Disponível em: https://medium.com/@srowen/common-probability-distributions-347e6b945ce4. Acesso em: 16 nov. 2020.
R PUBS. Estatística Básica - Bussab e Morettin (2017). Disponível em: https://rpubs.com/EstatBasica/Cap6. Acesso em: 15 nov. 2020.
SUPORTE AO MINITAB. Distribuição discreta. Disponível em: https://support.minitab.com/pt-br/minitab/18/help-and-how-to/probability-distributions-and-random-data/supporting-topics/distributions/discrete-distribution/. Acesso em: 17 nov. 2020.
SURVEYMONKEY. Diferença entre pesquisa quantitativa e qualitativa. Disponível em: https://pt.surveymonkey.com/mp/quantitative-vs-qualitative-research/. Acesso em: 15 nov. 2020.
WEBTECNICO. Família de distribuições. Disponível em: https://web.tecnico.ulisboa.pt/paulo.soares/pe/capitulo3.html#23.0. Acesso em: 17 nov. 2020.