Chapter 6 Tema
Existem inúmeros indicadores de localização e de dispersão da distribuição dos dados ecológicos que podem ser utilizados para a caracterizaação dos mesmos. Neste tema pretende-se que apresentem exemplos de indicadores de localização e de dispersão da distribuição de dados ecológicos.
6.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- Ana Catarina Garnecho Nº48009
- Catarina Fernandes Nº51977
- Dúnia Gregório Nº51194
- Jéssica RodriguesNº51196
- Marta Correia Nº40060
- Rita Ferrão Nº49599
- Sofia Dias Nº50840
6.2 Introdução Teórica
Neste capítulo fala-se sobre medidas estatísticas. O seu objetivo é apresentar um sumário de características significativas dos dados, que nos irão ajudar a fazer inferências acerca destes. Serão abordados dois tipos de caracterização estatística de dados amostrais: medidas de localização e medidas de dispersão.
Regra geral, numa análise exploratória de dados usa-se no mínimo uma medida de localização e uma de dispersão, normalmente, a média e a variância.
Medidas de Localização:
Indicam a localização dos valores observados na reta real. Fazem um resumo da amostra indicando o seu centro da distribuição e pontos importantes desta. Dividem-se em medidas de tendência central e tendência não-central.
Medidas de Tendência Central:
- Moda
A moda de uma amostra é o valor com maior frequência, ou seja, o valor mais observado. Caso existam poucas observações, onde frequentemente não há valores repetidos, não é possível obter uma moda, sendo esse conjunto de dados amodal. Contudo um conjunto de dados pode ter mais que uma moda e por isso ser multimodal. Quando se trata dados agrupados, o valor da moda é bastante afetado pela forma como as classes são construídas, pelo que o valor obtido poderá não ser a verdadeira moda. Esta medida não é afetada pelos valores extremos da amostra, desde que esses não correspondam ao próprio valor da moda.
- Mediana
A mediana localiza o valor central da amostra. É usada em dados discretos ou contínuos. Indepedentemente da ordenação crescente ou decrescente da amostra, a mediana encontra sempre o(s) valor(es) centrais, dado que é uma medida que não é influenciada pelos extremos. No caso de a amostra ser par, a mediana é obtida através da média da soma dos dois números centrais.
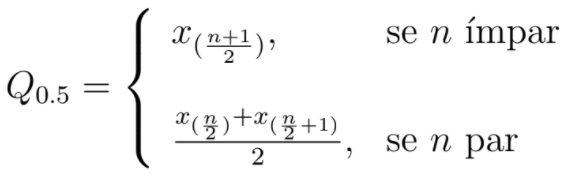
- Média
A média (mais formalmente, a média aritmética) é o resultado da soma do conjunto de dados divido pelo número total de observações. O valor obtido da média é inlfuenciado pelos extremos amostrais, bem como pela dimensão da amostra.

Medida de Tendência Não Central:
- Quantil (Qp)
Os quantis dividem uma amostra num determinado número de intervalos com a mesma dimensão, ou seja, o mesmo número de elementos. Por exemplo, os quartis são quantis que dividem a amostra em quatro partes, os decis dividem em dez partes e os percentis dividem em cem partes. A quantidade de intervalos estabelecidos depende do que se pretende com a utilização desta medida.
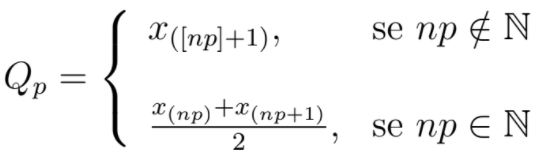
Medidas de dispersão:
Dão informação sobre a variabilidade dos dados, ou seja, como esses valores se distribuem sobre a reta real.
- Variância
A variância é igual à soma dos quadrados dos desvios das observações em relação à média (aritmética), dividida por (n-1), sendo n o número total da amostra. É, portanto, uma medida de dispersão relativamente à média observada, sendo considerada uma “média” dos desvios das observações em relação a esta. Consiste no somatório do quadrado das diferenças entre os valores da variável e da média, a dividir por n. É usada para obter o desvio-padrão.

- Desvio padrão
O desvio-padrão é o valor que, em média, cada observação da amostra se desvia da média (aritmética). Corresponde à raíz quadrada da variância.
- Amplitude total
A amplitude total é a diferença entre o valor máximo e o valor mínimo observados na amostra.
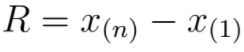
- Amplitude inter-quartil
A amplitude inter-quartil corresponde à amplitude do intervalo onde se encontram 50% das observações, ou seja, é a amplitude do intervalo limitado pelo Quartil Inferior (Q0.25) e Superior (Q0.75). Quanto maior a amplitude inter-quartil maior a dispersão da amostra.
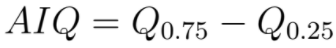
- Coeficiente de variação
O coeficientede de variação (ou coeficiente de dispersão) é o quociente entre o desvio-padrão e a média aritmética, apresentado em percentagem. Indica a grandeza da dispersão, um valor maior corresponde a uma distribuição mais dispersa. O coeficiente de variação é uma forma de comparação entre a dispersão de amostras, sendo por vezes usado para avaliar a qualidade da média como medida caracterizadora de uma distribuição.

6.3 Exemplo em R
A pergunta ecológica deste trabalho é se a diversidade de diferentes espécies de musgo e líquenes num tronco de árvore é influenciada por algum fator. Neste caso foram recolhidos dados sobre o número de espécies de líquenes e musgo presente em cada tronco (nsp), a espécie de cada árvore (spar), o seu perímetro à altura do peito (pap), entre outros dados.
Para a análise exploratória dos dados começa-se pela importação dos dados e aplicação da função ‘summary’.
## ID nsp spar pap
## Min. : 1.00 Min. :0.000 Length:190 Min. : 6.00
## 1st Qu.: 48.25 1st Qu.:3.000 Class :character 1st Qu.: 20.00
## Median : 95.50 Median :4.000 Mode :character Median : 43.00
## Mean : 95.50 Mean :4.037 Mean : 62.09
## 3rd Qu.:142.75 3rd Qu.:6.000 3rd Qu.: 84.75
## Max. :190.00 Max. :8.000 Max. :374.00
## dens hum reg local
## Length:190 Length:190 Length:190 Min. :1.0
## Class :character Class :character Class :character 1st Qu.:2.0
## Mode :character Mode :character Mode :character Median :3.0
## Mean :3.4
## 3rd Qu.:5.0
## Max. :6.0Algumas das informações que podem ser retiradas do sumário são: número de variáveis, os seus nomes e as suas classes, o número de observações, e, para variáveis numéricas, os dados relativos às médias, medianas, quartis, máximos e mínimos.
Pode-se, portanto, observar que a função ‘summary’ apresenta algumas medidas de localização. Há no entanto funções específicas para cada uma delas. Apresentam-se abaixo os códigos do R correspondentes, incluindo as que não constam no sumário:
- Moda:
#package para executar a função que calcula a Moda
library(modeest)
moda.sp<-mfv(moss$nsp)
moda.pap<-mfv(moss$pap)
moda.sp## [1] 3## [1] 13Conclui-se que na maioria das observações foram contadas 3 espécies, e que a medida mais frequente do perímetro à altura do peito foi 13cm.
- Mediana:
## [1] 4## [1] 43Constata-se que o valor mais central na contagem do número de espécies foi 4, e no perímetro à altura do peito foi 43cm.
- Média:
## [1] 4.04## [1] 62.09A média de espécies observadas por ramo foi aproximadamente 4 e o comprimento médio do perímetro à altura do peito foi 62cm.
- Quantil:
A função ‘quantile’ apresenta, por definição, os valores da amostra correspondentes às seguintes probabilidades: 0, 0.25, 0.5, 0.75, 1.
## 0% 25% 50% 75% 100%
## 0 3 4 6 8## 0% 25% 50% 75% 100%
## 6.00 20.00 43.00 84.75 374.00No entanto, é possível determinar as probabilidades que se pretende obter. Apresenta-se abaixo para a probabilidade 0.60:
## 60%
## 5## 60%
## 55O primeiro quarto de valores do número de espécies encontra-se entre 0 e 3, o segundo quarto entre 3 e 4, mas nos restantes dois quantis os valores avançam de dois em dois, ou seja, o terceiro quarto é entre 4 e 6 e o último é entre 6 e 8.
Para o perímetro à altura do peito também se pode observar que o primeiro quarto de valores varia entre 6 e 20cm, o segundo entre 20 e 43cm, o terceiro entre 43 e 85cm, e o último entre 85 e 374cm. Aqui também se pode concluir que mais de metade dos perímetros à altura do peito medidos tinham valores abaixo dos 50cm.
- Variância:
## [1] 3.86## [1] 3682.17Verifica-se que a variância do número de espécies é aproximademente 4 e que a variância do perímetro à altura do peito é aproximadamente 3682, o que indica que os perímetros medidos variam muito entre si. Pode-se concluir que a variância do número de espécies de musgos e líquenes é menor, ou seja, os valores desta variável estão mais próximos da média. Em relação ao perímetro à altura do peito, a variância é maior, logo os valores desta variável estão mais distantes da média.
- Desvio Padrão:
## [1] 1.96## [1] 60.68Com estes resultados, conclui-se que o desvio padrão do número de espécies é de quase 2 espécies, e que o do perímetro à altura do peito é de aproximadamente 61cm.
- Amplitude Total:
## [1] 8## [1] 368Relativamente à amplitude total, para o número de espécies é 8, o que indica pouca variabilidade destes dados, e para o perímetro à altura do peito é 368, o que indica uma maior variabilidade destes dados - o que está de acordo com os valores obtidos para a variância.
- Amplitude Inter-Quantil:
Várias maneiras de se calcular:
## [1] 3## [1] 64.75## 75%
## 3## 75%
## 64.75A amplitude inter-quartil para o número de espécies é 3 e para o perímetro à altura do peito é de aproximadamente 65. Assim sendo, também para esta medida se confirma uma dispersão pequena para o número de espécies e uma dispersão maior para as medidas do perímetro à altura do peito.
- Coeficiente de Variação:
cv.sp<-round(sd(moss$nsp)/mean(moss$nsp)*100,2)
cv.pap<-round(sd(moss$pap)/mean(moss$pap)*100,2)
cv.sp## [1] 48.64## [1] 97.72A coeficiente de variação do número de espécies é 48.64% e do perímetro à altura do peito é 97.72%. Pode-se assim concluir que a distribuição dos perímetros à altura do peito é bastante mais dispersa do que a distribuição do número de espécies de musgos e líquenes observados.
Representações gráficas:
- Boxplots:
Algumas medidas de localização, com exceção da média, podem ser graficamente representadas através de boxplots. Este tipo de representação gráfica é ainda útil para comparar estas medidas entre diferentes distribuições.
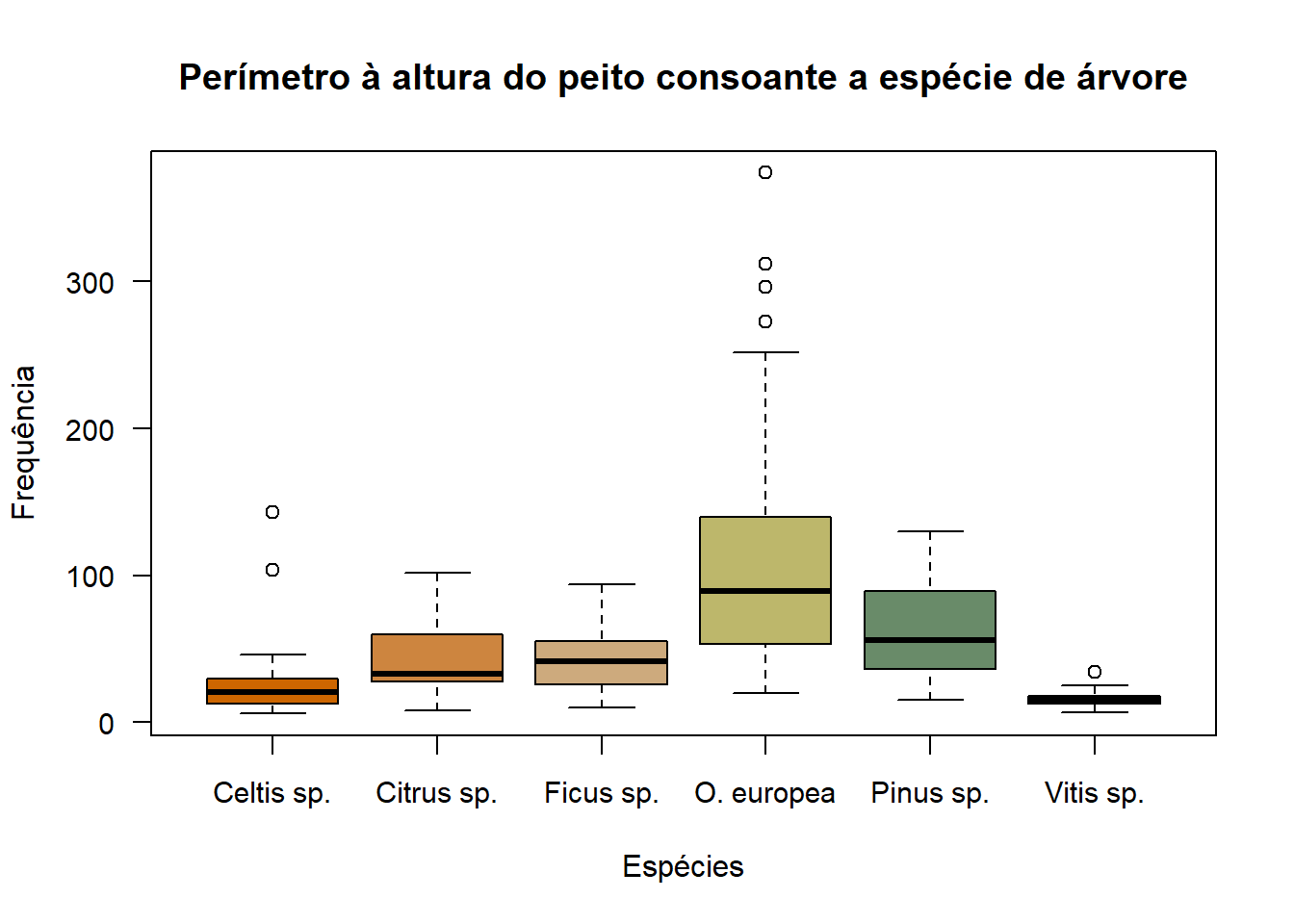
Na comparação dos boxplots representantes das medições feitas para o perímetro à altura do peito é possível observar que a Olea europea e o Pinus sp. são as espécies de árvore que, não só apresentaram maiores dimensões do perímetro, como também uma maior variedade nas medições. A espécie de árvore com menor dimensão e menor variedade é a Vitis sp..
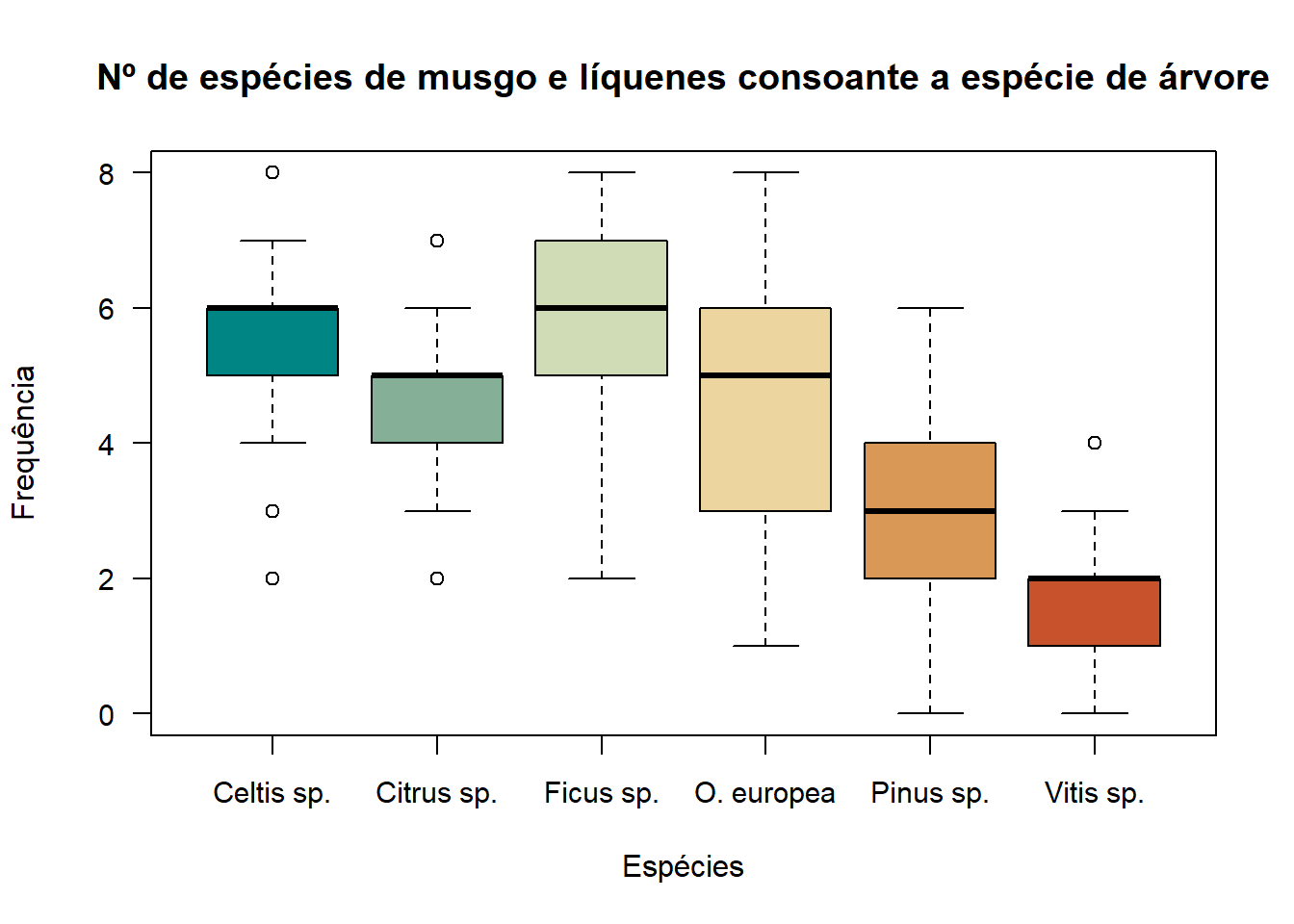
Já na comparação para o número de espécies de líquenes e musgo consoante a espécies de árvore, as espécies de árvore onde se identificaram mais espécies foram a Celtis sp. e a Ficus sp., e menos a Vitis sp.. No entanto, a Olea europea também mostra muita variedade no número de espécies observado no seu tronco.
- Histogramas:
Através do histograma podemos obter informação relativa à moda, média e mediana.
hist(moss$nsp,main="Espécies de Musgo e Líquenes por tronco", xlab="Número de Espécies",ylab = "Frequência", border="burlywood", col="wheat1",las=1)
abline(v=mean(moss$nsp),lty=2,lwd=3, col="darkorange3")
abline(v=median(moss$nsp),lty=2,lwd=3, col="darkslategrey")
abline(v=mfv(moss$nsp),lty=2,lwd=3, col="palevioletred4")
legend("topright",legend=c("Moda","Mediana","Média"),col=c("palevioletred4","darkslategrey","darkorange3"),lty=2,lwd=3)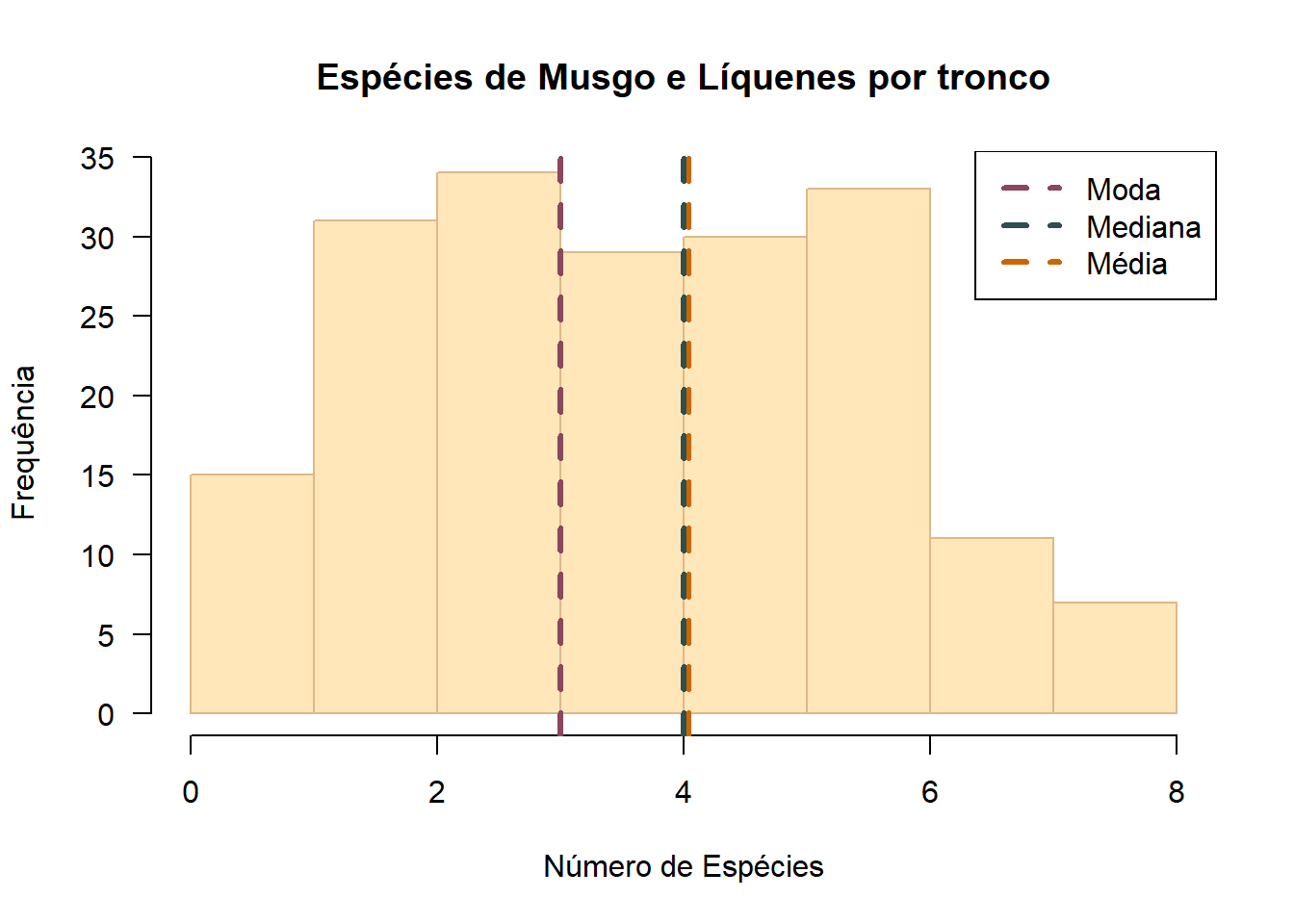
Neste gráfico, é possível observar que 3 foi o número de espécies de musgo e líquenes mais vezes identificado. Em relação à média e à mediana, estas encontram-se muito próximas, com um valor próximo de 4. Na análise da média, é importante relembrar que esta medida de tendência central é influenciada pelos valores extremos na amostra, já a mediana não é. O facto a média e a mediana terem valores próximos significa que a média é uma boa caracterizadora desta distribuição.
m <- mean(moss$nsp)
std <- sqrt(var(moss$nsp))
hist(moss$nsp, prob=TRUE, main="Espécies de Musgo e Líquenes por tronco", xlab="Número de Espécies",ylab = "Frequência", col="papayawhip", border = "wheat",las=1, ylim=c(0,0.20), xlim=c(-3, 11))
curve(dnorm(x, mean=m, sd=std), col="tomato3", lwd=1.5, add=TRUE, yaxt="n")
abline(v=(m-std), lty=3,lwd=1.75, col="chocolate4")
abline(v=(m+std), lty=3,lwd=1.75, col="chocolate4")
abline(v= m, lty=1,lwd=1.5, col="lightsalmon1")
arrows(x0=(m-std), y0=0.16, x1=(m+std), y1=0.16, code=3, length=0.15, col='turquoise4')
text(x=m, y=0.18, font = 4, labels='68%', col='turquoise4')
legend("topright",legend=c("Curva de distribuição","Desvio-padrão","Média"),col=c("tomato3","chocolate4","lightsalmon1"),lty=c(1,2,1),lwd=3,bty="n", inset = -0.0145)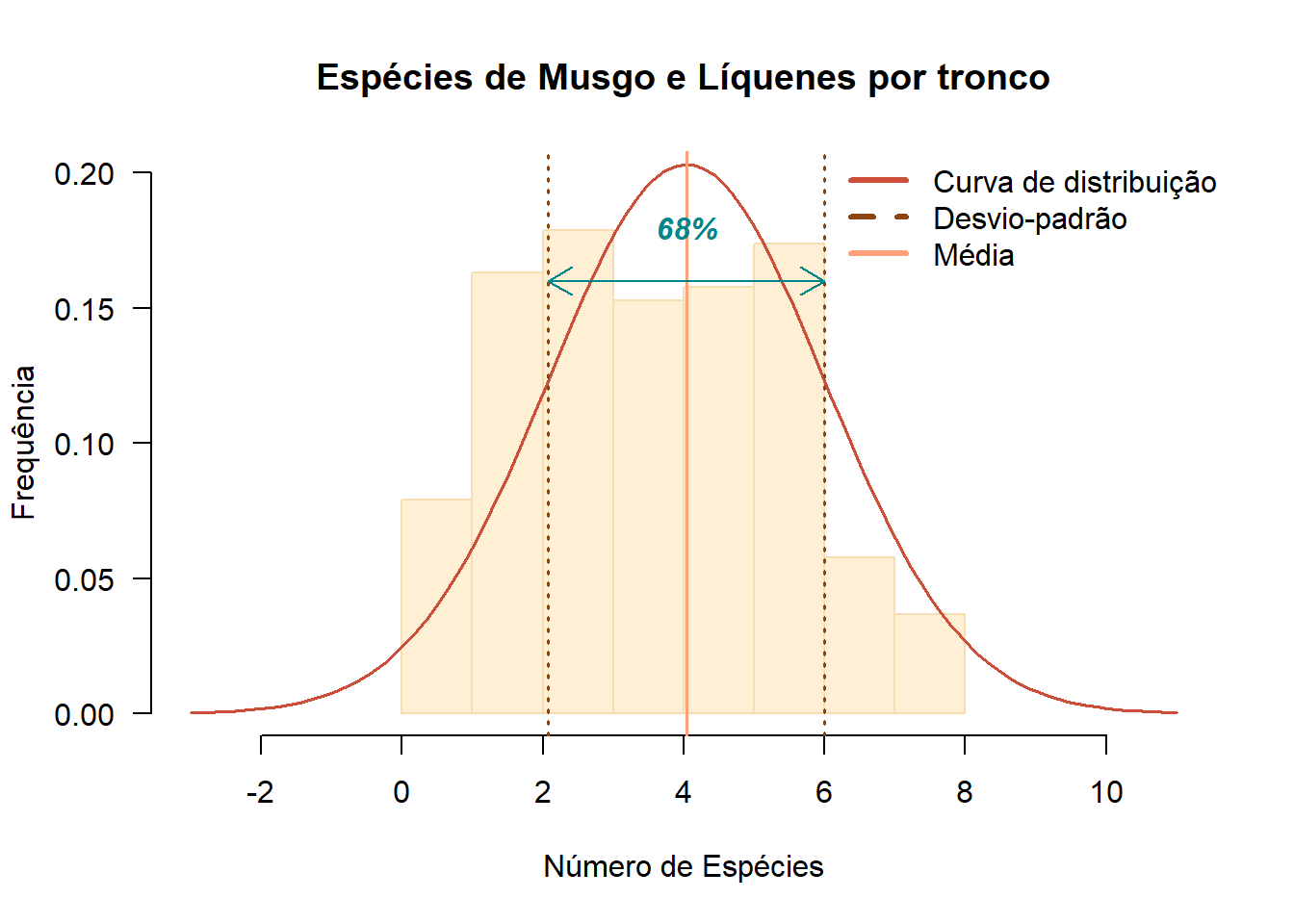
Este gráfico permite observar como se comporta a distribuição do número de espécies de líquenes por tronco relativamente à sua simetria. Em 68% das observações, o número de espécies de musgo e líquenes contadas esteve entre 2 e 6.
Nestes exemplos conseguimos assim perceber a utilidade das medidas de localização na análise exploratória de dados ecológicos.
6.4 Exemplos reais de aplicação
- Artigo 1:
Este artigo descreve como a perda de florestas para plantações de palma e borracha afeta as comunidades de aves podendo diminuir a sua riqueza até 60%. Para este objetivo foram estudadas 128 espécies ao longo de vários habitats, sendo estes: a floresta, plantações de óleo de palma e plantações de borracha. Realizaram-se modelos lineares e boxplots para se poder comparar a diferença de riqueza de espécies para cada habitat.
- Artigo 2:
https://digitalcommons.ric.edu/cgi/viewcontent.cgi?article=1106&context=honors_projects
Com esta pesquisa visaram estudar a variabilidade em características foliares em 3 biomas diferentes, usando para tal 4 espécies de arbustos dentro destes biomas. Para abordar as comparações entre os 3 biomas, foram calculados os valores médios de cada arbusto para depois serem sujeitos a um teste Tukey.
- Artigo 3:
http://www.ric.edu/faculty/rdegouvenain/Erichonors12.pdf
Este artigo analisou bolbos de plantas de várias famílias de geófitos presentes no sul de África, pretendendo estudar se estas fazem diferenciação espacial de nicho de modo a poderem coexistir no mesmo ambiente. Para se poder comparar a profundidade no solo a que estavam os bolbos dos vários grupos foram usados vários boxplots. A análise dos resultados também envolveu ANOVAs, testes-t e um modelo de regressão.
Estes artigos provam que as medidas de dispersão e localização são muito importantes para se poder analisar e comparar dados, sendo que as representações gráficas que as incluem (como boxplots) também são muito úteis. No entanto também se observa que, apesar de serem bastante usadas, não costumam ser a única análise aos dados observada na maior parte dos artigos, sendo complementadas ou servindo de base para outras análises dos dados.
6.5 Recursos adicionais
https://www.niustat.com/sites/default/files/elementosdeestatistica/medidasdesc.pdf
6.6 Considerações finais
Este trabalho mostra a importância da análise exploratória de dados, pois permite a interpretação e a comparação inicial dos mesmos, servindo de base para uma análise mais aprofundada posteriormente.
6.7 Referências
Statistics: A Beginning, Kuebler, R., Smith, H., John Wiley & Sons, Inc., 1976 ISBN 0-471-50928-0
Exercícios de Estatística Descritiva para as Ciências Sociais, Barroso, M., Ramos, M., Sampaio, M., Edições Sílabo, Lda., 1ª Edição, Lisboa, Fevereiro 2003, ISBN: 972-618-294-8
Introdução à Probabilidade e à Estatística, Pestana D., Velosa S.,Fundação Calouste Gulbenkian, 4ª ed. , Lisboa , 2010, ISBN: 978-972-31-1150-7
Bioestatística: Notas de Aula, Antunes, M., Capítulo 1, Faculdade de Ciências da Universidade de Lisboa