Chapter 17 Tema
Uma ANOVA não é mais do que um caso específico de um modelo de regressão. Explique porquê e ilustre com um conjunto de dados ecológicos a equivalencia entre estas análises.
17.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- Anaís Guerra nº 52627
- Fábio Celestino nº52509
- Hugo Jesus nº 53663
- Rafaela Reis nº52534
- Ricardo Guedes nº52578
- Sara Amaral nº52138
17.2 Introdução Teórica
17.2.1 Anova
A ANOVA é um teste de hipóteses paramétrico, muito utilizado no delineamento experimental, que permite testar mais de dois grupos de amostras e averiguar se estes possuem médias iguais (sendo esta a hipótese nula (H0) do teste). A ANOVA é também conhecida por ser uma análise de variâncias, pois, para testar a H0, analisa a variação total, isto é, a soma da variabilidade dentro de cada grupo (erros) e entre os grupos.

Para realizar a ANOVA é necessário que se verifiquem alguns pressupostos, tais como: os resíduos amostrais terem uma distribuição normal, haver homocedasticidade entre grupos e independência entre amostras. À semelhança de outros testes de hipóteses, a ANOVA compara a estatística de teste observada com a distribuição que seria esperada sobre H0. Seguidamente decide-se se a hipótese nula é rejeitada ou não em função do p-value encontrado.
A distribuição da estatística de teste da análise de variância é a estatística de F que apresenta dois graus de liberdade diferentes (associados aos grupos e aos erros). Esta estatística baseia-se no quão estatisticamente significativas são as diferenças entre as médias dos grupos, como podemos confirmar pela expressão apresentada.

17.2.2 Modelos de Regressão
Por sua vez, nos modelos de regressão é indispensável que haja uma variável resposta (y) e uma ou mais variáveis explicativas (x), ou seja, é avaliado se a primeira depende das outras e, se sim, como é que essas a fazem variar. Normalmente, as variáveis explicativas são numéricas, o que permite ao modelo criar uma reta de regressão cuja a linha minimiza a soma dos quadrados.
Equação da reta: y = a x + b + e , sendo:
a= declive da reta;
b= intercessão;
e = erro associado)
Para além de nos possibilitar fazer uma reta de regressão, o modelo linear utiliza esta mesma reta para fazer um teste de hipóteses. Neste teste, a hipótese nula é a=0, ou seja, não há relação entre x e y (reta: y=b) e para tomar a decisão de rejeição (ou não) de H0 observamos o p-value, utilizando a estatística de teste F, à semelhança da ANOVA (expressão abaixo).

Considerando o tema do trabalho, não é surpreendente constatar que os pressupostos do modelo linear são os mesmos que os da ANOVA e que, para além disso, ambas utilizam a variação total, medida através dos quadrados das somas, para chegar às suas conclusões. Contudo, neste trabalho vamos focar-nos no modelo linear (em que a variável explicativa é categórica) fazendo um teste de hipóteses, que será ligeiramente diferente do que foi apresentado agora. Com estas duas breves introduções, talvez ainda não seja claro como é que a ANOVA é um caso especial de um modelo linear em que todas as variáveis independentes são fatores, mas é precisamente isso que vamos demonstrar e aprofundar neste trabalho. STAY TUNED !
17.3 Exemplo em R
Começámos por importar os dados de um estudo feito sobre o que faz variar a distância a que uma gaivota foge de um indivíduo. Mais especificamente, decidimos abordar a variação desta variável em 3 praias com densidades populacionais diferentes.
Feito isto, procedemos à exploração dos dados. Primeiro, averiguando as médias dos diferentes grupos (que é isso que vamos comparar, mais especificamente) e depois visualizando um boxplot com as médias.
## [1] 6.55## [1] 7.95## [1] 6.85boxplot(dist~loc, col=c("orange","pink","skyblue"), ylab ="Distância" , xlab="Densidade Populacional", main= "Distâncias registadas nas diferentes praias ")
abline(h=mean(datahigh[,2]), lwd=3, lty=2, col= "darkorange3")
abline(h=mean(datamedium[,2]),lwd=3, lty=2, col= 2)
abline(h=mean(datalow[,2]), lwd=3, lty=2, col= "blue2")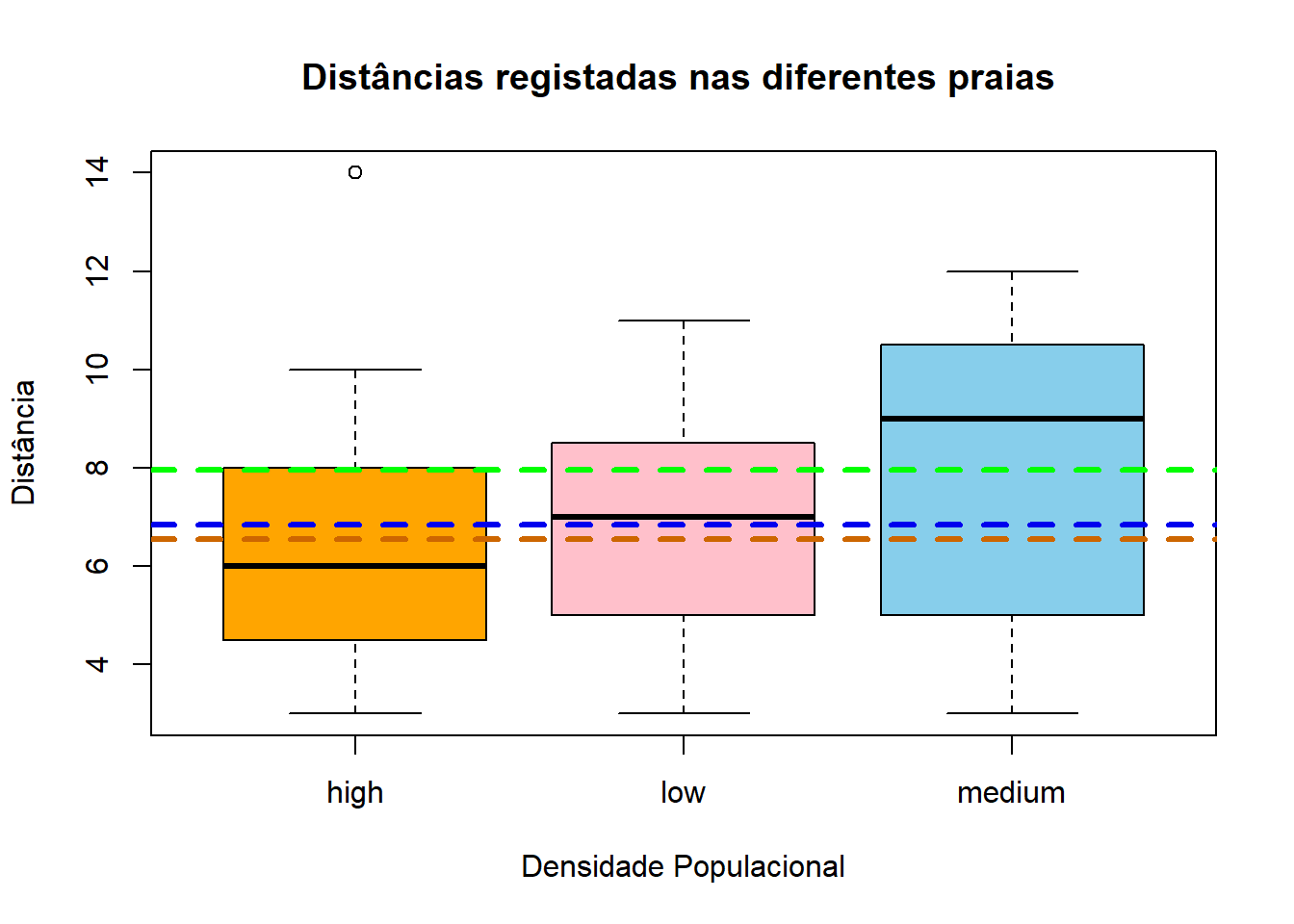
Como o nosso objetivo é comparar a média das distâncias de cada grupo com um teste ANOVA, então teremos de verificar se o conjunto de dados que temos cumpre os pressupostos necessários para a sua realização (sendo que também se aplicam ao modelo de regressão).
Deste modo, começámos por verificar a gaussianidade dos resíduos amostrados dentro de cada grupo, fazendo um shapiro.test.
##
## Shapiro-Wilk normality test
##
## data: residuals(aov(dist ~ loc))
## W = 0.97926, p-value = 0.3982Sendo o p-value= 0.3982, não rejeitámos H0, a um nível de significância de 5%, pelo que assumimos que os nossos resíduos cumprem o pressuposto. Logo, tendo o primeiro pressuposto verificado, passámos ao segundo, a homocedasticidade, aplicando o teste de bartlett.
##
## Bartlett test of homogeneity of variances
##
## data: dist by loc
## Bartlett's K-squared = 1.3504, df = 2, p-value = 0.5091Novamente, não rejeitámos H0 (p-value= 0,5091), logo nada nos impede de assumir que estamos perante homocedasticidade. .
## Warning in abline(linha1): only using the first two of 3 regression coefficients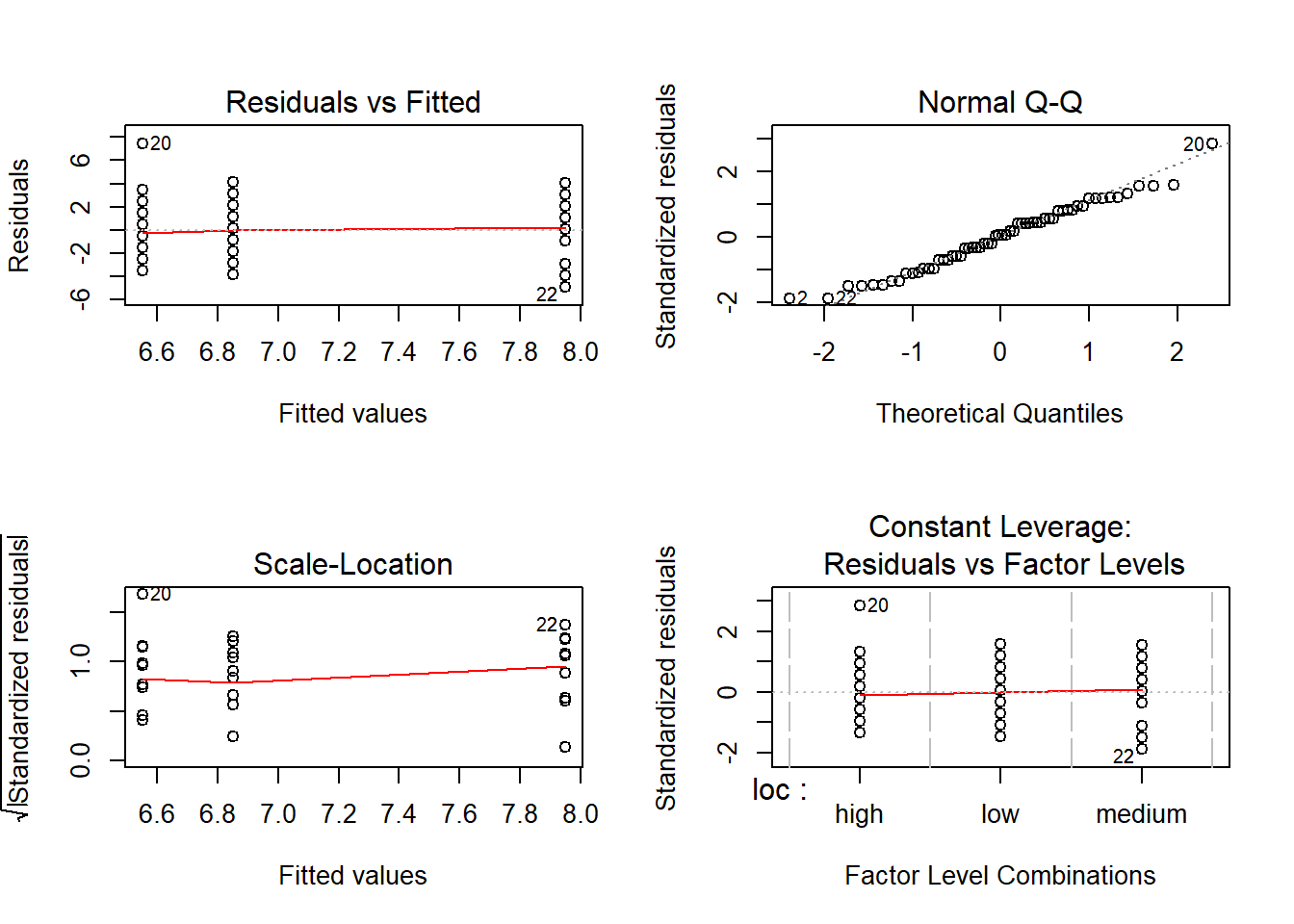
Tendo avaliado todos os pressupostos, bem como tendo uma noção gráfica dos mesmos, verificamos que os resíduos dos dados têm distribuição gaussiana, têm variâncias iguais e, uma vez que os dados amostrados são indepentes entre si, podemos prosseguir com a análise através da ANOVA.
## Call:
## aov(formula = dist ~ loc)
##
## Terms:
## loc Residuals
## Sum of Squares 21.7333 412.4500
## Deg. of Freedom 2 57
##
## Residual standard error: 2.689975
## Estimated effects may be unbalanced## Df Sum Sq Mean Sq F value Pr(>F)
## loc 2 21.7 10.867 1.502 0.231
## Residuals 57 412.5 7.236Verificámos que a hipótese nula não é rejeitada a um nível de significância 5% (p-value=0.231), o que significa que não obtivemos informação suficiente para concluir que as médias das distâncias nas diferentes praias são significativamente diferentes, o que é o mesmo que dizer que concluímos que a variação da distância entre grupos não é significativa. Como já referido anteriormente, a ANOVA é um caso específico de um modelo linear (quando a variável explicativa (x) é categórica). Mas o que é que isso significa? Bom, primeiro vamos ver o que é que acontece ao utilizar o modelo linear com este conjunto de dados.
##
## Call:
## lm(formula = dist ~ loc)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.95 -1.85 0.15 2.05 7.45
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.5500 0.6015 10.890 1.51e-15 ***
## loclow 0.3000 0.8506 0.353 0.726
## locmedium 1.4000 0.8506 1.646 0.105
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.69 on 57 degrees of freedom
## Multiple R-squared: 0.05006, Adjusted R-squared: 0.01672
## F-statistic: 1.502 on 2 and 57 DF, p-value: 0.2314Ora, como podemos ver o p-value é igual ao do teste da ANOVA, dando a mesma resposta: a não rejeição de H0. E para além disto, sabemos que, sendo x uma variável categórica, o modelo linear não é capaz de criar uma reta. Então como é que ele interpreta os dados?
##
## Call:
## lm(formula = dist ~ loc)
##
## Coefficients:
## (Intercept) loclow locmedium
## 6.55 0.30 1.40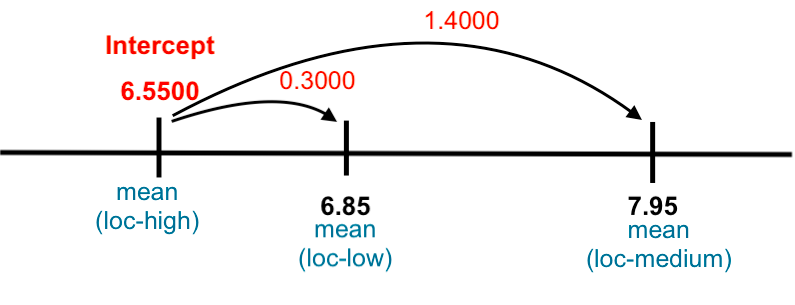 O modelo linear neste caso pega no valor basal (a menor média entre as médias dos grupos) que identifica como intercept, neste caso a média do lochigh. De seguida, subtrai à média dos outros grupos o valor do intercept, obtendo os valores das diferenças entre estas médias e o valor basal. O modelo vai, deste modo, interpretar se as variâncias entre estas médias são estatisticamente significativas, ou não. Neste caso, ao não rejeitarmos H0 concluímos que as diferenças entre médias não são significativas.
O modelo linear neste caso pega no valor basal (a menor média entre as médias dos grupos) que identifica como intercept, neste caso a média do lochigh. De seguida, subtrai à média dos outros grupos o valor do intercept, obtendo os valores das diferenças entre estas médias e o valor basal. O modelo vai, deste modo, interpretar se as variâncias entre estas médias são estatisticamente significativas, ou não. Neste caso, ao não rejeitarmos H0 concluímos que as diferenças entre médias não são significativas.
Resumindo, numa situação em que a variável explicativa é categórica o modelo da regressão linear não consegue correlacionar como é que a variável y varia com a x, acabando por avaliar apenas as diferenças entre as médias dos grupos. Dito isto, é de notar que isso é precisamente o que a ANOVA testa e avalia, daí não ser surpreendente o facto do p-value ser o mesmo e a decisão sobre H0 ser a mesma.
Em suma, percebemos que uma ANOVA avalia cada média e dá-nos um p-value que nos informa se pelo menos duas médias dos grupos de dados são significativamente diferentes. E uma regressão relata apenas uma média (como uma interceptação) e as diferenças entre essa e todas as outras médias, e o nosso p-value avalia essas comparações específicas. Ou seja, embora tomem caminhos, aparentemente, diferentes aquilo que está a ser concluído é o mesmo.
17.4 Exemplos reais de aplicação
Apresentamos abaixo dois exemplos de papers em que foram utilizados tanto o teste da ANOVA como o do Modelo Linear. Embora não ilustrem a ANOVA como um caso específico do modelo linear, são bons exemplos de como estas duas ferramentas completam um trabalho.
1) Habitat constraints and self-thinning shape Mediterranean red coral deep population structure: implications for conservation practice (Cau A., Bramanti, L., Cannas R, Follesa MC., Angiolillo M., Canese S., Bo M., Cuccu D., Guizien K.)
– FIG.13 –
V(coeficiente de variação) é utilizado para analisar a variação no tamanho das colónias de corais. V varia consoante as diferentes espécies (ANOVA, F13,42=24.82, p < 0.001) e é inversamente proporcional ao tamanho médio das colónias. A variação de tamanho nas populações é maior em espécies com colónias de reduzidas dimensões e menor em espécies com colónias de maior tamanho. O gráfico da figura 13 ilustra esta relação através de uma reta de regressão (a linha está meio sumida).
1) Population structure and local selection in Impatiens pallida (balsaminaceae), a selfing annual (Schemske D.)
–FIG.2–
Entre famílias de Impatiens pallida, a fecundidade, aferida através da produção de sementes (ANOVA of log10 [seeds + 1]: F17,344 = 13.3, p < 0.001), está negativamente correlacionada com a época de floração (ANOVA, F17,344= 20.4, p < 0 .001), como é sugerido pela reta de regressão do gráfico da figura 2.
17.5 Recursos adicionais
17.6 Considerações finais
A ANOVA é muito robusta, ou seja, o seu desempenho não é profundamente afectado por desvios moderados dos pressupostos. Mas se os pressupostos forem violados de uma maneira não moderada, podemos usar o Teste de Kruskal-Wallis que é o seu correspondente não paramétrico.
A ANOVA também pode ser utilizada para situações com mais do que um factor, sendo que é a ANOVA multifactorial. Há também casos particulares da ANOVA que podem resultar da falta de independência temporal e espacial: ANOVA Hierárquica (nested), ANOVA por Blocos e ANOVA para medidas repetidas (cada indivíduo em si funciona como um bloco).
No modelo de regressão ao dividir a soma dos quadrados de regressão pela soma dos quadrados total, obtemos o coeficiente de determinação R^2. Este coeficiente permite-nos dizer qual é a quantidade da variabilidade total que estava no y que é explicada pelo modelo da regressão. Sendo que varia de 0 a 1.
17.7 Referências
http://lite.acad.univali.br/rcurso/anova/ https://cran.ncc.metu.edu.tr/doc/contrib/Faraway-PRA.pdf https://www.researchgate.net/profile/Barbara_Tabachnick/publication/259465542_Experimental_Designs_Using_ANOVA/links/5e6bb05f92851c6ba70085db/Experimental-Designs-Using-ANOVA.pdf https://files.eric.ed.gov/fulltext/EJ689117.pdf https://www.theanalysisfactor.com/why-anova-and-linear-regression-are-the-same-analysis/ https://www.hackdeploy.com/anova-and-linear-regression-are-one-and-the-same/