Chapter 5 Tema

Existem diferentes metodologias de amostragem possíveis para obter uma amostra representativa de uma população. Neste tema pretende-se que apresentem exemplos de amostragem e que os implementem para seleccionar elementos de um conjunto de dados.

5.1 Membros do grupo

Este grupo era composto pelos seguintes elementos:

Alexandra Correia 51938
Gonçalo Fernandes 52553
Leonor Novais 52652
Raquel Oliveira 52658
Tomás Alves 52542
Tomás Pinto 52535

5.2 Introdução Teórica

Conceitos fundamentais

A população corresponde ao conjunto de unidades de amostragem sobre a qual se realiza a inferência.

Será fácil compreender como são selecionados animais numa população, porém, noutros contextos ecológicos, as unidades de amostragem podem ser mais difíceis de definir. Por exemplo, a população considerada na carga viral do ar corresponderia a todas as moléculas de ar?

Métodos de amostragem correspondem à forma como são selecionadas as unidades de amostragem e há que ter em conta que estas devem ser representativas da população e em quantidade adequada.

Dos métodos de amostragem existentes, alguns dos mais relevantes são:

Amostragem aleatória simples
Aleatória estratificada
Aleatória sistemática
Amostragem por conglomerados
Amostragem adaptativa

Amostragem aleatória simples

Amostragem aleatória simples: este método implica que todas as unidades de amostragem tenham a mesma probabilidade de ser selecionadas para fazerem parte da amostra.

Existem fórmulas que podem ser utilizadas para calcular a média e o erro padrão.

\(\underline{Estimativa\ da\ média}\) \[{\bar {x}} =\frac{\sum_{i=1}^n x_i}n\]

\(x_i\) corresponde ao valor da observação \(i\)

\(n\) corresponde ao número de unidades de amostragem

\(\underline{Estimativa\ do\ erro\ padrão}\) \[S{\bar{x}=\sqrt{\frac{s^2}{n}}(\sqrt{1-\frac{n}{N}})}\]

\(s^2\) corresponde à variância

\(N\) corresponde ao tamanho da população

Aleatória estratificada

Em situações concretas, como casos em que as estimativas diferem muito entre estratos ou a variância intraestrato é muito menor que a interestrato, pode ser relevante efetuar uma amostragem aleatória estratificada, obtendo estimativas específicas de cada um, com um maior grau de precisão. Por outro lado, pode haver problemas de amostragem intrínsecos a cada estrato, como por exemplo a detetabilidade ser diferente ou diferenças nas exigências de meios (ambiente, despesas, tecnologias).

Existem várias formas de alocar as unidades de amostragem aos estratos definidos: de forma equitativa, de forma proporcional à dimensão e de forma ótima (relativamente a custos e variância).

\(\underline{Estimativa\ da\ média}\) \[{\bar{x}_{ST}={\frac{\sum_{i=1}^L N_i\bar{x}_i}N}}\]

\(L\) corresponde ao número de estratos

\(\underline{Estimativa\ do\ erro\ padrão}\) \[S{_\bar{x}}={\sqrt{\sum_{i=1}^L[\frac{w_i^2 s_i^2}{n_i}(1-f_i)]}}\]

\(w_i\) é proporção do total das unidades de amostragem no estrato i=Ni/N

\(s_i^2\) é variância no estrato i

\(n_i\) é o número de replicados no estrato i

\(fi= ni/Ni\)

\(1-f_i\) é o fator de correção para populações finitas

Aleatória sistemática

A amostragem aleatória sistemática é um dos métodos mais utilizados em estudos ecológicos. As possíveis tendências existentes devem ser tidas em conta, uma vez que podem interferir com as estimativas a efetuar. Pode ser tratada como amostragem aleatória, nomeadamente na estimativa de parâmetros.

É possível obter uma amostra representativa de uma área ao longo do espaço ou do tempo. Por exemplo, pode-se amostrar uma área de 50 a 50 metros ou um local semanalmente.

Amostragem por conglomerados

É o método utilizado quando a população ocorre em clusters, agregados. As extrapolações efetuadas para a população devem ter em consideração a possível existência de diferenças entre estes conglomerados, uma vez que não são independentes. Este método pode ser tratado como amostragem aleatória ou estratificada.

Amostragem adaptativa

No método de amostragem adaptativa são escolhidas unidades de amostragem, de forma aleatória. Junto às unidades de amostragem em que se verifica a presença do objeto de estudo devem ser selecionadas para amostragem as unidades adjacentes nos quatro pontos cardeais.

Métodos de amostragem

Concluindo, para obter inferências estatísticas, são geralmente utilizadas amostragens aleatórias simples e estratificada. Contudo, outros métodos podem ser utilizados em situações particulares.

Dimensão da amostra

É possível calcular a dimensão da amostra, em função do erro desejado, recorrendo a expressões. Para se poderem aplicar há que obter conhecimentos relativos ao parâmetro de interesse, que pode ser a média, a variância ou a proporção, e à distribuição de probabilidade da variável aleatória, que descreve o evento.

É essencial definir a população e hipótese a testar. Selecionar o método de amostragem e a dimensão da amostra, de acordo com a população e hipótese em estudo.

A dimensão da amostra deverá aumentar se a variância do processo for elevada. Dependendo do erro que se estiver disposto a cometer, a dimensão da amostra deverá variar inversamente em relação ao erro pretendido.

\(\underline{Para\ estimar\ uma\ média\ com\ erro\ d}\) \[{n=({\frac{t_\alpha S}d})^2}\]

\(t_{\alpha}\) é o quantil \(\alpha\) da distribuição t ou Gaussiana

\(S\) é a estimativa do desvio padrão

\(d\) é o erro pretendido (em valor absoluto)

\(\underline{Proporções\ e \ percentagens - Para\ estimar\ uma\ proporção\ p\ com\ erro\ d}\) \[{n={\frac{t_\alpha^2 \hat{p}(1-\hat{p})}{d^2}}}\]

\(p\) é a proporção estimada

Então, qual a proporção mais difícil de estimar?

Como varia a expressão em função do p?

p<-0.1;p*(1-p)

## [1] 0.09

p = 0.1

p<-0.5;p*(1-p)

## [1] 0.25

p=0.5

p<-0.95;p*(1-p)

## [1] 0.0475

p=0.95

Assim, é mais difícil estimar uma proporção intermédia, uma vez que, quando a proporção é muito grande ou muito pequena, são observados quase só sucessos ou insucessos. Deste modo, tem-se a certeza da sua dimensão. Por outro lado, numa proporção intermédia, é observada uma grande variação.

\(\underline{Dimensão\ da \ amostra}\)

\(\underline{Contagens}\) \[\bar{x} {\cong} s^2 \]

\[n={({\frac{t_\alpha100}r})^2{\frac{1}{\bar{x}}}}{\approx}({\frac{200}r})^2{\frac{1}{\bar{x}}}\] \(r\) é o erro pretendido em percentagem

\(\underline{Contagens}\) \[\bar{x} < s^2 \]

\[n={({\frac{t_\alpha100}r})^2}{(\frac{1}{\bar{x}}+{\frac{1}k})}\]

\(k\) dado por: \[k={\frac{\bar{x}^2}{s^2-{\bar{x}}}}\]

Estudos piloto

Para efetuar esta seleção é indispensável obter informação sobre a variável a medir. Assim, os estudos-piloto não devem ser menosprezados, já que permitem a obtenção de dados e informações preliminares relativas às questões a resolver.

Captura e recaptura

O método de captura e recaptura permite estimar o tamanho de populações, a partir de uma recolha e marcação de espécimes e uma outra recolha posterior. É calculado o número de indivíduos total da população, com base no número de indivíduos marcados encontrados na recaptura.

Amostragem por distâncias

No método de amostragem por distâncias são definidos transectos, linhas ou pontos, em que o observador identifica indivíduos e calcula a distância a que se encontram em relação a si.

Delineamento experimental: mensurativas, manipulativas

O delineamento experimental é indispensável em experiências controladas. Assim, as experiências podem ser classificadas em mensurativas, que se caracterizam por medições em unidades ecológicas, não sendo aplicado nenhum tratamento, são comparáveis a estudos observacionais e permitem observar a correlação. Já as experiências manipulativas requerem, como o nome indica, manipulação em unidades ecológicas, com aplicação de tratamentos. Neste caso é possível identificar causalidade.

Aleatorização

Visto que muitos testes estatísticos implicam observações independentes, a alocação aleatória das unidades de amostragem aos vários tratamentos permite reduzir o enviesamento que pode ocorrer. Porém, nem sempre é possível atingir a aleatorização completa. A aleatorização permite minimizar, assim, os efeitos dos fatores de confundimento que dificultam a distinção entre variabilidade e erro e a compreensão dos efeitos dos tratamentos.

Replicação

Em amostragem, um dos conceitos mais relevantes é o de replicado, que consiste em observações independentes (unidades de amostragem independentes) sob o efeito do mesmo tratamento. A replicação permite estimar o erro, erro este que é fundamental para avaliar a significância estatística e determinar intervalos de confiança. Um replicado seria, por exemplo, medir alturas de diferentes árvores (da mesma espécie) para estimar a altura média dessa espécie, assegurando que estas observações são tão independentes quanto possível.

Pseudo Replicação

A pseudoreplicação ocorre quando as amostras são recolhidas de forma não independente, assim é essencial compreender como se distribuem as unidades experimentais no espaço e no tempo. A existência de um único replicado por tratamento e analisar verdadeiros replicados de forma conjunta (aglomerada) são também casos de pseudoreplicação.

Balancing e Blocking

Em design experimental é também essencial utilizar unidades de experimentais homogéneas, obter informação sobre as variáveis relacionadas, recolher um número elevado de replicados e realizar designs experimentais eficientes, utilizando balancing e blocking. Balancing: todos os tratamentos devem ter um tamanho de amostra igual. Blocking caracteriza-se por uma divisão de replicados, que pode ser natural, dentro das unidades de amostragem homogéneas.

5.3 Exemplo em R

Para o exemplo de implementação em RStudio, serão utilizados os dados do trabalho 1 de um dos membros do grupo. A questão a que se pretendeu responder foi “Como variou o número de vocalizações de aves em função da localização, período do dia e temperatura no local”.

Quanto às unidades de amostragem, estas devem ser bem definidas para evitar erros de contagem/medição. Assim, para garantir a consistência das unidades de amostragem estas foram definidas como vocalizações “discretas” - eventos que ocorreram num instante. Dessa forma, não poderiam prolongar-se no tempo, uma vez que isso iria classificá-las como um estado em vez de um evento.

Para responder a uma questão desta natureza poderiam ser usados diferentes métodos de amostragem, cuja escolha dependeria de vários fatores, como diferenças no coberto vegetal, proximidade a uma zona urbana, entre outros, visto que estes fatores influenciam diretamente o número de aves.

O método que mais se adequaria seria uma amostragem aleatória estratificada, uma vez que foram escolhidos 2 locais cuja extensão total apresenta alguma variância nos fatores mencionados anteriormente. Dessa forma, seria possível obter uma maior variabilidade e representatividade dos dados sem alterar os locais de amostragem originais.

Com o propósito de maximizar a aleatoriedade dos dados amostrados, os períodos de amostragem seriam repartidos ao longo de vários dias, e com alguns minutos de intervalo entre observações para reduzir possíveis fatores de confundimento. Também foram utilizados diferentes sítios aleatórios dentro dos dois locais definidos para reforçar a aleatorização.

\(\underline{Implementação\ dos\ dados\ em\ R}\)

library(readxl)
X52553GonFer <- read_excel("52553GonFer.xlsx")

Gráfico 1

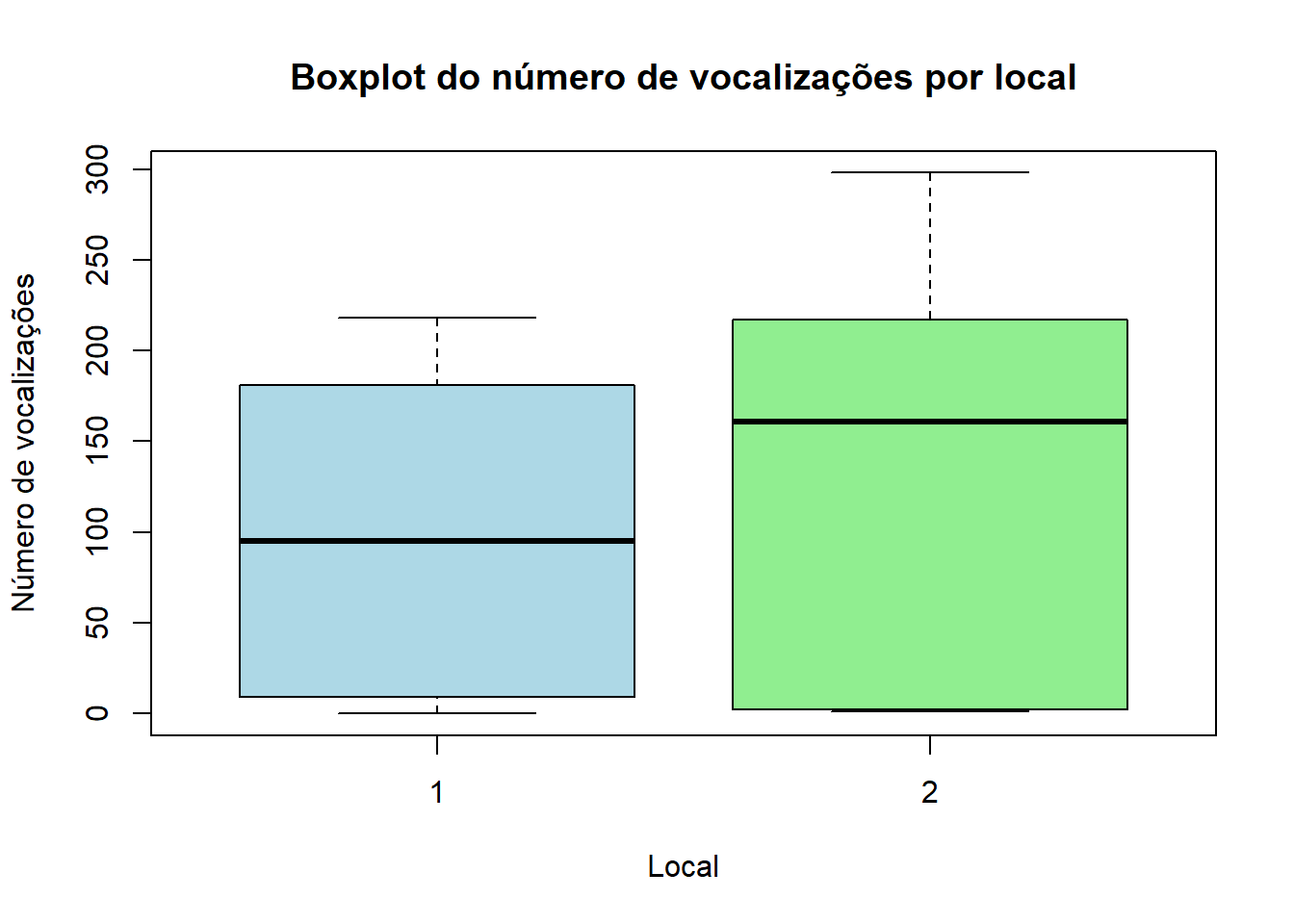boxplot(X52553GonFer$vocal~X52553GonFer$local,ylab="Número de vocalizações",xlab="Local",main = "Boxplot do número de vocalizações por local", col=c("lightblue","lightgreen") )

O gráfico representa o número de localizações por local em ambos os locais amostrados. É possível observar uma grande variabilidade do número de vocalizações, sendo que esta variabilidade é superior no local 2.

Gráfico 2

library(ggplot2)
model <- glm(X52553GonFer$vocal~X52553GonFer$temp, family=poisson, data=X52553GonFer)
ggplot(data=X52553GonFer,aes(x=temp,y=vocal))+
  geom_point(colour="royalblue1")+
  geom_line(aes(y=fitted(model)),colour="black",linetype = "dashed")+
  labs(title = "Número de vocalizações em função da temperatura do ar")+
  xlab("Temperatura do ar (Cº)")+
  ylab("Número de vocalizações")+
  theme_light()+
  theme(plot.title = element_text(size = 14))+
  theme(plot.title = element_text(hjust = 0.5))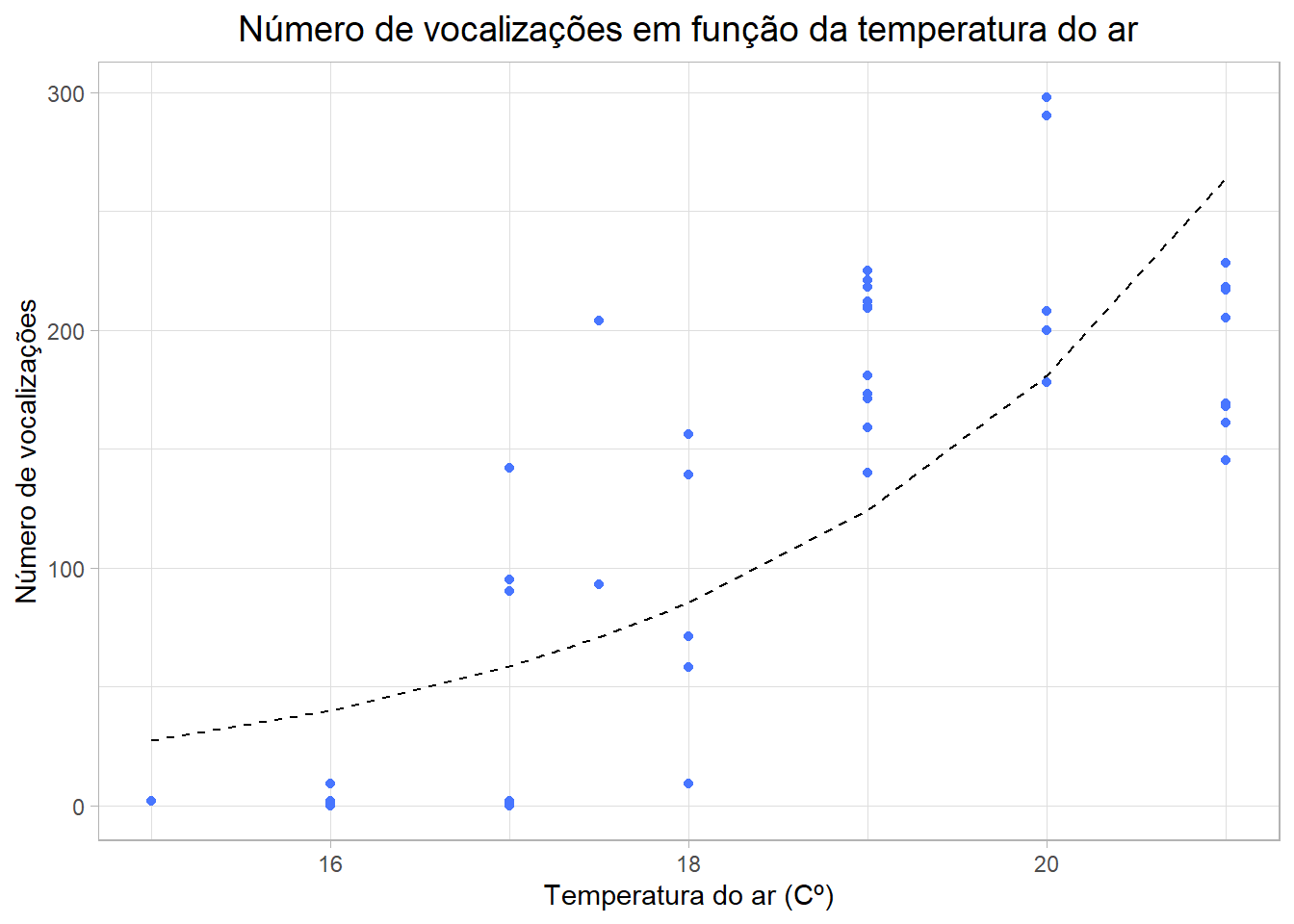

Neste gráfico está representado o número de vocalizações em função da temperatura atmosférica, e observa-se uma tendência crescente no número de vocalizações à medida que a temperatura aumenta, o que não implica causalidade, uma vez que o período de amostragem foi relativamente curto (3 dias) e seria necessário uma amostragem mais prolongada para perceber a verdadeira influência da temperatura.

Gráfico 3

X52553GonFer$priod <- factor(X52553GonFer$priod, levels=c("morning", "afternoon", "night"))
boxplot(X52553GonFer$vocal~X52553GonFer$priod,xlab="Período do dia",ylab="Número de vocalizações",main="Número de vocalizações em cada período considerado", col=c("lightgoldenrod1","orange2","blue"))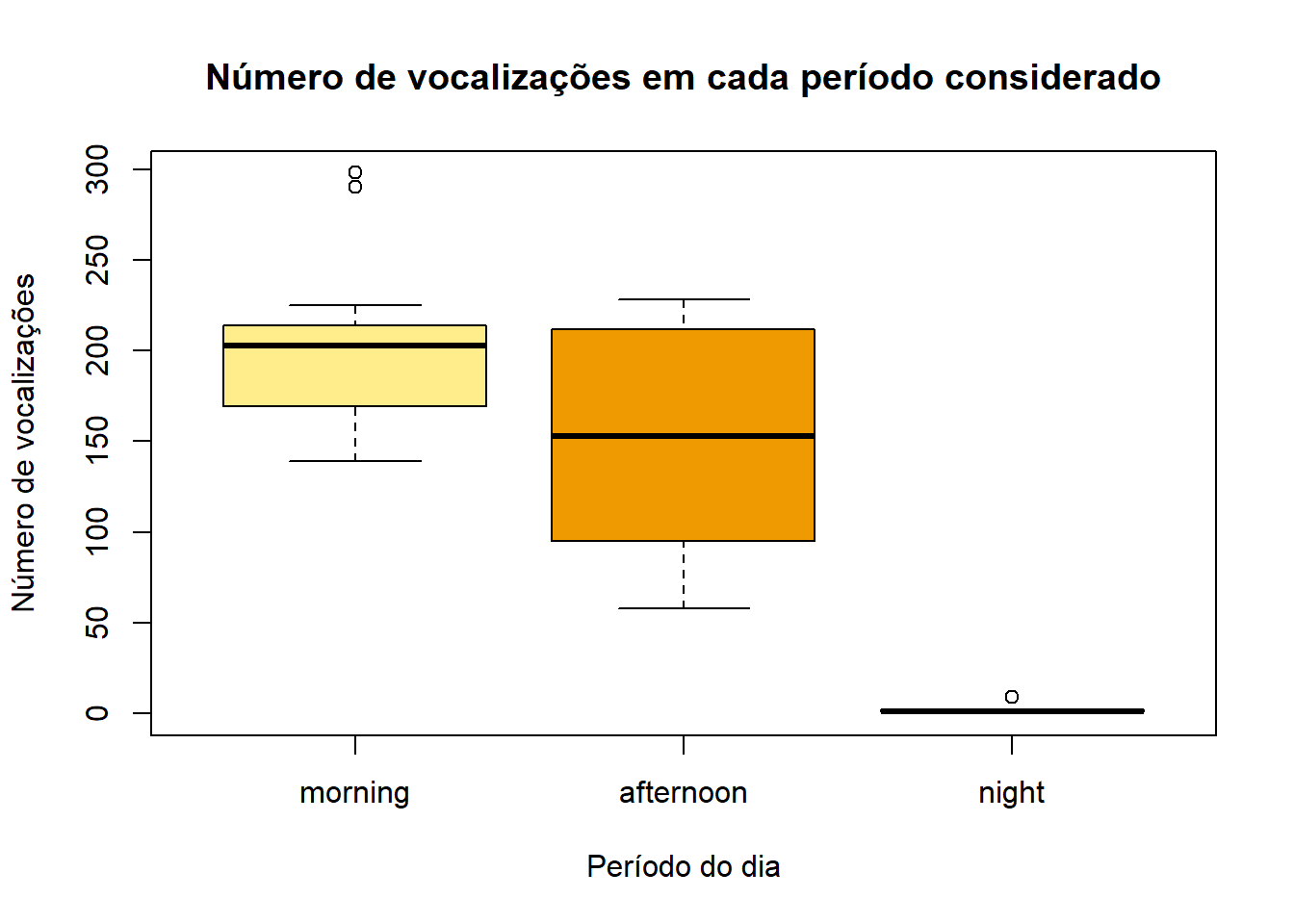

No gráfico acima está representado a variação do número de vocalizações em relação ao período do dia. Foram considerados três períodos, “morning”, “afternoon” e “night”, em que o maior valor da mediana se registou no período da manhã (“morning”), o período da tarde (“afternoon”) apresentou maior variabilidade no número de vocalizações observadas e no período da noite (“night”) foram registados os valores mínimos, aproximando-se do 0.

Dimensão da amostra com desvio padrão original

((qnorm(0.975,0,1)*93.68)/25)^2

## [1] 53.93987

Dimensão da amostra com maior desvio padrão

((qnorm(0.975,0,1)*150)/25)^2

## [1] 138.2925

Foi feito o cálculo de dimensão amostral necessária para uma população com um desvio padrão de 93.68, sabendo que se pretendia um erro de 25, tendo sido obtido um valor total de aproximadamente 54 amostras.

Se os dados apresentassem uma maior variação, ou seja maior desvio padrão (cerca de 150), e se o erro pretendido fosse o mesmo (25), seria necessário recolher um número de amostras superior.

5.4 Exemplos reais de aplicação

https://pubs.usgs.gov/of/2006/1337/pdf/ofr20061337.pdf

O estudo do paper Polar Bear Population Status in the Southern Beaufort Sea foi conduzido devido às grandes alterações no gelo do Oceano Ártico, provocadas pelo aquecimento global, com o objetivo de avaliar de que forma essas alterações afetam a população de ursos polares dessa região.

No paper são apresentadas estimativas, de individuos sobreviventes e do tamanho da população, extrapoladas a partir de dados recolhidos por captura e recaptura, durante 5 anos. Durante cada um desses 5 anos, os autores tentaram maximizar tanto o tamanho da amostra, como a distribuição geográfica da mesma na região em estudo, de forma a garantir que todos os indíviduos em estudo fossem igualmente expostos à captura.

Em estudos anteriores foram utilizados métodos de amostragem não aleatórios, que não incluiam toda a área de estudo e, por isso, existiam dificuldades em estimar parâmetros demográficos a partir dessas amostras, demonstrando assim a importância de utilizar um método de amostragem aleatório e maximizar tanto o tamanho amostral, como a distribuição geográfica onde essas amostras são recolhidas.

https://www.tandfonline.com/doi/pdf/10.1080/00063657.2014.942594

O paper Testing methods to estimate abundance of Magellanic Penguins Spheniscus magellanicus foca-se em descobrir qual o método de amostragem que melhor estima a abundância de pinguins de Magalhães.

Aplicaram-se vários métodos de amostragem (amostragem aleatória com quadrantes, amostragem sistemática com quadrantes e amostragem sistemática com transetos de largura fixa), a uma colónia virtual, que foi gerada a partir de um survey real. A abundância estimada com recurso a cada método de amostragem foi comparada com a abundância da colónia virtual. Concluiu-se que a amostragem sistemática é o melhor método, com uma accuracy de 100% e excelente precisão, com uma reduzida amostragem da colónia.

Ao longo do estudo são apresentados outros métodos de amostragem utilizados anteriormente e feitas considerações sobre as condições particulares de amostragem de pinguins de Magalhães.

Esta conclusão é relevante uma vez que pode permitir criar um standard para estudos com pinguins de Magalhães e permitir conclusões semelhantes noutras espécies de aves coloniais.

5.5 Recursos adicionais

Site com vários recursos sobre estatística, sendo que o link indicado incide sobre métodos de amostragem, mas com um table of contents cobrindo vários aspetos sobre amostragem e outros temas

https://www.scribbr.com/methodology/sampling-methods/

Site que apresenta diversos métodos de amostragem e exemplos

https://www.questionpro.com/blog/types-of-sampling-for-social-research/

Vídeo informativo que incide sobre design experimental e métodos de amostragem

https://youtu.be/Rf-fIpB4D50

Vídeo que explicita os métodos de amostragem

https://youtu.be/be9e-Q-jC-0

Vídeo curto e didático sobre o conceito de amostragem aleatória e captura-recaptura

https://youtu.be/0RSLmQzz_jg

5.6 Considerações finais

Em suma, a amostragem é um tema indissociável da investigação em ecologia, nunca devendo ser menosprezada.

5.7 Referências

Marques, T. (2020). EcolNumT6 29 09 2020 [PDF].

Marques, T. (2020). EcolNumT7 06 10 2020 [PDF].

Marques, T. (2020). EcolNumT11 20 10 2020 [PDF].

Marques, T. (2020). EcolNumT16 09 11 2020 [PDF].

Eric V. Regehr, Steven C. Amstrup e Ian Stirling (2006) Polar Bear Population Status in the Southern Beaufort Sea Open-File Report 2006-1337, disponível em https://pubs.usgs.gov/of/2006/1337/pdf/ofr20061337.pdf, consultado a 20 de novembro de 2020

Cecilia Villanueva & Marcelo Bertellotti (2014) Testing methods to estimate abundance of Magellanic Penguins Spheniscus magellanicus, Bird Study, 61:3, 421-427, DOI: 10.1080/00063657.2014.942594, disponível em https://www.tandfonline.com/doi/pdf/10.1080/00063657.2014.942594, consultado a 20 de novembro de 2020