Chapter 8 Tema

Existem testes de hipóteses que podem ser usados para testar dados em contextos ecológicos. Neste tema pretende-se que apresentem uma visão geral sobre testes de hipóteses com exemplos de testes de hipóteses a uma ou duas amostras, emparelhadas ou não emparelhadas.

8.1 Membros do grupo

Este grupo era composto pelos seguintes elementos:

Beatriz Garcia Nº52572
Catarina Talefe Nº49576
Diogo Janeiro Nº51207
Inês Cabeça Nº52538
Maria Inês Silva Nº52642
Tiago Miranda Nª49608

8.2 Introdução Teórica

Os testes de hipóteses são uma metodologia estatística que permite efetuar inferências acerca de uma população com base numa ou mais amostras dessa mesma população. Estes testes têm como objetivo ajudarem-nos a perceber se uma determinada hipótese testada, numa ou mais amostras, pode ser verdade para toda a população. Dito isto, os testes de hipóteses são usados para verificar a validade de uma hipótese.

Para testar um parâmetro é necessária a existência de duas hipóteses, uma representa uma afirmação, que expressa a inexistência de diferenças, e outra que nega a primeira, sendo o complementar dessa informação, a hipótese nula (H0) e a hipótese alternativa (H1), respetivamente.

Para chegarmos a uma conclusão acerca das hipóteses, comparamos a estatística de teste com uma distribuição de probabilidade conhecida chegando a uma de duas conclusões, manter ou rejeitar a H0. Para tomar a decisão também podemos utilizar o p-value, sendo rejeitada a H0 quando este é inferior ou igual ao nível de significância usado. Com esta decisão, podendo cometer dois tipos de erros, sendo os de Tipo I correspondentes à rejeição de H0 quando este é verdadeiro e os de Tipo II, manter a H0, sendo ele falso. O nível de significância (\(\alpha\)) representa o risco de cometer um erro de Tipo I e o \(\beta\), o risco de cometer um erro do Tipo II, estando os dois negativamente correlacionados. A potência do teste é dada por 1-\(\beta\), sendo a probabilidade de rejeitar a hipótese nula quando esta de facto é falsa.

Podemos resumir a criação de um teste de hipóteses em quatro passos:

1ºPasso: Elaborar hipóteses. O investigador faz uma hipótese nula (H0) acerca da população e uma hipótese alternativa que a contradiga (H1).
2ºPasso: Determinar um critério de decisão. O investigador decide um valor, o \(\alpha\), para o qual ele compara e decide se rejeita ou mantém a H0. Os níveis mais usuais são o 0,1 , 0,05 , 0,01.
3ªPasso: Para este passo temos 2 opções que podemos seguir: -Calcular a estatística de teste. Isto vai dar um valor que irá ser comparado com um valor esperado de uma distribuição conhecida de acordo com o \(\alpha\) escolhido, antes de analisar amostra. -Podemos calcular um p-value a partir da estatística de teste.
4ºPasso: Toma de decisão. Para decidir, podemos utilizar a estatística de teste. Contudo, a regra para rejeitar ou não o H0 varia consoante o teste utilizado. Assim, calculamos o p-value que, comparando com o valor de significância utilizado, rejeitamos o H0 se o p-value for menor que \(\alpha\) e mantemos H0 se o p-value for maior.

Estes testes podem ser unilaterais ou bilaterais consoante a região critica (a zona na qual rejeitamos a H0). Se quisermos saber o teste para um parâmetro superior ou inferior a uma determinada média, falamos em testes unilaterais, se, por outro lado, quisermos saber se o que acontece é diferente a essa média, então falamos em testes bilaterais. Essa região critica é igual ao valor de \(\alpha\) se o teste for unilateral, mas é metade do \(\alpha\) no caso de um teste bilateral.

Existem vários tipos de testes de hipóteses e a escolha do tipo de teste (paramétricos ou não) dependerá da natureza dos dados e do cumprimento ou não de pressupostos.

Em suma, os testes de hipóteses ajudam-nos a compreender de que forma a nossa população em estudo se comporta consoante um parâmetro, fazendo uma inferência através de uma amostra dessa mesma população.

8.3 Exemplo em R

Neste exemplo em R, apresentamos 3 tipos de testes de hipóteses aplicados aos dados do trabalho 1 de um integrante deste grupo.

1)Importadar dados para o Rmd

library(readxl)
G8 <- read_excel("G8.xlsx", col_types = c("numeric", "text"))

2)Colocar os dados em Data Frame

Dados <- data.frame(read_excel("G8.xlsx"))
Dados

##    cap dmar
## 1  214  mar
## 2  120  mar
## 3  117  mar
## 4  153  mar
## 5   82  mar
## 6  212  mar
## 7  170  mar
## 8  145  mar
## 9  296  mar
## 10 197  mar
## 11 141  mar
## 12 132  mar
## 13 117  mar
## 14 128  mar
## 15 113  mar
## 16 159  mar
## 17 100  mar
## 18  65  mar
## 19  46  mar
## 20  78  mar
## 21 163  est
## 22 170  est
## 23 140  est
## 24 152  est
## 25 178  est
## 26 229  est
## 27 233  est
## 28 183  est
## 29 177  est
## 30 186  est
## 31  90  est
## 32 101  est
## 33 100  est
## 34 209  est
## 35  86  est
## 36  99  est
## 37 105  est
## 38 126  est
## 39  82  est
## 40  48  est
## 41 294  rio
## 42 203  rio
## 43 220  rio
## 44 198  rio
## 45 188  rio
## 46  93  rio
## 47 176  rio
## 48 225  rio
## 49 260  rio
## 50 143  rio
## 51  58  rio
## 52  63  rio
## 53  88  rio
## 54 112  rio
## 55 214  rio
## 56 113  rio
## 57  68  rio
## 58 125  rio
## 59 135  rio
## 60  95  rio

Visualização gráfica dos dados

ycap<-Dados$cap
xmar<-Dados$dmar
xm<-ycap[xmar=="mar"]
xe<-ycap[xmar=="est"]
xr<-ycap[xmar=="rio"]
boxplot(ycap~xmar,xlab = "Distância ao Mar",ylab="Perímetro",main="Fig.8:Perímetro dos Pinheiros de acordo com a Distância ao Mar ",col="skyblue2")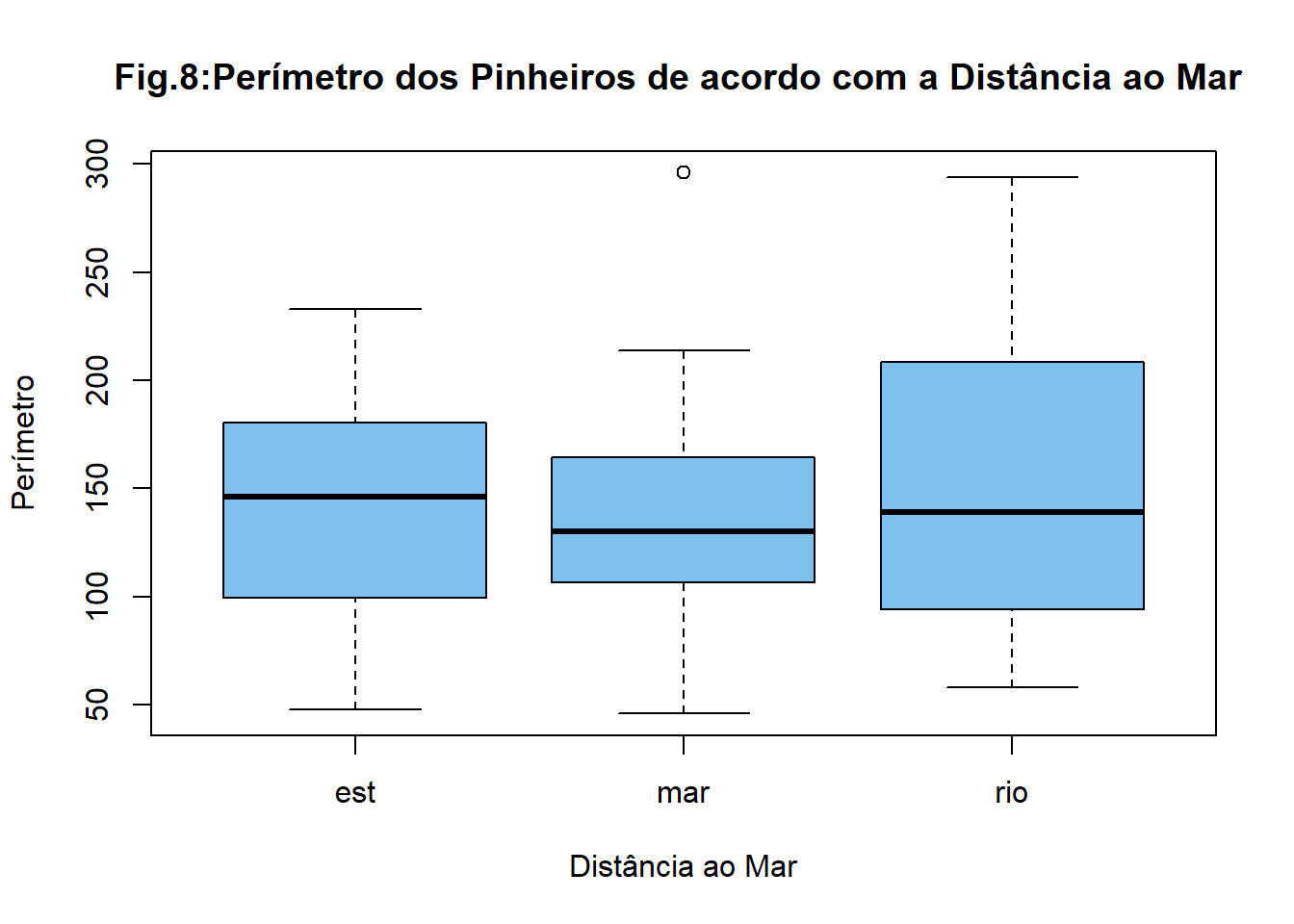

4)Vamos fazer um teste de hipóteses para testar a homogeneidade de variâncias. Neste caso, fazemos um Teste de Bartlett onde:

H0: As variâncias são iguais
H1: As variâncias são diferentes

grupo123<-rep(1:3,each=20)
grupo123

##  [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
## [39] 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3

bartlett.test(x=Dados$cap,g=grupo123)

## 
## 	Bartlett test of homogeneity of variances
## 
## data:  Dados$cap and grupo123
## Bartlett's K-squared = 1.4002, df = 2, p-value = 0.4965

Com um p-value de 0,4965 não rejeitamos a hipótese nula, para os níveis de significância usuais (0,1,0,05 e 0,01), de que as variâncias são iguais.

5)De seguida fazemos um outro teste de hipóteses, um para testar a normalidade. Neste caso, vamos fazer um teste de Shapiro onde:

H0: Os resíduos são normais
H1: Os resíduos não são normais

shapiro.test(xm-mean(xm))

## 
## 	Shapiro-Wilk normality test
## 
## data:  xm - mean(xm)
## W = 0.94899, p-value = 0.3521

shapiro.test(xr-mean(xr))

## 
## 	Shapiro-Wilk normality test
## 
## data:  xr - mean(xr)
## W = 0.949, p-value = 0.3522

shapiro.test(xe-mean(xe))

## 
## 	Shapiro-Wilk normality test
## 
## data:  xe - mean(xe)
## W = 0.95525, p-value = 0.4537

Para todos os casos, o p-value é superior a todos os níveis de significância usuais. Assim, não rejeitamos H0.

Com os dois testes a cima, sabemos que os dados cumprem os pressupostos necessários para realizar um teste paramétrico.

Como podemos realizar um teste paramétrico, vamos fazer outro tipo de testes de hipóteses que é o Teste T, aqui fazemos um para duas amostras. A nossa H0 é que não existe diferenças nas médias e a H1 é que existe diferenças nas médias.

t.test(xm,xr)

## 
## 	Welch Two Sample t-test
## 
## data:  xm and xr
## t = -0.70492, df = 37.003, p-value = 0.4853
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -55.40329  26.80329
## sample estimates:
## mean of x mean of y 
##    139.25    153.55

t.test(xe,xr)

## 
## 	Welch Two Sample t-test
## 
## data:  xe and xr
## t = -0.54964, df = 35.522, p-value = 0.586
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -50.20008  28.80008
## sample estimates:
## mean of x mean of y 
##    142.85    153.55

t.test(xe,xm)

## 
## 	Welch Two Sample t-test
## 
## data:  xe and xm
## t = 0.204, df = 37.589, p-value = 0.8395
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -32.1376  39.3376
## sample estimates:
## mean of x mean of y 
##    142.85    139.25

Tomamos a decisão, para todos os conjuntos em teste, de não rejeitar H0 pois o p-value, mais uma vez, é superior a todos os níveis de significância. Assim, podemos concluir que as médias dos perímetros dos pinheiros entre os 3 locais estudados não apresentam diferenças significativas.

Caso os dados não respeitassem os pressupostos, poderíamos fazer um teste não paramétrico como o de wilcoxon.

8.4 Exemplos reais de aplicação

Existem vários tipos de testes de hipóteses, nestes artigos encontramos alguns desses tipos aplicados a um contexto ecológico real.

Tarpy, D. Genetic diversity within honeybee colonies prevents severe infections and promotes colony growth Proceedings. Biological sciences / The Royal Society, 2003, 270, 99-103

Neste trabalho, tentou-se perceber se a variabilidade genética em colónias de abelhas pode desempenhar um papel importante na manutenção e desenvolvimento das colónias. Mais concretamente, se a Poliandria pode prevenir e diminuir as infeções por doenças graves.

Para tal, foram feitos dois tratamentos em duas abelhas rainhas irmãs:

• Uma foi inseminada com sémen de um macho geneticamente idêntico

• Outra foi inseminada com sémen de vários machos

Após o estabelecimento das duas colónias, estas foram inoculadas com esporos de Ascosphaera apis, um fungo patogénico responsável pela morte das ninhadas em desenvolvimento e foram contados o número de mortos por ninhada, sendo esta a variável que dá a prevalência da doença. Foram medidas mais duas variáveis, sendo estas a viabilidade das ninhadas e o nível de comportamento higiénico (retirada de mortos, etc…)

Para testas as diferenças nas médias destas três variáveis, consoante os dois tratamentos foram feitos teste-t unidirecionais, com H0 a prever uma igualdade de médias nos dois tratamentos e H1 a prever uma diferença das médias sendo que era expectável que a média fosse menor na colónia mais geneticamente diversa. O investigador utilizou um nível de significância de 0,1 para as tomadas de decisão.

Observou-se que a viabilidade média das ninhadas era igual nos dois tratamentos, e as variâncias eram bastante diferentes, com a variância da colónia geneticamente idêntica bastante maior (medido com recurso a um teste de Bartlett para homocedasticidade). Este padrão também se observou no que toca ao nível de comportamento higiénico. Na prevalência da doença nota-se que a variância é bastante superior na colónia com pouca variabilidade genética.

Assim, quem efetuou este estudo, concluiu que as colónias geneticamente diversas são menos propensas a doenças que afetem grande parte da colónia do que as colónias geneticamente idênticas, que por serem sensíveis aos mesmos tipos de fatores devido à sua predisposição genética, estão mais suscetíveis a estas doenças.

Aqui observa-se a utilização de vários tipos de testes de hipóteses e algumas noções importantes:

• Os testes para análise de pressupostos: Bartlett test

• Um teste para a igualdade de médias: Teste T

• A utilização de testes unilaterais

• A definição do nível de significância \(\alpha\)

Baltag, E.; Pocora, V.; Sfîcă, L. & Bolboaca, L. Common Buzzard (Buteo buteo) population during winter season in North-Eastern Romania: The influences of density, habitat selection, and weather Ornis Fennica, 2012, 90, 186-192

Este estudo tem como objetivo perceber os efeitos da densidade, do habitat e do clima nas populações de Búteo Comum, Buteo buteo.

Os dados foram recolhidos no nordeste da Roménia, numa região que combina habitats artificiais e naturais, através da contagem de indivíduos em transectos de 40km numa viatura, durante os meses de Inverno. Por cada Búteo observado retiraram-se os seguintes dados:

• A distância no transepto • A idade aparente • O tipo de habitat (classificados de acordo com Corine land cover classes)

Neste trabalho os testes de hipótese entram precisamente no estudo da escolha de habitat. Para testar se os indivíduos escolhem os habitats de forma aleatória foi utilizado um Teste G com H0 significando uma escolha aleatória. É também utilizado um Teste de Friedman para detetar diferenças nas abundâncias relativas de búteos entre meses e transectos

Neste trabalho podemos observar mais alguma variabilidade de testes de hipóteses que existem.

8.5 Recursos adicionais

Para mais informações, poderá consultar a seguinte seleção de links de forma a ter uma aprendizagem mais abrangente sobre o tema em estudo.

8.6 Considerações finais

É relevante ter em conta que os resultados estatísticos e as significâncias não são tudo. Quando trabalhamos com variáveis e problemas ecológicos temos de ver o seu contexto e tomar a decisão com base nos resultados estatísticos e nos fatores ecológicos, não apenas nos números.

É necessário realçar que certos conceitos abordados no nosso trabalho não foram tão desenvolvidos, uma vez que os trabalhos de outros colegas, nomeadamente os dos grupos que se seguirão a nós, já irão falar deles de forma mais pormenorizada e aprofundada.

8.7 Referências

Para este trabalho usamos as seguintes referências:

Firmino, Maria José de Almeida Caetano de Sousa. Testes de hipóteses: uma abordagem não paramétrica. 2015, 107 p. Dissertação (Mestrado em Matemática para professores) – Universidade de Lisboa, 2015,[Accessed 14 November 2020]. Link 1
1. [ebook] Available at: Link 2 [Accessed 14 November 2020].
Baltag, E.; Pocora, V.; Sfîcă, L. & Bolboaca, L. Common Buzzard (Buteo buteo) population during winter season in North-Eastern Romania: The influences of density, habitat selection, and weather Ornis Fennica, 2012, 90, 186-192 [Accessed 14 November 2020].
Tarpy, D. Genetic diversity within honeybee colonies prevents severe infections and promotes colony growth Proceedings. Biological sciences / The Royal Society, 2003, 270, 99-103 [Accessed 14 November 2020]
Failing to reject null hypothesis
Video