Chapter 15 Tema
Testes de comparações múltiplas à posteriori, são testes frequentemente utilizados para complementar os testes de análise de variância. Neste trabalho pretende-se que justifiquem em que contexto os testes à posteriori são implementados, que identifiquem alguns exemplos deste tipo de testes e que demonstrem, com um exemplo específico, a sua implementação em R (podem usar os dados do Trabalho 1).
15.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- Ana Botelho 52544
- Ana Catarina Fialho 52650
- Catarina Ferreira 52530
- Daniel Pereira 52606
- Renato Pereira 52599
- Sílvia Ferreira 52655
15.2 Introdução Teórica
15.2.1 Testes a posteriori
Os testes a posteriori podem ser utilizados como complemento aos testes de análise de variância entre grupos, como é o caso do Teste ANOVA e o Teste de Kruskal-Wallis. Só se aplicam estes testes complementares caso o p-value da ANOVA ou ANOVA não paramétrica for estatisticamente significativo. Caso contrário, não há razão para suspeitar que os dados diferem muito entre si. Os testes de análise de variância não especificam quais os grupos que diferem e, por isso, são necessários os testes a posteriori para se analisar os dados e se identificar as diferenças.
Os testes a posteriori abordados em aula foram o Teste de Tukey, o Teste de Newman-Keuls, o Teste de Scheffé e o Teste de Dunn. Os três primeiros requerem a realização prévia da ANOVA, e o teste de Dunn que, sendo um teste não paramétrico, é utilizado após um teste também não paramétrico, o teste de Kruskal-Wallis, ou one-way ANOVA. A H0 destes testes é a igualdade das médias.
Estes testes diferem na sua aplicabilidade, poder estatístico e quão conservadores são.
O poder estatístico de um teste reflete-se no quão provável o teste é de distinguir um efeito significativo de um efeito por mera chance. Ter um poder estatístico elevado significa que os resultados têm uma elevada probabilidade de serem válidos. Já ter um poder estatístico baixo significa que os resultados têm uma probabilidade baixa de serem válidos, acabando por serem questionáveis. Um teste poderoso tem baixa probabilidade de cometer um erro tipo II.
Um teste conservativo mantém a probabilidade de rejeitar a H0 abaixo do nível de significância. Isto significa que tem uma baixa probabilidade de rejeitar incorretamente H0 i.e. tem baixa probabilidade de cometer um erro tipo I.
15.2.2 Teste de Tukey
O Teste de Tukey compara as médias de cada tratamento com as médias de todos os outros tratamentos, ou seja, aplica-se simultaneamente ao conjunto de todas as comparações de pares e identifica qualquer diferença entre 2 médias que seja maior que o erro padrão esperado. Tipicamente, é utilizado após obtenção de um valor estatisticamente significativo na ANOVA. É também útil para grupos com diferentes tamanhos amostrais. Assume que as observações são independentes, os grupos têm distribuição normal e há homocedasticidade.
A estatística teste é:
Figura 1 - Estatística de teste para o Teste de Tukey.
Valor crítico:
Figura 2 - Valor crítico para o Teste de Tukey.
Critério de rejeição para H0:
Figura 3 - Critério de rejeição da H0 para o Teste de Tukey.
15.2.3 Teste de Newman-Keuls
O Teste de Newman-Keuls é um teste a posteriori para diferenças entre médias. Após realização da ANOVA com um resultado estatisticamente significativo, é possível realizar um Newman-Keuls para conferir, em sequência, que pares específicos de médias são diferentes. Tanto este como o teste de Tukey baseiam-se na Studentized range distribution (a diferença entre o maior valor e menor valor numa amostra, em termos de desvios padrões). Este teste assume que há independência das observações, homocedasticidade e distribuição normal dos resíduos.
Para determinar se uma diferença é significante ou não, aplica-se a seguinte fórmula, em que se divide a diferença entre as duas médias pelo erro padrão, para se obter a estatística de teste:
Figura 4 - Estatística de teste para o Teste de Newman-Keuls.
Onde MSE (Mean Squared Error) representa a variância do erro da ANOVA realizada no primeiro passo da análise dos dados.
No caso em que as amostras têm tamanhos diferentes (nA=/=nB), usa-se a seguinte fórmula:Figura 5 - Estatística de teste para o Teste de Newman-Keuls, quando existem diferentes tamanhos amostrais.
Depois, compara-se a estatística de teste ao valor crítico, rejeitando e mantendo H0 de acordo. Este método usa valores de significância diferentes para diferentes pares de comparações de médias, sendo assim mais provável que sejam reveladas diferenças significativas entre as médias das amostras. Comparativamente com o teste de Tukey, este teste é, assim, mais poderoso mas menos conservador, mas, apesar disto, o valor exato da probabilidade de cometer um erro de tipo I não pode ser calculado devido à natureza sequencial deste teste. É também necessário ter em conta que comparar um range de mais do que 4 médias é irrealista, visto que as probabilidades de erro sobem para níveis demasiados altos para consideração.
15.2.4 Teste de Scheffé
Após rejeição da hipótese nula da ANOVA, com um resultado estatisticamente significativo, realiza-se este teste para descobrir que pares de médias têm diferenças significativas.
Este teste corrige o alfa (valor de significância) para comparações de médias simples e complexas (comparar mais do que um par de médias simultaneamente). É escolhido em vez do teste de Tukey quando se pretende comparar mais do que diferenças emparelhadas, por exemplo quando se compara a média de dois grupos à média de outros dois grupos.
É um teste bastante conservativo e, dos três, é o mais flexível e com menor poder estatístico.
A estatística de teste é:
Figura 6 - Estatística de teste para o Teste de Scheffé.
15.2.5 Teste de Dunn
Este teste é o procedimento seguinte a um teste de Kruskal-Wallis, isto é, é o equivalente não paramétrico dos testes de comparações múltiplas usados após a ANOVA, ou seja, não assume que os seus resíduos provêm duma distribuição específica. A sua importância é constatada quando existe uma diferença entre três ou mais médias, e serve para averiguar quais as médias que são significativamente distintas. Assim, realizam-se comparações múltiplas de forma a redefinir o valor de significância (alfa), o que está muitas vezes associado à probabilidade de rejeitar equivocadamente a hipótese nula.
É um dos testes menos potentes mas altamente conservador, sendo principalmente utilizado quando só se pretende realizar um reduzido número de comparações.
Estatística de teste:
Figura 7 - Estatística de teste para o Teste de Dunn.
Onde SE é:
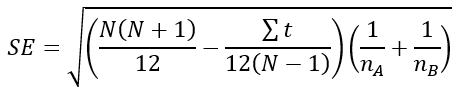
Figura 8 - SE para estatística de teste.
Valor crítico:
Figura 9 - Valor crítico para o Teste de Dunn, sendo k = número de grupos.
Critério de rejeição para H0:
Figura 10 - Critério de rejeição de H0 para o Teste de Dunn.
15.2.5.1 Outros testes a posteriori
Outros testes a posteriori incluem a correção de Bonferroni, um teste a posteriori conservativo que é utilizado para limitar a possibilidade de obter um resultado estatisticamente significante quando testamos múltiplas hipóteses. É bastante útil porque quantos mais testes corremos, maior é a chance de obtermos um resultado significante. Existe também o Duncan’s new multiple range test (MRT), uma alternativa ao Teste de Newman-Keuls com maior potência.
15.3 Exemplo em R
Começando por importar os dados, referentes à diferença de peso da comida ingerida por dois gatos, os grupos estão divididos por altura do dia, sendo estes:
- Morning, de manhã, das 6h-12h;
- Afternoon, durante a tarde, das 12h-18h;
- Evening, ao fim da tarde, das 18h-00h;
- Night, durante a noite, das 00h-6h.
Vamos realizar o teste de Tukey, um teste a posteriori, logo é primeiro necessário ajustar um modelo de regressão linear para a ANOVA - função aov(). Por conveniência, assumimos que os pressupostos da ANOVA são cumpridos, uma vez que o nosso objetivo é exemplificar a utilização dos testes a posteriori.
- A H0 é que as médias são iguais;
- A H1 é que as médias diferem.
## Df Sum Sq Mean Sq F value Pr(>F)
## time 3 6802 2267.5 22.27 2.69e-09 ***
## Residuals 50 5091 101.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1O valor retornado pela ANOVA é 2.69e-09, bastante menor que qualquer um dos níveis usuais de significância, logo, a H0 deverá ser rejeitada e o valor é estatisticamente significativo, então podemos prosseguir à utilização dos testes a posteriori.
Para investigar mais diferenças entre todos os grupos, o Teste de Tukey vai ser efetuado (função TukeyHSD(), requer o package agricolae).
##
## Attaching package: 'agricolae'## The following objects are masked from 'package:moments':
##
## kurtosis, skewness## The following object is masked from 'package:modeest':
##
## skewness## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = lmdados)
##
## $time
## diff lwr upr p adj
## Evening-Afternoon 20.307692 9.978607 30.636778 0.0000198
## Morning-Afternoon 12.923077 2.404451 23.441702 0.0103366
## Night-Afternoon -8.263736 -18.592822 2.065349 0.1588960
## Morning-Evening -7.384615 -17.713701 2.944470 0.2411317
## Night-Evening -28.571429 -38.707430 -18.435427 0.0000000
## Night-Morning -21.186813 -31.515898 -10.857728 0.0000090Analisando os p-values, é possível inferir que existem diferenças entre alguns grupos.
Evening-Afternoon: o p-value (
0.0000198) é bastante inferior aos níveis usuais de significância (0.1, 0.05 e 0.01), logo a H0 de que as médias são semelhantes deverá ser rejeitada. Estes dados diferem entre si;Morning-Afternoon: o p-value (
0.0103366) é inferior aos níveis de significância de 0.1 e 0.05, mas é ligeiramente superior ao nível de significância de 0.01. A H0 deverá então não ser rejeitada apenas para este nível, sendo rejeitada para os outros níveis usuais;Night-Afternoon: o p-value (
0.1588960) é superior aos níveis usuais de significância, logo não se deve rejeitar a H0;Morning-Evening (
0.2411317) é superior aos níveis usuais de significância, logo não se deve rejeitar a H0;Night-Evening (
0.0000000) é muito inferior aos níveis usuais de significância (0.1, 0.05 e 0.01), logo a H0 deverá ser rejeitada.Night-Morning (
0.0000090) é muito inferior aos níveis usuais de significância (0.1, 0.05 e 0.01), logo a H0 deverá ser rejeitada.
É possível concluir que os grupos Evening-Afternoon, Morning-Afternoon, Night-Evening e Night-Morning diferem entre si, ou seja, a quantidade de comida ingerida nestas alturas do dia é bastante diferente. Os grupos Night-Afternoon e Morning-Evening, por sua vez, não diferem tanto, e a quantidade de comida ingerida é mais semelhante.
Estas conclusões também podem ser tiradas a partir de uma análise gráfica:
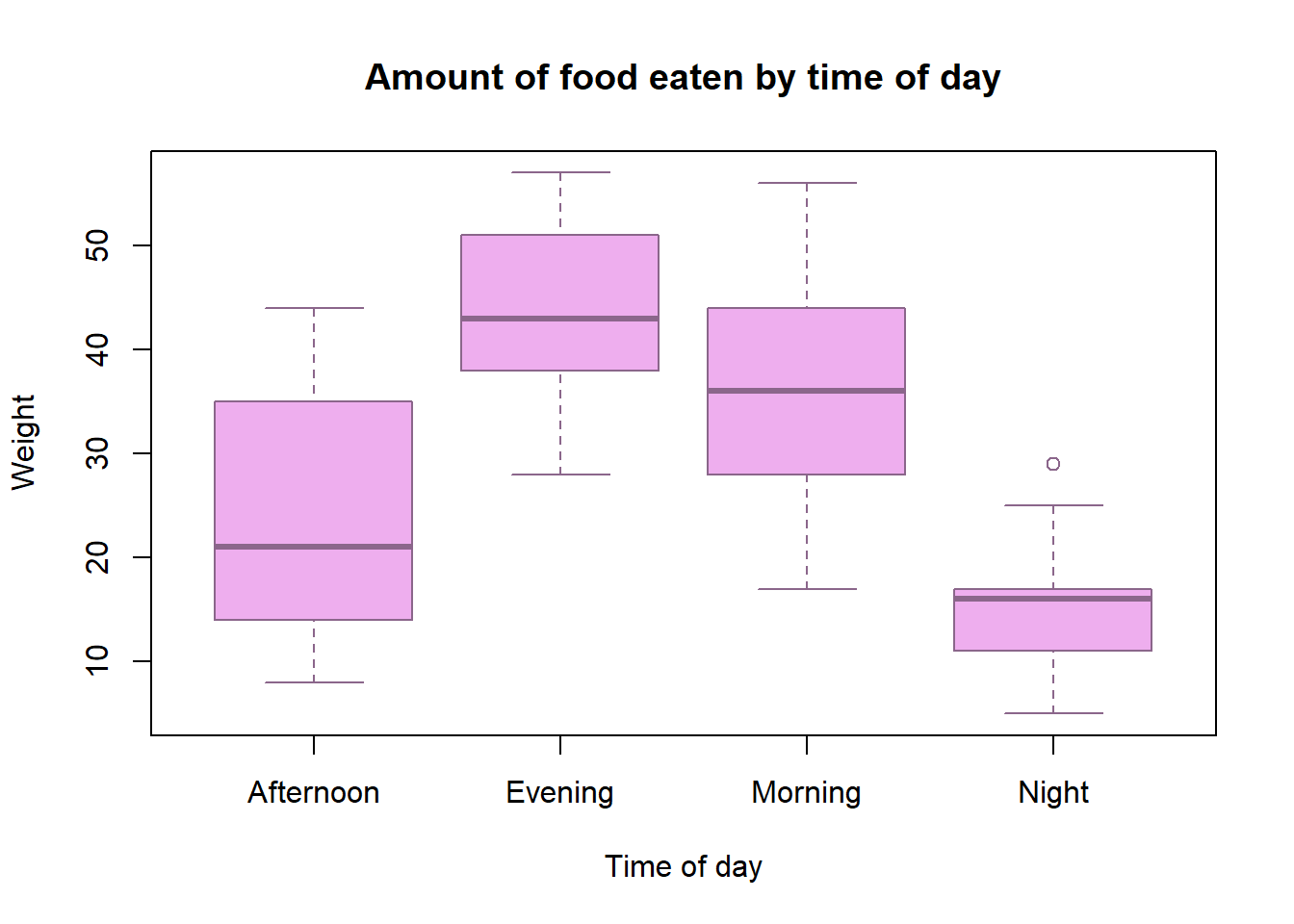
Observa-se que o grupo Afternoon difere bastante dos grupos Evening e Morning, e o grupo Night difere dos grupos Evening e Morning, como se concluiu também com o teste de Tukey.
De seguida, implementamos o teste de Newman-Keuls no R, através da função SNK.test() (também requer o package agricolae).
## $statistics
## MSerror Df Mean CV
## 101.8255 50 29.92593 33.71946
##
## $parameters
## test name.t ntr alpha
## SNK time 4 0.05
##
## $snk
## NULL
##
## $means
## wght std r Min Max Q25 Q50 Q75
## Afternoon 23.69231 12.756597 13 8 44 14.00 21 35.0
## Evening 44.00000 7.854445 14 28 57 38.25 43 50.5
## Morning 36.61538 12.093652 13 17 56 28.00 36 44.0
## Night 15.42857 6.687696 14 5 29 11.25 16 17.0
##
## $comparison
## NULL
##
## $groups
## wght groups
## Evening 44.00000 a
## Morning 36.61538 a
## Afternoon 23.69231 b
## Night 15.42857 c
##
## attr(,"class")
## [1] "group"O teste incluiu os grupos Evening e Morning no grupo a, uma vez que são os mais semelhantes entre si.
Agora, uma implementação de teste de Scheffe, através da função ScheffeTest(), que requer o package DescTools.
## Registered S3 method overwritten by 'DescTools':
## method from
## reorder.factor gdata##
## Attaching package: 'DescTools'## The following object is masked from 'package:gdata':
##
## reorder.factor##
## Posthoc multiple comparisons of means: Scheffe Test
## 95% family-wise confidence level
##
## $time
## diff lwr.ci upr.ci pval
## Evening-Afternoon 20.307692 9.063252 31.552132 6.5e-05 ***
## Morning-Afternoon 12.923077 1.472300 24.373854 0.0207 *
## Night-Afternoon -8.263736 -19.508176 2.980704 0.2241
## Morning-Evening -7.384615 -18.629055 3.859825 0.3182
## Night-Evening -28.571429 -39.605674 -17.537183 2.9e-08 ***
## Night-Morning -21.186813 -32.431253 -9.942373 3.1e-05 ***
##
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Para o Evening-Afternoon, Night-Evening e o Night-Morning rejeita-se H0 para todos os níveis usuais de significância e também para o nível ajustado pelo próprio teste, correspondente a 0.001. Para o Morning-Afternoon, rejeita-se H0 para um nível de significância de 0.05 e acima.
Os pares Night-Afternoon e Morning-Evening são os mais semelhantes, e o seu p-value excede os níveis usuais de significância, logo a H0 não será rejeitada.
Finalmente, implementamos em R o teste de Dunn, utilizando a função dunn.test(), que requer o package dunn.test.
## Kruskal-Wallis rank sum test
##
## data: x and group
## Kruskal-Wallis chi-squared = 29.9628, df = 3, p-value = 0
##
##
## Comparison of x by group
## (No adjustment)
## Col Mean-|
## Row Mean | Afternoo Evening Morning
## ---------+---------------------------------
## Evening | -3.562245
## | 0.0002*
## |
## Morning | -2.289555 1.230676
## | 0.0110* 0.1092
## |
## Night | 1.316442 4.971623 3.648011
## | 0.0940 0.0000* 0.0001*
##
## alpha = 0.05
## Reject Ho if p <= alpha/2Este teste dá-nos um alfa = 0.05 e o critério de rejeição para a H0 é se o p-value for menor ou igual a alpha/2, isto é, 0.025. Segundo este critério, rejeitamos a H0 para os grupos Evening-Afternoon, Morning-Afternoon, Night-Evening e Night-Morning, o que bate certo com os resultados do teste de Tukey, pois, assumindo um valor crítico de 0.05 também chegamos a esta conclusão.
15.4 Exemplos reais de aplicação
1:
Fidalgo, V. (2012). Ecologia trófica da Gaivota de patas-amarelas (Larus michahellis) e do Pintainho (Puffinus baroli): uma abordagem isotópica em áreas costeiras e pelágicas, Universidade de Coimbra (online)
O intuito deste trabalho consistiu em avaliar a ecologia trófica de duas espécies de aves marinhas, utilizando para isso uma abordagem isotópica, que consistiu na comparação dos rácios de isótopos de carbono (δ 13C) e azoto (δ15N) em tecidos sintetizados em diferentes épocas do ano (sangue, que em algumas análises se dividiu em células e plasma, e diferentes tipos de penas). No caso da Gaivota de patas-amarelas, para obter os valores isotópicos do sangue na sua totalidade (separado em células sanguíneas e plasma aquando do trabalho de campo) fez-se a média entre os valores isotópicos das células sanguíneas e do plasma. Posteriormente, para verificar se existia uma variação sazonal na ecologia trófica da Gaivota de patas-amarelas, comparam-se os diferentes tecidos (sangue e penas) entre si quanto aos valores de δ15N e δ13C, utilizando-se para isso a ANOVA de uma via. E para determinar quais tecidos apresentavam diferenças significativas entre si recorreu-se ao teste post-hoc de Tukey. No caso dos Pintainhos, para verificar se existiam diferenças na ecologia trófica de duas colónias distintas, compararam-se, através de uma ANOVA de duas vias, os valores de δ15N e δ13C entre os diferentes tipos de pena, as duas colónias e a interação entre estes dois factores. Após se verificar que existiam diferenças significativas, foi aplicado um teste post-hoc de Tuckey, para determinar quais os tecidos que apresentavam diferenças entre as duas colónias.
2:
https://pdfs.semanticscholar.org/bc99/6c50f54aa102cbeab3cc8fbaf3f7f4c32028.pdf
Johnson, K., Grabowski, J. and Smee, D. (2014). Omnivory dampens trophic cascades in estuarine communities. Marine Ecology Progress Series, [online] 507, pp.197–206.
Entender como os predadores de topo e intermédios afetam a estrutura da comunidade, isolando os efeitos predatórios e a sua influência ao nível das ostras e caranguejos. Usou-se um teste Tukey-Kramer para comparar de modo emparelhado as diferenças entre tratamentos que utilizaram diferentes tamanhos de caixas (de forma a excluir diferentes predadores) e os controlo.
3:
https://doi.org/10.1371/journal.pone.0148296
Lopes, F. A., Catão, E. C., Santana, R. H., Cabral, A., Paranhos, R., Rangel, T. P., de Rezende, C. E., Edwards, R. A., Thompson, C. C., Thompson, F. L., & Kruger, R. H. (2016). Microbial Community Profile and Water Quality in a Protected Area of the Caatinga Biome. PloS one, 11(2), e0148296.
Avaliação do efeito da proteção por parte do Parque Nacional da Chapada Diamantina sobre a qualidade da água e diversidade microbiana do rio Paraguaçu. Os valores dos parâmetros físico-químicos e microbianos das amostras de água, retiradas de locais distintos em diferentes estações, foram comparados por ANOVA (α <0,05), seguido de um teste de Tukey, com recurso ao R.
4:
https://sci-hub.st/https://doi.org/10.1111/j.1461-0248.2009.01383.x
Van de Waal, D. B., Verspagen, J. M. H., Lürling, M., Van Donk, E., Visser, P. M., & Huisman, J. (2009). The ecological stoichiometry of toxins produced by harmful cyanobacteria: an experimental test of the carbon-nutrient balance hypothesis. Ecology Letters, 12(12), 1326–1335.
Paper sobre composição das toxinas produzidas por bactérias em condições diferentes de limitação de carbono, nitrogénio ou luz. Foi então usado o teste de Tukey HSD para averiguar se existem ou não diferenças significativas entre estes grupos.
5:
Viana, D., Oliveira, A., Junior, J., Santos, A., Carvalho, A. (2012). The study of tests of average comparisons through the analysis of biochemical values of creatine obtained of four zebuine breeds. 32. 17-22.
Neste trabalho foi efetuado um estudo sobre os testes de comparações de médias, através da análise dos valores bioquímicos de creatinina obtidos de quatro raças zebuínas diferentes. Para isso foram usados os testes de comparações de médias: Tukey, Duncan, Dunnett, Scheffé e Student Newman Keuls (SNK). Sendo que o objetivo consistia em verificar qual era o teste mais adequado para explicar a resposta dos dados obtidos de maneira mais detalhada.
15.5 Recursos adicionais
Abdi, Herve & Williams, Lynne. (2010). Newman-Keuls Test and Tukey Test. Encyclopedia of Research Design;
Haynes W. (2013) Tukey’s Test. In: Dubitzky W., Wolkenhauer O., Cho KH., Yokota H. (eds) Encyclopedia of Systems Biology. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-9863-7_1212;
PowerPoint referente à aula teórica número 15 lecionada no dia 3 de Novembro;
Statistics Solutions. (2012). Bonferroni Correction - Statistics Solutions. Available at: https://www.statisticssolutions.com/bonferroni-correction/, acessado no dia 17 de Novembro de 2020;
Stephanie Glen. “Tukey Test/ Tukey Procedure/Honest Significant Difference” FromStatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/tukey-test-honest-significant-difference/, acessado no dia 16 de Novembro de 2020.
- Este site tem definições dos testes específicos, aconselhamos explorarem.
15.6 Considerações finais
Consideramos que as informações mais relevantes já foram incluídas nos tópicos acima.
15.7 Referências
Abdi, Herve & Williams, Lynne. (2010). Newman-Keuls Test and Tukey Test. Encyclopedia of Research Design;
Fidalgo, V. (2012). Ecologia trófica da Gaivota de patas-amarelas (Larus michahellis) e do Pintainho (Puffinus baroli): uma abordagem isotópica em áreas costeiras e pelágicas, Universidade de Coimbra (online)
Johnson, K., Grabowski, J. and Smee, D. (2014). Omnivory dampens trophic cascades in estuarine communities. Marine Ecology Progress Series, [online] 507, pp.197–206.
Haynes W. (2013) Tukey’s Test. In: Dubitzky W., Wolkenhauer O., Cho KH., Yokota H. (eds) Encyclopedia of Systems Biology. Springer, New York, NY. https://doi.org/10.1007/978-1-4419-9863-7_1212;
Lopes, F. A., Catão, E. C., Santana, R. H., Cabral, A., Paranhos, R., Rangel, T. P., de Rezende, C. E., Edwards, R. A., Thompson, C. C., Thompson, F. L., & Kruger, R. H. (2016). Microbial Community Profile and Water Quality in a Protected Area of the Caatinga Biome. PloS one, 11(2), e0148296.
PowerPoint referente à aula teórica número 15 lecionada no dia 3 de Novembro;
Statistics Solutions. (2012). Bonferroni Correction - Statistics Solutions. Available at: https://www.statisticssolutions.com/bonferroni-correction/, acessado no dia 17 de Novembro de 2020;
Stephanie Glen. “Tukey Test/ Tukey Procedure/Honest Significant Difference” FromStatisticsHowTo.com: Elementary Statistics for the rest of us! https://www.statisticshowto.com/tukey-test-honest-significant-difference/, acessado no dia 16 de Novembro de 2020.
Van de Waal, D. B., Verspagen, J. M. H., Lürling, M., Van Donk, E., Visser, P. M., & Huisman, J. (2009). The ecological stoichiometry of toxins produced by harmful cyanobacteria: an experimental test of the carbon-nutrient balance hypothesis. Ecology Letters, 12(12), 1326–1335.
Viana, D., Oliveira, A., Junior, J., Santos, A., Carvalho, A. (2012). The study of tests of average comparisons through the analysis of biochemical values of creatine obtained of four zebuine breeds. 32. 17-22.