Chapter 10 Tema
Existem pressupostos para testes paramétricos que podem ser usadas para modelar dados ecológicos. Neste tema pretende-se que apresentem os pressupostos dos testes paramétricos dando exemplos da sua utilização.
10.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- Catarina Barros 49324
- David Cabral 52547
- Gonçalo Graça 52536
- Miguel Leal e Rigor 53508
- Rafael Ricardo 52616
- Syra Alves 52667
10.2 Introdução Teórica
Para testarmos uma hipótese sobre um conjunto de dados podemos aplicar vários testes estatísticos. Estes estão divididos em dois grupos: testes paramétricos e testes não paramétricos.
10.2.0.1 Testes não paramétricos
Para a aplicação de um teste não-paramétrico, não são requeridos nenhum tipo de pressupostos, à exceção da independência das observações. Estes testes são muitas vezes usados quando se tem conhecimento que a distribuição das observações não é normal ou quando não existem dados suficientes para poder afirmar que o seja (quando n<30 - Teorema do Limite Central) Além disto, são utilizados em casos de variáveis medidas erm escalas ordinais e intervaladas ou de razão. No entanto existe a possibilidade de transformar os dados das observações de maneira a poder aplicar nos mesmos os testes paramétricos.
10.2.0.2 Testes paramétricos
Para podermos aplicar um teste paramétrico num conjunto de amostras é necessário que estas verifiquem três pressupostos: - A independência das observações - Distruibuição normal dos resíduos (erros) - Variâncias homogéneas (variâncias iguais) Ao contrário dos testes não-paramétricos, os paramétricos precisam de váriaveis, pelo menos, medidas em escalas intervaladas.
10.2.0.2.1 Testes formais e avaliação gráfica
É possível avaliar os pressupostos com testes formais ou a partir da análise de gráficos.
Independência das observações
Para analisar a independência das observações não é comum aplicar qualquer tipo de teste pois é um tipo de informação que já é suposto ter-se considerada à priori.
Distribuição Gaussiana
No que toca à distribuição normal dos resíduos das observações podem aplicar-se diversos testes de ajustamento, destacando o Teste de Kolmogorov-Smirnov, o Teste D’Agostino-Pearson e o Teste de Shapiro-Wilk.
Todos estes testes baseiam-se num mesmo princípio: se as amostras forem de facto gaussianas, estas apresentaram um conjunto de características conhecidas de uma distruibuição gaussiana. Estes testes verificam a normalidade dos dados através da rejeição ou da não-rejeição da H0 (hipótese nula) que afirma que a distruibuição é Gaussiana ou da H1 (hipótese alternativa) que nega a distribuição Gaussiana. Depois de aplicado o teste, este apresenta-nos um p-value que consoante este ser menor ou maior que um valor de significância (α) a decidir previamente, rejeitamos ou não a H0 (se p-value < α, rejeitamos a H0, se p-value > α, não rejeitamos H0).
No entanto, apesar dos testes avaliarem o mesmo pressuposto, os mesmos utilizam estatísticas de teste diferentes, o que pode levar a valores-p diferentes e consequentemente a uma decisão diferente em relação a rejeitar a H0.
Para além dos testes formais podemos ainda avaliar os nossos dados através de gráfico quantil-quantil (Q-Q) que nos permitem compreender o quão próximo estão as nossas observações de uma determinada distribuição.
Homogeneidade de variâncias
No que toca homogeneidade das variâncias podem aplicar-se diversos testes de homocedasticidade, destacando o Teste de Hartley, o Teste de Cochran e o Teste de Bartlett.
Ao aplicar estes testes vamos testar a H0 que diz que as variâncias são iguais. Caso o p-value < α, rejeitamos a H0, caso o p-value > α, não se rejeita H0.
Tal como nos testes de normalidade, os testes de homocedasticidade também apresentam estatístiscas de teste diferentes que podem levar a valores-p diferentes.
É de salientar que estes testes não são perfeitos e que podem levar a uma não rejeição de uma H0 falsa (erro do tipo II) ou a uma rejeição de uma H0 verdadeira (erro do tipo I).
10.3 Exemplo em R
Os dados utilizados para aplicar os testes estatísticos como exemplo envolvem o tempo (em segundos) que um pato-real demora até pegar no alimento, a diferentes distâncias (em metros). Realizaram-se 50 observações de patos macho e fêmea, com o alimento a diferentes distâncias e em diferentes dias, com consequentes temperaturas diferentes.
## ID tempo sexo dstnc tmprt
## 1 1 8.43 Femea 3.5 27
## 2 2 5.07 Macho 3.0 27
## 3 3 5.69 Macho 2.5 27
## 4 4 3.11 Femea 1.5 27
## 5 5 2.09 Macho 2.0 27
## 6 6 2.10 Macho 1.0 27
## 7 7 3.90 Femea 1.5 27
## 8 8 9.45 Macho 3.5 27
## 9 9 12.43 Macho 5.0 27
## 10 10 4.30 Femea 3.0 27
## 11 11 2.92 Femea 1.5 27
## 12 12 10.20 Macho 4.0 27
## 13 13 3.74 Macho 3.5 27
## 14 14 2.18 Macho 1.0 27
## 15 15 3.80 Macho 1.5 27
## 16 16 8.45 Femea 3.5 24
## 17 17 3.30 Macho 1.5 24
## 18 18 4.03 Macho 3.0 24
## 19 19 2.34 Femea 1.5 24
## 20 20 3.54 Femea 3.0 24
## 21 21 3.23 Macho 3.0 24
## 22 22 5.12 Femea 3.5 24
## 23 23 4.65 Macho 1.5 24
## 24 24 4.20 Femea 1.5 24
## 25 25 3.90 Femea 1.0 24
## 26 26 3.28 Macho 1.0 24
## 27 27 8.74 Macho 4.0 24
## 28 28 3.45 Macho 1.5 24
## 29 29 13.21 Macho 5.0 24
## 30 30 4.23 Femea 1.5 24
## 31 31 4.10 Femea 3.0 23
## 32 32 11.10 Macho 4.5 23
## 33 33 3.10 Femea 1.0 23
## 34 34 2.79 Macho 1.0 23
## 35 35 3.40 Femea 3.0 23
## 36 36 4.32 Femea 2.5 23
## 37 37 11.65 Macho 5.0 23
## 38 38 9.34 Macho 4.0 23
## 39 39 3.21 Macho 3.0 23
## 40 40 5.40 Femea 3.5 23
## 41 41 2.89 Macho 1.0 23
## 42 42 14.30 Femea 5.0 23
## 43 43 3.45 Macho 1.5 23
## 44 44 4.32 Femea 3.0 23
## 45 45 3.45 Macho 1.5 23
## 46 46 4.32 Femea 3.0 23
## 47 47 3.40 Femea 1.5 23
## 48 48 2.89 Femea 1.0 23
## 49 49 3.43 Macho 1.0 23
## 50 50 11.20 Femea 4.5 23##
## Attaching package: 'moments'## The following object is masked from 'package:modeest':
##
## skewness10.3.0.1 Testes de normalidade
Para decidir que tipo de teste (paramétrico ou não paramétrico) utilizar para analizar a variável “tempo”, iremos aplicar diversos testes de normalidades para podermos concluir sobre este pressuposto.
10.3.0.1.0.1 Teste de Kolmogorov-Smirnov
##
## One-sample Kolmogorov-Smirnov test
##
## data: dados$tempo
## D = 0.98169, p-value < 2.2e-16
## alternative hypothesis: two-sided10.3.0.1.0.2 Teste de Shapiro-Wilk
##
## Shapiro-Wilk normality test
##
## data: dados$tempo
## W = 0.78252, p-value = 3.55e-0710.3.0.1.0.3 Teste de D’Agostino-Pearson
##
## D'Agostino skewness test
##
## data: dados$tempo
## skew = 1.3157, z = 3.4984, p-value = 0.000468
## alternative hypothesis: data have a skewnessPela observação dos p-values, concluimos que rejeitamos a hipótese nula pois estes são, para os testes 3 feitos, muito baixos. Assim, assumimos que as observações não provêm de uma população com distribuição normal, pelo que teriamos ou de aplicar um teste não paramétrico ou uma transformação.
Para reforçar e confirmar a nossa conclusão, podemos ainda recorrer há análise de um gráfico Q-Q.
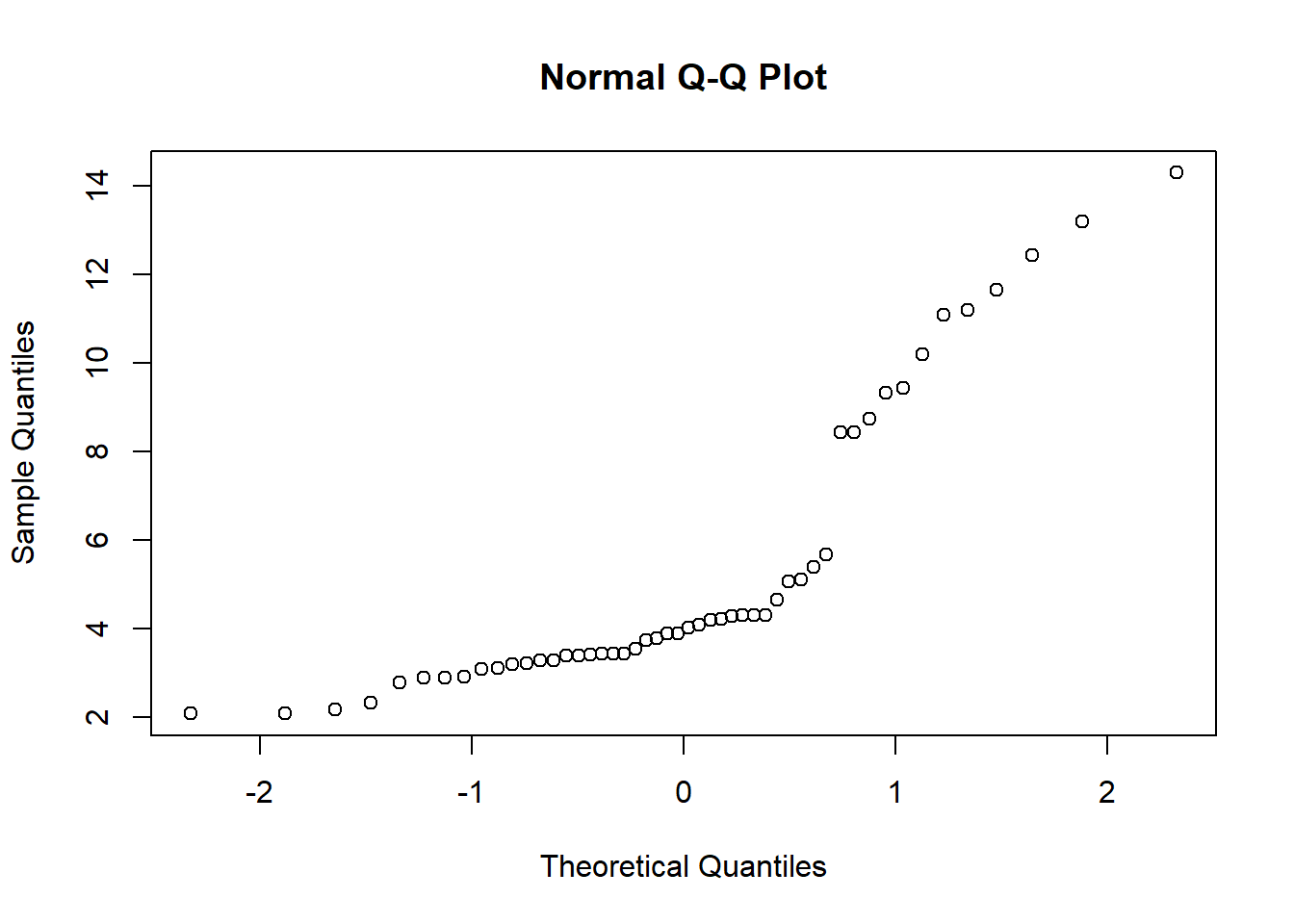
Pela análise do gráfico, podemos verificar que, para o número de observações que temos, os pontos não aparentam formar uma linha reta do tipo x=y, pelo nos faz ter mais certezas de que estas amostras não provêm de uma população com distribuição gaussiana.
10.3.0.2 Testes de homogeneidade de variâncias
Dentro da variável “tempo”, iremos analisar a homogeneidade das variâncias entre machos e fêmeas.
10.3.0.2.0.1 Teste de Bartlett
##
## Bartlett test of homogeneity of variances
##
## data: dados$tempo by dados$sexo
## Bartlett's K-squared = 1.013, df = 1, p-value = 0.314210.3.0.2.0.2 Teste de Cochran
var1<-var(c(5.07,5.69,2.09,2.10,9.45,12.43,10.20,3.74,2.18,3.80,3.30,4.03,3.23,4.65,3.28,8.74,3.45,13.21,11.10,2.79,11.65,9.34,3.21,2.89,3.45,3.45,3.43))
var2<-var(c(8.43,3.11,3.90,4.30,2.92,8.45,2.34,3.54,5.12,4.20,3.90,4.23,4.10,3.10,3.40,4.32,5.40,14.30,4.32,4.32,3.40,2.89,11.20))
cochran.test(c(var1,var2),c(27,23))##
## Cochran test for outlying variance
##
## data: c(var1, var2)
## C = 0.60362, df = 25, k = 2, p-value = 0.3097
## alternative hypothesis: Group 1 has outlying variance
## sample estimates:
## 1 2
## 12.833187 8.42718810.3.0.2.0.3 Teste de Hartley
Devido ao facto de não exisitir uma fórmula no R para a aplicação deste, o mesmo não será apresentado neste relatório.
Pela observação dos p-values, concluimos que não rejeitamos a hipótese nula pois estes são, para os 2 testes feitos, relativamente altos. Assim, conclui-se que as vâriancias são suficientemente homogéneas para estes dados cumprirem o pressuposto da homocedasticidade.
10.4 Exemplos reais de aplicação
https://www.sciencedirect.com/science/article/pii/S0301479719312927
O seguinte paper científico procurava otimizar, a nível ecológico e de forma sustentável, as práticas de restauração das zonas dunares costeiras e dos seagrass meadows. Foram criados recipientes biodegradáveis feitos a partir de algas marinhas e de um polímero bio-based para crescimento de plantas a partir de sementes. As espécies utilizadas foram as algas Cymodocea nodosa e Zostera noltei e as plantas dunares Euphorbia paralias e Thinopyrum junceum. O controlo utilizado na experiência foram os típicos recipientes de plástico já usados nestas práticas. No final do estudo, comprovou-se que os recipientes biodegradáveis melhoraram a performance das plantas em estudo a nível de crescimento, de colonização das áreas circundantes onde foram plantadas e que efetivamente estes se degradavam, quer em água, quer na areia, ao final de 3 anos. Nesta experiência, foram usados os testes de Shapiro-Wilk e Cochran para testar a distribuição Gaussiana e a homogeneidade das variâncias dos resultados obtidos, respetivamente, para poderem prosseguir com a utilização de uma ANOVA.
https://periodicos.ufsc.br/index.php/biotemas/article/view/2175-7925.2010v23n4p71/15977
Este artigo científico procurava estudar os impactos que a fragmentação do ecossistema das restingas – habitats de plantas que estão nos cordões dunares e que cobrem grande parte do litoral do Estado da Bahia, no Brasil - têm sobre o microhabitat ocupado pelo lagarto endémico Tropdurus hygomi. A conclusão do estudo provou que não houve uma redução dos recursos utilizados pela espécie. A normalidade dos dados obtidos - complexidade estrutural do ambiente (número de plantas presente, altura da cobertura e frequência das clareiras), distúrbio causado pelo Homem e o uso do habitat pela espécie - foi avaliada pelo teste D’Agostino-Pearson. Posteriormente foi feito o teste paramétrico ANOVA.
10.5 Recursos adicionais
http://www.forp.usp.br/restauradora/gmc/gmc_livro/gmc_livro_cap14.html
http://sweet.ua.pt/andreia.hall/Bioestat%C3%ADstica/TH2006continua.pdf
10.6 Considerações finais
Existem ainda outros tópicos relacionados com o nosso tema que poderiam ser mais aprofundados (como por exemplo, as transformações) mas que estão presentes nos temas dos trabalhos dos outros grupos.
10.7 Referências
https://www.sciencedirect.com/science/article/pii/S0301479719312927
https://periodicos.ufsc.br/index.php/biotemas/article/view/2175-7925.2010v23n4p71/15977
http://www.forp.usp.br/restauradora/gmc/gmc_livro/gmc_livro_cap14.html
http://sweet.ua.pt/andreia.hall/Bioestat%C3%ADstica/TH2006continua.pdf