Chapter 9 Tema
O valor de p (\(p-value\)), a hipótese nula e a hipótese alternativa são conceitos que têm um papel central na tomada de decisão na análise de dados ecológicos. Neste tema pretende-se que apresentem exemplos da sua utilização aplicada a dados ecológicos.
9.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- Alex Marnoto 52586
- Catarina Bernardo 52632
- Inês Pina 49211
- Luís Bastos 47948
- Sara Santos 43092
- Sofia Machado 53662
9.2 Introdução Teórica
Quando se pretende responder a uma questão ecológica, formula-se uma hipótese que depois será testada. Esta hipótese é denominada hipótese nula (H0) e expressa o conceito de igualdade (i.e., inexistência de diferenças). De seguida, formula-se também uma hipótese alternativa (HA ou H1) que tem a função de complementar H0 (i.e., há pelo menos uma diferença).
Por exemplo:
- H0 - As médias da velocidade das formigas no sentido do formigueiro e no sentido oposto são iguais.
- H1 - As médias da velocidade das formigas no sentido do formigueiro e no sentido oposto são diferentes.
A forma como se testam essas hipóteses é através de um teste de hipóteses em que se calcula a probabilidade, sendo H0 verdadeira, de obter um resultado tão extremo para a estatística de teste como o observado com base numa determinada amostra. Esta probabilidade é o p-value.
O p-value pode ser dado por um teste unilateral “à direita” ( P(X>x | H0 ) ), um teste bilateral - o dobro da probabilidade da menor cauda - (2*min(P(X>x | H0), P(X<x | H0)) ou por um teste unilateral “à esquerda” ( P(X<x | H0) ).
Abaixo encontram-se representações gráficas do que é um p-value:
plot(seq(-5, 5, by=0.001), dt(seq(-5, 5, by=0.001), df=3), type="l", lwd=2, xlab="Possibilidade de valores de estatística de teste", ylab="Densidade", main="Distribuição t com 3 graus de liberdade")
points(seq(2.5, 5, by=0.001), dt(seq(2.5, 5, by=0.001), df=3), type="l", lwd=3, col="red")
abline(v=2.5, col="blue", lwd=2)
text(3.95, 0.31, "Valor da estatística")
text(3.95, 0.29, "de teste")
text(4, 0.04, "p-value")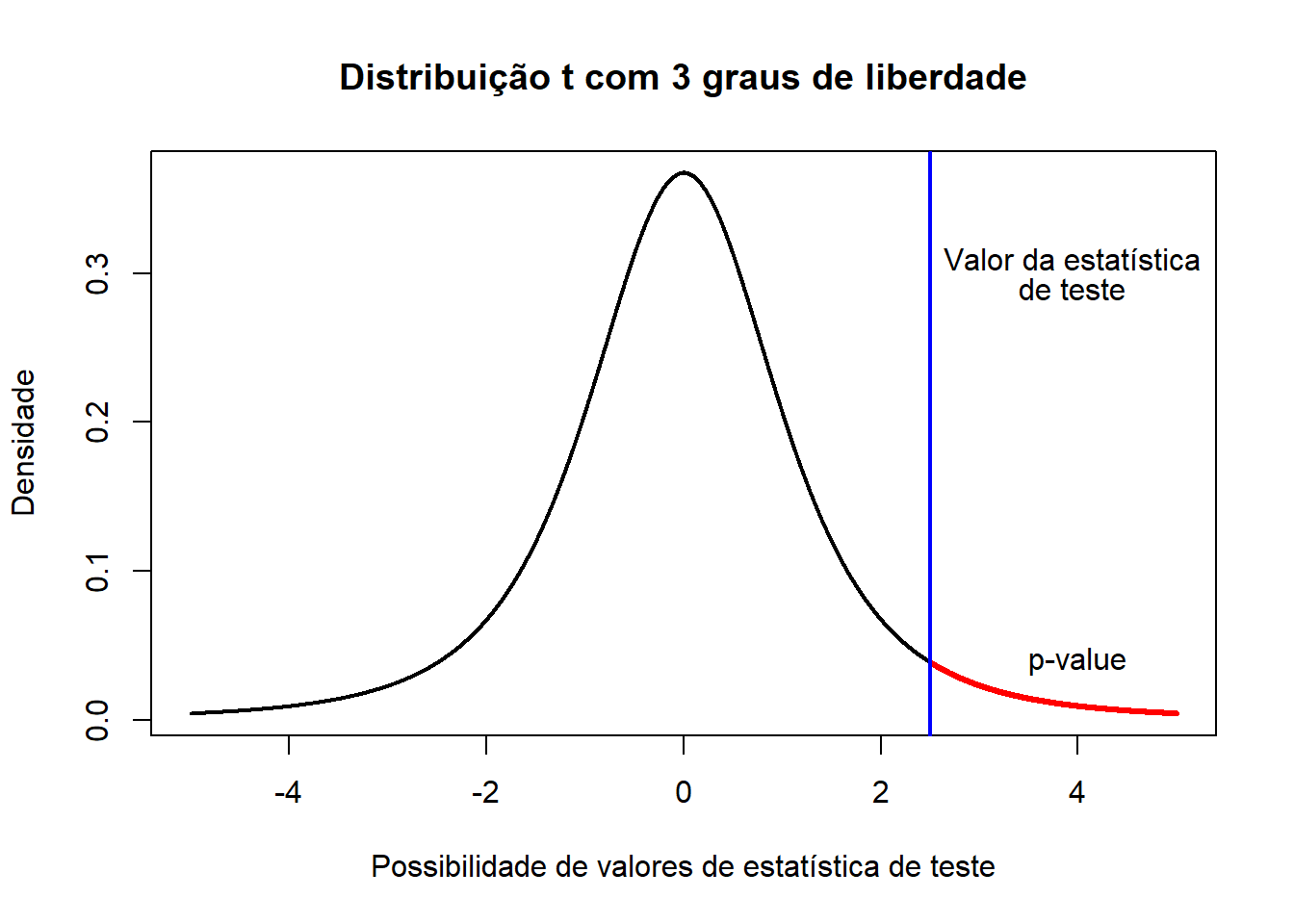
Realizou-se um teste-t unilateral “à direita” em que a estatística de teste deu 2.5. O p-value é então a área da função que se encontra à direita do valor da estatística de teste, que neste caso pode ser calculada no R da seguinte forma:
## [1] 0.04385332plot(seq(-5, 5, by=0.001), dt(seq(-5, 5, by=0.001), df=3), type="l", lwd=2, xlab="Possibilidade de valores de estatística de teste", ylab="Densidade", main="Distribuição t com 3 graus de liberdade")
points(seq(-5, -3.5, by=0.001), dt(seq(-5, -3.5, by=0.001), df=3), type="l", lwd=3, col="red")
abline(v=-3.5, col="blue", lwd=2)
text(-2, 0.31, "Valor da estatística")
text(-2, 0.29, "de teste")
text(-4.5, 0.04, "p-value")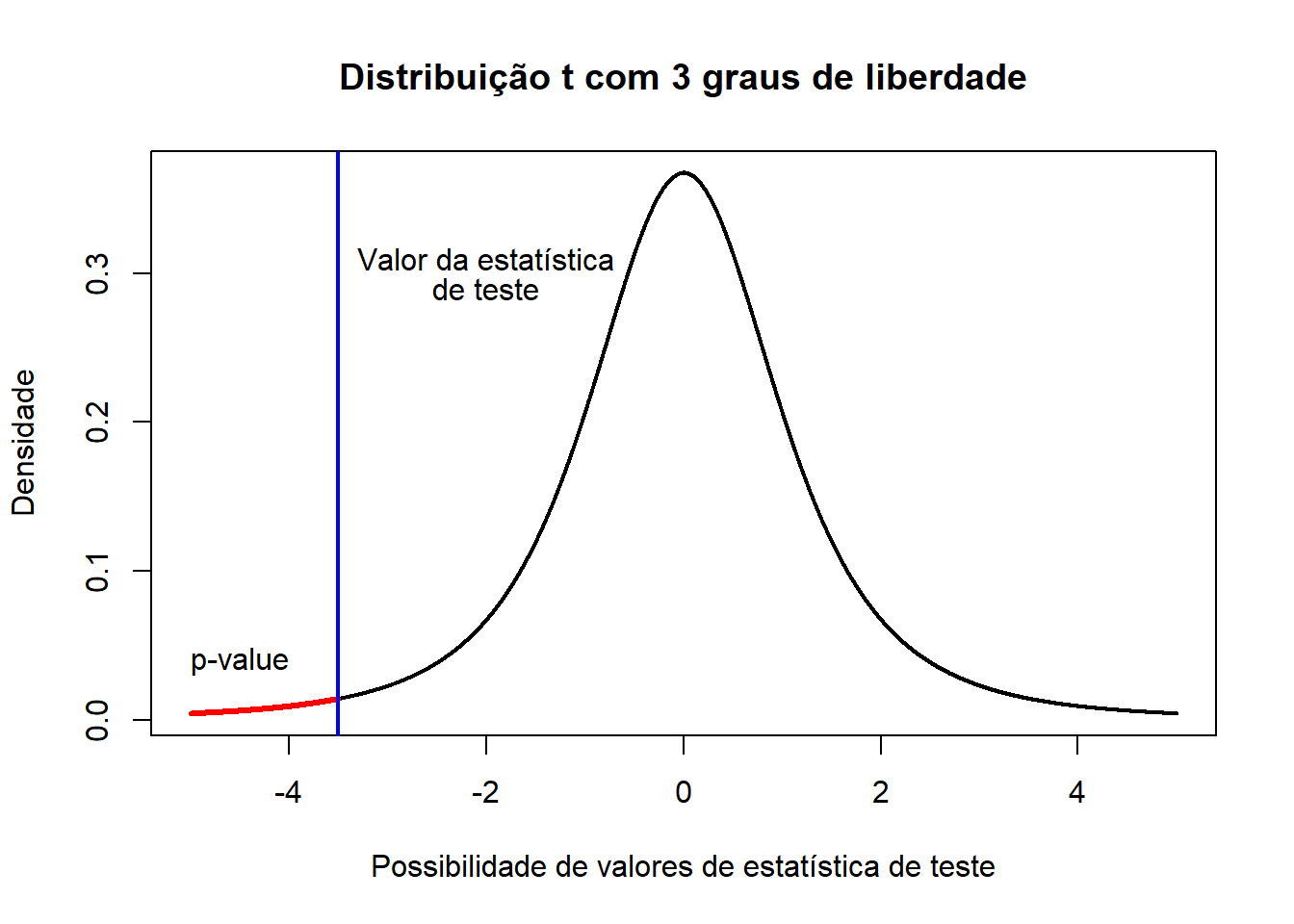
Realizou-se um teste-t unilateral “à esquerda” em que a estatística de teste deu -3.5. O p-value é então a área da função que se encontra à esquerda do valor da estatística de teste, que neste caso pode ser calculada no R da seguinte forma:
## [1] 0.01974052plot(seq(-5, 5, by=0.001), dt(seq(-5, 5, by=0.001), df=3), type="l", lwd=2, xlab="Possibilidade de valores de estatística de teste", ylab="Densidade", main="Distribuição t com 3 graus de liberdade")
points(seq(-5, -3.5, by=0.001), dt(seq(-5, -3.5, by=0.001), df=3), type="l", lwd=3, col="red")
abline(v=-3.5, col="blue", lwd=2)
points(seq(3.5, 5, by=0.001), dt(seq(3.5, 5, by=0.001), df=3), type="l", lwd=3, col="red")
abline(v=3.5, col="blue", lwd=2)
text(-2, 0.31, "Valor da estatística")
text(-2, 0.29, "de teste")
text(-4.5, 0.04, "p-value")
text(4.5, 0.04, "p-value")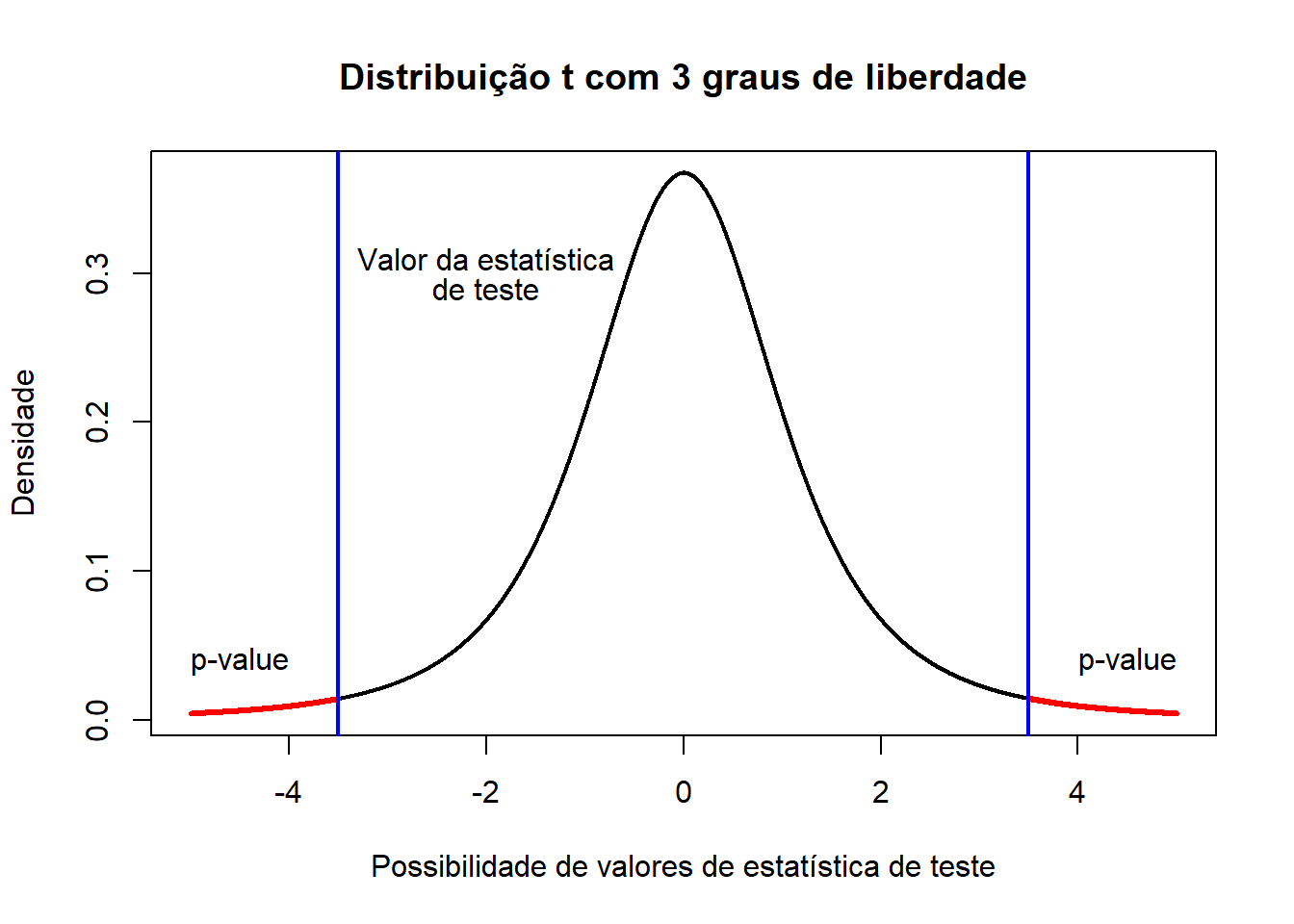
Realizou-se um teste-t bilateral em que a estatística de teste pode dar -3.5 ou 3.5. O p-value é então a área da função que se encontra a vermelho, que neste caso pode ser calculada no R da seguinte forma:
## [1] 0.03948104Ou então:
## [1] 0.03948104Isto porque, neste caso, como a distribuição t é simétrica, é indiferente a cauda cuja área se multiplica por 2. Mas se a distribuição fosse assimétrica, como, por exemplo, a distribuição qui-quadrado ou a de Fisher (ANOVA), teria de se multiplicar a menor área das caudas por 2.
O p-value deve depois ser comparado com um valor de significância (\(\alpha\)) considerado a priori. Vários níveis de significância podem ser utilizados para fazer referência ao p-value, sendo os valores mais usuais: 0.1, 0.05 e 0.01.
Se o p-value for menor ou igual ao nível de significância desejado, rejeita-se H0. Se for maior que o nível de significância desejado, não se rejeita H0.
No caso em que H0 não é rejeitada, não se diz que se aceita H0, apenas que não existem evidências para a rejeitar.
9.3 Exemplo em R
Para exemplificar este tema, foram utilizados parte dos dados do Trabalho 1 do aluno Alex Marnoto, que consistem na relação entre a velocidade média de deslocação das formigas e o sentido em que essa deslocação ocorre (sentido do formigueiro ou contrário ao mesmo).
#Para importar os dados
library(readxl)
ants <- read_excel("ants.xlsx")
#Para ver a estrutura dos dados
str(ants)## tibble [36 x 2] (S3: tbl_df/tbl/data.frame)
## $ formigueiro: num [1:36] 1.63 1.32 1.45 1.53 2.26 1.66 2.51 2.13 1.75 1.7 ...
## $ contrario : num [1:36] 1.4 1.3 1.27 1.78 1.51 1.07 1.96 1.76 1.65 2.32 ...## formigueiro contrario
## Min. :1.280 Min. :0.970
## 1st Qu.:1.583 1st Qu.:1.298
## Median :1.725 Median :1.535
## Mean :1.941 Mean :1.606
## 3rd Qu.:2.285 3rd Qu.:1.875
## Max. :3.090 Max. :2.780#Para obter uma representação gráfica dos dados
boxplot(ants, range=0, main="Velocidade média de formigas", ylab="Velocidade média (cm/s)", xlab="", names=c("Sentido Formigueiro", "Sentido Contrário"), col=c("darkorange1", "lightskyblue"))
#Média de sentido formigueiro
meanf <- mean(ants$formigueiro)
abline(h=meanf, col="darkred")
text(1, meanf+0.0825, bquote(bar(x) * " =" ~ .(round(meanf, 3)) * " cm/s"))
#Média de sentido contrário [ao formigueiro]
meanc <- mean(ants$contrario)
abline(h=meanc, col="blue")
text(2, meanc+0.0825, bquote(bar(x) * " =" ~ .(round(meanc, 3)) * " cm/s"))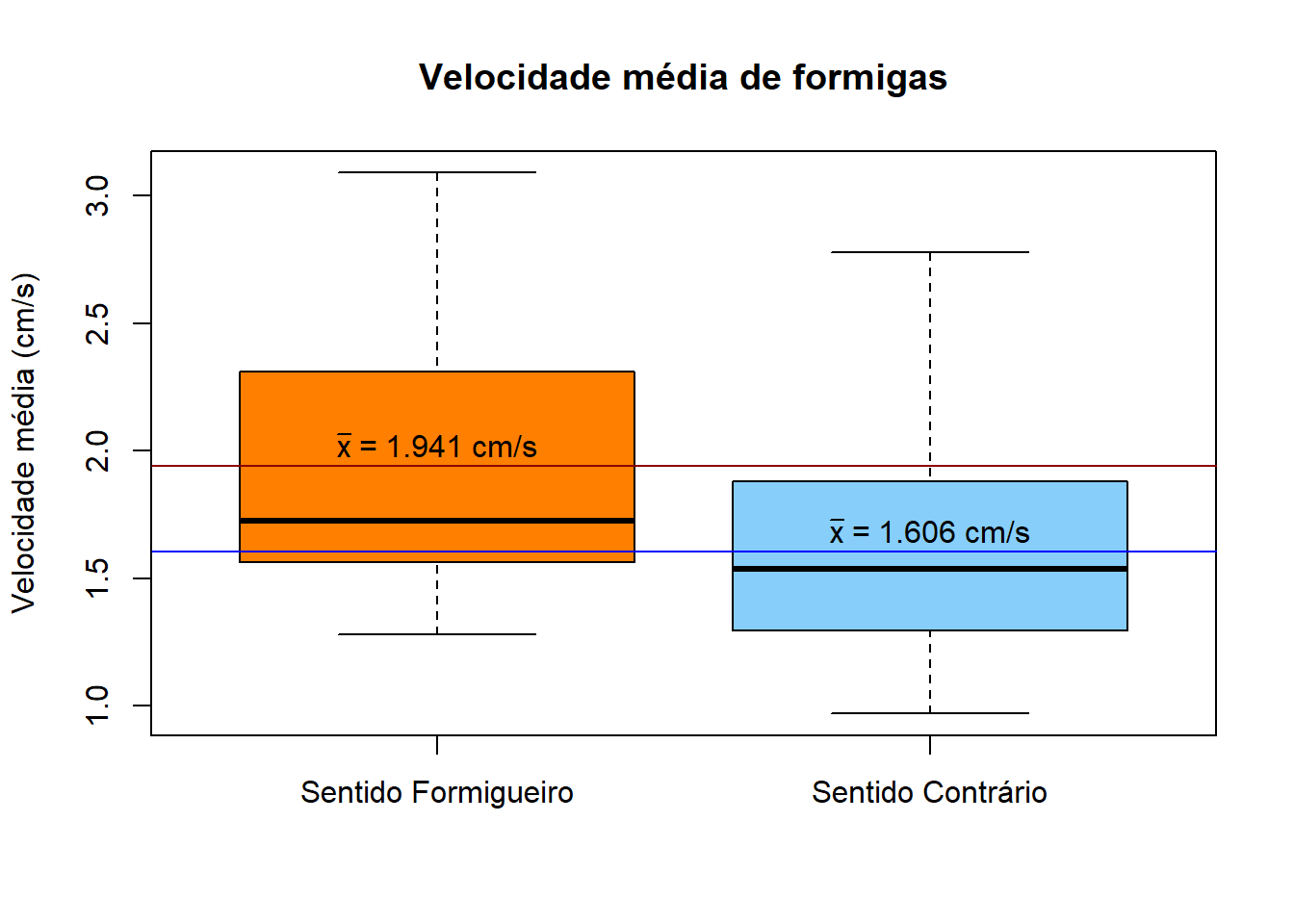
Neste exemplo a hipótese nula é a igualdade entre as médias das velocidades médias para cada um dos grupos - sentido formigueiro e sentido contrário. Diferentemente, a hipótese alternativa consiste na diferença entre as médias anteriores. Como apresentado no gráfico, os valores das velocidades no sentido do formigueiro aparentam ser superiores aos valores no sentido oposto.
Para testar se as médias são iguais ou não, poderá usar-se um teste não-paramétrico. Neste caso escolheu-se o teste de Mann-Whitney, em que a hipótese nula (H0) é que as médias dos grupos são iguais e a hipótese alternativa (H1) é que as médias dos grupos são diferentes.
##
## Wilcoxon rank sum test with continuity correction
##
## data: formigueiro and contrario
## W = 903, p-value = 0.00415
## alternative hypothesis: true location shift is not equal to 0O p-value é 0.00415, sendo inferior a qualquer um dos níveis usuais de significância (0.1, 0.05 e 0.01), logo rejeita-se H0, ou seja, não existem evidências para considerar que as médias sejam iguais.
Tendo em conta o acesso aos dados, é possível calcular os valores reais das médias (linhas nos boxplots). Os valores correspondem ao sentido do formigueiro e sentido contrário, respetivamente, 1.941 cm/s e 1.606 cm/s aproximadamente. Assim, não houve qualquer erro de decisão.
9.4 Exemplos reais de aplicação
Num estudo sobre populações de urso-polar, foram amostradas duas regiões - M’Clintock Channel (MC) e Gulf of Boothia (GB) - registando-se a distância máxima em linha reta entre locais em que cada indivíduo foi capturado, como forma de estimar o seu movimento (Campagna et al., 2013). Para comparar os padrões de movimento, foi posteriormente realizada uma análise de variância (ANOVA) de dois fatores: sexo e região. No caso do fator região, H0 é \(\mu_{reg_{MC}} = \mu_{reg_{GB}}\) e H1 é \(\mu_{reg_{MC}} ≠ \mu_{reg_{GB}}\), tendo os autores utilizado o nível de significância de 0.05. Obteu-se então \(F_{(1,52)}=\) 6.310 e um p-value de 0.015 e, como tal, os autores rejeitaram H0.
Noutro estudo pretendia-se determinar o potencial de dois compostos voláteis atrativos, nomeadamente, extratos de casca de Carica papaya (papaia) e de Ananas comosus (ananás) em duas espécies de insetos. No ensaio com Aedes aegypti, em que tinham ambos os extratos, os espécimes mostraram uma atração mais significativa ao extrato de casca de papaia (Nur Athen et al., 2020). Para tal, compararam uma amostra de um índice (Preference Index) com a média teórica se a escolha dos espécimes fosse 50/50. Utilizaram um teste-t para uma amostra, sendo H0: \(\mu = Y_{50/50}\) e H1: \(\mu ≠ Y_{50/50}\) e definiram o nível de significância de 0.05. Tendo obtido \(t_{(3)}=\) 4.60 e um p-value de 0.02, rejeitaram H0.
9.5 Recursos adicionais
9.6 Considerações finais
Este tema está interligado ao tema anterior “Testes de Hipóteses” e, portanto, para uma melhor compreensão de ambos, devem ser lidos conjuntamente.
9.7 Referências
Campagna, L. et al. (2013) “Extensive sampling of polar bears (Ursus maritimus) in the Northwest Passage (Canadian Arctic Archipelago) reveals population differentiation across multiple spatial and temporal scales”, Ecology and Evolution, 3(9), pp. 3152-3165. doi: 10.1002/ece3.662.
Ferreira, J. and Patino, C. (2015) “What does the p value really mean?”, Jornal Brasileiro de Pneumologia, 41(5), pp. 485-485. doi: 10.1590/s1806-37132015000000215.
Marques, T. (2020) “Slides Aula 9 13 10 2020”
Marques, T. (2020) “Slides Aula 10 19 10 2020”
Nur Athen, M., Nazri, C. and Siti Nazrina, C. (2020) “Bioassay studies on the reaction of Aedes aegypti & Aedes albopictus (Diptera: Culicidae) on different attractants”, Saudi Journal of Biological Sciences, 27(10), pp. 2691-2700. doi: 10.1016/j.sjbs.2020.06.016.