Chapter 4 Tema
Existem inúmeras distribuições teóricas que podem ser usadas para modelar dados ecológicos. Neste tema pretende-se que apresentem exemplos de dados univariados contínuos e as possíveis distribuições teóricas que poderiam ser usadas para os modelar.
4.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- André Campos, 49282
- Beatriz Ramos, 53617
- Inês Cabaço, 48382
- João Louro, 52893
- Madalena Matias, 52633
- Margarida Almeida, 47939
4.2 Introdução Teórica
Dados univariados são dados que, como o próprio nome indica, têm apenas uma variável. Quando se fala de dados univariados contínuos, estamos a referir-nos a dados como altura de um pinheiro, o comprimento de uma cobra ou a temperatura da água de uma poça; ou seja, estamos a falar de dados contínuos, que podem tomar qualquer valor infinito dentro de um determinado domínio.
Este tipo de dados pode ser modelado através de distribuições contínuas.
As distribuições contínuas descrevem a probabilidade de uma variável aleatória contínua tomar determinado valor. Estas distribuições também são chamadas de funções distribuição de densidade de probabilidade, onde os valores que a variável pode tomar se encontram representadas no eixo do x e as probabilidades de os obter são dados pela área abaixo da curva da função entre os valores de interesse. Como a probabilidade da variável tomar um determinado valor varia entre 0 e 1, e a soma das probabilidades de todos os valores possíveis de um dado fenómeno ou evento é igual a 1, a área total abaixo da curva também é igual a 1.
Ao contrário das distribuições discretas, onde cada valor particular tem uma probabilidade diferente de zero [por exemplo, P(X=6)=0,4], valores exatos nas distribuições contínuas têm probabilidade igual a zero. Na realidade, essa probabilidade é infinitesimal mas é tão baixa que, para todos os efeitos, é considerada zero. Assim, apenas faz sentido dizer que se está a calcular a probabilidade da variável aleatória X se encontrar num determinado intervalo de valores.
Como as variáveis aleatórias são quase sempre únicas, existem inúmeras distribuições de probabilidade diferentes. Neste trabalho iremos referir apenas as mais comumente usadas.
4.2.1 1. Distribuição Normal
Também conhecida como distribuição gaussiana, corresponde ao modelo mais amplamente utilizado e o mais popular. É muito versátil e simples de usar. É aplicado para fazer comparações entre pontuações ou para tomar outros tipos de decisões estatísticas.
A família gaussiana é caracterizada por dois parâmetros, o valor médio (\(\mu\) ou mean), ou seja onde está centralizada (parâmetro de localização), e a desvio-padrão (\(\sigma\) ou sd) que descreve o seu grau de dispersão (parâmetro de escala).
Graficamente, a forma desta distribuição é muitas vezes referida como “em forma de sino”.
A popularidade deste modelo corresponde ao facto da sua forma descrever adequadamente o comportamento de diversas variáveis de interesse prático, pois muitas variáveis apresentam uma distribuição que se aproxima muito da distribuição gaussiana, sobretudo se revelarem grande concentração em torno de um valor (o valor médio) e distribuição simétrica em torno deste mesmo valor.
Em linguagem R existem 4 funções integradas para gerar distribuição normal, que se encontram descritas a seguir:
dnorm(x, mean, sd) → mede a função densidade da distribuição
pnorm(x, mean, sd)→ função de distribuição cumulativa (mede a probabilidade de que um número aleatório X tenha um valor menor ou igual a X)
qnorm(p, mean, sd)→ o inverso da função pnorm()(útil para encontrar os percentis de uma distribuição normal)
rnorm(n, mean, sd)→ usada para gerar um vetor de comprimento n de números aleatórios normalmente distribuídos
A descrição dos parâmetros usados nas funções acima:
xé um vetor de números.pé um vetor de probabilidades.né o número de observações (tamanho da amostra).meané o valor médio dos dados da amostra. Seu valor padrão é zero.sdé o desvio padrão (e o seu valor padrão é 1).
**Representação gráfica
# cria uma sequência de valores
# entre -15 a 15 com a diferença de 0.1
x = seq(-15, 15, by=0.1)
y = dnorm(x, mean(x), sd(x))
# Plot o gráfico
plot(x, y)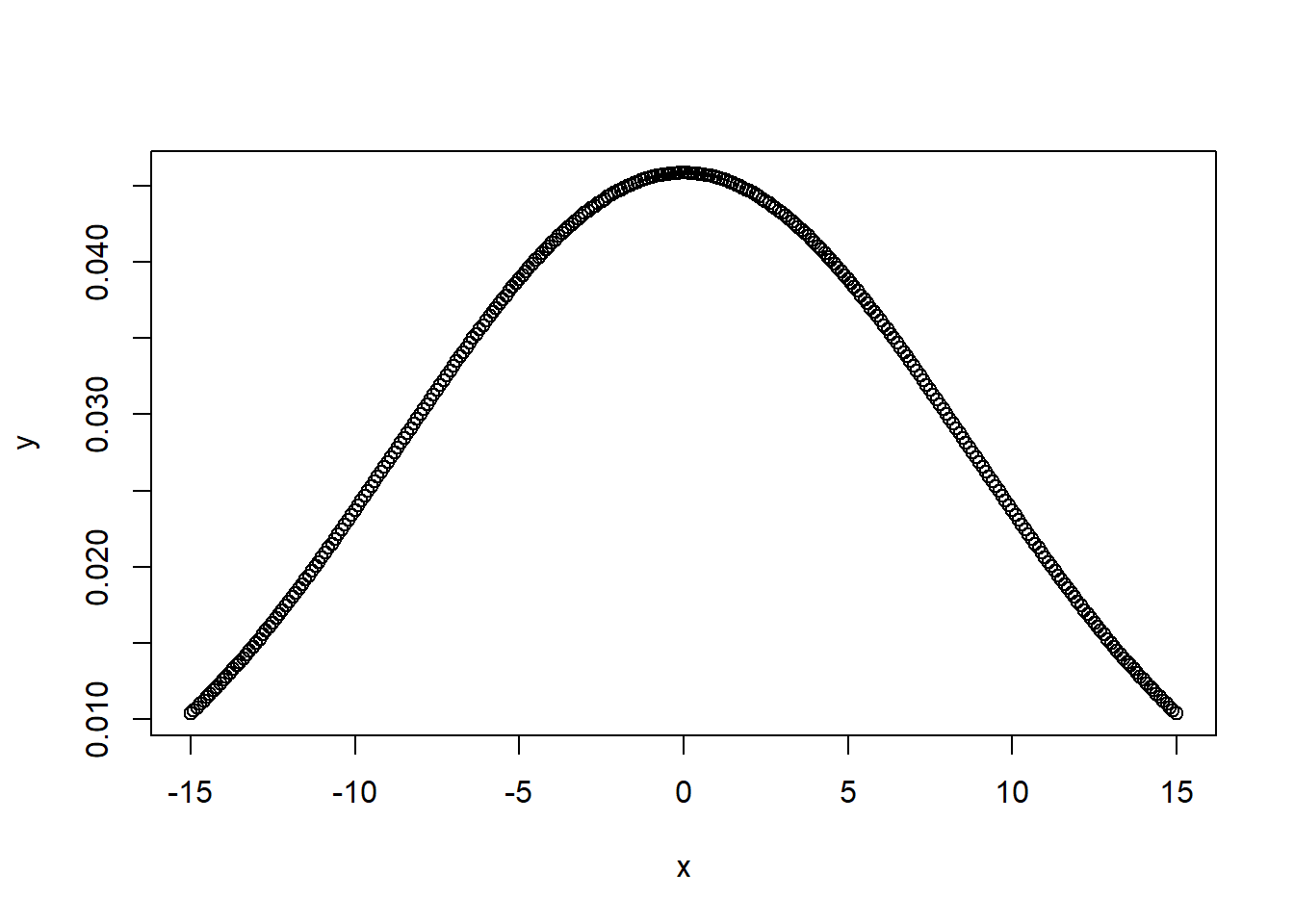
# cria uma sequência de valores
# entre -10 a 10 com a diferença de 0.1
x = seq(-10, 10, by=0.1)
y = pnorm(x, mean=2,5, sd=2)
# Plot o gráfico
plot(x, y)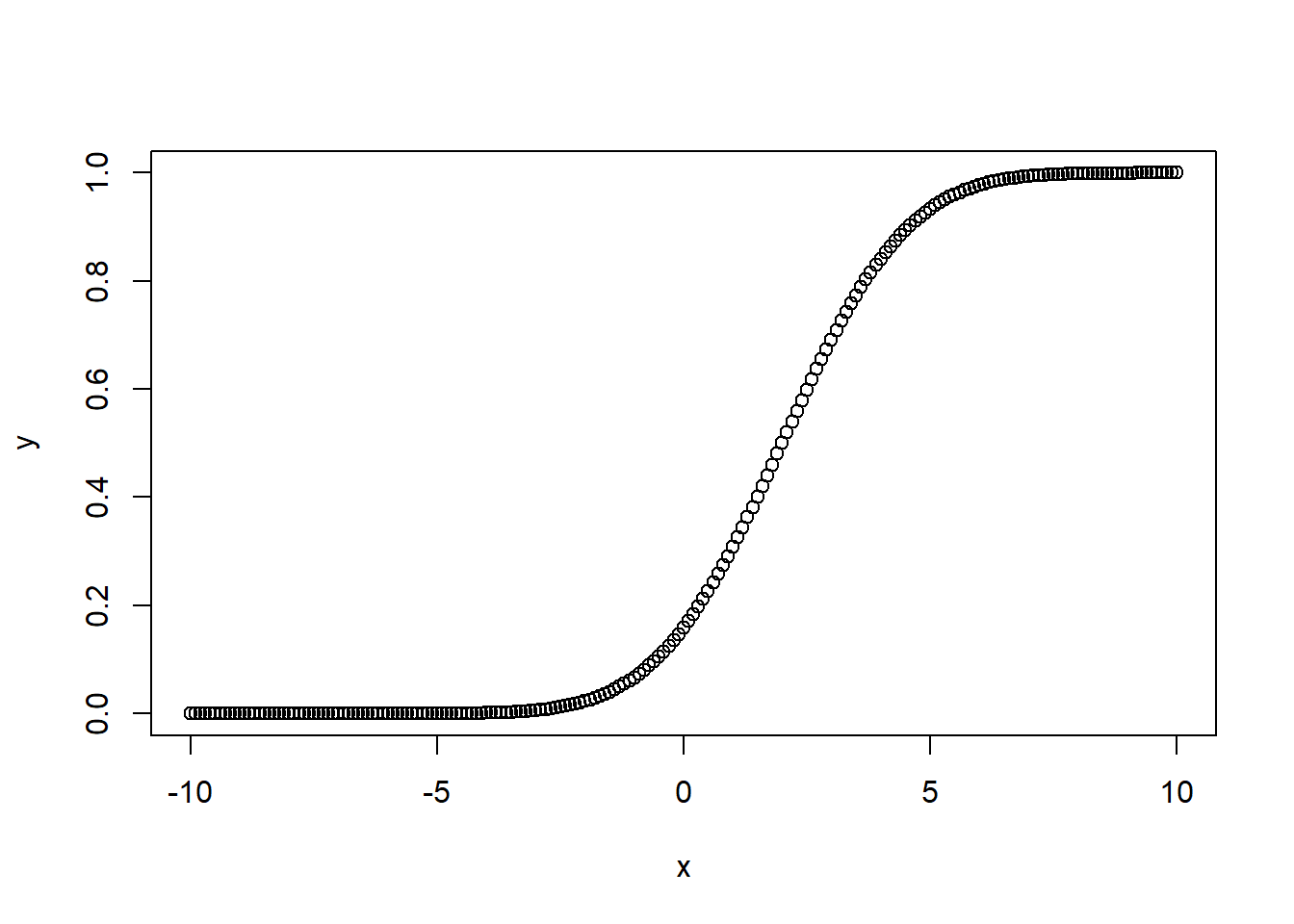
# Cria-se uma sequência de valores de probabilidade
# incrementa-se `by 0.02`
x = seq(0, 1, by = 0.02)
y = qnorm(x, mean(x), sd(x))
# O gráfico
plot(x, y,) 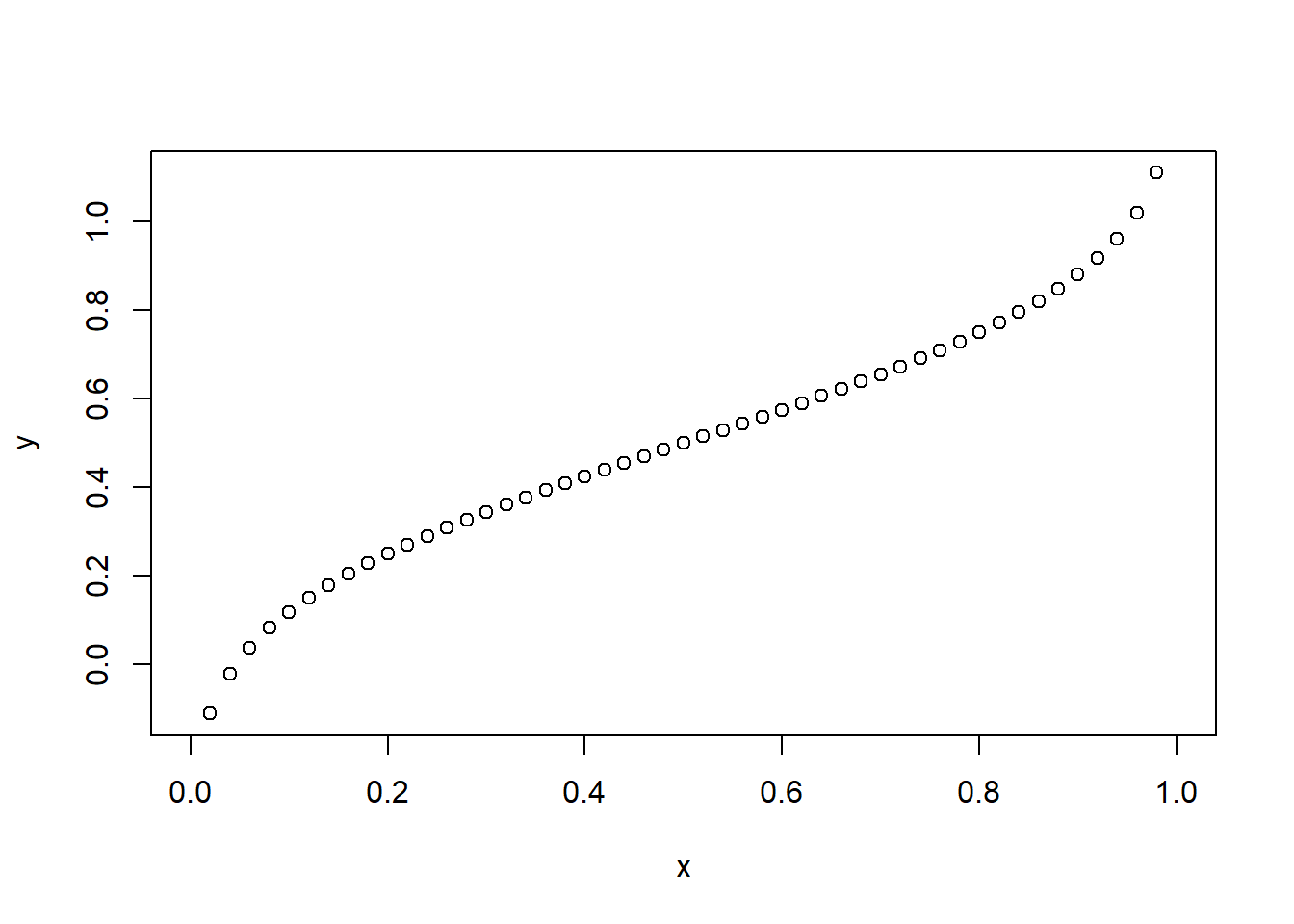
# CRia-se um vector com 1000 numeros aleatórios
# com mean=90 and sd=5
n = rnorm(10000, mean=90, sd=5)
# Histograma com 50 barras
hist(n, breaks=50, main="Histograma da Normal") 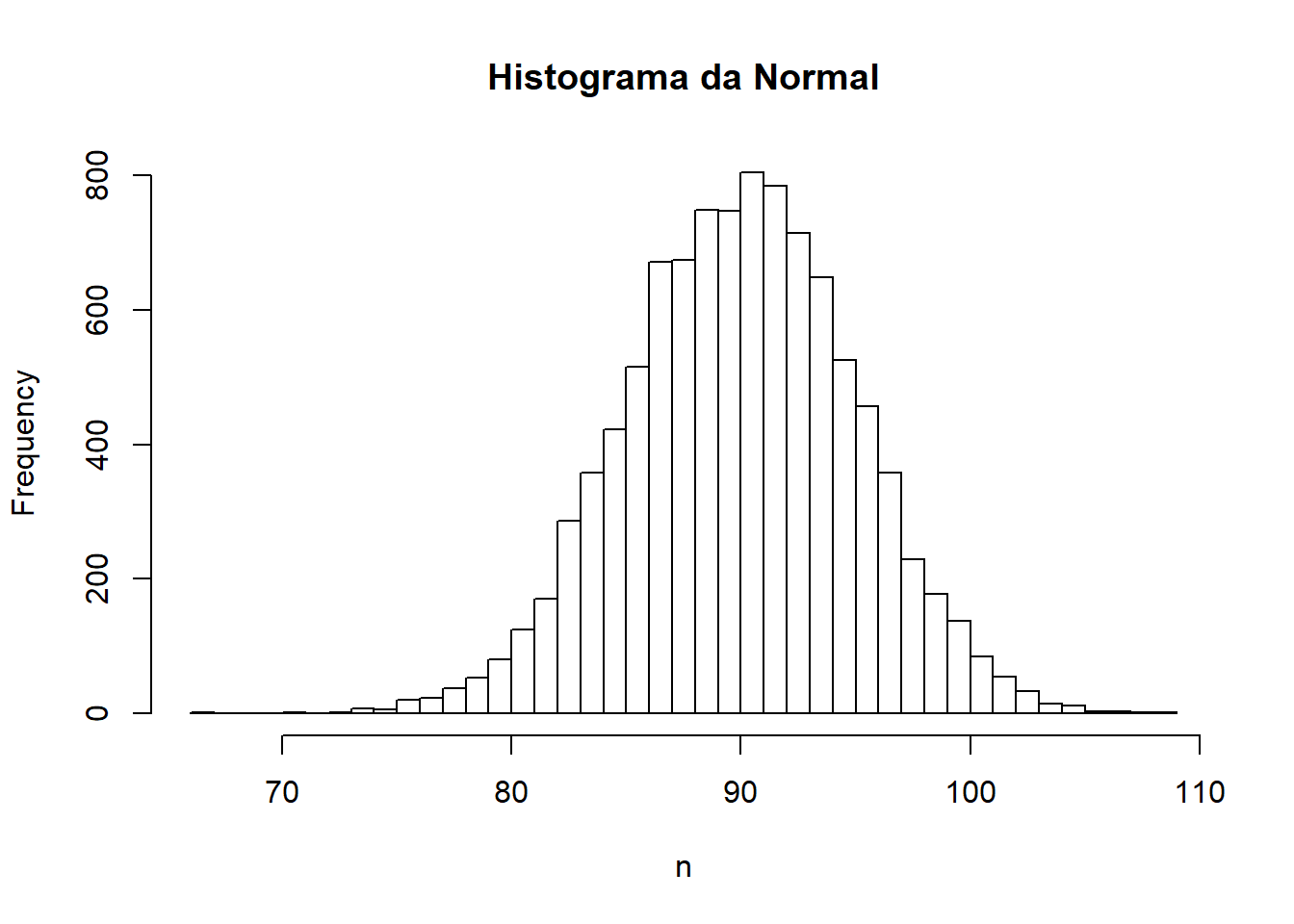
x <- seq(0, 60, 0.1)
plot(x, dnorm(x, 30, 10), type = "l", axes=FALSE, ylab="",main="Normal")
axis(1, at=seq(0, 60, 10), pos=0)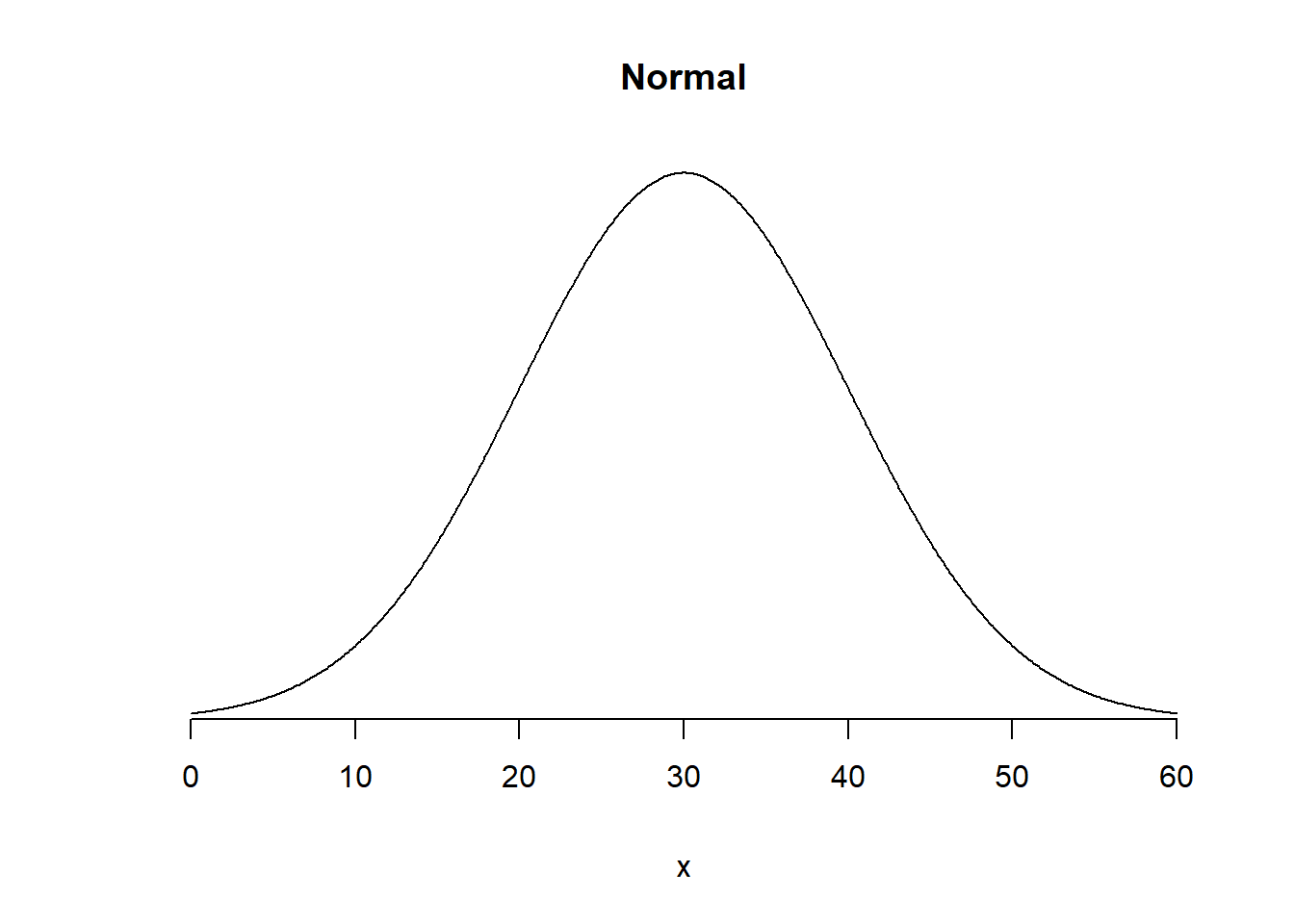
4.2.2 2. Distribuição T-student
A distribuição t-Student apresenta uma distribuição simétrica em torno da média próxima de zero, com um aspecto semelhante à curva normal padrão.
Tem como único parâmetro m ou df,número de graus de liberdade, obtidos com base no tamanho da amostra n onde n-1 = m, e irá definir a sua forma mais ou menos gaussiana. Regra geral, as caudas da t-Student são mais pesadas, pelo que é expectável encontrar valores mais extremados que numa normal padrão.
Sendo uma aproximação com base na normalidade dos dados, iremos encontrar semelhanças entre a estatística de teste Z (Normal) e T(student), em especial quando o espectro amostral de observações independentes, de T supera as 30 observações, ou seja df>30. Nestes casos T \(\approx\) Z para os mesmos graus de liberdade (TLC), sendo a sua semelhança tanto maior quanto maior o número de graus de liberdade da primeira.
É amplamente utilizada para testar as diferenças entre médias amostrais de duas distribuições Gaussianas diferentes. Da mesma forma que a estatística T também pode ser útil para testar se determinado parâmetro estimado é ou não diferente de zero, por ser simétrica em torno deste valor.
Muito provavelmente é das distribuições contínuas mais conhecidas em estatística, uma vez que foi adaptada de forma a que seja possível retirar conclusões válidas com base em amostras pequenas (n<30) — provenientes de populações normais. Este facto coloca em destaque a sua ampla utilização quando são disponibilizados poucos dados amostrais da população. Não estando dependente da variância como outras distribuições, a sua robustez na inferência sobre a população não é fortemente afectada.
→ No R não existe valor de default para os graus de liberdade. dt origina a função de densidade da distrbuição, pt dá a função de distribuição cumulativa, qt dá a função dos quantis e rt gera números aleatórios desta distribuição.
→ ATENÇÂO: Não confundir com Student’s t-test, um teste de hipóteses no qual a estatística de teste segue uma distribuição T sob H0.
**Representação gráfica
t<-seq(-4,4,length=200)
td<-dt(t,df=2)
plot(t,td,type="l",lwd=2,col="red",main="T-student",ylab="Densidade",ylim=c(0,0.5))
lines(t,dt(t,df=5),col="blue")
lines(t,dt(t,df=10),col="green")
lines(t,dt(t,df=20),col="pink")
lines(t,dt(t,df=30),col="black")
lines(t,dnorm(t,mean=0,sd=1),lty=3,lwd=4)
legend("topright",
legend = c("df=2", "df=5", "df=10","df=20","df=30","Normal Standard"),col = 1:5)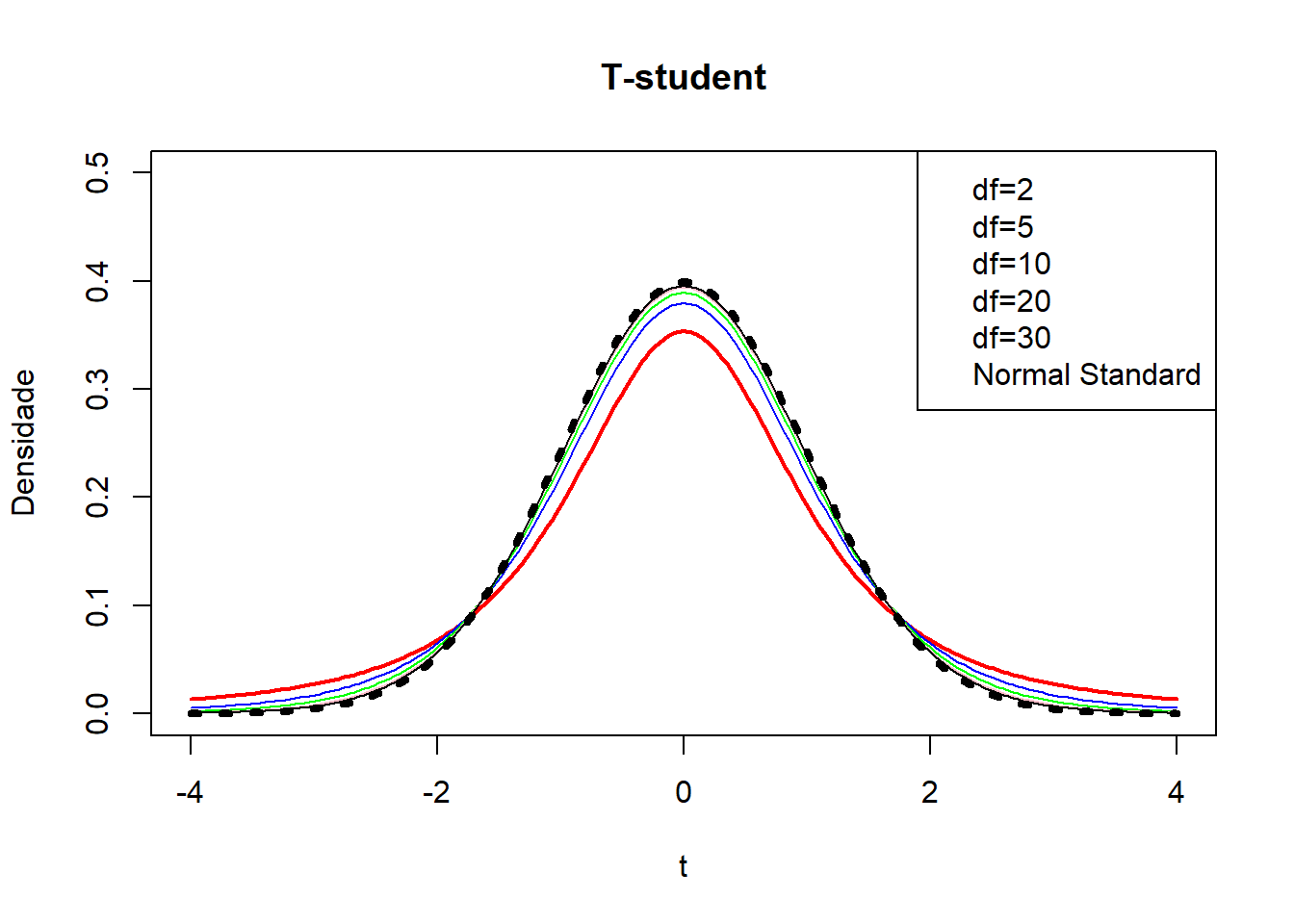
4.2.3 3. Distribuição Beta
A distribuição Beta é uma distribuição de dois parâmetros positivos, \(\alpha\) e \(\beta\), que lhe dão a sua forma. Esta é a única distribuição contínua, para além da uniforme, com um _range _finito, tomando valores apenas entre 0 e 1.
Neste modelo, os parâmetros definem a forma da distribuição: se \(\alpha=\beta\), a distribuição é simétrica em torno de 0.5; se \(\alpha>\beta\), a assimetria é na direção de 1 e, no caso de \(\alpha<\beta\), sua inclinação é na direção de 0. A distribuição B(1,1) é equivalente a U(0,1), tornando a distribuição uniforme um caso particular da Beta.
Dadas as particularidades desta distribuição (só pode tomar valores entre 0 e 1), a Beta é usada para modelar variações de probabilidade, percentagens ou qualquer outro tipo de dados proporcionais, como percentagem de cobertura vegetal, por exemplo. Contudo, é fácil redefinir a escala da distribuição (rescale the distribution) para que se aplique a outro conjunto de valores finitos em vez de ser exclusivamente para valores entre 0 e 1. Por exemplo, Tiwari et al. (2005) usaram a Beta para descrever a distribuição de tartarugas numa praia, por isso o seu range foi de 0 até ao comprimento total da praia.
→ No R não existem valores de default para os dois parâmetros de forma. dbetadá a função de densidade da distribuição, pbetadá a função de distribuição cumulativa, qbetadá a função dos quantis e rbetagera número aleatórios desta distribuição.
**Representação gráfica
beta<- seq(0,1, length=100)
#parâmetros iguais e >1
plot(beta, dbeta(beta, 100, 100), main="Beta",ylab="Densidade", type ="l",ylim=c(1,13),xlab="n")
# parâmetros diferentes e >1
lines(beta, dbeta(beta, 90, 10), type ="l", col="red")
# parâmetros iguais e <1
lines(beta, dbeta(beta, 0.5, 0.5), type ="l", col="green")
legend("topleft",legend=c("shape1=100,shape2=100","shape1=90,shape2=10","shape1=0.5,shape2=0.5"),col = 1:3,
lty = 1,lwd=2)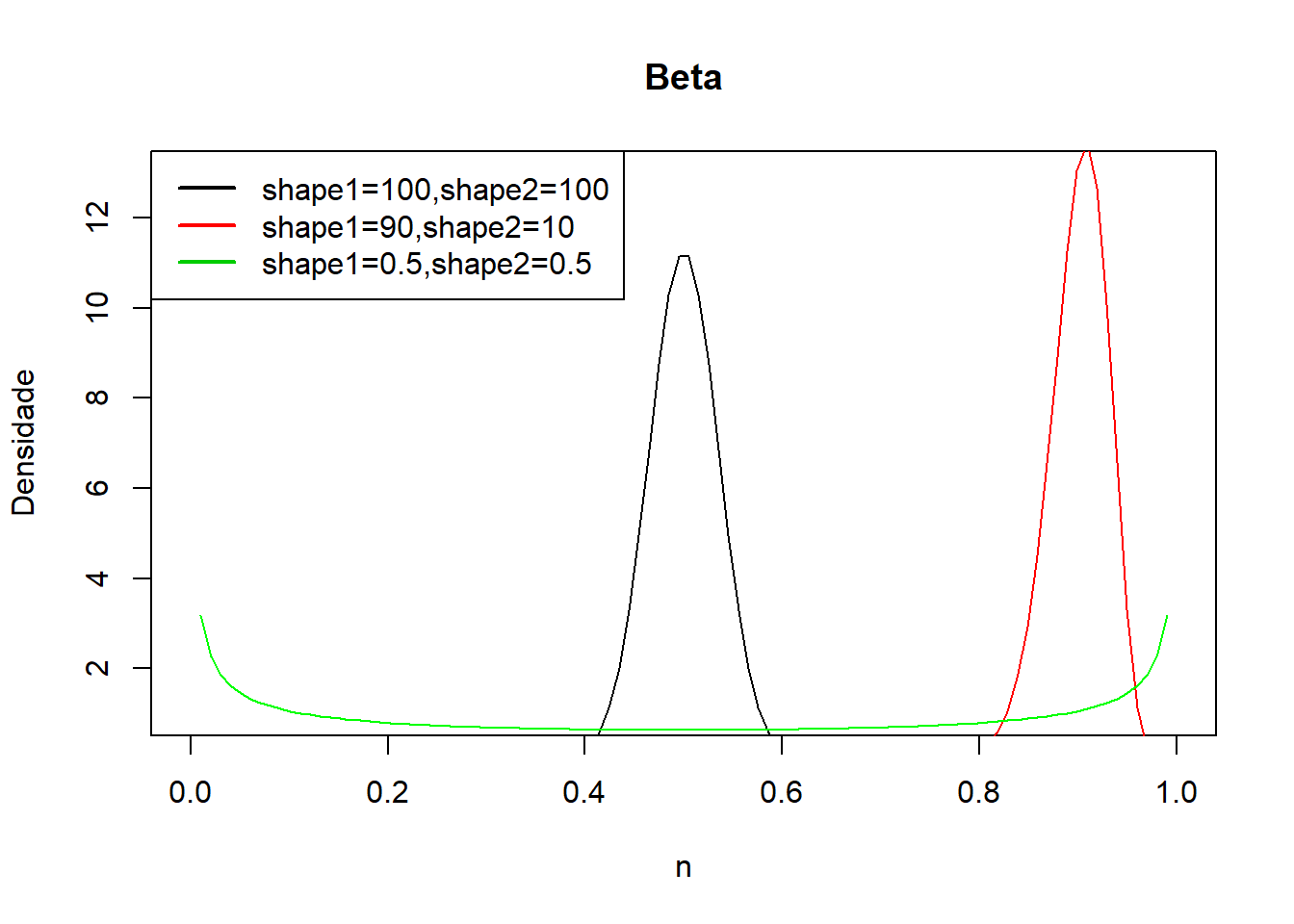
4.2.4 4. Distribuição Uniforme
A distribuição Uniforme está relacionada com eventos que tenham a mesma probabilidade de ocorrer. Apresenta como parâmetros, \(\alpha\) e \(\beta\), ou noutras notações a e b, representando o limite inferior e o limite superior, correspondentemente, do intervalo de valores que baliza a variável aleatória (onde \(\beta>\alpha\)).
Nesta distribuição, todos os valores que a variável aleatória pode tomar dentro do intervalo definido, apresentam igual densidade de probabilidade dentro do intervalo [0,1] sendo, por esse motivo, muitas vezes chamada de distribuição retangular. Fora deste intervalo, a variável independente não toma qualquer valor, tendo uma probabilidade nula de ocorrer.
A distribuição uniforme é um caso especial da distribuição Beta. Como descrito anteriormente, a Beta toma valores no mesmo intervalo da distribuição Uniforme, e os seus parâmetros definem a sua forma mais ou menos simétrica, sendo sempre não-negativos.
Se observarmos uma distribuição Beta de parâmetros \(\alpha=1\) e \(\beta=1\), temos a distribuição uniforme U (0,1). Quando ambos os parâmetros da distribuição beta são iguais a 1, a sua função densidade de probabilidade é proporcional a uma constante. Concluindo, ambas as distribuições são nestas condições idênticas, pelo cálculo da f.d.p.
→ No R, se os valores de mínimo e máximo não forem definidos, o sistema preenche com 0 e 1 por default.dunif é a função de densidade, punif faz a função de distribuição cumulativa, qunif faz a função dos quantis e runifgera números aleatórios uniformes.
**Representação gráfica:
a <- -2
b <- 3
rand.unif <- runif(10000, min = -2, max = 3)
hist(rand.unif,
freq = FALSE,
xlab = 'x',
ylim = c(0, 0.4),
xlim = c(-4,4),
density = 20,
main = "Uniforme, intervalo [-2,3]")
curve(dunif(x, min = a, max = b),
from = -5, to = 5,
n = 100000,
col = "light blue",
lwd = 2,
add = TRUE,
yaxt = "n",
ylab = 'Densidade')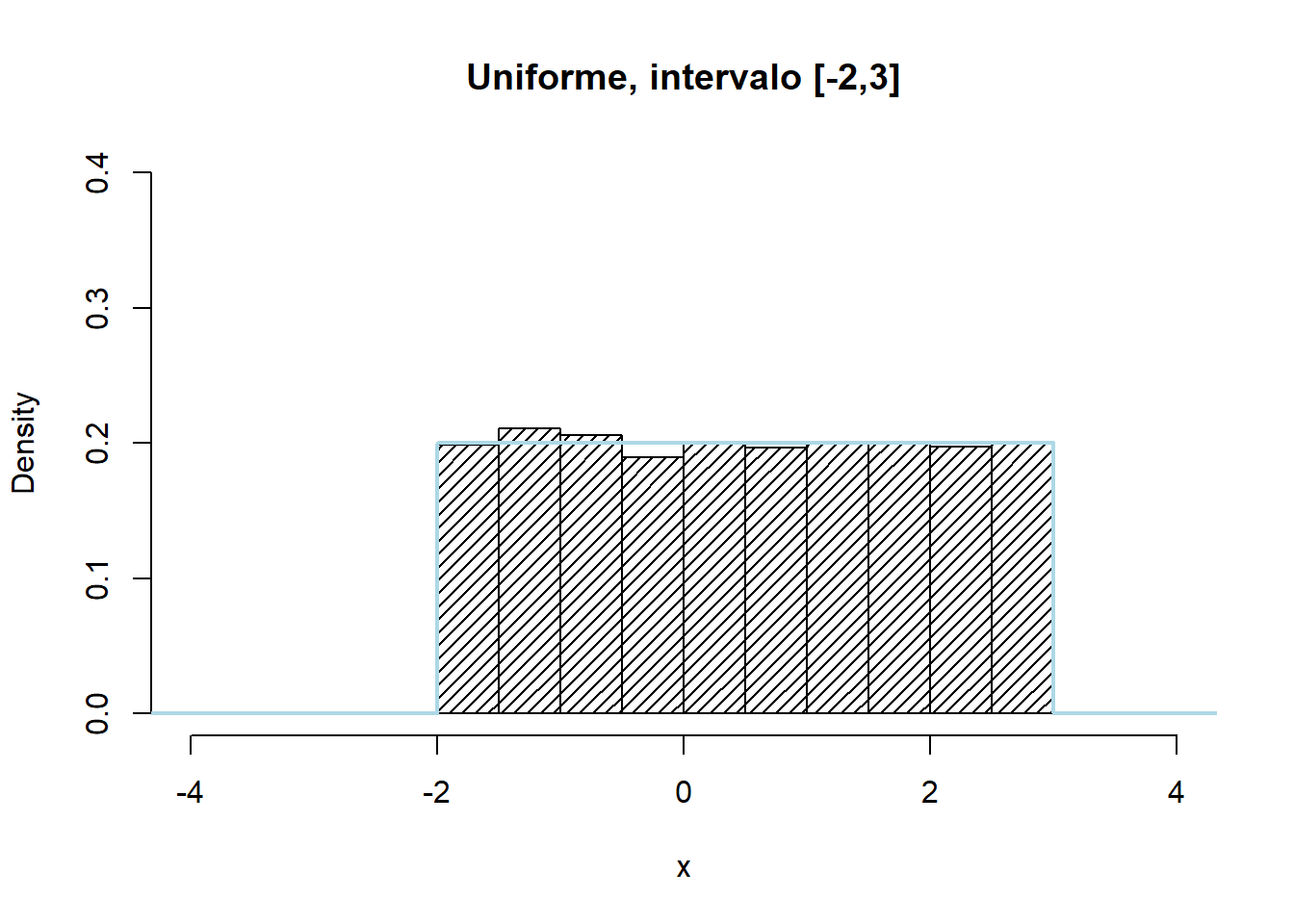
4.2.5 5. Distribuição Gama
A distribuição Gamma é uma distribuição positiva de valores reais que possui dois parâmetros: shapee scale, com scale=1/rate (rateé uma maneira alternativa de especificar scale).
A Gamma dá-nos a distribuição do tempo até um determinado acontecimento (parâmetro shape) ocorrer, tendo em conta a taxa a que cada sucesso se verifica, sendo essa taxa o parâmetro rate. Ocorre naturalmente em processos onde o tempo de espera entre eventos é relevante, prevê o tempo para mais do que o primeiro evento (ao contrário da exponencial) e é muitas vezes relacionada com o número de mortes (sucessos) numa população.
Por exemplo, uma Gamma (shape=3, scale=2) poderia ser a distribuição do tempo, em dias, que seria de esperar até se ter 3 mortes numa população, dado o tempo de sobrevivência média em 2 dias (com a taxa de mortalidade igual a ½ por dia). Outros exemplos de aplicação da Gamma, em termos ecológicos, incluem quase todas as variáveis ambientais com grande variância onde os valores negativos não fazem sentido, tais como a intensidade de luz ou as concentrações de nitrogénio.
Dadas as suas características, a Gamma é extremamente útil e resolve o problema que muitos investigadores enfrentam quando têm uma variável contínua com “muita variância”, com coeficiente de variação maior que 0,5. Modelar dados desse tipo com distribuições normais leva a valores negativos irrealistas, que depois têm de ser tratados com algum procedimento posterior, como truncá-los ou mesmo ignorá-los. Assim, a Gamma oferece uma alternativa mais realista para lidar com dados com grandes variâncias e com uma right skew (inclinação para a direita).
As distribuições exponencial e de qui-quadrado são dois dos casos especiais que derivam da distribuição gamma.
→ No R, se o parâmetro scale não for definido, o sistema preenche 1 por default, uma vez que este parâmetro é igual a \(1/rate\) e \(rate=1\). O comando dgamma dá a função de densidade, pgamma faz a função de distribuição cumulativa, qgamma faz a função dos quantis e rgammagera números aleatórios desta distribuição.
**Representação gráfica
x_dgamma<- seq(0, 1, by = 0.02)
y_dgamma <- dgamma(x_dgamma, shape = 6)
plot(y_dgamma,main="Gama",type="l",col="blue",xlab="n",ylab="Densidade") 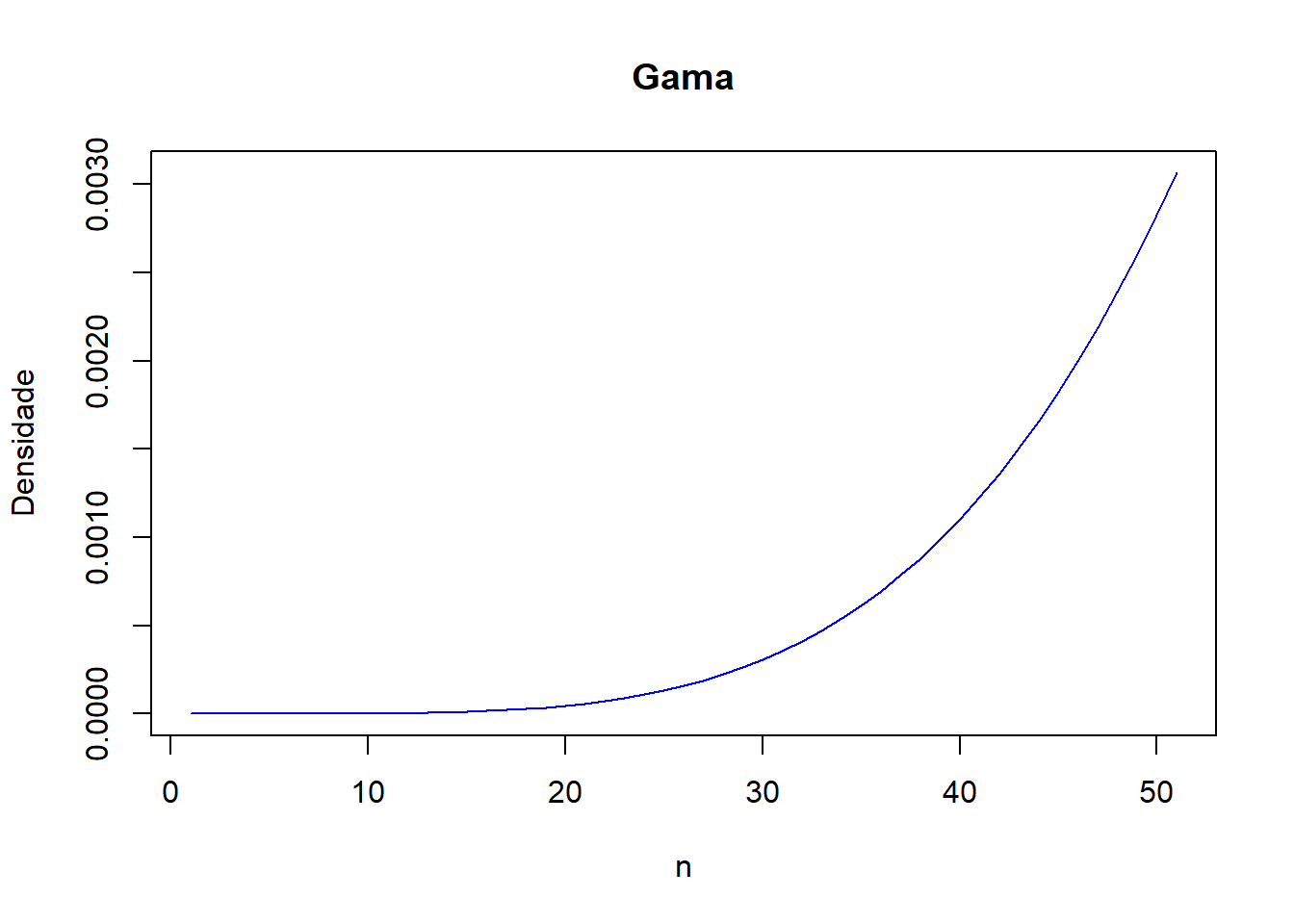
4.2.6 6. Distribuição Exponencial
A distribuição exponencial é um caso especial da distribuição Gamma (quando o parâmetro shape = 1). É definida por um parâmetro (λ) que representa a taxa do processo ou rate, semelhante ao da distribuição Gamma. Esta taxa de processo é o inverso da média.
A Exponencial dá-nos a distribuição de tempos de espera até que o primeiro evento ocorra, dada uma probabilidade por unidade de tempo (rate) constante.
É não só usada para modelar tempos de espera para um evento certo como para variáveis que tenham uma maior probabilidade de tomar o valor 0 ou perto disso. Os seus exemplos de aplicação em contexto ecológico são na modelação do tempo entre avistamentos de aves; amostras que decrescem exponencialmente, como os níveis de luz na canópia da floresta ou mesmo em análises de sobrevivência ou longevidade
→ No R, se o parâmetro rate (λ) não for definido, o sistema preenche 1 por default. Os comandos dexp,pexp, qexp e rexp funcionam de forma idêntica aos outros acima referidos.
**Representação gráfica
em<-rexp(2500000,rate=0.2)
hist(em,freq=FALSE,xlab="x",main="Exponencial", breaks = seq(-5,200,0.5), xlim=c(0,40),col="light grey",density=20,ylim=c(0,0.2),ylab="Densidade")
curve(dexp(x),add=TRUE, col="green")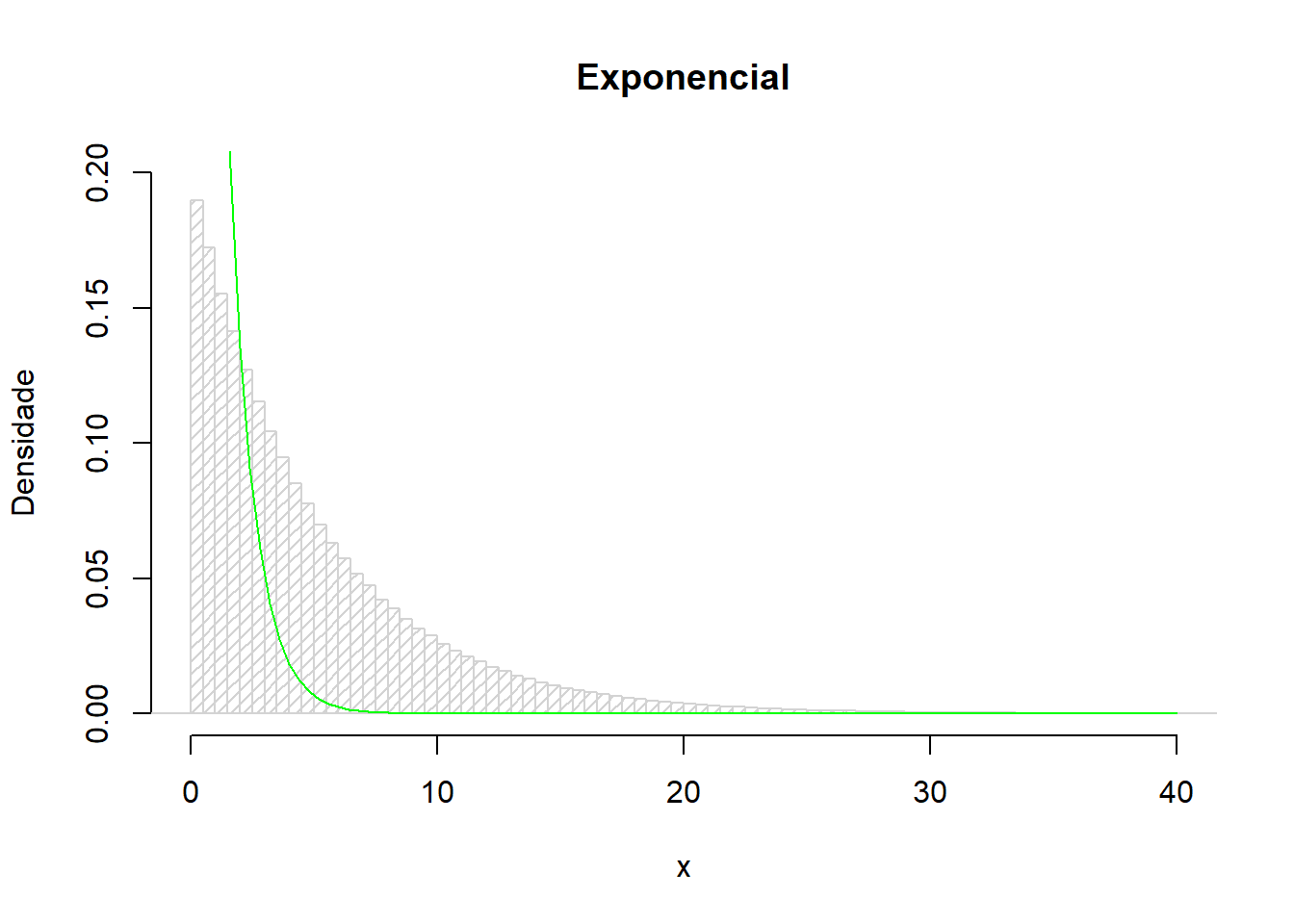
4.2.7 7. Distribuição Qui-Quadrado
A distribuição Qui-quadrado é uma distribuição positiva, com uma cauda à direita e que é definida apenas pelos graus de liberdade df. Esta distribuição, com k graus de liberdade, corresponde à distribuição da soma dos quadrados de k variáveis aleatórias normais independentes. Este modelo caracteriza-se como um caso especial da distribuição gamma e é utilizado para determinar a “goodness of the fit”, uma vez que toma a soma dos erros quadrados, normalizando-os para uma normal padrão N(0,1).
É uma distribuição utilizada na análise de tabelas de contingência (tabelas com a distribuição de uma variável em linhas e a outra em colunas para estudar a correlação entre essas duas variáveis) ou em testes de likehood ratios, que nos ajudam a escolher qual o melhor de dois modelos aninhados (nested).
A \(\chi\)2 também é particularmente útil para estimar intervalos de confiança para o desvio padrão, e estudar a variância de amostras onde a distribuição subjacente é normal, permitindo ainda testar desvios nas diferenças entre os valores de frequência expectáveis e observados. Um teste qui-quadrado pode ser aplicado, por exemplo, a dados provenientes de uma amostragem realizada pelo método dos quadrados, de forma a determinar se existe uma associação estatisticamente significativa na distribuição de duas espécies.
→ No R, os graus de liberdade df não têm valores de default. Os comandos dchisq,pchisq, qchisq e rchisq funcionam de forma idêntica aos outros acima referidos.`
Representação gráfica:
x_dchisq <- seq(0, 100, by = 1)
y_dchisq <- dchisq(x_dchisq, df = 5)
plot(y_dchisq,type="l",main="Qui-quadrado",ylab="Densidade",xlab="n")
lines(x_dchisq,dchisq(x_dchisq,df=10),col="red")
lines(x_dchisq,dchisq(x_dchisq,df=20),col="green")
lines(x_dchisq,dchisq(x_dchisq,df=30),col="blue")
legend("topright",legend=c("df=5","df=10","df=20","df=30"),col = 1:4,lty = 1,lwd=1)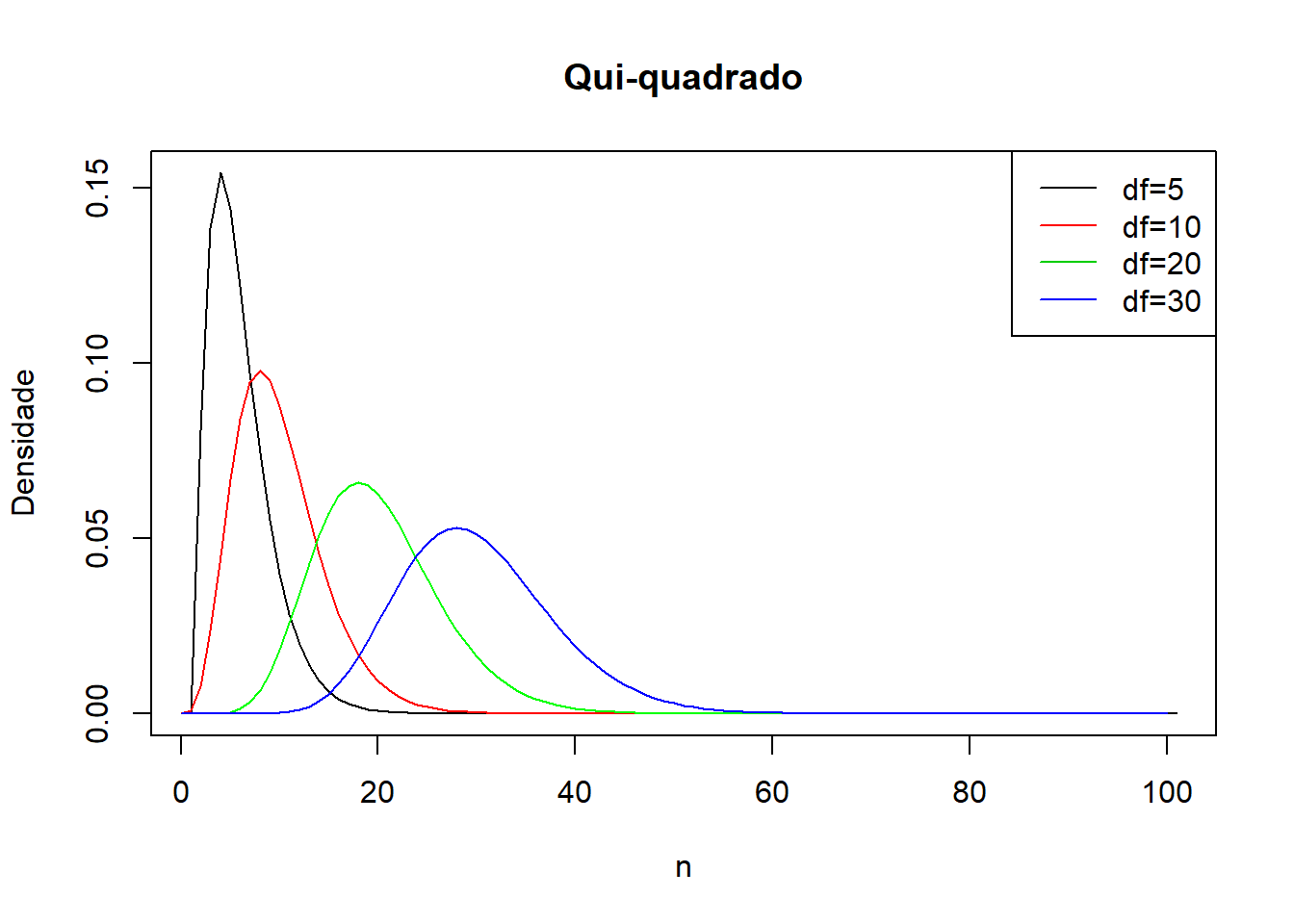
4.2.8 8. Distribuição Log-Normal
Esta distribuição é difinida por dois parâmetros: a média meanloge o desvio-padrão sdlog. Este último paarâmetro condiciona a forma da distribuição.
A distribuição log-normal está intimamente relacionada com a distribuição normal, uma vez que tem por base a gaussianidade de um conjunto de valores positivos que a variável aleatória pode assumir, posteriormente logaritmizados.
Alguns exemplos de relacionados com esta distribuição são sobre estudos de um determinado tecido que cresce de forma exponencial dependendo de fatores que variam aleatoriamente ao longo do tempo, curvas de abundância vs frequência em comunidades de plantas ou modelação de situações de avaliação de aumento de tamanho de indivíduos numa população, entre outros exemplos.
É tendencialmente útil em estudos de modelação quando, após visualização dos dados, estes se apresentem relativamente simétricos e positivamente distribuídos.
Tal como a distribuição Gamma, a Log-normal pode apresentar aparências significativamente diferentes consoante o seu parâmetro de escala, ou seja, o incremento no crescimento da variável que estamos a observar após x tempo. Visto ser uma distribuição skewed à esquerda, iremos observar mais valores extremados nesse sentido, pelo que em certos casos se pode aplicar uma transformação exponencial dos dados com distribuição log-normal.
Um factor que poderá ser problemático na escolha da melhor distribuição para os dados amostrados, é a grande semelhança na aparência geral dos dados entre uma Gamma e uma Log-normal, ambas positivamente distribuídas, o que cria diferenças qualitativas insignificantes.
Ambas são usadas para modelar acontecimentos similares, pelo que uma solução prática será observar a sua função densidade, sobre o histograma dos dados amostrados. No intuito de numa forma visual ajudar a resolver o problema.
→ No R, meanlog e sdlog têm valores 0 e 1 por default, respectivamente. As funções dlnorm, plnorm, qlnorm e rlnorm funcionam da mesma maneira que nas outras distribuições.
**Representação gráfica
x<- seq(0,10,length = 100)
alog_norm<-dlnorm(x,meanlog=0,sdlog=1,log=FALSE)
blog_norm<-dlnorm(x,meanlog=0,sdlog=2,log=FALSE)
clog_norm<-dlnorm(x,meanlog=1,sdlog=0.5,log=FALSE)
dlog_norm<-dlnorm(x,meanlog=1.5,sdlog=0.3,log=FALSE)
plot(x,alog_norm,lty=1,col="black",main="Log-normal",type="l",ylab="Densidade")
lines(x,blog_norm,lty=2,col="red",lwd=2)
lines(x,clog_norm,lty=3,col="green",lwd=2)
lines(x,dlog_norm,lty=4,col="blue",lwd=2)
legend("topright",
legend = c("mu = 0, sd = 1", "mu = 0, sd = 2", "mu = 1, sd = 0.5","mu=1.5,sd=0.3"),
col = 1:4,
lty = 1:4,lwd=2)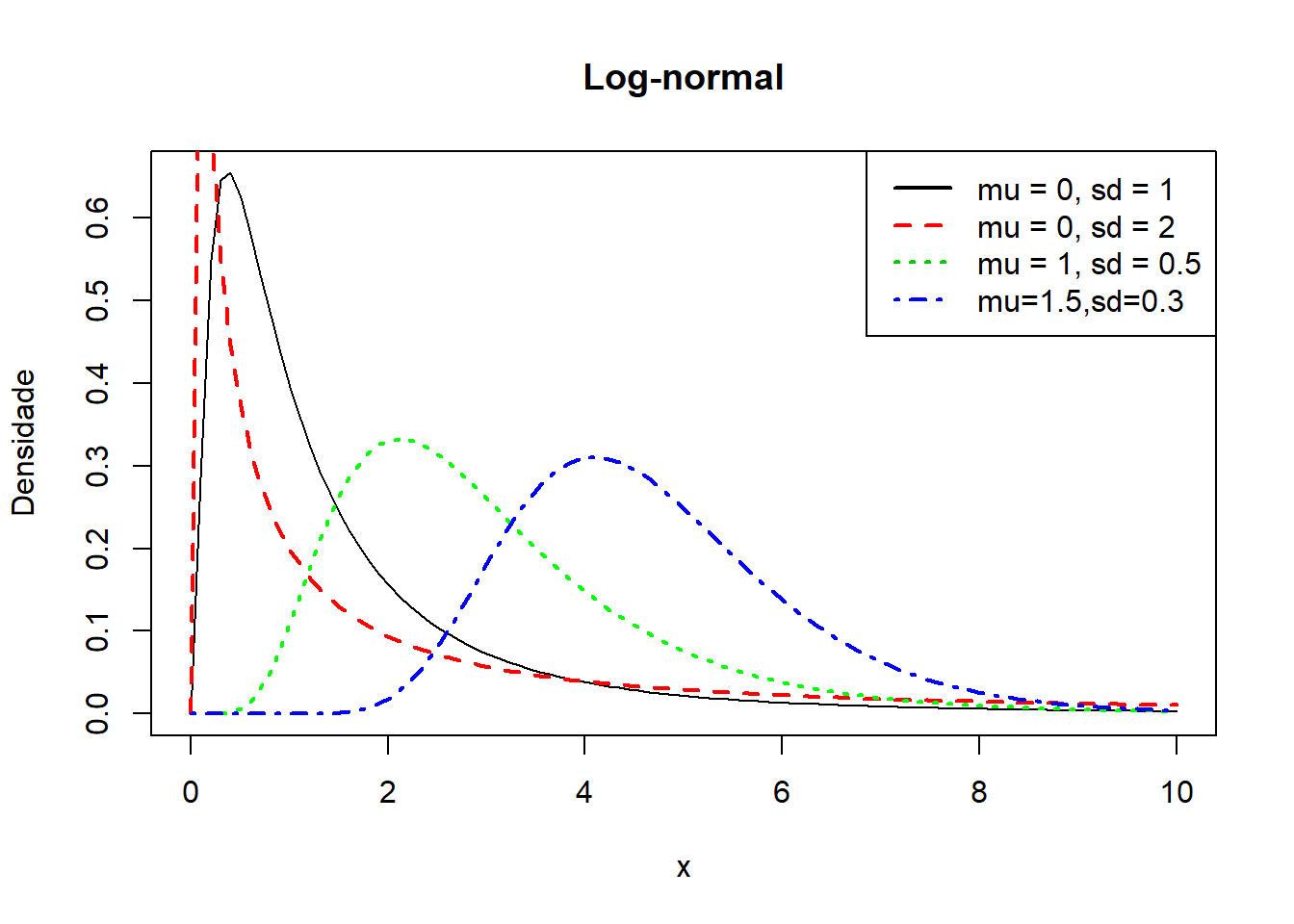
4.2.9 9. Distribuição Weibull
A distribuição de Weibull é um caso especial da distribuição exponencial definida por dois parâmetros shape e scale, ambos positivos. Esta distribuição transforma-se numa distribuição exponencial quando o parâmetro shape = 1. Por exemplo, Weibull (1,b) = Exp (b). A Weibull fica bastante próxima da Gaussiana quando o parâmetro scale = 3.25.
Esta distribuição é útil para modelar tempo até à ocorrência de um evento quando a probabilidade de ocorrência se altera com o tempo — o processo tem “memória”, ao contrário da distribuição exponencial, onde a probabilidade de ocorrência se mantém constante porque o processo não tem “memória”. A Weibull é muito muito utilizada em análises de sobrevivência, onde o parâmetro shapecontrola a taxa de alterações da taxa de mortalidade age-specific e, por isso, a forma geral da curva de sobrevivência. Outros usos incluem a análise do tempo de vida de produtos ou para previsões da velocidade do vento.
→ No R, o parâmetro shape não tem valores de default e scale assume valor 1 se não for definido. Os comandos dweibull,pweibull, qweibull e rweibull funcionam de forma idêntica aos outros acima referidos.
**Representação gráfica
x_weibull <- seq(0, 20, by = 0.1)
y_weibull <- dweibull(x_weibull, shape = 1,scale=0.5)
plot(y_weibull,type="l",main=" Weibull",ylab="Densidade",xlim=c(0,10))
lines(x_weibull,dweibull(x_weibull,shape=1,scale=1),col="red")
lines(x_weibull,dweibull(x_weibull,shape=3,scale=2.5),col="green")
# influência dos parâmetros shape e scale na forma da distribuição aproximando-a de uma normal
lines(x_weibull,dweibull(x_weibull,shape=3,scale=3.25),col="blue")
legend("topright",legend=c("shape=1,scale=0.5","shape=1,scale=1","shape=3,scale=2.5","shape=3,scale=3.25"),col = 1:4,
lty = 1,lwd=2)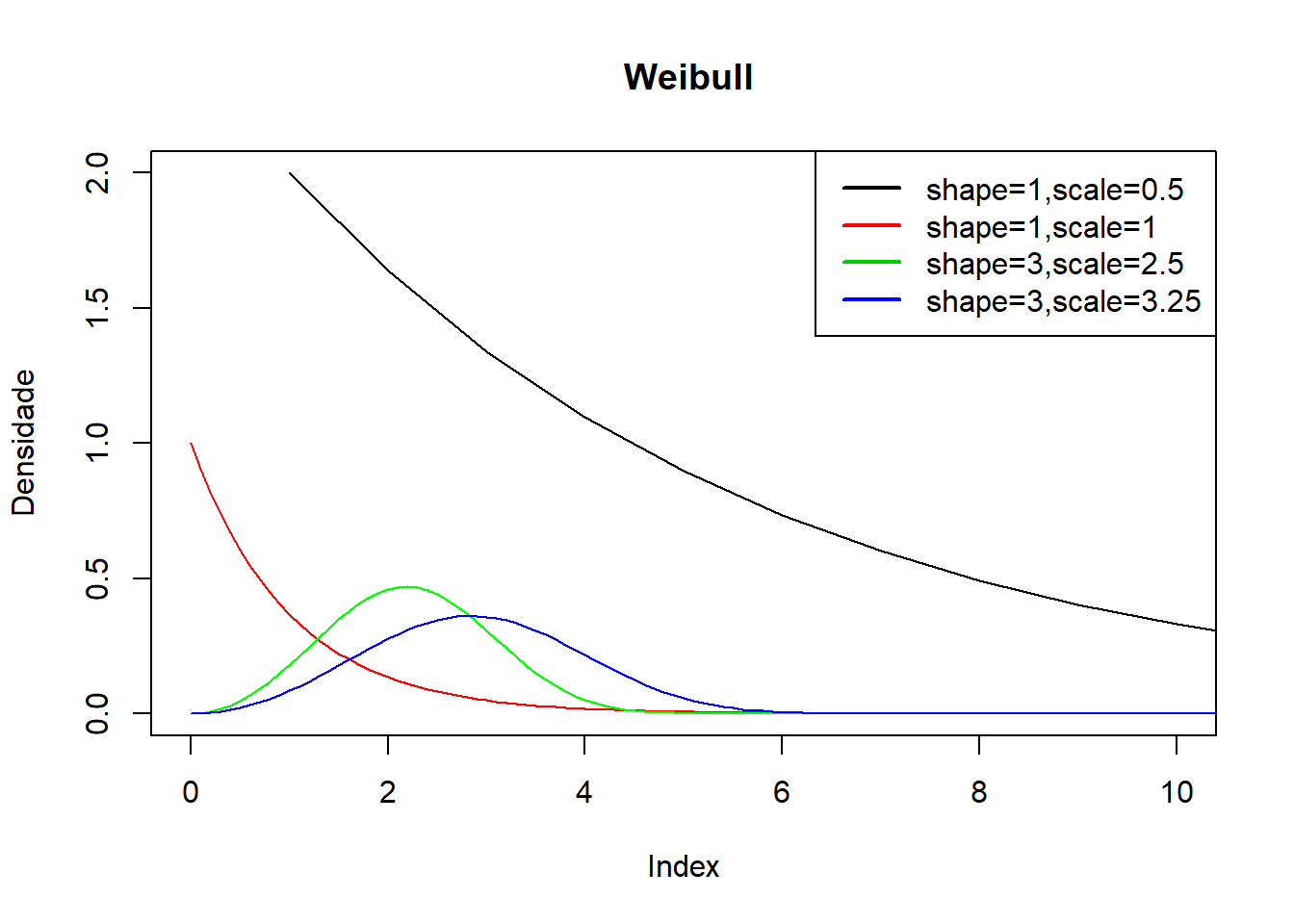
4.3 Exemplo em R
Como demonstrado na Ficha de trabalho nº7 das TPs, saber que diferentes tipos de distribuições contínuas existem pode ser útil para, por exemplo, aplicar um modelo geral de regressão linear (GLM) aos nossos dados.
Através do R torna-se possível analisar que tipo de distribuição poderá modelar uma variável do nosso interesse. Para o demonstrar, utilizámos um exemplo prático do primeiro trabalho de um dos elementos do grupo. Colocou-se a questão ecológica de como varia a dimensão das azeitonas, de três variedades diferentes de oliveira e provenientes de duas localizações diferentes, em que a variável resposta, “tg”, corresponde a um Tamanho global, obtido pela multiplicação do diâmetro do fruto pelo seu comprimento. Começamos por uma breve análise exploratória:
## ID arvr quant perim
## Min. : 1.00 Length:100 Length:100 Min. :3.000
## 1st Qu.: 25.75 Class :character Class :character 1st Qu.:4.300
## Median : 50.50 Mode :character Mode :character Median :4.800
## Mean : 50.50 Mean :4.809
## 3rd Qu.: 75.25 3rd Qu.:5.400
## Max. :100.00 Max. :6.200
## comp cf var loc
## Min. :1.300 Min. :1.700 Length:100 Min. :1.0
## 1st Qu.:2.000 1st Qu.:4.875 Class :character 1st Qu.:1.0
## Median :2.100 Median :5.600 Mode :character Median :1.5
## Mean :2.119 Mean :5.453 Mean :1.5
## 3rd Qu.:2.300 3rd Qu.:6.025 3rd Qu.:2.0
## Max. :3.000 Max. :8.000 Max. :2.0
## dir tg
## Length:100 Min. : 3.90
## Class :character 1st Qu.: 8.80
## Mode :character Median :10.19
## Mean :10.39
## 3rd Qu.:12.45
## Max. :17.70## tibble [100 x 10] (S3: tbl_df/tbl/data.frame)
## $ ID : num [1:100] 1 2 3 4 5 6 7 8 9 10 ...
## $ arvr : chr [1:100] "A1" "A1" "A1" "A1" ...
## $ quant: chr [1:100] "pa" "pa" "pa" "pa" ...
## $ perim: num [1:100] 4 3.9 4.1 3.6 3.8 4.7 4.4 4.1 4.35 4 ...
## $ comp : num [1:100] 1.9 1.7 1.6 1.3 1.6 2.4 2.2 2.4 2.1 1.7 ...
## $ cf : num [1:100] 5.2 5.25 3.95 5.82 5.79 6.47 6.3 5.8 6.5 5.1 ...
## $ var : chr [1:100] "gal" "gal" "gal" "gal" ...
## $ loc : num [1:100] 2 2 2 2 2 2 2 2 2 2 ...
## $ dir : chr [1:100] "W" "W" "W" "W" ...
## $ tg : num [1:100] 7.6 6.63 6.56 4.68 6.08 ...Como podemos observar, temos uma amostra de 100 observações e 9 variáveis. Sabe-se que a variável tg, uma vez que se trata da dimensão de um fruto, é uma variável contínua, apta para ser modelada por qualquer uma das distribuições acima descritas. A variável resposta encontra-se agora representada no histograma abaixo:
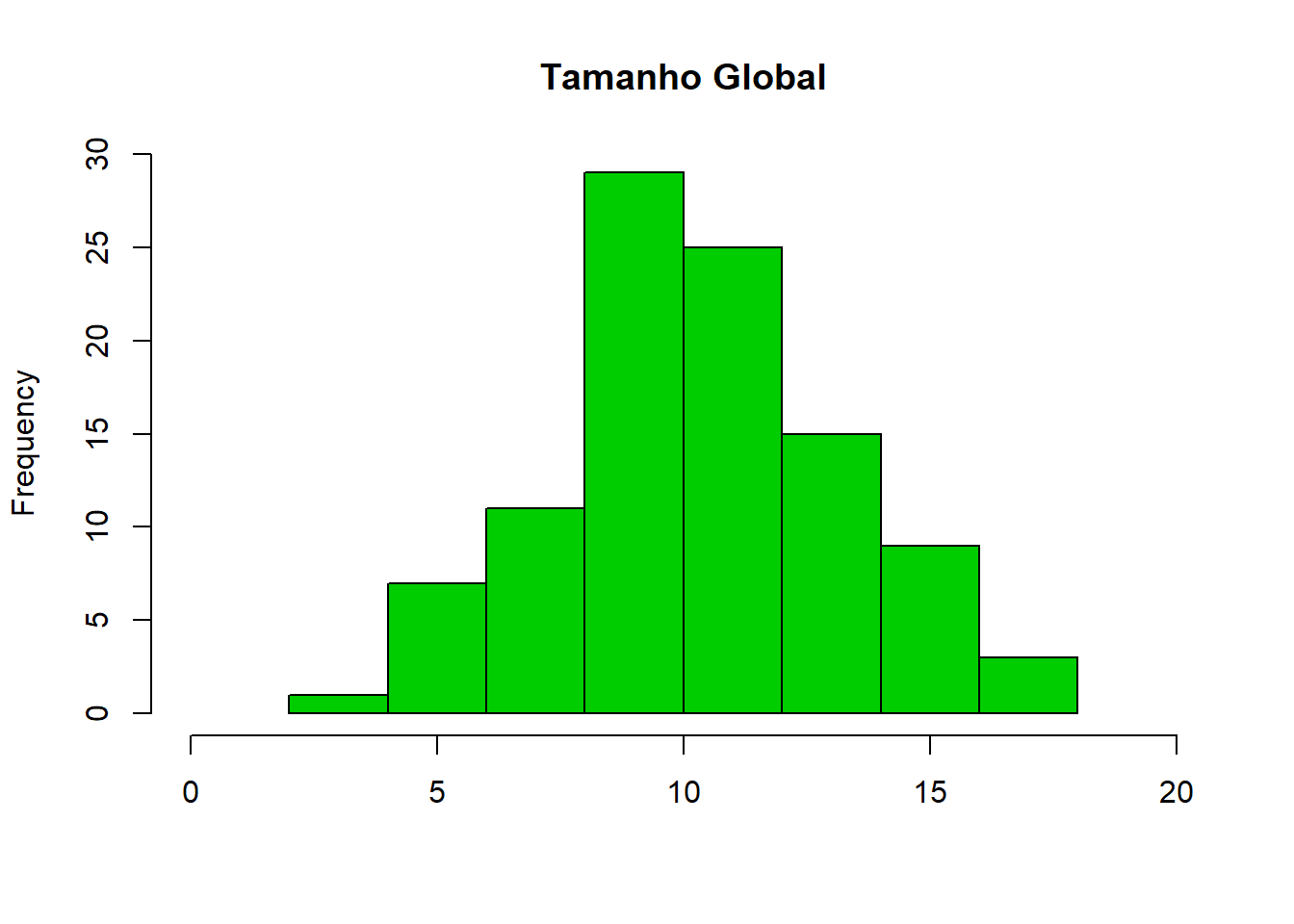
Se quisermos ajustar uma distribuição aos dados, a maneira mais comum de o fazer é através da função fitdistr. Esta função permite estimar os valores dos parâmetros da distribuição, através da maximização da função de probabilidade.
Assim, e como os dados aparentam ter uma distribuição gaussiana, como podemos verificar no histograma acima, assumimos que o Tamanho global “tg” ~ Normal (mean,sd).
## mean sd
## 10.3922000 2.9925225
## ( 0.2992523) ( 0.2116033)Estimados os parâmetros da distribuição, é possível representar no histograma uma linha de tendência:
hist(data$tg,main="Tamanho Global",xlab=NULL,xlim=c(0,20),col=3,freq=FALSE)
lines(seq(0,20,by=0.2),dnorm(seq(0,20,by=0.2),mean=10.3922000,sd= 2.9925225))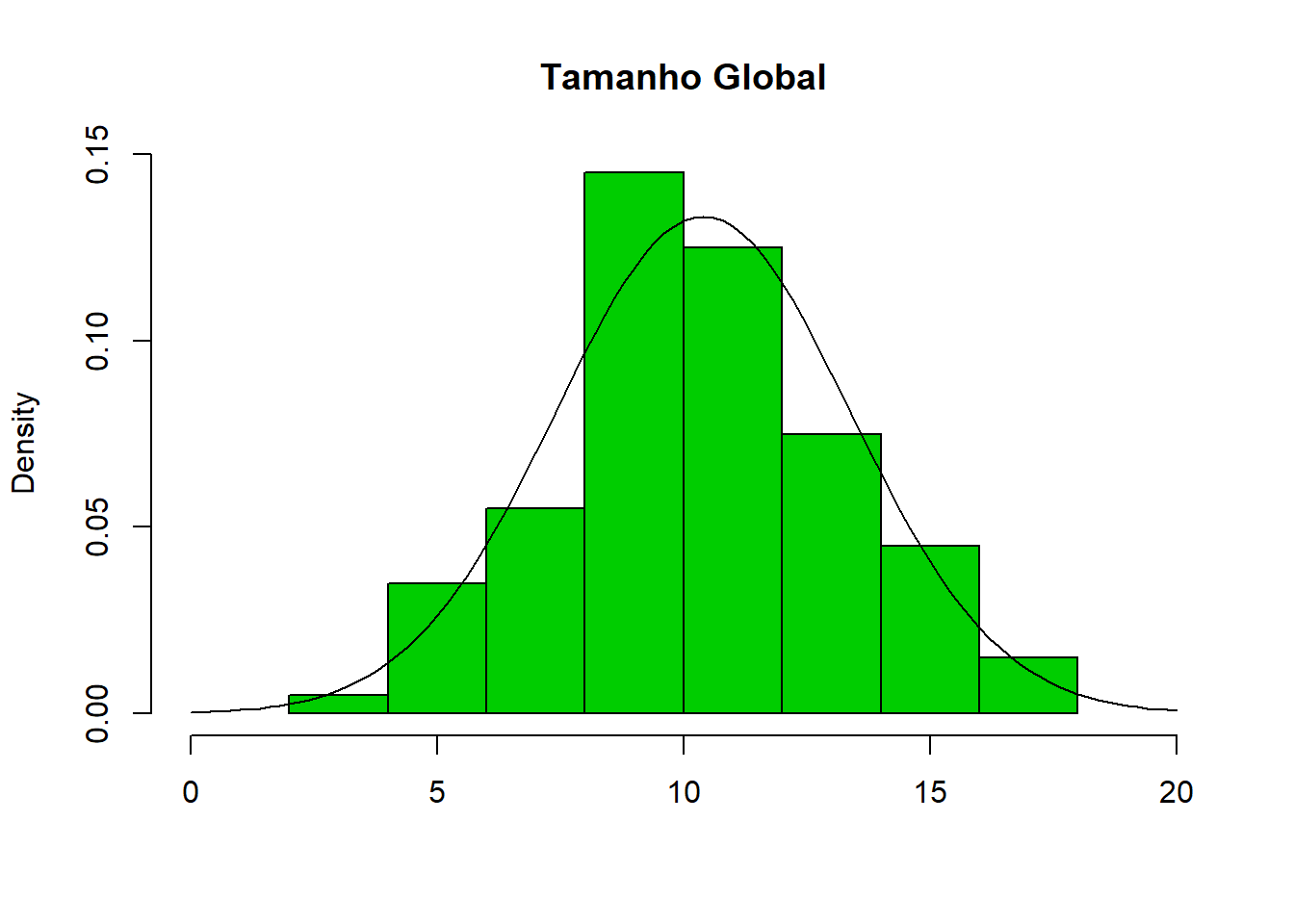
Assim, obtemos uma linha de tendência que aparenta ajustar-se corretamente aos dados. Embora apenas se possa testar a gaussianidade dos dados com recurso a testes de normalidade aplicados sobre os resíduos, segundo a representação acima, não existem fortes razões para suspeitar de que a distribuição dos dados não seja Gaussiana.
Em oposição, e a título de exemplo, se tentássemos ajustar uma outra distribuição mais “skewed”, como a distribuição Log-Normal, é expectável que não obtenhamos o mesmo ajuste dos dados a esta distribuição.
## meanlog sdlog
## 2.29565714 0.31149091
## (0.03114909) (0.02202573)hist(data$tg,main="Tamanho Global",xlab=NULL,xlim=c(0,20),col=3,freq=FALSE)
lines(seq(0,20,by=0.2),dlnorm(seq(0,20,by=0.2),meanlog= 2.29565714,sdlog=0.31149091),col="red")
lines(seq(0,20,by=0.2),dnorm(seq(0,20,by=0.2),mean=10.3922000,sd= 2.9925225))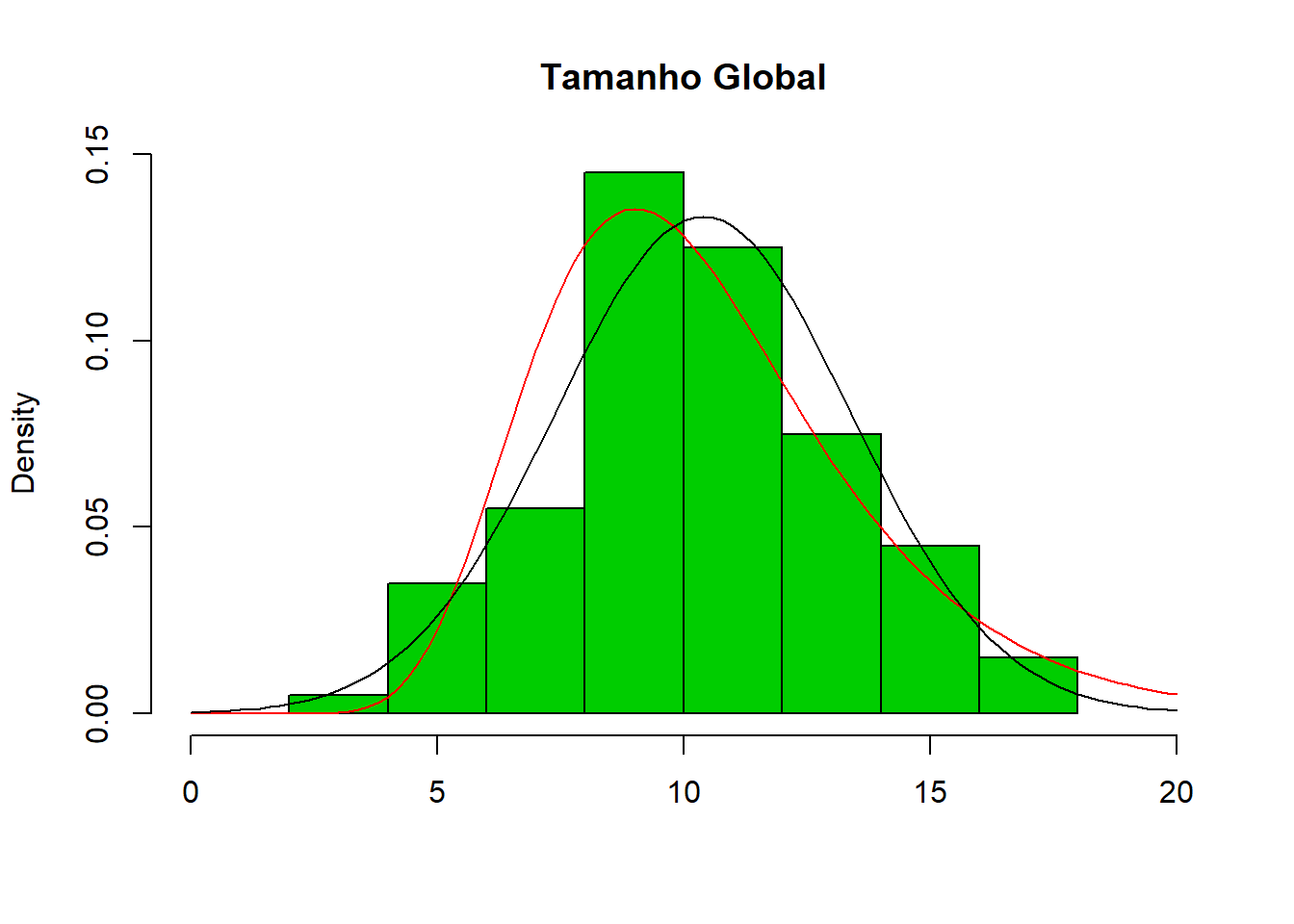
Nota: A linha de tendência representada a vermelho corresponde ao ajuste dos dados à distribuição Log-Normal
Para que não restem dúvidas, podemos analisar de que forma os valores amostrais da média e desvio padrão calculados para o tamanho global se aproximam dos valores estimados segundo as duas distribuições. Espera-se então que os valores obtidos para os parâmetros dos valores reais se aproximem mais aos calculados segundo uma distribuição normal, quando comparados com os obtidos segundo a Log-Normal.
## [1] 3.007598## [1] 10.3922## mean sd
## 10.3922000 2.9925225
## ( 0.2992523) ( 0.2116033)## meanlog sdlog
## 2.29565714 0.31149091
## (0.03114909) (0.02202573)- Desvio Padrão
dados: 3.007598
normal: 2.9925225
log-normal: 10^0.31149091 = 2.048759
- Média
dados: 10.3922
normal: 10.3922000
log-normal: 2.29565714
Conclui-se, dada a semelhança dos parâmetros, que de facto os dados se aproximam de uma distribuição Gaussiana.
4.4 Exemplos reais de aplicação
- Black-swan events in animal populations → https://www.pnas.org/content/pnas/early/2017/03/06/1611525114.full.pdf
Os Black Swan events são eventos estatisticamente improváveis e com profundas consequências, que ocorrem em meio social, financeiro ou biológico. Neste último caso, e especialmente em termos ecológicos, aplica-se muito a dinâmicas populacionais. Neste artigo são discutidas quais as melhores distribuições a usar em dados de dinâmica populacional para tornar possível a previsão de Black swan events, especialmente daqueles que levam à drástica diminuição da população, ou mesmo à sua extinção.
- Coral population structure: The hidden information of colony size-frequency distributions → https://www.int-res.com/articles/meps/162/m162p301.pdf
Neste artigo, as informações de tamanho e frequência de colónias de corais são modeladas com distribuições lognormal e, através dessas distribuições tamanho-frequência (size-frequency distributions), são analisadas diversas características das colónias que podem ser utilizadas para avaliar as condições e as alterações nas mesmas.
- Modeling observed animal performance using the Weibull distribution → https://jeb.biologists.org/content/jexbio/219/11/1603.full.pdf
Neste artigo compara-se o desempenho de várias distribuições na modelação de dados relativos à performance adesiva de geckos.
4.5 Recursos adicionais
Várias distribuições contínuas (e outros temas da cadeira) com recursos para o R: https://ms.mcmaster.ca/~bolker/emdbook/chap4A.pdf
Distribuição Normal: http://seankross.com/notes/dpqr/
Distribuição t de Studnet: https://www.mathworks.com/help/stats/students-t-distribution.html
Distribuição Beta: https://besjournals.onlinelibrary.wiley.com/doi/full/10.1111/2041-210X.13234
Distribuição Gamma: https://www.mathworks.com/help/stats/gamma-distribution.html
Distribuição Weibull: https://www.weibull.com/hotwire/issue14/relbasics14.htm
4.6 Considerações finais
Existem muitas mais distribuições contínuas para além daquelas que foram apresentadas neste trabalho. Esta família de distribuições está em constante expansão para melhor descrever e modelar a imensidão de dados, ecológicos e não só, que são gerados todos os dias.
Com tanta variedade de distribuições, é impossível memorizar tudo. Felizmente, existem descrições e explicações detalhadas para cada uma delas, disponibilizadas publicamente em diversos artigos e sites, de modo a que a comunidade científica possa usufruir do conhecimento que já existe em caso de necessidade.
Se os teus dados não tiverem as características descritas neste documento ou se as distribuições abordadas não tiverem o melhor ajuste aos dados, não desesperes! Em princípio já existe uma distribuição que te salve. No pior dos casos, podes sempre criar a tua própria distribuição.
4.7 Referências
Bak, R., & Meesters, E. (1998). Coral population structure: The hidden information of colony size-frequency distributions. Marine Ecology Progress Series, 162, 301-306.
Anderson SC, Branch TA, Cooper AB, Dulvy NK. Black-swan events in animal populations. Proc Natl Acad Sci U S A. 2017 Mar 21;114(12):3252-3257.
Travis J. Hagey, Jonathan B. Puthoff, Kristen E. Crandell, Kellar Autumn, Luke J. Harmon. Modeling observed animal performance using the Weibull distribution. Journal of Experimental Biology 2016 219: 1603-1607; doi: 10.1242/jeb.129940
https://www.umass.edu/landeco/teaching/ecodata/schedule/distributions.pdf
http://www.portalaction.com.br/probabilidades/modelos-probabilisticos-continuos