Chapter 18 Tema

Todo o texto a itálico neste template deverá ser apagado para entregar. O texto que estivel a bold deve ser substituido por texto normal com os vossos dados. Nenhum cabeçalho deverá ser apagado. Nenhum cabeçalho deverá ser adicionado

Depois de realizar uma análise de regressão devemos avaliar se os pressupostos do modelo linear se verificam. Neste trabalho pretende-se que apliquem uma regressão a um dos conjuntos de dados que tenham recolhido no Trabalho 1 e avaliem os pressupostos do modelo. Dica: para tal devem fazer uma análise aos resíduos.

18.1 Membros do grupo

Este grupo era composto pelos seguintes elementos:

Catarina Ribeiro, nº 50887
Fabiana Tavares, nº 50784
Jessica Matos, nº 55181
João Mendes, nº 50855
Katerina Moniz, nº 45883
Mónica Lima, nº 49204

18.2 Introdução Teórica

Colocar aqui contexto teórico suficiente para um aluno de EN que não tenha ido a esta aula compreender o tema

Um modelo de regressão linear é usado quando uma reta resume os dados de um diagrama de dispersão e que pode ser usado para fazer previsões a partir dos dados.

Para aplicarmos testes estatísticos é necessário verificar que os nossos resíduos cumprem determinados pressupostos: os pressupostos de normalidade, homocedasticidade, independência dos erros, linearidade dos dados e inexistência de outliers influentes. Para tal, efectua-se uma análise aos resíduos, pois assim percebe-se se o modelo de regressão utilizado é adequado. A normalidade dos dados resíduos pode ser testada pelos testes de Kolmogorov-Smirnov, Pearson e Shapiro-Wilk, por exemplo, enquanto que a homocedasticidade pode ser testada pelos testes de Bartlett e Levene e a independência pelo teste de Durbin-Watson. O último teste a aplicar é o teste de hipóteses.

18.3 Exemplo em R

Implementar em R o tema. Por exemplo se for um teste de hipóteses aplicar sobre um conjunto de dados e tirar as conclusões devidas. Se for para ilustrar um conceito, poderão realizar uma pequena simulação.

usar isto - > lm([target variable] ~ [predictor variables], data = [data source])

Devem usar um dos conjuntos de dados que um dos elementos do grupo tenha recolhido no trabalho 1. Explicar brevemente os dados, fazendo uma curta análise exploratória dos mesmos.

arvores <- read.csv2("50855JoaMen 1.csv")

str(arvores)

## 'data.frame':	70 obs. of  5 variables:
##  $ ï..ID: int  1 2 3 4 5 6 7 8 9 10 ...
##  $ arvor: Factor w/ 2 levels "A","B": 1 1 1 1 1 1 1 1 1 1 ...
##  $ cor  : Factor w/ 3 levels "amarelo","castanho",..: 3 2 3 1 2 1 2 1 2 2 ...
##  $ comp : num  5.1 8.6 6.5 7.2 8.4 7 6.7 5 8.5 6.5 ...
##  $ larg : num  2.7 5 4.5 3.2 4.5 4.2 3.5 2.7 4 4 ...

summary(arvores)

##      ï..ID       arvor        cor          comp             larg       
##  Min.   : 1.00   A:35   amarelo : 5   Min.   : 4.000   Min.   : 2.700  
##  1st Qu.:18.25   B:35   castanho:46   1st Qu.: 6.825   1st Qu.: 4.000  
##  Median :35.50          verde   :19   Median : 8.200   Median : 6.350  
##  Mean   :35.50                        Mean   : 8.377   Mean   : 7.714  
##  3rd Qu.:52.75                        3rd Qu.: 9.300   3rd Qu.:10.925  
##  Max.   :70.00                        Max.   :15.900   Max.   :18.000

par(mfrow=c(1,2))
boxplot(comp~arvor,arvores, main="Comprimento das árvores") 

boxplot(larg~arvor,arvores, main="Largura das árvores")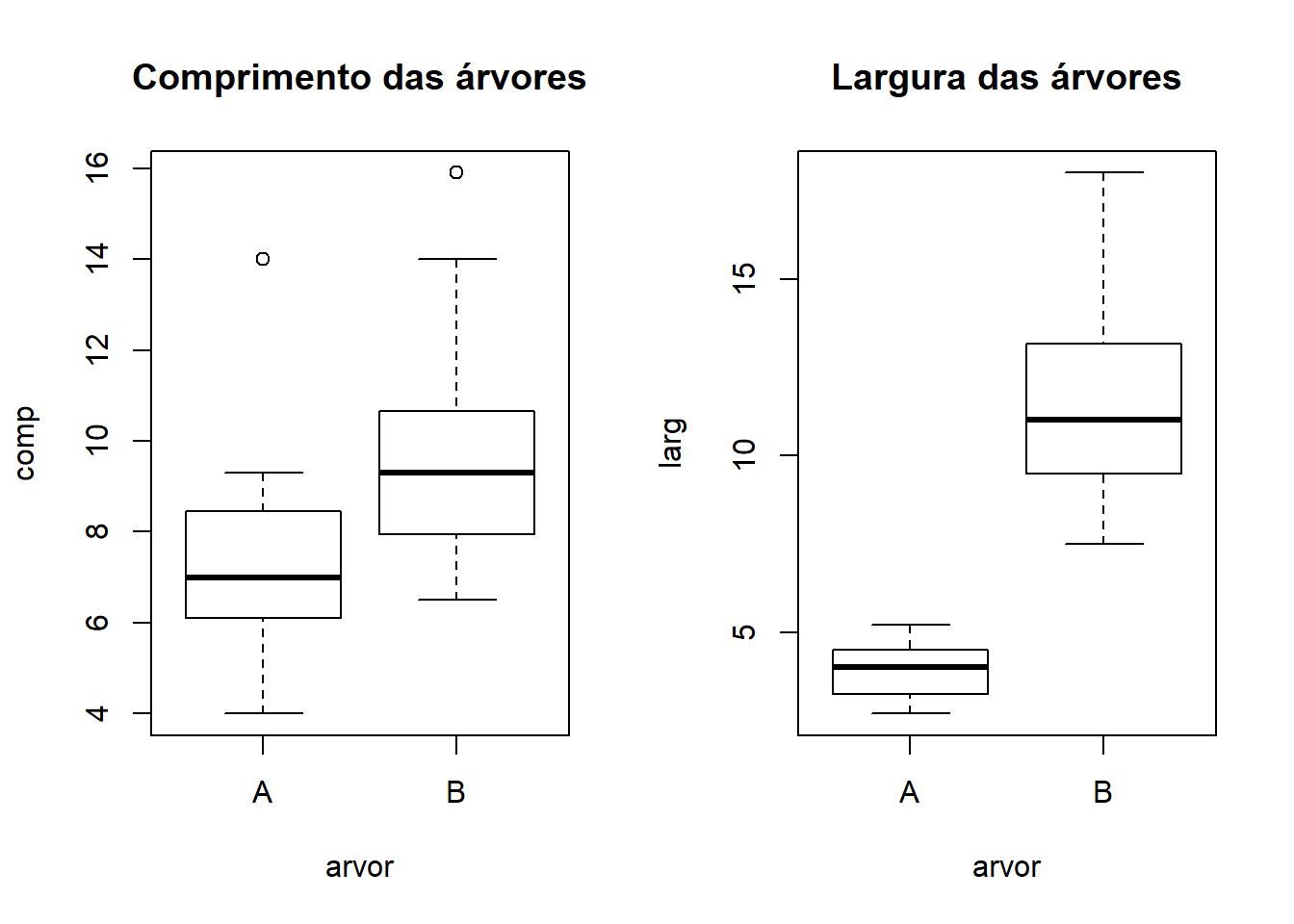

#Nos boxplots com o comprimento das árvores, consegue-se perceber que há 1 outlier para as árvores A e outro para as árvores B. Nos boxplots com a largura das árvores não há outliers.

Pressupostos da análise de regressão

Distribuição dos erros é normal de média 0 e variância constante \(\sigma\)^2 (homocedasticidade de variâncias).

Teste de Shapiro:

H0: erros têm uma dist. Normal; H1: erros NÃO têm uma dist. Normal.

with(arvores,tapply(comp,arvor,shapiro.test))

## $A
## 
## 	Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.90566, p-value = 0.005633
## 
## 
## $B
## 
## 	Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.92105, p-value = 0.01528

with(arvores,tapply(larg,arvor,shapiro.test))

## $A
## 
## 	Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.95191, p-value = 0.1297
## 
## 
## $B
## 
## 	Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.92043, p-value = 0.01467

#Para o comprimento das árvores A temos como resultado p-value=0.005633, que é menor que α=0.05, logo podemos rejeitar H0.

#Para o comprimento das árvores B obtém-se p-value=0.01528, que é um valor menor que α=0.05, logo rejeita-se H0.

#Para a largura das árvores A obtém-se p-value=0.1297, que é um valor maior que α=0.05, portanto não se rejeita H0.

#Para a largura das árvores B obtém-se p-value=0.01467, que é um valor menor que α=0.05, portanto rejeita-se H0.

#Apesar de a grande maioria dos nossos dados não seguirem uma distribuição Normal, é possível realizar-se uma regressão linear. Isto porque, o método de estimativa usado é o método dos quadrados mínimos que não requer o pressuposto de normalidade.

Teste de Bartlett:

H0: erros têm variância constante; H1: erros NÃO têm variância constante.

bartlett.test(x=arvores$comp, g=arvores$arvor)

## 
## 	Bartlett test of homogeneity of variances
## 
## data:  arvores$comp and arvores$arvor
## Bartlett's K-squared = 0.77433, df = 1, p-value = 0.3789

#Deu p-value=0.3789 que é um valor maior que α=0.05, logo não rejeitamos H0.

Os erros são independentes (não correlacionados).
Não há erros em X (ou na prática as medições de X são obtidas com erro negligível comparativamente às de Y).

Teste de Durbin-Watson

H0: os erros NÃO estão auto-correlacionados; H1: os erros estão auto-correlacionados.

lm1=lm(comp~larg, data=arvores[1:35,])

lm2=lm(comp~larg, data=arvores[36:70,])

library(lmtest)

## Loading required package: zoo

## 
## Attaching package: 'zoo'

## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric

dwtest(lm1)

## 
## 	Durbin-Watson test
## 
## data:  lm1
## DW = 2.2099, p-value = 0.7309
## alternative hypothesis: true autocorrelation is greater than 0

#Deu p-value=0.7309 que é um valor maior que α=0.05, portanto não rejeitamos H0.

dwtest(lm2)

## 
## 	Durbin-Watson test
## 
## data:  lm2
## DW = 1.5133, p-value = 0.07406
## alternative hypothesis: true autocorrelation is greater than 0

#Deu p-value=0.07406 que é um valor maior que α=0.05, logo não podemos rejeitar H0.

library(ggplot2)

arvores.ols <-lm(comp~larg, data=arvores)
arvores.resi<-arvores.ols$residuals
ggplot(data = arvores, aes(y = comp, x = larg)) + geom_point(col = 'blue') + geom_abline(slope=0)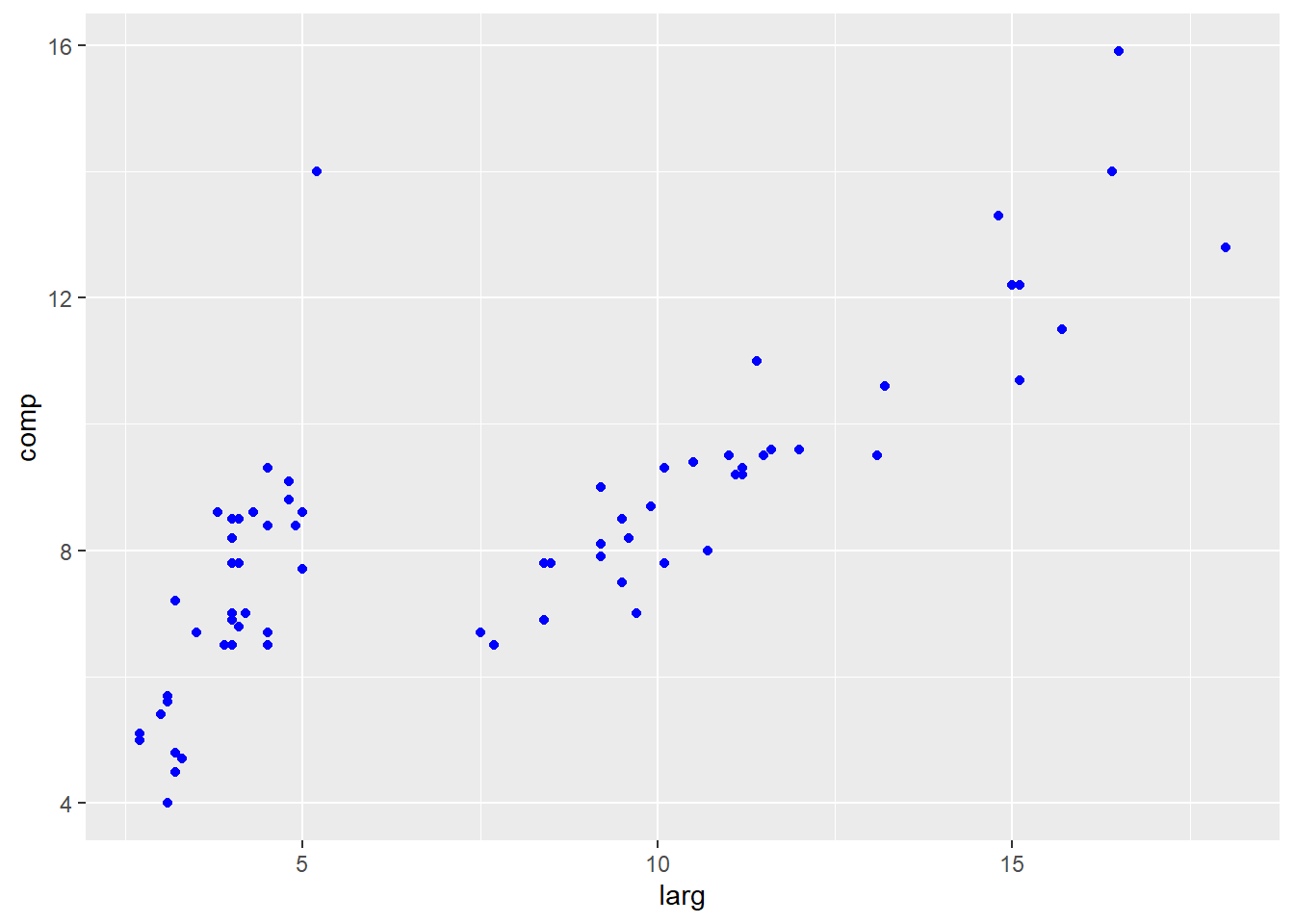

scatter.smooth(x=arvores[1:35,]$larg, y=arvores[1:35,]$comp, main="Árvores A", xlab="Largura", ylab="Comprimento")

lm1=lm(comp~larg, data=arvores[1:35,])
abline(lm1, lty=1, col="red")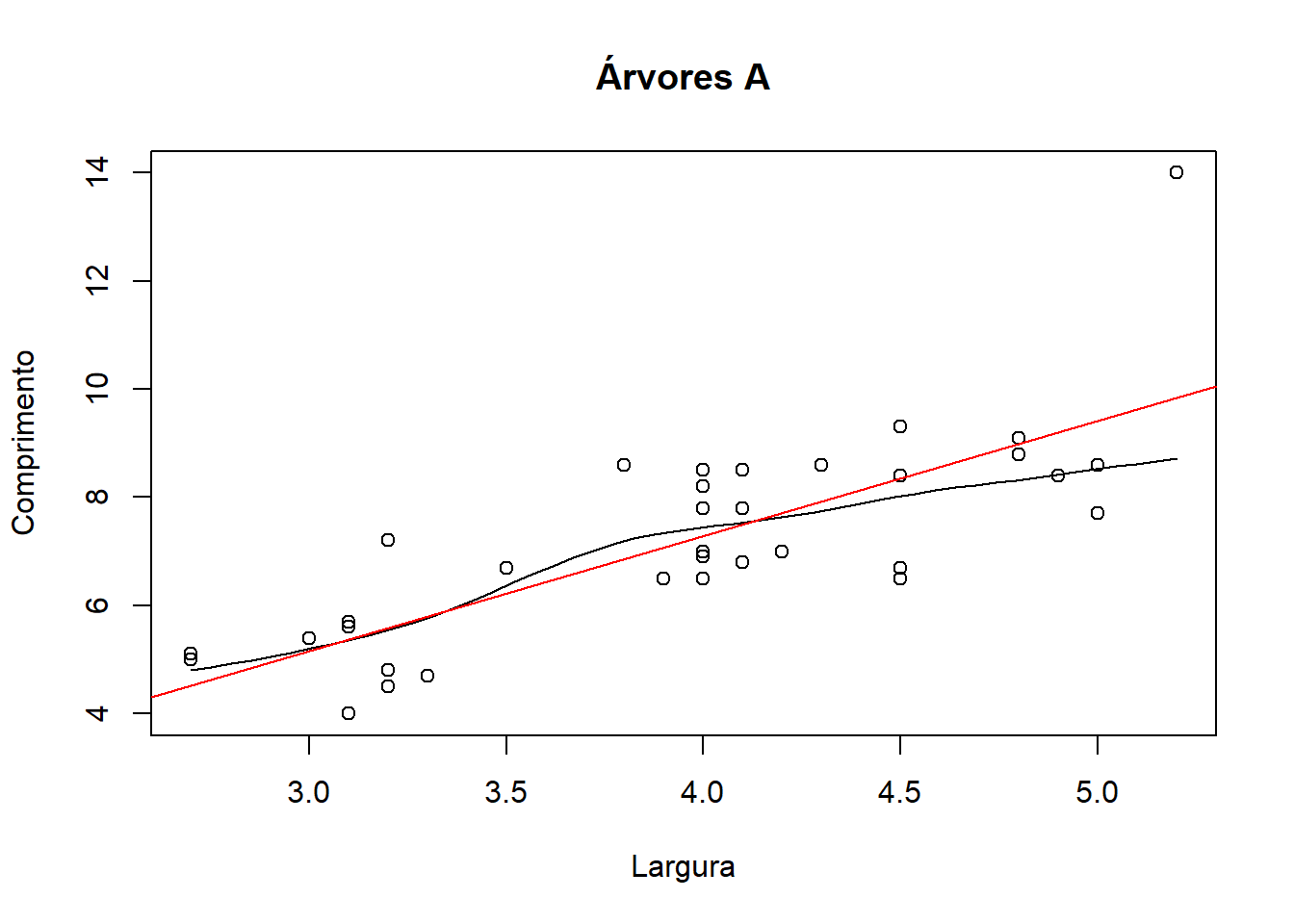

scatter.smooth(x=arvores[36:70,]$larg, y=arvores[36:70,]$comp, main="Árvores B", xlab="Largura", ylab="Comprimento")

lm2=lm(comp~larg, data=arvores[36:70,])
abline(lm2, lty=1, col="blue")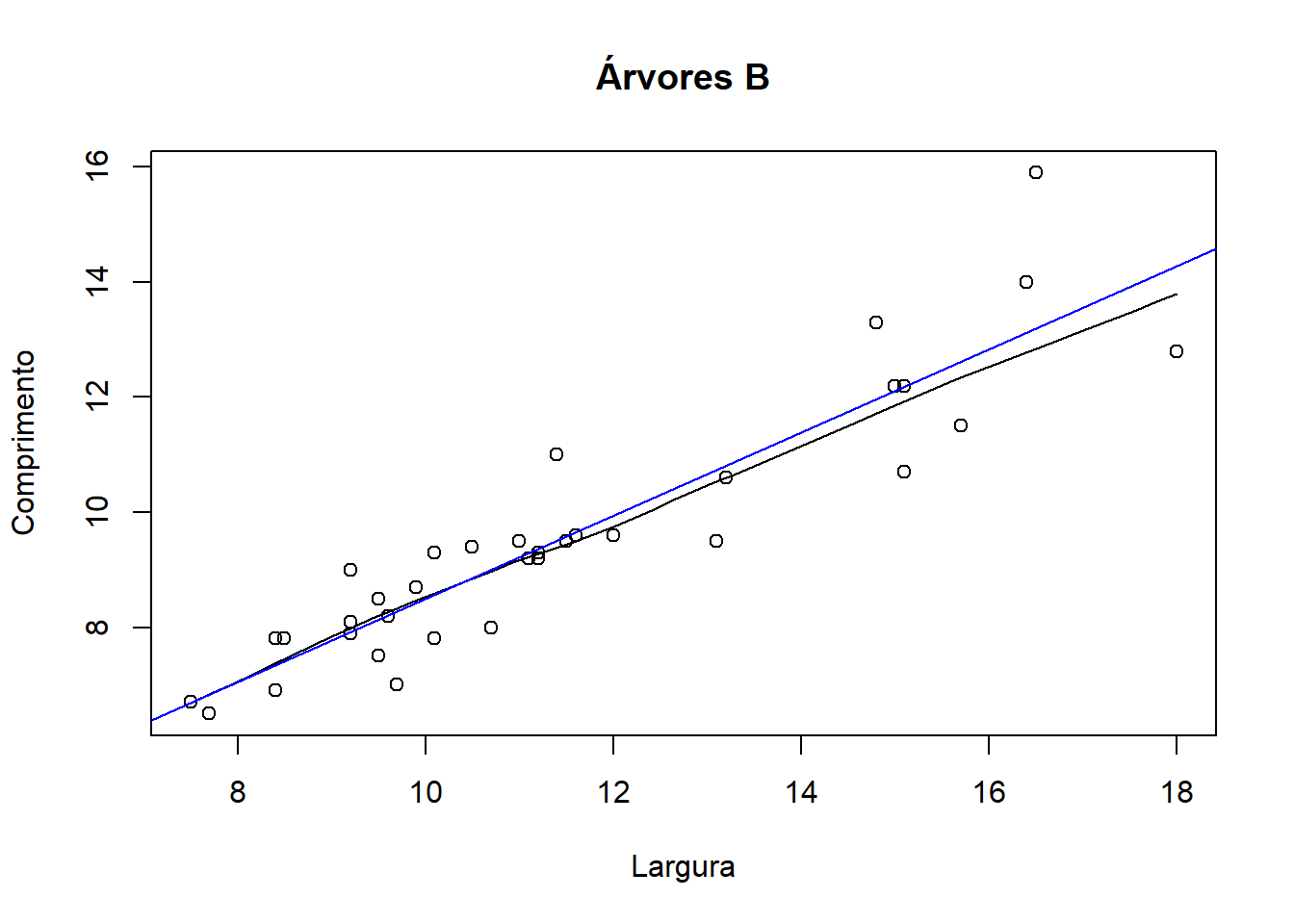

#Pelo teste de Durbin-Watson e pelos plots obtidos acima consegue-se cumprir o 2º e o 3º pressuposto.

Regressões lineares e análise de resíduos

par(mfrow=c(2,2))

lmA<-lm(comp~larg,data=arvores[1:35,])
summary(lmA)

## 
## Call:
## lm(formula = comp ~ larg, data = arvores[1:35, ])
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.8539 -0.7867  0.0461  0.5458  4.1549 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -1.2321     1.1910  -1.034    0.308    
## larg          2.1302     0.2969   7.176 3.18e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.193 on 33 degrees of freedom
## Multiple R-squared:  0.6094,	Adjusted R-squared:  0.5976 
## F-statistic: 51.49 on 1 and 33 DF,  p-value: 3.178e-08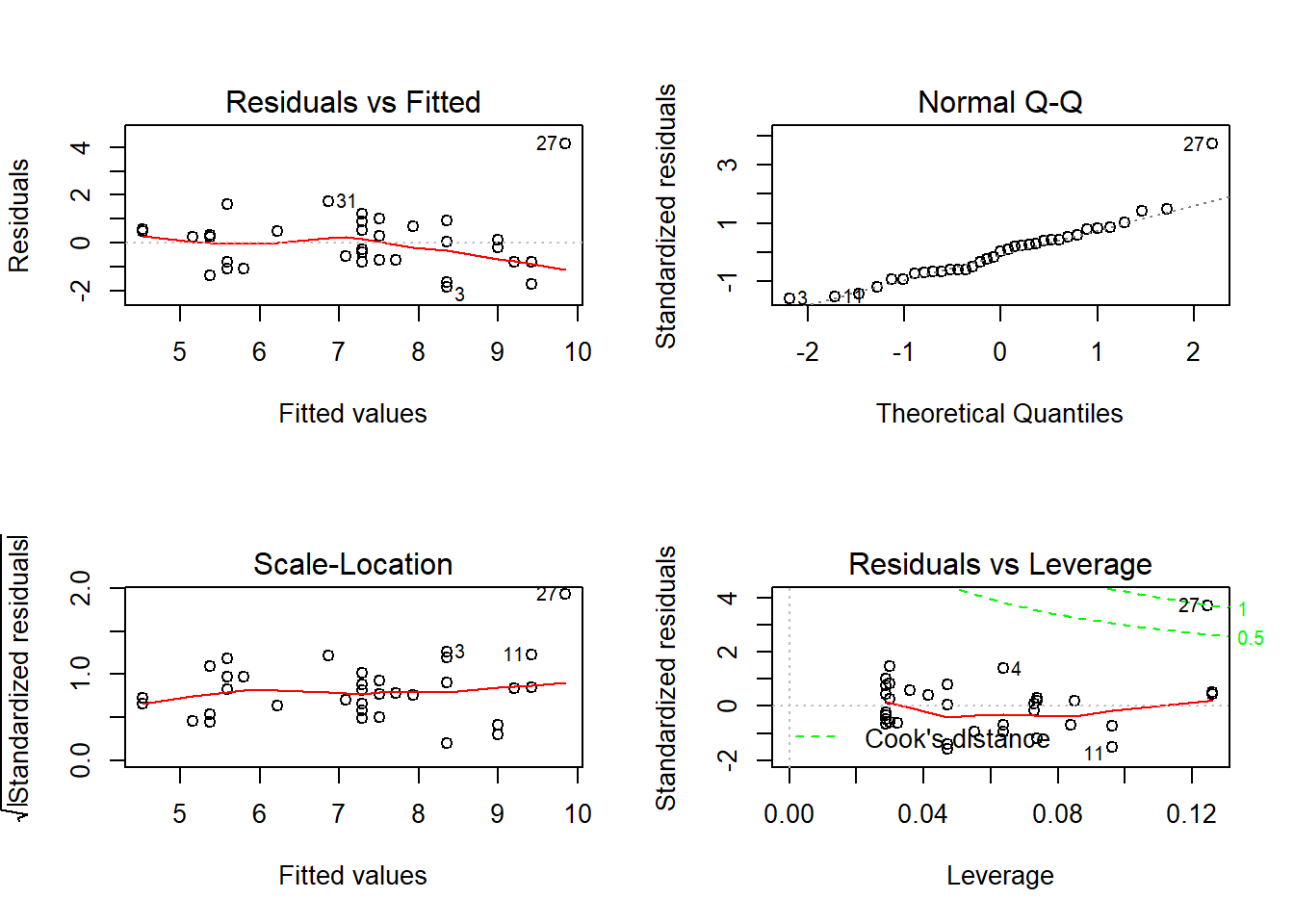

plot(lmA)

Para as árvores A fez-se uma regressão linear simples, que comparou a variável comprimento com a variável largura. Pelo output consegue-se perceber que a variável largura é a que mais contribui para explicar os resultados. Obtiveram-se 4 gráficos no output.

O gráfico “Residuals vs Fitted” apresenta os resíduos em função dos valores estimados. Permite verificar os pressupostos de linearidade entre as variáveis e a homocedasticidade das variâncias. No nosso caso, o pressuposto de linearidade cumpre-se porque os resíduos não se encontram muito longe de y=0. Quanto ao pressuposto de homocedasticidade, este também se cumpre porque não há nenhum padrão nos resíduos e estes encontram-se espalhados em torno de y=0.

O gráfico “Normal Q-Q” avalia a normalidade dos resíduos. A linha a tracejado representa a distribuição Normal teórica, enquanto os pontos representam a distribuição de resíduos observados. Neste caso, os pontos tendem a seguir a recta, por isso a distribuição pode ser considerada normal.

O gráfico “Scale-Location” é semelhante ao gráfico “Residuals vs Fitted”, mas com valores positivos e tem os resíduos padronizados como referência. Este gráfico permite detectar heterocedasticidade de variâncias, ou seja, variâncias que não sejam constantes. No nosso caso, observou-se a homocedasticidade de variâncias, reforçando assim o que foi observado no 1º gráfico.

O gráfico “Residuals vs Leverage” mostra os pontos que mais influênciam os resultados da regressão em causa. Isto é possível ver-se através da proximidade entre os pontos e a linha “Cook’s distance”. Percebe-se que os pontos 4, 11 e 27 são os que têm mais influência nos resultados, sendo o ponto 27 um outlier.

par(mfrow=c(2,2))

lmB<-lm(comp~larg,data=arvores[36:70,])
summary(lmB)

## 
## Call:
## lm(formula = comp ~ larg, data = arvores[36:70, ])
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.48541 -0.39114 -0.01782  0.37684  2.70195 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.26328    0.64838   1.948   0.0599 .  
## larg         0.72332    0.05497  13.159 1.11e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8893 on 33 degrees of freedom
## Multiple R-squared:  0.8399,	Adjusted R-squared:  0.8351 
## F-statistic: 173.2 on 1 and 33 DF,  p-value: 1.112e-14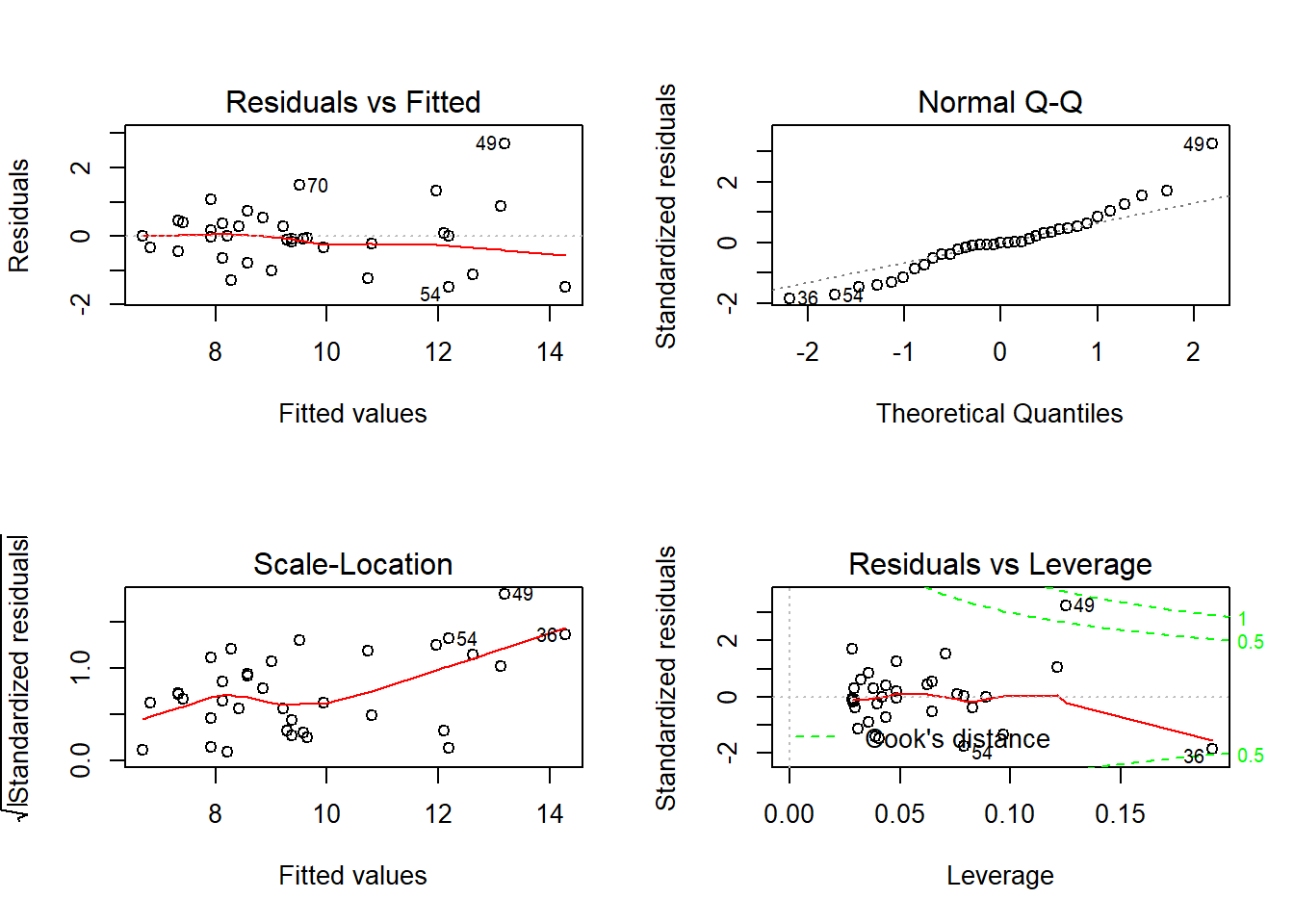

plot(lmB)

Para as árvores B repetiu-se o mesmo procedimento que foi feito para as árvores A. Pelo output consegue-se perceber que ambas as variáveis (comprimento e largura) contribuem para explicar os resultados. Obtiveram-se novamente os 4 gráficos no output.

O gráfico “Residuals vs Fitted” permitiu cumprir o pressuposto de linearidade, mas não o de homocedasticidade das variâncias. Isto porque, os resíduos não se encontram muito longe de y=0, mas parece haver um padrão ou um “cluster” em torno de y=0.

No gráfico “Normal Q-Q” os pontos tendem a seguir a recta, com alguns desvios. Por esta razão, a distribuição pode ser considerada normal.

O gráfico “Scale-Location” mostra a existência de heterocedasticidade de variâncias, o que evidência que este modelo provavelmente não seria o mais adequado aos nossos dados referentes às árvores B. Se quisessemos continuar a usar uma regressão linear simples, seria necessário proceder a uma transformação de dados ou então escolher outro modelo.

No gráfico “Residuals vs Leverage” observa-se que os pontos 36, 49 e 54 são os que mais influenciam os resultados, sendo o ponto 49 um outlier e provavelmente o ponto 36 também.

18.4 Exemplos reais de aplicação

Aqui deverá colocar no mínimo dois artigos que se refiram ao seu tema num contexto ecológico ou biológico

https://www.sciencedirect.com/science/article/pii/S1871402120302939

https://www.sciencedirect.com/science/article/pii/S0269749120316961#fig3

18.5 Recursos adicionais

Aqui deverá colocar no mínimo dois links para páginas que apresentem mais informação sobre o tema

https://pt.khanacademy.org/math/statistics-probability/describing-relationships-quantitative-data/introduction-to-trend-lines/a/linear-regression-review

http://r-statistics.co/Assumptions-of-Linear-Regression.html

http://r-statistics.co/Linear-Regression.html

http://www.stat.yale.edu/Courses/1997-98/101/linreg.htm

18.6 Considerações finais

Comentários ou outras considerações finais que não caibam em nenhum dos tópicos acima

Num trabalho de carácter experimental, nomeadamente estatístico, é preciso ter em consideração o tamanho da amostra, isto é, quanto maior a amostra, menor será a probabilidade de ocorrerem erros. O facto de existirem diversos métodos para chegar a um certo fim, pode influenciar os resultados finais do estudo. O mais certo seria fazer diversos testes para verificarmos se os pressupostos são verdadeiros, de modo a que o resultado possa ser considerado mais fidedigno.

18.7 Referências

Deverá aqui no mínimo ter as referencias que usou na secção dos exemplos reais de aplicação

Tratam-se do mesmos links.