Chapter 13 Tema
A análise de variância (ANOVA) é um procedimento estatístico usado frequentemente em estudos ecológicos. Neste trabalho pretende-se que contextualizem em que situações é que este teste estatístico deve ser aplicado, sob que condições e que demonstrem, com um exemplo específico, a sua implementação em R (podem usar os dados do Trabalho 1).
13.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- Mafalda Cordeiro, 52596
- Maria Machado, 52580
- Maria Vasconcelos, 52601
- Nuno Fialho, 52634
- Omar Moura, 52624
- Rui Antunes, 52637
13.2 Introdução Teórica
A ANOVA é um teste de análise de variância aplicado quando se pretende comparar a distribuição de três ou mais grupos de amostras e que simplifica bastante a sua avaliação. É bastante utilizado em muitos estudos devido à necessidade de repetir colheitas efetuadas em diversas condições, testando vários fatores ou usando vários grupos. A ANOVA permite verificar o quão distante a média de cada grupo está da média global e com isso também estudar a variabilidade das amostras consideradas, a diversos níveis, são estes:
- Variabilidade total: corresponde à diferença entre cada grupo de observações e uma média global (ao quadrado - de forma a que os valores se anulem ). A variação total é também igual à soma da variação entre grupos com a variação dos resíduos (SQ TOTAL=SQ GRUPOS+SQ ERRO).
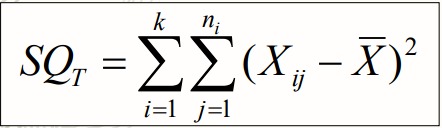
- Variabilidade entre-grupos
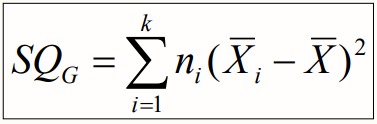
- Variabilidade intra-grupos: corresponde aos resíduos, mais concretamente ao desvio de cada componente do grupo em relação à média desse mesmo grupo. Dado que os elementos de cada grupo são sujeitos às mesmas condições, esta variabilidade surge como fonte do acaso.
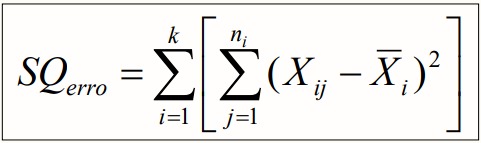
Idealmente, a variância entre grupos deve ser pequena quando comparada com a variância dentro de cada grupo.
13.2.1 Pressupostos do teste
Este teste possui alguns pressupostos que incidem sobre os resíduos das amostras:
As variâncias devem ser iguais (homocedasticidade);
Os resíduos devem ser provenientes de uma distribuição gaussiana (com média 0).
Para além disso, para realizar a ANOVA, as amostras devem ser independentes. A análise de variância, através deste método, é bastante robusta sendo que, por isso, o seu desempenho não é profundamente afectado por desvios moderados dos pressupostos.
Em geral os resultados da ANOVA são apresentados numa tabela que será posteriormente analisada. A ANOVA é útil quando temos mais do que dois níveis na variável independente.
13.2.2 Caso os pressupostos acima descritos forem cumpridos:
Sendo a ANOVA um teste de hipóteses é necessário, portanto, defini-las a priori. Neste caso, a hipótese nula é a igualdade das médias, pelo que a hipótese alternativa, e o que geralmente queremos provar, é que há pelo menos um valor diferente.
H0 : µA=µB=µC.
H1 : As médias não são todas iguais.
13.2.3 Estatística de teste:
A estatística de teste F é a razão entre duas variâncias: a variância das médias entre-grupos e intra-grupos e é utilizada para decidir se se rejeita ou aceita H0.
Para o cálculo são utilizados a soma dos quadrados e os graus de liberdade associados a cada fator, no numerador o grau de liberdade é calculado através de k-1, onde k é o número de grupos e, no denominador, por N-k, onde N é o número de observações. Pode-se também simplificar esta expressão para a razão entre o Quadrado Médio(QM) entre-grupos e intra-grupos.
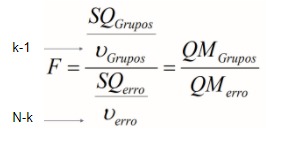
Seguindo esta linha de pensamento, quanto aos graus de liberdade:
- gl TOTAL = gl GRUPOS + gl ERRO , ou seja, N-1 = (k-1) + (N-k)
13.2.4 Valor Crítico e Critério de Decisão:
O valor crítico é dado pela expressão abaixo. Devemos rejeitar H0 caso a nossa estatística de teste F seja maior que o valor crítico estabelecido a priori. Caso contrário, não devemos rejeitar H0 e podemos assumir que as médias das diferentes amostras são todas iguais.
Valor crítico:
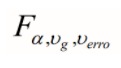
Rejeitar H0 se:
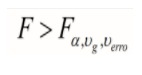
13.3 Exemplo em R
Para ajudar na compreensão desta matéria decidimos pô-la em prática com dados obtidos no trabalho 1, em que se estudou o que pode influenciar o comprimento dos juvenis da espécie Procambarus Clarkii.
Para tentar perceber o que influencia o comprimento destes lagostins foram registadas 3 variáveis diferentes: uma contínua (temperatura), uma binária (vegetação predominante), e uma categórica (tipo de sedimentação principal). Dado que o trabalho foi realizado na época seca, os lagostins foram encontrados em charcos.
No âmbito deste trabalho, apenas se irá utilizar a variável categórica para estudar o impacto no comprimento da espécie em questão, pois é a única que tem o número necessário de grupos para a realização do teste. O registo desta variável teve como objetivo observar indiretamente se a distância à foz influenciava o comprimento dos lagostins, isto porque, sabemos que os sedimentos vão sofrendo erosão à medida que se dirigem para jusante, o que implica que quanto mais próximo da foz, mais pequenos serão os sedimentos.
Realizámos o teste de Bartlett e de Shapiro-Wilk para verificar se se cumpriam os pressupostos da homogeneidade das variâncias e da distribuição gaussiana, respetivamente.
##
## Bartlett test of homogeneity of variances
##
## data: dados$tam. by grupos
## Bartlett's K-squared = 6.4456, df = 2, p-value = 0.03984##
## Shapiro-Wilk normality test
##
## data: dados$tam.
## W = 0.92261, p-value = 0.0007909Como se obteve um p-value de 0.04 no teste de Bartlett, H0 foi rejeitado para dois dos níveis de significância comuns, logo o pressuposto não foi cumprido. No teste de Shapiro-Wilk o p-value é de 0.0008, pelo que, o pressuposto mais uma vez não foi cumprido. Sendo assim, não se pode prosseguir para a realização do teste da ANOVA, visto que, bastava um dos pressupostos não ser cumprido para se ter de transformar os dados ou, eventualmente, optar por um teste não paramétrico.
Decidimos fazer um histograma para perceber o porquê do resultado do teste de Shapiro ser tão baixo.
# Código para a realização do histograma com os dados originais
hist(dados$tam., xlab = "Comprimento dos lagostins (cm)", ylab = "Frequência", main = "Distribuição do comprimento dos lagostins", col = "lightblue", ylim= c(0,30))
# Código para a realização da curva da distribuição dos dados no histograma
# Neste caso, como a função densidade probabilidade tem um intervalo de 0 a 1, multiplicámos por 31.5 para a curva ficar à escala do histograma
curve(31.5*dnorm(x, mean (dados$tam.),sqrt(var(dados$tam.))), col="dark blue", lwd=2, add=TRUE, yaxt="n")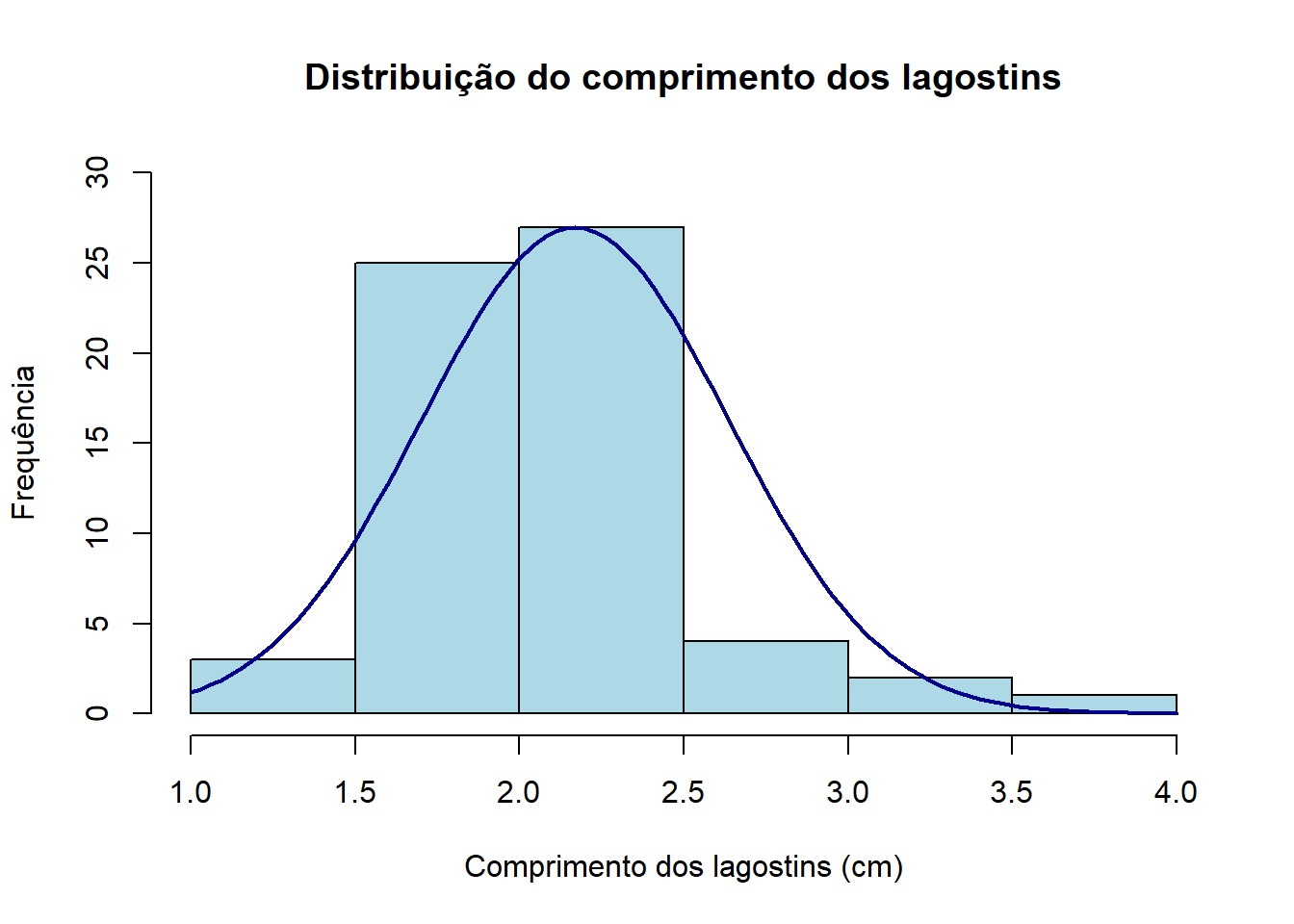
De seguida, transformou-se os dados para tentar cumprir os pressupostos necessários para a realização do teste da ANOVA. Para tal, utilizou-se a função logarítmica.
# Transformação dos dados do comprimento dos lagostins numa função logarítmica
trans<-log(dados$tam.)Após a transformação dos dados, voltou-se a realizar os testes para verificar se os pressupostos são cumpridos.
# Código para a realização do teste de Bartlett com os dados transformados
bartlett.test(trans,grupos)##
## Bartlett test of homogeneity of variances
##
## data: trans and grupos
## Bartlett's K-squared = 4.2627, df = 2, p-value = 0.1187No teste de Bartlett, H0 não é rejeitado, pois o p-value é superior a todos os níveis de significância normalmente utilizados. Assim sendo, o pressuposto da homogeneidade das variâncias é cumprido.
# Verificámos a variância dos valores dos três grupos de sedimentos em relação à média total dos dados
tapply(trans,grupos,FUN = var)## Areia Argila Seixos
## 0.02393971 0.06536739 0.03886928# criar uma palete de cores com as cores pretendidas
col.list <- c("red","green","blue")
palette(col.list)
#criar um gráfico utilizando os nossos dados com as cores de acordo com a família de sedimentos
family <- as.factor(grupos)
plot(dados$ID,trans, pch=19, col=family,xlab="Observações",ylab="log do comprimento dos lagostins",main="Variância entre-grupos")
#criar as linhas horizontais que representam as variâncias dos grupos
la<-mean(trans)+0.02393971
lb<-mean(trans)+0.06536739
lc<-mean(trans)+0.03886928
ld<-mean(trans)
abline(h=(mean(trans)))
#a função clip permite selecionar entre os valores de x e y que queremos as linhas
clip(1,25,ld,la)
abline(v=13,col="blue")
clip(26,43,ld,lb)
abline(v=35,col="red")
clip(44,62,ld,lc)
abline(v=53,col="green")
clip(1,25,ld,la)
abline(h=mean(trans)+0.02393971,col="blue")
clip(26,43,ld,lb)
abline(h=mean(trans)+0.06536739,col="red")
clip(44,62,ld,lc)
abline(h=mean(trans)+0.03886928,col="green")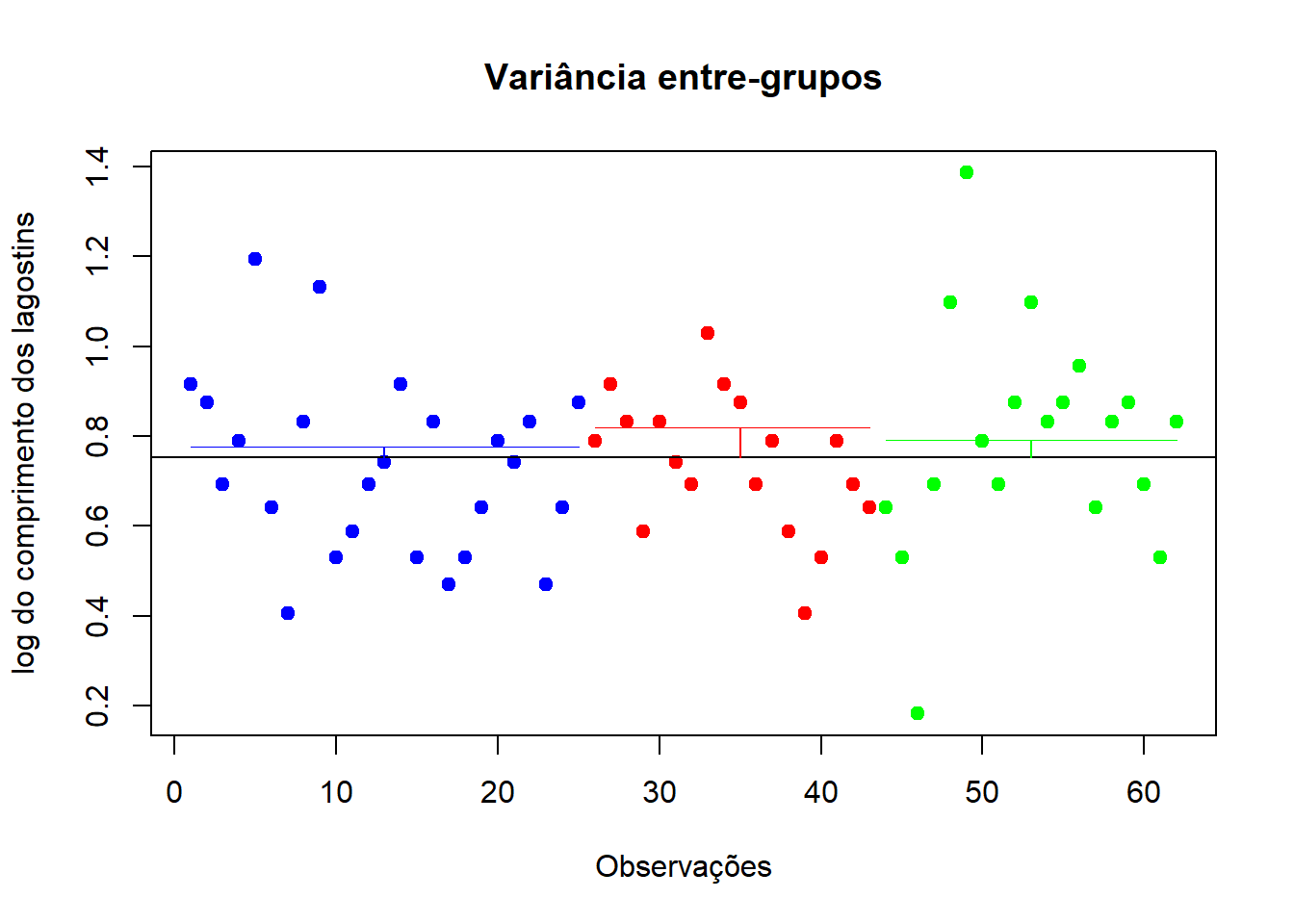
Este gráfico ilustra a semelhança entre as variâncias dos vários grupos e o porquê de não rejeitarmos H0 para este teste.
##
## Shapiro-Wilk normality test
##
## data: trans
## W = 0.97513, p-value = 0.2395Também o p-value, no teste de Shapiro-W, é superior a todos os níveis de significância comuns, tendo um valor igual a 0.24, o que significa que H0 não é rejeitado e o pressuposto é cumprido.
# Código para a realização do histograma com os dados transformados
hist(trans, xlab = "log do comprimento dos lagostins", ylab = "Frequência", main = " Distribuição logarítmica do comprimento dos lagostins", col="lightblue", ylim= c(0,25), cex.main= 1.1)
# Código para a realização da curva da distribuição dos dados transformados no histograma
# Neste caso, como a função densidade probabilidade tem um intervalo de 0 a 1, multiplicámos por 11.85 para a curva ficar à escala do histograma
curve(11.85*dnorm(x, mean(trans), sqrt(var(trans))), col="darkblue", lwd=2, add=TRUE, yaxt="n")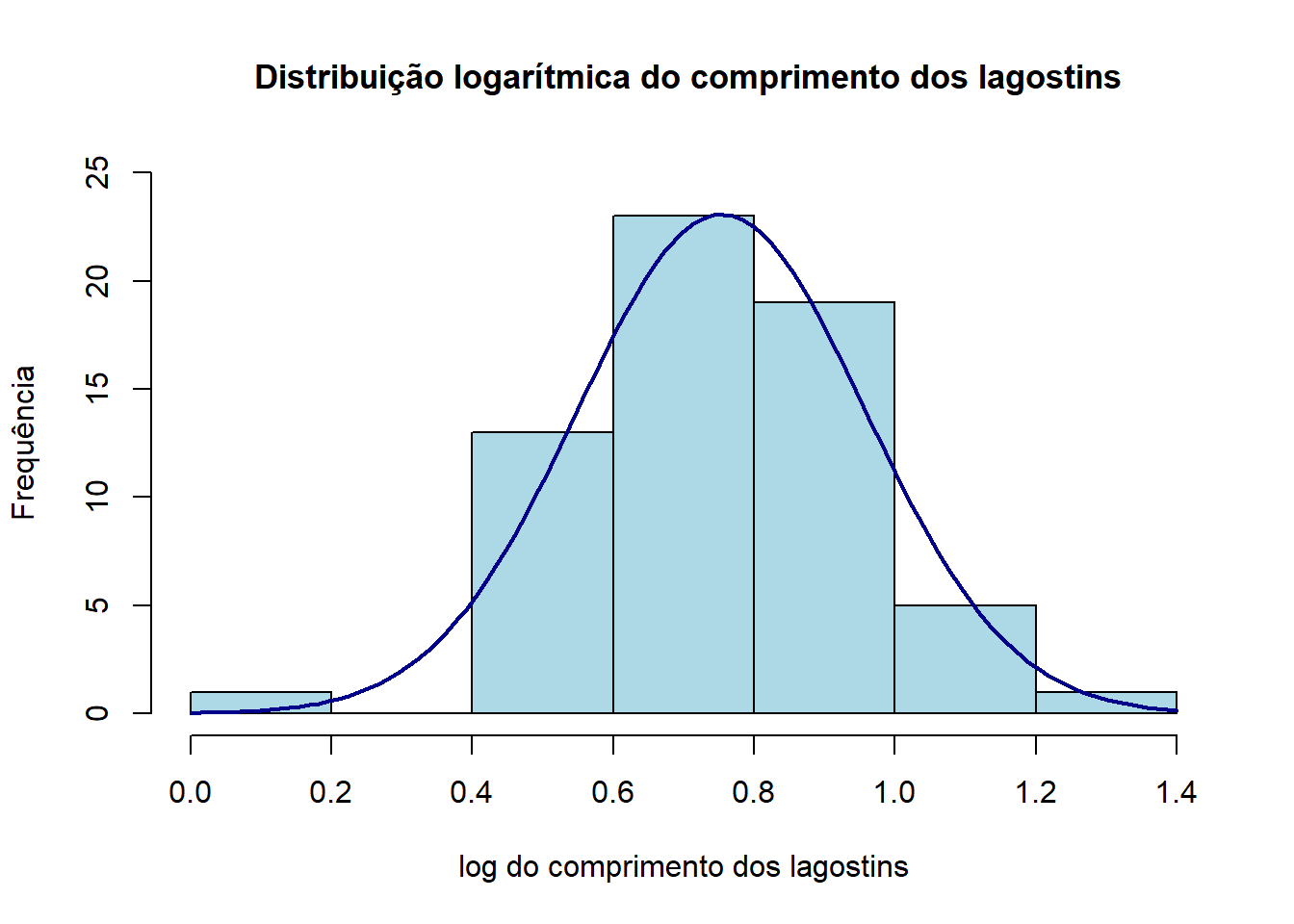
Realizou-se novamente um histograma, desta vez com os dados dos comprimentos transformados, para se poder vizualizar a sua distribuição e comparar com a distribuição anterior, podendo assim perceber a diferença entre os p-values e justificando a razão pela qual o pressuposto não foi cumprido inicialmente.
Assumindo que as variáveis são independentes e sabendo que os outros dois pressupostos foram cumpridos, podemos passar para a fase da realização do teste da ANOVA.
## Analysis of Variance Table
##
## Response: trans
## Df Sum Sq Mean Sq F value Pr(>F)
## grupos 2 0.04304 0.021520 0.5045 0.6064
## Residuals 59 2.51645 0.042652Analisando a tabela da ANOVA, observamos que:
Em relação aos resíduos:
Temos 59 graus de liberdade (N-k, em que N=62 e k=3)
A soma dos quadrados é igual a 2.51645
A média dos quadrados é igual a 0.042652
Em relação aos dados:
Temos dois graus de liberdade (k-1, em que k=3)
A soma dos quadrados é igual a 0.04304
A média dos quadrados é igual a 0.021520
A nossa estatística de teste é menor do que o valor crítico (0.5045<0.6064), pelo que não rejeitamos H0, sendo as médias consideradas estatisticamente iguais.
# Código para a realização do boxplot com os dados transformados
plot(trans~as.factor(grupos),names= c("Seixos", "Areias", "Argilas"), xlab= "Tipos de sedimentos", ylab = "log do comprimento dos lagostins", main= "Influência do tipo de sedimentação no tamanho dos lagostins", col=brewer.pal(3, "Blues"), cex.main= 1)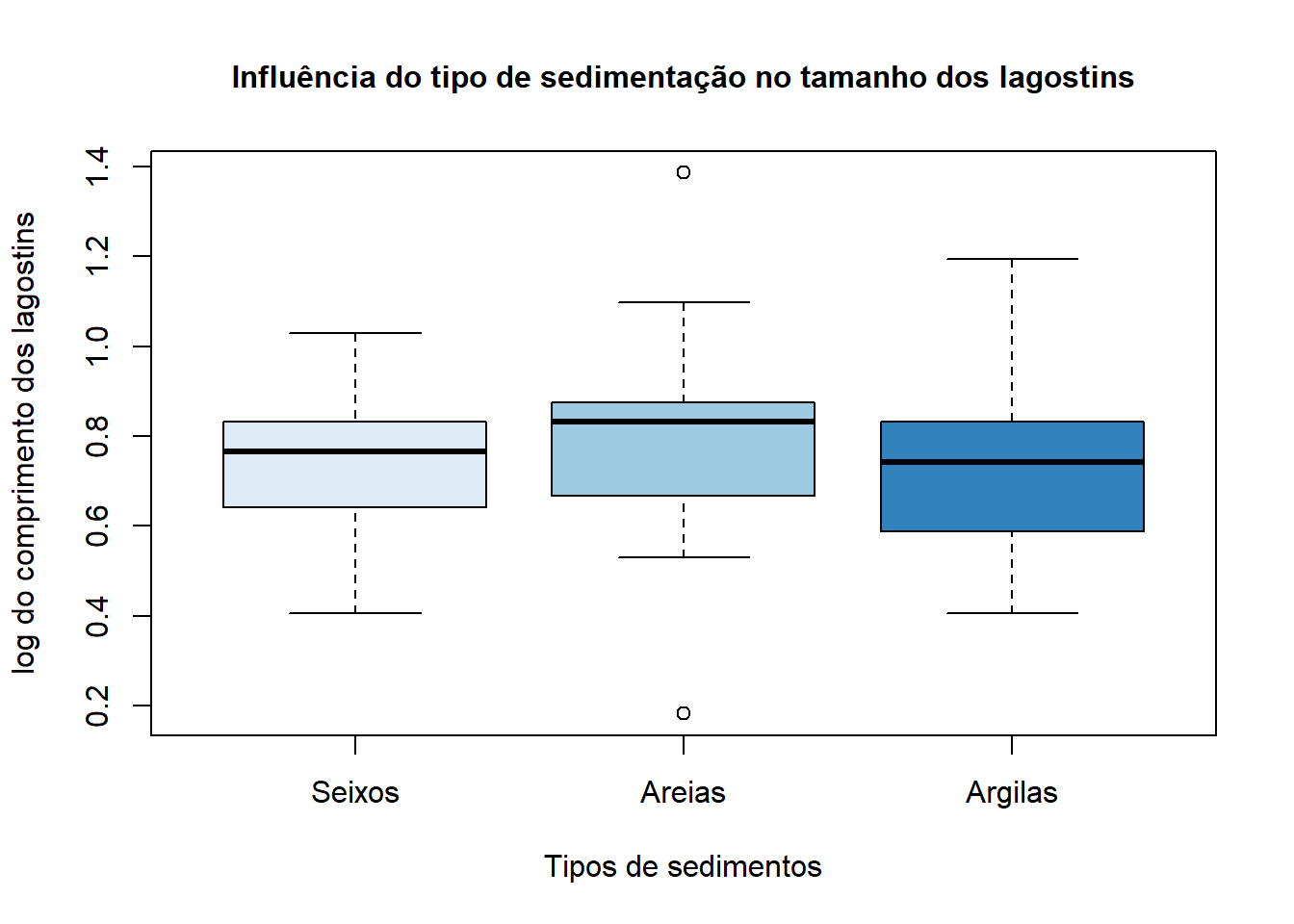
O boxplot apresentado ilustra a semelhança das médias para os três grupos, reforçando o porque de não rejeitarmos H0.
Tendo isto em conta, concluímos que o tipo de sedimentos e consequentemente a distância à foz não influencia o comprimento dos juvenis desta espécie de lagostins.
13.4 Exemplos reais de aplicação
13.4.0.1 Ecologia trófica da Gaivota de patas-amarelas (Larus michahellis) e do Pintainho (Puffinus baroli): uma abordagem isotópica em áreas costeiras e pelágicas.
Este artigo aborda a ecologia trófica da gaivota de patas-amarelas (Larus michahellis) e do pintainho (Puffinus baroli), onde foram avaliados individualmente três fatores distintos, utilizando um método experimental semelhante em todos estes fatores. É referido nos métodos que é utilizada a ANOVA como análise estatística para verificar se existiam diferenças significativas entre os valores de dois isótopos (15N e 13C) no sangue e em diferentes tipos de tecido testados (primeira pena primária, oitava pena secundária e penas do peito) e assim poder verificar se há evidências para rejeitar ou não rejeitar H0.
Este método permitiu averiguar se:
A ecologia trófica se modifica com a sazonalidade numa população de gaivotas, na ilha das Berlengas;
Existe variação interpopulacional entre Pintainhos nas ilhas de Porto Santo e Selvagens;
Há diferenças na mesma população de Puffinus baroli em dois anos consecutivos.
O resultado da realização de um teste ANOVA permitiu dar evidências para rejeitar H0, devido ao baixo p-value obtido, em cada uma das três situações investigadas, o que indica que estas aves marinhas podem alterar as suas estratégias alimentares consoante as condições alimentares no meio.
No sentido de averiguar onde se encontravam essas diferenças, foram realizados testes a posteriori.
13.4.0.2 The ecological stoichiometry of toxins produced by harmful cyanobacteria: an experimental test of the carbon-nutrient balance hypothesis
Neste artigo os investigadores testaram se a disponibilidade de luz, carbono e azoto afetava a estequiometria N:C (azoto:carbono) de microcistinas (toxinas) produzidas pelas cianobactérias Microcystis aeruginosa. Para isso, cresceram diferentes culturas em quimiostatos sujeitas a diferentes condições limitantes, luz, carbono e azoto limitado. Algumas variáveis foram logaritmizadas, tendo-se recorrido de seguida a uma one way ANOVA para verificar se existiam diferenças significativas nos rácios de N:C celulares entre os grupos sujeitos a diferentes condições, e de facto isso verificou-se (p-value < 0.01).
O baixo p-value permitiu rejeitar H0 para todas as situações analisadas de que há diferenças nos rácios N:C celulares em diferentes condições de carbono, azoto e luminosidade limitadas, permitindo aos autores provar experimentalmente a carbon-nutrient balance hypothesis e concluir que o aumento dos níveis de CO2 atmosférico tenderá a favorecer o crescimento destas bactérias e possivelmente a estequiometria das suas toxinas.
13.5 Recursos adicionais
https://rstudio-pubs-static.s3.amazonaws.com/201742_ba0f209e7e2c47619342c0112d616e7a.html
13.6 Considerações finais
Caso os resíduos não cumpram os pressupostos da ANOVA, dever-se-á tentar transformar os dados sendo que, se mesmo assim não forem cumpridos, deverá optar-se pela alternativa não paramétrica da ANOVA, o Teste de Kruskal-Wallis.
Este teste é um tipo de regressão linear de uma variável dependente em função de um fator. Tendo esta definição como base, podemos aplicar vários outros testes derivados da ANOVA simples:
Two way ANOVA: já se considera uma variável dependente em função de dois fatores. Nesta abordagem, precisam de ser analisados os efeitos isolados e combinados das variáveis independentes na variável dependente;
ANCOVA: considera-se uma variável dependente em função de um fator e de uma variável quantitativa;
ANOVA multifatorial: considera-se uma variável dependente em função de mais de dois fatores.
13.6.0.1 Casos particulares, para dados não independentes:
ANOVA hierárquica
ANOVA por blocos
Estes testes permitem avaliar o efeito da dependência dos dados.
13.7 Referências
Fernández-Juricic, César García; Daniel Renison; Ana M. Cingolani; Esteban. 2008. “Avifaunal Changes as a Consequence of Large-Scale Livestock Exclusion in the Mountains of Central Argentina.” Journal of Applied Ecology. https://besjournals.onlinelibrary.wiley.com/doi/pdfdirect/10.1111/j.1365-2664.2007.01388.x.
Fidalgo, Vera Alexandra Correia. 2012. “Ecologia Trófica Da Gaivota de Patas Amarelas E Do Pintainho: Uma Abordagem Isotópia Em áreas Costeiras E Pelágicas.” Master’s thesis, Faculdade de Ciências e Tecnologia da Universidade de Lisboa. https://eg.uc.pt/bitstream/10316/26187/1/Ecologia Trófica da Gaivota de Patas-amarelas (Larus michahellis) e do Pintainho (Puffinus baroli)- uma abordagem isotópi~1.pdf.
Fukuchi, Reginaldo K. 2017. “Análise de Variância (Anova).” https://rstudio-pubs-static.s3.amazonaws.com/201742_ba0f209e7e2c47619342c0112d616e7a.html.