Chapter 16 Tema
A regressão linear constitui um procedimento estatístico amplamente utilizado em ecologia. Neste trabalho pretende-se que identifiquem o seu principal objetivo, descrevam e contextualizem a sua aplicação e que demonstrem, com um exemplo específico, a sua implementação em R (podem usar os dados do Trabalho 1).
16.1 Membros do grupo
Este grupo é composto pelos seguintes elementos:
- Beatriz Arzeni- 50817
- David Vaz- 49228
- Luis Dias- 28978
- Marisa Mendes- 55673
- Marta Silva- 55192
- Sara Cabral- 55615
16.2 Introdução Teórica
A regressão linear é um procedimento estatístico que permite avaliar a relação entre duas (simples) ou mais (múltipla) variáveis com o objetivo de modelar um evento ou fazer previsões. Consiste na colocação de dados num modelo estatístico, geralmente utilizando-se um eixo cartesiano na sua representação gráfica, isto é, para cada variável estudada, existem diversos pontos de encontro entre os eixos X e Y. A tendência de linha reta criada a partir destes pontos é o que se chama de regressão linear. Esta linha pode ser obtida a partir de métodos tradicionais ou a partir de programas computacionais e machine learning.
16.3 Exemplo em R
Importação dos dados :
## tibble [51 x 4] (S3: tbl_df/tbl/data.frame)
## $ dia: num [1:51] 26 29 22 31 32 29 19 35 34 26 ...
## $ tam: num [1:51] 38 41 39 35 36 40 31 32 38 36 ...
## $ cor: Factor w/ 3 levels "amarela","azul",..: 2 2 2 2 2 2 2 2 2 2 ...
## $ con: logi [1:51] FALSE FALSE TRUE TRUE FALSE TRUE ...## dia tam cor con
## Min. : 5.00 Min. : 10.00 amarela:17 Mode :logical
## 1st Qu.: 9.00 1st Qu.: 12.25 azul :17 FALSE:23
## Median :29.00 Median : 36.00 rosa :17 TRUE :28
## Mean :27.14 Mean : 43.40
## 3rd Qu.:38.50 3rd Qu.: 67.50
## Max. :57.00 Max. :125.00
## NA's :1Regressão linear e correlação entre variáveis :
##
## Call:
## lm(formula = diametro ~ tamanho, data = flores)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.910 -5.125 -2.203 3.498 26.797
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.88717 1.85599 4.25 9.8e-05 ***
## tamanho 0.43901 0.03429 12.80 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.841 on 48 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.7735, Adjusted R-squared: 0.7687
## F-statistic: 163.9 on 1 and 48 DF, p-value: < 2.2e-16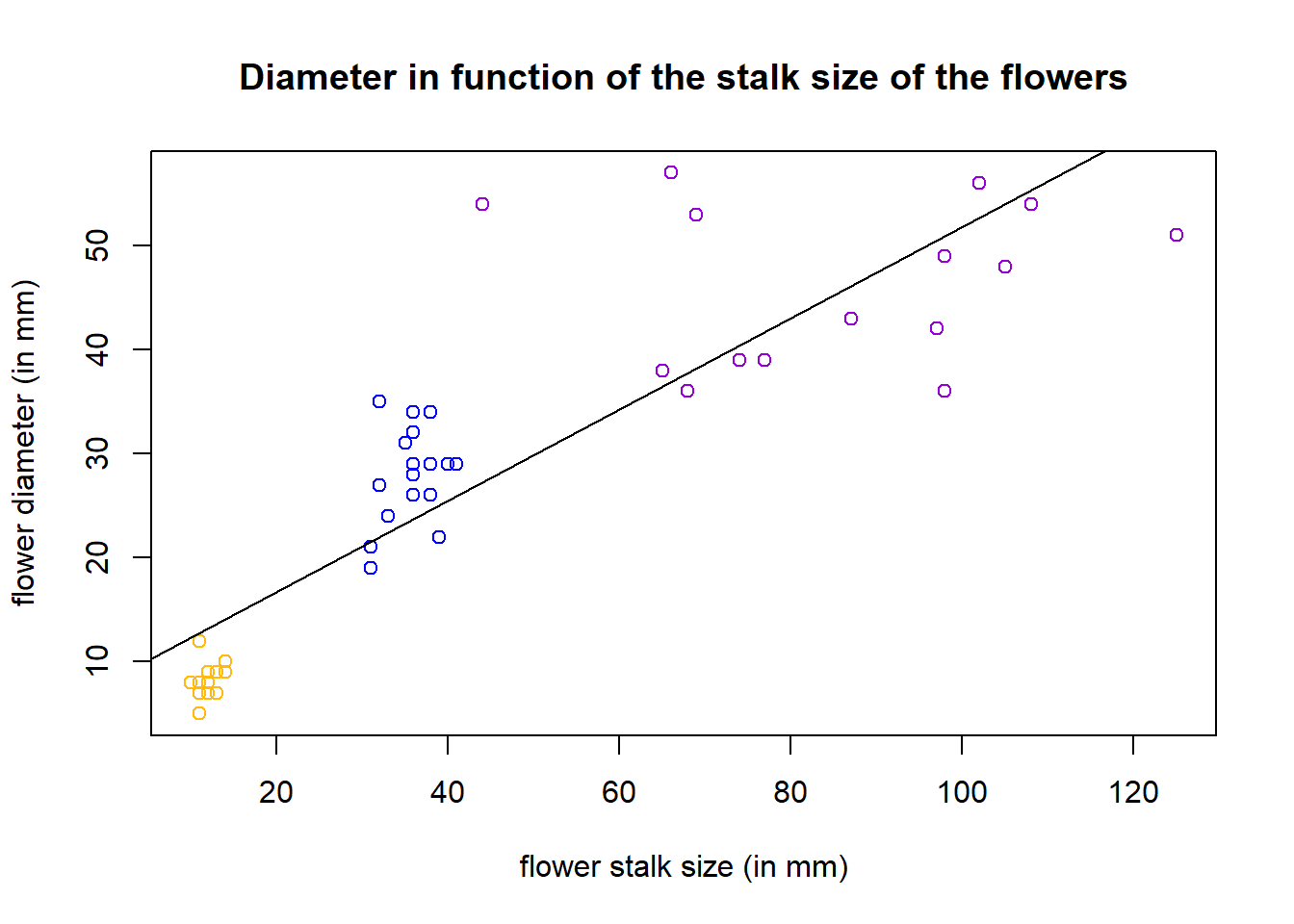
Depois de termos implementado em R o nosso exemplo vemos neste gráfico o nosso modelo de regressão linear. Podemos ver que a nossa variável explicativa (o tamanho) tem um efeito positivo sobre a nossa variável resposta (o diâmetro da flor). Mostra-nos uma correlação entre as duas: quanto maior o tamanho é, maior o diâmetro da flor será e vemos isso, com as diferentes cores de flores (uma cor = uma espécie de flor). Aliás, temos confirmação com nosso output, onde vemos que há uma diferença significativa entre as duas variáveis, revelando uma possível correlação (rejeita-se H0 porque p-value está significativamente baixo).
16.4 Exemplos reais de aplicação
- Vertical distribution and diel migration of mesopelagic fishes on the northern slope of the South China sea¹
Usam regressão linear simples para relacionar a densidade acústica em função da temperatura média e do oxigénio nas zonas de profundidade.
- Body size and season influence elemental composition of tissues in ocean sunfish Mola mola juveniles²
Usam regressão linear múltipla para relacionar a concentração de um elemento num tecido específico (Copper (Cu) in gills, cobalt (Co) in gelatin, cadmium (Cd) in white muscle and zinc (Zn) in gills and red muscle) com o comprimento total de espécimes Mola Mola do sul de Portugal na primavera e no outono.
16.5 Recursos adicionais
16.6 Considerações finais
Antes de se aplicar uma regressão linear, devem sempre ser verificados os seus pressupostos:
- A distribuição dos erros deve ser Gaussiana (com média=0 e variância constante \(\sigma\)²)
- Os erros são independentes
- Os erros nas medições da variável independente (x) são negligenciáveis comparativamente aos erros da variável resposta (y)
Caso algum dos pressupostos não se verifique, deve recorrer-se a outros procedimentos estatísticos.
16.7 Referências
- Wang, X. et al. Vertical distribution and diel migration of mesopelagic fishes on the northern slope of the South China sea. Deep Sea Res. Part II Top. Stud. Oceanogr. 167, 128–141 (2019).
- Baptista, M. et al. Body size and season influence elemental composition of tissues in ocean sunfish Mola mola juveniles. Chemosphere 223, 714–722 (2019).