Chapter 7 Tema

Existem inúmeras transformações que podem ser usadas para modelar dados ecológicos. Neste tema pretende-se que apresentem exemplos de transformações e verificação dos efeitos das mesmas através de estatísticas descritivas e de métodos gráficos.

7.1 Membros do grupo

Este grupo era composto pelos seguintes elementos:

  • Ana Pires, nº 53656
  • Filipa Mendes, nº 52618
  • Joana Rocha, nº 52628
  • Sérgio Reis, nº 52560
  • Tiago Carrapiço, nº 52511
  • Tomás Chainho, nº 52622

7.2 Introdução Teórica

O Teorema do Limite Central (TLC) diz-nos que na maioria das situações, a média da amostra varia normalmente se esta for grande. No entanto, se uma for amostra pequena ou tiver dados enviesados, a aproximação por este teorema poderá não ser a mais adequada, com um intervalo de confiança superior aos usualmente utilizados. Assim, havendo provas de enviesamento, é bastante comum proceder à transformação dos dados antes de criar esse intervalo de confiança. O objetivo é tornar a distribuição dos dados em algo mais parecido com uma distribuição normal, para que possam ser aplicados testes paramétricos, mais robustos, para proceder à análise dos dados.

Os objetivos principais desta transformação de dados são obter uma melhor visualização de determinadas características de um processo ou atingir certos pressupostos, sendo os mais considerados a normalidade, a linearidade e a homoscedasticidade. Porém, nem sempre é algo legítimo, sendo necessário ter alguma reservas dependendo do procedimento analítico e verificar se as conclusões retiradas a partir de transformações de dados serão válidas e relevantes para a sua análise e testagem de hipóteses, sendo muitas vezes preferível seguir soluções alternativas, como métodos não paramétricos ou a utilização de modelos que não tenham pressupostos tão estritos como gaussianidade ou igualdade de variâncias.

Existem dois tipos de transformações- lineares e não lineares. Lineares são aquelas obtidas através de combinações lineares (tal como soma/ subtração ou produto/divisão), padronizacão pela variância (ou desvio padrão) e pela média- redução e centragem; padronização por totais ou máximos (neste caso todas as variáveis ficam com um peso semelhante). As não lineares serão, por exemplo, logaritmização, que contribui para tornar as variâncias muito menores e desta forma obter homocedasticidade, e radiciação (raízes quadradas) e funções trigonométricas (como arcsin, p.e.), que contribuem para alterar as formas das distribuições.

A transformação de dados só serve para fazer inferências, ou seja, testar hipóteses, e neste sentido os resultados finais devem ser apresentados respeitando a escala original. Os cálculos deverão ser feitos sobre a escala transformada e esta transformação para a escala original só deverá ser feita no fim. Além disto, deverá ser apresentado um sumário dos dados na sua escala original (raw data).

7.3 Exemplo em R

Os dados utilizados foram do trabalho 1 do nosso colega Sérgio Reis, em que foi medida a distância de aproximação do Sérgio a pombos (variável resposta) e relacionada com diversos fatores, entre os quais a distância de voo dos pombos em fuga e a presença de alimento (variáveis explicativas).

##        ID             dist            voa            grupo          
##  Min.   : 1.00   Min.   :0.000   Min.   : 0.000   Length:94         
##  1st Qu.:24.25   1st Qu.:0.000   1st Qu.: 0.000   Class :character  
##  Median :47.50   Median :1.000   Median : 2.500   Mode  :character  
##  Mean   :47.50   Mean   :1.266   Mean   : 7.069                     
##  3rd Qu.:70.75   3rd Qu.:2.000   3rd Qu.: 4.875                     
##  Max.   :94.00   Max.   :8.000   Max.   :80.000                     
##      parq              saúde              aprox               alim          
##  Length:94          Length:94          Length:94          Length:94         
##  Class :character   Class :character   Class :character   Class :character  
##  Mode  :character   Mode  :character   Mode  :character   Mode  :character  
##                                                                             
##                                                                             
##

Como exemplo para as transformações de dados utilizamos o gráfico que relaciona a distância de voo com a presença de alimento (gráfico original).

  • Transformações lineares

Scale (redução e centragem)
Se isto funcionasse, as duas caixas teriam as suas médias centradas a zero. O que vemos neste gráfico é uma redução da escala associada à divisão pela variância. Porém, a centralização é uniforme para todo o gráfico em vez de separada para as duas caixas, o que faz com que os valores “com alimento” sejam todos abaixo de zero.

O mesmo se verifica na padronização pelos máximos- a padronização deveria ser feita para as duas caixas em separado, mas isso não aconteceu, e por isso o gráfico não muda de aspeto, apenas fica limitada ao intervalo [0;1].

As nossas transformações lineares não foram feitas de forma correta porque era necessário separar os dados da variável “presença de alimento” em duas colunas, de forma a que o scale e a padronização fossem aplicados a cada uma das colunas e não à totalidade dos dados. Nós não conseguimos encontrar um método eficaz para fazer esta separação que não implicasse fazer novas tabelas e novas transformações em separado.

  • Transformações não-lineares

Logaritmização
Efetuámos uma transformação logarítmica utilizando “log+1” porque existiam zeros nos dados referentes à distância de voo (pombos que não voaram), e logaritmos de 0 geram erros na transformação.
Ao transformarmos os dados utilizando a função log temos uma redução da escala, correspondente a uma redução na variância.

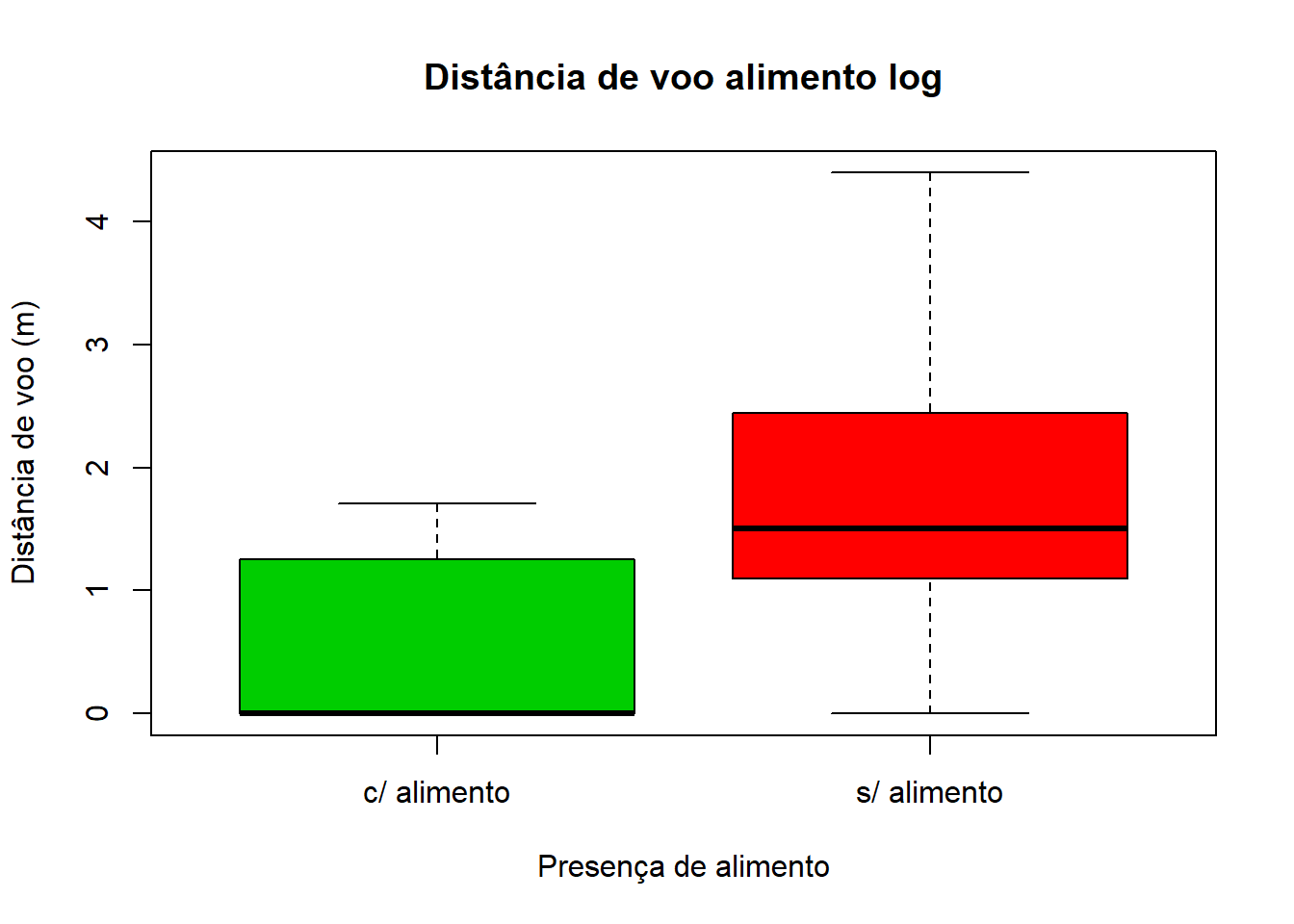
Radiciação
Efetuámos uma transformação através da utilização de raízes quadradas.

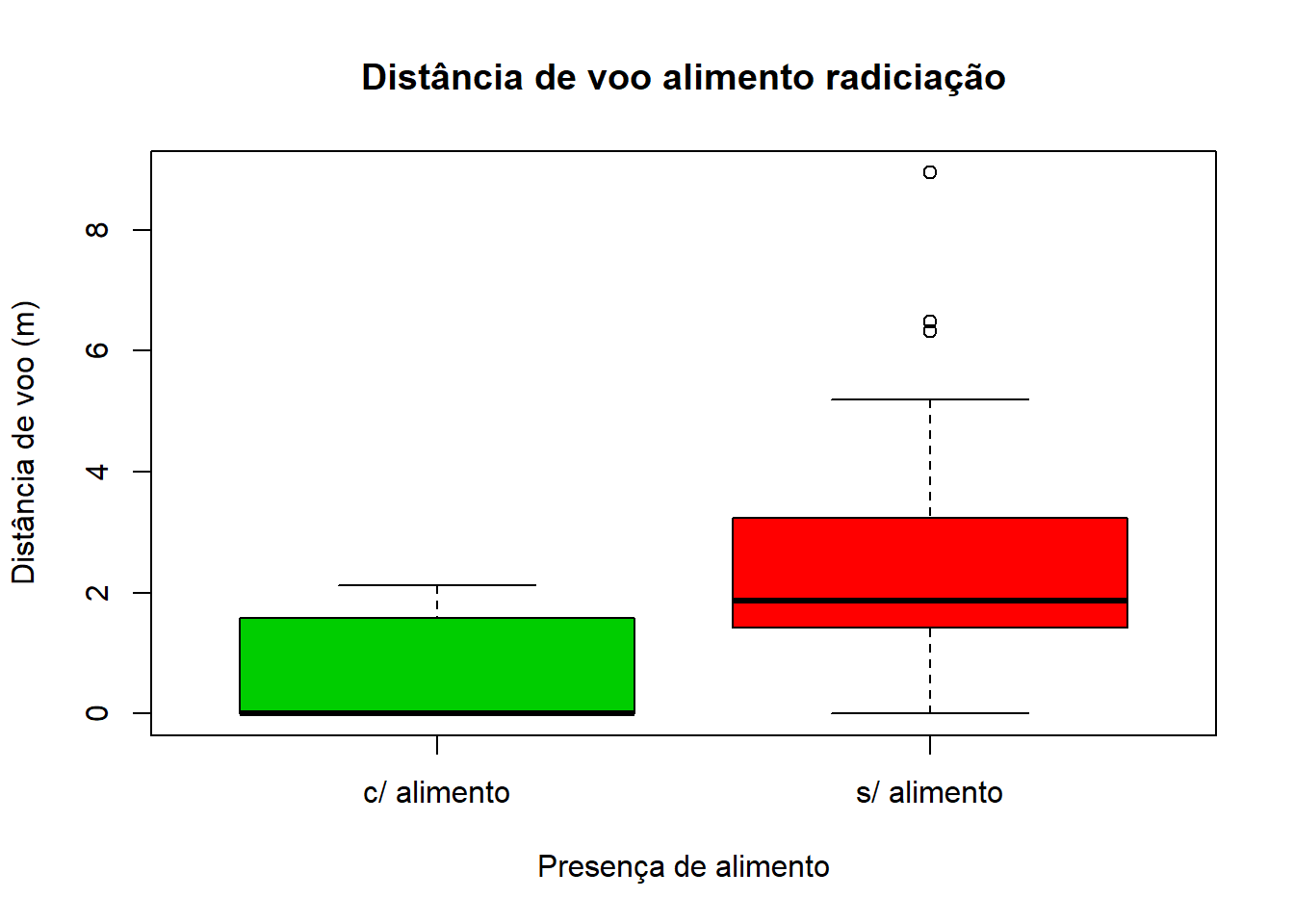
Nota: Não é necessário representar graficamente as transformações efetuadas, visto serem numéricas, mas recomendamos que o façam, de forma a entender se estas transformações foram bem executadas.

7.4 Exemplos reais de aplicação

O primeiro exemplo apresentado provém do paper “Evaluating Functional Diversity: Missing Trait Data and the Importance of Species Abundance Structure and Data Transformation”. Este artigo foca-se na utilização de índices para explicar diversidade funcional e se, na falta de informação acerca de todas as espécies, é aceitável transformar os dados.

A diversidade funcional trata-se de uma medida de biodiversidade que tem em conta as caraterística das espécies, dando assim uma ideia da função que as espécies têm num ecossistema . De modo a estudar a diversidade funcional, são utilizados muitas vezes índices de diversidade funcional, índices estes que muitas vezes dependem da quantidade de informação que se tem acerca do ecossistema para serem considerados representativos. Neste estudo, foram testados índices de riqueza funcional, equidade funcional e divergência funcional com variantes níveis de informação acerca das espécies de três diferentes comunidades - plantas, formigas e pássaros. Foi ainda testada a abundância das espécies em cada ecossistema.

Ao recolher dados acerca das espécies dos ecossistemas (para serem calculados os índices mencionados, são recolhidos dados acerca de caraterísticas e composição de espécies), dá-se prioridade a espécies dominantes, pois assume-se que têm mais funcionalidades no ecossistema. Contudo, espécies raras podem ter papéis importantes no ecossistema mesmo sendo encontradas em menor quantidade. Para evitar que o papel de espécies dominantes ofusque o das espécies raras, são por vezes utilizadas transformações nos dados recolhidos. De modo a simular amostras nas quais falta informação de certas espécies, foi removida informação acerca de algumas espécies de forma metódica e os resultados obtidos foram transformados e, através do cálculo dos índices, comparados com os dados originais. Foi ainda feita distinção entre análise conjunta ou separada de espécies. Os índices foram também ordenados, de modo a verificar se, ao transformar e/ou remover dados, a ordem era afetada. Ao remover diferentes quantidades de dados, os valores também são afetados, logo, quando comparadas entre si, as espécies avaliadas através destes índices alteram o quão funcionalmente diversas são em relação umas às outras, alterando consequentemente as ordens dos índices. Demonstra-se assim como alterações nos dados afetam as conclusões ecológicas que se podem retirar de um certo conjunto de dados.

Neste estudo, para caraterísticas contínuas foram aplicadas transformações com raíz quadrada e logarítmicas (base 10). Para dados acerca da abundância de espécies foi aplicada uma transformação log (x+1) e log (x/min (x) + 1) onde x é a abundância de espécies e min (x) representa o valor mínimo de abundância positiva das espécies.

Foi, por fim, averiguado o efeito das transformações na robustez dos índices. Para isto, comparou-se a distorção dos dados de caraterísticas contínuas antes e após as transformações. Como as transformações aproximam os dados de uma distribuição normal, quanto menores forem as diferenças de distorção entre os dados antes e depois das transformações, mais próximos de uma distribuição normal os dados estão. Se os dados utilizados estiverem muito perto de uma distribuição normal, o índice é muito robusto (e vice-versa). Assim, transformar dados em que há lacunas na informação obtida aumenta a robustez dos índices utilizados.

Contudo, o estudo confirmou que diferentes índices têm diferentes sensibilidades a lacunas e transformação de dados. O índice de equidade funcional foi o mais sensível a faltas de informação, possivelmente pois a falta de informação acerca de espécies raras leva a que alguns dos valores mais extremos não sejam contados. Por esta razão, este foi o índice que beneficiou sempre com a realização de transformações, sendo que estas ajudam a dar igual peso a todas as espécies. Pelo contrário, o índice de divergência funcional foi o que beneficiou menos (ou até nada) com a transformação de dados, sendo que transformar os dados diminui a variedade dos valores. No que toca à transformação de dados referentes à abundância, estas alteram a noção que temos da estrutura das comunidades ao achatar as curvas de dominância-diversidade, por isso deve-se a questão em estudo em conta quando transformamos este tipo de dados. Por exemplo, se formos fazer estudos comparativos entre populações, standartizar os dados através de transformações pode ser útil, mas comparar espécies da mesma população pode tornar-se difícil.

Em geral, transformar dados ecológicos resulta em normalizar a sua distribuição, o que vai alterar os índices em causa, por isso escolher utilizar ou não transformações depende da questão ecológica em causa. Neste paper conclui-se que as relações e comparações entre espécies caracterizam-se bem através da diferença entre os logaritmos dos dados, enquanto que se a questão envolver extrapolar ao nível do ecossistema, os valores brutos são a melhor escolha.

Outro exemplo real de aplicação foi retirado do paper “Statistical convenience vs biological insight: consequences of data transformation for the analysis of fitness variation in heterogeneous environments” e aborda a utilização de transformações, neste caso logarítmicas, quando os dados desobedecem o pressuposto de homocedasticidade da ANOVA. Em particular, neste artigo discute-se a sua utilização em dados de fitness de plantas (Sinapis arvenses) em ambientes heterogéneos. Esta seria a opção usualmente tomada, mas discute-se neste artigo se esta é a prática mais correta ou não.

Plantas têm uma grande capacidade de adaptação e quando as condições ambientais são mais favoráveis pode dar-se um drástico aumento de fitness médio e variância de fitness. O estudo de fitness de plantas pretende documentar como é que a heterogeneidade ambiental natural influencia a evolução. Neste artigo, foi discutido o uso da análise de variância para a interpretação dos dados em tais estudos, sendo usualmente utilizada a ANOVA. No entanto, em estudos de respostas de plantas a ambientes contrastantes, os dados de fitness individual geralmente violam os pressupostos da ANOVA (são geralmente L-shaped e heterocedásticos), recorrendo-se usualmente a transformações logarítmicas. Estas são quase universalmente usadas em modelos ANOVA para estudos de genética ecológica de plantas.

Começaram por demonstrar como mudanças de fitness e mudanças em genótipos em diversos ambientes ou uma combinação desses fatores influenciam a significância do efeito principal do genótipo e a interação genótipo x ambiente, numa ANOVA. Consideram quatro resultados potenciais da experiência, cada um representando diferentes respostas de fitness de genótipos aos diferentes ambientes. Para cada um desses quatro cenários, compararam os resultados de ANOVA usando fitness absoluto (1), fitness relativo (2) de cada ambiente ou transformações logarítmicas de fitness como variável resultado. As análises sugerem que a transformações logarítmicas de fitness produziriam resultados de ANOVA relativamente pouco informativos. Em contraste, a análise de fitness absoluto e de fitness relativo deve refletir o resultado da hard vs soft selection (3), respetivamente, dentro do contexto de heterogeneidade ambiental natural.

São apontados diversos problemas com a aplicação de transformações logarítmicas neste tipo de estudo. Não prevêem com precisão a acção do genótipo e isto leva a uma interpretação imprecisa da variação de fitness genotípico e da interação genótipo x ambiente em diversos cenários de seleção. Produzem estimativas de fitness enviesadas que não prevêem contribuições genéticas para gerações futuras. Pela mesma razão, não recomendam a sua utilização para calcular gradientes ou diferenciais de seleção, uma vez que altera a relação entre o genótipo e o fitness, obscurecendo a natureza da seleção. A transformação de variáveis acaba por complicar a interpretação, sendo que os dados já estão expressos numa escala de interesse biológico inerente, comprometendo assim interpretações evolutivas.

Noutros casos, transformações logarítmicas continuam a ser uma técnica útil. No entanto, em análises evolutivas, visto que é o próprio fitness que determina o resultado da seleção natural, devem-se utilizar técnicas estatísticas que não requeiram transformações de fitness. Recomendam por isso que deixem de ser o padrão para estudos de genética ecológica, propondo a ANOVA ponderada como um método preferível para lidar com heterocedasticidade e um maior uso de técnicas como regressão de quantis ou reamostragem para descrever e avaliar a variação de fitness em ambientes heterogéneos.

1 Fitness absoluto: É uma medida de fitness biológico expressa como o número total de cópias de genes transmitidos à geração subsequente ou o número total de descendentes sobreviventes que um indivíduo produz durante sua vida. (https://www.biologyonline.com/dictionary/absolute-fitness)
2 Fitness relativo: É uma medida de fitness biológico em que a taxa reprodutiva (de um genótipo ou fenótipo) é comparada com a taxa reprodutiva máxima (de outros genótipos ou fenótipos) numa determinada população. (https://www.biologyonline.com/dictionary/relative-fitness)
3 Hard selection: É quando a seleção natural substitui um gene por outro, fazendo-o por meio de mortalidade extra, para além da mortalidade de fundo que existe de qualquer maneira. ; Soft selection: É quando as mortes selectivas são substituídas pela mortalidade não-selectiva de fundo. Se toda a mortalidade sofrida por uma população fosse seletiva, a evolução poderia ocorrer a uma grande velocidade. (https://www.blackwellpublishing.com/ridley/a-z/Hard_&_soft_selection.asp)

7.6 Considerações finais

As transformações são extremamente úteis e podem ser feitas de várias maneiras, mas é de extrema importância aplicá-las com reservas e muito pensamento crítico em relação à sua legitimidade e relevância no contexto dos dados.