Chapter 14 Tema
Teste de Kruskal-Wallis
14.1 Membros do grupo
Este grupo era composto pelos seguintes elementos:
- Afonso Barrocal, nº 52504
- André Jorge, nº 52517
- António Vaz Pato, nº 50889
- Carolina Dias, nº 51944
- Diogo Cabrita, nº 52890
- M. Carolina Marques, nº 52569
- Rita Moreira, nº 52531
14.2 Introdução Teórica
- Contextualização
O teste de Kruskal-Wallis foi criado para que se pudessem testar amostras que não cumprissem com os pressupostos do teste F da ANOVA.
Os estatísticos envolvidos na sua criação foram William Kruskal e W.Allen Wallis, ambos estatísticos da América, e o seu trabalho foi publicado no Journal of the American Statistical Association (Kruskal & Wallis 1952).
O teste F da ANOVA é utilizado quando os resíduos (ou erros) das amostras em estudo seguem uma distribuição Normal ou quando as amostras têm dimensões “suficientemente” elevadas. Se algum destes parâmetros não se verificar é utilizado o teste de Kruskal-Wallis. Sendo que, em todos os casos, as amostras têm que ser independentes. O teste de Kruskal-Wallis é feito para testar a homogeneidade entre três ou mais amostras.
- Funcionamento do Teste
No teste de Kruskal-Wallis, considera-se \(m\) como o número de amostras, e (\(X_{1,m}, X_{2,m}, ..., X_{nm,m}\)) como as observações de cada amostra. O objetivo deste teste consiste em avaliar se as funções de distribuição das \(m\) amostras são idênticas.
Para tal, a hipótese nula estipula que todas as amostras apresentam uma função de distribuição idêntica, ou, de forma equivalente, \(H_0: F_1 = ... = F_m\). Em oposição, a hipótese alternativa sugere que, pelo menos, uma das amostras apresenta uma função de distribuição diferente das restantes amostras, ou seja, \(H_1: \exists_{i \neq j} (i, j = 1, ..., m): F_i \neq F_j\). Em seguida encontram-se outros exemplos de testes de hipóteses que são possíveis num teste de Kruskal-Wallis:
Hipóteses de Interesse:
ou
ou
Perante estas hipóteses, a decisão de rejeitar ou não a hipótese nula depende do valor \(p\), em relação ao nível de significância, ou \(\alpha\), estabelecido. Se o valor \(p\) for maior do que \(\alpha\), não há evidências para rejeitar a hipótese nula. Por outro lado, se o valor \(p\) for menor do que \(\alpha\), há indícios para rejeitar a hipótese nula.
- Estatística de Teste
Na expressão de estatistica de teste vai ser apresentada a seguinte notação:
\(N\): Número total de observações \(\Rightarrow\) \(N = \sum_{j=1}^m n_j\)
\(R(X_{i,j})\): Ordem de \(X_{i,j}\) na ordenação das \(N\) observações (ordem na amostra conjunta das \(m\) amostras), \(j\) = 1, …, \(m\); \(i\) = 1, …, \(n_j\). No caso de existirem empates associa-se a cada conjunto de observações iguais a média aritmética das ordens que elas teriam se não fossem iguais.
\(R_j\): Soma das ordens atribuídas às observações da \(j\)-ésima observação (da amostra \(X_j\)) \(\Rightarrow\) \(R_j = \sum_{i=1}^{n_j} R(X_{i,j})\), \(j\) = 1, …, \(m\)
Estatística de Teste:
\(K_{n_1,n_2, ...,n_m} = \frac{1}{S^2} \Bigg\{ \sum_{j=1}^m \frac{R_j^2}{n_j} - \frac{N(N+1)^2}{4} \Bigg\}\) com \(S^2 = \frac{1}{N-1} \Bigg\{ \sum_{j=1}^m \sum_{i=1}^{n_j} R^{2}(X_{i,j}) - \frac{N(N+1)^2}{4} \Bigg\}\)
Se não existirem empates
\(\Rightarrow\) \(\sum_{j=1}^m \sum_{i=1}^{n_j} R^{2}(X_{i,j}) = \sum_{k=1}^N k^2 = \frac{N(N+1)(2N+1)}{6}\)
\(\implies S^2 = \frac{N(N+1)}{12}\)
\(\implies K_{n_1,n_2, ..., n_m} = \frac{12}{N(N+1)} \sum_{j=1}^m \frac{R_j^2}{n_j} - 3(N+1)\)
14.3 Exemplo em R
14.3.1 Os dados
# Pergunta: Será que as dietas têm o mesmo efeito no crescimento de Zophobas morio?
# 3 dietas utilizadas: controlo, rica em proteínas e rica em hidratos de carbono. variáveis em estudo: crescimento e peso do escaravelho
# Obtenção dos dados
library(readxl)
data<-read_excel("51944CarDia.xlsx")
# Adição de colunas com a variação do peso e do comprimento dos indivíduos
data$Weigf<- as.numeric(data$Weigf)## Warning: NAs introduced by coerciondata$Weigi<- as.numeric(data$Weigi)
# Obter a diferença entre o peso inicial e o peso final
data$varw <- (data$Weigf - data$Weigi)
data$varw<- as.numeric(data$varw)
data$Lengf<- as.numeric(data$Lengf)## Warning: NAs introduced by coerciondata$Lengi<- as.numeric(data$Lengi)
# Obter a diferença entre o comprimento inicial e o comprimento final
data$varl <- (data$Lengf - data$Lengi)
data$Diet<- as.factor(data$Diet)
# Verificar as características dos dados
summary(data)## ID Box Num Diet Temp
## Min. : 1.00 Length:66 Min. : 1 Both :22 Min. :0.0
## 1st Qu.:17.25 Class :character 1st Qu.: 3 Carbo:22 1st Qu.:0.0
## Median :33.50 Mode :character Median : 6 Prot :22 Median :0.5
## Mean :33.50 Mean : 6 Mean :0.5
## 3rd Qu.:49.75 3rd Qu.: 9 3rd Qu.:1.0
## Max. :66.00 Max. :11 Max. :1.0
##
## Lengi Weigi Lengf Weigf
## Min. :3.650 Min. :0.7200 Min. :4.000 Min. :0.920
## 1st Qu.:4.250 1st Qu.:0.7925 1st Qu.:4.700 1st Qu.:1.010
## Median :4.650 Median :0.8800 Median :5.000 Median :1.060
## Mean :4.589 Mean :0.8924 Mean :4.943 Mean :1.078
## 3rd Qu.:4.950 3rd Qu.:0.9750 3rd Qu.:5.200 3rd Qu.:1.140
## Max. :5.650 Max. :1.3200 Max. :5.600 Max. :1.330
## NA's :13 NA's :13
## Pupa varw varl
## Length:66 Min. :0.0400 Min. :0.3500
## Class :character 1st Qu.:0.2000 1st Qu.:0.3500
## Mode :character Median :0.2000 Median :0.3500
## Mean :0.1908 Mean :0.3915
## 3rd Qu.:0.2000 3rd Qu.:0.3500
## Max. :0.3000 Max. :0.7500
## NA's :13 NA's :13## [1] "Both" "Carbo" "Prot"14.3.2 Para o Peso dos Indivíduos
## Warning in ks.test(data$varw, y = "pnorm"): ties should not be present for the
## Kolmogorov-Smirnov test##
## One-sample Kolmogorov-Smirnov test
##
## data: data$varw
## D = 0.51595, p-value = 1.112e-12
## alternative hypothesis: two-sided##
## Shapiro-Wilk normality test
##
## data: data$varw
## W = 0.56022, p-value = 2.337e-11# como podemos ver o p-value em ambos os testes é muito baixo, assim sendo rejeitamos H0
# ou seja os vários grupos não têm distribuições normais.
library(dplyr)
# Estatísticas resumidas por grupos:
group_by(data, Diet) %>%
summarise(
count = n(),
mean = mean(varw, na.rm = TRUE),
sd = sd(varw, na.rm = TRUE),
median = median(varw, na.rm = TRUE),
IQR = IQR(varw, na.rm = TRUE))## `summarise()` ungrouping output (override with `.groups` argument)## Diet count mean sd median IQR
## 1 Both 22 0.1816667 0.04730999 0.2 1.110223e-16
## 2 Carbo 22 0.2000000 0.05163978 0.2 1.110223e-16
## 3 Prot 22 0.1915789 0.02609026 0.2 1.110223e-16library("ggpubr")
ggboxplot(data, x = "Diet", y = "varw",
color = "Diet", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
ylab = "Variação do Peso dos Indivíduos", xlab = "Dieta")## Warning: Removed 13 rows containing non-finite values (stat_boxplot).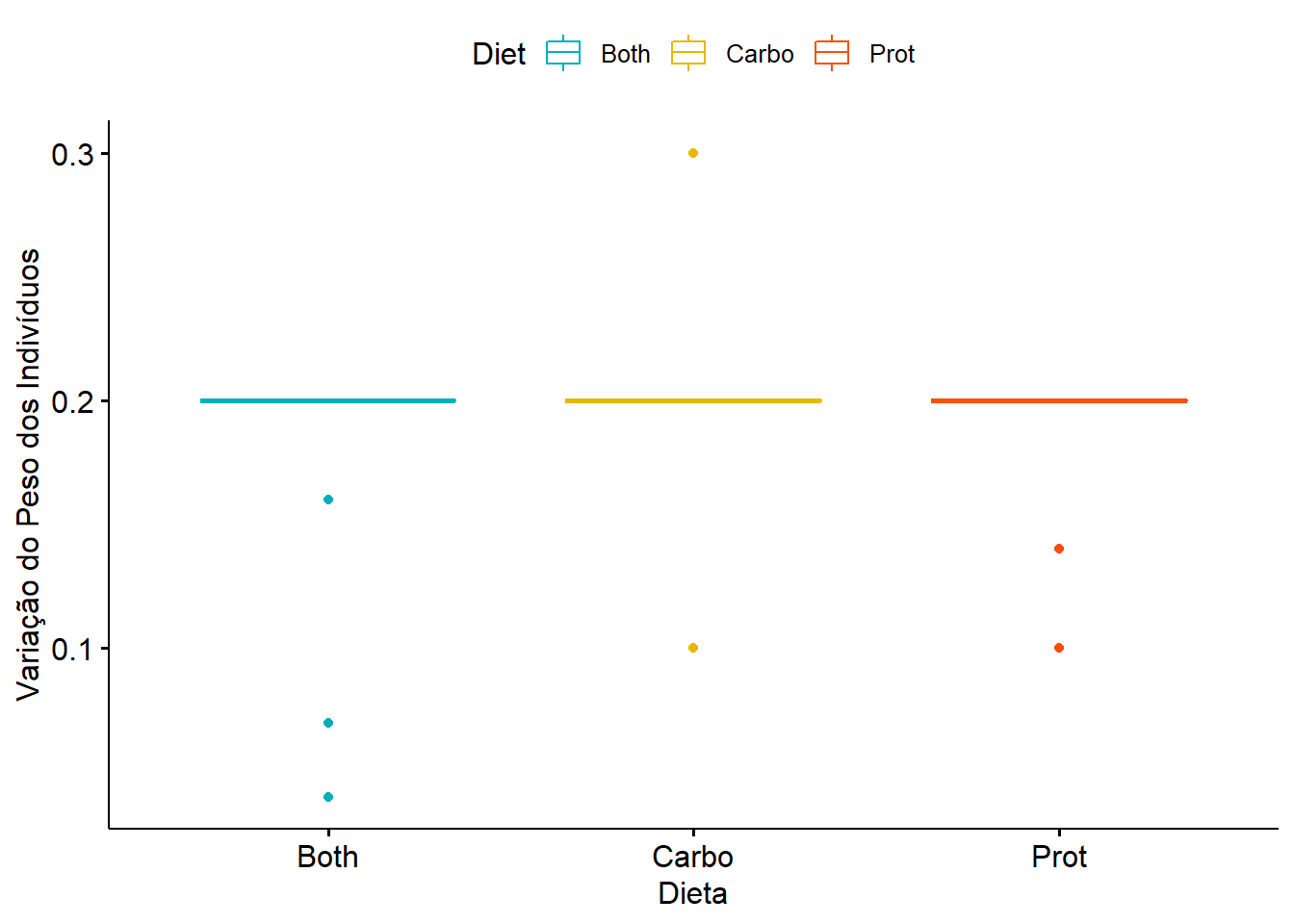
# adicionar barras de erro
ggline(data, x = "Diet", y = "varw",
add = c("mean_se", "jitter"),
ylab = "Variação do Tamanho dos Indivíduos", xlab = "Dieta")## Warning: Removed 13 rows containing non-finite values (stat_summary).## Warning: Removed 13 rows containing missing values (geom_point).
##
## Kruskal-Wallis rank sum test
##
## data: varw by Diet
## Kruskal-Wallis chi-squared = 4.097, df = 2, p-value = 0.128914.3.3 Para o Comprimento dos Indivíduos
## Warning in ks.test(data$varl, y = "pnorm"): ties should not be present for the
## Kolmogorov-Smirnov test##
## One-sample Kolmogorov-Smirnov test
##
## data: data$varl
## D = 0.63683, p-value < 2.2e-16
## alternative hypothesis: two-sided##
## Shapiro-Wilk normality test
##
## data: data$varl
## W = 0.51786, p-value = 6.102e-12# como podemos ver o p-value em ambos os testes é muito baixo, assim sendo rejeitamos H0
# ou seja os vários grupos não têm distribuições normais.
group_by(data, Diet) %>%
summarise(
count = n(),
mean = mean(varw, na.rm = TRUE),
sd = sd(varl, na.rm = TRUE),
median = median(varl, na.rm = TRUE),
IQR = IQR(varl, na.rm = TRUE))## `summarise()` ungrouping output (override with `.groups` argument)## Diet count mean sd median IQR
## 1 Both 22 0.1816667 0.09217772 0.35 8.881784e-16
## 2 Carbo 22 0.2000000 0.11528949 0.35 2.500000e-02
## 3 Prot 22 0.1915789 0.07334928 0.35 8.881784e-16library("ggpubr")
ggboxplot(data, x = "Diet", y = "varl",
color = "Diet", palette = c("#00AFBB", "#E7B800", "#FC4E07"),
ylab = "Variação do Comprimento dos Indivíduos", xlab = "Dieta")## Warning: Removed 13 rows containing non-finite values (stat_boxplot).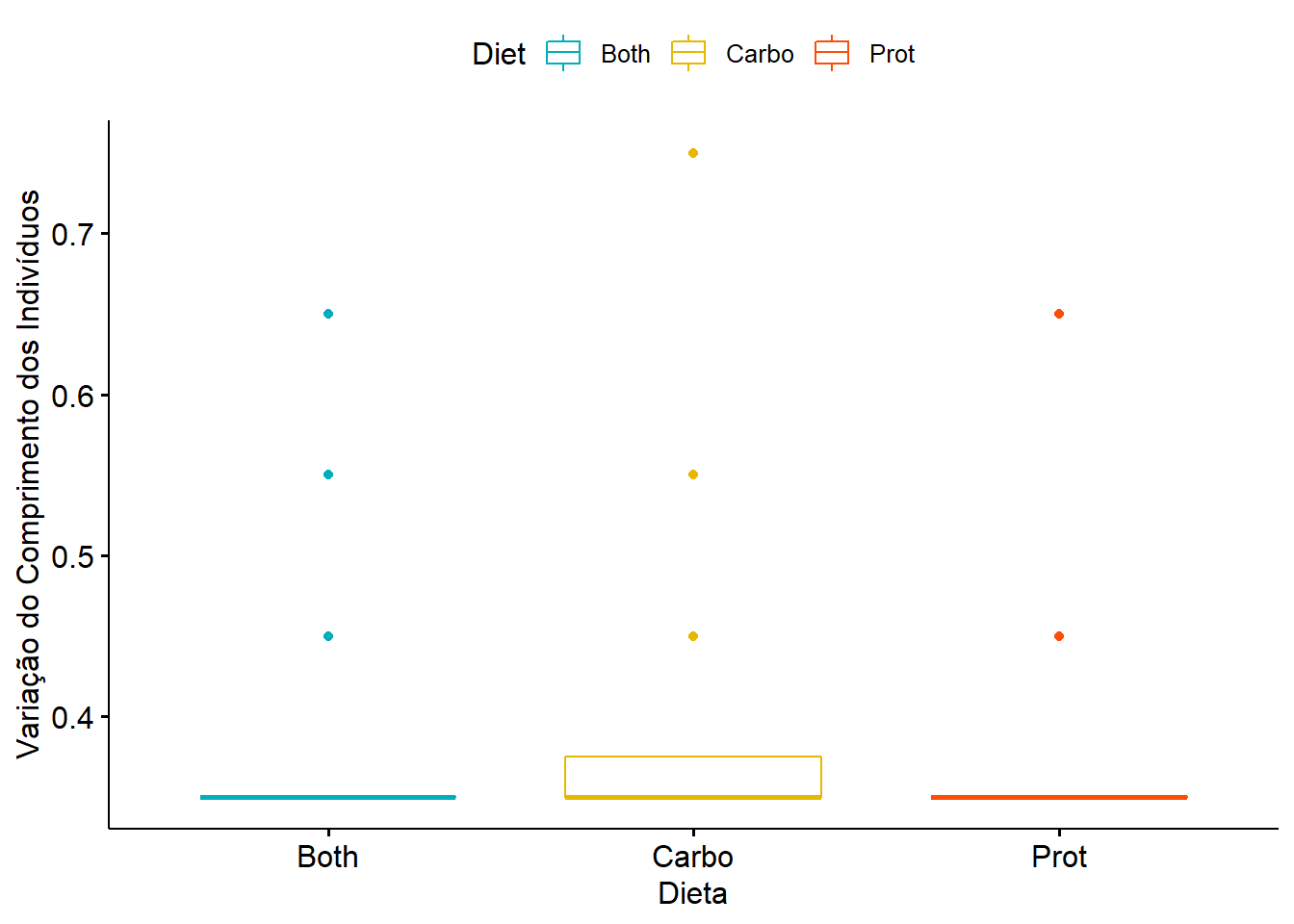
# adicionar barras de erro
ggline(data, x = "Diet", y = "varl",
add = c("mean_se", "jitter"),
ylab = "Variação do Comprimento dos Indivíduos", xlab = "Dieta")## Warning: Removed 13 rows containing non-finite values (stat_summary).## Warning: Removed 13 rows containing missing values (geom_point).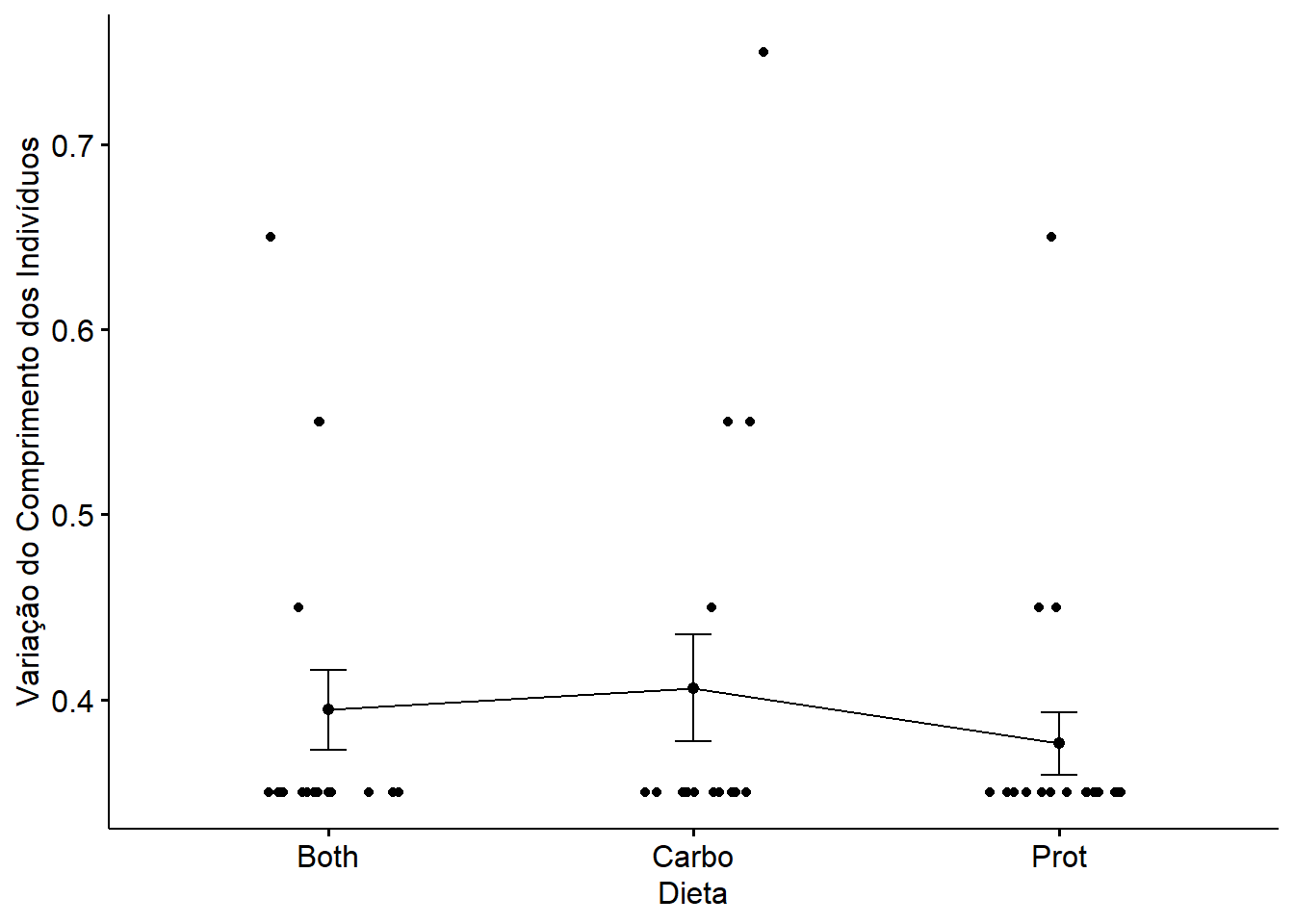
##
## Kruskal-Wallis rank sum test
##
## data: varl by Diet
## Kruskal-Wallis chi-squared = 1.958, df = 2, p-value = 0.375714.4 Exemplos reais de aplicação
- Immune-mediated hookworm clearance and survival of a marine mammal decrease with warmer ocean temperatures (Seguel et al. 2018).
No paper Immune-mediated hookworm clearance and survival of a marine mammal decrease with warmer ocean temperatures por Seguel et al. (2018), foi usado um teste de Kruskal-Wallis, seguido de um teste de Dunn, para comparar os valores médios de glicose, colesterol, basófilos, linfócitos e IgG específica do parasita para os períodos de reprodução entre 2012 e 2017, que são usados para avaliar o estado de saúde das crias de lobo-marinho-sul-americano (Arctocephalus australis). Porém qual o motivo para usar Teste de Kruskal-Wallis ao invés da mais standard ANOVA?
Como o teste de Kruskal-Wallis é um teste não-paramétrico, este é usado se um ou mais dos 3 pressupostos necessários para executar uma ANOVA não são respeitadas. Tendo isso em mente, decidimos testar com um teste de Bartlett e um teste de Shapiro-Wilkins os dados1 do paper para ver se existe homogeneidade das variâncias e se os dados são distribuídos normalmente, respectivamente.
Após as análises, concluímos que não há homogeniedade das variâncias e a distribuição não é normal e, por isso, é justificado a utilização do teste de Kruskal-Wallis.
- Bleaching causes loss of disease resistance within the threatened coral species Acropora cervicornis (Muller et al. 2018).
O teste de Kuskall-Wallis foi usado num artigo sobre o coral Acropora cervicornis na Florida. Este paper teve como objectivo perceber se um evento de branqueamento (ou seja a dissociação da alga simbiótica Symbiodinium do coral) pode aumentar ou não a susceptibilidade de diferentes tipos genéticos de coral (chamados genets) à doença de banda branca, causada por uma bactéria. Para o efeito foram feitas várias análises estatísticas a vários genets que poderiam ter alguma influência na reação à exposição do agente patogénico bacteriano.
Aqui o teste de Kruskal-Wallis foi determinante, entre outras coisas, para verificar se houve diferenças significativas na eficiência fotoquímica (Fv/Fm) do Symbiodinium para cada um dos grupos dos genets de coral entre um momento pré-branqueamento e um momento pós-branqueamento. Os investigadores optaram por usar o Kruskal-Wallis, uma vez que as amostras não cumpriam o pressuposto da normalidade. O passo é crucial na experiência pois este parâmetro é usado como proxy do branqueamento, isto é, os investigadores sabiam de antemão que uma diminuição considerável do valor de Fv/Fm da alga é um indicador (ainda que indirecto) do fenómeno de dissociação que leva à perda da cor do coral. Esta análise complementa as pistas visuais dadas pela mudança de cor. Neste contexto, o teste de Kruskal-Wallis seguido do teste post hoc de Dunn confirmaram que há diferenças assinaláveis nas médias de eficiência fotoquímica nas amostras dos vários genets, fornecendo maior suporte aos investigadores para estes concluírem que houve de facto branqueamento em todos os tipos genéticos em experiência.
- Outros:
- Antagonism between parasites within snail hosts impacts the transmission of human schistosomiasis (Laidemitt et al. 2019).
- Biophysical and physiological processes causing oxygen loss from coral reefs (Silveira et al. 2019).
- Awareness of Bacterial Resistance to Antibiotics among Healthcare Providers in Sana’a City, Yemen (Halboup et al. 2018).
14.5 Recursos adicionais
14.6 Considerações finais
Como observações finais convém fazer a ressalva de que o teste de Kruskal-Wallis não é conclusivo quando se rejeita \(H_0\), uma vez que não descrimina qual ou quais os grupos de amostras cuja análise à média leva à rejeição dessa mesma hipótese. Nesta situação, podemos recorrer ao teste de Dunn, um teste à posteriori (ou post hoc test) que nos permite fazer comparações múltiplas entre as amostras, e nos diz exacta e individualmente os grupos de amostras cujas médias não poderão ser consideradas iguais. A \(H_0\) deste teste é que não existe diferença entre os grupos, sendo indiferente se têm o mesmo tamanho ou não.
Para se visualizar melhor este conceito, temos este exemplo prático onde após a realização de um teste Kruskal-Wallis (com consequente rejeição da sua \(H_0\) por os valores das médias serem significativamente diferentes entre amostras), poderíamos recorrer ao teste de Dunn para comparar individualmente os grupos e perceber que entre \(G_1\) e \(G_2\), e \(G_3\) e \(G_4\), não se rejeita \(H_0\).
14.7 Referências
Halboup, A., Karem Alzoubi, Othman, G. & and. (2018). Awareness of bacterial resistance to antibiotics among healthcare providers in sana’a city, yemen. Yemeni Journal for Medical Sciences, 12, 12–21.
Kruskal, W.H. & Wallis, W.A. (1952). Use of ranks in one-criterion variance analysis. Journal of the American Statistical Association, 47, 583–621.
Laidemitt, M.R., Anderson, L.C., Wearing, H.J., Mutuku, M.W., Mkoji, G.M. & Loker, E.S. (2019). Antagonism between parasites within snail hosts impacts the transmission of human schistosomiasis. eLife, 8.
Muller, E.M., Bartels, E. & Baums, I.B. (2018). Bleaching causes loss of disease resistance within the threatened coral species acropora cervicornis. eLife, 7.
Seguel, M., Montalva, F., Perez-Venegas, D., Gutiérrez, J., Paves, H.J., Müller, A., Valencia-Soto, C., Howerth, E., Mendiola, V. & Gottdenker, N. (2018). Immune-mediated hookworm clearance and survival of a marine mammal decrease with warmer ocean temperatures. eLife, 7.
Silveira, C.B., Luque, A., Roach, T.N., Villela, H., Barno, A., Green, K., Reyes, B., Rubio-Portillo, E., Le, T., Mead, S., Hatay, M., Vermeij, M.J., Takeshita, Y., Haas, A., Bailey, B. & Rohwer, F. (2019). Biophysical and physiological processes causing oxygen loss from coral reefs. eLife, 8.
No paper, não foi referido o motivo pelo qual foi usado o teste de Kruskal-Wallis ao invés da ANOVA e, por isso, vimos-nos obrigados a analisar os dados.↩