Capítulo 5 Distribuicoes de Probabilidade

Além das análises utilizando estatísticas descritivas, o R contém pacotes que nos permitem trabalhar com probabilidades. Ao longo das disciplinas de estatística, vamos nos deparar com diversos exercícios de probabilidade, e o R é uma boa ferramenta para se fazer conferências referentes aos cálculos feitos nestes exercícios. Além do mais, a probabilidade no R amplia nossas possibilidades no âmbito dos estudos em que queremos checar o quão provável é a ocorrência de um evento, mas nem sempre conseguimos encontrar tais probabilidades efetuando cálculos à mão. Neste tópico vamos abordar três distribuições conhecidas, são elas: Poison (Variável discreta), Binomial (Variável discreta) e Normal (Variável contínua). Nos pacotes referentes a cada modelo encontramos funções que calculam os quantis das distribuições e probabilidades exatas, dados os parâmetros de cada distribuição.

5.1 Binomial

Um dos principais modelos discretos de probabilidade é o modelo Binomial. Quando possuímos uma sequência de n experimentos independentes entre si,com variáveis binárias como resposta (sucesso ou fracasso), dada uma determinada probabilidade constante de sucesso, podemos obter a probabilidade de ocorrência de k sucessos através da distribuição binomial.

Contextualizando

Em uma fábrica de empacotar café, espera-se que o peso do produto final esteja entre 498 e 502 gramas. Cerca de 90% das embalagens continham a quantidade de café dentro dos padrões desejados. Se escolhermos aleatoriamente 10 embalagens, podemos muito bem encontrar 10 pacotes de café com o peso aceitável. Entretanto, pode ser também que, na nossa amostra, nenhum pacote esteja dentro desse padrão.

Mas como mensurar as probabiliidades desses eventos? Eles são prováveis ou não? Podemos perfeitamente calcular as probabilidades desejadas usando o modelo binomial: neste caso, nosso n seria igual a 10 e p seria 0.90, assumindo que a exposição referente quantidade de café seja independente para cada indivíduo da nossa amostra.

\[ P(X=k) = \frac{n!}{k!(n-k)!}p^k(1-p)^{n-k}\] ### Função dbinom

Suponha que na nossa amostra de 10 pacotes, n = 10, estejamos interessados na probabilidade de encontrarmos 8 pacotes com peso ideal, k =8, com p =0.90. Calculamos a probabilidade P(X = 8 ) da seguinte maneira:

dbinom(x = 8, size = 10, prob = 0.9)

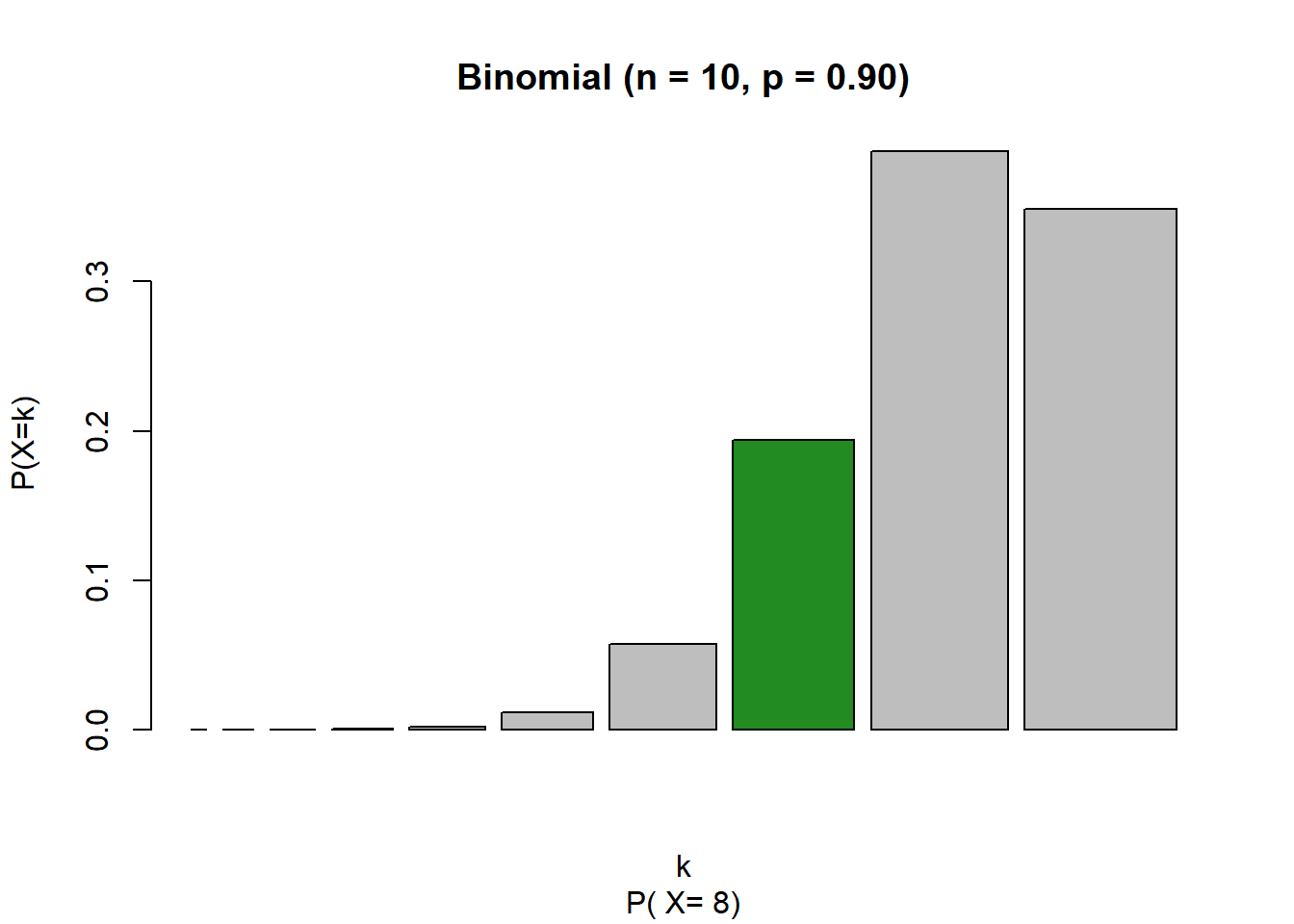
## [1] 0.1937102

E para P(X =9)?

dbinom(x = 9, size = 10, prob = 0.9)

## [1] 0.3874205

Repare que o argumento size em dbinom representa o número de replicações do experimento (peso ideal ou não), referente ao parâmetro n da binomial.

5.1.1 Função pbinom

Agora, suponha o mesmo contexto do exemplo anterior. Porém, desta vez, queremos encontrar a probabilidade de no máximo oito pacotes da nossa amostra terem o peso ideal, ou seja, estamos interessados na probabilidade acumulada da binomial com n = 10 e p = 0.90 avaliada no caso em que X = 8. No exemplo anterior estávamos interessados na probabilidade da ocorrência de 8 sucessos, e agora, buscamos a probabilidade da ocorrência de 8, 7,…, 2, 1 e 0 sucessos, P(X ≤ 8).

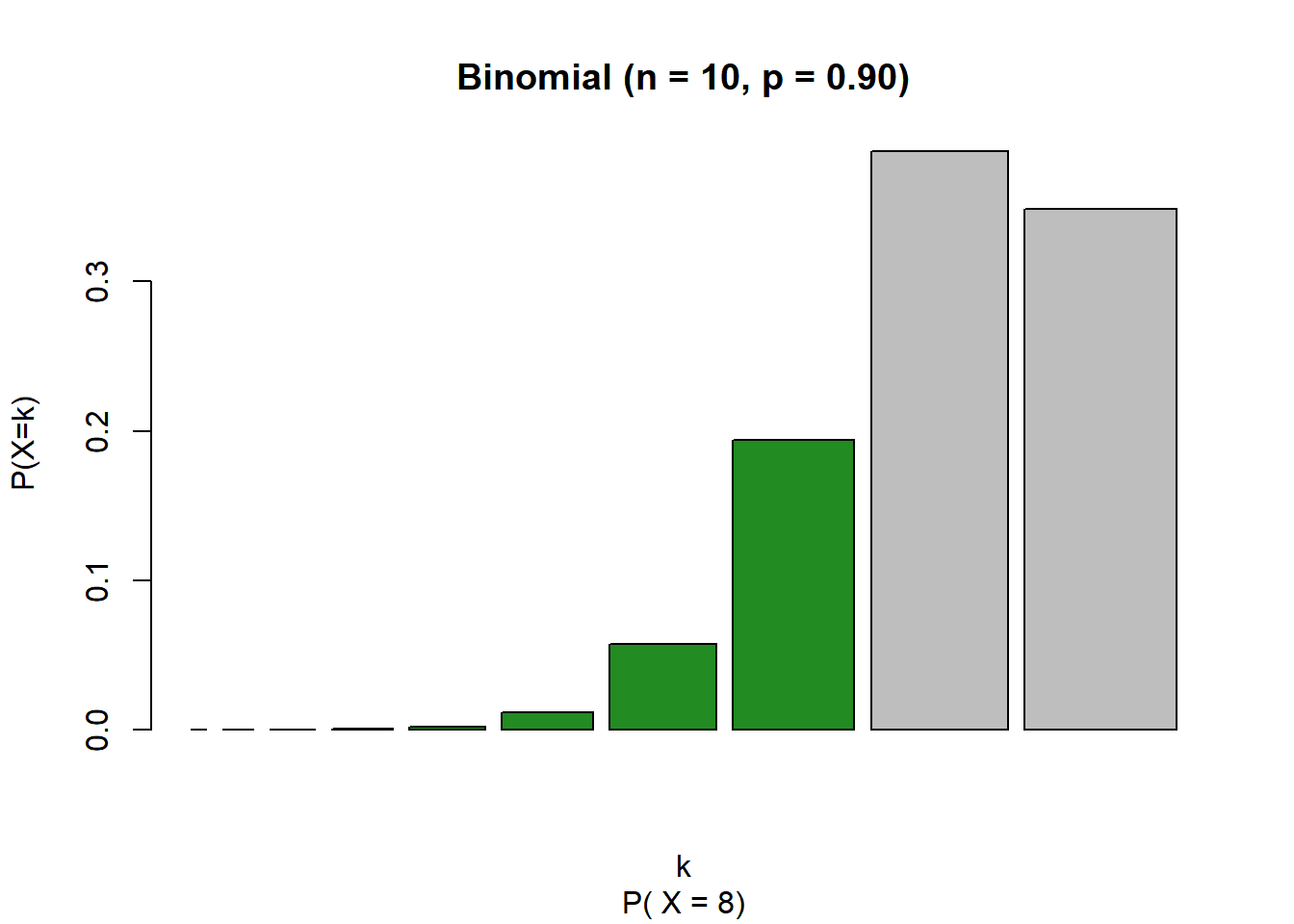
Sendo assim:

pbinom(q = 5, size = 10, prob = 0.9)

## [1] 0.001634937

Como P(X ≤5)= P(X =5)+P(X =4)+P(X =3)+P(X =2)+P(X =1)+P(X =0), repare que se calcularmos as probabilidades separadamente utilizando dbinom e somarmos todas, devemos encontrar o mesmo resultado obtido com o comando pbinom.

Veja:

dbinom(x = 8, size = 10, prob = 0.90)+
dbinom(x = 7, size = 10, prob = 0.9)+ 
dbinom(x = 6, size = 10, prob = 0.9)+ 
dbinom(x = 5, size = 10, prob = 0.9)+
dbinom(x = 4, size = 10, prob = 0.9)+ 
dbinom(x = 3, size = 10, prob = 0.9)+ 
dbinom(x = 2, size = 10, prob = 0.9)+ 
dbinom(x = 1, size = 10, prob = 0.9)+
dbinom(x = 0, size = 10, prob = 0.9)

## [1] 0.2639011

E se quisermos obter P(X > 8) ?

Neste caso, queremos descobrir a probabilidade de mais de pacotes de café terem o peso ideal.

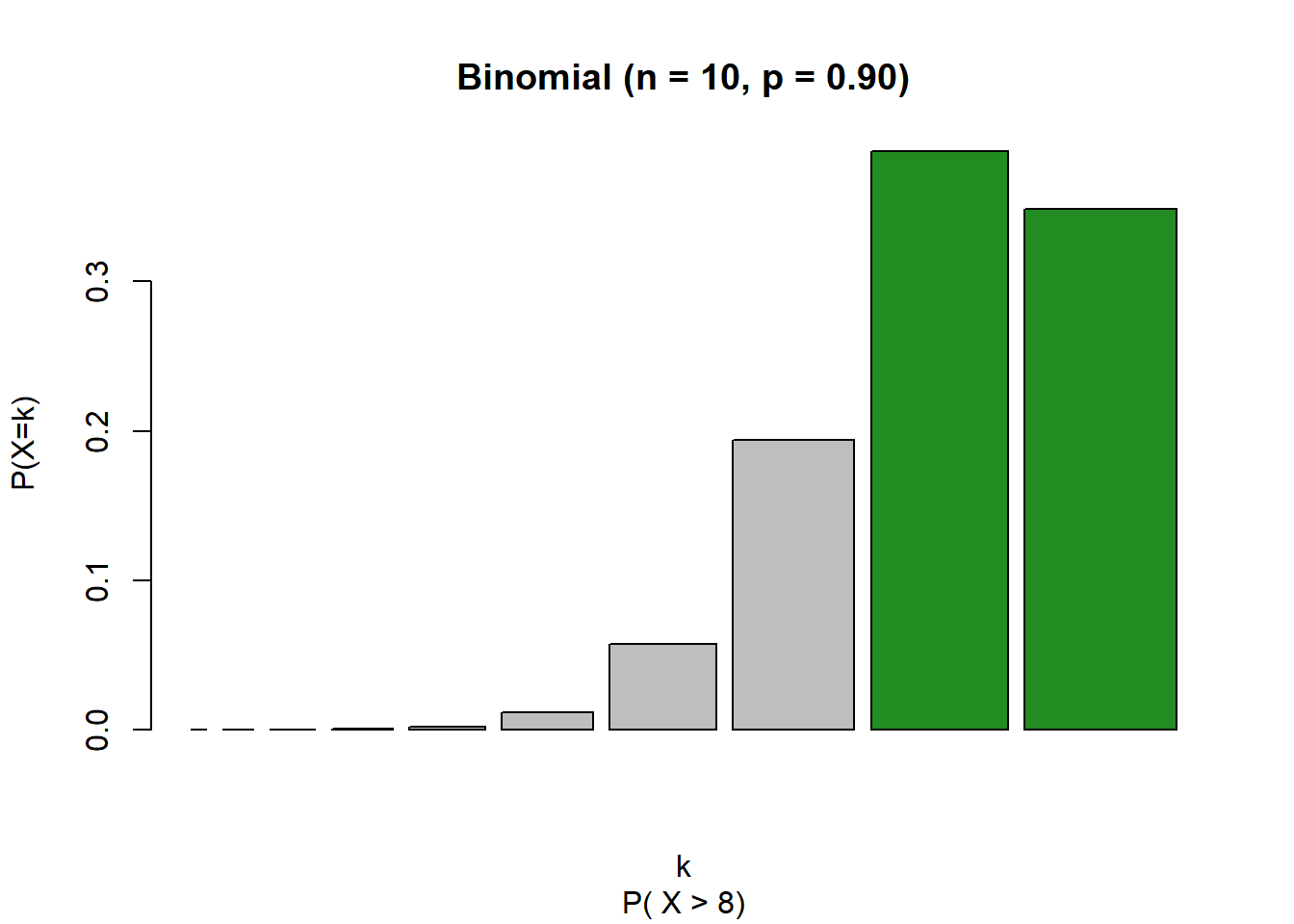
Sabemos que P(X >8)=1−P(X ≤ 8), então:

1 - pbinom(q = 8, size = 10, prob = 0.9)

## [1] 0.7360989

O comando pbinom nos fornece uma facilidade que nos permite obter a mesma probabilidade encontrada acima. Basta utilizar o parâmetro lower.tail como “FALSE”.

Veja:

pbinom(q = 8, size = 10, prob = 0.9, lower.tail = FALSE)

## [1] 0.7360989

Se o comando lower.tail não for especiﬁcado, o R vai interpretá-lo como “TRUE”, calculando a probabilidade dos valores acumulados à esquerda, P(X ≤8). Defenindo o parâmetro como “FALSE”, o R retorna a probabilidade dos valores acumulados à direita, P(X > 8).

5.1.2 Função qbinom

A função qbinom nos fornece o caminho “inverso” da função dbinom. Quando utilizamos qbinom estamos interessados em obter os quantis da distribuição binomial. Ou seja, se queremos o quantil referente ao percentil de ordem 0.95,estamos interessados num determinado valor de sucessos que seja maior do que 95% dos valores de sucesso possíveis.

Exemplo:

qbinom(p = 0.95, size = 10, prob = 0.9)

## [1] 10

Nos exemplos anteriores, mostramos que na binomial de tamanho 10 e p = 0.90 , a probabilidade de sucessos associada a x =8 é 0.1937102. Portanto, se utilizarmos a função qbinom(p =0.1937102, size = 10, prob = 0.90), devemos obter o valor 8 como resposta.

qbinom(p =0.1937102, size = 10, prob = 0.90)

## [1] 8

5.1.3 Função rbinom

Por motivo de curiosidade, vamos introduzir a funcionalidade da função rbinom para exempliﬁcar um experimento modelado pela distribuiçao Binomial. Suponha que um aluno esteja fazendo uma prova de 20 questões independentes entre si e a probabilidade do estudante acertar cada questão é de 0.4. Utilizando a função rbinom, é como se estivessemos simulando a aplicação da prova para o aluno em questão. Portanto, nosso experimento conterá 20 replicações e a probabilidade de sucesso de cada replicação independente é p =0.4

rbinom(n = 1, size = 20, prob = 0.4)

## [1] 7

Interpretando o resultado: desenvolvemos um experimento (n = 1) com 20 replicações (size = 20) e obtivemos 10 sucessos em nosso experimento. Neste caso, o estudante teria acertado 10 questões da prova. E se aplicássemos a prova de 20 questões para 5 alunos com a mesma probabilidade igual a 0.4 de acertar uma questão na avaliação?

Nosso experimento seria simulado da seguinte maneira:

rbinom(n = 5, size = 20, prob = 0.4)

## [1]  8 11 12 10  9

Interpretando o resultado: desenvolvemos cinco experimentos (n =5) com 20 replicações (size =20) cada um e obtivemos 6, 4, 7, 9 e 10 sucessos em nossos experimentos. Através dessa função, conseguimos simular nosso experimento da Binomial quantas vezes desejarmos.

P(X > 5) :

ppois(q = 5, lambda = 3, lower.tail = FALSE)

## [1] 0.08391794

A utilização da do parâmetro lower.tail foi devidamente discutida no tópico da função pbinom.

5.2 Poisson

É comum encontrarmos problemas em que o número de ocorrência de determinado evento é obtido a partir da distribuição Poisson com uma taxa λ. Neste tópico apresentaremos funções bem similares às que vimos no tópico referente à distribuição binomial, são elas: ppois, dpois e qpois.

A probabilidade de eventos envolvendo a distribuição de Poisson podem ser calculadas através da seguinte função de probabilidade:

\[ P(X=k) = \frac{e^{-λ}λ^k}{x!}\]

5.2.1 Função dpois

Assim como em dbinom, a função dpois nos retorna a probabilidade associada a um valor de X. A diferença entre dbinom e dpois são os parâmetros que passamos para a função, devido à característica de cada modelo. No caso da binomial, devemos informar o tamanho do experimento e a probabilidade de sucesso, na Poisson precisamos informar apenas o valor do parâmetro λ.

Exemplo

Suponha que um determinado em uma fábrica de laticínios, na etapa de embalagens podem ocorrer falhas, de acordo com uma variável aleatória X que segue uma distribuição de Poisson de parâmetro λ = 3.

Estamos interessados na probabilidade de 5 caixas de leite apresentarem alguma deformação.

Usando a funçao dpois, calculamos o valor de P(X=5)com λ =3.

dpois(x = 5, lambda = 3)

## [1] 0.1008188

A função ppois retorna o valor da prababilidade acumulada avaliada em um X qualquer. No nosso exemplo deﬁnimos X = 5 e λ = 3.

P(X ≤ 5):

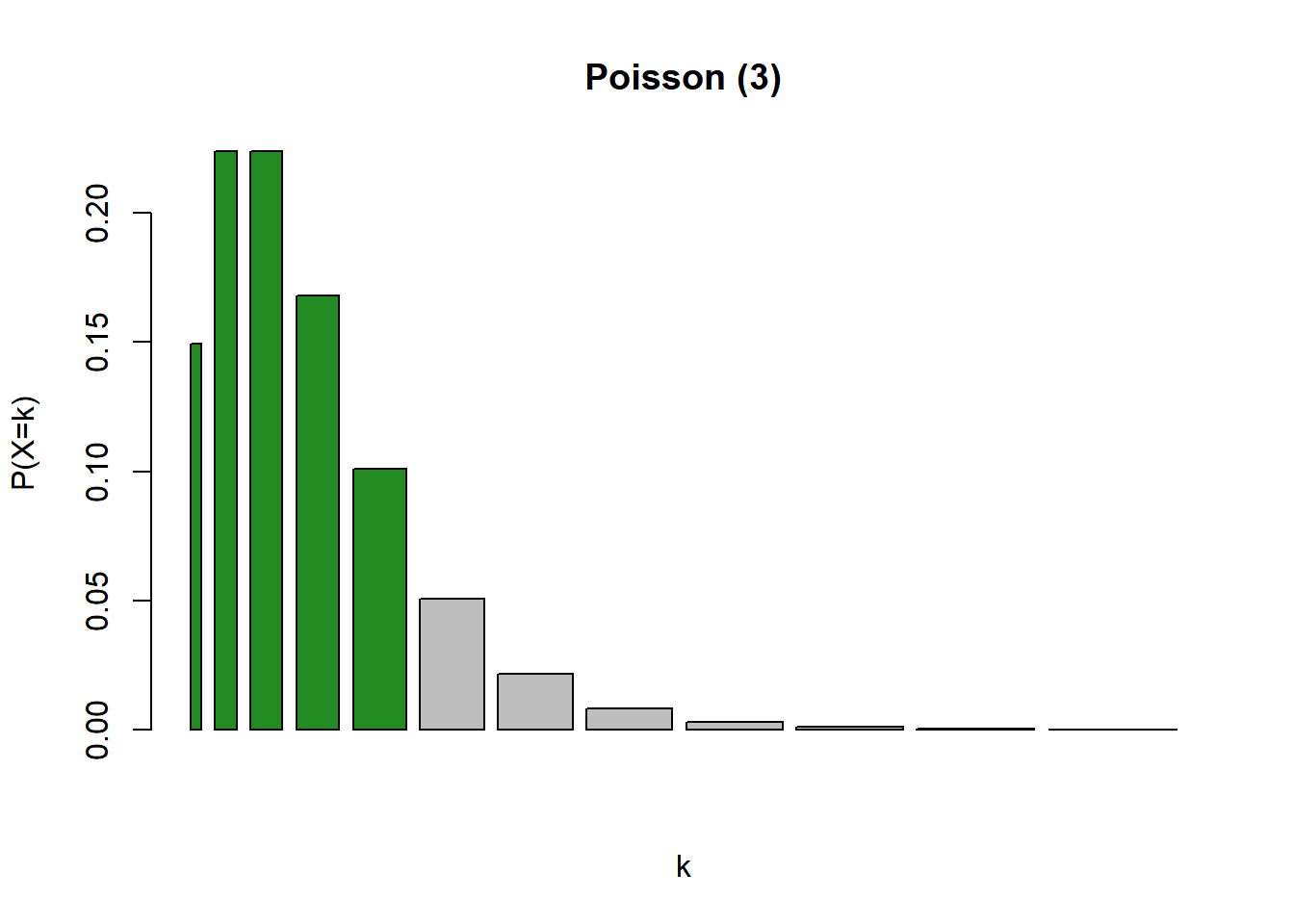No nosso exemplo sobre a etapa de embalagens, se estivéssemos interessados na probabilidade de 5 caixas de leite, ou menos,apresentar defeito, bastaria utilizar o comando ppois da seguinte maneira:

ppois(q = 5, lambda = 3)

## [1] 0.9160821

Assim como ﬁzemos com a função pbinom, podemos conferir o resultado obtido com a função ppois comparando com o resultado obtido com a soma de probabilidades utilizando a função dpois. Veja:

dpois(x = 5, lambda = 3)+
dpois(x = 4, lambda = 3)+
dpois(x = 3, lambda = 3)+ 
dpois(x = 2, lambda = 3)+
dpois(x = 1, lambda = 3)+
dpois(x = 0, lambda = 3)

## [1] 0.9160821

P(X > 5) :

ppois(q = 5, lambda = 3, lower.tail = FALSE)

## [1] 0.08391794

A utilização da do parâmetro lower.tail foi devidamente discutida no tópico da função pbinom.

5.2.2 Função qpois

Ao utilizar a funçao qpois estamos interessados em descobrir os quantis da distribuição Poisson, exemplo: Dado o caso da fábrica de laticínios abordado nos tópicos acima, suponha que queiramos encontrar um número x de caixas de leite onde, em 95% dos casos, a quantidade de itens deformados seja menor do que x. Isso é equivalente a obter o quantil 0.95 da Poison(λ = 3). Utilizamos então, o comando qpois:

qpois(p =0.95, lambda = 3)

## [1] 6

O quantil referente ao percentil de ordem 0.95 da Poisson(3) é 6. Ou seja, em 95% dos casos, a produção tem menos do que 6 caixas de leite com defeito.

5.3 Distribuição Normal

A distribuição normal é provavelmente a mais famosa entre todas as distribuições de probabilidade e apresenta inúmeras aplicações. Trata-se de uma distribuição contínua, onde uma variável com essa distribuição pode assumir qualquer valor na reta real e é totalmente simétrica, apresentando uma forma de sino, como pode ser visto a seguir:

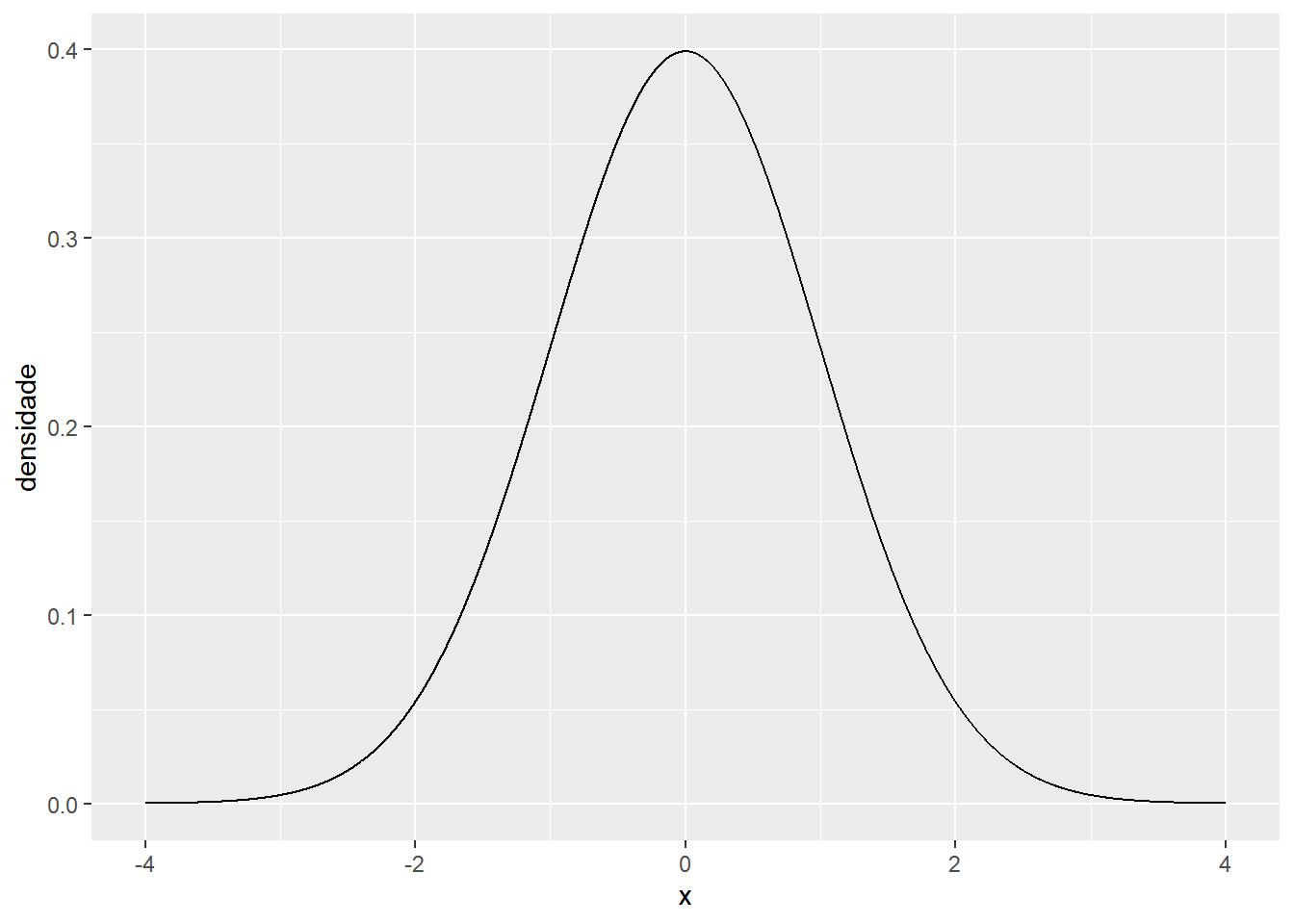
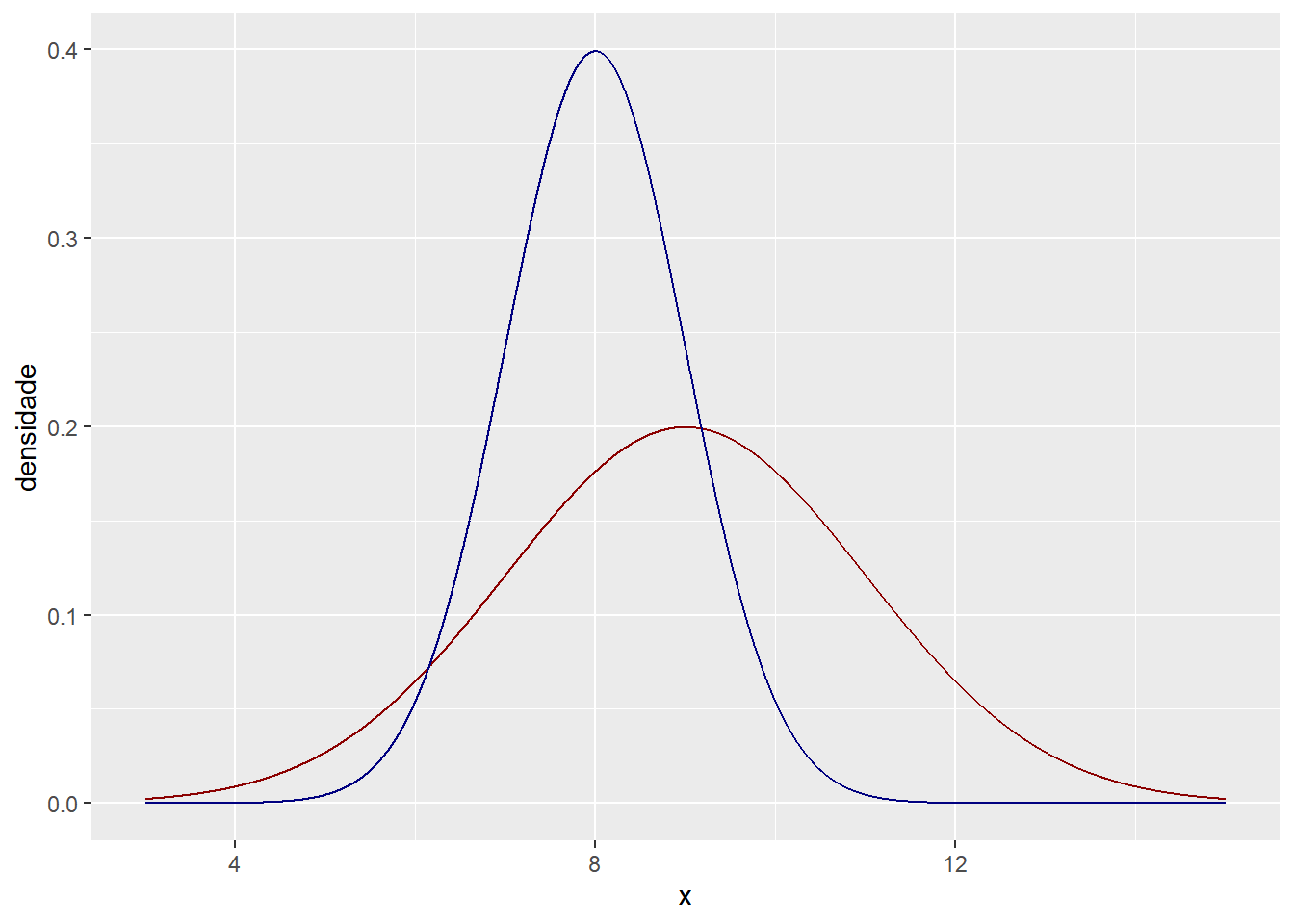
A curva normal é definida por dois parâmetros, a média \(\mu\) e o desvio padrão \(\sigma\) (ou a variância \(\sigma^2\)), que determinam onde a probabilidade está mais concentrada e o quão dispersa ela é, respectivamente. Veja as curvas normais com \(\mu\)=9 e \(\sigma\)=2 (em vermelho) e com \(\mu\)=8 e \(\sigma\)=1 (em azul). Vale lembrar que a curva não representa a probabilidade daquele ponto, mas sim a densidade de probabilidade.

5.3.1 Função dnorm

Para calcularmos a densidade da distribuição normal em um certo ponto, usamos o comando ‘dnorm’,colocando como parâmetros o ponto desejado, além da média e do desvio padrão da curva normal em questão:

dnorm(0.5,mean=0,sd=1)

## [1] 0.3520653

5.3.2 Função pnorm

A probabilidade de uma variável aleatória que tem distribuição normal assumir um valor menor que ‘b’ pode ser calculada pela área abaixo da curva de densidade e à esquerda do valor b. Por exemplo, veja a probabilidade de uma variável Z (normal com média 0 e desvio padrão 1), assumir um valor menor que 1.

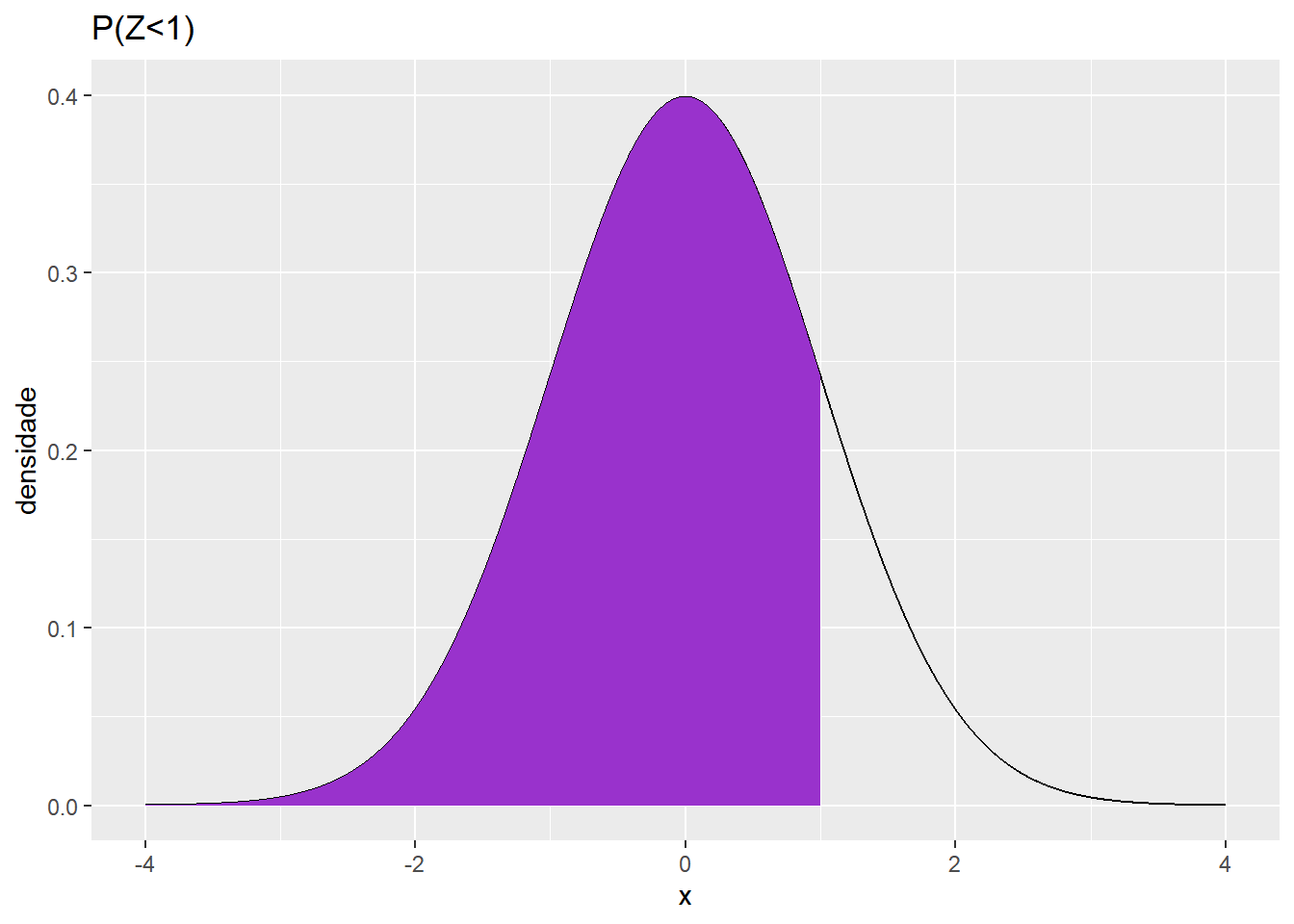
Para calcular probabilidades desse tipo (probabilidade de a variável ser menor que um valor b), podemos usar o comando “pnorm”, colocando como parâmetros b, a média e o desvio padrão:

pnorm(1,mean=0,sd=1)

## [1] 0.8413447

Para alcular a probabilidade de uma variável assumir um valor maior que “a”, basta calcular a área abaixo da curva e à direta do valor a.

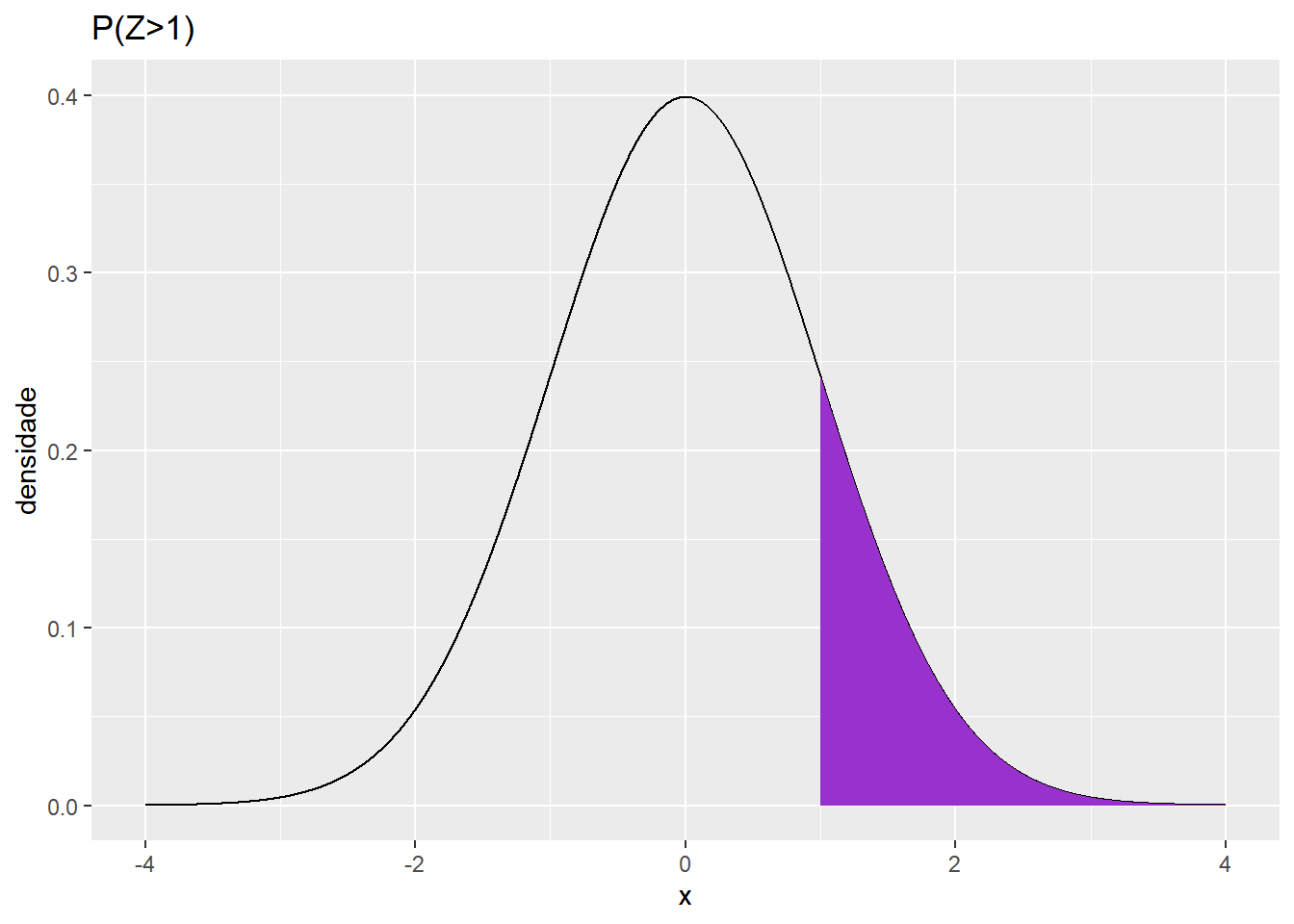
Para calcular probabilidades desse tipo, é simplesmente subtrair de 1 a probabilidade de a variável assumir um valor menor que ‘b’. Assim, fazemos assim:

1-pnorm(1,mean=0,sd=1)

## [1] 0.1586553

Para calcular a probabilidade de a variável assumir um valor entre a e b, devemos calcular a área abaixo da curva entre ‘a’ e ‘b’:

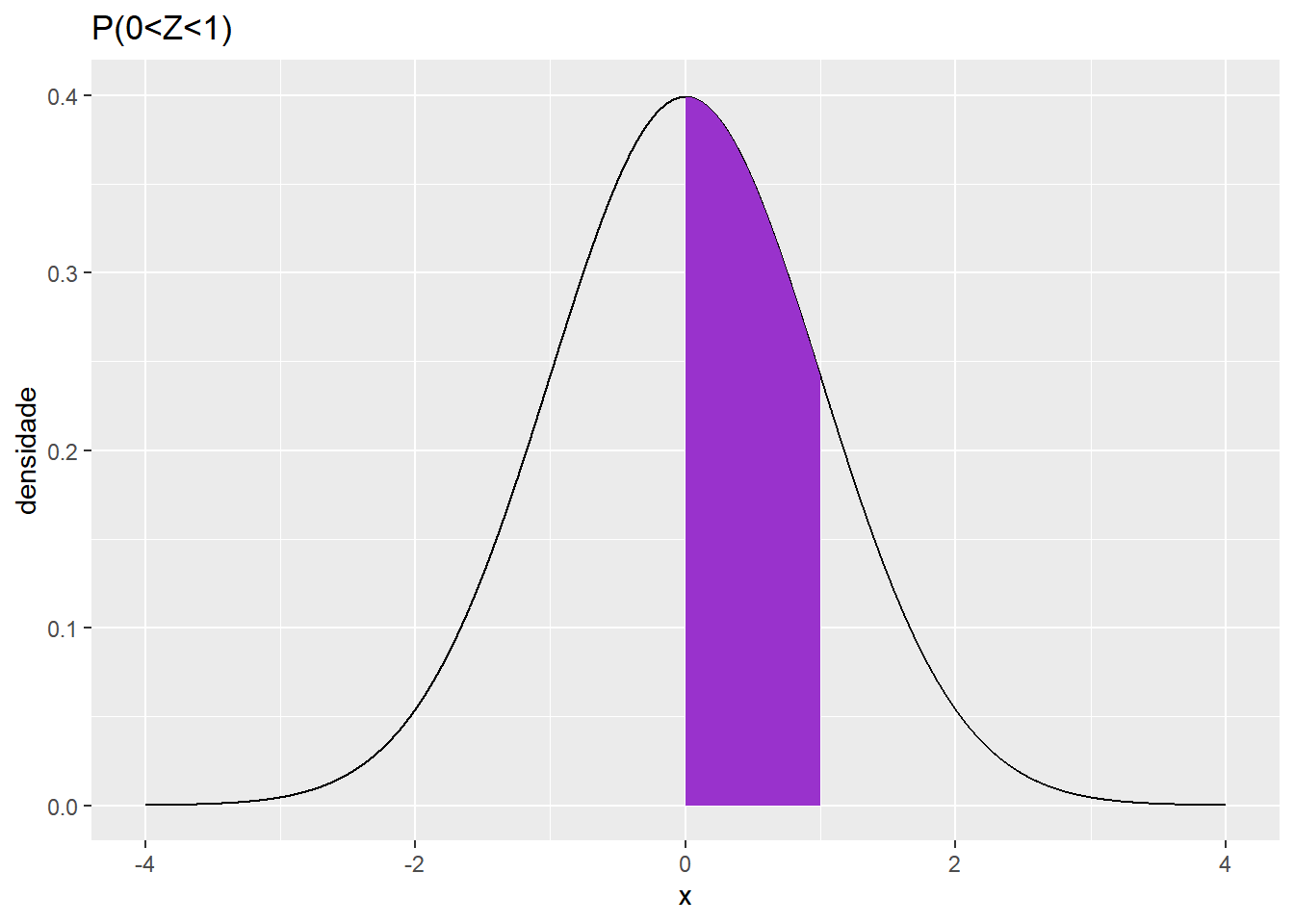
Para calcular probabilidades desse tipo, basta subtrair a probabilidade de a variável ser menor que b pela probabilidade da variável ser menor que a.

pnorm(1,mean=0,sd=1)-pnorm(0,mean=0,sd=1)

## [1] 0.3413447

5.3.3 Função qnorm

Para calcular o quantil da curva (o valor da variável) com o qual se associa certa probabilidade de a variável assumir um valor menor, usamos o comando “qnorm”, colocando como parâmetro a probabilidade, além da média e do desvio padrão da curva:

qnorm(0.95,mean=0,sd=1)

## [1] 1.644854

Vale lembrar que para calcular o quantil que deixa certa probabilidade p acima, basta calcular o quantil que deixa 1-p abaixo, assim, para calcularmos o quantil que deixa 0.1 acima, basta calcular o que deixa 0.9 abaixo:

qnorm(0.9,mean=0,sd=1)

## [1] 1.281552

5.3.4 Função rnorm

Para gerar amostras aleatórias da distribuição normal, usamos o comando “rnorm”, colocando como parâmetros o tamanho da amostra e a média e o desvio padrão da curva normal de onde você deseja gerá-la.

rnorm(5,mean=0,sd=1)

## [1]  0.3743569  0.2719775  0.5276041 -1.5395248  0.1653094

5.4 Outras distribuições de probabilidade

O R também nos permite fazer funções análogas para muitas outras distribuições de probabilidade. O funcionamento é quase idêntico ao das anteriores e não entraramos em exemplos e detalhes específicos. Algumas distribuições e funções associadas a elas são:

Distribuição Geométrica: pgeom, dgeom, qgeom, rgeom
Distribuição Binomial Negativa: pnbinom, dnbinom, qnbinom, rnbinom
Distribuição Hipergeométrica: phyper, dhyper, qhyper, rhyper
Distribuição Qui-Quadrado: pchisq, dchisq, qchisq, rchisq
Distribuição T de Student: pt, dt, qt, rt

5.5 Distribuições no RCommander

As funções apresentadas neste capítulo também podem ser utilizadas no R Commander, e de maneira bem simples. Para executar as funções desejadas basta clicar em “Distribuições”, depois escolher o tipo de distribuição desejada (Contínua ou Discreta), em seguida selecionar a distribuição desejada (Normal, Binomial, Poisson etc) e por ﬁm, clicar na função que será processada. Suponha que queiramos utilizar a função qnorm através do R Commander:

Distribuições -> Distribuições Contínuas -> Distribuição Normal -> Quantis da Normal...

Depois de seguir esses passos, basta deﬁnir os parâmetros da distribuição e o quantil desejado. Agora, suponha que queiramos utilizar a função pbinom através do R Commander:

Distribuições -> Distribuições Discretas -> Distribuição Binomial -> Probabilidades das caudas da Binomial...

5.6 Exercícios

1- Para X ~ Binomial(n = 20, p = 0.3), calcule: a) P(X ≤3) b) P(X =3) c) P(5 < X ≤15) d) P(12 < X < 18) e) P(X > 10|X ≥3)

2- Para X ~ Poisson(λ =100), calcule: a) P(50 < X ≤ 70) b) P(X > 200) c) P(X < 100|X > 50) d) P(50 < X < 100) e) P(X ≤ x)=0.2. Qual o valor de x?

3- Para X ~ Normal(µ =100, σ =10), calcule: a) P(µ−3σ ≥ X ≤ µ+3σ) b) P(X > x)=0.875. Qual o valor de x? c) P(x1 < X < x2)=0.8. Qual o valor de x1 e x2? d) P(X > 50|X ≤100) e) P(X ≥50|X ≤100)

4- Um dado não viciado é jogado 6 vezes em sequência. Levando em consideração que as jogadas são independentes umas das outras, calcule a probabilidade de se obter o número 4 duas vezes.

5- Considere o mesmo experimento do exercicio 4. Desta vez, calcule a probabilidade de se obter um número menor ou igual a 2 três vezes.

6- Numa turma de 36 alunos, suponha que, em média, haja 4 notas máximas em cada exame de matemática. Calcule a probabilidade de 10 alunos tirarem nota máxima em um exame de matemática. Suponha também que as notas dos alunos são independentes entre si.

7- Num estacionamento,a taxa média de entrada de veículos é de 10 por hora. Calcule: a) a probabilidade de chegarem 27 veículos em três horas. b) a probabilidade de chegarem 10 veículos em apenas meia hora. c) a probabilidade de não chegar veículo em seis horas.

8- Numa oficina mecânica, estima-se que, em média, 2 clientes novos cheguem a cada meia hora. Dado que em 15 minutos não chegou nenhum cliente, calcule a probabilidade de que cheguem 3 clientes nos próximos 15 minutos.

9- Sabe-se que a vida útil de um pneu de determinada marca segue uma distribuição normal com µ = 60 meses e σ = 20 meses. Calcule a probabilidade de um pneu dessa marca estragar em apenas 20 meses.

10- Assumindo que o tamanho de determinada planta tenha distribuição normal com media µ = 10 cm e σ = 3 cm, calcule: a) a probabilidade de encontrar uma planta com menos de 5 cm. b) a probabilidade de encontrar uma planta que tenha entre 6cm e 10 cm. c) a probabilidade de que em uma amostra de 20 plantas, 15 tenham mais de 12 cm. d) a probabilidade de que em uma amostra de 50 plantas, todas tenham entre 8 cm e 12 cm.

5.7 Gabarito

1- a) 0.1070868 b) 0.07160367 c) 0.7624867 d) 0.001278842 e) 0.01777555

2- a) 0.00097142 b) 0 c) 0.4867012 d) 0.4867012 e) 80

3- a) 0.9973002 b) 88.496504 c) 87.18449 e 112.815514, respectivamente d) 0.9999994 e) 0.9999994

4- 0.2009388

5- 0.2194787

6- 0.003410063

7- a) 0.06553248 b) 0.01813279 c) 8.756511e-27

8- 0.06131324

9- 0.02275013

10- a) 0.04779035 b) 0.4087888 c) 3.910648e-06 d) 5.381627e-16