8 Lab 4 (Stata)
8.1 Lab Goals & Instructions
We’re using a new dataset today. This is from the World Health Organization, containing various measures related to health outcomes.
Research Question: What measures are associated with a country’s life expectancy?
Goals
- Transform variables in your dataset in a few new ways
- Predict marginal effects from your regression
- Visualize marginal effects to communicate your regression results
Instructions
- Download the data and the script file from the lab files below.
- Run through the script file and reference the explanations on this page if you get stuck.
- If you have time, complete the challenge activity on your own.
Jump Links to Commands in this Lab:
Generating related variables
log()
xtile()
ggpredict()
Graphing Margins
Saving plots
8.2 Generating Related Variables
At various point in your data cleaning, you will want to create related variables, something that shows the same information but in a different form. By related variables, I mean you are using some variables in your dataset to calculate or configure a new variable.
For these related variables, we will rely on the mutate() function and various calculations.
Example 1: New variables with simple calculations
You can always manipulate numeric variables in your dataset with basic math operations (adding, subtracting, multiplying, and so on). This is a relatively simple process, you just need to do it carefully.
For our first example, let’s say we want to know the percent population change between years. This data set contains measures from 2010, but it also has a variable for the 2005 population.
A) Lets take a look at our two population variables for an example country, say Lebanon…
list population if country == "Lebanon"
list pop_2005 if country == "Lebanon"- 2010: 4337141
- 2005: 3986852
We could calculate the percent change manually
display 4337141 - 3986852
display 350289 / 4337141 * 100350289
8.0764956B) You can generate a simple variable based on a basic calculation
generate pop_change = (population - pop_2005) / population * 100C) Let’s check out our new variable
summarize pop_change Variable | Obs Mean Std. dev. Min Max
-------------+---------------------------------------------------------
pop_change | 143 -1416.076 8407.399 -97846.89 99.89945And for extra measure, the percent change for Lebanon…
tab pop_change if country == "Lebanon" pop_change | Freq. Percent Cum.
------------+-----------------------------------
8.076495 | 1 100.00 100.00
------------+-----------------------------------
Total | 1 100.00There are clearly some funky populations in this dataset we would need to look closer at, but right now I want you to focus on knowing how to calculate the new variable.
Example 2: Logging variables
This next example is really an extension of the last. We’re just explicitly using the log function to address nonlinearity in our model.
Let’s take a closer look at GDP and life expectancy.
A) Scatter plot of life expectency vs gdp
scatter lifeexpectancy gdp || lowess lifeexpectancy gdp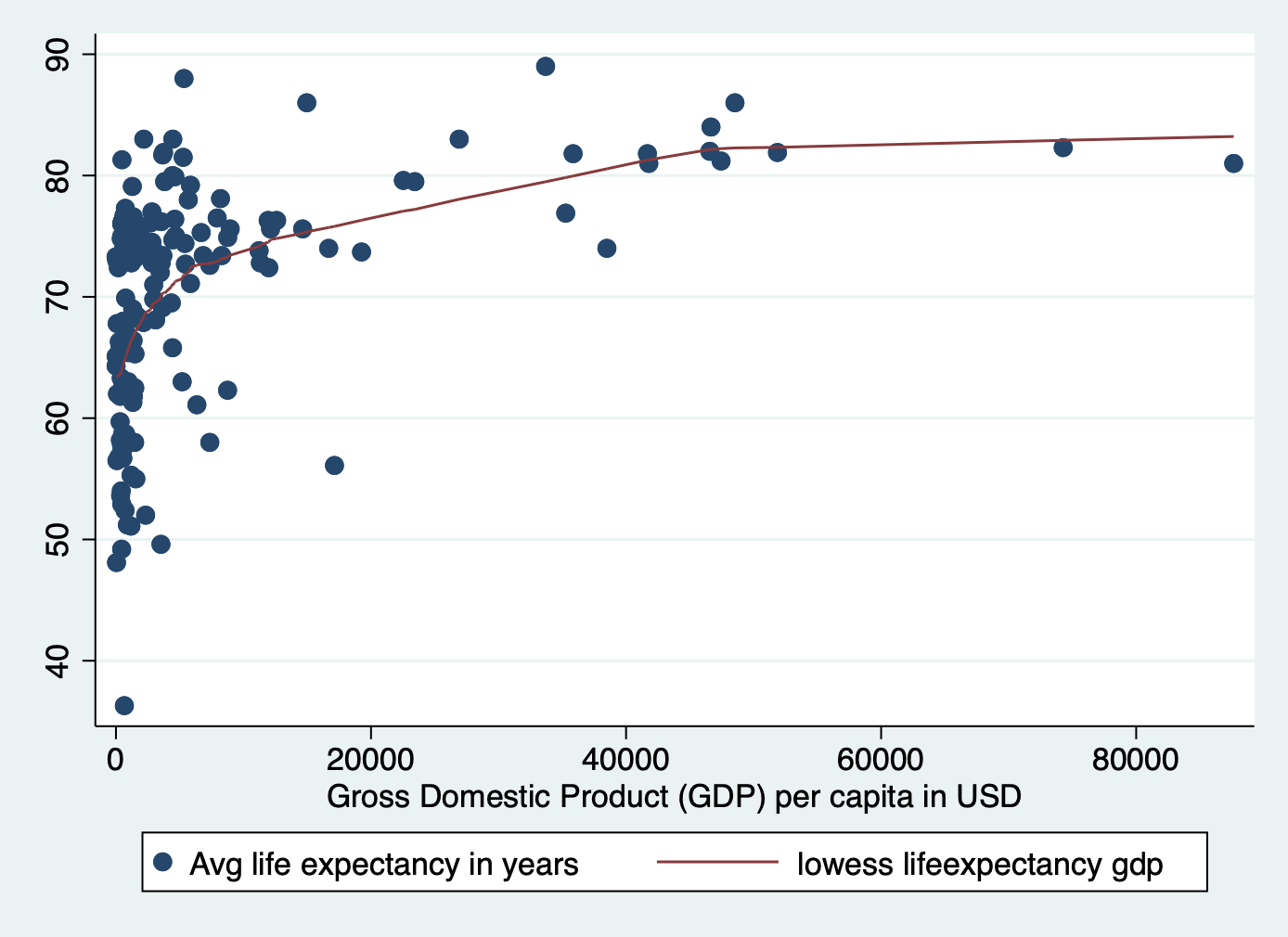
There is a clear nonlinear relationship between these two variables
B) Create a new logged version of the variable to deal with the nonlinearity
gen log_gdp = log(gdp)C) Now let’s look at the scatter plot again
scatter lifeexpectancy log_gdp || lowess lifeexpectancy log_gdp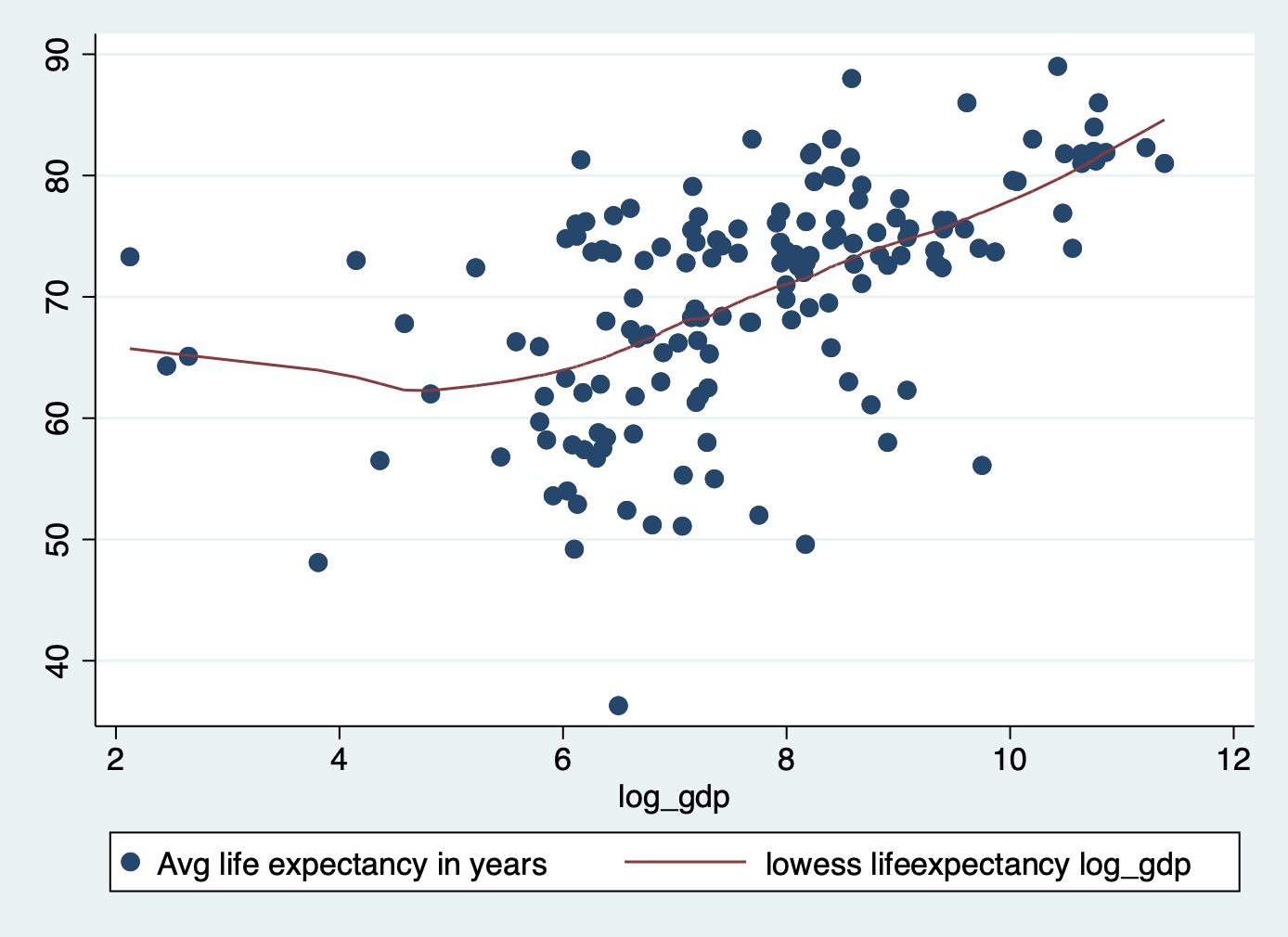
It’s not perfectly linear, but it’s a lot better!
Example 3: From continuous to categorical via quantiles
There are other ways to deal with nonlinearity besides logging the variable. In this case we are going to divide a continuous variables into categories based on the quantiles. Essentially, we will now be asking in our regression–does it matter whether someone is in the bottom quantile vs the second, third, or top quantile?
But first, let’s learn how to go from continuous to quantile categories.
A) Scatterplot of life expectancy vs infant death rate
scatter lifeexpectancy infantdeaths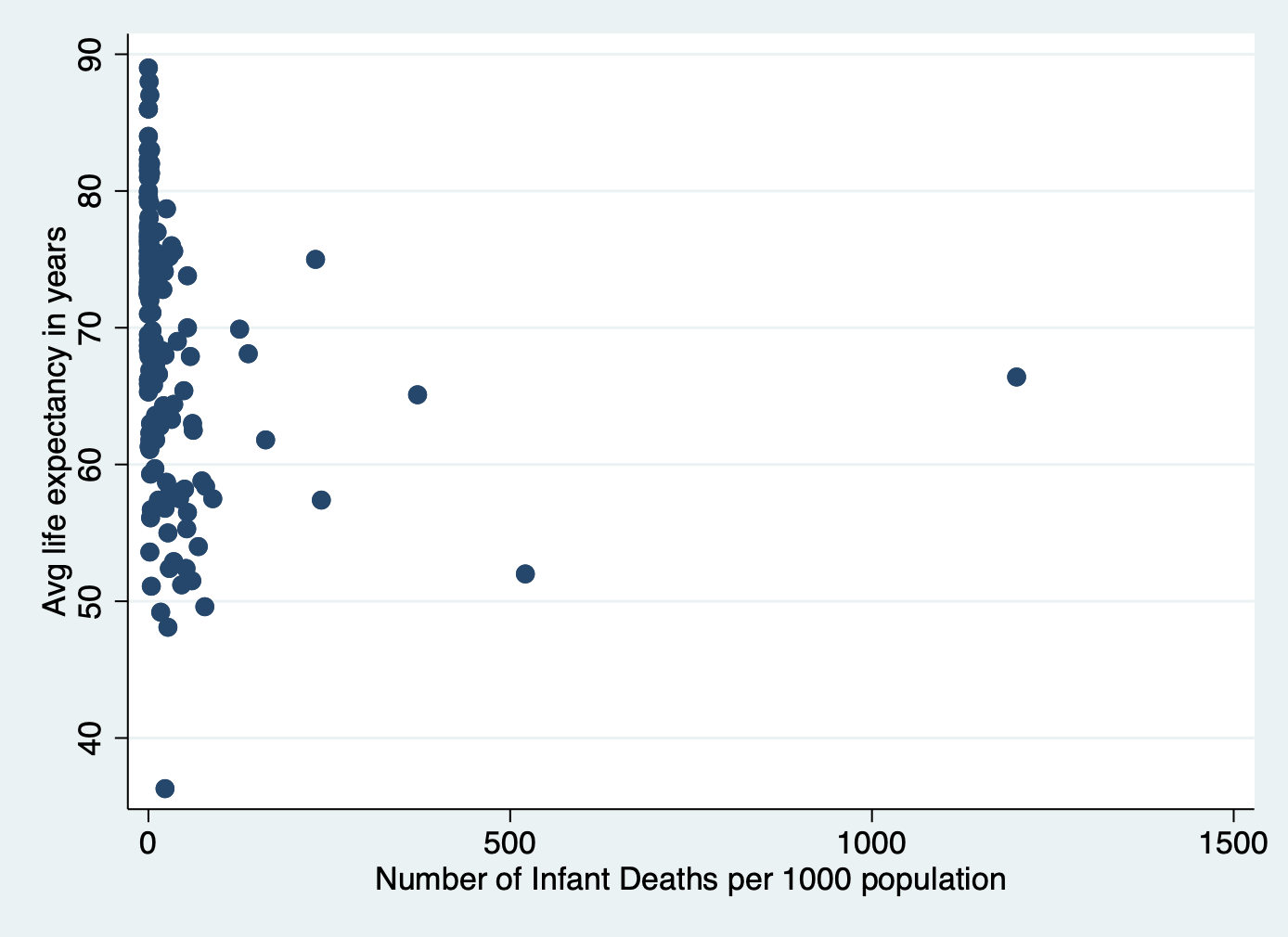
summarize infantdeaths, detail Number of Infant Deaths per 1000 population
-------------------------------------------------------------
Percentiles Smallest
1% 0 0
5% 0 0
10% 0 0 Obs 183
25% 0 0 Sum of wgt. 183
50% 3 Mean 27.92896
Largest Std. dev. 104.0253
75% 21 239
90% 54 372 Variance 10821.26
95% 79 521 Skewness 8.770086
99% 521 1200 Kurtosis 92.69153We can see that the infant death rate has a huge positive skew. Now let’s turn it into a categorical variable with quantiles. Quantiles refer to the values from 0-25%, 26-50%, 51-75%, and 76-100% of the range.
B) Use egen and xtile to make quantiles
Use “egen” and a command from the egenmore package, which automatically sorts the values into quantile ranges and assigns a category number 1-4.
First download the package and the ‘xtiles’ command
ssc install egenmoreThen generate the new variable
egen infant_quantiles = xtile(infantdeaths), nq(4)
label variable infant_quantiles "Infant death rate quantile" C) Let’s take a look at the new variable
tab infant_quantiles Infant |
death rate |
quantile | Freq. Percent Cum.
------------+-----------------------------------
1 | 54 29.51 29.51
2 | 46 25.14 54.64
3 | 38 20.77 75.41
4 | 45 24.59 100.00
------------+-----------------------------------
Total | 183 100.00scatter lifeexpectancy infant_quantiles || lowess lifeexpectancy infant_quantiles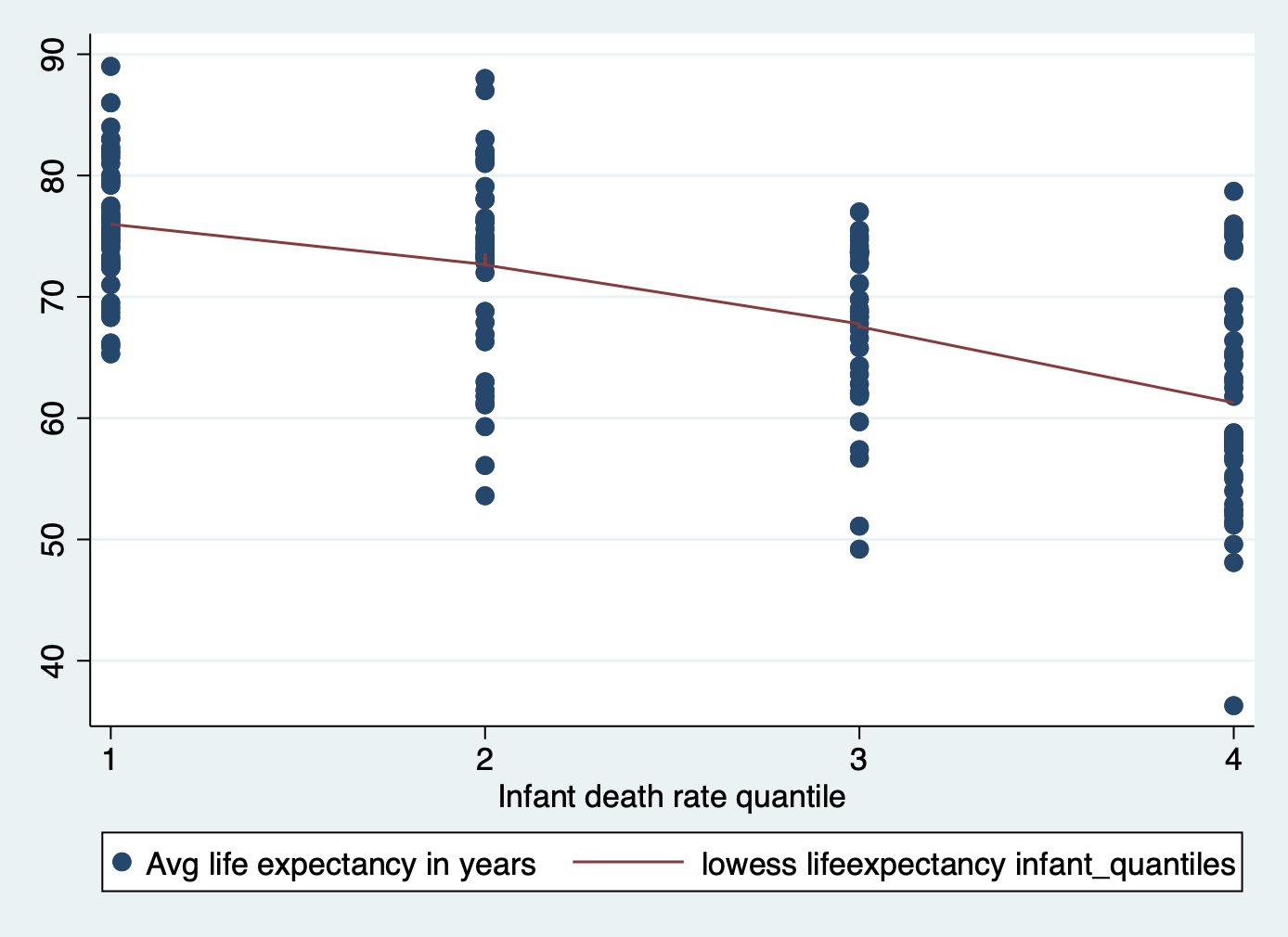
And just like that we are linear!
Now we have a categorical variable for infant deaths
where the bottom part of the range (0-25%) is category 1, the second
quantile (25-49%) is category 2, and so on. You can see where each value
fell into the range. It has a much more linear relationship
8.2.1 A note on gen vs egen
gen and egen are the two commands in Stata to calculate new variables based on other variables. Why are there two different commands? There’s not a good answer. The two commands a relic of how stata code has evolved over the years. Here’s what each command can do.
Here are some common math operations and functions that generate or gen can be used with:
- addition
- subtraction
- multiplication
- / division
- ^ power
- abs(x) absolute value of x
- exp(x) antilog of x
- ln(x), log(x) natural logarithm of x
- sqrt(x)square root of x
- round(x) rounds to the nearest integer of x
- round(x,y) x rounded in units of y (i.e., round(x,.1) rounds to one decimal place)
egen is often used with more complex functions like:
- xtile() to create quantiles
- std()
- anycount() to help you sum counts across variables
- rank() to assign a rank value to every observation based on a variable
- rowmean() to calculate the mean across variables in a row
- rowmiss() to calculate the total number of missing variables across a row
This is just a sample of what each command can do. If you need to do some type of calculation or transformation across variables, google the options you can do with each command.
8.3 Interpreting Results with Margins
This is what the margins command tells us. “Marginal effects” refer to the average predicted values for groups of observations, the groups being defined by levels of some variable(s) in the model, or for certain values of continuous variables (like the average). Marginal values will give us a lot of ways to visualize the
results of our linear regression model.
Margins for Categorical Variables
‘Margins’ is easy for categorical variables: as long as you told STATA it was a categorical/binary variable (used the i.), you can just write ‘margins [var]’ to see predicted variables for each category.
Run the regression first
regress lifeexpectancy i.infant_quantiles Source | SS df MS Number of obs = 183
-------------+---------------------------------- F(3, 179) = 37.95
Model | 6123.27377 3 2041.09126 Prob > F = 0.0000
Residual | 9627.92326 179 53.7872808 R-squared = 0.3887
-------------+---------------------------------- Adj R-squared = 0.3785
Total | 15751.197 182 86.5450386 Root MSE = 7.334
-------------------------------------------------------------------------------
lifeexpecta~y | Coefficient Std. err. t P>|t| [95% conf. interval]
--------------+----------------------------------------------------------------
infant_quan~s |
2 | -2.468357 1.471513 -1.68 0.095 -5.372101 .4353864
3 | -8.218129 1.552906 -5.29 0.000 -11.28249 -5.153772
4 | -14.71667 1.480315 -9.94 0.000 -17.63778 -11.79555
|
_cons | 75.99444 .9980284 76.14 0.000 74.02503 77.96386
-------------------------------------------------------------------------------Predict the marginal effects for x (infant_quantiles).
margins infant_quantilesAdjusted predictions Number of obs = 183
Model VCE: OLS
Expression: Linear prediction, predict()
-------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
--------------+----------------------------------------------------------------
infant_quan~s |
1 | 75.99444 .9980284 76.14 0.000 74.02503 77.96386
2 | 73.52609 1.081337 68.00 0.000 71.39228 75.65989
3 | 67.77632 1.189729 56.97 0.000 65.42862 70.12401
4 | 61.27778 1.093285 56.05 0.000 59.12039 63.43516
-------------------------------------------------------------------------------In a bivariate regression, the regression tells us the predicted values of people who are in each infant death rate quantile.
Interpretation: Countries in the lowest infant death quantile have an average life expectancy of 76 years whereas countries in the highest infant death quantile have an average life expectancy of 61 years.
Margins for Continuous Variables
When you are using the margins command for continuous variables, you have
to tell it more information. You have to specify the specific value of x
you want to predict the outcome for.
Run the regression first (not displaying the results this time for brevity)
regress lifeexpectancy total_hlthWith this command you specify the values that you want to calculate the marginal effects for inside the brackets. You can specify a single value, a range of values, or more.
Margins for 5% total health expenditures.
margins, at(total_hlth = 5)Adjusted predictions Number of obs = 180
Model VCE: OLS
Expression: Linear prediction, predict()
At: total_hlth = 5
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
_cons | 69.12835 .7166116 96.47 0.000 67.7142 70.54249
------------------------------------------------------------------------------Interpretation: Countries who spend 5% of total government expenditures on health are associated with a life expectancy of 69 years.
Margins for a range of total health expenditure levels. This code reads:
- calculate margins (GGPREDICT)
- for the model (FIT2)
- with the variable total_hlth (TERMS = "total_hlt …)
- starting from 0
- to a maximum of 15
- by increments of 5 I chose these cut points based on the range of total_hlth
margins, at(total_hlth = (0(5)15))Adjusted predictions Number of obs = 180
Model VCE: OLS
Expression: Linear prediction, predict()
1._at: total_hlth = 0
2._at: total_hlth = 5
3._at: total_hlth = 10
4._at: total_hlth = 15
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
_at |
1 | 64.31708 1.628695 39.49 0.000 61.10305 67.53112
2 | 69.12835 .7166116 96.47 0.000 67.7142 70.54249
3 | 73.93961 1.141811 64.76 0.000 71.68638 76.19283
4 | 78.75087 2.24126 35.14 0.000 74.32801 83.17373
------------------------------------------------------------------------------Interpretation: As health expenditure increases, the life expectancy in that country also increases. At a 5% health expenditure, the associated life expectancy is 69 years, where as at a 15% health expenditure, the associated life expectancy is 79 years.
Margins for regressions with more than one X variable
Run the regression first
regress lifeexpectancy i.infant_quantiles total_hlthCalculate the margins for the infant death rate quantiles
margins infant_quantilesPredictive margins Number of obs = 180
Model VCE: OLS
Expression: Linear prediction, predict()
-------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
--------------+----------------------------------------------------------------
infant_quan~s |
1 | 75.54355 .9861075 76.61 0.000 73.59736 77.48975
2 | 73.41128 1.057689 69.41 0.000 71.32382 75.49875
3 | 68.22427 1.18852 57.40 0.000 65.87859 70.56995
4 | 61.90537 1.096809 56.44 0.000 59.7407 64.07005
-------------------------------------------------------------------------------Like the previous example, we are asking Stata to generate the predicted values for the variable infant death rate quantiles (coded as 1, 2, 3, 4). But when calculating the predicted value for a person in each quantile, we now have to take into account our other x variable - total health expenditures. So what does this function do?
The function makes an assumption: that the other x values are being held at their mean (for continuous variables) or the “reference category” (for categorical variables). When you put just one variable, what the function actually calculates is the predicted value for each value of x when age is at its mean in the dataset.
mean total_hlthMean estimation Number of obs = 180
--------------------------------------------------------------
| Mean Std. err. [95% conf. interval]
-------------+------------------------------------------------
total_hlth | 6.151222 .2038742 5.748916 6.553528
--------------------------------------------------------------Interpretation: Countries in the lowest infant death quantile have an average life expectancy of 75 years whereas countries in the highest infant death quantile have an average life expectancy of 61 years, holding total health expenditures constant at the average.
Other variations of margins
We can do a lot with ggpredict() and the margins it produces. For example, Let’s say we want to know…
A) The predicted life expectancy for at various levels of health expenditure, but only for countries in the first infant death quantile:
margins, at(total_hlth = (0(5)15) infant_quantiles = 1)Adjusted predictions Number of obs = 180
Model VCE: OLS
Expression: Linear prediction, predict()
1._at: infant_quantiles = 1
total_hlth = 0
2._at: infant_quantiles = 1
total_hlth = 5
3._at: infant_quantiles = 1
total_hlth = 10
4._at: infant_quantiles = 1
total_hlth = 15
------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
-------------+----------------------------------------------------------------
_at |
1 | 71.6689 1.686734 42.49 0.000 68.33994 74.99786
2 | 74.8184 1.044886 71.60 0.000 72.7562 76.8806
3 | 77.9679 1.160133 67.21 0.000 75.67824 80.25755
4 | 81.11739 1.899327 42.71 0.000 77.36886 84.86593
------------------------------------------------------------------------------Interpretation: For countries in with the lowest infant death rate, at a 5% health expenditure, the associated life expectancy is 74 years, where as at a 15% health expenditure, the associated life expectancy is 81 years.
B) The predicted values for each quantile at different levels of health expenditure.
margins infant_quantiles, at(total_hlth = (0(5)15))Adjusted predictions Number of obs = 180
Model VCE: OLS
Expression: Linear prediction, predict()
1._at: total_hlth = 0
2._at: total_hlth = 5
3._at: total_hlth = 10
4._at: total_hlth = 15
-------------------------------------------------------------------------------
| Delta-method
| Margin std. err. t P>|t| [95% conf. interval]
--------------+----------------------------------------------------------------
_at#|
infant_quan~s |
1 1 | 71.6689 1.686734 42.49 0.000 68.33994 74.99786
1 2 | 69.53663 1.651616 42.10 0.000 66.27698 72.79628
1 3 | 64.34962 1.598282 40.26 0.000 61.19523 67.504
1 4 | 58.03072 1.583146 36.66 0.000 54.90621 61.15524
2 1 | 74.8184 1.044886 71.60 0.000 72.7562 76.8806
2 2 | 72.68613 1.090304 66.67 0.000 70.53429 74.83797
2 3 | 67.49911 1.181185 57.15 0.000 65.16791 69.83032
2 4 | 61.18022 1.102643 55.49 0.000 59.00403 63.35641
3 1 | 77.9679 1.160133 67.21 0.000 75.67824 80.25755
3 2 | 75.83563 1.287284 58.91 0.000 73.29503 78.37623
3 3 | 70.64861 1.497765 47.17 0.000 67.6926 73.60462
3 4 | 64.32972 1.390216 46.27 0.000 61.58597 67.07347
4 1 | 81.11739 1.899327 42.71 0.000 77.36886 84.86593
4 2 | 78.98513 2.032941 38.85 0.000 74.97289 82.99736
4 3 | 73.79811 2.258056 32.68 0.000 69.34158 78.25464
4 4 | 67.47922 2.158006 31.27 0.000 63.22015 71.73828
-------------------------------------------------------------------------------Interpretation: (Choosing one example from these margins) In countries with the highest level of health expenditure (15%), those with the highest infant death rates have an associated life expectancy of 67 years whereas those with the lowest infant death rates have a life expectancy of 81 years.
NOTE: This is a good example of why you have to be precise with ggpredict() margins. By changing our specification of infant_quantiles, we can find out the predicted life expectancy for a) only the first quantile at different levels of health expenditure OR b) each quantile at different levels of health expenditure.
8.4 Graphing Results with Margins
Knowing the margins can help you translate your findings into comprehensible statements. Displaying them is a great visual way to communicate those findings.
marginsplot is a command that can be used after margins to visualize our
predicted values. Let’s visualize the margins from the last section.
Plot A
Predict your margins first, then add a marginsplot command.
regress lifeexpectancy i.infant_quantiles total_hlthmargins, at(total_hlth = (0(5)15) infant_quantiles = 1)
marginsplot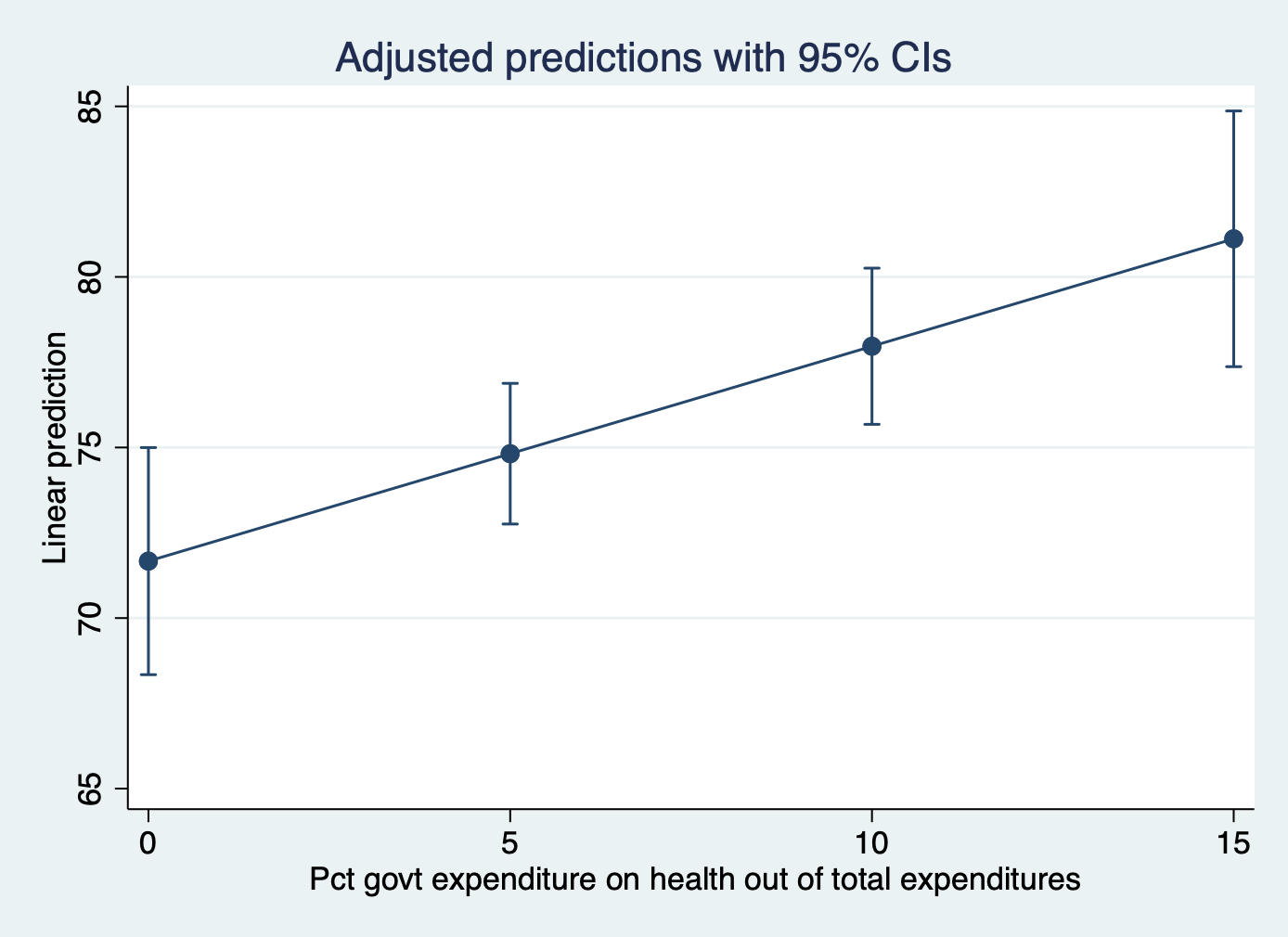
Plot B
Predict your margins first, then add a marginsplot command.
margins infant_quantiles, at(total_hlth = (0(5)15))
marginsplot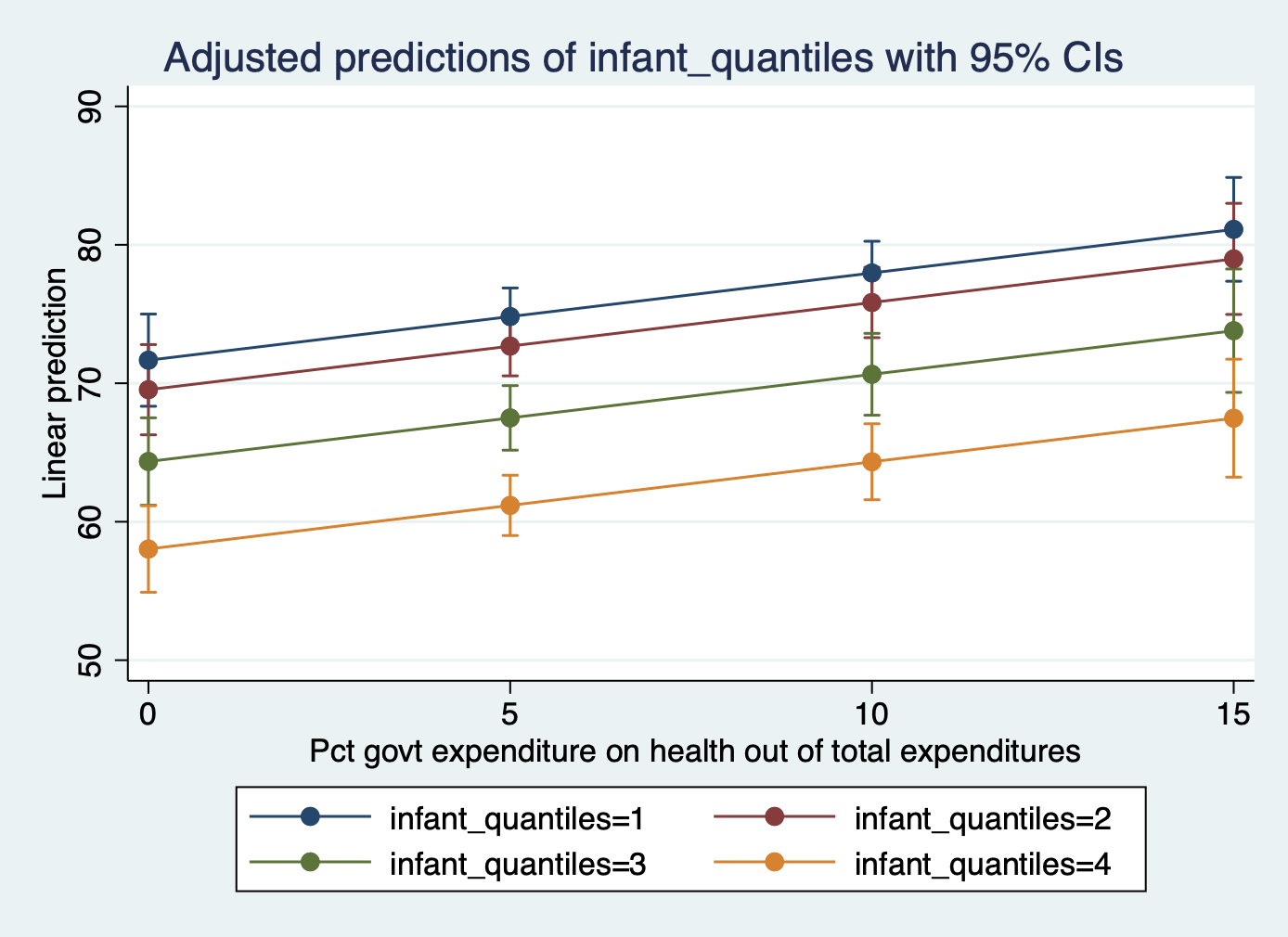
Plotting the margins allows us to actually make easier the visualization of what we are trying to describe with the predicted results. There are also some fun things we can do while visualizing relationships.
Here is an option with a bar graph
margins infant_quantiles
marginsplot, recast(bar)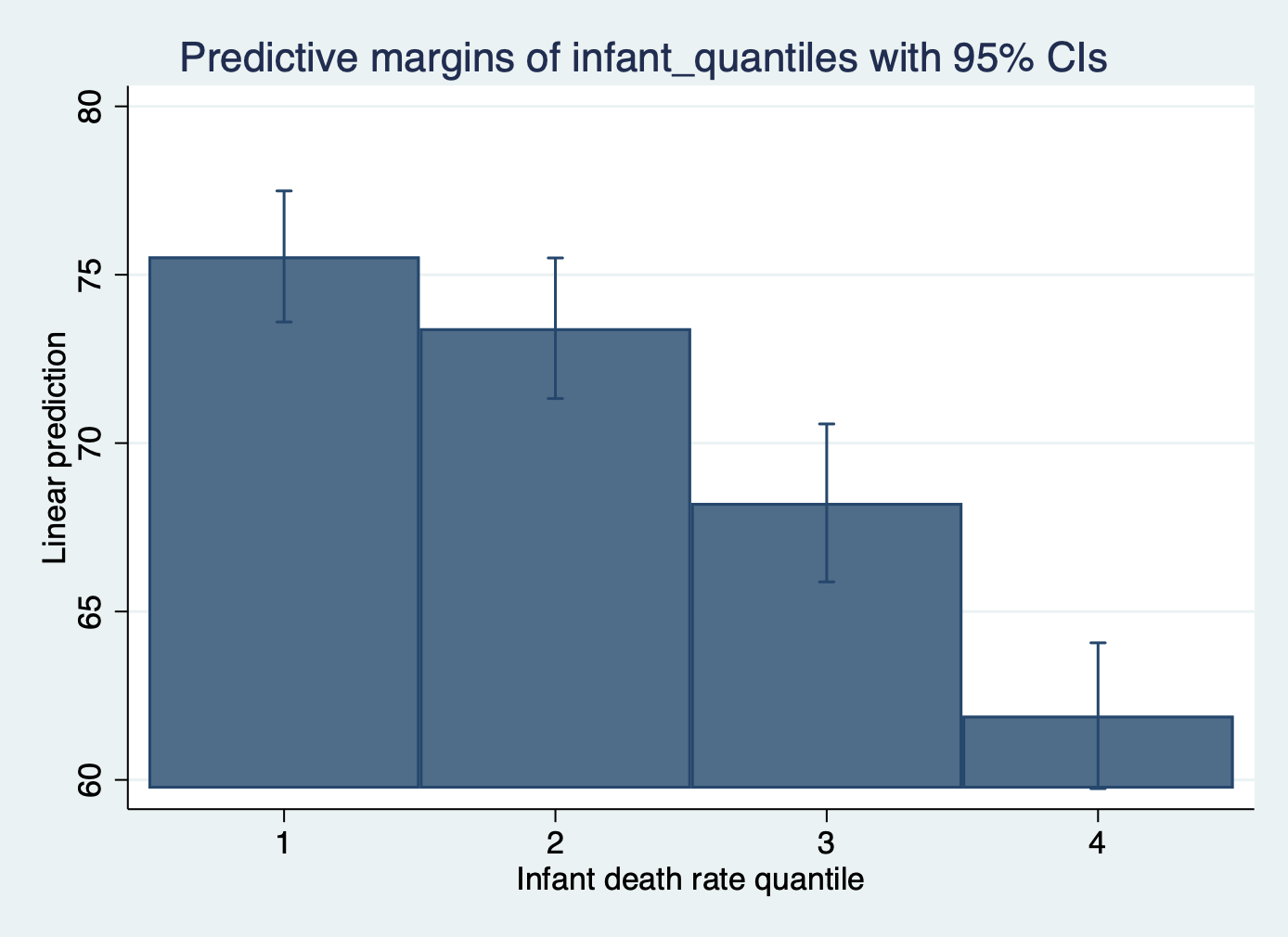
Here is an option with the lines split to multiple graphs
margins infant_quantiles, at(total_hlth = (0(5)15))
marginsplot, by(infant_quantiles)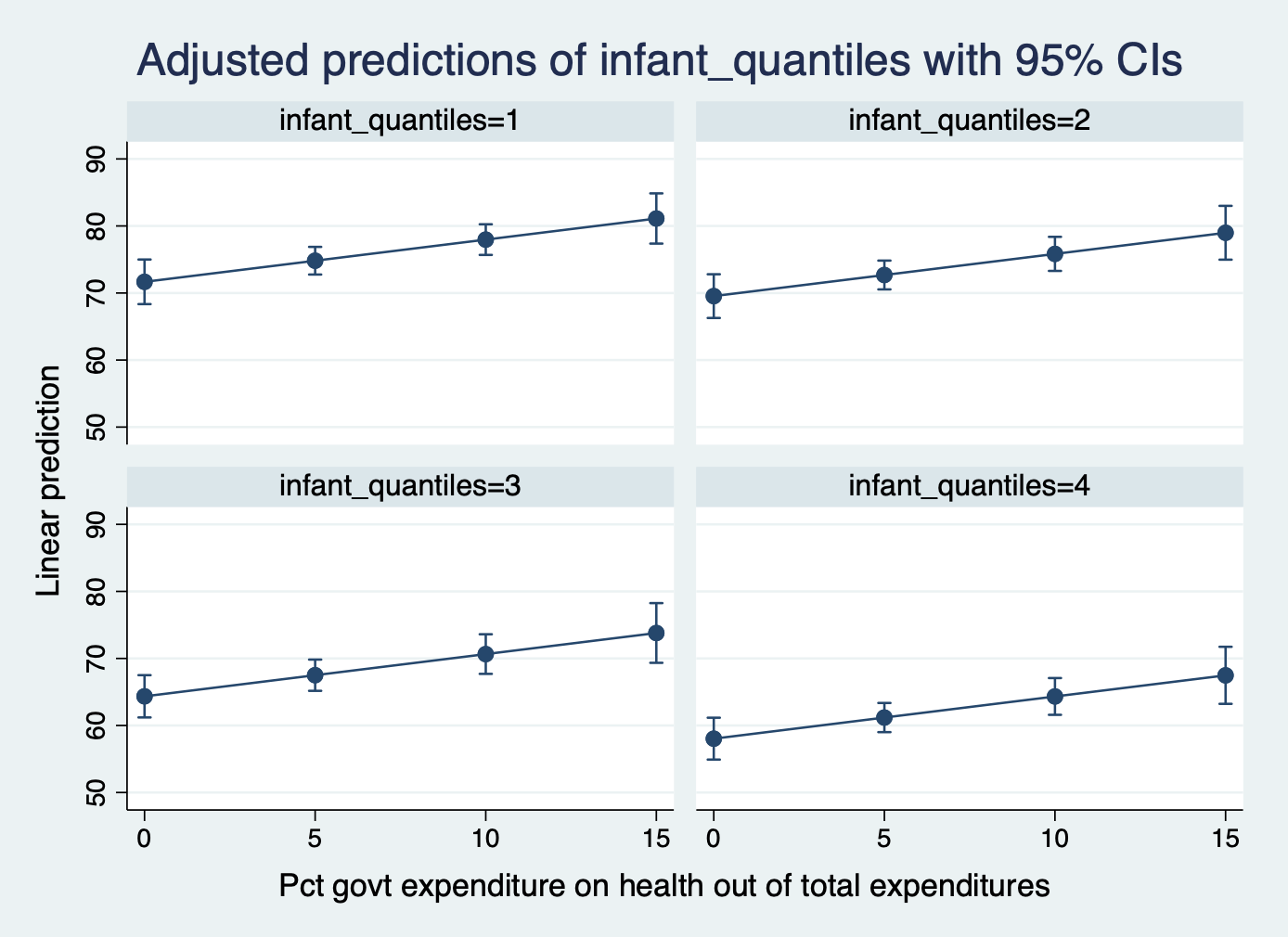
8.5 BONUS: Saving and Improving your Graphs
You may be manually saving your plots or taking screenshots, but here is some other helpful code to save a graph in code. If you tweak anything in your previous code that would affect the graph, your new graph will be saved when you rerun your code. It saves times as you are iterating your findings
FIRST: Create the graph
margins infant_quantiles, at(total_hlth = (0(5)15))
marginsplotSECOND: Save the most recent graph
graph export "figs_output/infantdeath_plot.png", replace8.6 Challenge Activity
Run a regression of life expectancy (lifeexpectancy) and child HIV/AIDS death rate (child_hivaids).
Create a new variable that addresses the skew of the HIV/AIDS variable. There are multiple ways to do this.
Produce a margins plot that clearly communicates the effect of the child HIV/AIDS death rate on life expectancy.
This activity is not in any way graded, but if you’d like me to give you feedback email me your script file and a few sentences interpreting your results.