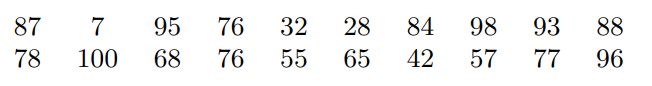5 Day 4

Announcements:

• Supplemental Homework Review

  • One of the other instructors made this

  • Thanks Eli!

• No office hours today

  • Thursday 9 AM - 10 AM

  • After 2:45 PM please do not talk to me

• Stat Help Lab

  • Should open next week

• Homework point recovery will open after this class

  • No due date but please respect my time

    • Don’t give me 10 homeworks on November $1^{st}$

  • I’m not going to grade them yet

    • Don’t stress email me, I won’t reply

• Extracurricular questions and supplemental material

Review

• When we have one quantitative variable we have several options:

Histograms

• Histogram: visual representation of a frequency distribution

  • Not a bar graph

• Start by making a frequency distribution:

  • Define classes (numeric intervals)

  • Record the frequency of occurrences

Class	Frequency
0.00-0.99	9
1.00-1.99	26
2.00-2.99	11
3.00-3.99	13
4.00-4.99	3
5.00-5.99	1
6.00-6.99	2

• Lower class limit: the smallest value that can appear in that class

• Upper class limit: largest value that can appear in that class

• Class width: the difference between consecutive lower class limits

• General requirements for quantitative frequency distributions:

  • Every observation must fall into one of the classes

  • The classes must not overlap

  • The classes must be of equal width

  • There must be no gaps between classes

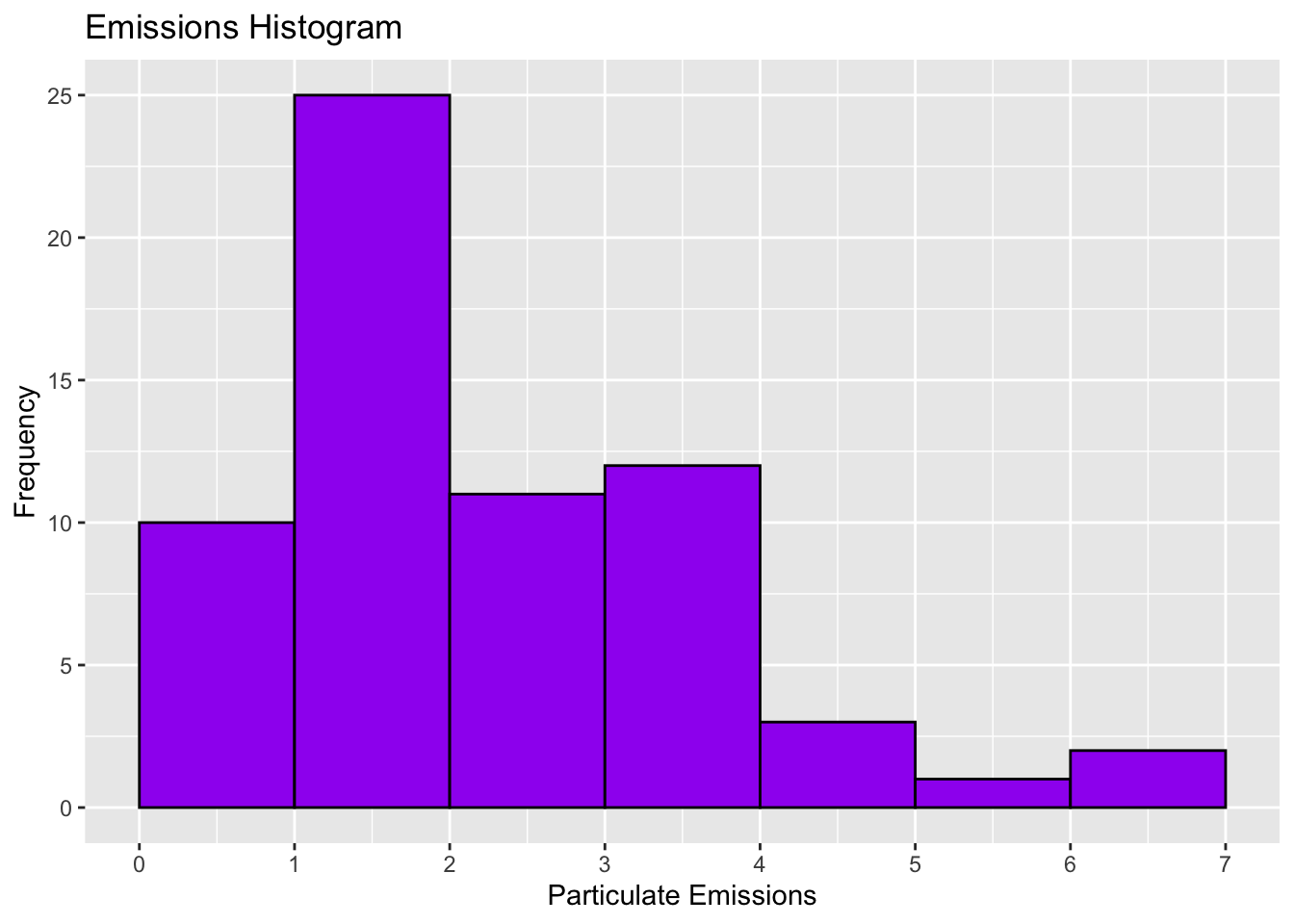
• Bar height (y-axis) represents class frequency

• Bar width (x-axis) represents class width

• Left edge of each bar corresponds to the lower class limit

• No gaps between classes so no gaps between bars of a histogram

• We care about the shape of our data

• The shape of our data can help us observe the distribution of our data

• Vocabulary for describing the shape of data:

  • Symmetric - mirror image on both sides of it’s center

  • Positively-skewed - Long, narrow tail to the right

  • Negatively-skewed - Long, narrow tail to the left

  • Unimodal - One peak/hump

  • Bimodal - two peaks/humps

  • Uniform - b o x

• Histograms can be used to summarize both small and large data sets

• Sometimes we prefer more detailed visualizations for smaller data sets

Steam-and-leaf plots

• Each observation should have at least two digits

  • The digit furthest to the right is the “leaf”

  • The digits to the left form the “stem”

• The data:

• The stem-and-leaf plot:

Dotplots

• We can represent each observation by a dot above its value on a number line

• Data:

3

6

2

5

1

2

3

4

3

4

• Dotplot:

Numerical Descriptions

• Graphics are good for taking data and making it easier to view

• Numerical summaries are how we take data and make it easier to understand

• We’re going to specifically cover:

  • Mean

  • Median

  • Mode

• Refresher:

  • A parameter describes a population

  • A statistic describes a sample

• “Use of sample statistics to describe population parameters”

  • Statistical Inference in a nutshell

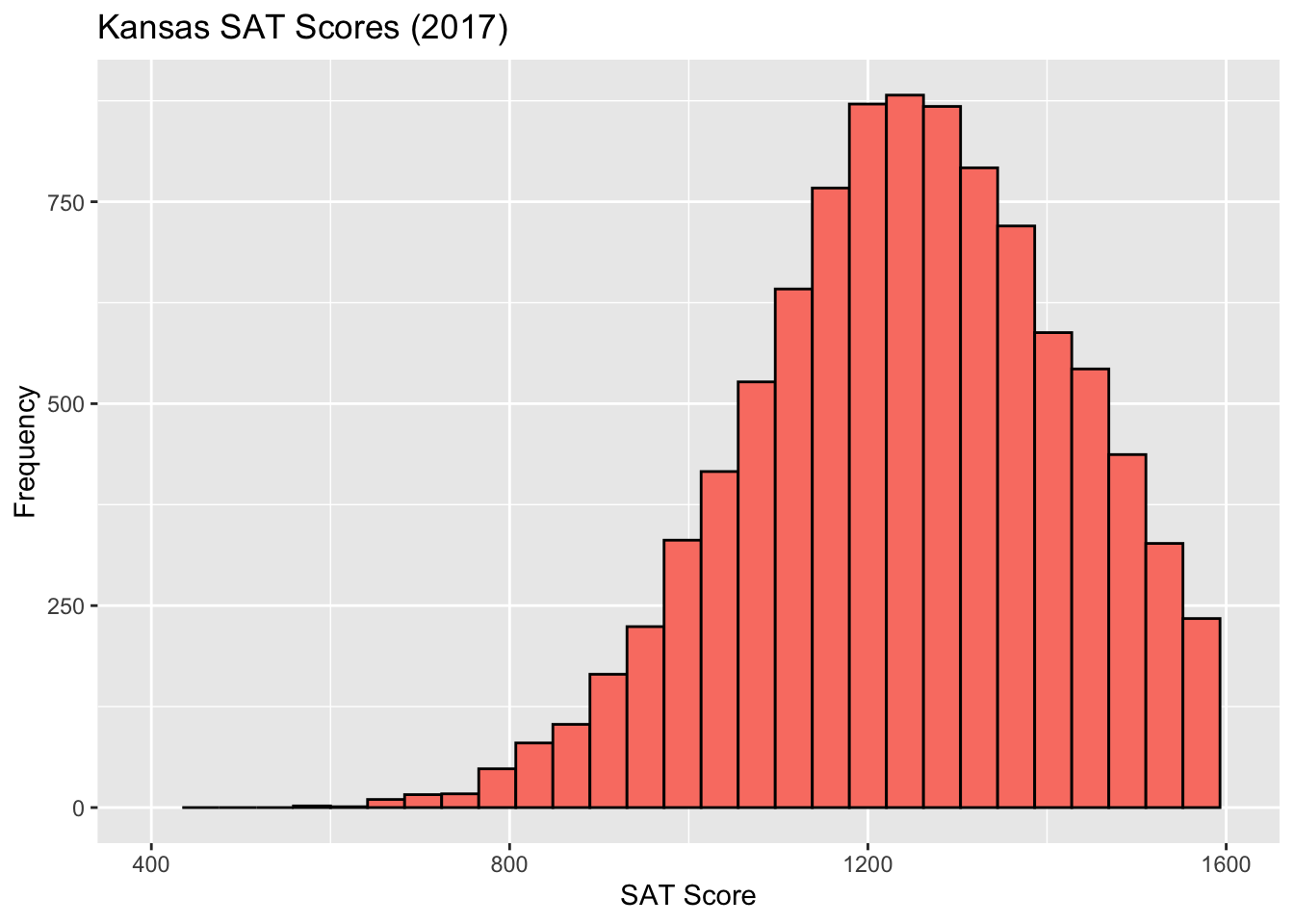
• Which way is this histogram skewed?

• How would you describe the “center” of this data?

  • Mean or average: Balance point (fulcrum) of the dataset.

  • Median: Half of the data points are above the median, half are below.

  • Mode: Where the peak is.

Mean

• Most commonly used metric for summarizing data

• Sum all of the data then divide by the number of observations

7

3

12

3

5

$$Mean \ = \ {7+3+12+3+5 \over 5} = {30 \over 5} = 6$$ - If the data we calculated a mean for comes from a sample:

• Sample mean

• If the data we calculated a mean for comes from a population:

  • Population mean

• Which one is a parameter?

  • A statistic?

• Mathematical Notation Soapbox

  • “Letter math”

  • I resisted it forever

  • But trust me, it does end up being helpful

• Data values can be denoted as $x_1,x_2,x_3,...$

  • $x_1$ refers to the observed value of the variable $x$ from individual 1

  • $x$ can be anything

    • It doesn’t even have to be $x$

    • It’s convention, not law

• Sample size (the number of individuals in the sample)

  • Denoted with $n$ (Note: lower-case)

• Population size

  • Denoted with $N$ (Note: capital)

• Summation:

  • This is referring to the sum (addition) of everything contained in the expression

  • We denote this with the Greek letter $\Sigma$

• With this notation we can describe:

$$\sum\limits_{i=1}^nx_i=x_1+x_2+...+x_n$$

• “The summation of $x_i$ to the $n^{th}$ term, indexed by 1”

• With sigma notation we can express the sample and population mean formulas:

  • Sample mean (denoted $\bar{x}$):

  $${1 \over n}\sum\limits_{i=1}^nx_i$$

  • Population mean (denoted $\mu$):

  $${1 \over N}\sum\limits_{i=1}^Nx_i$$

• Greek letters usually mean population parameters

• Lower-case letters usually mean sample statistics

• In practice:

Table 5.1: Sample of College Seniors

Student	Absences
1	2
2	6
3	1
4	2
5	4
6	0
7	1
8	3
9	0
10	2

$${1 \over n}\sum\limits_{i=1}^nx_i$$ $${1 \over 10}(x_1+x_2+x_3+x_4+x_5+x_6+x_7+x_8+x_9+x_{10})$$

$${1 \over 10}(2+6+1+2+4+0+1+3+0+2)$$

$${1 \over 10} *21 = {21 \over 10} = 2.1$$ - Properties of mean:

• Common

• Easy to interpret

• Susceptible to outliers

  • The average number of Super Bowl rings between me and Tom Brady is 3.5

  • (As of 2021) the top 1% of households in the United States hold 32.3% of the country’s wealth, while the bottom 50% hold 2.6%

• A statistic is resistant if its value is not affected heavily by outliers

  • Is the mean resistant?

Median

• Middle value, half the data are below and half are above

7

3

12

3

5

• Sort your data in increasing order (low to high)

3

3

5

7

12

• The median is 5

• If $n$ is odd: choose position ${(n+1)\over2}$ in the ordered dataset

• So $n=5$

  $${(n+1)\over2}={(5+1)\over2}=3$$

  • We pick the $3^{rd}$ data point after sorting

7

3

12

3

5

8

• If $n$ is even after ordering:

  • Pick $n\over 2$ and ${n \over 2}+1$

  • Average the two data points

3

3

5

7

8

12

• So $n=6$

  $${6\over 2}=3 \ ,\ {6 \over 2}+1=4$$

  • 3rd data point: $5$

  • 4th data point: $7$

  $${(5+7)\over 2}=6$$

  • The median is $6$

• Properties of median:

  • It doesn’t use all of the data directly

  • This makes it resistant

    • Outliers have little/no effect

  • Sometimes a more realistic measurement:

    • Median Household Income (Kansas): $\$57,422$

    • Average Household Income (Kansas): $\$77,509$

    • Why does median make more sense than average here?

  • Difference between median and mean depend on skew of the histogram

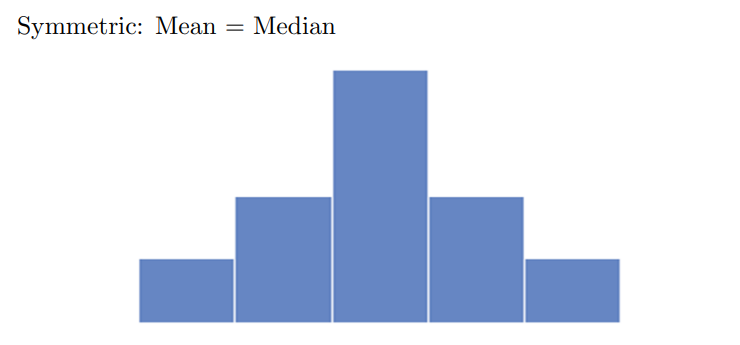
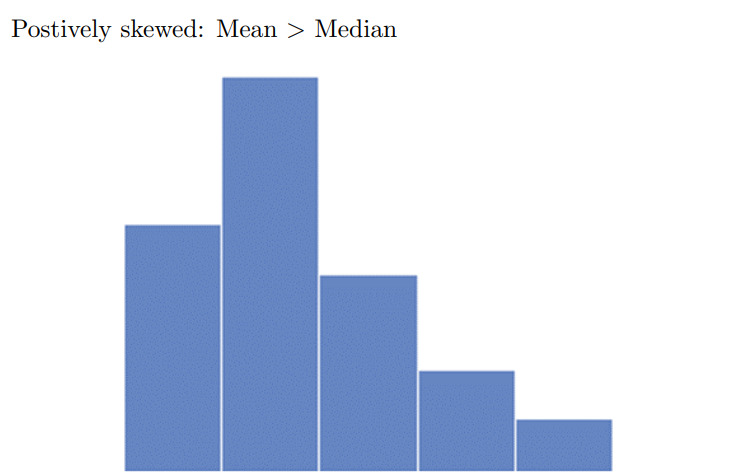
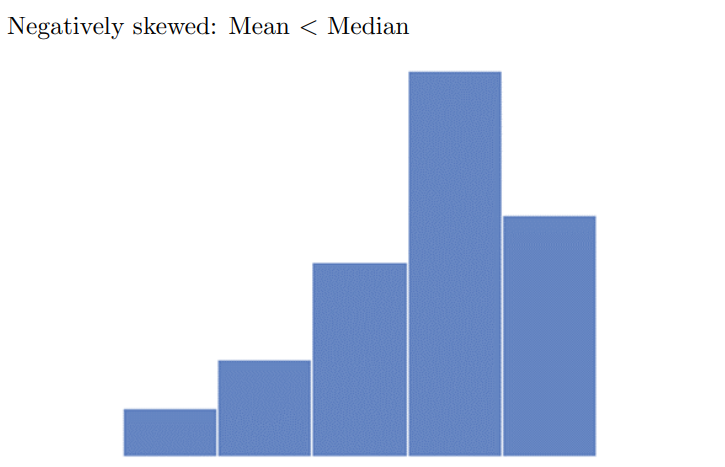
Mode

• The most frequent observation

• Useful for qualitative data

  • “Which credit card is most commonly used by our customers?”

• Not as useful for quantitative data

  • “What’s the most common weight of cattle on our research farms?”

  • Why isn’t this a helpful metric?

• A data set can have any number of modes (0,1,2,…)

7

3

12

3

5

• The most frequently observed value in this data set is $3$

  • So the mode is $3$

• The below data set displays a sample of $n=7$ observations:

2

1

3

4

3

5

4

1. Find the mean, round to two decimal places if necessary:

2. Find the median, round to two decimal places if necessary:

3. Find the mode(s):

A group of restaurants reported in a recent year that the mean price for their dinner was $\$18$, and the median was $\$22$. If a histogram was constructed for the price of dinner at the group of restaurants, would you expect it to be skewed to the right, skewed to the left, or approximately symmetric?