Chapter 4 練就基礎統計數感續談分配首部曲

4.1 「數字會不會說話」活動紀實

我計畫在「數字會不會說話」系列文章的前四篇各出一道與數字有關的小問題，徵集逢甲大學讀者的答題回覆，並且在活動結束後致送勝選文章一篇一份神祕禮物。嚴格說起來一開始這四篇不能被歸類為文章，它們只是一個引子，引領有興趣、有創意的讀者進入數據分析的殿堂。請有意願參與競賽的讀者在2012年3月15日到2012年4月30日活動期間回覆我的每週一問。

4.1.1 報到率

4.1.1.1 第一週的題目

「假如逢甲大學某個單位經過計算之後發現現在大一這一屆的入學報到率是100%。請讀者諸君從各種可能的角度（諸如學校經費、學習資源、大學同儕等等）論述100%這個數字可能帶出來的意義，或是背後可能隱藏某種角度的真實面貌。」

關於大一新生報到率，基本上是這麼算的：

實際大一報到人數除以錄取名額（不含外加名額）

大家都知道逢甲大學是一所教研並重的私立綜合大學，並沒有某某企業的奧援，意味著營運學校的每一分錢大大半來自學生繳交的學雜費以及教育部的補助。這也透露出每一位學生每一學期分配到的教育經費其實只有多少？如果你的理財觀念與數學夠好的話，你或許可以概算一個數字出來估計一下每一位逢甲大學生分配到的資源。關於大家熱愛的逢甲大學，她的財務狀況其實可以在學校官網找得到，加上財務並不是我的專長，我應該要閉嘴才是。

上面這一段文字只是本週一問「報到率」的引子，或許是一個不錯的起點讓你深入理解100%這個數字。為了避免誤導您理解與創作的思緒，我話先說到這裡。竭誠歡迎您來挑戰！

4.1.1.2 學生的回應

4.1.1.2.1 第一篇：作者，鄭育昇、發表時間，2012年03月17日9:45下午。

放榜之後只有一間學校可以讀，因此，如果不去讀這所學校，意味著必須花一年重考，因此學生們可能不想要重考所以就來讀這逢甲了!!!

因此我們開始從什麼原因讓學生不想要重考?!!

重考班就讓人想到什麼立志要讀台大等等的志願，如果有這種志願的人想必會重考，因此得到了一個論點逢甲入學的學生並沒有想要讀台大之類的企圖心。

再讓我們用另一個觀點提重考，會重考通常是因為想讀特定科系卻考不上，如醫科、電機之類的。那麼逢甲的新生真的如自己所願都讀到自己興趣的科系了嗎？想要在私立大學內進入自己想要的科系，沒有台清交這種學校來的困難，如果以人高中就立志要讀什麼系，想這些人只要認真讀自己有興趣的科目，填榜單要重自己的興趣並非難事，因此，逢甲應該不會有因為讀不到自己要的科系而想一重考的學生。另外，在逢甲要轉系只要肯讀書，學校都不會為難。

因此學生不想要重考?!!的原因可以歸於學生沒有打算考名聲響亮的國立大學的企圖心。

那我們又得到了一個問題，為什麼學生們沒有想要讀名聲響亮的國立大學的企圖心。以下就要問這些學生了啊:~~。不過還是可以做假設:

  1. 逢甲威望深植人心
  2. 大家都認為讀名聲響亮的國立大學出來工作薪水沒有比較神奇
  3. 親戚朋友從逢甲畢業都有不錯的工作因此很放心
  4. 學生已經有了人生目標了剩下是實踐但這和大學是哪沒關係
  5. 今朝有酒今朝醉
  6. 等等…

以上5點假設需要數據求證。

4.1.1.2.2 第二篇：作者，黃一臻、發表時間，2012年03月18日12:37上午。

題目假設了逢甲大學(後簡稱逢甲)某單位計算出大一新生入學報到率為100%，從字面上看來「100%」，這是一個非常漂亮的數字，可以說是領先於全國各個大學。但是，我們忽略了這漂亮的數據，也許存在著「美麗的錯誤」，我們常被數據給騙了。這是我進入逢甲的第二年，也就是步入大二生活，初次觸碰統計學(嚴格說來還真的算是初次接觸，在國高中因對數字感不佳，總是有聽沒有懂，上過統計學才明白是國高中的老師教得太淺了，並沒有想像中的難念。)，最近老師剛教到「誤差」(Error)，所以

在我認為100%，很可能是存有誤差的，我想可以套在這個例子上，也許負責的單位是隨機抽取學生樣本，而被抽到的學生剛好都有來報到，抑或是，在大學校園內同學間十分盛行的代理簽到、代理刷學生證，諸如此類的等等，因此掩蓋了這個誤差，讓我們看到了這不真實的100%。

然而，若是此誤差事實上是不存在的，那麼100%的實質報到率，真的是非常驚人，更何況是出現在全國大學人數名列前茅的逢甲，更是不容易。從這個數據我們也可以推斷出逢甲學生素質是相當良好的，在國內各界的風評也定會是多有讚許。我認為這100%是一條連帶的關係，老師引文中提到的「逢甲並沒有某某企業的奧援，意味著營運學校的每一分錢大大半來自學生繳交的學雜費以及教育部的補助。」，逢甲是國內私立的大專院校，學雜費比起公立學校當然是不便宜，而學生報到率如此高，也就代表學費的繳交率自然不會低，學生繳交了學費，因此逢甲才有錢在校園、設備、圖書館、健身房…等等的地方做建樹，讓我們學校的學生也因此才能享受到比其他學校更高等的教育品質。

4.1.1.2.3 第三篇：作者，卓宛穎、發表時間，2012年03月18日12:24下午。

可能因為

  1. 社團吸引新生，也很積極的關心新生

（例如：舉”南聯“來說，在還沒報到前就會打電話邀請新生參加迎新茶會，藉此讓新生更了解大學的生活！此外，在此社團都為同一地區且為相同高中的學生，因此，在逢甲遇到問題時還有學長的可以請教！他們也很貼心的為新生提供客運定位，讓還不熟悉台中的新生能安心地給學長姐們帶領）

  1. 學校們很關心新生

（例如：在開學前，導師主動打電話問新生是否有意願參加新生茶會等）

  1. 學校的資源也很吸引人

（圖書館資源豐，體育館也很誘人。外語中心也提供許許多多的學習英語的管道，讓想增強英語能力的人有環境可以學習：他們會不定期開TOEIC,TOEFL等課程讓學生免費報名，每週三和四也都有免費的活動，參加校園的英檢考試也都有補助）

  1. 外界對逢甲的評價

  2. 宿舍的設備與環境

4.1.1.2.4 第四篇：作者，劉韋伶、發表時間，2012年03月19日7:51上午。

  1. 由整體的財務狀況可以看出主要收入來源為學生繳納的學雜費，而主要支出為人事費用，而簡單的看每一位學生的資源便是主要來收入減主要支出再除以總人數，學校一開始會以錄取名額來預估應該支出的人事費用，100%的報到率的意思就是報到人數等於錄取名額，那麼每一位學生就會得到的應有的整體資源，可是只要報到人數不等於錄取名額，因為收支餘絀會減少，換句話來說，大家得多負擔固定的人事費用，則每一位學生所得到的整體資源也會減少。

  2. 假設報到人數不等於錄取名額，就師生比來說會減少，但不會因為老師負擔的學生比較少，就給老師較少的錢，所以100%的報到率就學校來講可以充分的運用師資，不造成浪費的情形，但就學生來講從老師獲得的資源則會減少，因為一個老師所提供的資源有限，越多學生反而會讓每個人得到較少老師提供的資源。

  3. 就同儕競爭方面，以100%的報到率來看，每一個學生所需面臨的競爭對手會多於報到人數不等於錄取名額，但有競爭就有合作，以人脈的角度來分析，100%的報到率，可以讓每個學生有機會認識更多的人。

  4. 100%的報到率意思是報到人數等於錄取名額，我認為100%這個數字，代表的是分子等於分母，例如：以機率來說100%就是一定會發生，以統計來說要100%的準確，則其樣本就等於母體。

4.1.1.2.5 第五篇：作者，邱喜華、發表時間，2012年03月19日10:30上午。

身為統計系的學生，曾經聽老師這樣說過：「你真的相信所謂的統計數字嗎？」，因為我們常常在醫院的公佈欄上看到「抽菸的人得到肺癌機率的會比不抽菸的人高Ｘ％」，而這個數字的由來可能只是很小的數字差，但是只要換上百分比，數字說的話卻會讓人怯步。所以一開始我看到本周的題目時，我直覺得想到所謂的「報到率」只是比較值，或許失真了吧！

「實際大一報到人數除以錄取名額（不含外加名額）」是報到率的算法，

顯然的，實際人數與錄取名額之間的多寡嚴重關係到「報到率」。往壞處想，有種情況是錄取名額很低，此時只針對會考慮就讀逢甲大學學生的人數來決定錄取名額，所以只要分母越小，百分比的數字就會越大；而往好處想，報到學生可能會因為逢甲大學的教學資源豐富、教育評鑑高或者同儕影響，來選擇逢甲大學，但是究竟學生們選擇的依據是什麼？我們無從得知。

我認為，雖然外界認為學校經費很高，但是上過經濟學的我曾聽老師分析過學校的經費，雖然大多的錢是學生繳交的學費，但是因為一個學校上上下下所有的教職員工的薪水大概就把學生的學費使用殆盡，所以經費的由來對於小小的學生來說，只能單純的認為那是政府根據教學評鑑所撥下來的款項，因為得來不易，所以我們身在逢甲則更應該好好珍惜身邊的資源，或許就是這個原因，塑造了逢甲的好形象，使得報到率如此之高吧！

4.1.1.2.6 第六篇：作者，倪偉倫、發表時間，2012年03月20日7:46下午。

依上面所述，100%可以有很多不同的意義：就字面上來講，上述的報到率計算方式為

\(p＝83.33%\)（例如:實際報到新生數50人/實際錄取60人＊100%)

  1. 從計算方式來講，表示今年度學生的入學人數。承前所述，表示未來四年”大部分”學生將會留在學校的人數。就錄取人數不等於報到人數來講，也代表有更吸引人的學校開出更低的條件吸引學生放棄目前的選項。

  2. 從社會的觀點來說，報到率最能表現學生及家人的接受程度。假如學生長期受到企業高度期許勢必提高入學意願。報到率的高低，相對間接反應出學生對(系所/學校)的興趣。(例如:台灣大學與私立大學相較。)

  3. 從財務方面來講，對學校來說，是補助外資金資源的主要收入(例如:逢甲大學最近幾年總人數大約在20,615人左右，可見光學費部分可提供的資金相對可觀。)

  4. 從教育方面來講，在一個完善的”教育體制”的前提下，報到率也是反應學生在此學習制度下的成效(例如:”聰明才智在前段”但成績中段的學生，想進去更好的學校但會因為成績不足所以只好降低目標)。成效與報到率的關係，比較像把學校作為職場的跳板，影響著學生未來的走向，所以在選學校時會考慮到未來的發展。

  5. 從素質方面來講，會直接反映在報到率上(例如:學校的教育品質、硬體設備…)。

最後100%的意義在數學及統計上的意義：

指某項測驗或評估中的滿分，在文化上亦可指全面性的。

大致上報到率可以分析出以上幾點，接著100%指的就是最全面的喜愛，以上大概為報到率的分析。

4.1.2 全球化

4.1.2.1 第二週的題目

【溫加寶】今年在股市賺進100萬新台幣這樣的事實，會不會改變你在股市賺進100萬新台幣的機會？[提示] 統計獨立性。 這一週我決定除了題目再加上一段小提示。讓有意競逐神祕獎品的讀者能聚焦在某個統計的議題。

上一週的數字是100%，這一週的數字是100萬。並不是因為喜歡100這個數字，而是它影響我們太深、太深了。考試要考100分、人生的第一桶金就是要存個100萬。

這一週的提示：【統計獨立性】是一項重要的假設。獨立性談的是變數與變數之間的一種關係，也會是樣本與樣本之間的關係。這裡我們想先談變數與變數之間的獨立性。不論那一項專業領域都充斥著各種變數，統計分析首重隨機變數，它是一種會跟著機率起舞的變數。意味著，不保證看到變數的那一個數字，想要看到股市衝過8000點，得問問機率大神！機率到底是什麼？體會一下這句話：

下一秒的你比現在的你老一秒，這是肯定的，表示看到比現在老一秒的你的機率等於1.0。除非！

機率現象俯拾即是，但我們卻只會看到數字。數字暗藏著機率，數據分析師用盡心機就是為了把數字背後的機率挖出來。如果兩變數是統計獨立的，那麼它們彼此帶著關於機率的資訊是不重疊的。意思就是說，如果【溫加寶今年在股市賺進新台幣】這個變數，跟【你今年在股市賺進新台幣】這個變數是統計獨立的，那麼兩變數所帶關於賺進100萬新台幣的資訊不會重複。上述這一句話對不對，請讀者諸君仔細評論。你注意到全球化出現在哪裡了嗎？

下週再見。

4.1.2.2 學生的回應

4.1.2.2.1 第一篇：作者，邱喜華、發表時間，2012年03月26日12:20上午。

假如兩者變數是統計獨立的，那麼溫加寶是否能在股市賺進100萬與你是否能在股市賺進100萬是沒有關係的，所以我們可能會因為「溫加寶能在股市賺進100萬新台幣」而認為「溫加寶可以，我也可以」以致大家都對股市有更多的注意，甚至研究。我認為溫加寶在股市賺進100萬新台幣，並不會改變其他人在股市賺錢的機會，只要對股市有些鑽研的人，都會希望能在股市賺進大把鈔票，而對於100萬這個數字，溫加寶賺來的原因可能是因為:

  1. 他對企業與政府、政策之間的關係有強大的洞悉能力。
  2. 他在市場上有足夠能力了解企業間的競爭關係以及各方能力。
  3. 他經長期研究股市，根據經驗法則，成功的機率會提高很多。
  4. 他對於挑對股票有很高的信心以及額外的幸運。

…等等。

而是否改變我在股市賺錢的機會呢?

並不會，因為根據上述4點，只要我也具備這4點能力的話，要賺進100萬也不是困難的。又因為股票市場千變萬化，可說在一定期間內，不會有相同的股票走勢出現，所以，因為我們與溫加寶投入股市的時間不同，所以我認為「時間」是使得兩著變數為統計獨立。 除此之外，我認為是否會改變其他人賺進100萬的因素有：

  1. 時間。
  2. 種類(例如:觀光股、銀行股…等)。
  3. 政策(政府推行的政策會影響到股市的發展)。
  4. 全球化(世界脈動當然也會影響到股市走向)。

…等等。

以上淺見。

4.1.2.2.2 第二篇：作者，倪偉倫、發表時間，2012年03月31日3:05上午。

以統計的角度看這個事件，在統計學的方面，各個理論上的定義都告訴我們，當兩個隨機過程保持統計獨立時他們必然是不相關的，但反過來則不一定成立，意即不相關的兩個隨機過程不一定能保持統計獨立。在機率論裡，說兩件事件是獨立的，直覺上是指一件事的發生不會影響到另一件是發生的機率。兩者的差別在於前者是長久收集資訊，後者估計事件不相關。

全球化的題目中提到”溫家寶投資一百萬與我們投資一百萬互相比較”，暫且撇開股票技術資訊來講，就統計方面來講這個事件，可以比喻為，兩個人花錢進入充滿珍寶的山上，開始無條件的帶走珍寶，沒有上限想拿多少就拿多少，但第一個問題出現了，珍寶就這麼多大家都要。所以就統計的角度來看這個事件，是相關的事件。

第二個問題，為了提高壓對寶的事件機率，是不是有許多的消息提示、股市上的內線？相繼接下來遇到的問題，自己所在區塊的寶不能挖了，那解決的方法當然就是去別人家（國）挖寶，反正大家現在都說地球是平的嘛！在這我們可以假設溫家寶是指有錢人，那全球化指的是全球的有錢人都在用錢賺錢。相對的，我們投資錢進去的時後到底是賺還是給別人賺？以上內容見仁見智，但可以確定的是你的一百萬我的一百萬，只要拿出來想要讓他變多都是相關的，只是影響程度的多少。

4.1.2.2.3 第三篇：作者，黃一臻、發表時間，2012年04月29日10:08下午。

如果【溫加寶今年在股市賺進新台幣】這個變數，跟【你今年在股市賺進新台幣】這個變數是統計獨立的，那麼兩變數所帶關於賺進100萬新台幣的資訊不會重複。

我與其他人持不一樣的觀點，我認為是錯誤的，因為就現金流量的觀念來看，股市有一筆100萬元的錢被別人賺走了，有人賺錢了，那必然會有人賠錢，只是損失錢的人是否是我？我不知道，但它應該存在著機率，也就是說，有可能是我也可能是別人，我們所努力的，就是把賠錢的機率壓到最低，把賺錢的機率拉到最高而已。在此我們假設：

  1. 溫家寶在股市賺進100萬元 ＝ 事件Ａ
  2. 我在股市賺進100萬元 ＝ 事件Ｂ

題目提到下一秒的你比現在的你老一秒，這是肯定的，表示看到比現在老一秒的你的機率等於1.0，在Ａ尚未成為事實前，它的機率也是小於1.0的一個值，但既然Ａ已然成為一項事實，那也是肯定的，代表它發生的機率也是1.0，我們將之記為

\(P(A) = 1.0\)

我在股市賺進100萬元的機會記為

\(P(B) = 機率為多少我們尚且不知道\)

Ａ發生是必然的，而Ａ發生是否影響到了Ｂ的發生？我想是的，正如我前面說到，有人賺錢必然會有人賠錢，當溫家寶在股市內賺進了100萬元，那麼我以及其他人賺到錢的機率就變小了，而且還有可能因此賠錢，因為原本Ｐ(Ａ)也是小於1.0的一個數值，但如今它已成為事實，我的股票賺錢的機率仍小於1.0，可能還因此小於它原本的機率值，那麼我們就該承認溫家寶在股市賺到錢的機率變成事實時，會影響我在股市賺到錢的機會了。

4.1.3 瞎說

4.1.3.1 第三週的題目

如果統計二甲的每個人都是19歲，那麼統計系的每位大學生也是19歲？[提示]邏輯推理與研究方法。直到我寫第三週題目，依然無人試圖回答第二週的問題。希望不是我的題目太難！

這一週的問題真的是瞎說。

怎麼可能統計系不分大一、大二、大三、大四都是同一個年紀！這絕對是瞎說。但是你如何透過統計手段找到推翻瞎說的確切證據？統計推論首重證據力，就像法官論斷嫌疑犯有沒有罪一樣。統計學家或是專業人士透過調查、實驗、觀察收集數字證據。人文社會科學家常用調查；工程科學家常用實驗；自然科學家常用觀察。不論哪一種數字收集手段，都不能沒有對象。對象可能是問卷調查的受訪者、工程師試圖延長壽命的電池、生物學家試驗新藥的白老鼠等等。『找到對象』是讀者回答這一週問題的關鍵。請努力找到他們吧！大家加油不要放棄！

4.1.3.2 學生的回應

4.1.3.2.1 第一篇：作者，邱喜華、發表時間，2012年03月31日1:26上午。

首先，這個題目看似很容易被推翻，但是要根據一些證據來推翻這個假設，並不容易。以下是我對此題目所做的證據推測：

假設以下無跳級或晚讀的因素，一般來說台灣的大學生年紀介於17歲到22歲之間，平均分配在大一到大四的年級層，而大一到大四的學生中，二年級的學生只占四分之一，又統計系每個年級有兩個班，所以就算我們已知統計二甲的學生都是19歲，那也只占整個統計系的八分之一，這個原因足以證明本題目的假設嚴重錯誤。

如果前項證據還不夠充足的話，我認為我們可以做實地調查，或許普查或許抽樣，以抽樣來說雖然有可能會有樣本數過少導致抽樣結果偏頗，但是這也是一種表達真實面的做法。針對統計系所有學生以亂數表抽取所需樣本進行調查，假設抽到的學生多為19歲學生，那麼我們只能大膽假設統計系學生大多為19歲學生，但是不無可能恰巧的都抽到統計二甲的學生。所以我認為可以先把統計二甲的學生先排除在外，對於未知其年齡的其他學生做抽樣調查，這樣一來，根據第二段的假設，我可以大膽推測，第二次抽樣所抽到的學生不會百分之百都是19歲的學生，由此可知，我們知道「所有統計系的學生都為19歲」這個假設，產生了嚴重的瑕疵。

以上淺見。

4.1.3.2.2 第二篇：作者，黃一臻、發表時間，2012年04月29日10:51下午。

如果統計二甲的每個人都是19歲，那麼統計系的每位大學生也是19歲。

這句話說不通，本周的題目的確是瞎說，怎麼可能統計系大一～大四的學生都同樣是19歲呢？除非統計系三、四年級所有人從小就都是跳級的學生，大三的學生都資優跳級一年、大四的學生都資優跳級兩年，一年級的學生就大家都是留級生，都留級了一年，而且二年級以及其他所有的統計系學生大家還要同樣都在十九年前的今天以後才出生，不然比起其他人，他今天就先成年了，而這有可能嗎？

機率簡直微乎其微，那麼我們要如何拆穿這個瞎說呢？其實不難，方法也百百種，諸如抽樣調查、問卷調查、調閱學校的紀錄…等。

第一種我們使用抽樣調查、問卷調查，我們務必要避免的就是其可能產生的誤差，因為在抽樣的過程中，可能抽樣人員抽樣調查的人都剛好是19歲，所以抽樣的母體相對要大一點以避免這個誤差出現，或者準確的抽統計系各個年級的人來做問卷調查(例如各班的前四名…等)。

第二種我們使用調閱學校的紀錄，此種方法可以一個不漏的涵蓋整個母體(也就是統計系所有的學生)。而當抽樣抽到或查到小於19歲或大於19歲的統計系學生時，哪怕是只有一、兩個人，我們即可推翻這個假說了。

利用統計出來的數據我們可以直接的看出「統計系的每位大學生都是19歲」這句事實並非如此，我想本周的題目「瞎說」是以偏概全了。

4.1.4 窮人的風險

4.1.4.1 第四週的題目

##                                       
## 1 第一組    2    4    6    8   10   12
## 2 第二組 2002 2004 2006 2008 2010 2012

如何表達上下兩組數據的不一樣？[提示]設計一個跟風險有關的數字。

本週題目出現兩組數據。它們是經過設計的，一般而言，現實環境裡不會看到這麼整齊劃一的數據集。針對這兩組數據，我做了一些基本的假設：

  1. 第一組跟第二組來自不一樣的母體。
  2. 它們有著一樣的單位。
  3. 第二組確實是第一組加上2000得到的，會看到這麼整齊畫一的數學關係，純粹是我故意的。
  4. 這兩組數據集都跟財富有關。
  5. 兩組數據集的其中一組可以假設跟窮人有關。（這純粹是為了呼應我的題目，當然也是我刻意的，請讀者海涵。）

窮人的生命風險比富人高（希望你同意！）。

統計學家通常會用一些數字試圖理解原始數據，諸如透過平均數、中位數、眾數發現原始數據的位置；透過全距、四分位數間距、變異數、標準差發現原始數據的分散程度。位置與分散是統計學家的言語。為了讓學生理解統計學家的「分散」，我在課堂上常用「胖瘦」試著解釋因為分散程度不一所帶出來各種分配的形狀。但是不管我多努力，還是有許多人無法弄懂變異數。後來經驗多了，我會跟學生這麼說：「變異數大代表意見（比較）不一致、變異數小代表意見（比較）一致。」學生好像比較懂了。

但是問題又來了。保險從業人員如何解釋變異數呢？財務管理專家又如何解釋變異數呢？在某一個特定領域，所謂的意見一致又是什麼意思呢？變異數是一個學過統計學的人都聽過的數字，大部分的人們認為它是不好懂、不好算的統計數字。事實上，變異數再怎麼不討喜，人們依舊大量採用。但是變異數也有詞窮的時候，現實世界裡確實有那種原始數據集明明大不同但是變異數算出來卻相等的案例。這時候專業人士或是該領域的統計學家會試著發明一個新的、足以區分彼此的數字，取代變異數在該專業領域的角色。

最後一週的題目，希望讀者試著找找看，想辦法找到或是發明一個跟窮人風險有關的數字（包含它的算法）。接著分別把題目提供的第一組跟第二組原始數據代入之後，因為我們假設窮人承擔的風險比較高（跟第六項假設有關），所以窮人那一組數據的計算結果應該會得到比較大的數字。

以往的案例告訴我，對一位沒有經驗、希望吸收經驗的新進數據分析師而言，第一時間沒有那一絲絲線索是正常的。我的引言到此，希望各位讀者諸君努力想答案；或是努力Google一下找答案。

4.1.4.2 學生的回應

4.1.4.2.1 第一篇：作者，邱喜華、發表時間，2012年04月15日1:04上午。

假設錢對於窮人來說是非常重要的，所以只要身邊有一塊錢，能存則存；而富人則是把錢拿來投資，剩下的錢才拿去儲蓄。所以我根據這個假設來設計一個式子：

風險(R) =存入(i)*[1+利率(r)]^年-未存入(o)

假設題目的兩組數字同在相同的r=0.01，這兩組數字代表著存入(i)的值，令每組數字的第一個為未存入(o)，每個數字都隔一年。帶入數字後：

第一組數字 → \[2*(1+0.01)^1-2=0.02；\] \[4*(1.01)^2-2=2.0804；\] \[6*(1.01)^3-2=4.1018；\] \[8*(1.01)^4-2=6.3248；\] \[10*(1.01)^5-2=8.5101\]

第二組數字 → \[2002*(1.01)^1-2002=20.02；\] \[2004*(1.01)^2-2002=42.2804；\] \[2006*(1.01)^3-2002=64.7838；\] \[2008*(1.01)^4-2002=87.5329；\] \[2010*(1.01)^5-2002=110.5302\]

根據上面式子算出來的值來做個簡單的分析，我發現第一組數字的風險顯然小於第二組數字所算出的風險，故我大膽假設第二組數字是屬於窮人的。因為窮人非常注重儲蓄所以會把所有積蓄都寄託在銀行或者郵局內，相對的，富人因為對於儲蓄較不重視，所以多把金錢拿來投資，僅剩的錢才拿去做小儲蓄。簡單定義本式子的「風險」，是指金錢擁有者把錢寄託給郵局或銀行的風險。

由上面的式子看來，因為富人不重視儲蓄，每年增加的風險比較少；而窮人因為都把錢存入郵局或銀行，使得每年風險增加的速度遠遠高過於富人。以上是我根據題目所設計得式子，不知道是否符合題意或者是否合理，希望能夠得到老師的肯定與批評。

4.1.4.2.2 第二篇：作者，倪偉倫、發表時間，2012年04月29日10:36下午。

風險大概分類成以下幾種：

  • (1)市場風險、
  • (2)信用風險、
  • (3)市場流動性風險、
  • (4)資金調度流動性風險、
  • (5)系統及事件風險、
  • (6)法律風險、
  • (7)作業風險、
  • (8)模型風險、
  • (9)其他。

一般情況下大家都不用承擔風險，但是當你投資的時候就無可避免的承擔風險，不論資金多寡。到這裡聽起來都算合理。但是你”只能”投資一塊錢時跟你投資一百萬時風險真的一樣嗎?

假設：

  1. 題目是在敘述一個社會或國家，情況假設為M型社會
  2. 第一組數字是指一群社會中最左端(極貧)
  3. 第二組數字是指一群社會中最右端(極富)

這兩群人的物價指數相同。按照上述理論，我們把所有財務投資出去，所要承擔的風險應該相同，現實上我們要生活，但我們也真的需要投資，有2000萬的人損失了200萬。可能只是飯後閒聊。但是2萬塊的人損失了2000塊。可能已經在想這個月要捨棄什麼開銷了。此處照上面風險的計算到最會是相同的，但是事實真的一樣嗎?

假設我們計算改成

(X(總資產)*(1+R(投資報酬率)))/CPI(物價指數)，其中CPI: 108.0 (民國100年12月by國家統計月報)

  1. 第一組：\(20,000*1.01/108= 187.04\)
  2. 第二組：\(20,000,000*1.01/108= 187,037.04\)

這樣相較下是不是比較符合現實感受?

這些只是粗淺的估計，但是我想表達的是，市面上大多的指數(EX:痛苦指數、CPI、…)都沒有把大家的財產，生存風險計算進去，大家都忽略掉、沒看到，但現實呢?

4.1.4.2.3 第三篇：作者，黃一臻、發表時間，2012年04月30日5:30上午。

其實當我看完題目時，對於本題的確有些卻步，也許是對我來說太難了，讓我無法思考出更佳的解答。而我第一個想到的就是之前修投資學時有上過…以變異數衡量風險的算法，統計學也學過變異數、標準差，但當我利用課本裡的公式時，兩個求出來的解竟然相同(都為14)，因此我開始產生疑惑，後來發現這樣有規律的數字(差都相同)，求出來的結果當然會相同…，此題變異數的確辭窮了，所以我得自己設計出一個和風險有關的公式讓結果能得出窮人的生命風險比富人來得高，由於窮人相對於富人較沒有經濟能力去購買各式各樣的保險，當碰到事故時，相對就少一份保障，所以相對富人，窮人的生命風險必然較為高。

我先假設了　

  1. 第一組數據是窮人
  2. 第二組數據是富人
  3. 他們都能利用一半的錢去買保險

富人第一年能利用1001萬元去買保險，則窮人僅能用1萬元去買保險。

富人第二年能利用1002萬元去買保險，則窮人僅能用2萬元去買保險。

…

富人第五年能利用1005萬元去買保險，則窮人僅能用5萬元去買保險。

富人第六年能利用1006萬元去買保險，則窮人僅能用6萬元去買保。

而我設計了一個簡單的公式為：

\[R＝\frac{1}{賺進的錢－投保金額}\]

第一組～窮人：

  1. 第一期：\(1/1=1.000\)　　　　　　　
  2. 第二期：\(1/2=0.500\)
  3. 第三期：\(1/3=0.333\)
  4. 第四期：\(1/4=0.250\)
  5. 第五期：\(1/5=0.200\)
  6. 第六期：\(1/6=0.167\)

第二組～富人：

  1. 第一期：\(1/1001=0.000999\)
  2. 第二期：\(1/1002=0.000998\)
  3. 第三期：\(1/1003=0.000997\)
  4. 第四期：\(1/1004=0.000996\)
  5. 第五期：\(1/1005=0.000995\)
  6. 第六期：\(1/1006=0.000994\)

因此我們可以看出，計算出風險較大的第一組的確是窮人，第二組則是富人。

4.1.4.2.4 第四篇：作者，黃一臻、發表時間，2012年04月30日5:52上午。

而我的另一個想法是…

數據為窮人、富人投入保險的金額，並將原有的變異數公式做點改良～

\[R = \sum \frac{X_i^2 - \bar{X}^2}{(n- 1)X_i}\]

如此可得出第一組～窮人：　　　　　　　　　　　　

  1. 第一期：\(14/2=7\)
  2. 第二期：\(14/4=3.5\)
  3. 第三期：\(14/6=2.333\)
  4. 第四期：\(14/8=1.75\)
  5. 第五期：\(14/10=1.4\)
  6. 第六期：\(14/12=1.167\)

第二組～富人：

  1. 第一期：\(14/2002=0.006993\)
  2. 第二期：\(14/2004=0.006986\)
  3. 第三期：\(14/2006=0.006979\)
  4. 第四期：\(14/2008=0.006972\)
  5. 第五期：\(14/2010=0.006965\)
  6. 第六期：\(14/2012=0.006958\)

因此我們也可看出，第一組為窮人，第二組為富人，隨著投入保險的金額增加，所需要承擔的生命風險也會越來越小，但窮人仍是比富人須承擔更多的生命風險，畢竟富人投入的金額也較多，因此所需擔負的風險也趨小。

4.2 排序

為什麼選讀這個主題，基本上，至少有以下幾個理由：

  1. 見證莖葉圖如何得到數字由小到大的排序結果？
  2. 見證莖葉圖如何得到數字由大到小的排序結果？

4.2.1 建議優先閱讀：莖葉圖

1900年代，Arthur Bowley倡議莖葉圖這一項技術。

…

讓我們回顧以下這一組摘錄自維基百科數據的莖葉圖：

  1. 呼叫套件aplpack：
library(aplpack)
  1. 直接抓網頁上的數據然後用「c」形成向量然後指定給「<-」給「Data」這個名字就能永久存放在記憶體裡：
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
  1. 讓stem.leaf自行決定怎麼畫莖葉圖但是設定不理會離群值：
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6

4.2.2 打亂原始數據的順序再畫一次莖葉圖

  1. 指定隨機種子等於1233。
set.seed(1233)
  1. 產生「Data」的隨機排列然後回存給「Data」。
Data <- sample(Data)
  1. 呼叫「Data」檢視成果。
Data
##  [1]  84  88  68  72  46  44  75  76  68  64  81  49  63  66 106  47  72
  1. 繪製「Data」打亂後的莖葉圖。
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6

我們得到的莖葉圖一模一樣，沒變！

4.2.3 排序84, 88, 68, 72, 46, 44, 75, 76, 68, 64, 81, 49, 63, 66, 106, 47, 72的結果是…

  1. 先產製莖葉圖。
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6
  1. 再根據上述莖葉圖，一路往下抄下來，得到遞增的數列。

記得起點是數字「44」，然後「從左而右」、「從上而下」的順序一路抄到數字「106」。

##  [1]  44  46  47  49  63  64  66  68  68  72  72  75  76  81  84  88 106
  1. 再根據上述莖葉圖，一路往上抄上去，得到遞減的數列。

記得起點是數字「106」，然後「從右而左」、「從下而上」的順序一路抄到數字「44」。

##  [1] 106  88  84  81  76  75  72  72  68  68  66  64  63  49  47  46  44

4.2.4 實際上，作者並沒有一路抄下來，而是用這一句話得到答案：

  1. 由小到大排序。
sort(Data)
##  [1]  44  46  47  49  63  64  66  68  68  72  72  75  76  81  84  88 106
  1. 由大到小排序。
sort(Data, decreasing = TRUE)
##  [1] 106  88  84  81  76  75  72  72  68  68  66  64  63  49  47  46  44

4.3 四分位數

為什麼選讀這個主題，基本上，至少有以下幾個理由：

  1. 見證莖葉圖如何得到數字由小到大的排序結果？
  2. 見證莖葉圖如何得到一群數字的中位數？
  3. 見證莖葉圖如何得到一群數字的第一個四分位數？
  4. 見證莖葉圖如何得到一群數字的第二個四分位數？
  5. 見證莖葉圖如何得到一群數字的第三個四分位數？

4.3.1 建議優先閱讀：莖葉圖

1900年代，Arthur Bowley倡議莖葉圖這一項技術。

…

讓我們回顧以下這一組摘錄自維基百科數據的莖葉圖：

  1. 呼叫套件aplpack。
library(aplpack)
  1. 直接抓網頁上的數據然後用「c」形成向量然後指定給「<-」給「Data」這個名字就能永久存放在記憶體裡。
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
  1. 讓stem.leaf自行決定怎麼畫莖葉圖但是設定不理會離群值。
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6

4.3.2 哪一個數字位在正中間？

我們再看一次「44, 46, 47, 49, 63, 64, 66, 68, 68, 72, 72, 75, 76, 81, 84, 88, 106」的莖葉圖：

stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6
  1. 什麼是正中間？

所謂的「正中間」的意思是，「有一半的數字小於等於『它』，而且有一半的數字大於等於『它』」。

  1. 再一次觀察莖葉圖最左邊的數字

注意看，莖葉圖裡一定有一個數字被「小括號」包起來，表示上下累加葉子個數到那一株莖會超過半數，所以，正中間的數字會出現在那一株莖裡。因為現在是「17」個數字，是奇數個，所以莖葉圖上第「9」個數字會在「正中間」。找到位置後，計算這些位置上數字的平均數就是中位數的答案。

  1. 讓我們一起數！
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6

答案是「68」。我們稱這一個數字，叫做「中位數」。

4.3.3 如果不畫莖葉圖，如何找到中位數？

首先，先排序(請記得，莖葉圖會給我們排序的結果。繪製莖葉圖本身就是一種排序的演算法。)

sort(Data)
##  [1]  44  46  47  49  63  64  66  68  68  72  72  75  76  81  84  88 106

接著，計算正中間的位置。如果有「奇數個」數字，那中位數的位置是「個數加一除以二」；如果有「偶數個」數字，那中位數的位置是「個數除以二與個數除以二再加一」。

if(length(Data) %% 2 == 1){
  print((length(Data)+1)/2)
} else {
 print(c(length(Data)/2, length(Data)/2+1))
}
## [1] 9

所以，中位數等於

mean(sort(Data)[(length(Data)+1)/2])
## [1] 68

用R找中位數：

quantile(Data)[3]
## 50% 
##  68

4.3.4 找「最小值」跟「最大值」

如果我們有莖葉圖，

stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6

那麼看著圖，最上方的那一株莖的最左邊葉子所代表的數字是「最小值」；而最下方的那一株莖的最右邊葉子所代表的數字是「最大值」。所以，答案是

  1. 最小值等於「44」。
  2. 最大值等於「106」。

4.3.4.1 用R靠「sort」找答案

最小值是

sort(Data)[1]
## [1] 44

最大值是

sort(Data)[length(Data)]
## [1] 106

4.3.4.2 用R靠「quantile」找答案

最小值是

quantile(Data)[1]
## 0% 
## 44

最大值是

quantile(Data)[5]
## 100% 
##  106

4.3.5 找第一個四分位數之「Q1」跟第三個四分位數「Q3」

sort(Data)
##  [1]  44  46  47  49  63  64  66  68  68  72  72  75  76  81  84  88 106

「Q1」是排序後，下半段的「中位數」；而「Q3」是排序後，上半段的「中位數」。R官方的函式(function)，quantile可以一次給我們以下這五個數字：

quantile(Data)
##   0%  25%  50%  75% 100% 
##   44   63   68   76  106

它們依序是「最小值」、「第一個四分位數」、「中位數」(也是「第二個四分位數」)、「第三個四分位數」、「最大值」。

4.3.5.1 找Q1

4.3.5.1.1 第一種算法：Q1等於
quantile(Data)[2]
## 25% 
##  63
4.3.5.1.2 第二種算法：因為下半段有偶數個數字
mean(sort(Data)[1:8][c(4,5)])
## [1] 56
4.3.5.1.3 第三種算法：因為下半段加上中位數有奇數個數字
mean(sort(Data)[1:9][5])
## [1] 63

4.3.5.2 找Q3

4.3.5.2.1 第一種算法：Q3等於
quantile(Data)[4]
## 75% 
##  76
4.3.5.2.2 第二種算法：因為上半段有偶數個數字
mean(sort(Data)[10:17][c(4,5)])
## [1] 78.5
4.3.5.2.3 第三種算法：因為上半段加上中位數有奇數個數字
mean(sort(Data)[9:17][5])
## [1] 76

4.3.6 關於中位數的理論結果

統計理論學家告訴我們，如果用「中位數」代表整組數字，那「中位數」會最小化下面這一個算式：

\[\sum |數字 - 中位數|\]

這一個總和，後來叫做「誤差和」。

4.4 十分位數

為什麼選讀這個主題，基本上，至少有以下幾個理由：

  1. 發現如何從莖葉圖發現中位數？
  2. 發現除了電算十分位數，如何手算十分位數？
  3. 發現中位數與十分位數的關係？

4.4.1 建議優先閱讀：莖葉圖

1900年代，Arthur Bowley倡議莖葉圖這一項技術。

…

讓我們回顧以下這一組摘錄自維基百科數據的莖葉圖：

  1. 呼叫套件aplpack。
library(aplpack)
  1. 直接抓網頁上的數據然後用「c」形成向量然後指定給「<-」給「Data」這個名字就能永久存放在記憶體裡。
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
  1. 讓stem.leaf自行決定怎麼畫莖葉圖但是設定不理會離群值。
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6

4.4.2 建議優先閱讀：中位數 = 一個位在正中間的數字

為了示範有別於「四分位數」這一本微微書的場景，我們先把「莖葉圖」建議的「HI」離群值「106」刪除，也就是說，從「Data」移除它。

Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88)

4.4.2.1 檢查原始數據是否由小到大依序排列？

4.4.2.1.1 不檢查，直接排序再回存：
Data <- sort(Data)
4.4.2.1.2 檢查是否已經按順序再決定是否需要「排序後再回存」
  1. (第一步) 根據數字的大小關係，前後相減的結果可以協助發現一串數字是否由小到大依序排列？
diff(Data)
##  [1]  2  1  2 14  1  2  2  0  4  0  3  1  5  3  4
  1. (第二步) 檢查相減之後是否大於0？
diff(Data) >= 0
##  [1] TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE
  1. (第三步) 總共幾個大於等於0？
sum(diff(Data) >= 0)
## [1] 15
  1. (第四步) 大於等於0的個數是不是等於15？
sum(diff(Data) >= 0) == (length(Data) - 1)
## [1] TRUE
  1. (第三步) 或是「總共幾個小於0」？
sum(!(diff(Data) >= 0))
## [1] 0
  1. (第四步) 小於0的個數是不是等於0？
sum(!(diff(Data) >= 0)) == 0
## [1] TRUE
sum(diff(Data) < 0) == 0
## [1] TRUE
sum(diff(Data) < 0) != 0
## [1] FALSE
  1. (第五步) 決定需不需要排序？記得，排序是一項大工程，不要隨隨便便要求電腦幫我們排序！
if(sum(diff(Data) < 0) != 0){
  Data <- sort(Data)
}

我們看看新「Data」，「44, 46, 47, 49, 63, 64, 66, 68, 68, 72, 72, 75, 76, 81, 84, 88」的莖葉圖：

stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 16
##    1    4* | 4
##    4    4. | 679
##         5* | 
##         5. | 
##    6    6* | 34
##   (3)   6. | 688
##    7    7* | 22
##    5    7. | 56
##    3    8* | 14
##    1    8. | 8

4.4.2.2 檢查「Data」擁有偶數個還是奇數個數字？

  1. (第一步) 求得「Data」這一個向量的長度，也就是說，「Data」擁有幾個數字。
length(Data)
## [1] 16
  1. (第二步) 長度除以2取餘數？
length(Data) %% 2
## [1] 0
  1. (第三步) 透過得知餘數是否為0決定是偶數還是奇數？
length(Data) %% 2 == 0
## [1] TRUE

看到「TRUE」就是偶數，看到「FALSE」就是奇數。

4.4.2.3 決定中位數所在的位置

決定規則：

  1. 如果有奇數個數字，位置就是中間那一個位置。
  2. 如果有偶數個數字，位置就是中間那兩個位置。
if(length(Data) %% 2 == 1){
  print((length(Data)+1)/2)
} else {
 print(c(length(Data)/2, length(Data)/2+1))
}
## [1] 8 9

4.4.2.4 留下位置資訊

if(length(Data) %% 2 == 1){
  Q2pos <- (length(Data)+1)/2
} else {
  Q2pos <- c(length(Data)/2, length(Data)/2+1)
}
Q2pos
## [1] 8 9

4.4.2.5 計算中位數：所以答案是

mean(Data[Q2pos])
## [1] 68

我們稱這一個數字，叫做「中位數」。

4.4.3 從位置下手找尋十分位數

4.4.3.1 電動：請「quantile」幫忙。先定義「十分位」再丟給「quantile」找答案。

seq(0, 1, 0.1)
##  [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
quantile(Data, probs = seq(0, 1, 0.1))
##   0%  10%  20%  30%  40%  50%  60%  70%  80%  90% 100% 
## 44.0 46.5 49.0 63.5 66.0 68.0 72.0 73.5 76.0 82.5 88.0
4.4.3.1.1 解讀「quantile」的輸出
  1. 第一個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[2]
##  10% 
## 46.5
  1. 第二個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[3]
## 20% 
##  49
  1. 第三個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[4]
##  30% 
## 63.5
  1. 第四個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[5]
## 40% 
##  66
  1. 第五個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[6]
## 50% 
##  68
  1. 第六個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[7]
## 60% 
##  72
  1. 第七個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[8]
##  70% 
## 73.5
  1. 第八個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[9]
## 80% 
##  76
  1. 第九個十分位數
quantile(Data, probs = seq(0, 1, 0.1))[10]
##  90% 
## 82.5

4.4.3.2 一樣從位置下手「手動」找十分位數。可能嗎？

4.4.3.2.1 定義「十分位」
seq(0, 1, 0.1)
##  [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
4.4.3.2.2 計算位置
seq(0, 1, 0.1) * length(Data)
##  [1]  0.0  1.6  3.2  4.8  6.4  8.0  9.6 11.2 12.8 14.4 16.0
4.4.3.2.3 示範計算第一個十分位數「(Data[2] - Data[1]) * 0.6 + Data[1]」
pos <- seq(0, 1, 0.1) * length(Data)
pos[2]
## [1] 1.6
pos[2] %/% 1 + 1
## [1] 2
pos[2] %/% 1
## [1] 1
pos[2] %% 1
## [1] 0.6
(Data[2] - Data[1]) * 0.6 + Data[1]
## [1] 45.2

得到「第一個十分位數」，45.2。

4.4.3.2.4 接下來，是一次算完全部十分位數的『自力救濟程式碼』：
decile <- numeric(0)
pos <- seq(0, 1, 0.1) * length(Data)
for (i in 1:11) {
  if(pos[i] == 0){
    print(pos[i])
    decile <- c(decile, Data[1])
  } else if(pos[i] == length(Data)) {
    print(pos[i])
    decile <- c(decile, Data[length(Data)])
  } else {
    up <- pos[i] %/% 1 + 1
    low <- pos[i] %/% 1
    plus <- pos[i] %% 1
    print(c(pos[i], low, up, plus))
    decile <- c(decile, (Data[up] - Data[low]) * plus + Data[low])
  }
}
## [1] 0
## [1] 1.6 1.0 2.0 0.6
## [1] 3.2 3.0 4.0 0.2
## [1] 4.8 4.0 5.0 0.8
## [1] 6.4 6.0 7.0 0.4
## [1] 8 8 9 0
## [1]  9.6  9.0 10.0  0.6
## [1] 11.2 11.0 12.0  0.2
## [1] 12.8 12.0 13.0  0.8
## [1] 14.4 14.0 15.0  0.4
## [1] 16
decile
##  [1] 44.0 45.2 47.4 60.2 64.8 68.0 70.4 72.6 75.8 82.2 88.0

對照

quantile(Data, probs = seq(0, 1, 0.1))
##   0%  10%  20%  30%  40%  50%  60%  70%  80%  90% 100% 
## 44.0 46.5 49.0 63.5 66.0 68.0 72.0 73.5 76.0 82.5 88.0
4.4.3.2.5 不完全一樣。看來只有一招了，讓我們變身為「駭客」試著找專家、找源頭、找原始碼…

4.4.3.3 求助「?quantile」的原始碼

4.4.3.3.1 第一次，直接向R求助
quantile
## function (x, ...) 
## UseMethod("quantile")
## <bytecode: 0x555a4f3f13a0>
## <environment: namespace:stats>

看不懂！

4.4.3.3.2 第二次，上網搜尋

我們用這一句話

how to see the source code of quantile in r

餵給Google搜尋引擎，找到

quantile.R

仔細看過之後，發現點選右邊一個叫做「Raw」的按鈕，可以到

quantile.R的個人網頁

於是乎，我們的第二個問題來了，如何「抓到它」？如果可以抓到它，那我們的工作區就會有一支跟「quantile」同名同姓的函式「quantile」了。為此，我繼續餵這一句話

how to read the source code file online from web in r

給Google搜尋引擎，找到

Sourcing R script over HTTPS

往下滑到綠色勾勾處，發現了「source」這一個字可以幫忙。所以，先把「quantile.R」的網址放在「URL」裡，然後呼叫「source」，

URL<-"https://raw.githubusercontent.com/SurajGupta/r-source/master/src/library/stats/R/quantile.R"
source(URL)

成功之後，呼叫「quantile」。發現跟第一次直接呼叫R的「quantile」，得到類似的結果：

quantile
## function (x, ...) 
## UseMethod("quantile")

再檢視過一次源頭，發現實際上應該呼叫「quantile.default」：

quantile.default
## function (x, probs = seq(0, 1, 0.25), na.rm = FALSE, names = TRUE, 
##     type = 7, ...) 
## {
##     if (is.factor(x)) {
##         if (!is.ordered(x) || !type %in% c(1L, 3L)) 
##             stop("factors are not allowed")
##         lx <- levels(x)
##     }
##     else lx <- NULL
##     if (na.rm) 
##         x <- x[!is.na(x)]
##     else if (anyNA(x)) 
##         stop("missing values and NaN's not allowed if 'na.rm' is FALSE")
##     eps <- 100 * .Machine$double.eps
##     if (any((p.ok <- !is.na(probs)) & (probs < -eps | probs > 
##         1 + eps))) 
##         stop("'probs' outside [0,1]")
##     n <- length(x)
##     if (na.p <- any(!p.ok)) {
##         o.pr <- probs
##         probs <- probs[p.ok]
##         probs <- pmax(0, pmin(1, probs))
##     }
##     np <- length(probs)
##     if (n > 0 && np > 0) {
##         if (type == 7) {
##             index <- 1 + (n - 1) * probs
##             lo <- floor(index)
##             hi <- ceiling(index)
##             x <- sort(x, partial = unique(c(lo, hi)))
##             qs <- x[lo]
##             i <- which(index > lo)
##             h <- (index - lo)[i]
##             qs[i] <- (1 - h) * qs[i] + h * x[hi[i]]
##         }
##         else {
##             if (type <= 3) {
##                 nppm <- if (type == 3) 
##                   n * probs - 0.5
##                 else n * probs
##                 j <- floor(nppm)
##                 h <- switch(type, (nppm > j), ((nppm > j) + 1)/2, 
##                   (nppm != j) | ((j%%2L) == 1L))
##             }
##             else {
##                 switch(type - 3, {
##                   a <- 0
##                   b <- 1
##                 }, a <- b <- 0.5, a <- b <- 0, a <- b <- 1, a <- b <- 1/3, 
##                   a <- b <- 3/8)
##                 fuzz <- 4 * .Machine$double.eps
##                 nppm <- a + probs * (n + 1 - a - b)
##                 j <- floor(nppm + fuzz)
##                 h <- nppm - j
##                 if (any(sml <- abs(h) < fuzz)) 
##                   h[sml] <- 0
##             }
##             x <- sort(x, partial = unique(c(1, j[j > 0L & j <= 
##                 n], (j + 1)[j > 0L & j < n], n)))
##             x <- c(x[1L], x[1L], x, x[n], x[n])
##             qs <- x[j + 2L]
##             qs[h == 1] <- x[j + 3L][h == 1]
##             other <- (0 < h) & (h < 1)
##             if (any(other)) 
##                 qs[other] <- ((1 - h) * x[j + 2L] + h * x[j + 
##                   3L])[other]
##         }
##     }
##     else {
##         qs <- rep(NA_real_, np)
##     }
##     if (is.character(lx)) 
##         qs <- factor(qs, levels = seq_along(lx), labels = lx, 
##             ordered = TRUE)
##     if (names && np > 0L) {
##         names(qs) <- format_perc(probs)
##     }
##     if (na.p) {
##         o.pr[p.ok] <- qs
##         names(o.pr) <- rep("", length(o.pr))
##         names(o.pr)[p.ok] <- names(qs)
##         o.pr
##     }
##     else qs
## }

4.4.4 但是看不懂「quantile.R」的開放原始碼！

雖然作者功力不夠，無法百分百看懂「quantile.R」，但是，作者努力找「滿足一開始與『自力救濟程式碼』同樣思緒的段落」。作者個人認為可能是

  1. n <- length(x)
  2. index <- 1 + (n - 1) * probs

於是乎，作者把『自力救濟程式碼』改寫為

decile <- numeric(0)
n <- length(Data)
pos <- 1 + (n - 1) * seq(0, 1, 0.1)
for (i in 1:11) {
  if(pos[i] == 0){
    print(pos[i])
    decile <- c(decile, Data[1])
  } else if(pos[i] == length(Data)) {
    print(pos[i])
    decile <- c(decile, Data[length(Data)])
  } else {
    up <- pos[i] %/% 1 + 1
    low <- pos[i] %/% 1
    plus <- pos[i] %% 1
    print(c(pos[i], low, up, plus))
    decile <- c(decile, (Data[up] - Data[low]) * plus + Data[low])
  }
}
## [1] 1 1 2 0
## [1] 2.5 2.0 3.0 0.5
## [1] 4 4 5 0
## [1] 5.5 5.0 6.0 0.5
## [1] 7 7 8 0
## [1] 8.5 8.0 9.0 0.5
## [1] 1.000000e+01 1.000000e+01 1.100000e+01 1.776357e-15
## [1] 11.5 11.0 12.0  0.5
## [1] 13 13 14  0
## [1] 14.5 14.0 15.0  0.5
## [1] 16
decile
##  [1] 44.0 46.5 49.0 63.5 66.0 68.0 72.0 73.5 76.0 82.5 88.0

對照

quantile(Data, probs = seq(0, 1, 0.1))
##   0%  10%  20%  30%  40%  50%  60%  70%  80%  90% 100% 
## 44.0 46.5 49.0 63.5 66.0 68.0 72.0 73.5 76.0 82.5 88.0

竟然一模一樣。大成功！我們確實可以透過找位置算出十分位數。

4.4.5 十分位數與中位數的關係

4.4.5.1 中位數Q2是第五個十分位數

quantile(Data, probs = seq(0, 1, 0.1))[6]
## 50% 
##  68

4.5 百分位數

為什麼選讀這個主題，基本上，至少有以下幾個理由：

  1. 發現如何從莖葉圖發現中位數？
  2. 發現除了電算百分位數，如何手算百分位數？
  3. 發現中位數與百分位數的關係？
  4. 發現十分位數與百分位數的關係？

4.5.1 建議優先閱讀：莖葉圖

1900年代，Arthur Bowley倡議莖葉圖這一項技術。

…

讓我們回顧以下這一組數據(取自維基百科並刪除最大值)的莖葉圖：

library(aplpack)
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88)
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 16
##    1    4* | 4
##    4    4. | 679
##         5* | 
##         5. | 
##    6    6* | 34
##   (3)   6. | 688
##    7    7* | 22
##    5    7. | 56
##    3    8* | 14
##    1    8. | 8

4.5.2 建議優先閱讀：中位數 = 一個位在正中間的數字

我們不再觀察莖葉圖，直接請「quantile」協尋「44, 46, 47, 49, 63, 64, 66, 68, 68, 72, 72, 75, 76, 81, 84, 88」的四分位數：

quantile(Data)
##    0%   25%   50%   75%  100% 
## 44.00 59.50 68.00 75.25 88.00
  1. 第一個四分位數，Q1。
quantile(Data)[2]
##  25% 
## 59.5
  1. 第二個四分位數，也就是中位數，Q2。
quantile(Data)[3]
## 50% 
##  68
  1. 第三個四分位數，Q3。
quantile(Data)[4]
##   75% 
## 75.25

4.5.3 百分位數

4.5.3.1 (第一步) 定義「百分位」

seq(0, 1, 0.01)
##   [1] 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.10 0.11 0.12 0.13 0.14
##  [16] 0.15 0.16 0.17 0.18 0.19 0.20 0.21 0.22 0.23 0.24 0.25 0.26 0.27 0.28 0.29
##  [31] 0.30 0.31 0.32 0.33 0.34 0.35 0.36 0.37 0.38 0.39 0.40 0.41 0.42 0.43 0.44
##  [46] 0.45 0.46 0.47 0.48 0.49 0.50 0.51 0.52 0.53 0.54 0.55 0.56 0.57 0.58 0.59
##  [61] 0.60 0.61 0.62 0.63 0.64 0.65 0.66 0.67 0.68 0.69 0.70 0.71 0.72 0.73 0.74
##  [76] 0.75 0.76 0.77 0.78 0.79 0.80 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 0.89
##  [91] 0.90 0.91 0.92 0.93 0.94 0.95 0.96 0.97 0.98 0.99 1.00

4.5.3.2 (第二步) 跟向量「Data」一起餵給「quantile」

quantile(Data, probs = seq(0, 1, 0.01))
##    0%    1%    2%    3%    4%    5%    6%    7%    8%    9%   10%   11%   12% 
## 44.00 44.30 44.60 44.90 45.20 45.50 45.80 46.05 46.20 46.35 46.50 46.65 46.80 
##   13%   14%   15%   16%   17%   18%   19%   20%   21%   22%   23%   24%   25% 
## 46.95 47.20 47.50 47.80 48.10 48.40 48.70 49.00 51.10 53.20 55.30 57.40 59.50 
##   26%   27%   28%   29%   30%   31%   32%   33%   34%   35%   36%   37%   38% 
## 61.60 63.05 63.20 63.35 63.50 63.65 63.80 63.95 64.20 64.50 64.80 65.10 65.40 
##   39%   40%   41%   42%   43%   44%   45%   46%   47%   48%   49%   50%   51% 
## 65.70 66.00 66.30 66.60 66.90 67.20 67.50 67.80 68.00 68.00 68.00 68.00 68.00 
##   52%   53%   54%   55%   56%   57%   58%   59%   60%   61%   62%   63%   64% 
## 68.00 68.00 68.40 69.00 69.60 70.20 70.80 71.40 72.00 72.00 72.00 72.00 72.00 
##   65%   66%   67%   68%   69%   70%   71%   72%   73%   74%   75%   76%   77% 
## 72.00 72.00 72.15 72.60 73.05 73.50 73.95 74.40 74.85 75.10 75.25 75.40 75.55 
##   78%   79%   80%   81%   82%   83%   84%   85%   86%   87%   88%   89%   90% 
## 75.70 75.85 76.00 76.75 77.50 78.25 79.00 79.75 80.50 81.15 81.60 82.05 82.50 
##   91%   92%   93%   94%   95%   96%   97%   98%   99%  100% 
## 82.95 83.40 83.85 84.40 85.00 85.60 86.20 86.80 87.40 88.00

4.5.3.3 (第三步) 取得任意一個百分位數

4.5.3.3.1 觀察「quantile」輸出結果。
quantile(Data, probs = seq(0, 1, 0.01))
##    0%    1%    2%    3%    4%    5%    6%    7%    8%    9%   10%   11%   12% 
## 44.00 44.30 44.60 44.90 45.20 45.50 45.80 46.05 46.20 46.35 46.50 46.65 46.80 
##   13%   14%   15%   16%   17%   18%   19%   20%   21%   22%   23%   24%   25% 
## 46.95 47.20 47.50 47.80 48.10 48.40 48.70 49.00 51.10 53.20 55.30 57.40 59.50 
##   26%   27%   28%   29%   30%   31%   32%   33%   34%   35%   36%   37%   38% 
## 61.60 63.05 63.20 63.35 63.50 63.65 63.80 63.95 64.20 64.50 64.80 65.10 65.40 
##   39%   40%   41%   42%   43%   44%   45%   46%   47%   48%   49%   50%   51% 
## 65.70 66.00 66.30 66.60 66.90 67.20 67.50 67.80 68.00 68.00 68.00 68.00 68.00 
##   52%   53%   54%   55%   56%   57%   58%   59%   60%   61%   62%   63%   64% 
## 68.00 68.00 68.40 69.00 69.60 70.20 70.80 71.40 72.00 72.00 72.00 72.00 72.00 
##   65%   66%   67%   68%   69%   70%   71%   72%   73%   74%   75%   76%   77% 
## 72.00 72.00 72.15 72.60 73.05 73.50 73.95 74.40 74.85 75.10 75.25 75.40 75.55 
##   78%   79%   80%   81%   82%   83%   84%   85%   86%   87%   88%   89%   90% 
## 75.70 75.85 76.00 76.75 77.50 78.25 79.00 79.75 80.50 81.15 81.60 82.05 82.50 
##   91%   92%   93%   94%   95%   96%   97%   98%   99%  100% 
## 82.95 83.40 83.85 84.40 85.00 85.60 86.20 86.80 87.40 88.00
4.5.3.3.2 取得每一個「quantile」輸出結果的名字。
names(quantile(Data, probs = seq(0, 1, 0.01)))
##   [1] "0%"   "1%"   "2%"   "3%"   "4%"   "5%"   "6%"   "7%"   "8%"   "9%"  
##  [11] "10%"  "11%"  "12%"  "13%"  "14%"  "15%"  "16%"  "17%"  "18%"  "19%" 
##  [21] "20%"  "21%"  "22%"  "23%"  "24%"  "25%"  "26%"  "27%"  "28%"  "29%" 
##  [31] "30%"  "31%"  "32%"  "33%"  "34%"  "35%"  "36%"  "37%"  "38%"  "39%" 
##  [41] "40%"  "41%"  "42%"  "43%"  "44%"  "45%"  "46%"  "47%"  "48%"  "49%" 
##  [51] "50%"  "51%"  "52%"  "53%"  "54%"  "55%"  "56%"  "57%"  "58%"  "59%" 
##  [61] "60%"  "61%"  "62%"  "63%"  "64%"  "65%"  "66%"  "67%"  "68%"  "69%" 
##  [71] "70%"  "71%"  "72%"  "73%"  "74%"  "75%"  "76%"  "77%"  "78%"  "79%" 
##  [81] "80%"  "81%"  "82%"  "83%"  "84%"  "85%"  "86%"  "87%"  "88%"  "89%" 
##  [91] "90%"  "91%"  "92%"  "93%"  "94%"  "95%"  "96%"  "97%"  "98%"  "99%" 
## [101] "100%"
4.5.3.3.3 假如我們想知道「中位數」的答案，我必須把「50%」的「50」取出來。
strsplit("50%", "%")
## [[1]]
## [1] "50"
strsplit("50%", "%")[[1]]
## [1] "50"
strsplit("50%", "%")[[1]][1]
## [1] "50"
as.numeric(strsplit("50%", "%")[[1]][1])
## [1] 50
4.5.3.3.4 開始抓中位數。
pos <- "50%"
pos <- as.numeric(strsplit(pos, "%")[[1]][1])
quantile(Data, probs = seq(0, 1, 0.01))[(pos + 1)]
## 50% 
##  68
4.5.3.3.5 開始抓第三十八個百分位數。
pos <- "38%"
pos <- as.numeric(strsplit(pos, "%")[[1]][1])
quantile(Data, probs = seq(0, 1, 0.01))[(pos + 1)]
##  38% 
## 65.4
4.5.3.3.6 開始抓第六十二個百分位數。
pos <- "62%"
pos <- as.numeric(strsplit(pos, "%")[[1]][1])
quantile(Data, probs = seq(0, 1, 0.01))[(pos + 1)]
## 62% 
##  72

4.5.4 從位置下手仿「十分位數」手動找「百分位數」

4.5.4.1 轉印「十分位數」的「自力救濟程式碼」，然後改幾個地方

  1. 「seq(0, 1, 0.1)」變成「seq(0, 1, 0.01)」
  2. 「i in 1:11」變成「i in 1:101」
# 記得要檢查是否需要排序？因為現在數字不多，就直接排序了。
Data <- sort(Data)
decile <- numeric(0)
n <- length(Data)
pos <- 1 + (n - 1) * seq(0, 1, 0.01)
for (i in 1:101) {
  if(pos[i] == 0){
    # print(pos[i])
    decile <- c(decile, Data[1])
  } else if(pos[i] == length(Data)) {
    # print(pos[i])
    decile <- c(decile, Data[length(Data)])
  } else {
    up <- pos[i] %/% 1 + 1
    low <- pos[i] %/% 1
    plus <- pos[i] %% 1
    # print(c(pos[i], low, up, plus))
    decile <- c(decile, (Data[up] - Data[low]) * plus + Data[low])
  }
}
decile
##   [1] 44.00 44.30 44.60 44.90 45.20 45.50 45.80 46.05 46.20 46.35 46.50 46.65
##  [13] 46.80 46.95 47.20 47.50 47.80 48.10 48.40 48.70 49.00 51.10 53.20 55.30
##  [25] 57.40 59.50 61.60 63.05 63.20 63.35 63.50 63.65 63.80 63.95 64.20 64.50
##  [37] 64.80 65.10 65.40 65.70 66.00 66.30 66.60 66.90 67.20 67.50 67.80 68.00
##  [49] 68.00 68.00 68.00 68.00 68.00 68.00 68.40 69.00 69.60 70.20 70.80 71.40
##  [61] 72.00 72.00 72.00 72.00 72.00 72.00 72.00 72.15 72.60 73.05 73.50 73.95
##  [73] 74.40 74.85 75.10 75.25 75.40 75.55 75.70 75.85 76.00 76.75 77.50 78.25
##  [85] 79.00 79.75 80.50 81.15 81.60 82.05 82.50 82.95 83.40 83.85 84.40 85.00
##  [97] 85.60 86.20 86.80 87.40 88.00

對照

quantile(Data, probs = seq(0, 1, 0.01))
##    0%    1%    2%    3%    4%    5%    6%    7%    8%    9%   10%   11%   12% 
## 44.00 44.30 44.60 44.90 45.20 45.50 45.80 46.05 46.20 46.35 46.50 46.65 46.80 
##   13%   14%   15%   16%   17%   18%   19%   20%   21%   22%   23%   24%   25% 
## 46.95 47.20 47.50 47.80 48.10 48.40 48.70 49.00 51.10 53.20 55.30 57.40 59.50 
##   26%   27%   28%   29%   30%   31%   32%   33%   34%   35%   36%   37%   38% 
## 61.60 63.05 63.20 63.35 63.50 63.65 63.80 63.95 64.20 64.50 64.80 65.10 65.40 
##   39%   40%   41%   42%   43%   44%   45%   46%   47%   48%   49%   50%   51% 
## 65.70 66.00 66.30 66.60 66.90 67.20 67.50 67.80 68.00 68.00 68.00 68.00 68.00 
##   52%   53%   54%   55%   56%   57%   58%   59%   60%   61%   62%   63%   64% 
## 68.00 68.00 68.40 69.00 69.60 70.20 70.80 71.40 72.00 72.00 72.00 72.00 72.00 
##   65%   66%   67%   68%   69%   70%   71%   72%   73%   74%   75%   76%   77% 
## 72.00 72.00 72.15 72.60 73.05 73.50 73.95 74.40 74.85 75.10 75.25 75.40 75.55 
##   78%   79%   80%   81%   82%   83%   84%   85%   86%   87%   88%   89%   90% 
## 75.70 75.85 76.00 76.75 77.50 78.25 79.00 79.75 80.50 81.15 81.60 82.05 82.50 
##   91%   92%   93%   94%   95%   96%   97%   98%   99%  100% 
## 82.95 83.40 83.85 84.40 85.00 85.60 86.20 86.80 87.40 88.00

4.5.4.2 太多個了，很難比對！

decile - quantile(Data, probs = seq(0, 1, 0.01))
##            0%            1%            2%            3%            4% 
##  0.000000e+00 -7.105427e-15  0.000000e+00 -7.105427e-15  0.000000e+00 
##            5%            6%            7%            8%            9% 
##  0.000000e+00 -7.105427e-15 -7.105427e-15  0.000000e+00  7.105427e-15 
##           10%           11%           12%           13%           14% 
##  0.000000e+00 -7.105427e-15 -7.105427e-15  7.105427e-15  0.000000e+00 
##           15%           16%           17%           18%           19% 
##  0.000000e+00  0.000000e+00  0.000000e+00 -7.105427e-15  0.000000e+00 
##           20%           21%           22%           23%           24% 
##  0.000000e+00  0.000000e+00 -7.105427e-15  0.000000e+00  0.000000e+00 
##           25%           26%           27%           28%           29% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           30%           31%           32%           33%           34% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           35%           36%           37%           38%           39% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           40%           41%           42%           43%           44% 
##  0.000000e+00 -1.421085e-14  0.000000e+00  0.000000e+00  0.000000e+00 
##           45%           46%           47%           48%           49% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           50%           51%           52%           53%           54% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           55%           56%           57%           58%           59% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           60%           61%           62%           63%           64% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           65%           66%           67%           68%           69% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           70%           71%           72%           73%           74% 
##  0.000000e+00  0.000000e+00 -1.421085e-14  0.000000e+00  0.000000e+00 
##           75%           76%           77%           78%           79% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           80%           81%           82%           83%           84% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           85%           86%           87%           88%           89% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           90%           91%           92%           93%           94% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##           95%           96%           97%           98%           99% 
##  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00  0.000000e+00 
##          100% 
##  0.000000e+00
op <- options(scipen=999) # 關掉科學記號的輸出模式。
sum(abs(decile - quantile(Data, probs = seq(0, 1, 0.01))))
## [1] 0.00000000000009947598

雖然前後相減的誤差沒有全部都是0，但是誤差總和非常小，幾乎就是0。

options(op) # 還原這一段之前的科學記號輸出模式設定。

4.5.5 百分位數與四分位數的關係

4.5.5.1 Q1

quantile(Data, probs = seq(0, 1, 0.01))[26]
##  25% 
## 59.5

4.5.5.2 Q2

quantile(Data, probs = seq(0, 1, 0.01))[51]
## 50% 
##  68

4.5.5.3 Q3

quantile(Data, probs = seq(0, 1, 0.01))[76]
##   75% 
## 75.25

4.5.6 百分位數與十分位數的關係

4.5.6.1 第一個十分位數

quantile(Data, probs = seq(0, 1, 0.01))[11]
##  10% 
## 46.5

4.5.6.2 第二個十分位數

quantile(Data, probs = seq(0, 1, 0.01))[21]
## 20% 
##  49

4.5.6.3 第三個十分位數

quantile(Data, probs = seq(0, 1, 0.01))[31]
##  30% 
## 63.5

4.5.6.4 諸如此類

…

4.6 平均數

為什麼選讀這個主題，基本上，至少有以下幾個理由：

  1. 見證平均數與中位數的異中求同。
  2. 學習計算平均數的第一種手動作法。
  3. 學習計算平均數的第二種手動作法。
  4. 學習計算平均數的電動作法與電動手動作法。
  5. 在同一張圖上結合直方圖、中位數、平均數。

4.6.1 建議優先閱讀：中位數 = 一個位在正中間的數字

library(aplpack)
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6

我們不再試著從觀察莖葉圖取得中位數，直接請「quantile」協尋「44, 46, 47, 49, 63, 64, 66, 68, 68, 72, 72, 75, 76, 81, 84, 88, 106」的第二個四分位數，也就是中位數：

quantile(Data)
##   0%  25%  50%  75% 100% 
##   44   63   68   76  106

我們已經知道第二個四分位數，也就是中位數，Q2。除了「quantile」可以幫我們找到「44, 46, 47, 49, 63, 64, 66, 68, 68, 72, 72, 75, 76, 81, 84, 88, 106」的中位數，也可以請「median」幫忙找。

quantile(Data)[3]
## 50% 
##  68

或者是

median(Data)
## [1] 68

記得，驗證這兩個數字的「class」。

class(quantile(Data)[3])
## [1] "numeric"
class(median(Data))
## [1] "numeric"

4.6.2 關於中位數的理論結果

統計理論學家告訴我們，如果用「中位數」代表整組數字，那「中位數」會最小化下面這一個算式：

\[\sum |數字 - 中位數|\]

這一個總和，後來叫做「誤差和」。

4.6.3 假如把「誤差和」變成「誤差平方和」

「誤差平方和」的定義是

\[\sum (數字 - 某一個數字)^2\]

  1. 理論結果一：中位數不一定最小化「誤差平方和」。

  2. 理論結果二：算術平均數最小化「誤差平方和」。

也就是說，

\[\sum (數字 - 算術平均數)^2 \le \sum (數字 - 某一個數字)^2\]

  1. 理論結果三：算術平均數等於

\[\frac{\sum 數字}{分子的總和加了幾個數字}\]

這也就是我們常在任何層級統計學教科書裡頭看到的「平均數」。

綜合來看：假如我們用「誤差平方和」為取捨標準，那麼「平均數」就是代表整組數字的最佳數字。

4.6.4 示範算術平均數最小化「誤差平方和」

SSE <- function(x, a){
  sum((x - a)^2)
}
SAE <- function(x, a){
  sum(abs(x - a))
}
###
a <- numeric(0)
sse <- numeric(0)
sae <- numeric(0)
###
for (i in 1:length(Data)) {
  a <- c(a, Data[i])
  sse <- c(sse, SSE(Data, Data[i]))
  sae <- c(sae, SAE(Data, Data[i]))
}
###
a <- c(a, mean(Data))
sse <- c(sse, SSE(Data, mean(Data)))
sae <- c(sae, SAE(Data, mean(Data)))
a <- c(a, median(Data))
sse <- c(sse, SSE(Data, median(Data)))
sae <- c(sae, SAE(Data, median(Data)))
###
DF <- data.frame(a = a, sse = sse, sae = sae, stringsAsFactors = FALSE)
row.names(DF) <- c(1:length(Data), "mean", "median")
DF
##                a       sse      sae
## 1       44.00000 14737.000 421.0000
## 2       46.00000 13121.000 391.0000
## 3       47.00000 12364.000 378.0000
## 4       49.00000 10952.000 356.0000
## 5       63.00000  4876.000 230.0000
## 6       64.00000  4697.000 223.0000
## 7       66.00000  4441.000 213.0000
## 8       68.00000  4321.000 207.0000
## 9       68.00000  4321.000 207.0000
## 10      72.00000  4489.000 211.0000
## 11      72.00000  4489.000 211.0000
## 12      75.00000  4972.000 226.0000
## 13      76.00000  5201.000 233.0000
## 14      81.00000  6856.000 278.0000
## 15      84.00000  8257.000 311.0000
## 16      88.00000 10601.000 363.0000
## 17     106.00000 27881.000 633.0000
## mean    68.76471  4311.059 207.7647
## median  68.00000  4321.000 207.0000
DF <- DF[order(DF$sse),]
DF
##                a       sse      sae
## mean    68.76471  4311.059 207.7647
## 8       68.00000  4321.000 207.0000
## 9       68.00000  4321.000 207.0000
## median  68.00000  4321.000 207.0000
## 7       66.00000  4441.000 213.0000
## 10      72.00000  4489.000 211.0000
## 11      72.00000  4489.000 211.0000
## 6       64.00000  4697.000 223.0000
## 5       63.00000  4876.000 230.0000
## 12      75.00000  4972.000 226.0000
## 13      76.00000  5201.000 233.0000
## 14      81.00000  6856.000 278.0000
## 15      84.00000  8257.000 311.0000
## 16      88.00000 10601.000 363.0000
## 4       49.00000 10952.000 356.0000
## 3       47.00000 12364.000 378.0000
## 2       46.00000 13121.000 391.0000
## 1       44.00000 14737.000 421.0000
## 17     106.00000 27881.000 633.0000
DF <- DF[order(DF$a),]
plot(DF$a, 
     DF$sse, 
     type = "b", 
     ylim = c(3000, 30000), 
     main = "SSE Curve")
abline(v = mean(Data), col = "blue")
abline(v = median(Data), col = "red")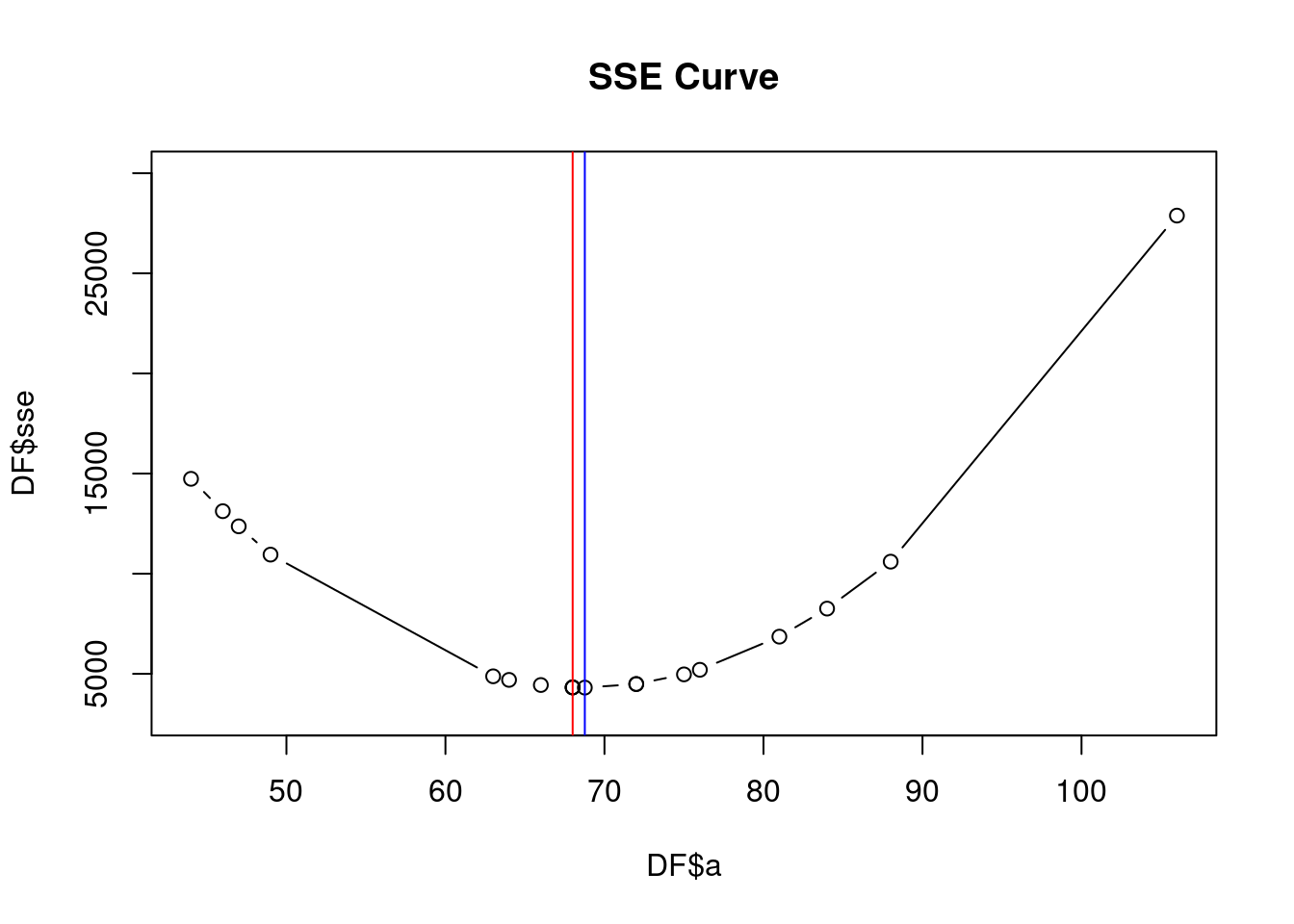

DF <- DF[order(DF$sae),]
DF
##                a       sse      sae
## 8       68.00000  4321.000 207.0000
## 9       68.00000  4321.000 207.0000
## median  68.00000  4321.000 207.0000
## mean    68.76471  4311.059 207.7647
## 10      72.00000  4489.000 211.0000
## 11      72.00000  4489.000 211.0000
## 7       66.00000  4441.000 213.0000
## 6       64.00000  4697.000 223.0000
## 12      75.00000  4972.000 226.0000
## 5       63.00000  4876.000 230.0000
## 13      76.00000  5201.000 233.0000
## 14      81.00000  6856.000 278.0000
## 15      84.00000  8257.000 311.0000
## 4       49.00000 10952.000 356.0000
## 16      88.00000 10601.000 363.0000
## 3       47.00000 12364.000 378.0000
## 2       46.00000 13121.000 391.0000
## 1       44.00000 14737.000 421.0000
## 17     106.00000 27881.000 633.0000
DF <- DF[order(DF$a),]
plot(DF$a, 
     DF$sae, 
     type = "b", 
     ylim = c(150, 700), 
     main = "SAE Curve")
abline(v = mean(Data), col = "blue")
abline(v = median(Data), col = "red")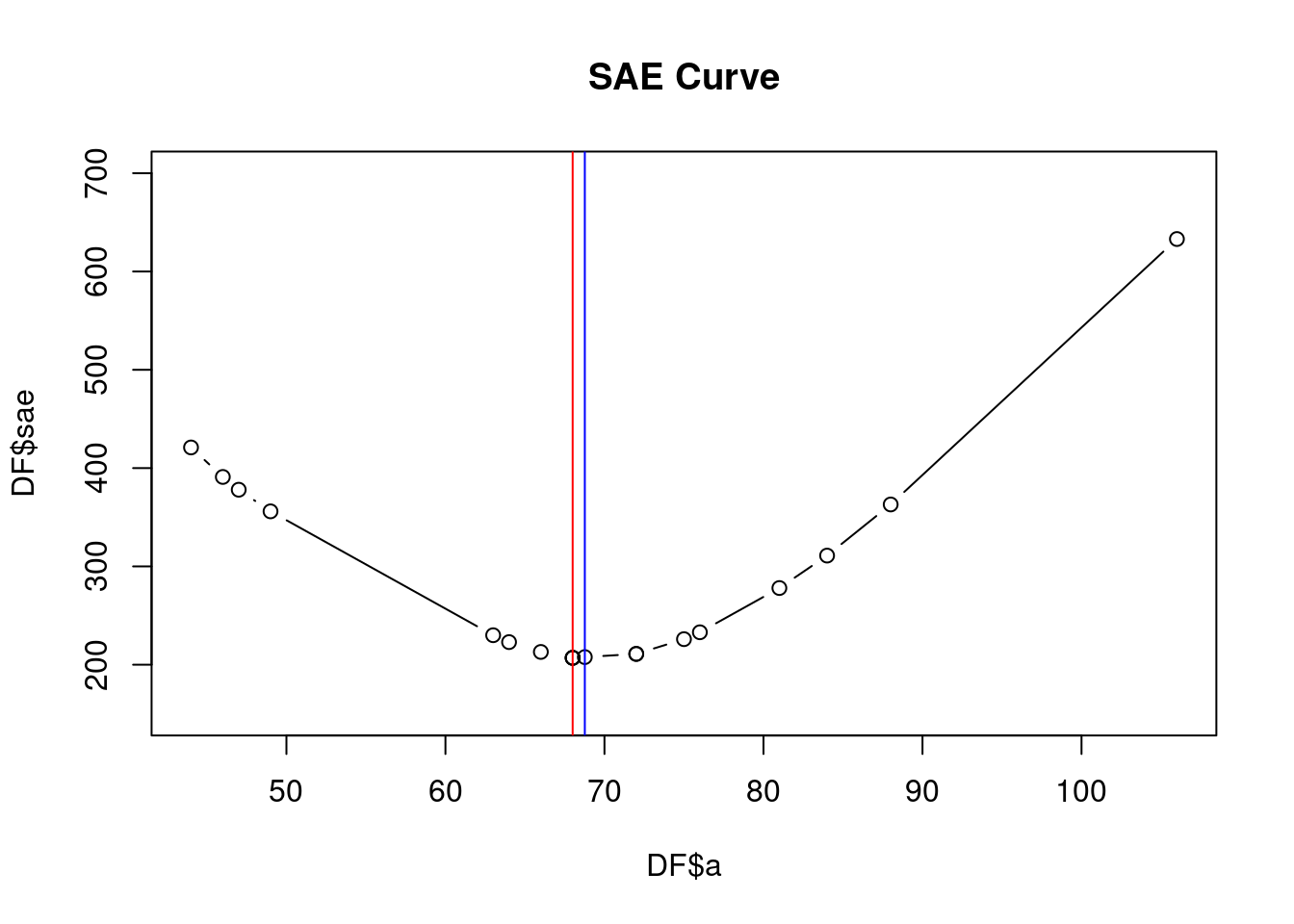

4.6.5 計算平均數

4.6.5.1 手動(電動手動)第一招

sum(Data)/length(Data)
## [1] 68.76471

4.6.5.2 手動(電動手動)第二招(請注意小括號放在哪裡？)

sum(Data/length(Data))
## [1] 68.76471

4.6.5.3 電動

mean(Data)
## [1] 68.76471

4.6.6 結合「直方圖」、「中位數」以及「平均數」

Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
hist(Data, 
 col = "peachpuff", 
 border = "black", 
 prob = TRUE,
 xlim = c(40, 310),
 ylim = c(0,0.038),
 main = "Data的直方圖")
lines(density(Data), # density plot
 lwd = 2, # thickness of line
 col = "chocolate3")
abline(v = mean(Data),
 col = "royalblue",
 lwd = 2)
abline(v = median(Data),
 col = "red",
 lwd = 2)
legend(x = "topright", # location of legend within plot area
 c("Density plot", "Mean", "Median"),
 col = c("chocolate3", "royalblue", "red"),
 lwd = c(2, 2, 2))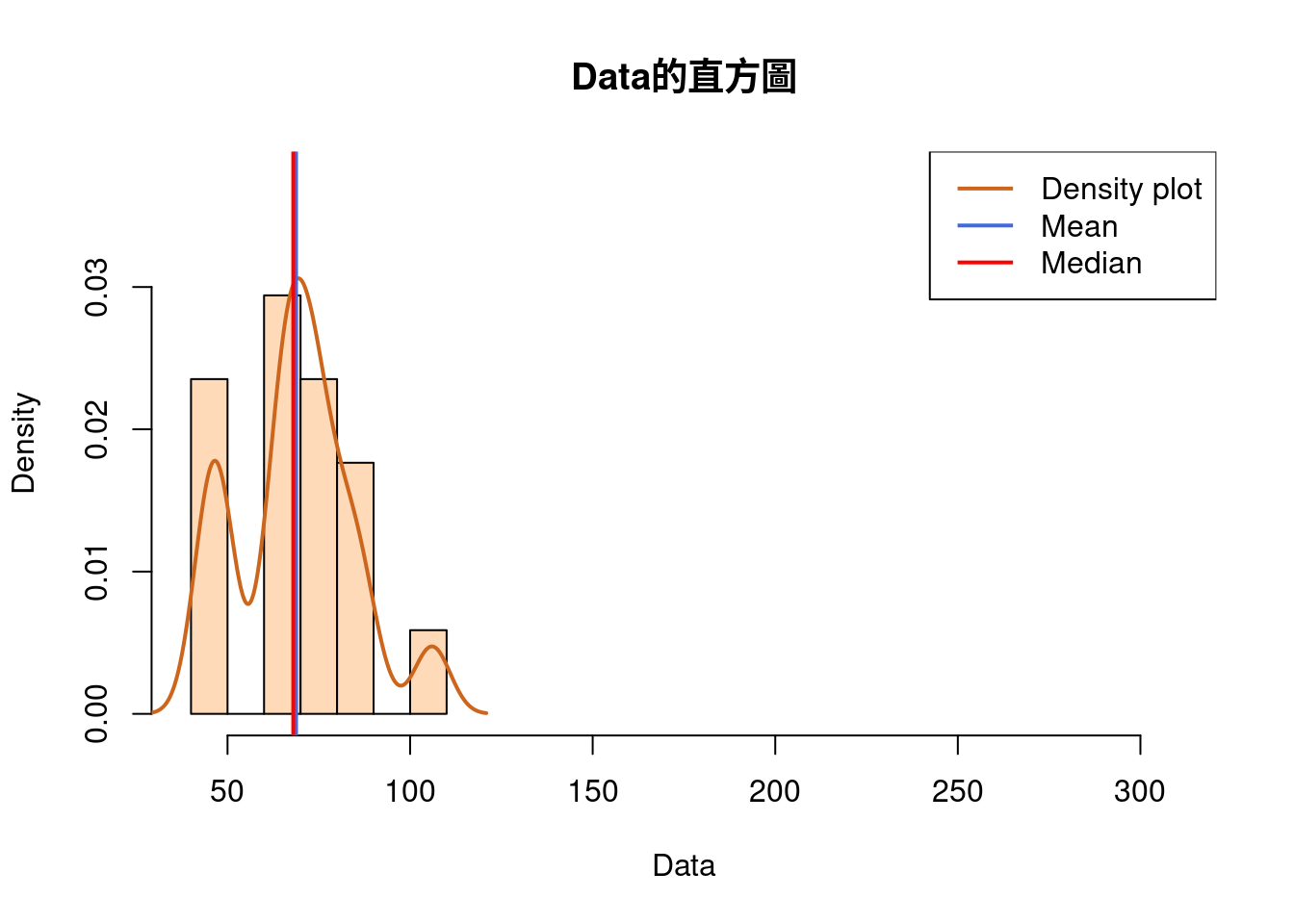

Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,206)
hist(Data, 
 col = "peachpuff", 
 border = "black", 
 prob = TRUE,
 xlim = c(40, 310),
 ylim = c(0,0.038),
 main = "Data的直方圖")
lines(density(Data), # density plot
 lwd = 2, # thickness of line
 col = "chocolate3")
abline(v = mean(Data),
 col = "royalblue",
 lwd = 2)
abline(v = median(Data),
 col = "red",
 lwd = 2)
legend(x = "topright", # location of legend within plot area
 c("Density plot", "Mean", "Median"),
 col = c("chocolate3", "royalblue", "red"),
 lwd = c(2, 2, 2))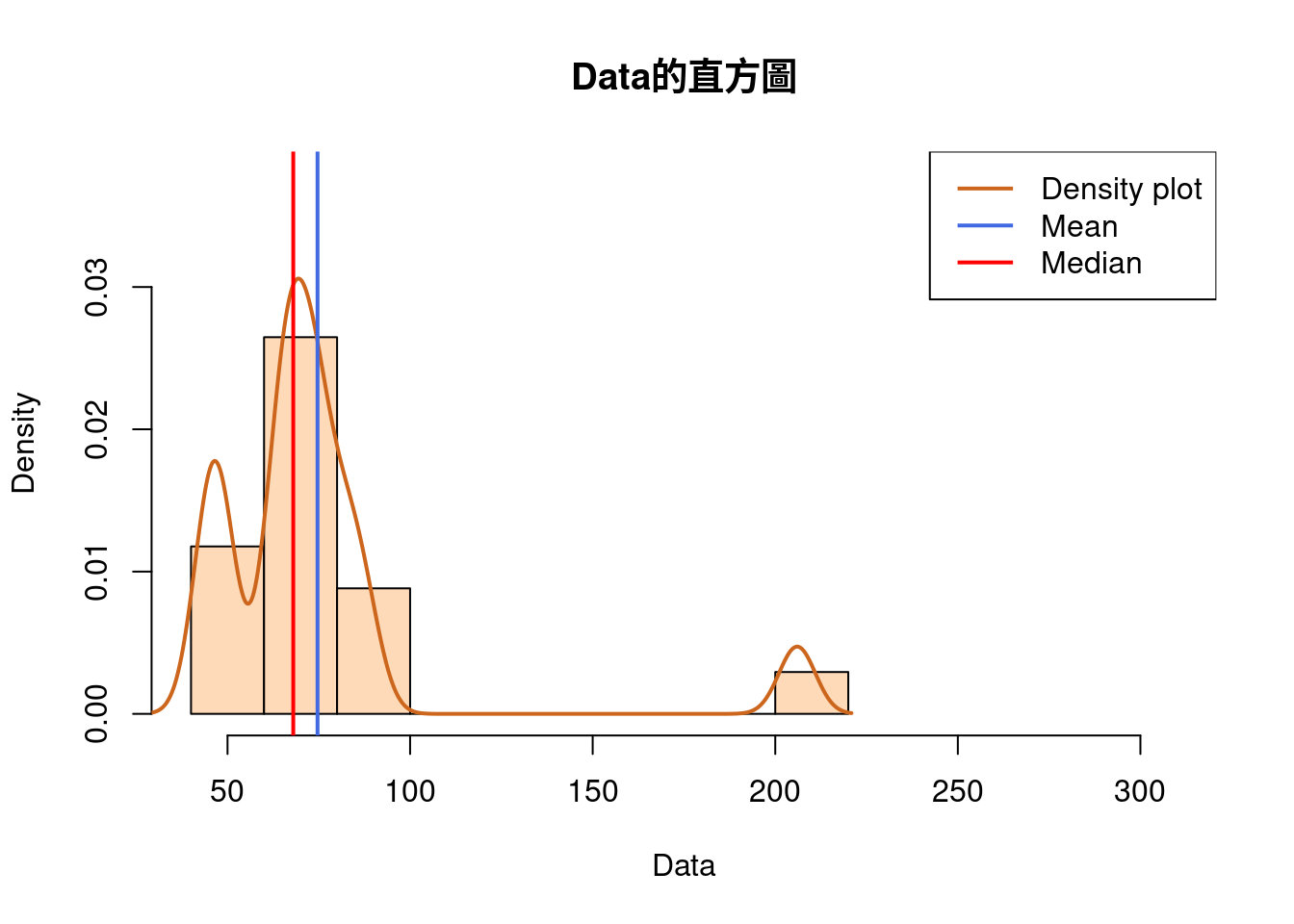

Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,306)
hist(Data, 
 col = "peachpuff", 
 border = "black", 
 prob = TRUE,
 xlim = c(40, 310),
 ylim = c(0,0.038),
 main = "Data的直方圖")
lines(density(Data), # density plot
 lwd = 2, # thickness of line
 col = "chocolate3")
abline(v = mean(Data),
 col = "royalblue",
 lwd = 2)
abline(v = median(Data),
 col = "red",
 lwd = 2)
legend(x = "topright", # location of legend within plot area
 c("Density plot", "Mean", "Median"),
 col = c("chocolate3", "royalblue", "red"),
 lwd = c(2, 2, 2))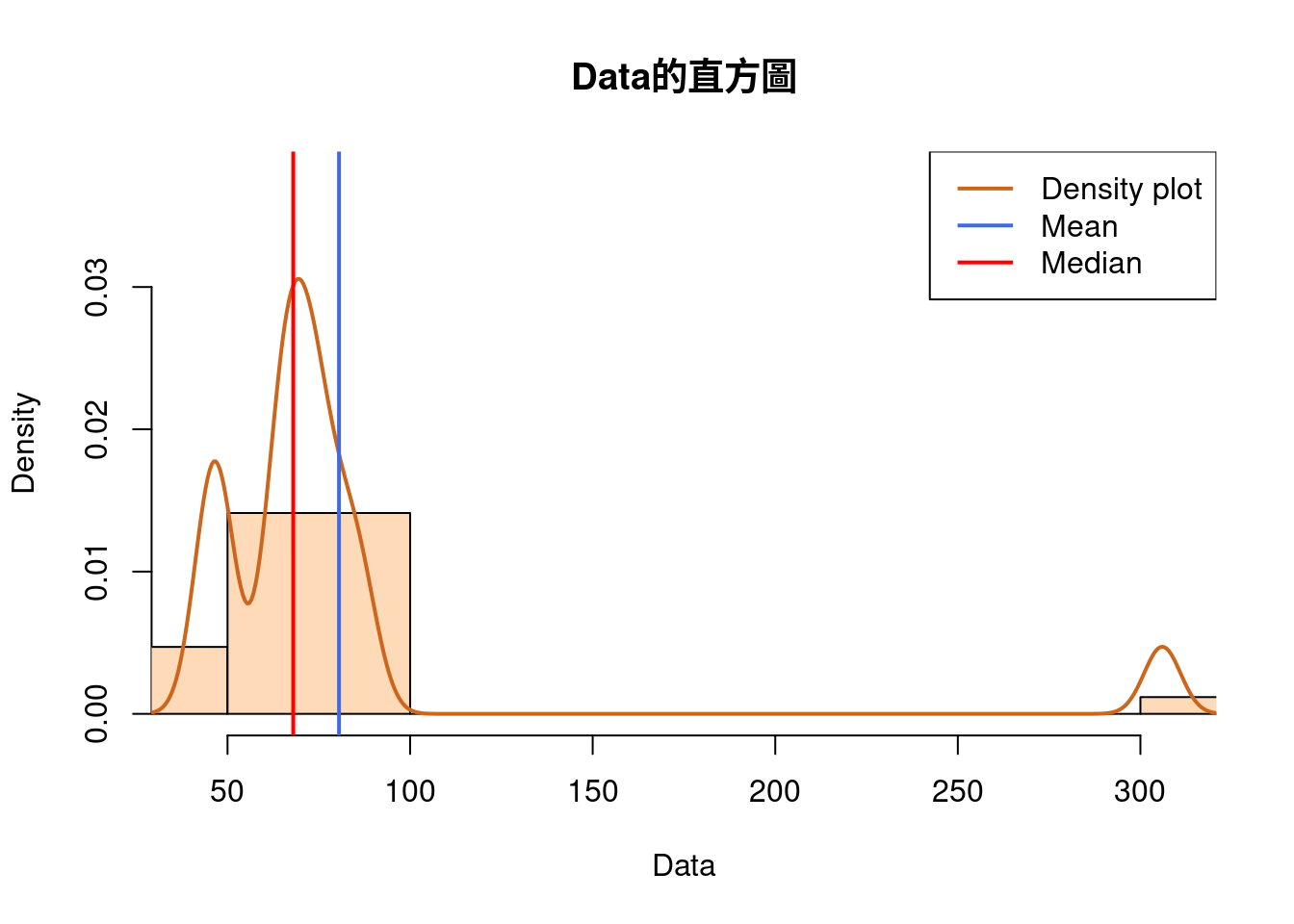

4.6.7 中位數與平均數的特徵

  1. 請看「中位數」與「平均數」的變化。我們發現「中位數」不動、「平均數」越來越大。這是看極端數字對「平均數」的影響。
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
(c(median(Data), mean(Data)))
## [1] 68.00000 68.76471
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,206)
(c(median(Data), mean(Data)))
## [1] 68.00000 74.64706
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,306)
(c(median(Data), mean(Data)))
## [1] 68.00000 80.52941
  1. 請看樣本數對「中位數」與「平均數」的影響。
set.seed(1233)
MEAN <- numeric(0)
MEDIAN <- numeric(0)
N <- integer(0)
x <- rnorm(10)
for (i in 1:1000) {
  N <- c(N, length(x))
  MEAN <- c(MEAN, mean(x))
  MEDIAN <- c(MEDIAN, median(x))
  x <- c(x, rnorm(1))
}
plot(N,MEAN,type = "l",ylim = c(-0.5,0.5),main = "請看平均數逼進0。")
abline(h = 0, col = "red")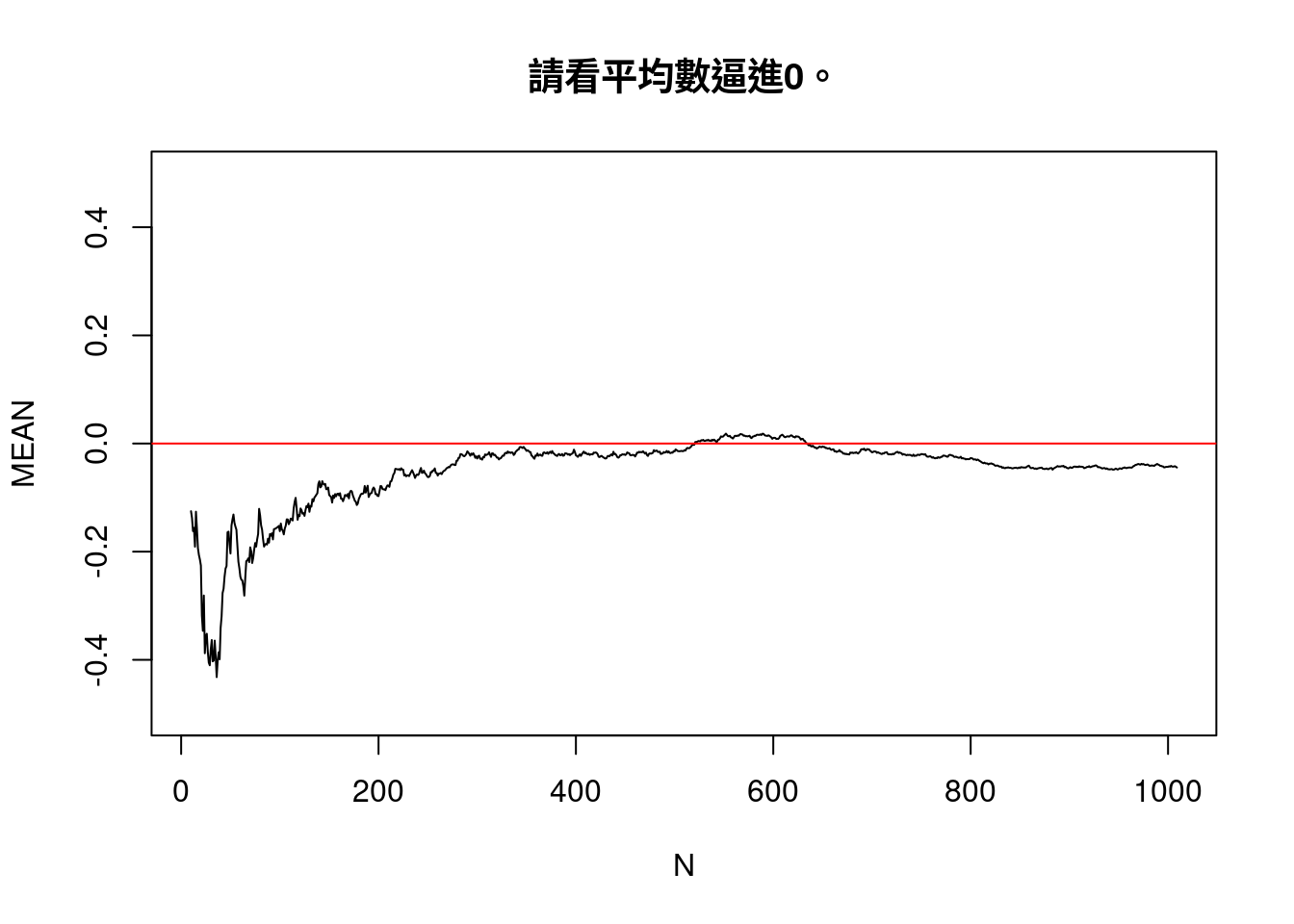

plot(N,MEDIAN,type = "l",ylim = c(-0.5,0.5),main = "請看中位數逼進0。")
abline(h = 0, col = "red")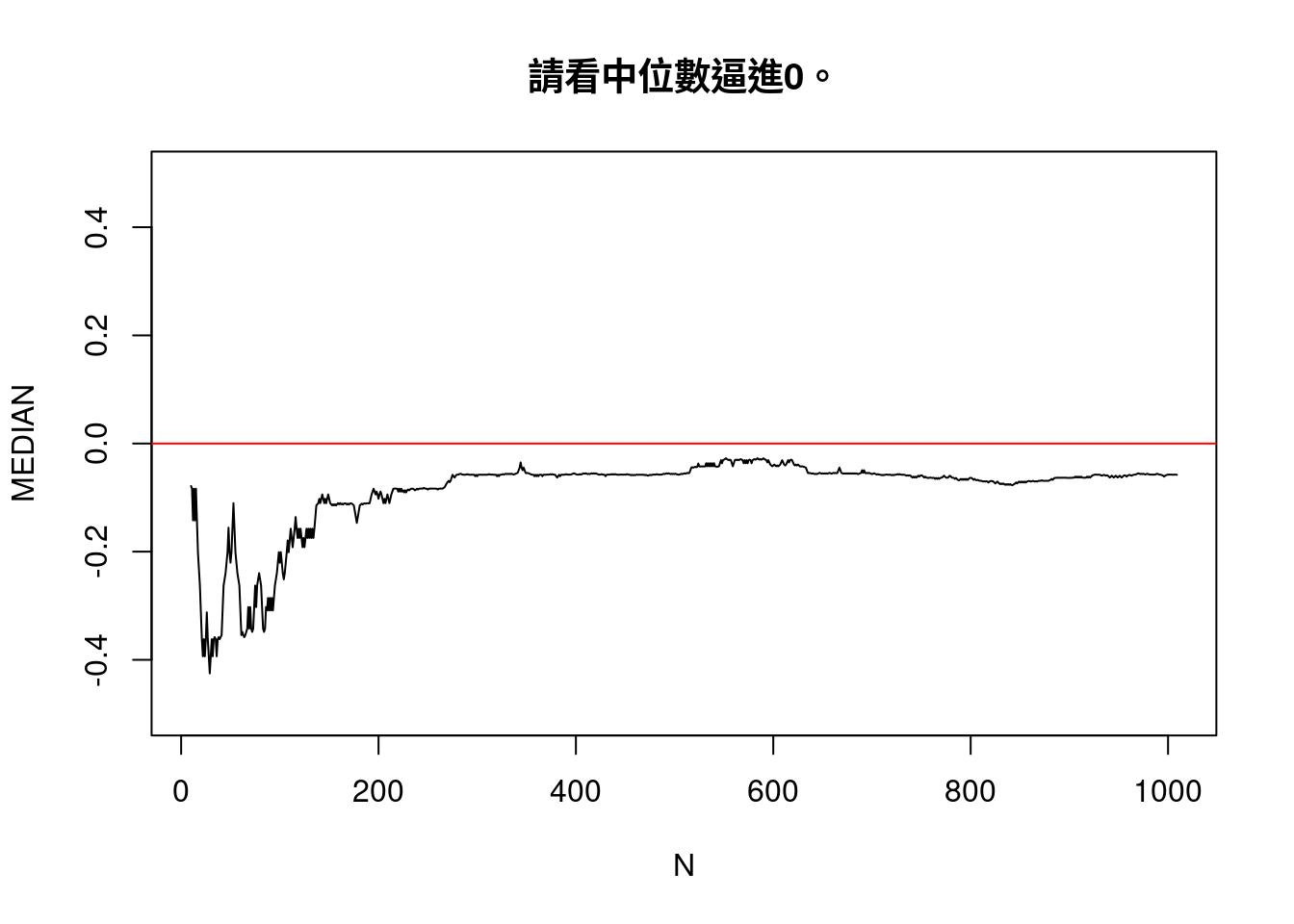

  1. 再看一次樣本數對「中位數」與「平均數」的影響。
set.seed(1288)
MEAN <- numeric(0)
MEDIAN <- numeric(0)
N <- integer(0)
x <- rnorm(10)
for (i in 1:1000) {
  N <- c(N, length(x))
  MEAN <- c(MEAN, mean(x))
  MEDIAN <- c(MEDIAN, median(x))
  x <- c(x, rnorm(1))
}
plot(N,MEAN,type = "l",ylim = c(-0.5,0.5),main = "請看平均數逼進0。")
abline(h = 0, col = "red")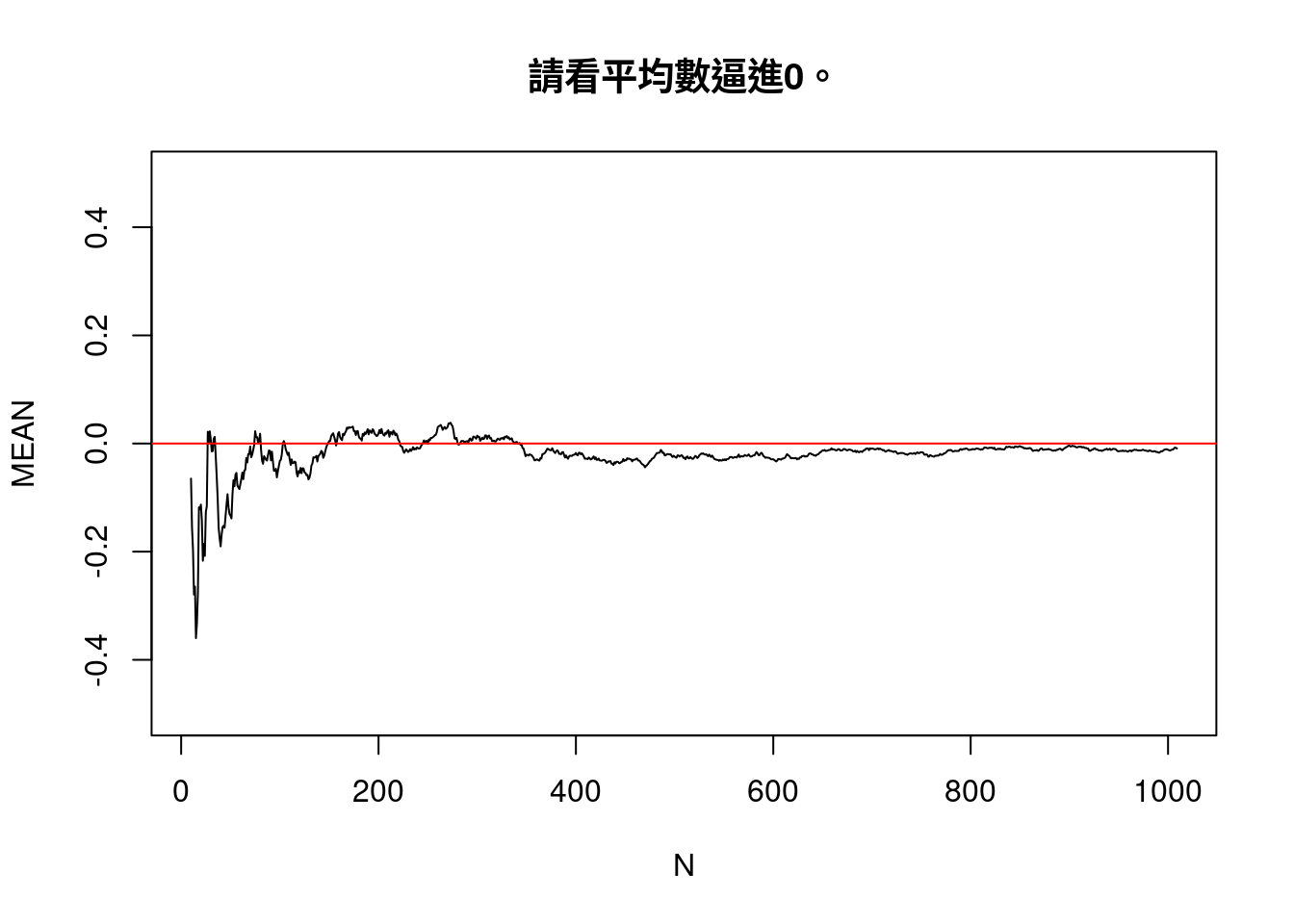

plot(N,MEDIAN,type = "l",ylim = c(-0.5,0.5),main = "請看中位數逼進0。")
abline(h = 0, col = "red")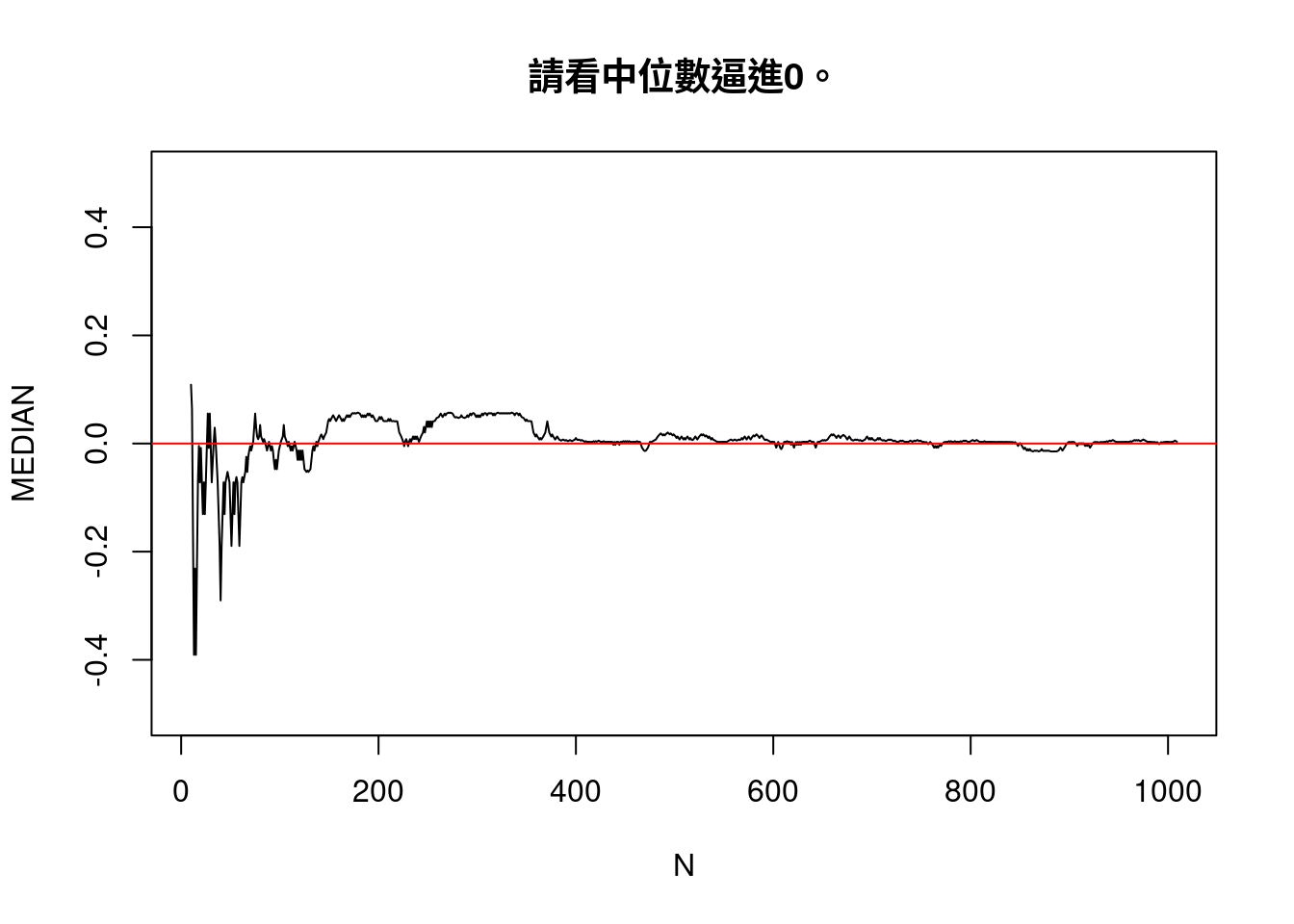

結論：

4.7 標準差

為什麼選讀這個主題，基本上，至少有以下幾個理由：

  1. 學習樣本變異數、樣本標準差的演化過程。
  2. 學習樣本數如何影響樣本變異數跟樣本標準差？
  3. 學習手算、電算手算、電算樣本變異數跟樣本標準差。
  4. 嘗試了解兩種手算樣本變異數跟樣本標準差的計算複雜度。
  5. 學習如何透過程式感受兩種平均誤差平方和的理論結果。
  6. 再一次學習如何透過程式感受中位數與平均數的理論結果。

4.7.1 建議優先閱讀：平均數

library(aplpack)
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6
median(Data)
## [1] 68
mean(Data)
## [1] 68.76471

4.7.2 關於平均數的理論結果

統計理論學家告訴我們，如果用「中位數」代表整組數字，那「中位數」會最小化下面這一個算式：

\[\sum |數字 - 中位數|\]

這一個總和，後來叫做「誤差和」。假如把「誤差和」變成「誤差平方和」，其中「誤差平方和」等於

\[\sum (數字 - 某一個數字)^2\]

  1. 理論結果一：中位數不一定最小化「誤差平方和」。

  2. 理論結果二：算術平均數最小化「誤差平方和」。

也就是說，

\[\sum (數字 - 算術平均數)^2 \le \sum (數字 - 某一個數字)^2\]

  1. 理論結果三：算術平均數等於

\[\frac{\sum 數字}{分子的總和加了幾個數字}\]

這也就是我們常在任何層級統計學教科書裡頭看到的「平均數」。

綜合來看：假如我們用「誤差平方和」為取捨標準，那麼「平均數」就是代表整組數字的最佳數字。

4.7.3 平均誤差平方和，也叫做樣本變異數

4.7.3.1 定義

\[\frac{\sum (數字 - 平均數)^2}{n}\] 其中\(n\)是樣本數，「樣本數」等於「Data」擁有幾個數字。也就是

length(Data)
## [1] 17

4.7.3.2 平均誤差平方和的代號

\[s^2\]

4.7.3.3 平均誤差平方和的理論結果帶出另一個版本的平均誤差平方和

\[\frac{\sum (數字 - 平均數)^2}{n - 1}\] 的理論結果比較好，因為長遠(數字越來越多之後)來看，上述這一個數字會比較快接近「真實的平均誤差平方和」。

4.7.4 觀察樣本數對「平均數」與「平均誤差平方和」的影響

MSE1 <- function(x, a){
  sum((x - a)^2)/length(x)
}
MSE2 <- function(x, a){
  sum((x - a)^2)/(length(x) - 1)
}

set.seed(1233)
MEAN <- numeric(0)
MEDIAN <- numeric(0)
mse1 <- numeric(0)
mse2 <- numeric(0)
N <- integer(0)

x <- rnorm(10)
for (i in 1:1000) {
  N <- c(N, length(x))
  MEAN <- c(MEAN, mean(x))
  MEDIAN <- c(MEDIAN, median(x))
  mse1 <- c(mse1, MSE1(x, mean(x)))
  mse2 <- c(mse2, MSE2(x, mean(x)))
  x <- c(x, rnorm(1))
}
plot(N,
     MEAN,
     type = "l",
     ylim = c(-0.5,0.5),
     main = "請看平均數逼進0。")
abline(h = 0, col = "red")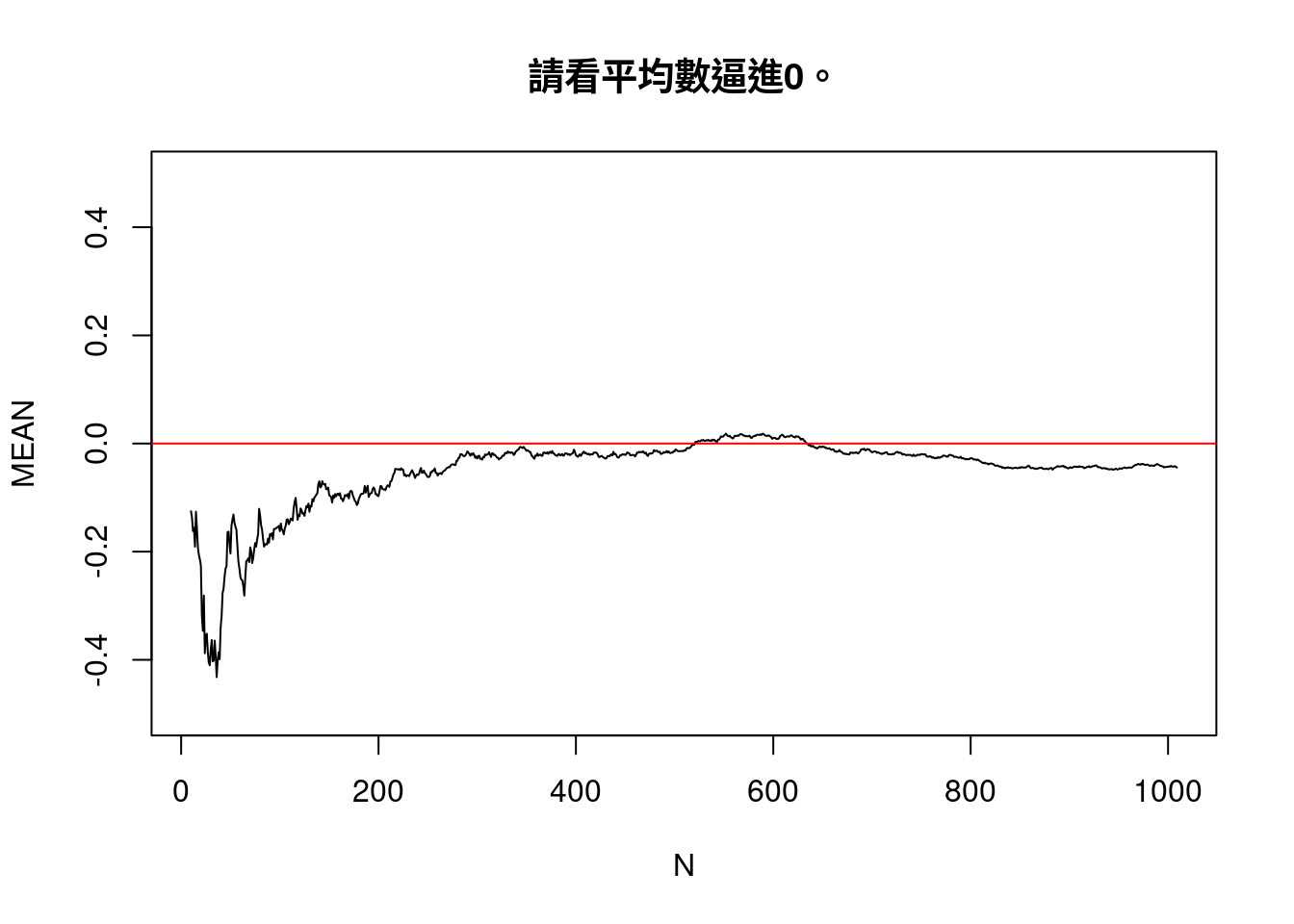

plot(N,
     MEDIAN,
     type = "l",
     ylim = c(-0.5,0.5),
     main = "請看中位數逼進0。")
abline(h = 0, col = "red")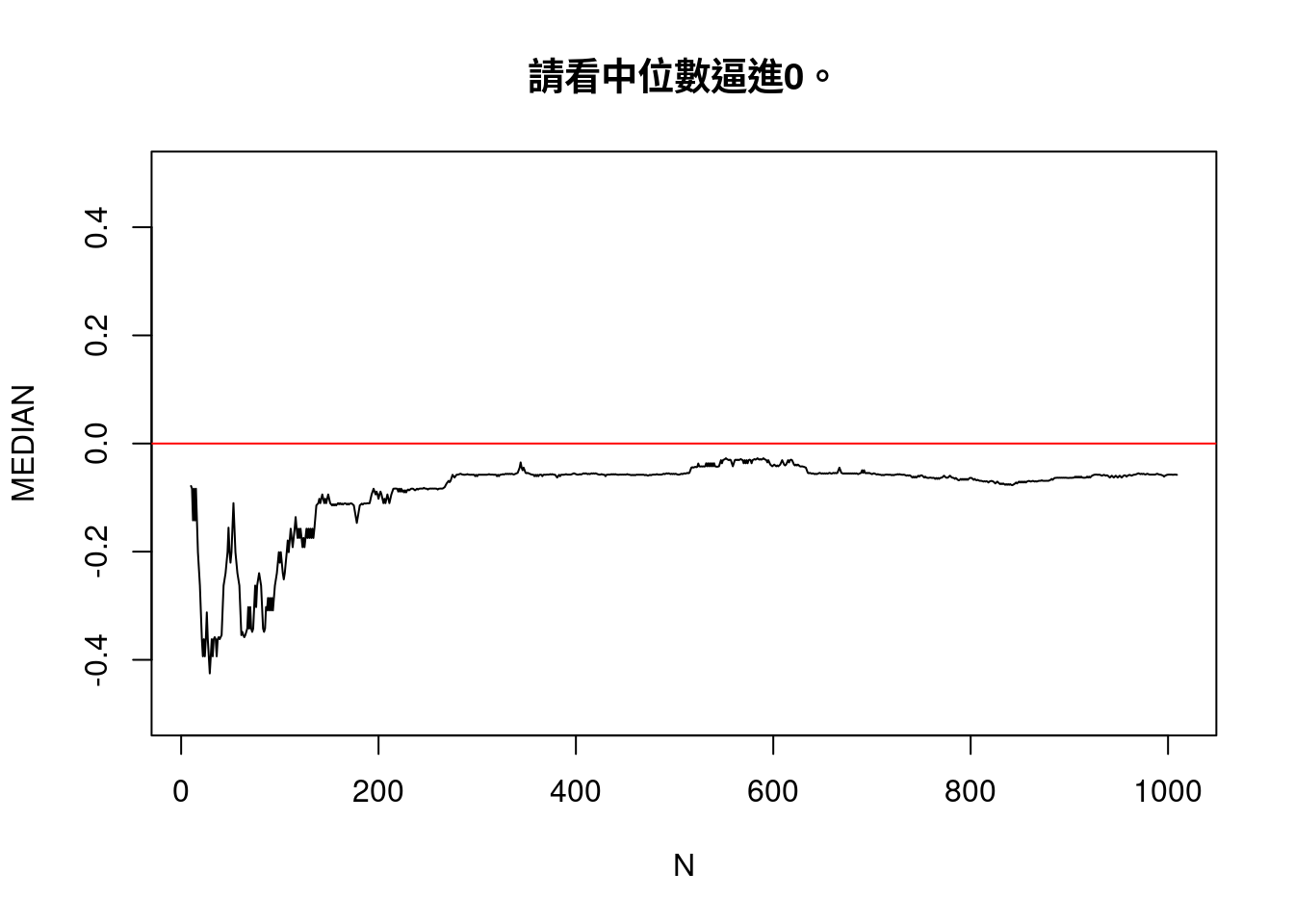

plot(N,
     mse1,
     type = "l",
     ylim = c(0.0,1.5),
     main = "請平均誤差平方和(除以n)看數逼進1。")
abline(h = 1, col = "red")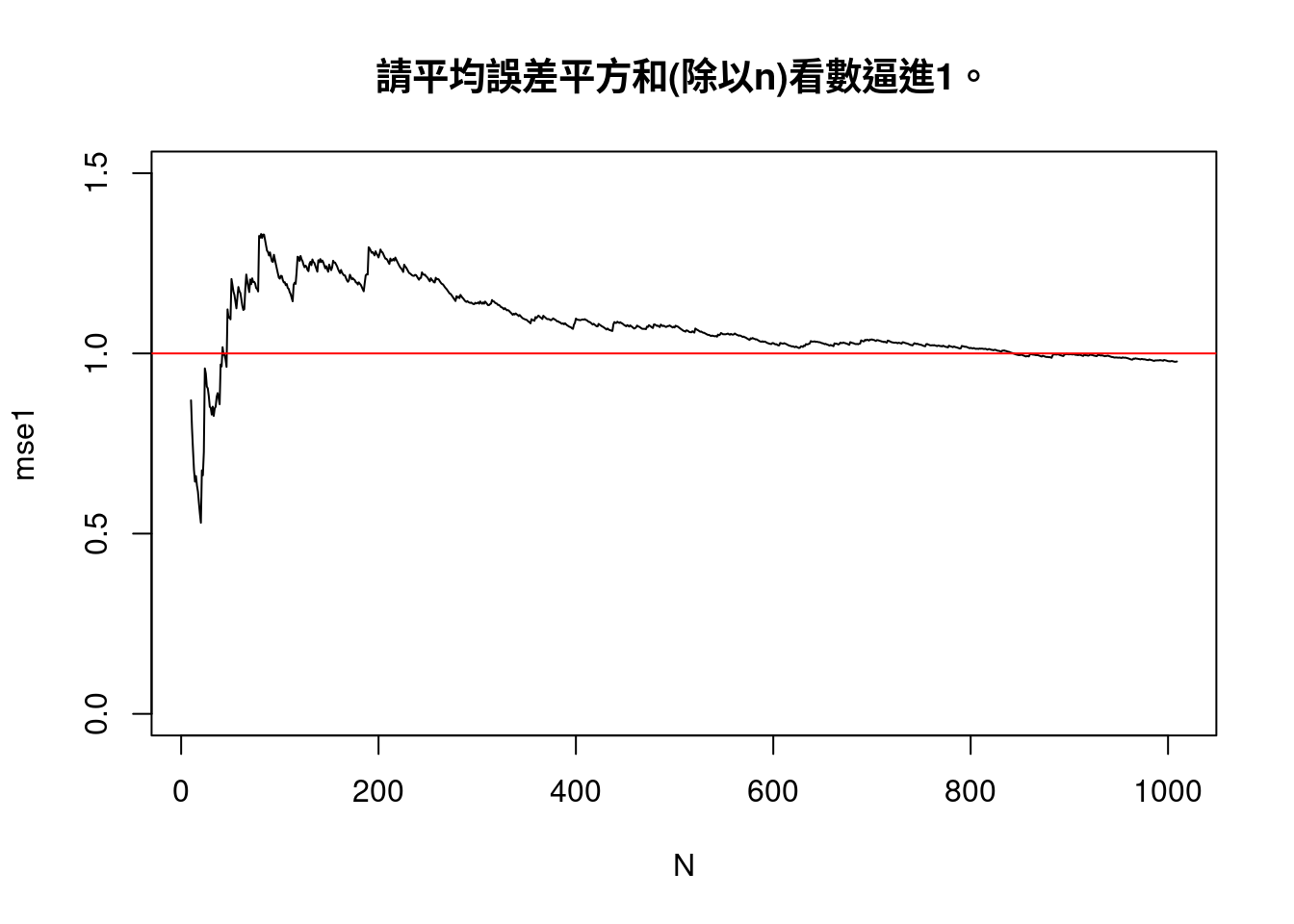

plot(N,
     mse2,
     type = "l",
     ylim = c(0.0,1.5),
     main = "請看平均誤差平方和(除以n-1)逼進1。")
abline(h = 1, col = "red")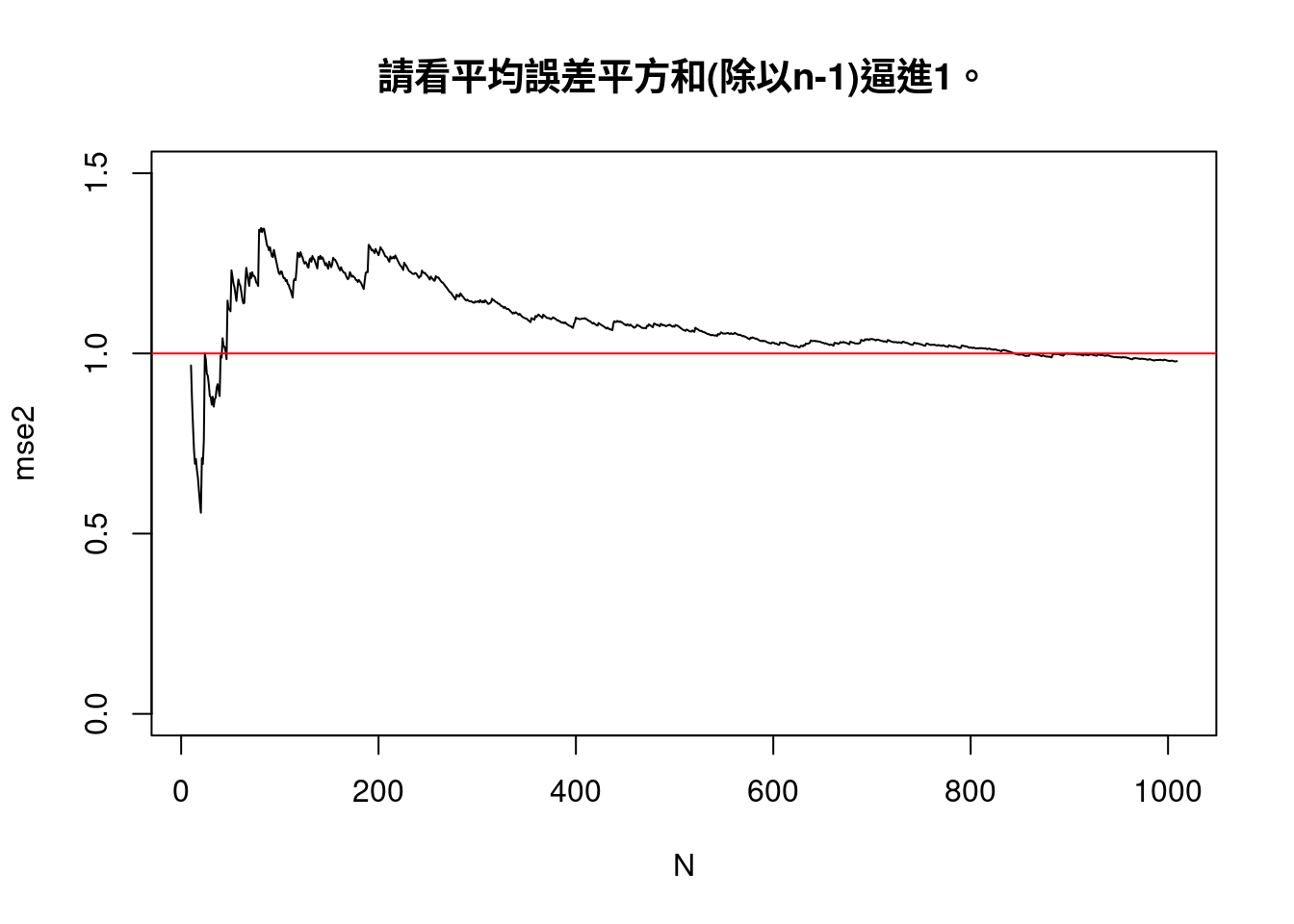

4.7.4.0.1 計算思維練習題：請觀察上述兩組圖形，並下結論。你同意以下論點嗎？
  1. 平均數比中位數更快接近0？
  2. 平均誤差平方和(除以n-1)比平均誤差平方和(除以n)更快接近1？

4.7.5 計算樣本變異數跟樣本標準差

4.7.5.1 第一種手動算法(手算，或是電算手算)

Data
##  [1]  44  46  47  49  63  64  66  68  68  72  72  75  76  81  84  88 106
Data^2
##  [1]  1936  2116  2209  2401  3969  4096  4356  4624  4624  5184  5184  5625
## [13]  5776  6561  7056  7744 11236
sum(Data^2)
## [1] 84697
(sum(Data))^2
## [1] 1366561
sum(Data^2) - (sum(Data))^2/length(Data)
## [1] 4311.059
(sum(Data^2) - (sum(Data))^2/length(Data))/length(Data)
## [1] 253.5917
sqrt((sum(Data^2) - (sum(Data))^2/length(Data))/length(Data))
## [1] 15.92456
(sum(Data^2) - (sum(Data))^2/length(Data))/(length(Data) - 1)
## [1] 269.4412
sqrt((sum(Data^2) - (sum(Data))^2/length(Data))/(length(Data) - 1))
## [1] 16.41466

4.7.5.2 第二種手動算法(手算，或是電算手算)

千萬不要這樣

sum((Data - mean(Data))^2)/(length(Data) - 1)
## [1] 269.4412
sqrt(sum((Data - mean(Data))^2)/(length(Data) - 1))
## [1] 16.41466

4.7.5.3 計算手動算法的複雜度

compComp <- data.frame(運算 = c("+","-","x","/","開根號","總和"),
                       第一種算法需要的次數 = rep("", 6),
                       第二種算法需要的次數 = rep("", 6),
                       stringsAsFactors = FALSE)
compComp
##     運算 第一種算法需要的次數 第二種算法需要的次數
## 1      +                                          
## 2      -                                          
## 3      x                                          
## 4      /                                          
## 5 開根號                                          
## 6   總和

請讀者諸君試著填滿上述表格，進而暸解兩種手算過程的計算複雜度。

4.7.5.4 電算

var(Data)
## [1] 269.4412
sd(Data)
## [1] 16.41466

或是利用我們自己定義的函式「MSE2」(請往前看)，

MSE2(Data, mean(Data))
## [1] 269.4412
sqrt(MSE2(Data, mean(Data)))
## [1] 16.41466

4.7.6 解讀樣本變異數跟樣本標準差

  1. 樣本標準差是樣本變異數的正方根。
  2. 樣本變異數沒有單位，或者可以說它的單位是原單位(數字向量「Data」的單位)的平方，但這已經不是原單位了。
  3. 樣本標準差的單位跟原單位是同一個單位。
  4. 樣本標準差跟樣本變異數都可以提供「以平均數代表全部數字的可靠度」，就像「誤差和」可以提供「以中位數代表全部數字的可靠度」。數字越小越可靠。
  5. 樣本標準差跟樣本變異數也可以視為「全部數字以平均數為中心分散的程度」，就像「誤差和」可以視為「全部數字以中位數為中心分散的程度」。樣本標準差跟樣本變異數的數字「越大」，表示「越分散」，也可以這麼說「數字越大分配越分散」。

4.8 間距

為什麼選讀這個主題，基本上，至少有以下幾個理由：

  1. 定義間距並且學習如何計算間距。
  2. 定義四分位數間距並且學習如何計算四分位數間距。
  3. 定義十分位數間距並且學習如何計算十分位數間距。
  4. 定義百分位數間距並且學習如何計算百分位數間距。
  5. 比較間距、四分位數間距、十分位數間距、百分位數間距與標準差衡量分配分散程度的可靠度。

4.8.1 建議優先閱讀：標準差

library(aplpack)
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
stem.leaf(Data, trim.outliers = FALSE)
## 1 | 2: represents 12
##  leaf unit: 1
##             n: 17
##    4     4 | 4679
##          5 | 
##   (5)    6 | 34688
##    8     7 | 2256
##    4     8 | 148
##          9 | 
##    1    10 | 6
median(Data)
## [1] 68
mean(Data)
## [1] 68.76471
var(Data)
## [1] 269.4412
sd(Data)
## [1] 16.41466

4.8.2 間距

range(Data)
## [1]  44 106
diff(range(Data))
## [1] 62
min(Data)
## [1] 44
max(Data)
## [1] 106
max(Data) - min(Data)
## [1] 62

4.8.3 四分位數間距

median(Data)
## [1] 68
quantile(Data, seq(0, 1, 0.25))
##   0%  25%  50%  75% 100% 
##   44   63   68   76  106
quantile(Data, seq(0, 1, 0.25))[2]
## 25% 
##  63
quantile(Data, seq(0, 1, 0.25))[4]
## 75% 
##  76
diff(quantile(Data, seq(0, 1, 0.25))[c(2,4)])
## 75% 
##  13

4.8.4 十分位數間距

quantile(Data, seq(0, 1, 0.1))
##    0%   10%   20%   30%   40%   50%   60%   70%   80%   90%  100% 
##  44.0  46.6  51.8  63.8  66.8  68.0  72.0  75.2  80.0  85.6 106.0
diff(quantile(Data, seq(0, 1, 0.1))[c(2,10)])
## 90% 
##  39
diff(quantile(Data, seq(0, 1, 0.1))[c(3,9)])
##  80% 
## 28.2
diff(quantile(Data, seq(0, 1, 0.1))[c(4,8)])
##  70% 
## 11.4

以下是計算細節：

quantile(Data, seq(0, 1, 0.1))
##    0%   10%   20%   30%   40%   50%   60%   70%   80%   90%  100% 
##  44.0  46.6  51.8  63.8  66.8  68.0  72.0  75.2  80.0  85.6 106.0
quantile(Data, seq(0, 1, 0.1))[2]
##  10% 
## 46.6
quantile(Data, seq(0, 1, 0.1))[10]
##  90% 
## 85.6
range9010 <- diff(quantile(Data, seq(0, 1, 0.1))[c(2,10)])
names(range9010) <- "10% ~ 90%"
range9010
## 10% ~ 90% 
##        39
quantile(Data, seq(0, 1, 0.1))[3]
##  20% 
## 51.8
quantile(Data, seq(0, 1, 0.1))[9]
## 80% 
##  80
range8020 <- diff(quantile(Data, seq(0, 1, 0.1))[c(3,9)])
names(range8020) <- "20% ~ 80%"
range8020
## 20% ~ 80% 
##      28.2
quantile(Data, seq(0, 1, 0.1))[4]
##  30% 
## 63.8
quantile(Data, seq(0, 1, 0.1))[8]
##  70% 
## 75.2
range7030 <- diff(quantile(Data, seq(0, 1, 0.1))[c(4,8)])
names(range7030) <- "30% ~ 70%"
range7030
## 30% ~ 70% 
##      11.4

4.8.5 百分位數間距

quantile(Data, seq(0, 1, 0.01))
##     0%     1%     2%     3%     4%     5%     6%     7%     8%     9%    10% 
##  44.00  44.32  44.64  44.96  45.28  45.60  45.92  46.12  46.28  46.44  46.60 
##    11%    12%    13%    14%    15%    16%    17%    18%    19%    20%    21% 
##  46.76  46.92  47.16  47.48  47.80  48.12  48.44  48.76  49.56  51.80  54.04 
##    22%    23%    24%    25%    26%    27%    28%    29%    30%    31%    32% 
##  56.28  58.52  60.76  63.00  63.16  63.32  63.48  63.64  63.80  63.96  64.24 
##    33%    34%    35%    36%    37%    38%    39%    40%    41%    42%    43% 
##  64.56  64.88  65.20  65.52  65.84  66.16  66.48  66.80  67.12  67.44  67.76 
##    44%    45%    46%    47%    48%    49%    50%    51%    52%    53%    54% 
##  68.00  68.00  68.00  68.00  68.00  68.00  68.00  68.64  69.28  69.92  70.56 
##    55%    56%    57%    58%    59%    60%    61%    62%    63%    64%    65% 
##  71.20  71.84  72.00  72.00  72.00  72.00  72.00  72.00  72.24  72.72  73.20 
##    66%    67%    68%    69%    70%    71%    72%    73%    74%    75%    76% 
##  73.68  74.16  74.64  75.04  75.20  75.36  75.52  75.68  75.84  76.00  76.80 
##    77%    78%    79%    80%    81%    82%    83%    84%    85%    86%    87% 
##  77.60  78.40  79.20  80.00  80.80  81.36  81.84  82.32  82.80  83.28  83.76 
##    88%    89%    90%    91%    92%    93%    94%    95%    96%    97%    98% 
##  84.32  84.96  85.60  86.24  86.88  87.52  88.72  91.60  94.48  97.36 100.24 
##    99%   100% 
## 103.12 106.00
diff(quantile(Data, seq(0, 1, 0.01))[c(11,91)])
## 90% 
##  39
diff(quantile(Data, seq(0, 1, 0.01))[c(21,81)])
##  80% 
## 28.2
diff(quantile(Data, seq(0, 1, 0.01))[c(31,71)])
##  70% 
## 11.4
4.8.5.0.1 計算思維練習題：請提供更多關於「十分位數間距」與「百分位數間距」的可能性。

4.8.6 比較「間距」與「標準差」

c(median(Data),
  mean(Data),
  sd(Data),
  diff(range(Data)),
  diff(quantile(Data, seq(0, 1, 0.25))[c(2,4)]),
  diff(quantile(Data, seq(0, 1, 0.1))[c(3,9)]),
  diff(quantile(Data, seq(0, 1, 0.01))[c(11,91)]))
##                                          75%      80%      90% 
## 68.00000 68.76471 16.41466 62.00000 13.00000 28.20000 39.00000
SUm <- c(median(Data),
  mean(Data),
  sd(Data),
  diff(range(Data)),
  diff(quantile(Data, seq(0, 1, 0.25))[c(2,4)]),
  diff(quantile(Data, seq(0, 1, 0.1))[c(3,9)]),
  diff(quantile(Data, seq(0, 1, 0.01))[c(11,91)]))
names(SUm) <- c("中位數",
                "平均數",
                "標準差",
                "間距",
                "25%~75%",
                "20%~80%",
                "10%~90%")
SUm
##   中位數   平均數   標準差     間距  25%~75%  20%~80%  10%~90% 
## 68.00000 68.76471 16.41466 62.00000 13.00000 28.20000 39.00000
SUm <- as.data.frame(SUm)
SUm
##              SUm
## 中位數  68.00000
## 平均數  68.76471
## 標準差  16.41466
## 間距    62.00000
## 25%~75% 13.00000
## 20%~80% 28.20000
## 10%~90% 39.00000
colnames(SUm) <- c("敘述統計量")
SUm
##         敘述統計量
## 中位數    68.00000
## 平均數    68.76471
## 標準差    16.41466
## 間距      62.00000
## 25%~75%   13.00000
## 20%~80%   28.20000
## 10%~90%   39.00000
4.8.6.0.1 計算思維練習題：請設計程式實驗到底「標準差」、「間距」還是「四分位數間距」，哪一個比較能「代表」分配的分散程度？

參考碼

MSE1 <- function(x, a){
  sum((x - a)^2)/length(x)
}
MSE2 <- function(x, a){
  sum((x - a)^2)/(length(x) - 1)
}

set.seed(1233)
MEAN <- numeric(0)
MEDIAN <- numeric(0)
mse1 <- numeric(0)
mse2 <- numeric(0)
N <- integer(0)

x <- rnorm(10)
for (i in 1:100) {
  N <- c(N, length(x))
  MEAN <- c(MEAN, mean(x))
  MEDIAN <- c(MEDIAN, median(x))
  mse1 <- c(mse1, MSE1(x, mean(x)))
  mse2 <- c(mse2, MSE2(x, mean(x)))
  x <- c(x, rnorm(1))
}
plot(N,
     MEAN,
     type = "l",
     ylim = c(-0.5,0.5),
     main = "請看平均數逼進0。")
abline(h = 0, col = "red")

plot(N,
     MEDIAN,
     type = "l",
     ylim = c(-0.5,0.5),
     main = "請看中位數逼進0。")
abline(h = 0, col = "red")
plot(N,
     mse1,
     type = "l",
     ylim = c(0.0,1.5),
     main = "請平均誤差平方和(除以n)看數逼進1。")
abline(h = 1, col = "red")
plot(N,
     mse2,
     type = "l",
     ylim = c(0.0,1.5),
     main = "請看平均誤差平方和(除以n-1)逼進1。")
abline(h = 1, col = "red")

4.9 參考文獻