Chapter 13 簡單線性迴歸分析首部曲
13.1 續
先回顧我們已經有什麼了?在寫一段下載數據集的耙蟲,我們已經取得波士頓數據集,不論是得力於R,還是「天助自助」。接下來,
- 在探索式數據分析首部曲,我們因為「莖葉圖」,因為「次數分配表」,因為「敘述(摘要)統計量」,深入認識「房價中位數」的「分配」。
- 在探索式數據分析二部曲,我們延伸第二章學到的技巧到整個波士頓數據集,取得每一個連續型變數的「次數分配表」、「相對次數分配表」、「累加次數分配表」、「累加相對次數分配表」跟「直方圖」,也得到每一個離散型變數的「次數分配表」跟「長條圖」。除了統計學定義的「探索式分析」,我們也利用程式深入了解波士頓數據集的零零總總。
- 在探索式數據分析安可曲,我們從「一次探索一個變數」延伸到「一次探索兩個變數」,試圖理解「兩個連續型變數的關係」、「兩個離散型變數的關係」、「一個連續型變數跟一個離散型變數的關係」。我們學到「散佈圖」、「共變異數」、「相關係數」、「列聯表」、「獨立性檢定」、「t檢定」、「變異數分析F檢定」等等相關的「探索式分析工具」。
繼續往前走之前,作者小編一定要再一次提醒大家,本波士頓數據集案例分析微微書的總目標是
搜尋「1970年代波士頓都會區的最佳『hedonic housing price model』」,某一種迴歸模型。
接下來,我們繼續研究「兩個連續型變數的迴歸模型」,尤其是固定一個變數在「房價中位數」。「房價中位數」是我們「散佈圖」的「y變數」,其他連續型變數則是我們的「x變數」,而且一次只來、只看一個。沿著、順著這樣的「探索之路」,作者小編想在這一章好好解釋、分析、視覺化「簡單線性迴歸模型」。「簡單線性迴歸模型」是最簡單的「兩個連續型變數的迴歸模型」:
\[y = \beta_0 + \beta_1 x + \epsilon\]
接下來幾章,除了介紹「最小平方法(LS)」,也會介紹「LASSO」跟「Ridge」。進而介紹作者小編土耳其同學反對的「機器學習(ML)」。以上不論是
- LS
- LASSO
- Ridge
- ML
- …
都是「挑選模型」的標準,或說是「估計模型」的演算法。「估計」兩個字對讀者諸君而言,或許太遙遠,但「估計」其實骨子裡就是「猜測」,不只是「有憑有據的猜測」,而且這些「猜測」都必須根據「樣本」。現實裡的「樣本」,讓「估計、猜測」的辦法不會只有一種,也就是說,現實裡沒有打遍天下無敵手的猜測辦法,意思是說「沒有贏家演算法」。即便如此,無論如何,接下來R將協助我們全掌握「簡單線性迴歸分析」,並且學習各種演算法的優缺點。
…
作者小編一路寫下來,感覺上,好像我們已經遠離了「分配」。事實上不然,因為「簡單線性迴歸模型」,「x變數」把「y變數的分配」切成許許多多的「小分配」。然後,統計學家企圖把這一些「小分配的平均數」連成「一條直線」:
\[E(y|x = x_0) = \beta_0 + \beta_1 x_0\]
只是不知道,\(\beta_0\)跟\(\beta_1\)到底在哪裡?到底有多大?而已。接下來,我們將好好想辦法
發展
找到\(\beta_0\)跟\(\beta_1\)的辦法、技術、數學、…,任何科學的辦法。
…
13.3 準備工作
require(MASS) # 用「require」不用「library」,是因為如果R已經將套件MASS載入環境,就不需要再載一次。
data(Boston)
boston <- Boston
# 「不動」原始數據集,不論它有「多原始」,是R程式設計的一項絕佳習慣。
# 即便一般使用者是無法任意改變套件MASS的內容物!
### rad (index of accessibility to radial highways)
boston[,"rad"] <- factor(boston[,"rad"], ordered = TRUE)
### chas (= 1 if tract bounds river; 0 otherwise)
boston[,"chas"] <- factor(boston[,"chas"])
### 讀取自製的波士頓數據集中文資訊。
DISvars <- colnames(boston)[which(sapply(boston, class) == "integer")]
CONvars <- colnames(boston)[which(sapply(boston, class) == "numeric")]
colsBostonFull<-readRDS("output/data/colsBostonFull.rds")
colsBostonFull$內容物 <- sapply(boston, class)
colsBostonFull## 變數名
## 1 crim
## 2 zn
## 3 indus
## 4 chas
## 5 nox
## 6 rm
## 7 age
## 8 dis
## 9 rad
## 10 tax
## 11 ptratio
## 12 black
## 13 lstat
## 14 medv
## 說明
## 1 per capita crime rate by town
## 2 proportion of residential land zoned for lots over 25,000 sq.ft.
## 3 proportion of non-retail business acres per town
## 4 Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
## 5 nitric oxides concentration (parts per 10 million)
## 6 average number of rooms per dwelling
## 7 proportion of owner-occupied units built prior to 1940
## 8 weighted distances to five Boston employment centres
## 9 index of accessibility to radial highways
## 10 full-value property-tax rate per $10,000
## 11 pupil-teacher ratio by town
## 12 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
## 13 % lower status of the population
## 14 Median value of owner-occupied homes in $1000's
## 中文翻譯 中文變數名稱 內容物
## 1 每個城鎮人均犯罪率。 犯罪率 numeric
## 2 超過25,000平方呎的住宅用地比例。 住宅用地比例 numeric
## 3 每個城鎮非零售業務英畝的比例。 非商業區比例 numeric
## 4 是否鄰近Charles River。 河邊宅 factor
## 5 氮氧化合物濃度。 空汙指標 numeric
## 6 每個住宅的平均房間數。 平均房間數 numeric
## 7 1940年之前建造的自用住宅比例。 老房子比例 numeric
## 8 距波士頓五大商圈的加權平均距離。 加權平均距離 numeric
## 9 環狀高速公路的可觸指標。 交通便利性 ordered, factor
## 10 財產稅占比(每一萬美元)。 財產稅率 numeric
## 11 生師比。 生師比 numeric
## 12 黑人的比例。 黑人指數 numeric
## 13 (比較)低社經地位人口的比例。 低社經人口比例 numeric
## 14 以千美元計的房價中位數。 房價中位數 numeric13.4 當anscombe在轉角遇上散佈圖
作者小編寫到這裏,有點詞窮!還誤按出全形的阿拉伯數字:
1234567890
在第四章,作者小編第一次介紹「散佈圖」。當時少看了一本書,
Tufte, Edward R. (1989). The Visual Display of Quantitative Information, 13–14. Graphics Press.
作者小編忘了向「統計藝術家Tufte教授」請益。話不多說,我們先看Tufte教授怎麼看一張「統計好圖」。好圖一定要:
- clarity
- precision
- efficiency
Tufte教授在「The Visual Display of Quantitative Information」的第十頁就舉了一個「散佈圖」的例子,示範上述的「一定要」。這一組數據集源自於
Anscombe, Francis J. (1973). Graphs in statistical analysis. The American Statistician, 27, 17–21.
R當然要收錄,而且以作者,統計學家Anscombe之名(anscombe)保留下來。我們先呼叫它:
require(datasets) # 通常我們是這麼寫「library(datasets)」。
data("anscombe") # 載入。
anscombe # 呼叫它。## x1 x2 x3 x4 y1 y2 y3 y4
## 1 10 10 10 8 8.04 9.14 7.46 6.58
## 2 8 8 8 8 6.95 8.14 6.77 5.76
## 3 13 13 13 8 7.58 8.74 12.74 7.71
## 4 9 9 9 8 8.81 8.77 7.11 8.84
## 5 11 11 11 8 8.33 9.26 7.81 8.47
## 6 14 14 14 8 9.96 8.10 8.84 7.04
## 7 6 6 6 8 7.24 6.13 6.08 5.25
## 8 4 4 4 19 4.26 3.10 5.39 12.50
## 9 12 12 12 8 10.84 9.13 8.15 5.56
## 10 7 7 7 8 4.82 7.26 6.42 7.91
## 11 5 5 5 8 5.68 4.74 5.73 6.89請「anscombe」自我介紹,先講講在R的性質,
class(anscombe) # 一張表。## [1] "data.frame"dim(anscombe) # 高與寬。## [1] 11 8sapply(anscombe, class) # 每一個欄位都是實數。## x1 x2 x3 x4 y1 y2 y3 y4
## "numeric" "numeric" "numeric" "numeric" "numeric" "numeric" "numeric" "numeric"再說說「摘要統計量」(我們在此第一次使用sapply的嫡系apply):
apply(anscombe, 2, mean) # 幾乎相同的平均數。## x1 x2 x3 x4 y1 y2 y3 y4
## 9.000000 9.000000 9.000000 9.000000 7.500909 7.500909 7.500000 7.500909apply(anscombe, 2, sd) # 幾乎相同的標準差。## x1 x2 x3 x4 y1 y2 y3 y4
## 3.316625 3.316625 3.316625 3.316625 2.031568 2.031657 2.030424 2.030579sapply(1:4, function(w){
cor(anscombe[,w], anscombe[,(w+4)])
}) # 幾乎相同的相關係數。## [1] 0.8164205 0.8162365 0.8162867 0.8165214我們為什麼檢查anscombe數據集以上這三種數字呢?因為
anscombe這一個字,在統計界已經是「幾乎一樣的平均數、標準差加相關係數卻完全不一樣的兩維數據集」的「代名詞」了!
作者小編先賣個關子,先不給「Tufte教授一開始就給,表達了「統計好圖」意念的四張『散佈圖』」。先給「全部x」對上「全部y」(當然沒有破壞彼此的配對關係)的「散佈圖」:
plot(unlist(anscombe[,1:4]),
unlist(anscombe[,5:8]),
xlab = "x",
ylab = "y",
main = "Scatterplot of the stacked x and y of Anscombe’s quartet")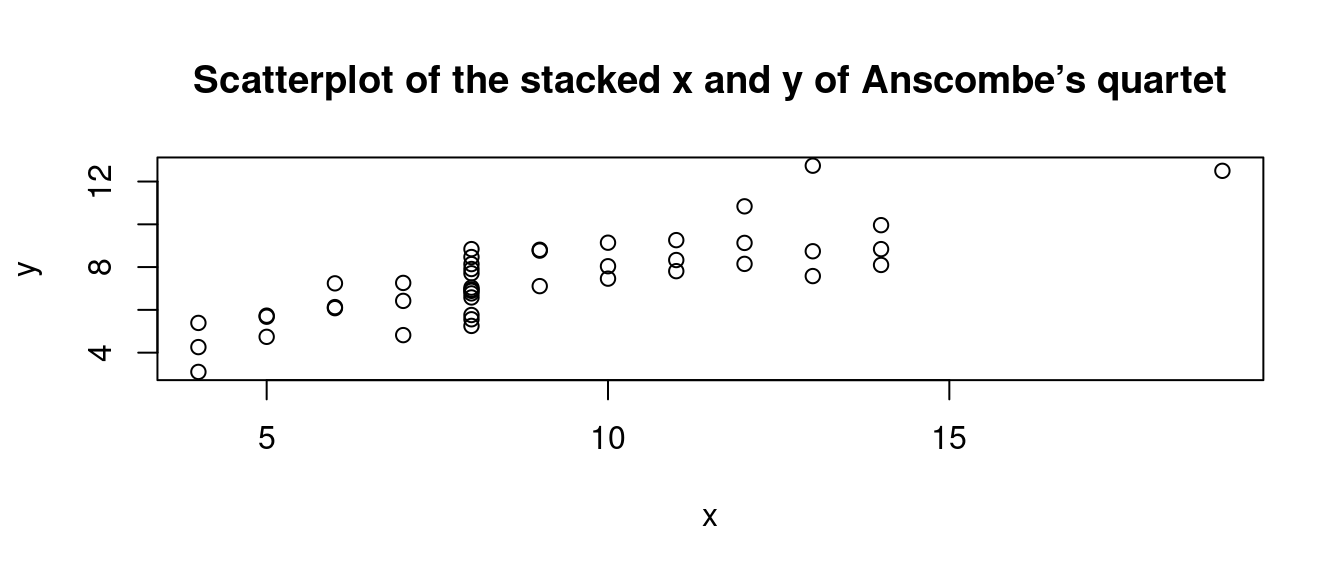
作者小編寫到這裏,相當開心,因為看到
小分配。請讀者諸君,固定某一個「x」然後視線往上,會發現有好幾個點,那幾個點的「y座標」就會形成「y的『小分配』」。
這一組數據集雖然是「統計學家Anscombe」為了示範他在
Anscombe, Francis J. (1973). Graphs in statistical analysis. The American Statistician, 27, 17–21.
企圖表達的、傳達的意念所創造出來的「假」數據集,但竟然在接近半世紀「38+10年後(1973 ~ 2021)」遇上「小分配」,何其巧合啊!!!接下來,讓我們親眼目睹「Tufte教授的2x2散佈圖矩陣」加上「統計學家Anscombe的最小平方法迴歸線」:
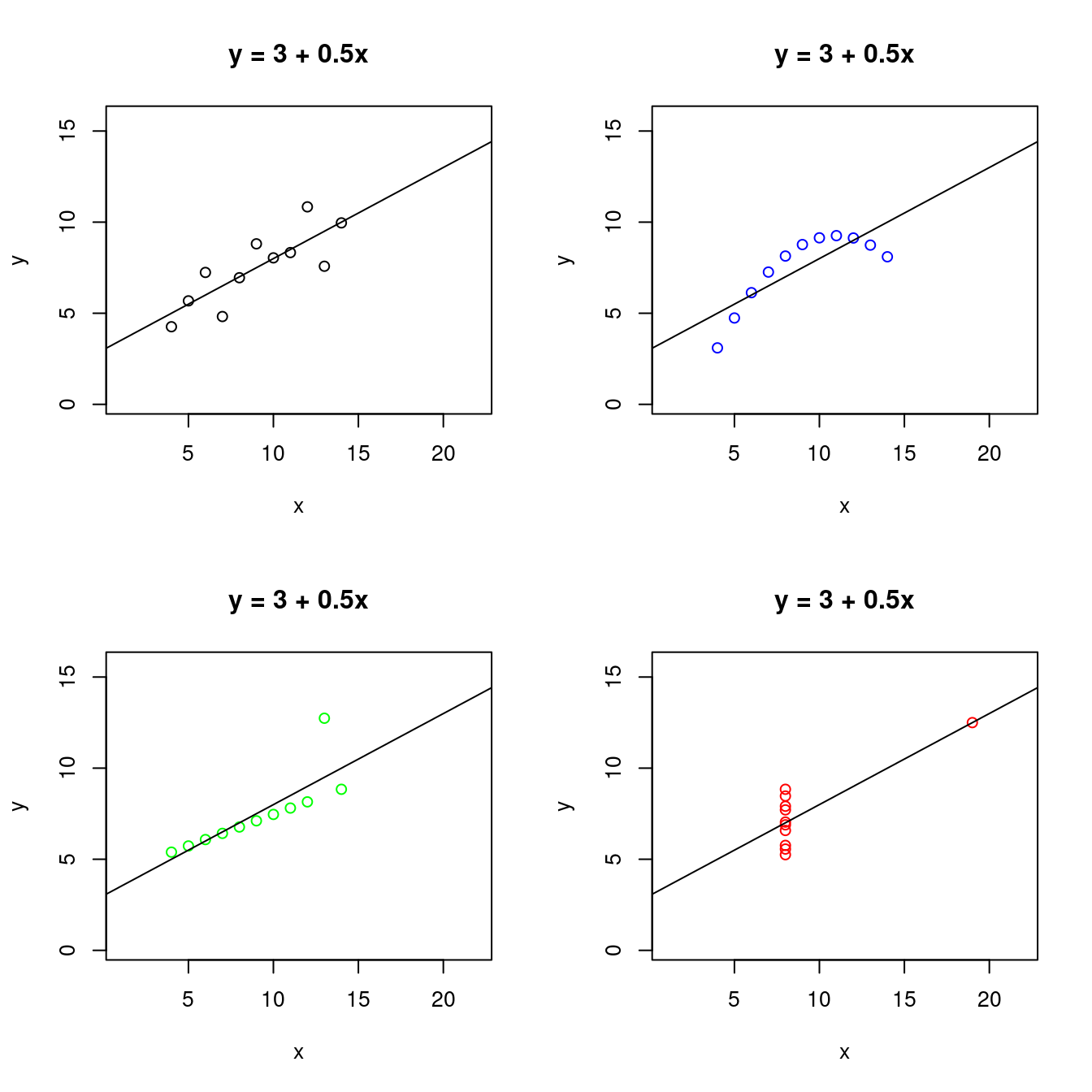
畫了上述四張「散佈圖」,也算了個別的「摘要統計量」跟「最小平方法迴歸線」,請讀者諸君務必記得,
不只看「摘要統計量」也要看「散佈圖」。
也意味著,統計世界裡存在著「幾乎一樣」的「平均數、標準差、相關係數、最小平方法迴歸線」卻完全不一樣的數據集。說到這裡,作者小編在Anscombe’s quartet(anscombe)這一篇維基百科發現了「比anscombe更anscombe」的數據集,
作者小編暫時把「Datasaurus」翻譯為「數據蜥蜴」。請看它們的精彩「散佈圖」:
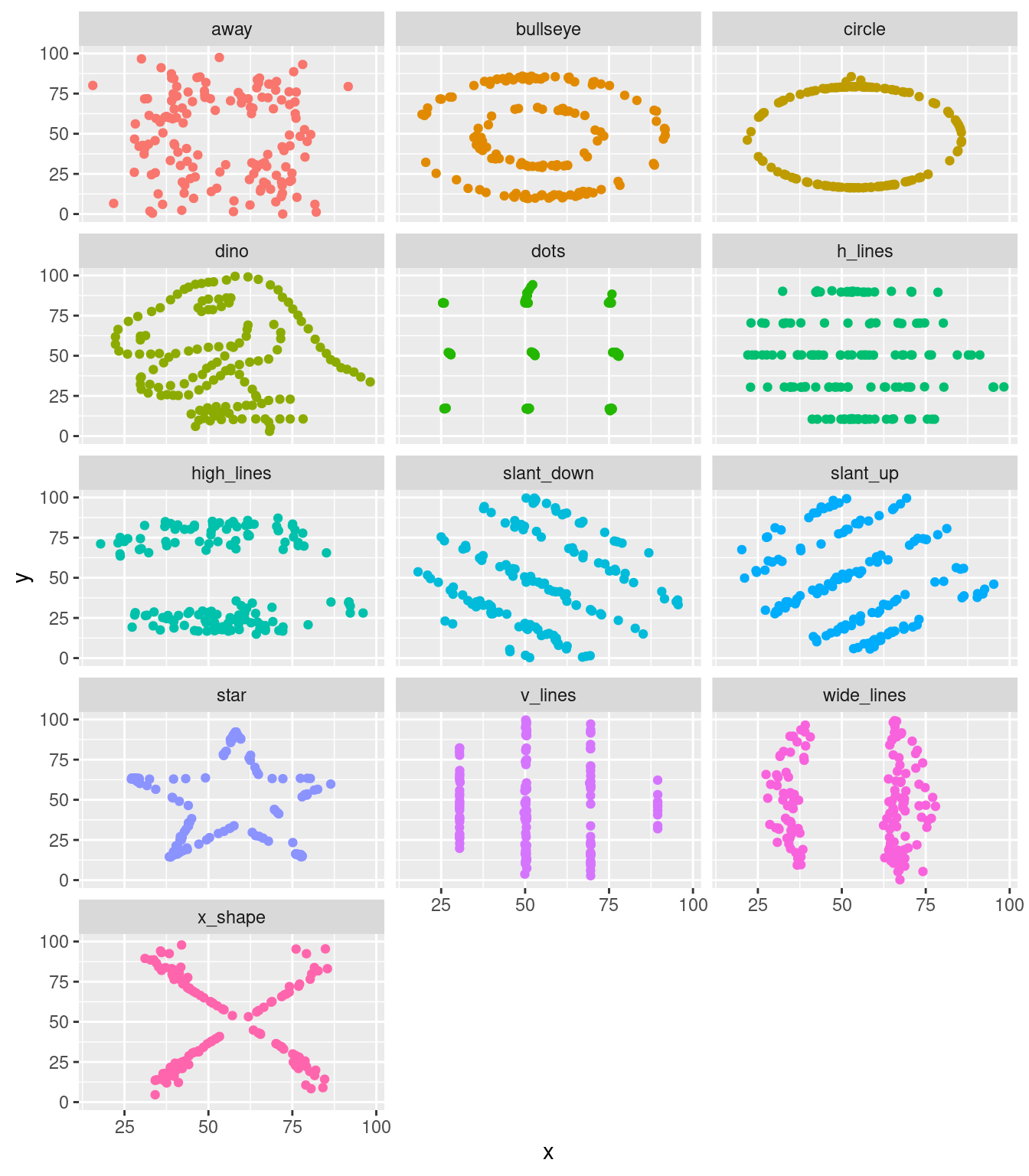
作者小編一邊喝咖啡一邊慢慢欣賞過後,驚覺竟然有人可以用作者小編在1998 (1998 ~ 2017)年任職於中央研究院統計所時代學過的「演算法」,創造出「dino」數據集,它可不是藝術家在畫紙上一筆一筆刻出來的!這幾位學者專家就是以下這一篇文章的作者:
Matejka, Justin; Fitzmaurice, George (2017). “Same Stats, Different Graphs: Generating Datasets with Varied Appearance and Identical Statistics through Simulated Annealing”. Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems: 1290–1294.
最後,讓作者小編提示以下程式碼,總結這一小段,個人認為如果「散佈圖」這樣畫,我們更容易發現其他現象:
### 先「堆疊」x座標跟y座標。
quartet <- data.frame(x = unlist(anscombe[,1:4]), y = unlist(anscombe[,5:8]))
par(mfrow = c(2,1)) # 切成畫布。
plot(quartet[, "x"],
quartet[, "y"],
xlab = "x",
ylab = "y") # 最簡單的散佈圖。
abline(lm(y ~ x, data = quartet)) # 畫簡單線性迴歸線。
ab <- round(lm(y ~ x,data = quartet)$coefficients, 2) # 取得直線的「截距」跟「斜率」。
title(paste0("y = ", ab[1], " + ", ab[2], "x")) # 把直線方程式貼上標題。
plot(quartet[, "x"],
quartet[, "y"],
xlab = "x",
ylab = "y",
main = "四色的anscombe",
col = c(rep(1,11),rep(2,11),rep(3,11),rep(4,11))) # 加味散佈圖。
abline(lm(y ~ x, data = quartet)) # 畫簡單線性迴歸線。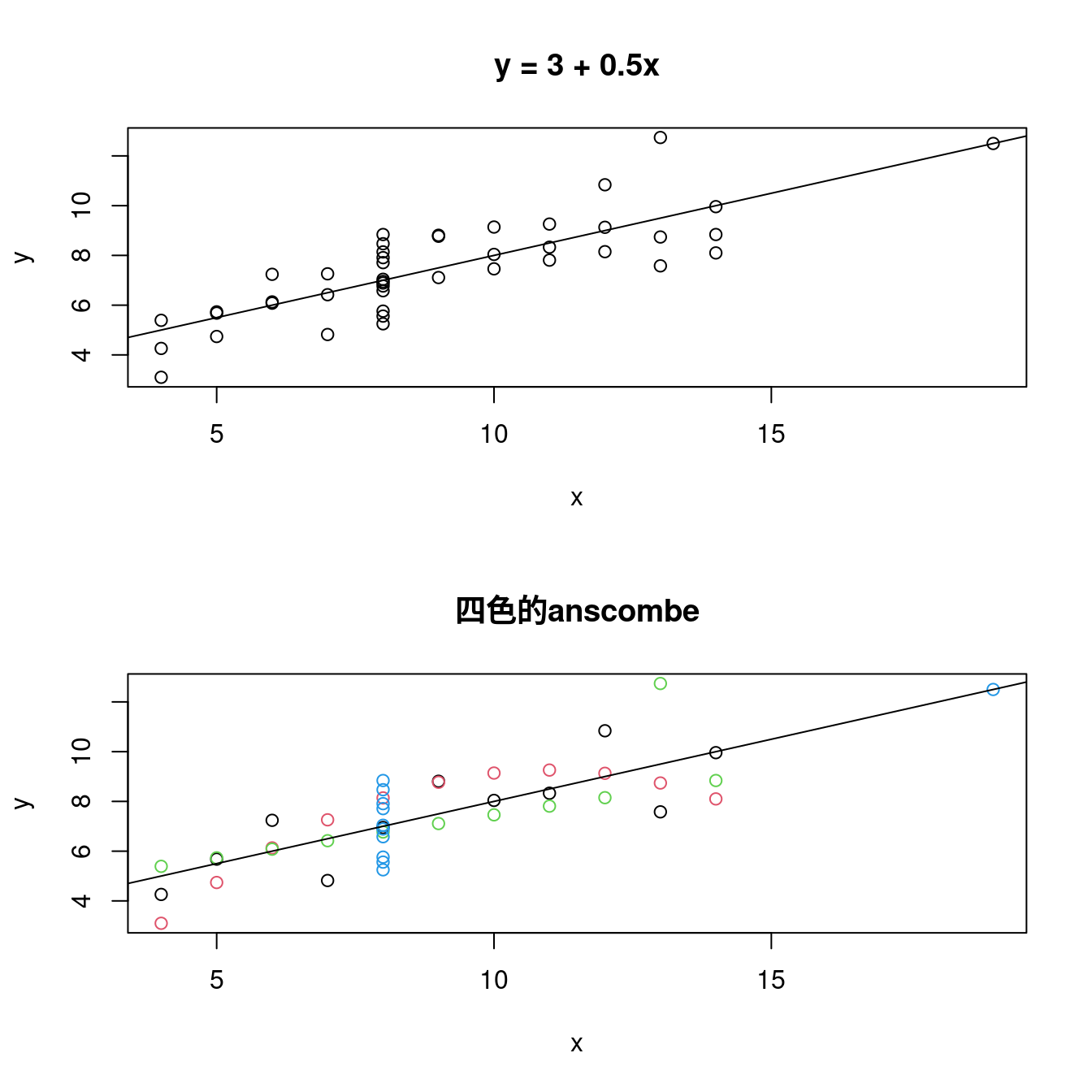
…
13.5 什麼是最小平方法?最小平方法迴歸線?
在這一章,我們開始
搜尋「1970年代波士頓都會區的最佳『hedonic housing price model』」,某一種迴歸模型。
也就是搜尋,
把「房價中位數」固定在「y變數」,把「其他變數放在x變數這一邊」的「迴歸模型」。
作者小編說過,
凡事從簡單的開始。
所以,我們的第一個搜尋任務是「一條直線」,一種「兩兩連續型變數間的『直線數學關係』」:
\[房價中位數 = \beta_0 + \beta_1 x = a + b x\]
其中「\(\beta_0\)跟\(a\)」是直線的截距,「\(\beta_1\)跟\(b\)」是直線的斜率。也就是說,我們要搜尋「合適的『\(\beta_0 (a)\)』跟『\(\beta_1 (b)\)』」。所謂的「合適的」到底是什麼意思呢?
這絕對是大哉問?
為什麼呢?
…
13.5.1 準備示範數據
小量示範
是教學現場的限制,雖然在這裡,在「微微書的世界」,這不是問題,但
凡事從簡單的開始。
所以,作者小編決定請「anscombe」數據集幫忙解釋「什麼是最小平方法?」。「anscombe」數據集有「四組」,根據個人初步、淺顯的觀察結果,認為其中的
- 第一組是四組裡面「散佈圖樣子」最隨機的、
- 第二組是曲線的樣子、
- 第三組是一條直線加一點組間內離群值、
- 第四組是一條垂直線加一點組間外離群值。
所以,作者小編請「anscombe數據集」的第一組為大家示範「什麼是最小平方法?」:
df <- anscombe[, c("x1", "y1")] # 取出「x1」跟「y1」,其中「1」代表第一組。
colnames(df) <- c("x", "y") # 劃掉其中的「1」。
df # 呼叫出來再一次檢視這一組數據集。## x y
## 1 10 8.04
## 2 8 6.95
## 3 13 7.58
## 4 9 8.81
## 5 11 8.33
## 6 14 9.96
## 7 6 7.24
## 8 4 4.26
## 9 12 10.84
## 10 7 4.82
## 11 5 5.68# 繪製散佈圖。左右上下各加3個單位,方便大家觀察。
plot(df,
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3))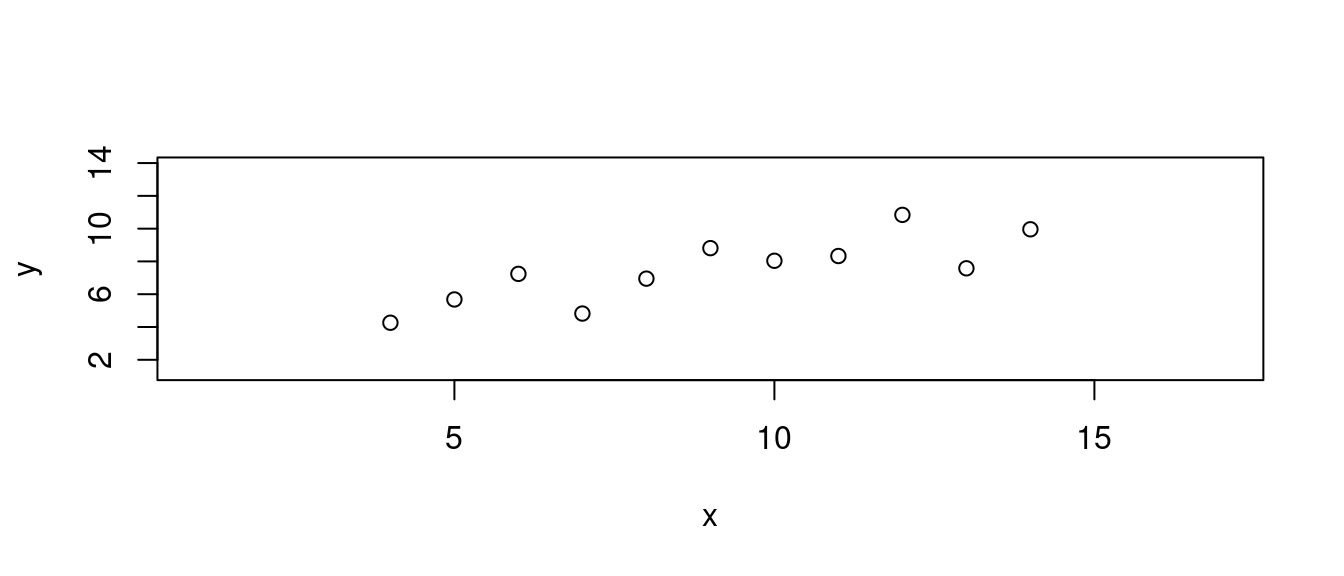
13.5.2 如果只有兩個點
這是最簡單的問題:
為兩筆觀察值搜尋一條合適的直線。
plot(df[1:2,],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3))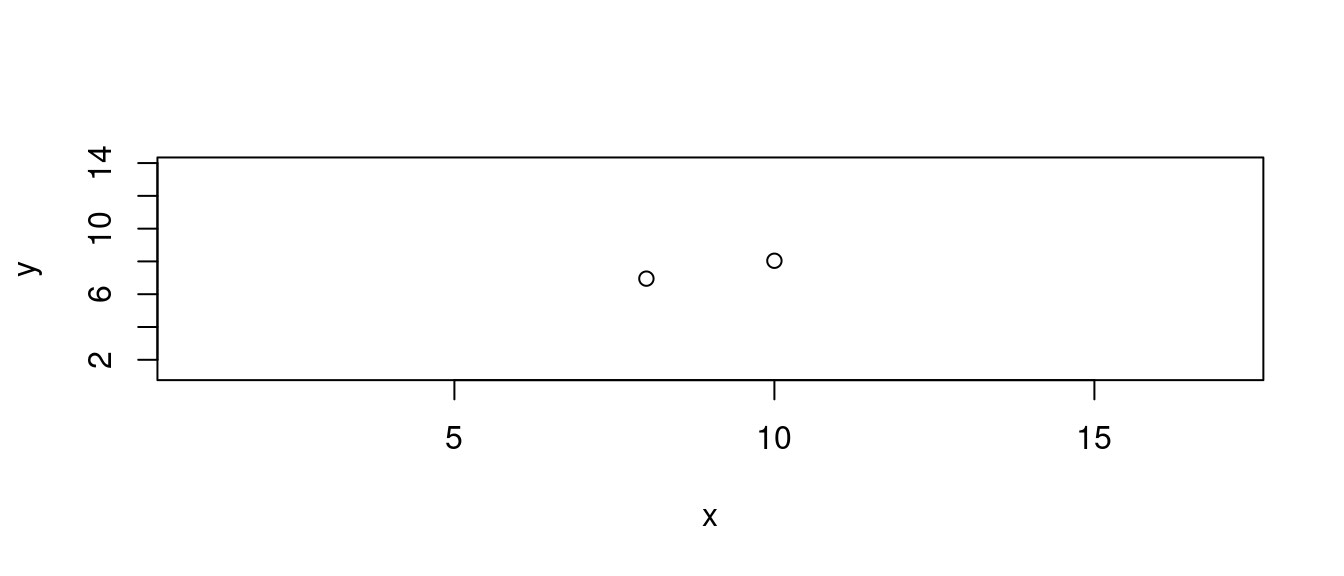
「兩點決定一條直線」,這一個「數學結果」,被我們(統計學家加統計學生)「借用」,所以「答案」是
\[y = y1 + \frac{y2 - y1}{x2 - x1} \times (x - x1)\]
其中「(\(x_1\), \(y_1\))」是第一個點的座標,而「(\(x_2\), \(y_2\))」是第二個點的座標。對應我們的「df」,第一個點的座標就是「第一個觀察值」,而第二個點的座標就是「第二個觀察值」。
df[1:2, c("x", "y")] # 先看座標。## x y
## 1 10 8.04
## 2 8 6.95b <- diff(df[1:2,"y"])/diff(df[1:2,"x"]) # 直接翻譯上述答案。「斜率」等於「y座標的差距」除以「x座標的差距」。
a <- df[1,"y"] - b * df[1,"x"] # 「截距」等於第一點的y座標減去斜率乘以第一點的x座標。
LINE <- c(a, b) # 報告成果。
names(LINE) <- c("a", "b")
LINE## a b
## 2.590 0.545plot(df[1:2, c("x", "y")],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3))
abline(a = LINE["a"], b = LINE["b"], col = "red") # 「abline」名字取得好!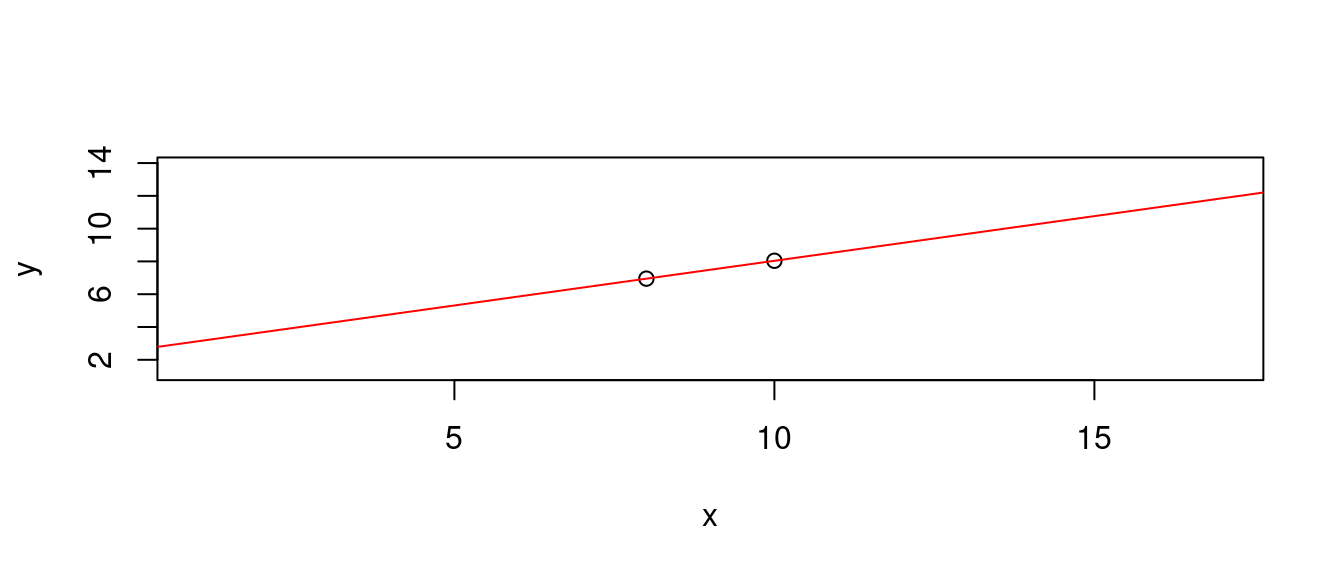
13.5.3 如果只有三個點
接下來,解題過程過了第一階段,來到第二個階段,這時候,多了第三點、第三筆觀察值,13, 7.58。散佈圖上「紅色的」那一點。
plot(df[1:3, c("x", "y")],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3),
col = c(1,1,2)) # 注意,作者小編怎麼給顏色?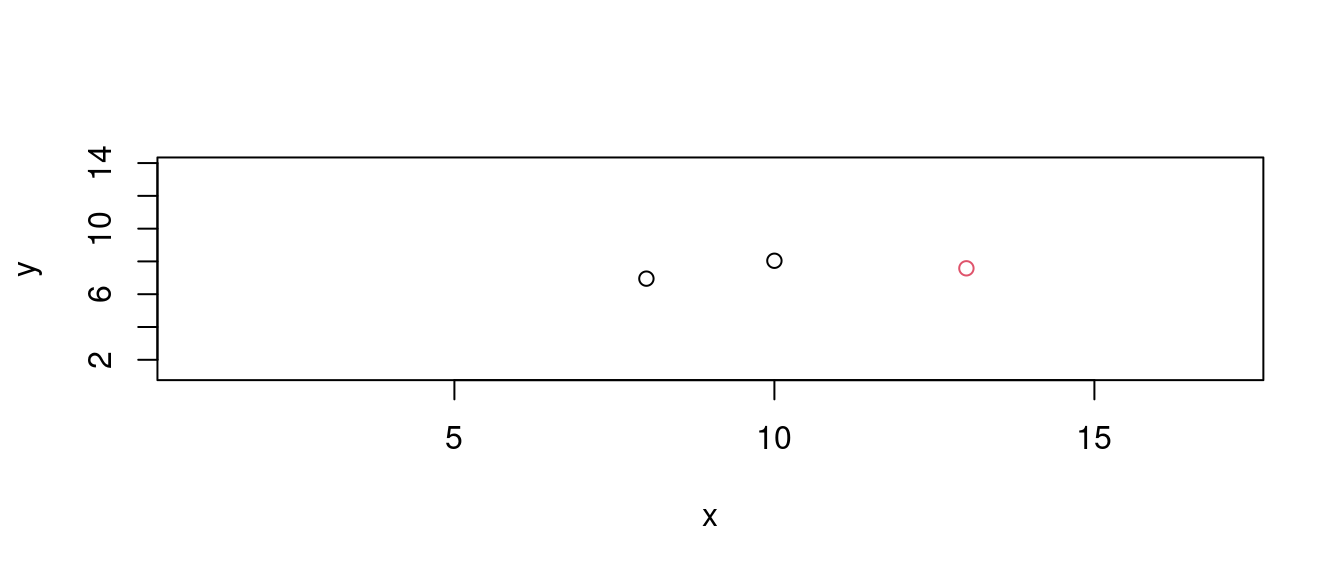
根據上一小節的答案,我們會有三條線。
請讀者諸君特別注意作者小編堅持的程式一致性,注意到作者小編的寫法。
- 穿過第一點跟第二點的直線
df[c(1,2), c("x", "y")]## x y
## 1 10 8.04
## 2 8 6.95b <- diff(df[c(1,2),"y"])/diff(df[c(1,2),"x"])
a <- df[1,"y"] - b * df[1,"x"]
LINE1 <- c(a, b) # 報告成果。
names(LINE1) <- c("a", "b")
LINE1## a b
## 2.590 0.545plot(df[c(1,2,3),],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3))
abline(a = LINE1["a"], b = LINE1["b"], col = "red")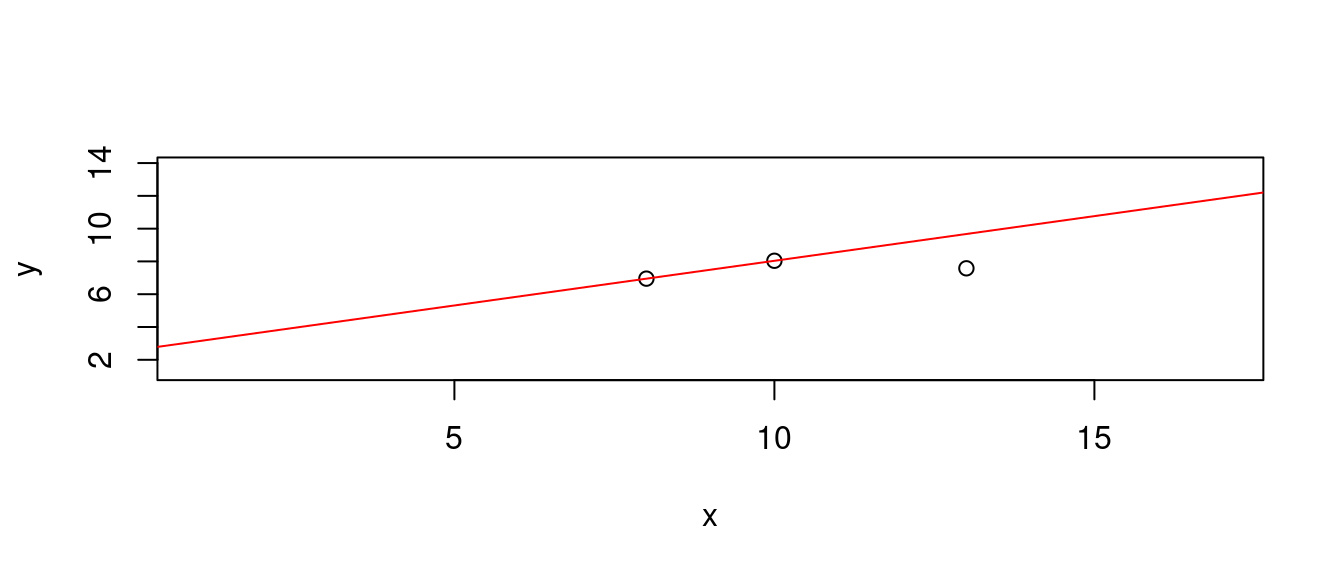
- 穿過第一點跟第三點的直線
df[c(1,3), c("x", "y")]## x y
## 1 10 8.04
## 3 13 7.58b <- diff(df[c(1,3),"y"])/diff(df[c(1,3),"x"])
a <- df[1,"y"] - b * df[1,"x"]
LINE2 <- c(a, b) # 報告成果。
names(LINE2) <- c("a", "b")
LINE2## a b
## 9.5733333 -0.1533333plot(df[c(1,2,3),],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3))
abline(a = LINE2["a"], b = LINE2["b"], col = "green")
abline(a = LINE1["a"], b = LINE1["b"], col = "red")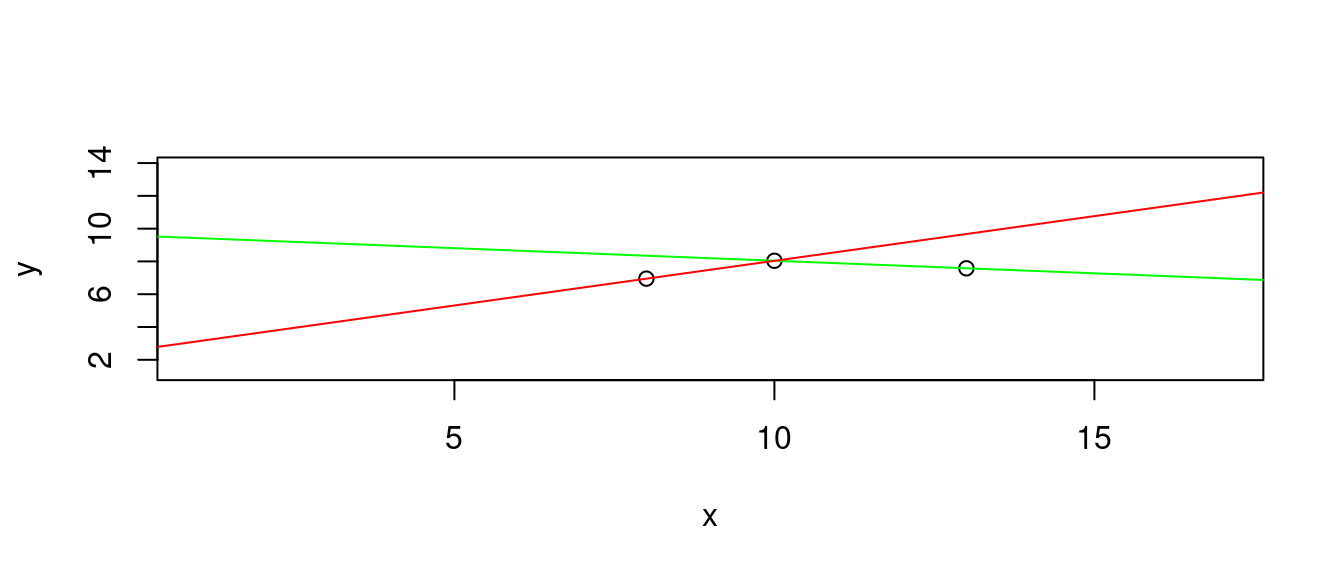
- 穿過第二點跟第三點的直線
df[c(2,3), c("x", "y")]## x y
## 2 8 6.95
## 3 13 7.58b <- diff(df[c(2,3),"y"])/diff(df[c(2,3),"x"])
a <- df[2,"y"] - b * df[2,"x"]
LINE3 <- c(a, b) # 報告成果。
names(LINE3) <- c("a", "b")
LINE3## a b
## 5.942 0.126plot(df[c(1,2,3),],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3))
abline(a = LINE3["a"], b = LINE3["b"], col = "blue")
abline(a = LINE2["a"], b = LINE2["b"], col = "green")
abline(a = LINE1["a"], b = LINE1["b"], col = "red")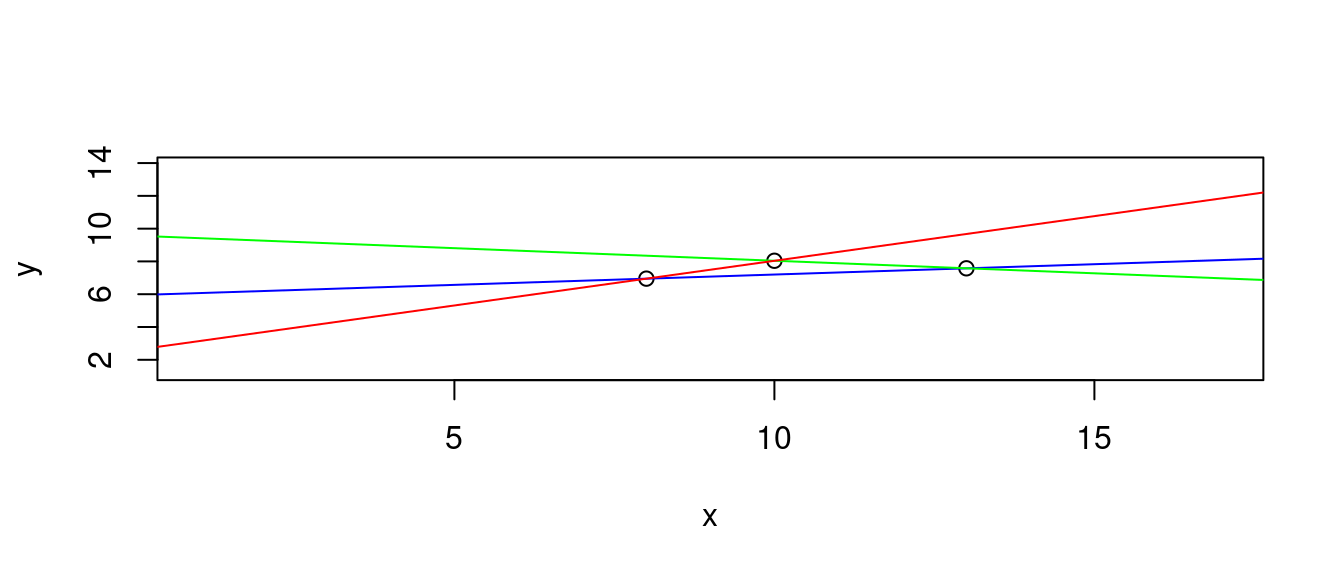
但是,我們只要一條。挑哪一條呢?
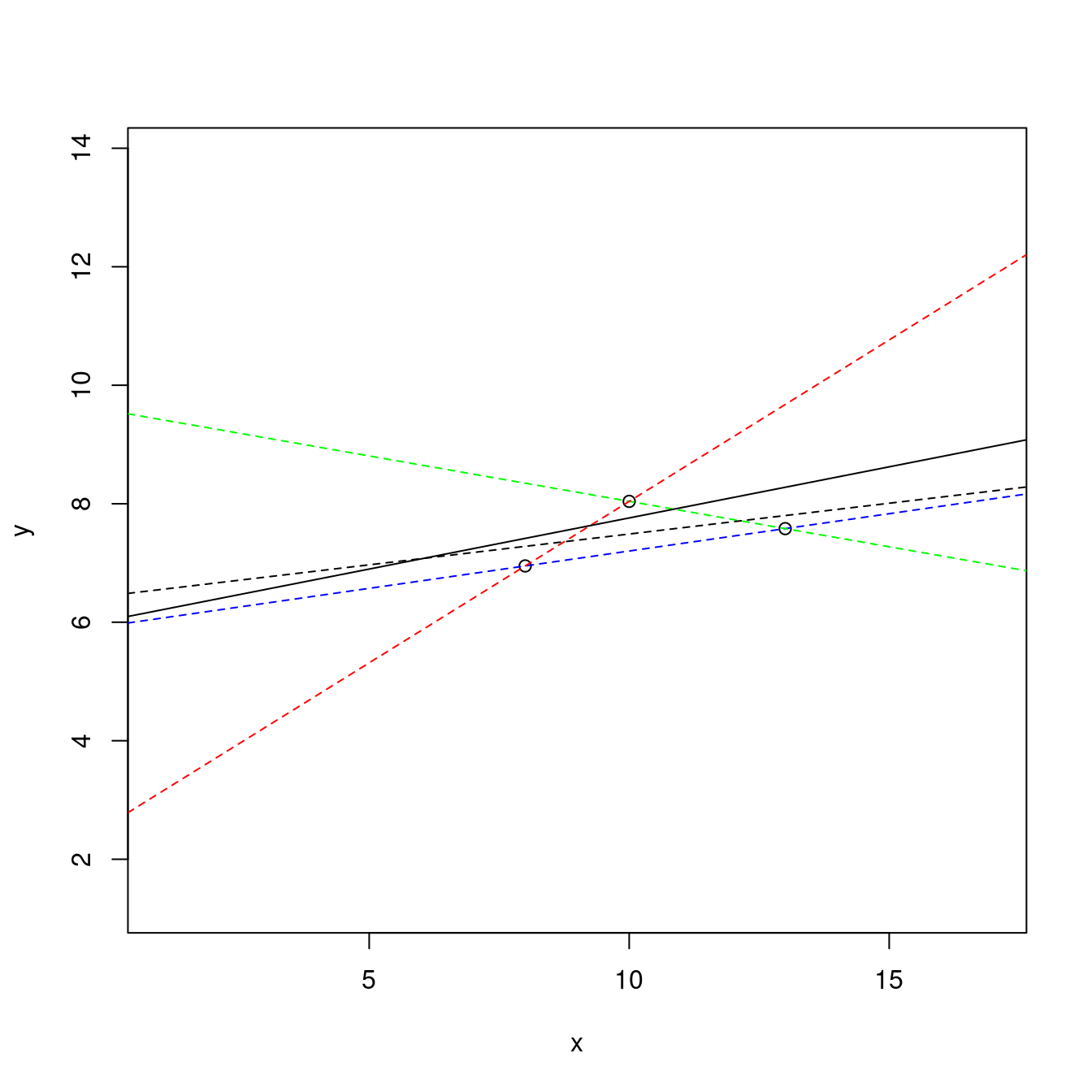
作者小編在這裡故意「遮掉」得到上述「加味散佈圖」的程式碼,請讀者諸君試著用自身的背景、知識、運氣,
猜猜哪一條是R算出來的「最小平方法」答案?
…
13.5.4 解析最小平方法迴歸線
前一小節,作者小編留下一個大問題:
從「五條線」挑出一條「合適的直線」。
作者小編,一直無力、無法、無方表達、說明、解釋「什麼是合適的直線」。不急,請繼續看作者小編怎麼
發展
怎麼「推演出」一種「合適的直線」?
- (步驟一) 只用前三點得到的「最小平方法迴歸線」合適嗎?
m0 <- lsfit(df[c(1,2,3), "x"], df[c(1,2,3), "y"]) # 取得前三筆觀察值的最小平方法迴歸線。
plot(df[c(1,2,3,4,5,6,7,8,9,10,11), c("x", "y")],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3),
col = c(1,1,1,rep(2,8))) # 全部數據的散佈圖,並且用顏色區分前三筆跟後八筆。
abline(m0) # 畫上前三筆觀察值的最小平方法迴歸線。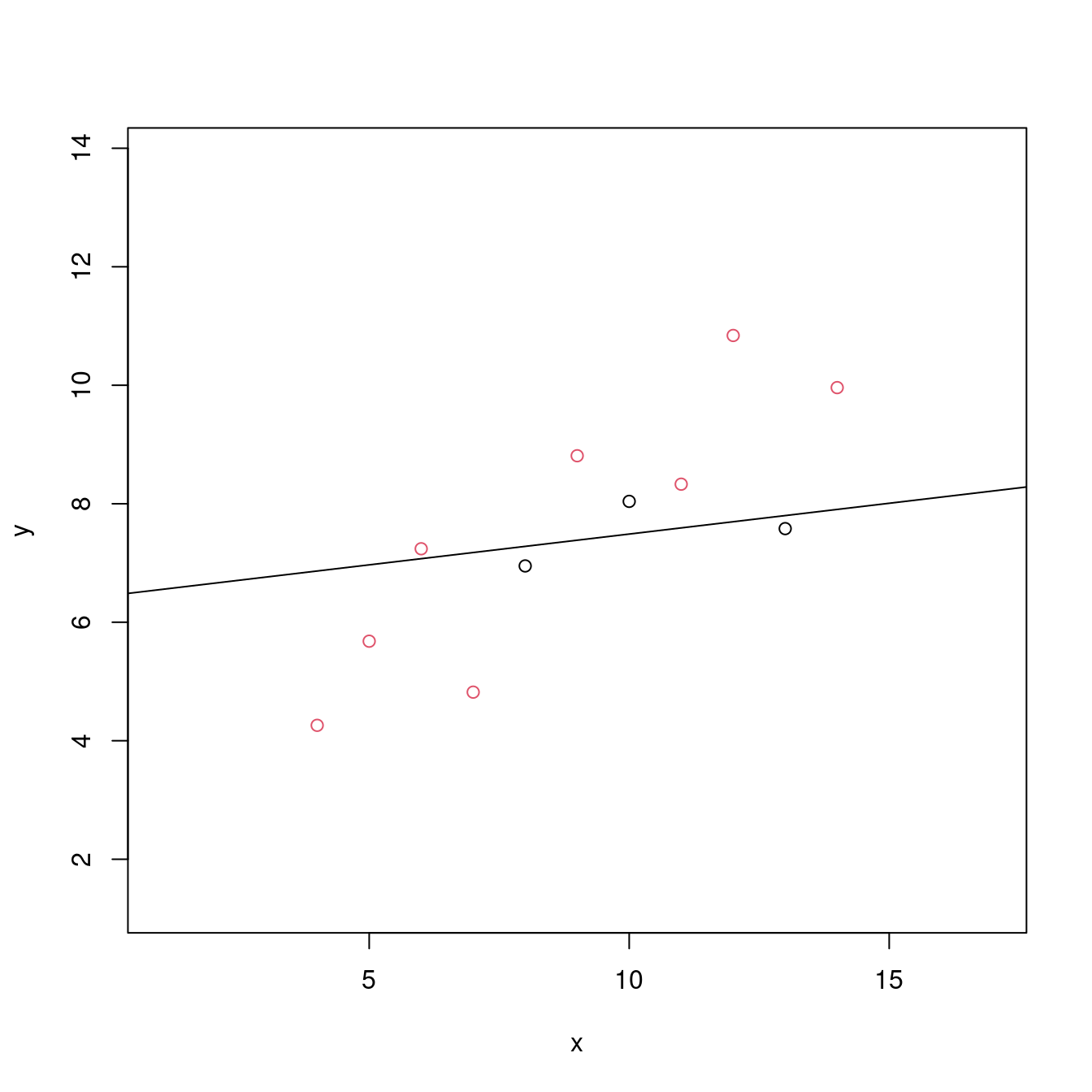
- (步驟二) 看過上圖之後,我們想問
這一條線的表現如何?適當嗎?
讓我們從「m0」抓「截距」跟「斜率」,計算「點與直線的『y』距離」以及「這些距離的平方和」。
a <- m0$coefficients[1] # 截距。請注意R的命名。
a## Intercept
## 6.449211b <- m0$coefficients[2] # 斜率。請注意R的命名。
b## X
## 0.1039474predy <- a + b * df[,"x"] # 戴帽子的y(一種對「猜測y」的說法,這是作者小編慣用的說法),也就是前三筆觀察值取得之直線上對應x的y。
predy## [1] 7.488684 7.280789 7.800526 7.384737 7.592632 7.904474 7.072895 6.865000
## [9] 7.696579 7.176842 6.968947df$predy0 <- predy # 擺入原始數據集的右邊欄位。注意,統計學裡,後生晚輩之欄位擺右邊。
df$SPE0 <- (df[,"y"] - df[, "predy0"])^2 # 計算誤差平方,並且擺入df。
df## x y predy0 SPE0
## 1 10 8.04 7.488684 0.30394910
## 2 8 6.95 7.280789 0.10942168
## 3 13 7.58 7.800526 0.04863186
## 4 9 8.81 7.384737 2.03137507
## 5 11 8.33 7.592632 0.54371219
## 6 14 9.96 7.904474 4.22518843
## 7 6 7.24 7.072895 0.02792417
## 8 4 4.26 6.865000 6.78602500
## 9 12 10.84 7.696579 9.88109591
## 10 7 4.82 7.176842 5.55470471
## 11 5 5.68 6.968947 1.66138532SSPE <- sum(df$SPE0) # 計算誤差平方和。
# 「SSPE = sum of squares of prediction error」
SSPE # 通常用「SSE = sum of squares of error」這一個代號。## [1] 31.17341plot(df[c(1,2,3,4,5,6,7,8,9,10,11), c("x", "y")],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3),
col = c(1,1,1,rep(2,8))) # 全部數據的散佈圖。
abline(m0) # 畫上前三筆觀察值的最小平方法迴歸線。
points(df[, c("x", "predy0")], col = "green") # 打上最小平方法迴歸線對應x的點。
lines(c(df[8, "x"], df[8, "x"]), c(df[8, "y"], df[8, "predy0"]), col = "blue") # 示意一段差距。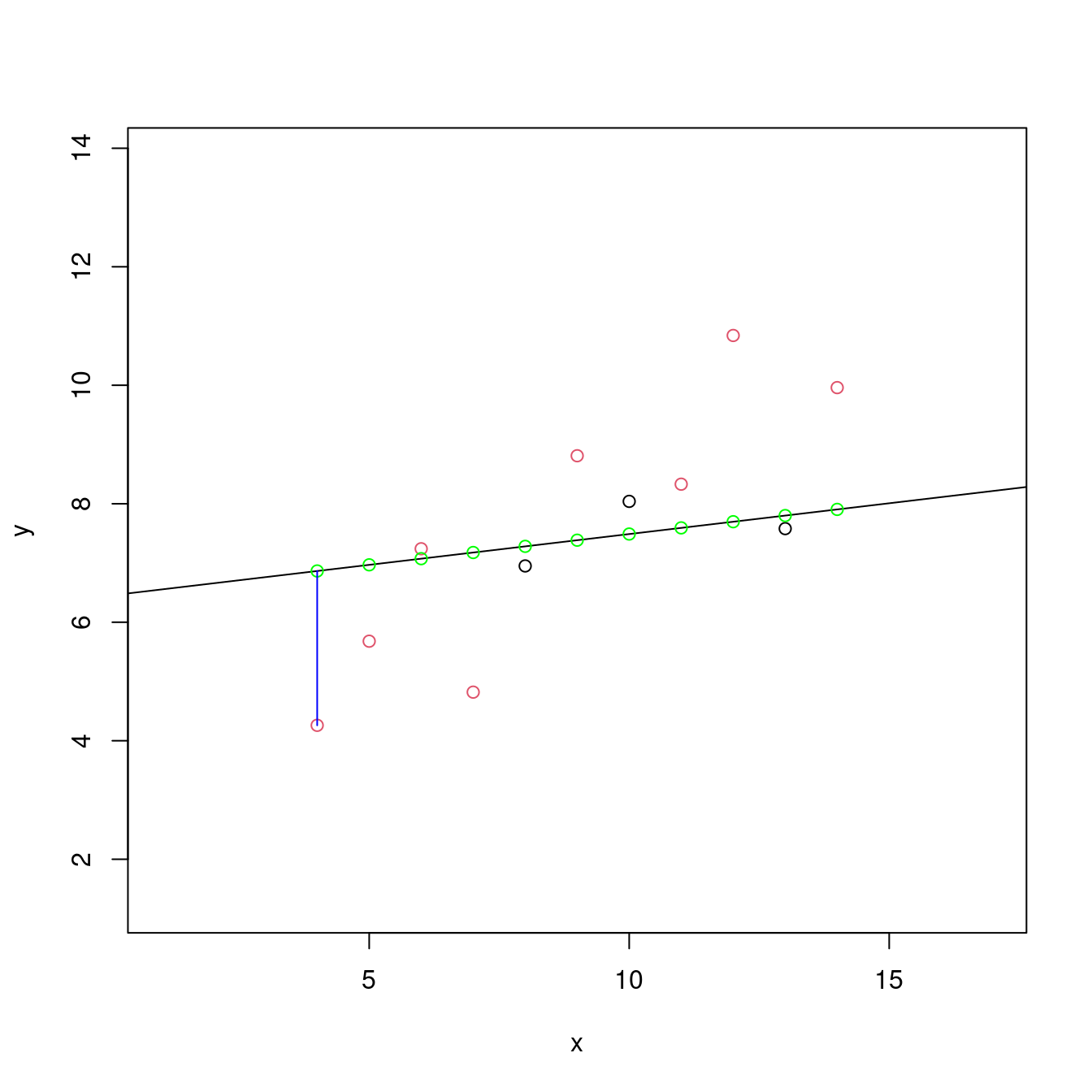
作者小編總結一下這一張圖,
- 「黑色點點」找到一條直線,「y = 6.4492105 + 0.1039474 x」、
- 「紅色點點」是剩下來的八個點、
- 「綠色點點」是把全部「x」代入上述方程式得到的點、
- 「y = 6.4492105 + 0.1039474 x」的表現可以用「31.1734134」來衡量、
- 作者小編認為應該有機會降低「31.1734134」這個數字?
- 假如可以讓「圖上的那條藍色線段變短」,應該有機會降低「31.1734134」這個數字?
怎麼做?
…
- (步驟三) 「最小平方法」就是答案!讀者諸君可能會問
這答案怎麼來的?
天外飛來一筆嗎?
什麼是「最小平方法」可能才是關鍵問題!
「最小平方法」搜尋那一條可以讓以下這一個數字,也就是「SSPE (SSE)」最小的直線:
\[\sum_{\hat y} (y - \hat y)^2 = \sum_{x} (y - (\hat \beta_0 + \hat \beta_1 \times x))^2\]
寫到這裡,作者小編「不禁」想要問,如果把「平方和」改成「絕對值和」,也就是以下這一個數字,那麼答案跟「最小平方法」的答案會一樣嗎?
\[\sum_{\hat y} | y - \hat y | = \sum_{x} | y - (\hat \beta_0 + \hat \beta_1 \times x) |\]
…
m1 <- lsfit(df[c(1,2,3,4,5,6,7,8,9,10,11), "x"], df[c(1,2,3,4,5,6,7,8,9,10,11), "y"])
a <- m1$coefficients[1] # 截距
a## Intercept
## 3.000091b <- m1$coefficients[2] # 斜率
b## X
## 0.5000909predy <- a + b * df[, "x"] # 戴帽子的y
predy## [1] 8.001000 7.000818 9.501273 7.500909 8.501091 10.001364 6.000636
## [8] 5.000455 9.001182 6.500727 5.500545df$predy1 <- predy
df$SPE1 <- (df[, "y"] - df[, "predy1"])^2
df## x y predy0 SPE0 predy1 SPE1
## 1 10 8.04 7.488684 0.30394910 8.001000 0.001521000
## 2 8 6.95 7.280789 0.10942168 7.000818 0.002582488
## 3 13 7.58 7.800526 0.04863186 9.501273 3.691288893
## 4 9 8.81 7.384737 2.03137507 7.500909 1.713719008
## 5 11 8.33 7.592632 0.54371219 8.501091 0.029272099
## 6 14 9.96 7.904474 4.22518843 10.001364 0.001710950
## 7 6 7.24 7.072895 0.02792417 6.000636 1.536022223
## 8 4 4.26 6.865000 6.78602500 5.000455 0.548272934
## 9 12 10.84 7.696579 9.88109591 9.001182 3.381252306
## 10 7 4.82 7.176842 5.55470471 6.500727 2.824844165
## 11 5 5.68 6.968947 1.66138532 5.500545 0.032203934SSPE <- sum(df$SPE1) # 誤差平方和
SSPE## [1] 13.76269plot(df[c(1,2,3,4,5,6,7,8,9,10,11), c("x", "y")],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3),
col = c(1,1,1,rep(2,8)))
abline(m0, lty = 2)
abline(m1)
points(df[, c("x", "predy0")], col = "green")
points(df[, c("x", "predy1")], col = "green")
lines(c(df[8, "x"], df[8, "x"]), c(df[8, "y"], df[8, "predy0"]), col = "blue", lty = 2)
lines(c(df[8, "x"], df[8, "x"]), c(df[8, "y"], df[8, "predy1"]), col = "blue")
points(mean(df[, "x"]), mean(df[, "y"]), pch = 19)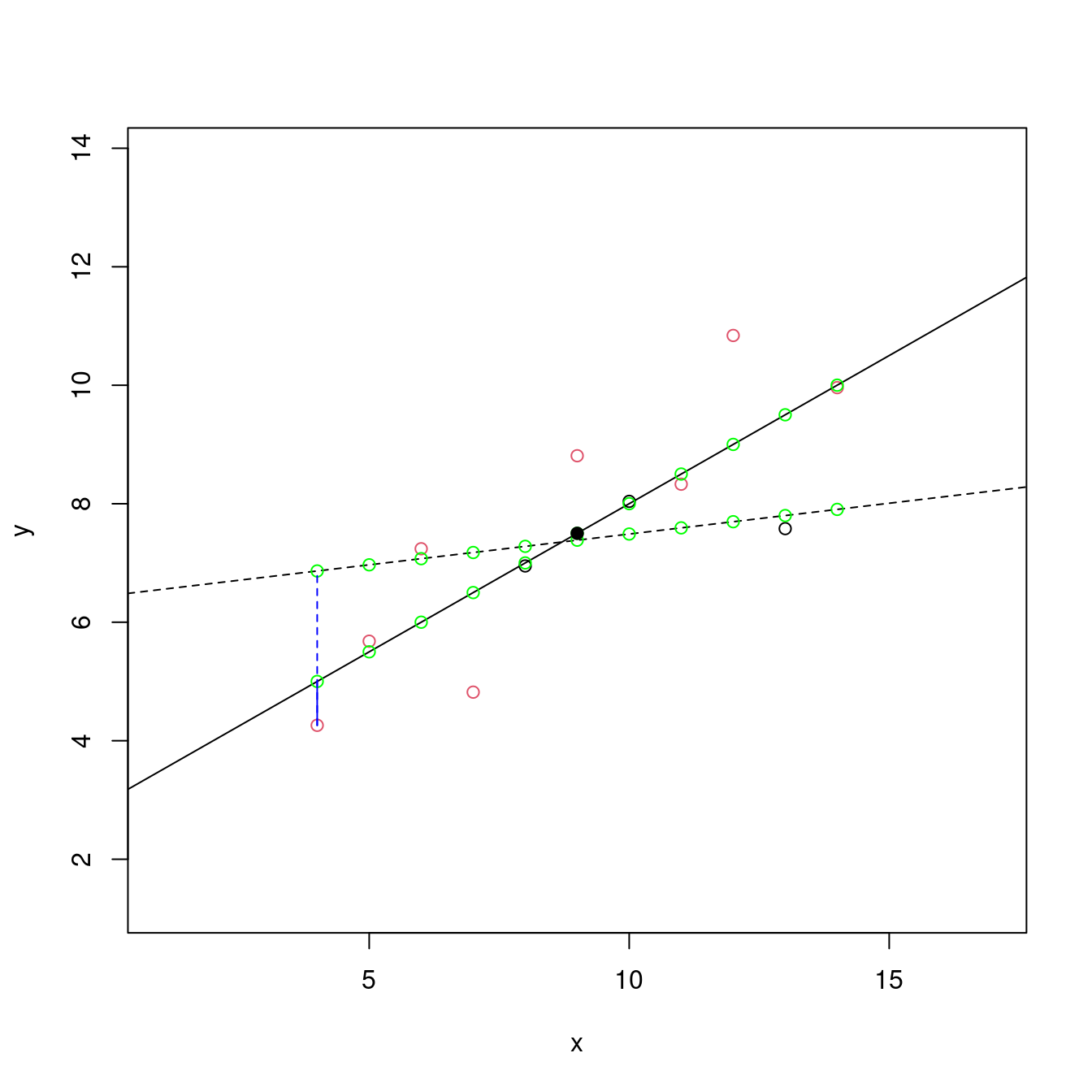
…
13.5.5 小結論
所謂的「最小平方法」概念下的「合適的迴歸直線」,就是那一條讓
\[\sum_{\hat y} (y - \hat y)^2 = \sum_{x} (y - (\hat \beta_0 + \hat \beta_1 \times x))^2\]
最小的直線。統計學家會這樣表達
\[\min_{\beta_0, \beta_1} \sum (y - \hat y)^2 = \min_{\beta_0, \beta_1} \sum (y - (\beta_0 + \beta_1 \times x))^2\]
科學上,這是一種「優化的問題」。所謂的「優化」,就是「讓某一個數字最大」,或是「讓某一個數字最小」。比如說,「最小平方法」概念下的「合適的迴歸直線」讓
\[預測誤差平方和 = SSPE = 誤差平方和 = SSE\]
最小。至於,如果像現在,只有「一個x」加「一個y」,那「最小平方法迴歸線」在幾何上,就是「按著那顆『黑點』轉動『直線』直到『\(SSE\)』出現最小值為止」,得到的那一條直線就是答案,就是「最小平方法迴歸線」。
請看作者小編示範:
SSE <- numeric(0) # 準備放置各種可能直線的SSE。
ybar <- mean(df[, "y"]) # 全部y座標的平均數。
xbar <- mean(df[, "x"]) # 全部x座標的平均數。
# 透過觀察散佈圖,或是計算幾組點對點的斜率,定調「斜率」可能的範圍。
# 加上改變「一條直線的斜率」就是「旋轉一條直線」。
# 再加上「最小平方法迴歸線」一定通過(xbar,ybar)這一點,就可以取得對應某一個斜率的「截距」。
for (b in seq(-1, 1, 0.1)) {
a <- ybar - b * xbar
predy <- df[, "y"] - (a + b * df[, "x"])
SSE <- c(SSE, sum(predy^2))
}
plot(seq(-1, 1, 0.1), SSE, type = "l") # 顯示SSE的搜尋成果。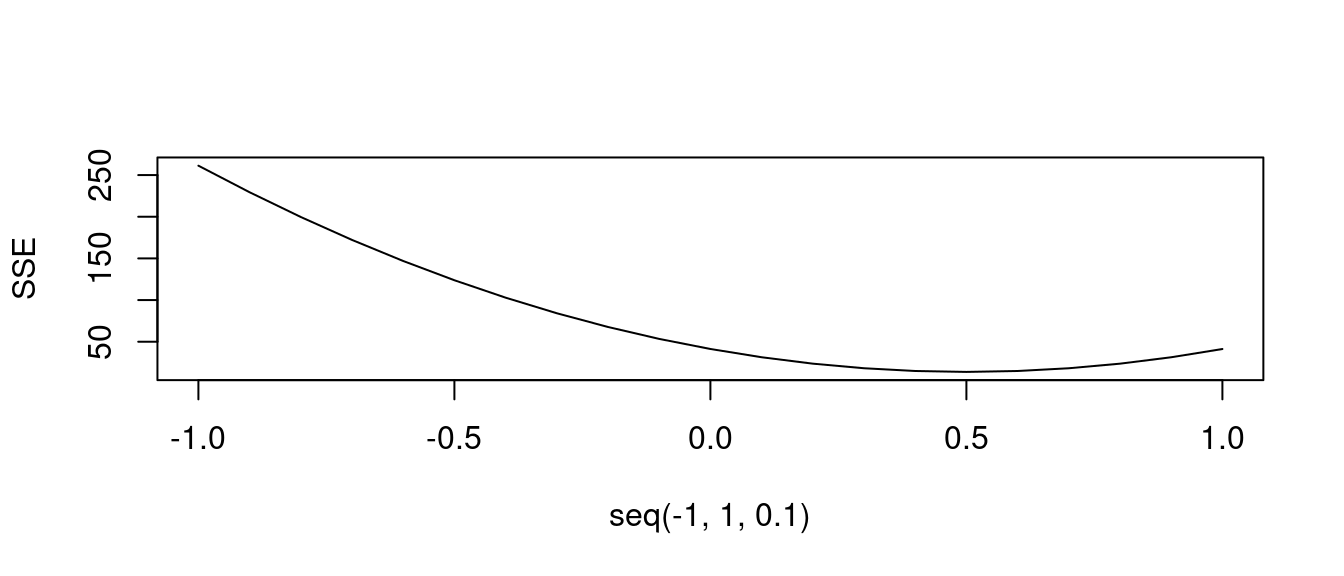
b <- seq(-1, 1, 0.1)[which.min(SSE)] # 最小化SSE的斜率等於多少?
a <- ybar - b * xbar # 對應上述斜率的截距。
LINE <- c(a, b)
names(LINE) <- c("a", "b")
LINE # 報告成果。## a b
## 3.000909 0.500000plot(df[, c("x", "y")],
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3)) # 最簡散佈圖。
abline(a = LINE["a"], b = LINE["b"], col = "red", lwd = 8) # 畫上搜尋成果的直線。
abline(m1, lwd = 3) # 畫上R提供的答案直線。
title(paste0("迴圈搜尋成果:", "y = ",
round(LINE["a"], 2),
" + ", round(LINE["b"], 2), "x",
"; R提供的成果:",
"y = ",
round(m1$coefficients[1], 2),
" + ", round(m1$coefficients[2], 2), "x"))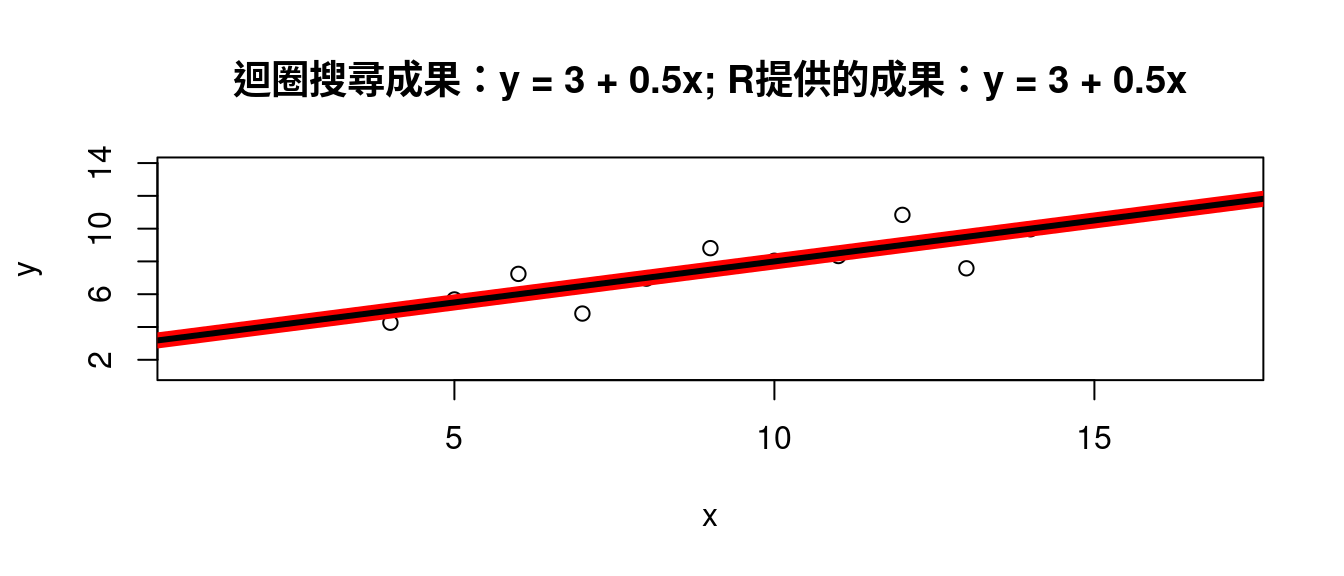
…
答案是一樣的!
13.6 回顧房價中位數與其他連續型變數的相關係數
繼續搜尋「房價中位數」的最小平方法迴歸線之前,先讓我們再一次回顧以下這幾個波士頓數據集內的連續型變數跟「房價中位數」的相關係數:
cor(x = boston[, CONvars[-12]], y = boston[, "medv"])## [,1]
## crim -0.3883046
## zn 0.3604453
## indus -0.4837252
## nox -0.4273208
## rm 0.6953599
## age -0.3769546
## dis 0.2499287
## tax -0.4685359
## ptratio -0.5077867
## black 0.3334608
## lstat -0.7376627我們發現
CORmedv <- cor(x = boston[, CONvars[-12]], y = boston[, "medv"])
rownames(CORmedv)[which(abs(CORmedv[,1]) <= 0.3)] # 小於0.3。## [1] "dis"rownames(CORmedv)[which(abs(CORmedv[,1]) > 0.3 & abs(CORmedv[,1]) <= 0.5)] # 大於0.3且小於0.5。## [1] "crim" "zn" "indus" "nox" "age" "tax" "black"rownames(CORmedv)[which(abs(CORmedv[,1]) > 0.5 & abs(CORmedv[,1]) <= 0.7)] # 大於0.5且小於0.7。## [1] "rm" "ptratio"rownames(CORmedv)[which(abs(CORmedv[,1]) > 0.7)] # 大於0.7。## [1] "lstat"也發現
rownames(CORmedv)[which.max(abs(CORmedv[,1]))] # 最大相關係數發生在哪一個變數?## [1] "lstat"rownames(CORmedv)[which.min(abs(CORmedv[,1]))] # 最小相關係數發生在哪一個變數?## [1] "dis"因為這個發現,作者小編寫了這一段程式碼示範「中文版說明『colsBostonFull』的用途與用處」。
maxCOR <- rownames(CORmedv)[which.max(abs(CORmedv[,1]))]
plot(boston[, maxCOR], boston[, "medv"],
xlab = colsBostonFull$中文變數名稱[which(colsBostonFull$變數名 == maxCOR)],
ylab = "房價中位數")
title(paste0("最高相關係數", " = ",
cor(boston[, maxCOR],
boston[, "medv"])))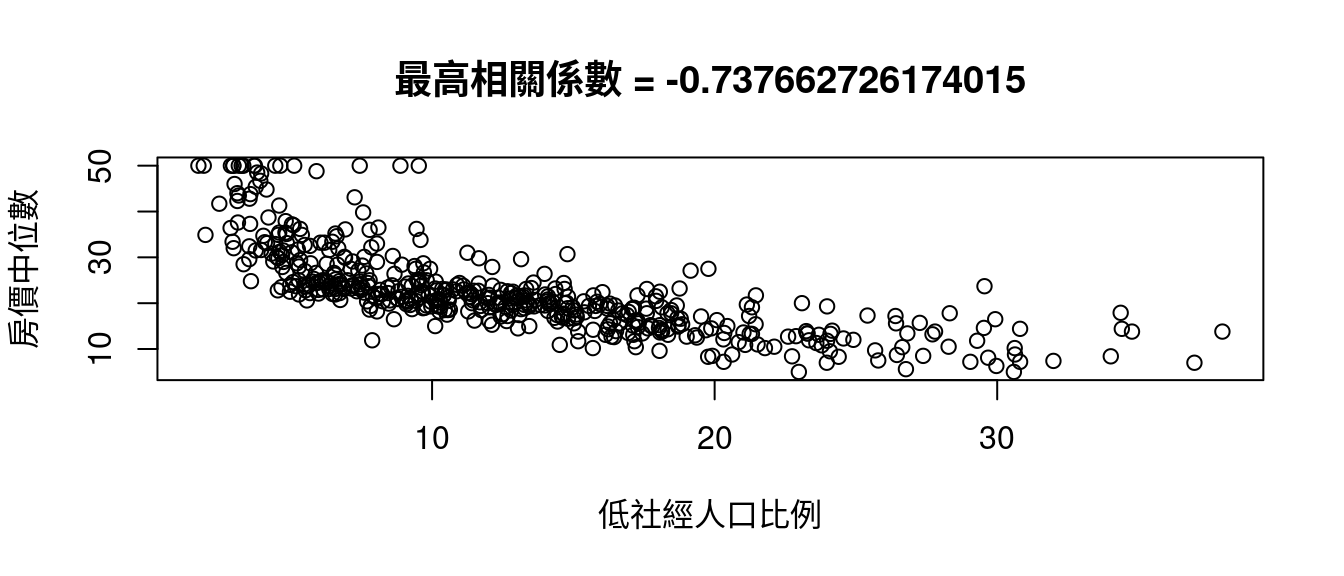
跟
minCOR <- rownames(CORmedv)[which.min(abs(CORmedv[,1]))]
plot(boston[, minCOR], boston[, "medv"],
xlab = colsBostonFull$中文變數名稱[which(colsBostonFull$變數名 == minCOR)],
ylab = "房價中位數")
title(paste0("最低相關係數", " = ",
cor(boston[, minCOR],
boston[, "medv"])))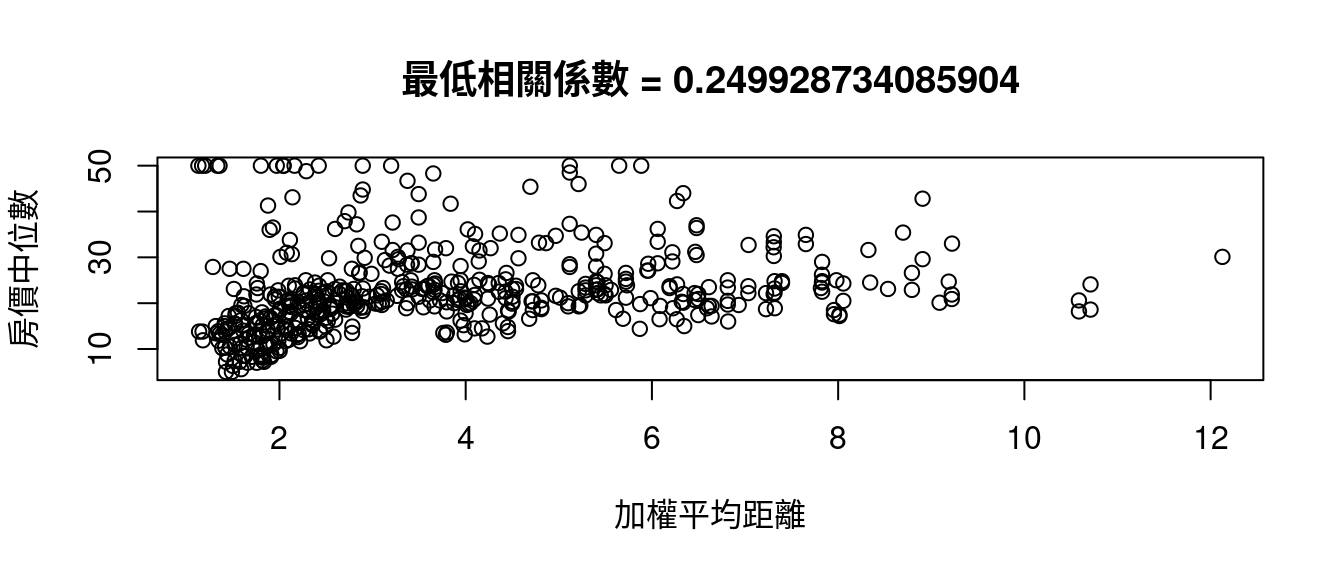
13.7 當x變數是低社經人口比例時的最小平方法迴歸線
先看「散佈圖」,
maxCOR## [1] "lstat"plot(boston[, "lstat"], boston[, "medv"], xlab = "低社經人口比例", ylab = "房價中位數")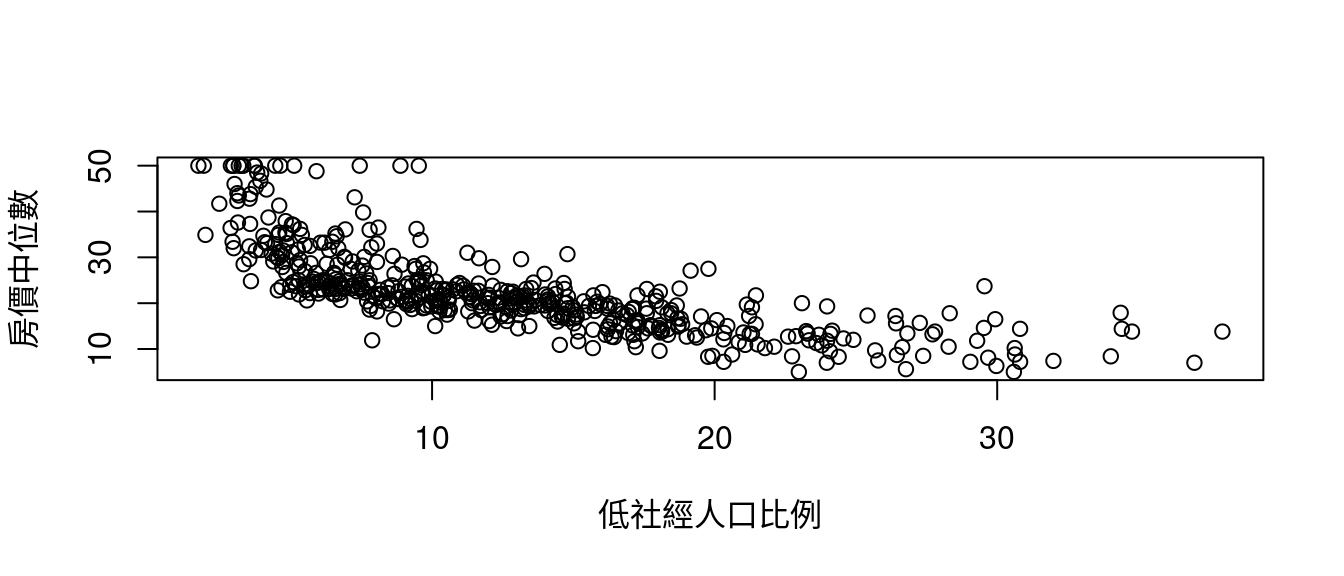
plot(sqrt(boston[, "lstat"]), boston[, "medv"], xlab = "低社經人口比例的正方根", ylab = "房價中位數")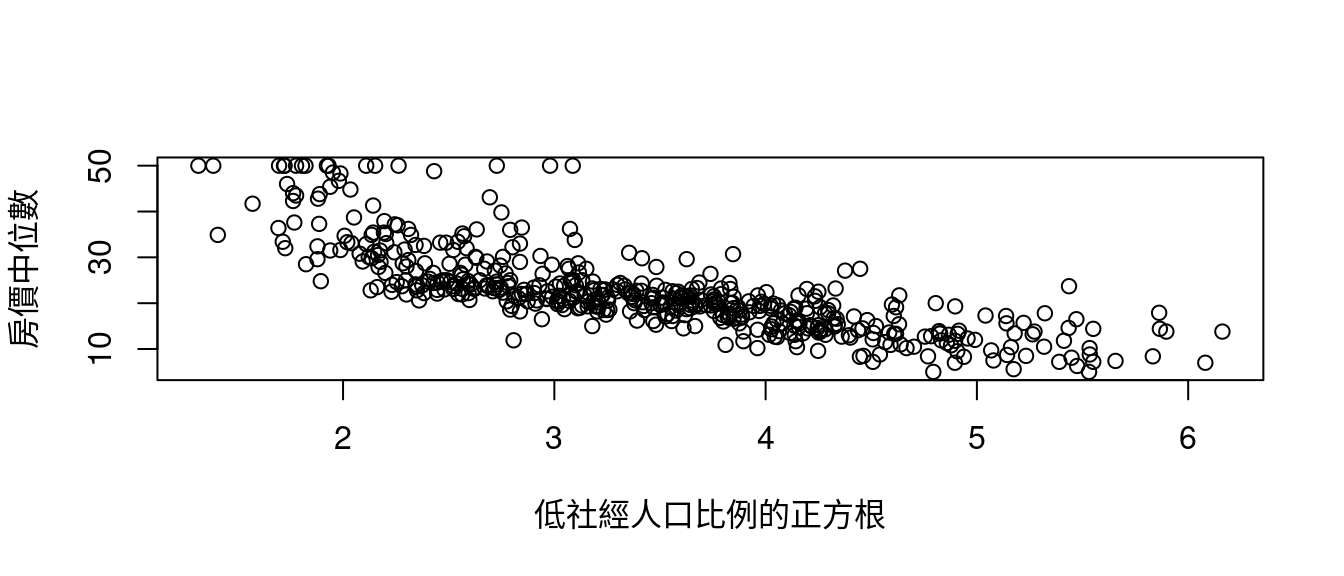
plot((boston[, "lstat"])^(1/3), boston[, "medv"], xlab = "低社經人口比例的三次方根", ylab = "房價中位數")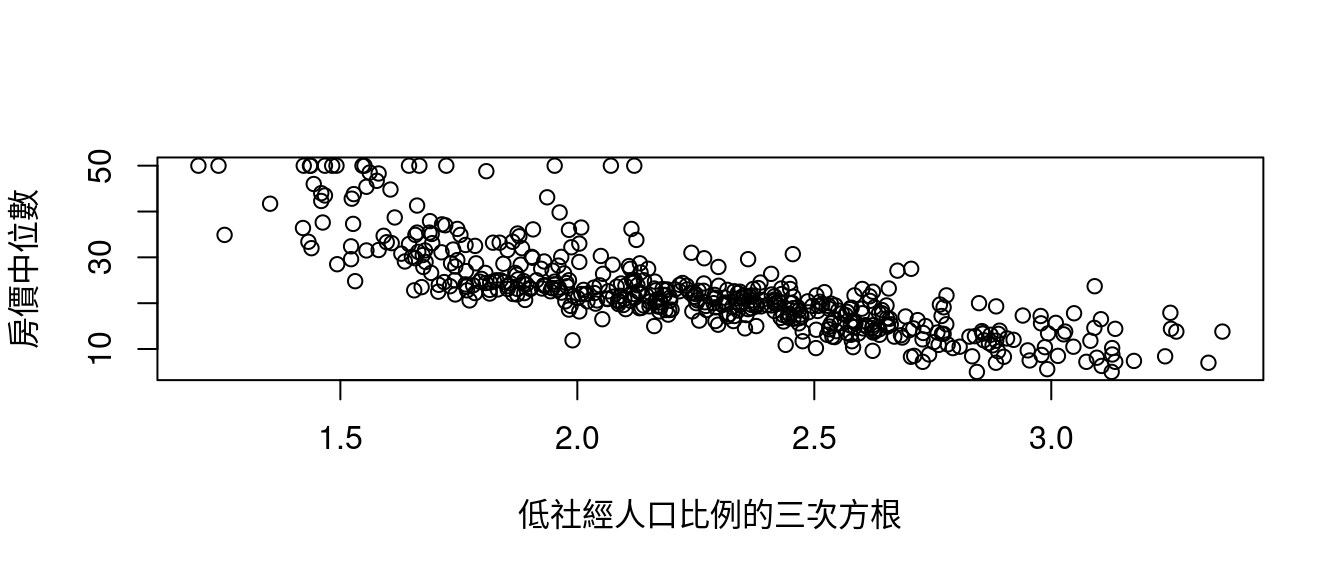
作者小編試過幾輪(多加了幾句plot)之後,決定這麼做:
miniBoston <- boston[, c("lstat", "medv")]
miniBoston$lstat2 <- sqrt(miniBoston$lstat)
miniBoston$lstat3 <- (miniBoston$lstat)^(1/3)
head(miniBoston)## lstat medv lstat2 lstat3
## 1 4.98 24.0 2.231591 1.707693
## 2 9.14 21.6 3.023243 2.090814
## 3 4.03 34.7 2.007486 1.591360
## 4 2.94 33.4 1.714643 1.432570
## 5 5.33 36.2 2.308679 1.746797
## 6 5.21 28.7 2.282542 1.733588tail(miniBoston)## lstat medv lstat2 lstat3
## 501 14.33 16.8 3.785499 2.428932
## 502 9.67 22.4 3.109662 2.130470
## 503 9.08 20.6 3.013304 2.086229
## 504 5.64 23.9 2.374868 1.780026
## 505 6.48 22.0 2.545584 1.864340
## 506 7.88 11.9 2.807134 1.989950m1 <- lsfit(miniBoston$lstat, miniBoston$medv)
sum(m1$residuals^2)## [1] 19472.38m2 <- lsfit(miniBoston$lstat2, miniBoston$medv)
sum(m2$residuals^2)## [1] 16386.13m3 <- lsfit(miniBoston$lstat3, miniBoston$medv)
sum(m3$residuals^2)## [1] 15546.59看過每一條最小平方法迴歸線的「SSE」之後,感覺上
「SSE」好像可以越來越小,
基於作者小編倡導的「連戲學習法」,作者小編再一次請「sapply」來幫忙,多算幾個「對『低社經人口比例(lstat)』開幾次方根的轉換之後的最小平方法迴歸線」:
SSE <- sapply(1:20, function(w){
m <- lsfit((miniBoston$lstat)^(1/w), miniBoston$medv)
sum(m$residuals^2)
}) # 算「20」個。
plot(SSE) # 繪製「SSE」的成果。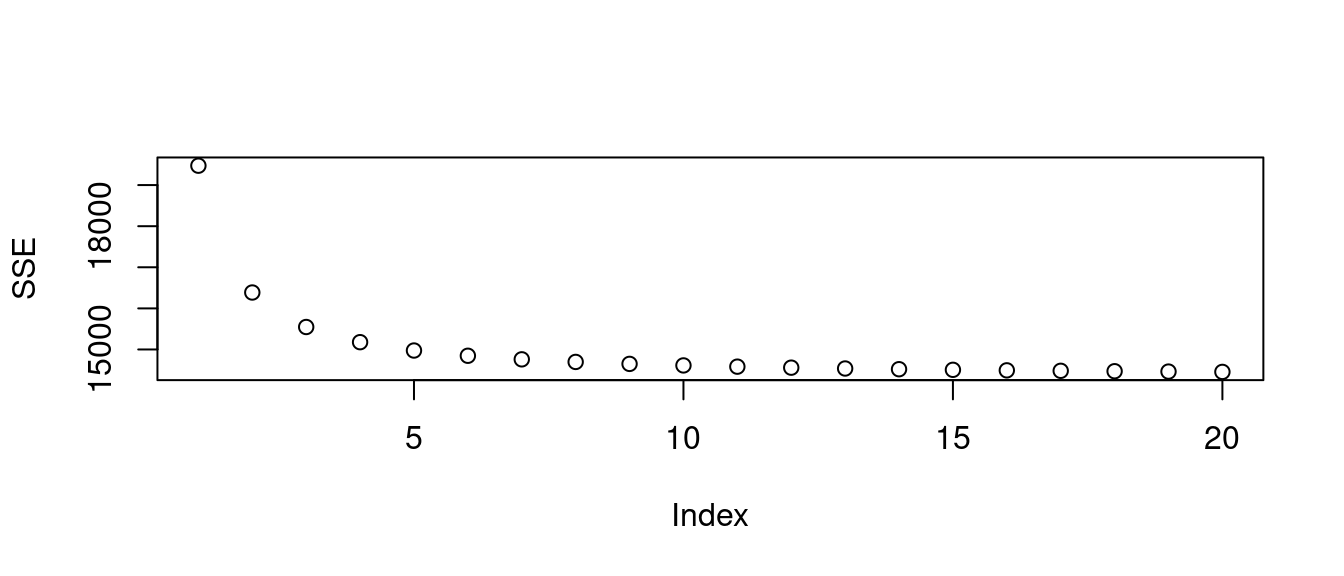
plot(diff(SSE)) # 繪製「SSE」前後相減的成果。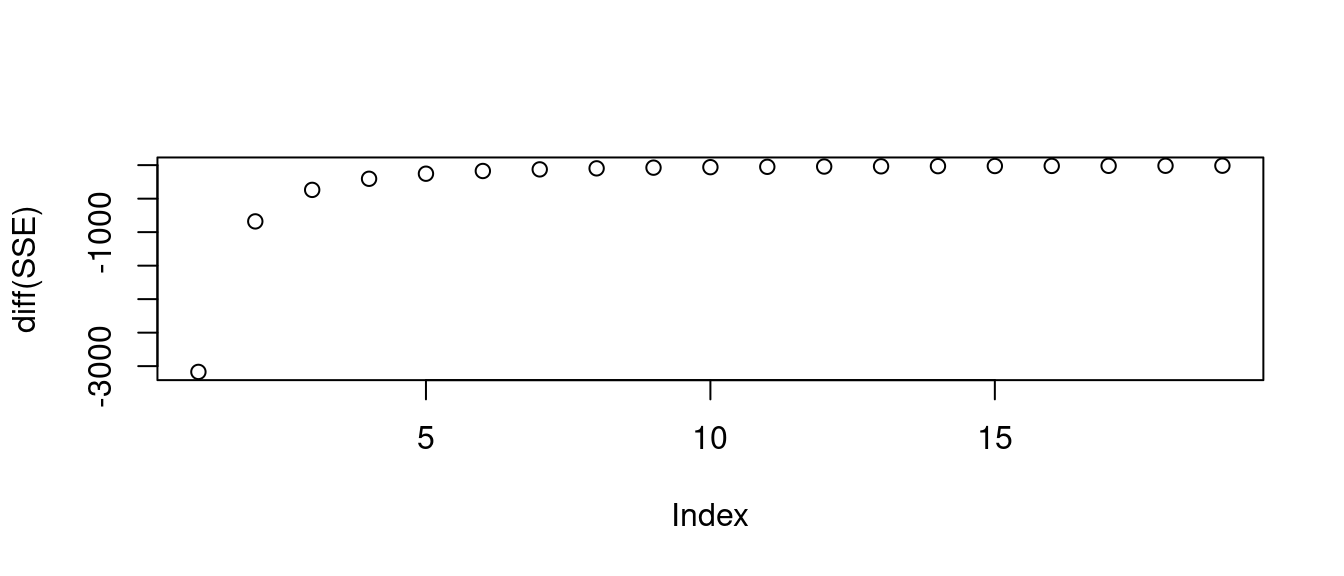
觀察過後,作者小編挑「10」,然後檢查成果。
m <- lsfit((miniBoston$lstat)^(1/10), miniBoston$medv)
sum(m$residuals^2) # SSE。## [1] 14611.59plot((miniBoston$lstat)^(1/10),
miniBoston$medv,
xlab = "低社經人口比例的十次方根",
ylab = "房價中位數",
main = paste0("y = ",
m$coefficients[1],
" + (",
m$coefficients[2],
") x"))
abline(m, col = "green") # 畫上最小平方法迴歸線。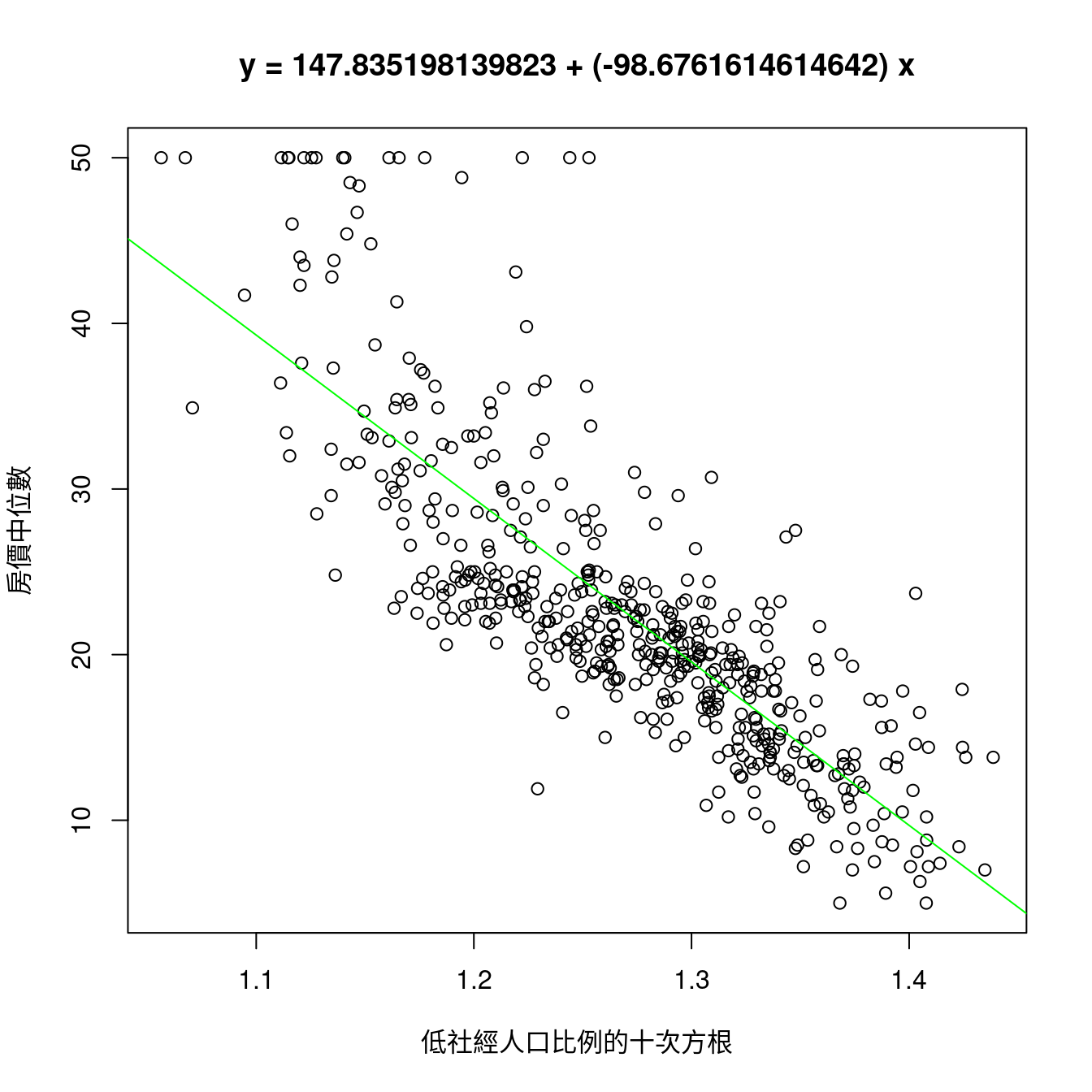
那「加權平均距離」有機會嗎?
為了對照「與房價中位數有著最高相關係數的『低社經人口比例(lstat)』的表現」,作者小編接下來,把上述程式碼「拷貝」過來,換掉「低社經人口比例」,改成「加權平均距離」,再研究「SSE」的現象。
miniBoston <- boston[, c("dis", "medv")]
SSE <- sapply(1:20, function(w){
m <- lsfit((miniBoston$dis)^(1/w), miniBoston$medv)
sum(m$residuals^2)
})
plot(SSE)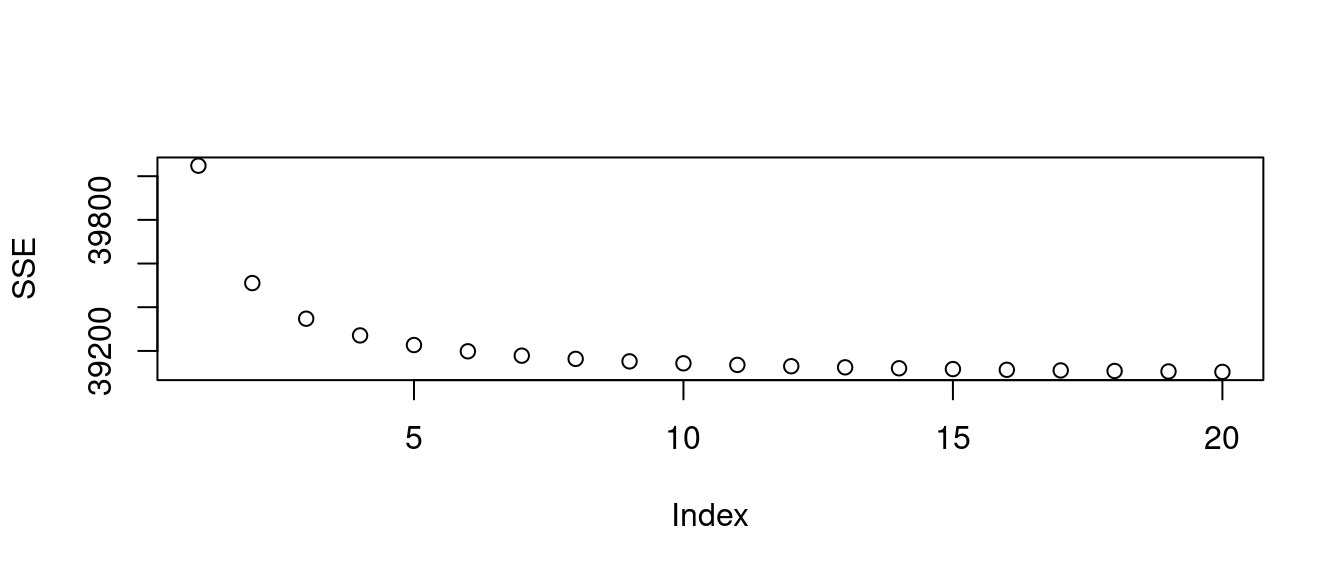
plot(diff(SSE))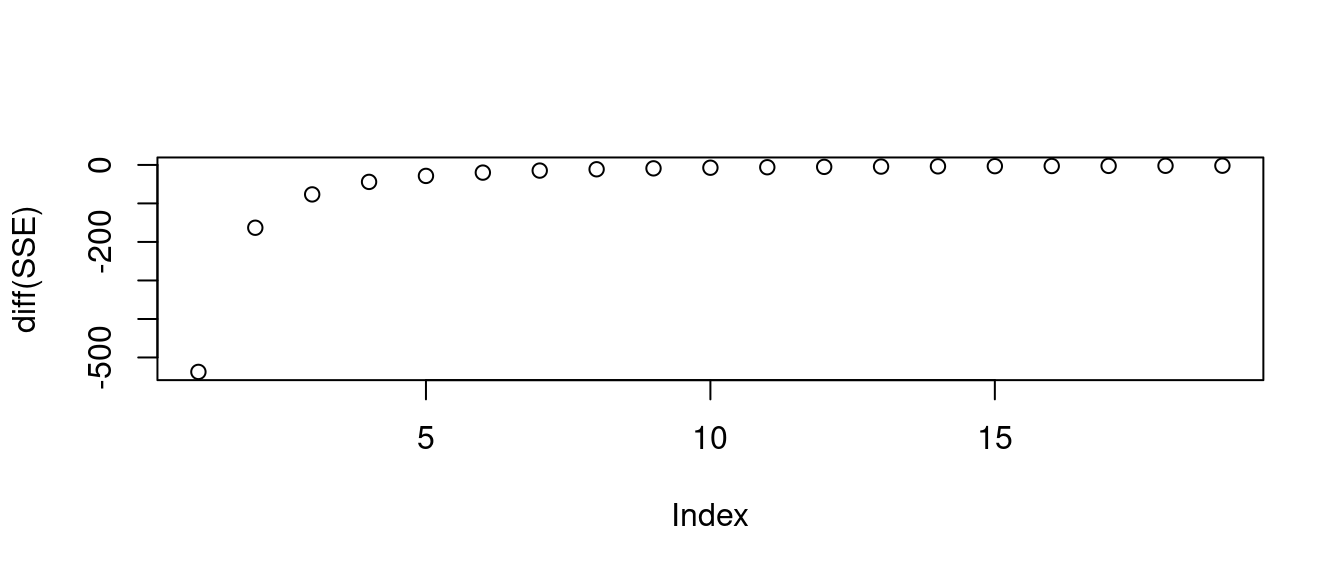
經過觀察,作者小編一樣挑「10」,然後檢查成果。
m <- lsfit((miniBoston$dis)^(1/10), miniBoston$medv)
sum(m$residuals^2) # 「SSE」確實比較高。「低相關係數的x確實帶出高SSE」。## [1] 39143.17plot((miniBoston$dis)^(1/10),
miniBoston$medv,
xlab = "加權平均距離的十次方根",
ylab = "房價中位數",
main = paste0("y = ",
m$coefficients[1],
" + (",
m$coefficients[2],
") x"))
abline(m, col = "green")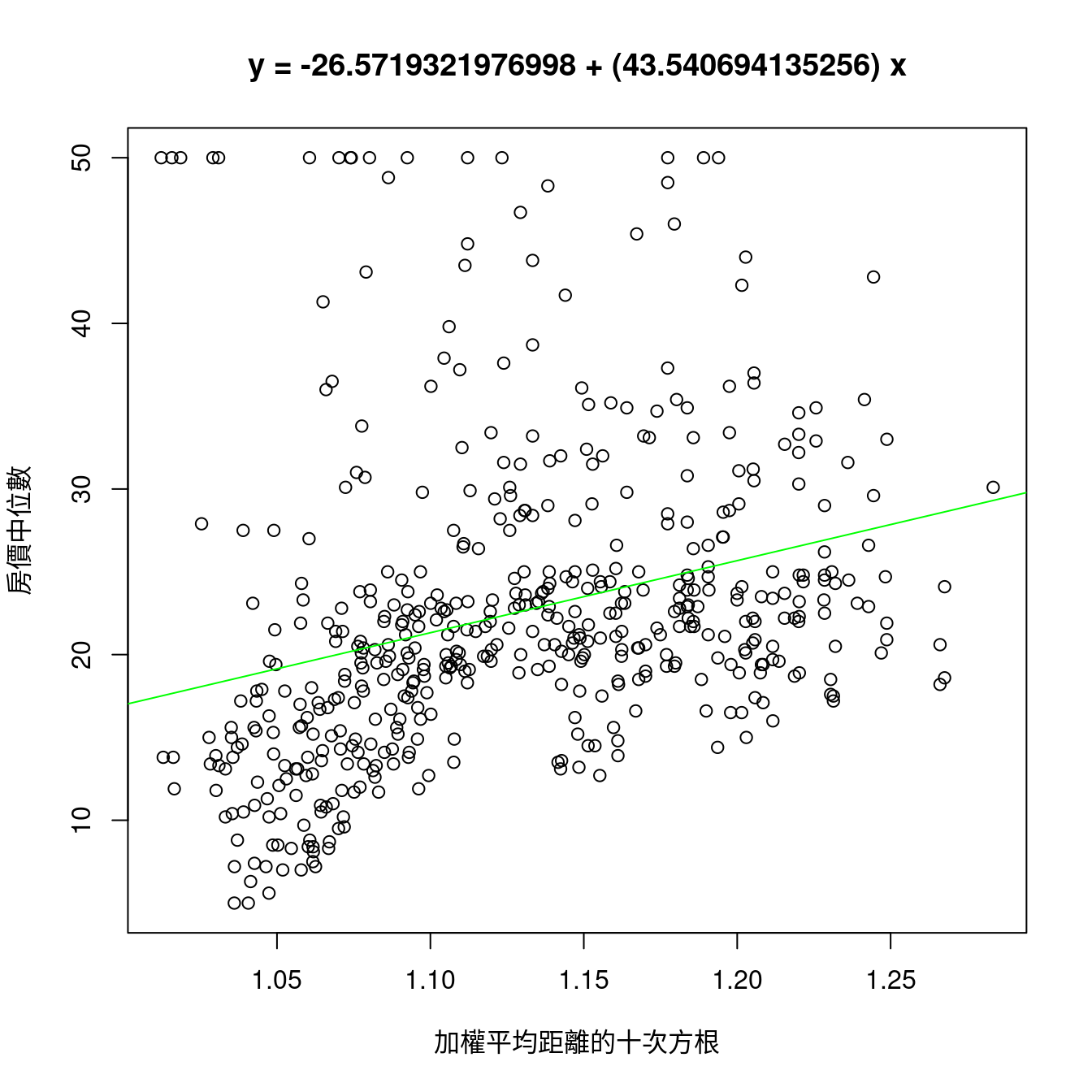
…
觀察過後,作者小編發現
「低」相關係數的x變數確實帶出「高」SSE。
接下來,作者小編想知道「低社經人口比例」在「\(R^2\)」的表現,這時候,「lsfit」就要讓位給「lm」了!
miniBoston <- boston[, c("lstat", "medv")]
miniBoston$lstat10 <- (miniBoston$lstat)^(1/10)
head(miniBoston)## lstat medv lstat10
## 1 4.98 24.0 1.174148
## 2 9.14 21.6 1.247655
## 3 4.03 34.7 1.149557
## 4 2.94 33.4 1.113871
## 5 5.33 36.2 1.182150
## 6 5.21 28.7 1.179462tail(miniBoston)## lstat medv lstat10
## 501 14.33 16.8 1.305042
## 502 9.67 22.4 1.254708
## 503 9.08 20.6 1.246834
## 504 5.64 23.9 1.188852
## 505 6.48 22.0 1.205473
## 506 7.88 11.9 1.229285m0 <- lm(medv ~ lstat, data = boston)
summary(m0)##
## Call:
## lm(formula = medv ~ lstat, data = boston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.168 -3.990 -1.318 2.034 24.500
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 34.55384 0.56263 61.41 <0.0000000000000002 ***
## lstat -0.95005 0.03873 -24.53 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.216 on 504 degrees of freedom
## Multiple R-squared: 0.5441, Adjusted R-squared: 0.5432
## F-statistic: 601.6 on 1 and 504 DF, p-value: < 0.00000000000000022m <- lm(medv ~ lstat10, data = miniBoston)
summary(m)##
## Call:
## lm(formula = medv ~ lstat10, data = miniBoston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -14.6341 -3.5815 -0.6994 2.0581 25.7941
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 147.835 4.032 36.67 <0.0000000000000002 ***
## lstat10 -98.676 3.169 -31.14 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.384 on 504 degrees of freedom
## Multiple R-squared: 0.6579, Adjusted R-squared: 0.6573
## F-statistic: 969.4 on 1 and 504 DF, p-value: < 0.00000000000000022通常,我們會先觀察「Multiple R-squared」的變化,結果是,從「未轉換的『低社經人口比例(lstat)』的0.5441463」,成長到「『低社經人口比例(lstat)十次方根』的0.6579388」。
漲幅是0.1137925。
13.7.1 小結論
在這一節,作者小編把「相關係數」的「強弱」與「最小平方法迴歸線」的「搜尋」結合起來。實驗證實:
- 「高相關係數變數」的「
SSE」低於「低相關係數變數」的「SSE」。 - 開方根變數變換可以繼續降低「低社經人口比例」跟「加權平均距離」的「
SSE」。 - 但是,「低社經人口比例」帶出來的「最小平方法迴歸線」依舊是「簡單線性迴歸線的冠軍」。
再繼續鑽研「1970年代波士頓都會區的最佳『hedonic housing price model』」之前,先來認識幾個基本迴歸分析專有名詞。
作者小編一直沒介紹「迴歸分析」相關的專有名詞,趁現在趕快介紹幾個最重要的專有名詞:
- 解釋變數:就是變數「
x」。它們是工程師、科學家、統計學家從「實驗設計」,「觀察研究」,或是「歷史資料」收集來、抓取來、變換來的變數。基本上,現階段的「x」,需要是那些「可被控制的」,或是「隨機性可被忽略的」變數。 - 反應變數:就是變數「
y」。在研究裡,某一個「隨機性無法被忽略的」變數。某一個需要被解釋的變數。像在這裏,搜尋「1970年代波士頓都會區的最佳「hedonic housing price model」,「房價」就是我們的「y」。由於,波士頓數據集來自1970年美國的普查「歷史資料」,其中的「x」變數都是「town」等級,所以「房價」這個「y」變身為「房價中位數」,某一個「town」全部「房價」的「中位數」是我們的「y」。 - 迴歸係數:如果是「簡單線性迴歸模型」,那就是「跟著變數『
x』的斜率」,也就是「改變『x』一個單位帶出多少個『y』的那個數字」。如果,變數「x」的範圍涵蓋「0」,那麼「x = 0」的「y」就是另一個迴歸係數,叫做「截距」。 - 隨機誤差:為了捕抓變數「
y」的「不可忽略隨機性」,模型\(y = \beta_0 + \beta_1 x\)之後再加上「\(\epsilon\)」,試圖把變數「x」的直線抓不到的「資訊」通通放在這個符號裡。根據這個「想像」,我們有可能可以發展出這樣的模型:\(y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon\)。 - 殘差:就是\(y - (\hat \beta_0 + \hat \beta_1 x)\)
- \(R^2\):一個衡量「
SSE」被降低多少的相對數字。 - \(\bar R^2\):跟\(R^2\)一樣的思維,只是加上「平均」這樣的想法。
13.7.2 課堂練習
- 回顧Harrison and Rubinfeld (1979)當年關心的變數「
nox(空汙指標)」在「最小平方法迴歸線」的表現。
CORmedv["lstat",1]## lstat
## -0.7376627CORmedv["nox",1]## nox
## -0.4273208miniBoston <- boston[, c("nox", "medv")]
plot(medv ~ nox, data = miniBoston)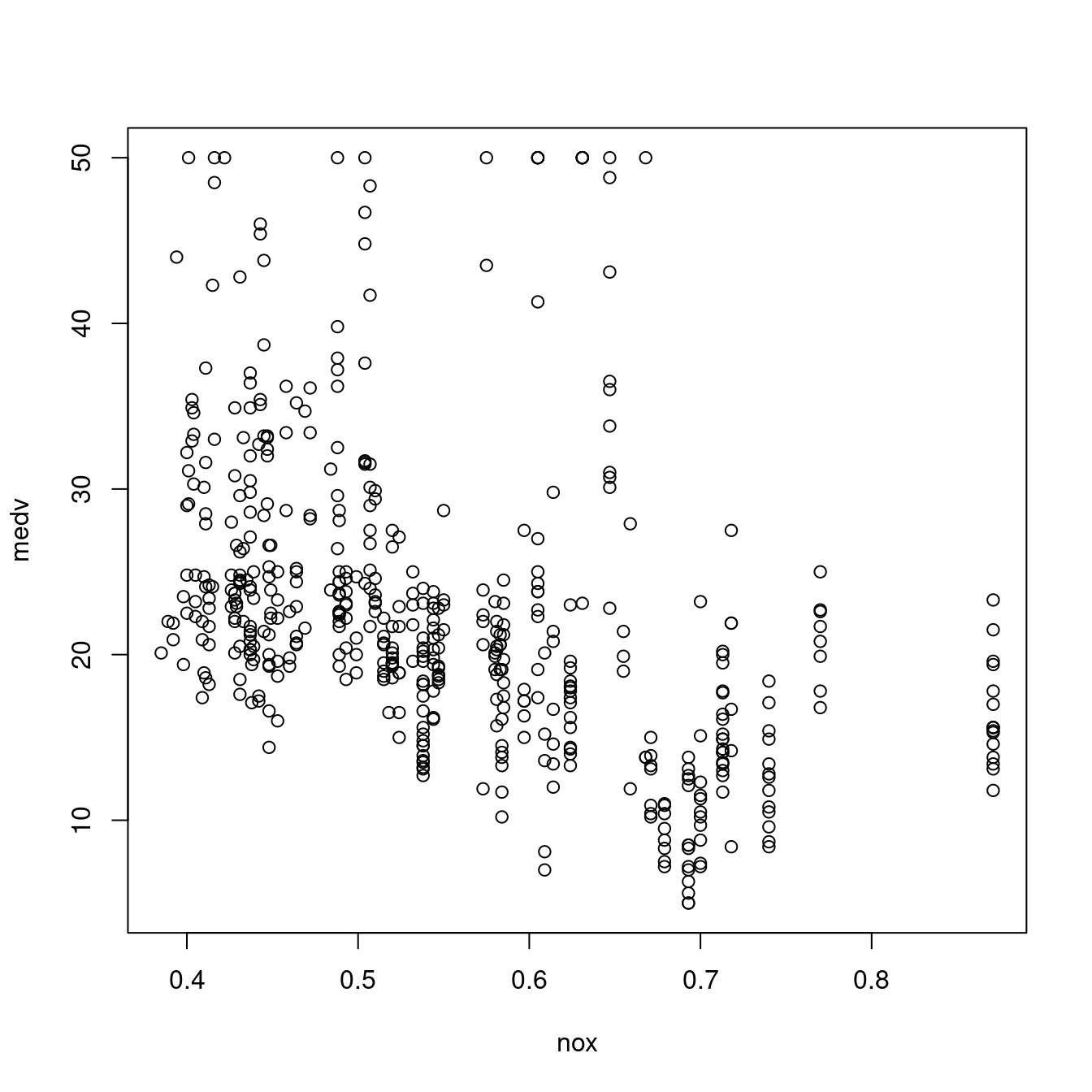
SSE <- sapply(1:20, function(w){
m <- lsfit((miniBoston$nox)^(1/w), miniBoston$medv)
sum(m$residuals^2)
})
plot(SSE)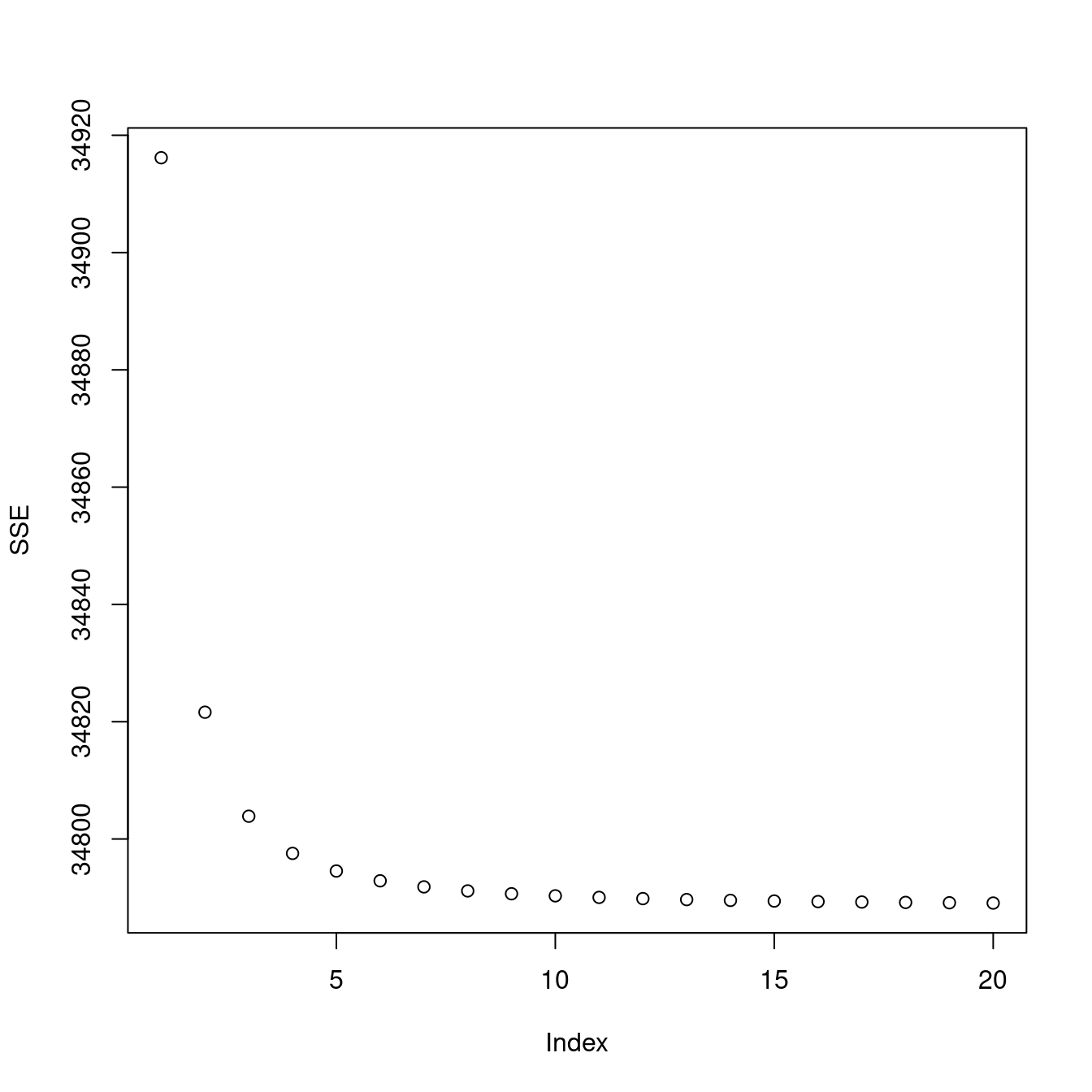
plot(diff(SSE))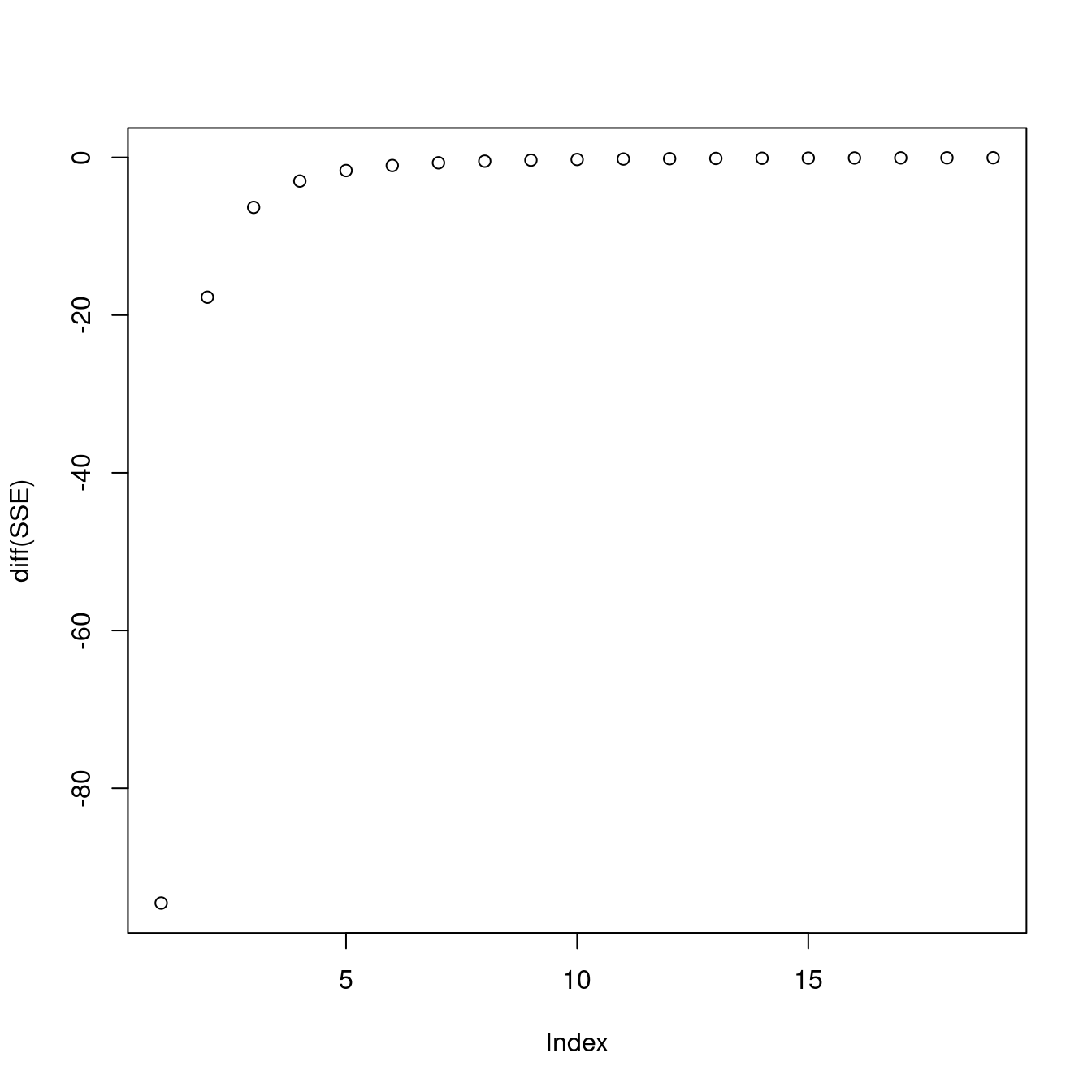
miniBoston$nox10 <- (miniBoston$nox)^(1/10)
head(miniBoston)## nox medv nox10
## 1 0.538 24.0 0.9398926
## 2 0.469 21.6 0.9270802
## 3 0.469 34.7 0.9270802
## 4 0.458 33.4 0.9248825
## 5 0.458 36.2 0.9248825
## 6 0.458 28.7 0.9248825tail(miniBoston)## nox medv nox10
## 501 0.585 16.8 0.9477976
## 502 0.573 22.4 0.9458352
## 503 0.573 20.6 0.9458352
## 504 0.573 23.9 0.9458352
## 505 0.573 22.0 0.9458352
## 506 0.573 11.9 0.9458352m0 <- lm(medv ~ nox, data = miniBoston)
summary(m0)##
## Call:
## lm(formula = medv ~ nox, data = miniBoston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.691 -5.121 -2.161 2.959 31.310
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 41.346 1.811 22.83 <0.0000000000000002 ***
## nox -33.916 3.196 -10.61 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.323 on 504 degrees of freedom
## Multiple R-squared: 0.1826, Adjusted R-squared: 0.181
## F-statistic: 112.6 on 1 and 504 DF, p-value: < 0.00000000000000022m <- lm(medv ~ nox10, data = miniBoston)
summary(m)##
## Call:
## lm(formula = medv ~ nox10, data = miniBoston)
##
## Residuals:
## Min 1Q Median 3Q Max
## -13.325 -5.088 -2.042 2.768 31.516
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 218.45 18.29 11.95 <0.0000000000000002 ***
## nox10 -208.20 19.43 -10.72 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 8.308 on 504 degrees of freedom
## Multiple R-squared: 0.1855, Adjusted R-squared: 0.1839
## F-statistic: 114.8 on 1 and 504 DF, p-value: < 0.0000000000000002213.8 特徵值工程對最小平方法的影響
我們已經經歷過「開方根變數變換」可以
- 降低殘差平方和(
SSE) - 提升\(R^2\)
「變數變換」是「搜尋工程」裡的一項可能性。除了,「開方根變數變換」,還有其他可能性。在這裡,作者小編順應「機器學習」潮流,介紹、實驗兩種「變數變換」:
- 常態轉換
- 0-1轉換
13.8.1 常態轉換對最小平方法的影響
# 呼叫套件「bestNormalize」。
require(bestNormalize)
# 抓「房價中位數」。
medv <- boston[, "medv"]
# 請「bestNormalize」把「房價中位數」變得更像「常態分配變數」。
medv2 <- bestNormalize(medv)
# 抓「低社經人口比例」。
lstat <- boston[, "lstat"]
# 請「bestNormalize」把「低社經人口比例」變得更像「常態分配變數」。
lstat2 <- bestNormalize(lstat)
# 繪製直方圖,檢視「是不是變得比較『常態』?」
par(mfrow = c(1,4))
hist(medv, main = "變換前")
hist(medv2[["x.t"]], main = "變換後")
hist(lstat, main = "變換前")
hist(lstat2[["x.t"]], main = "變換後")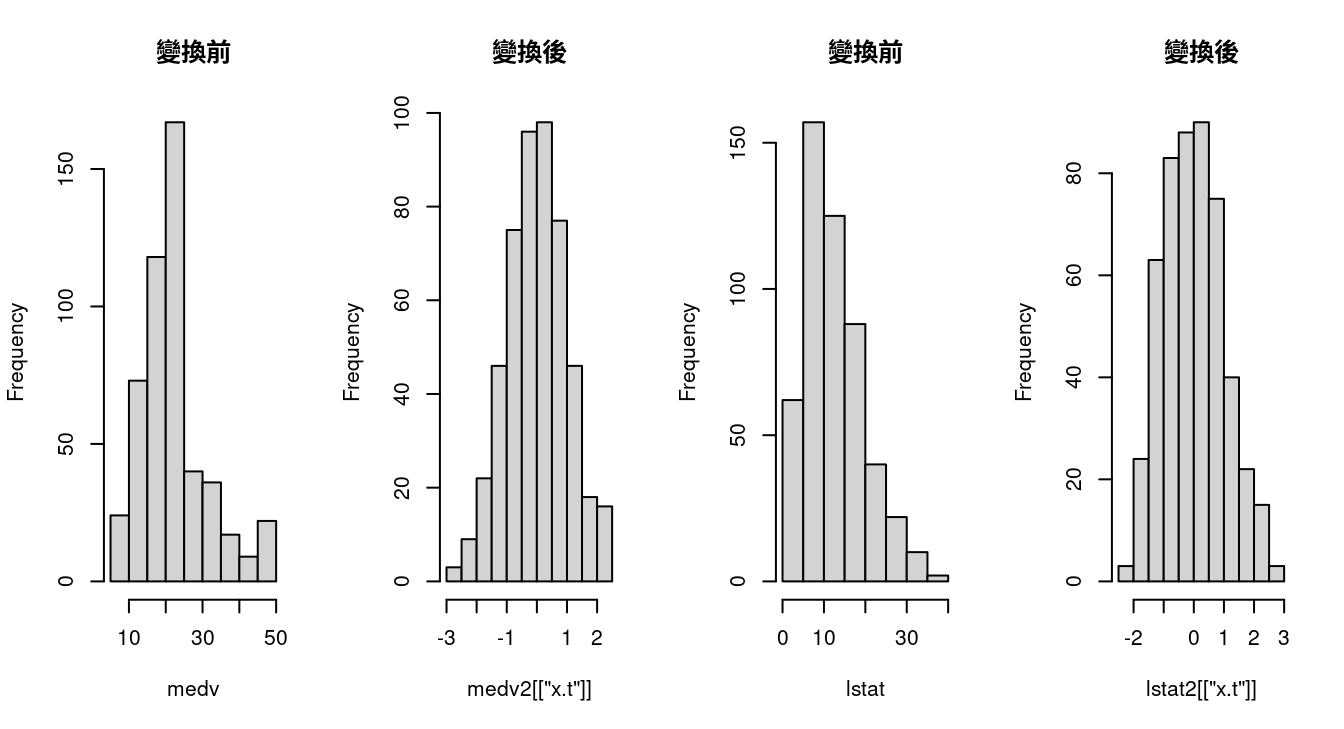
# 抓「加權平均距離」
dis <- boston[, "dis"]
# 請「bestNormalize」把「加權平均距離」變得更像「常態分配變數」。
dis2 <- bestNormalize(dis)
# 把畫布變為一整張。
par(mfrow = c(1,1))
# 摘要新變數之間的最小平方法迴歸線。
plot(lstat2[["x.t"]], medv2[["x.t"]])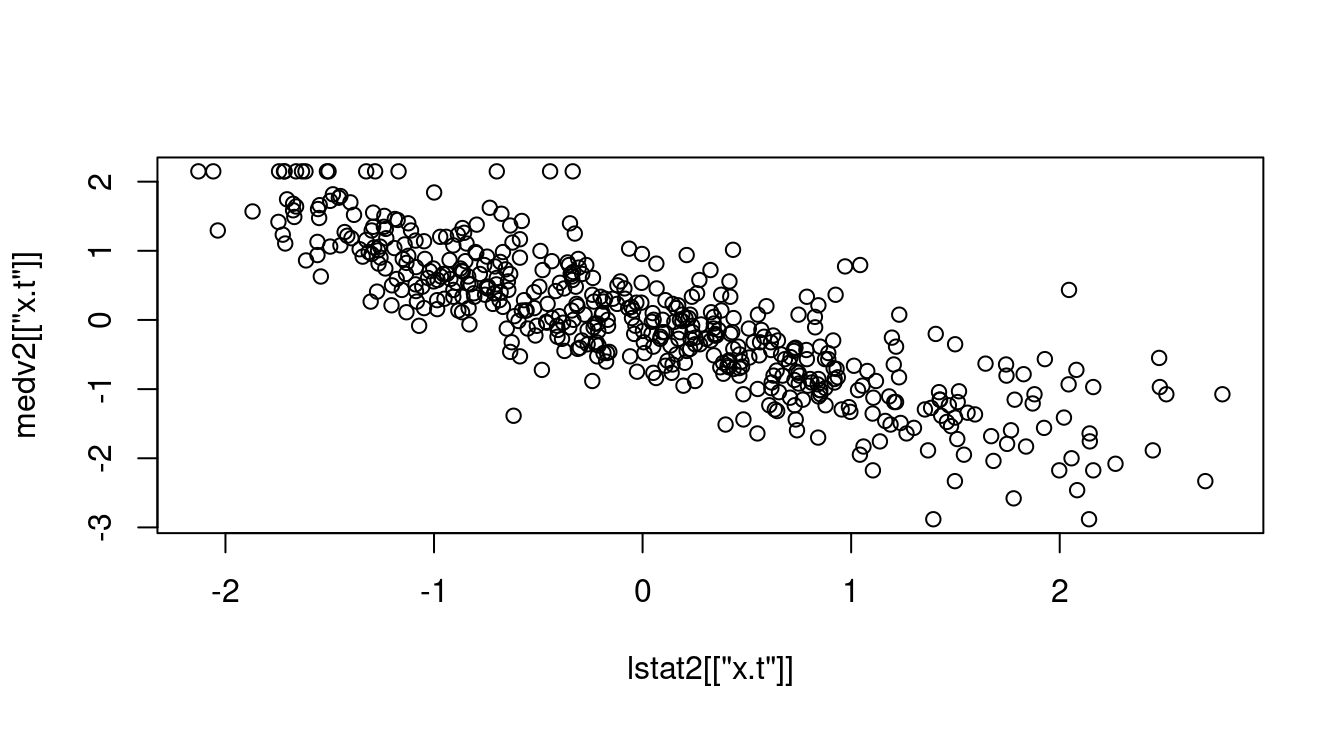
summary(lm(medv2[["x.t"]] ~ lstat2[["x.t"]]))##
## Call:
## lm(formula = medv2[["x.t"]] ~ lstat2[["x.t"]])
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.89660 -0.33550 -0.04472 0.30498 2.13694
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.002746 0.023989 -0.114 0.909
## lstat2[["x.t"]] -0.831399 0.024013 -34.623 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5396 on 504 degrees of freedom
## Multiple R-squared: 0.704, Adjusted R-squared: 0.7034
## F-statistic: 1199 on 1 and 504 DF, p-value: < 0.00000000000000022plot(dis2[["x.t"]], medv2[["x.t"]])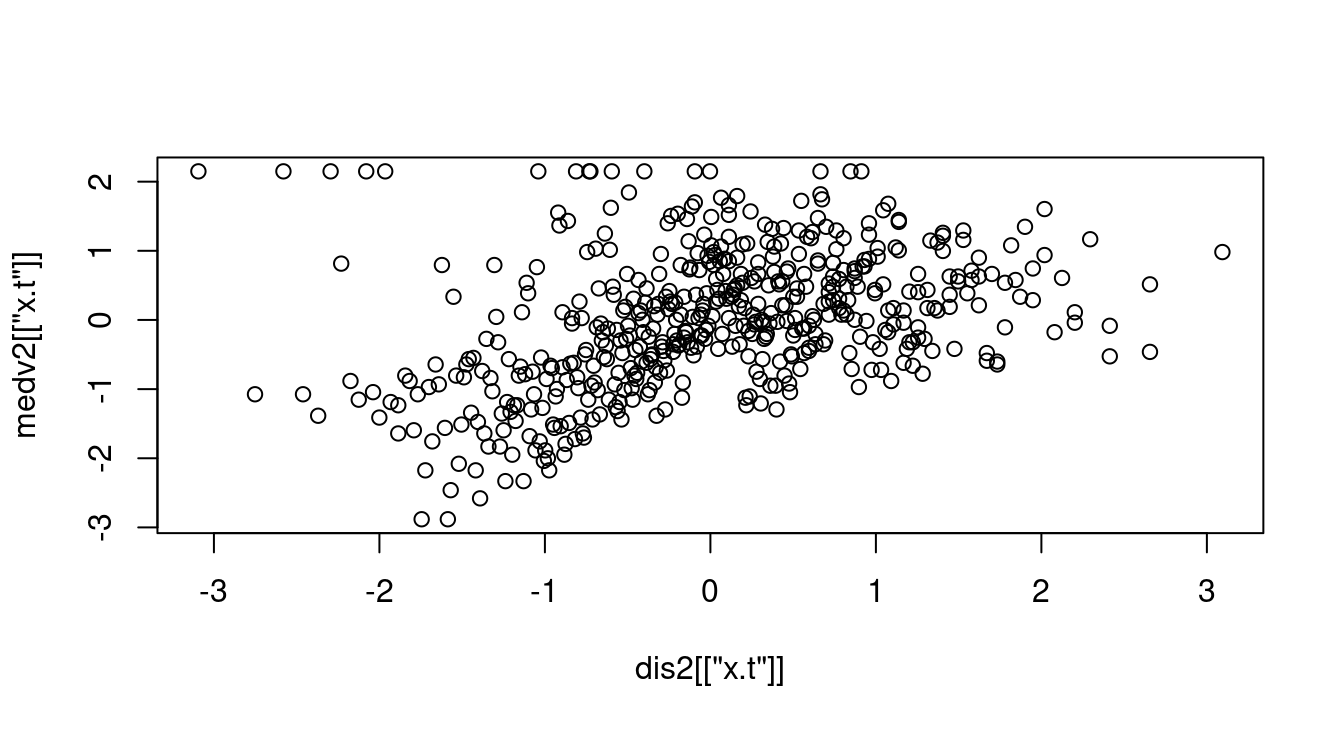
summary(lm(medv2[["x.t"]] ~ dis2[["x.t"]]))##
## Call:
## lm(formula = medv2[["x.t"]] ~ dis2[["x.t"]])
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.2629 -0.6139 -0.1062 0.5163 3.3538
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.002723 0.040567 -0.067 0.947
## dis2[["x.t"]] 0.388488 0.040626 9.563 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.9125 on 504 degrees of freedom
## Multiple R-squared: 0.1536, Adjusted R-squared: 0.1519
## F-statistic: 91.44 on 1 and 504 DF, p-value: < 0.00000000000000022成果如何呢?
13.8.2 0-1轉換對最小平方法的影響
medv <- boston[, "medv"]
medv3 <- (medv - min(medv))/diff(range(medv))
lstat <- boston[, "lstat"]
lstat3 <- (lstat - min(lstat))/diff(range(lstat))
par(mfrow = c(1,4))
hist(medv, main = "變換前")
hist(medv3, main = "變換後")
hist(lstat, main = "變換前")
hist(lstat3, main = "變換後")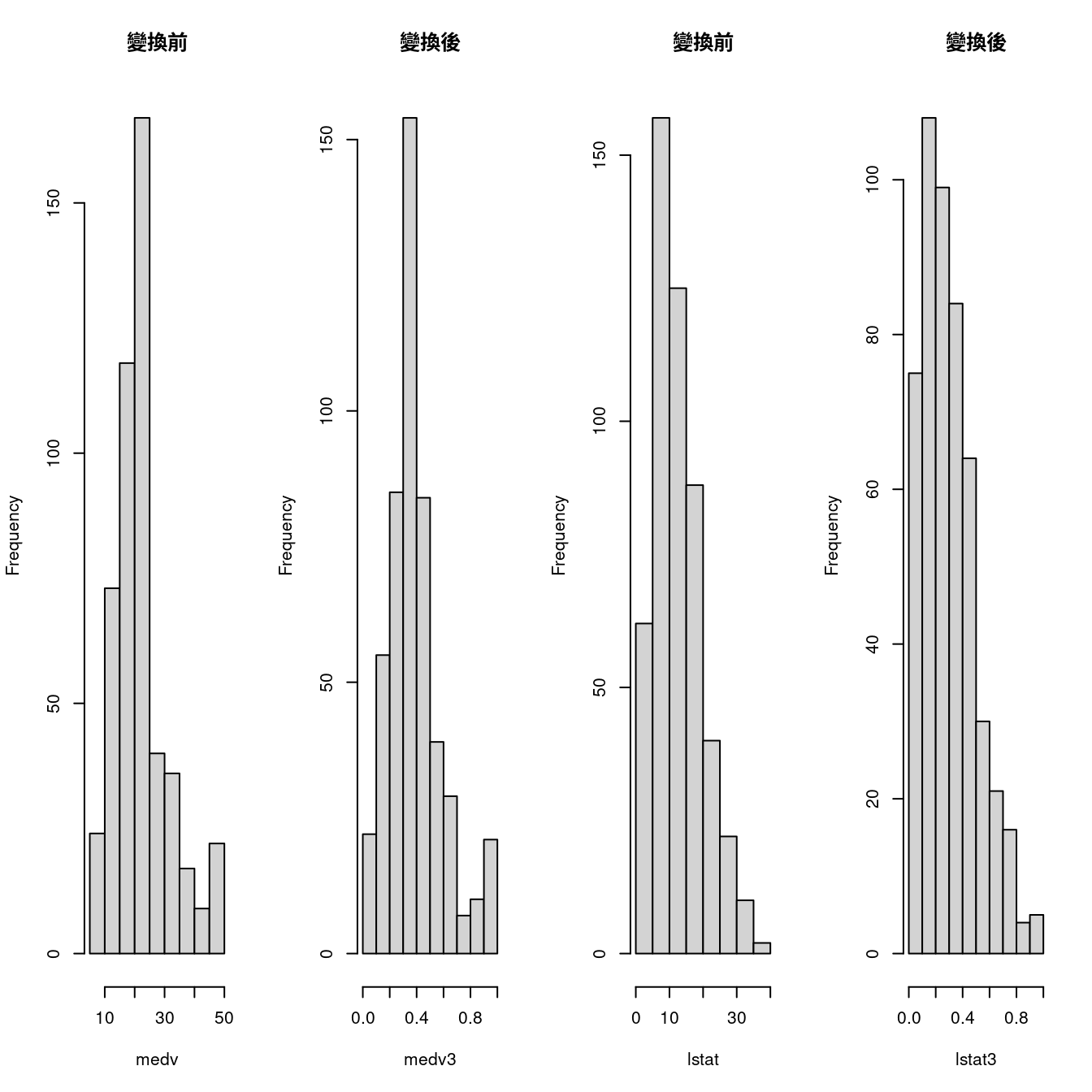
dis <- boston[, "dis"]
dis3 <- (dis - min(dis))/diff(range(dis))
par(mfrow = c(1,1))
plot(lstat3, medv3)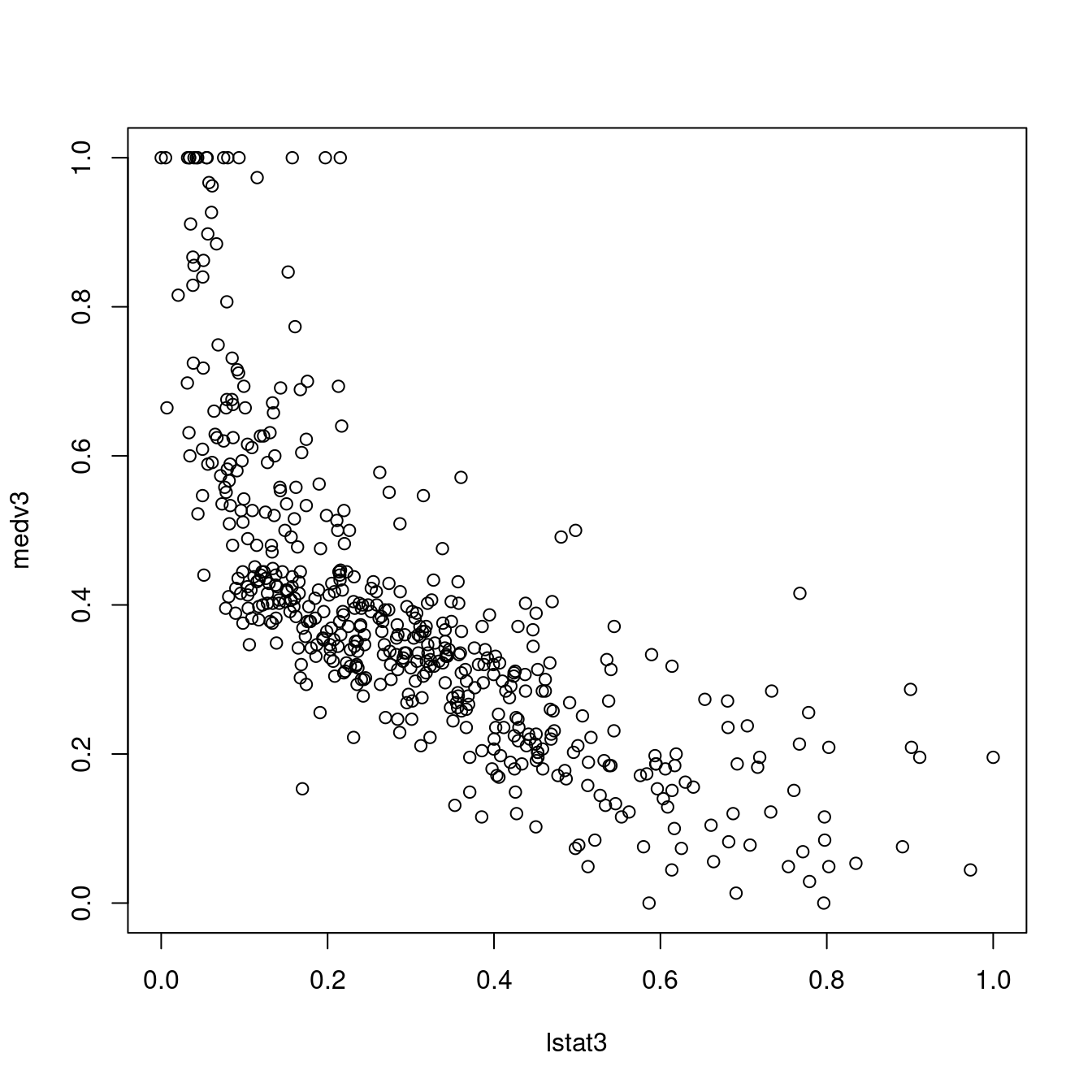
summary(lm(medv3 ~ lstat3))##
## Call:
## lm(formula = medv3 ~ lstat3)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.33705 -0.08866 -0.02929 0.04519 0.54445
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.62023 0.01123 55.23 <0.0000000000000002 ***
## lstat3 -0.76511 0.03119 -24.53 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1381 on 504 degrees of freedom
## Multiple R-squared: 0.5441, Adjusted R-squared: 0.5432
## F-statistic: 601.6 on 1 and 504 DF, p-value: < 0.00000000000000022plot(dis3, medv3)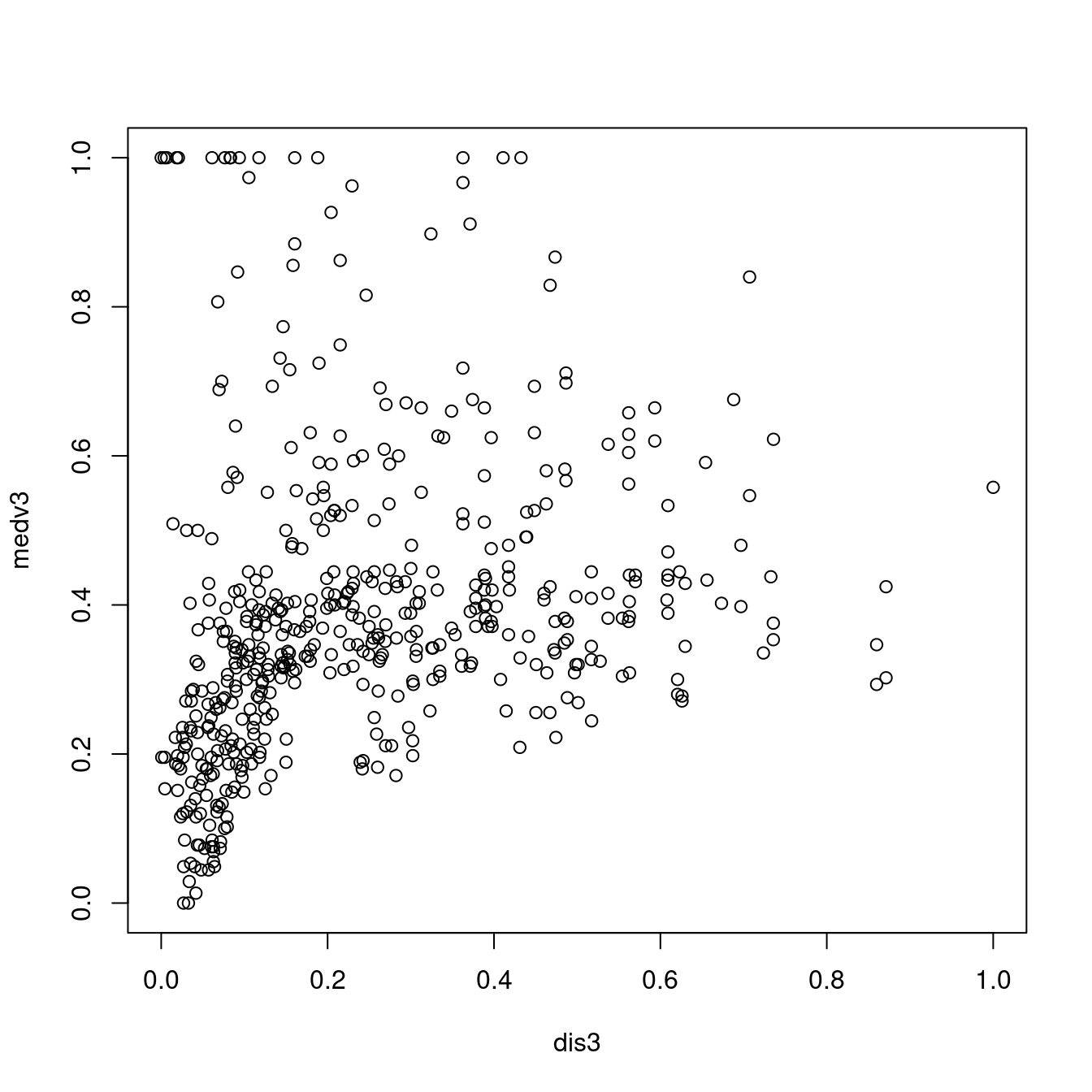
summary(lm(medv3 ~ dis3))##
## Call:
## lm(formula = medv3 ~ dis3)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.33369 -0.12346 -0.04145 0.05084 0.67504
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.32496 0.01421 22.861 < 0.0000000000000002 ***
## dis3 0.26676 0.04604 5.795 0.0000000121 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1981 on 504 degrees of freedom
## Multiple R-squared: 0.06246, Adjusted R-squared: 0.0606
## F-statistic: 33.58 on 1 and 504 DF, p-value: 0.00000001207plot(lstat3^(1/10), medv3)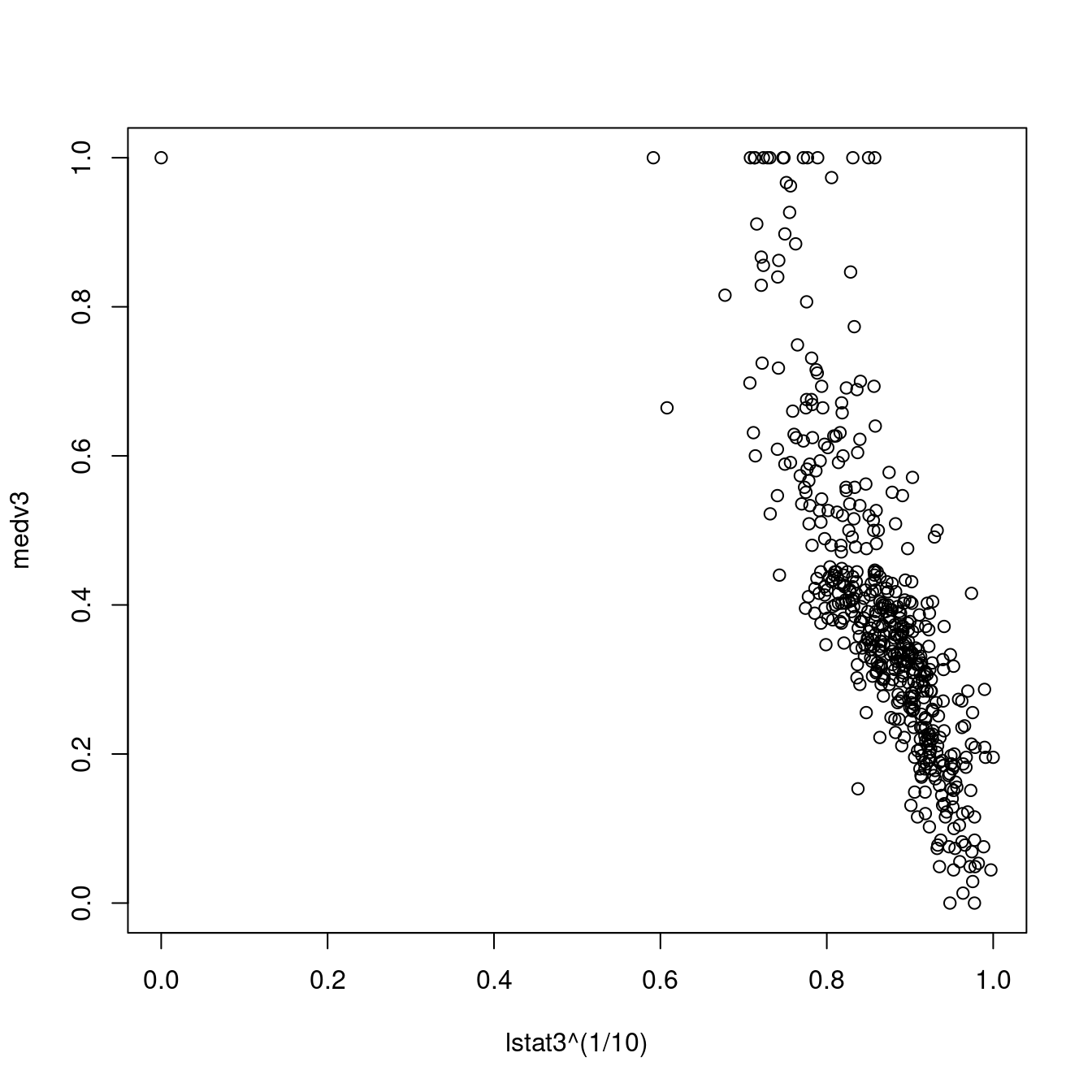
lstat3 <- lstat3^(1/10)
summary(lm(medv3 ~ lstat3))##
## Call:
## lm(formula = medv3 ~ lstat3)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.16170 -0.07367 -0.02163 0.04338 0.59321
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.16170 0.06694 32.30 <0.0000000000000002 ***
## lstat3 -2.04628 0.07700 -26.58 <0.0000000000000002 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.132 on 504 degrees of freedom
## Multiple R-squared: 0.5836, Adjusted R-squared: 0.5828
## F-statistic: 706.3 on 1 and 504 DF, p-value: < 0.00000000000000022plot(dis3^(1/10), medv3)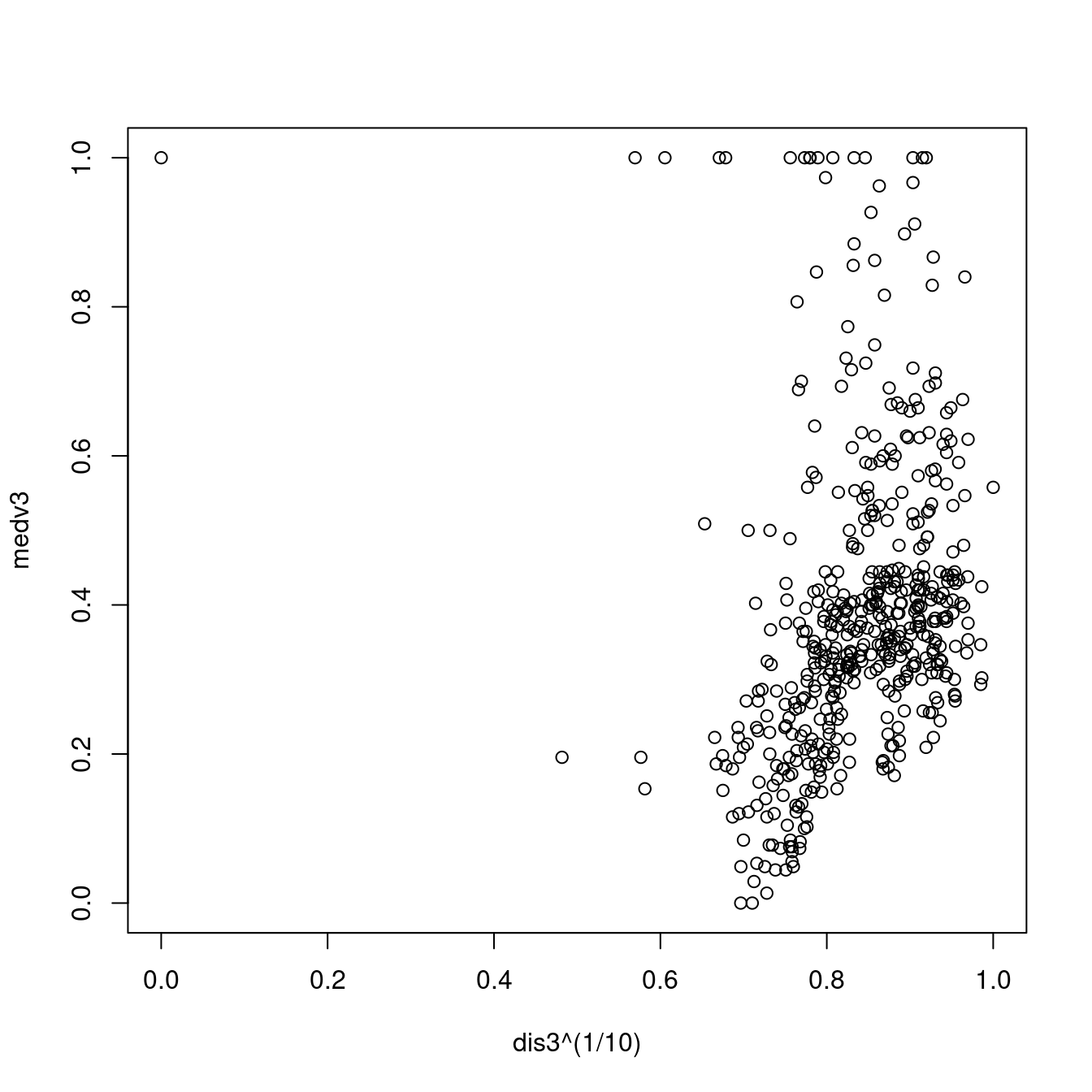
dis3 <- dis3^(1/10)
summary(lm(medv3 ~ dis3))##
## Call:
## lm(formula = medv3 ~ dis3)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.32580 -0.11650 -0.04541 0.04845 1.02955
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.02955 0.08532 -0.346 0.729
## dis3 0.50021 0.10126 4.940 0.00000107 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.1998 on 504 degrees of freedom
## Multiple R-squared: 0.04618, Adjusted R-squared: 0.04428
## F-statistic: 24.4 on 1 and 504 DF, p-value: 0.00000106613.8.2.1 課堂練習
- 請解釋上述程式碼以及R輸出的報表。
13.9 簡單線性迴歸分析全攻略
在這一節,作者小編趁本章結束之前,再一次回顧幾個「建置、搜尋」「簡單線性迴歸模型」的重點,包括:
- 基礎建模過程
- 各式各樣的摘要統計量
- 報表
在進入小節之前,作者小編想盡我所能跟讀者諸君討論「迴歸模型(regression models)」有什麼用處呢?統計學家這麼說
- 摘要數據。工程師或是科學家常用「方程式」描述數據集。有時候,一張表、一張圖,有時候還要再加上一條方程式。
- 估計係數(參數)。假如數據來自一個多方、多時的研究議題,甚至理論證實了,業界、學術界已經接受了「某一條(成熟的)方程式」,那新數據來了之後,研究者可以用「迴歸技術」取得「方程式的係數」的估計。
- 估計反應變數。如果實驗有了「
x」變數的新數據,研究者可以用先前取得的「迴歸方程式」計算、估計「y」變數的數值與區間。 - 預測反應變數。當然,也可以計算、預測「
y」變數的數值與區間。 - 控制解釋變數。假如研究者想控制「
y」變數的數值區間,那「x」變數應該是多少呢?
企圖清楚了!那計算工具呢?
接著,作者小編的學生可能會繼續問這一個問題:
為什麼我們更需要R呢?
建置「迴歸模型」是一項藝術、一項科學、一項智能,需要多次互動、來來回回的過程。對有意「自我養成」且希望「精通迴歸分析」的任何人,R絕對是「得力助手」。
為什麼呢?
…
13.9.1 從散佈圖到迴歸診斷圖談基礎建模過程
為了降低背景材料的複雜度,作者小編依舊請「anscombe」的第一組數據集協助我們示範建置「簡單線性迴歸模型」的全過程。
- 準備「
anscombe」的第一組數據集加一張簡單的散佈圖。
require(datasets) # 通常我們是這麼寫「library(datasets)」。
data("anscombe") # 載入。
anscombe # 呼叫它。## x1 x2 x3 x4 y1 y2 y3 y4
## 1 10 10 10 8 8.04 9.14 7.46 6.58
## 2 8 8 8 8 6.95 8.14 6.77 5.76
## 3 13 13 13 8 7.58 8.74 12.74 7.71
## 4 9 9 9 8 8.81 8.77 7.11 8.84
## 5 11 11 11 8 8.33 9.26 7.81 8.47
## 6 14 14 14 8 9.96 8.10 8.84 7.04
## 7 6 6 6 8 7.24 6.13 6.08 5.25
## 8 4 4 4 19 4.26 3.10 5.39 12.50
## 9 12 12 12 8 10.84 9.13 8.15 5.56
## 10 7 7 7 8 4.82 7.26 6.42 7.91
## 11 5 5 5 8 5.68 4.74 5.73 6.89df <- anscombe[, c("x1", "y1")] # 取出「x1」跟「y1」,其中「1」代表第一組。
colnames(df) <- c("x", "y") # 劃掉其中的「1」。
df # 呼叫出來再一次檢視這一組數據集。## x y
## 1 10 8.04
## 2 8 6.95
## 3 13 7.58
## 4 9 8.81
## 5 11 8.33
## 6 14 9.96
## 7 6 7.24
## 8 4 4.26
## 9 12 10.84
## 10 7 4.82
## 11 5 5.68# 繪製散佈圖。左右上下各加3個單位,方便大家觀察。
plot(y ~ x, data = df,
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3),
col = "dodgerblue",
pch = 20,
cex = 1.5,
main = "Anscombe x1 vs y1") 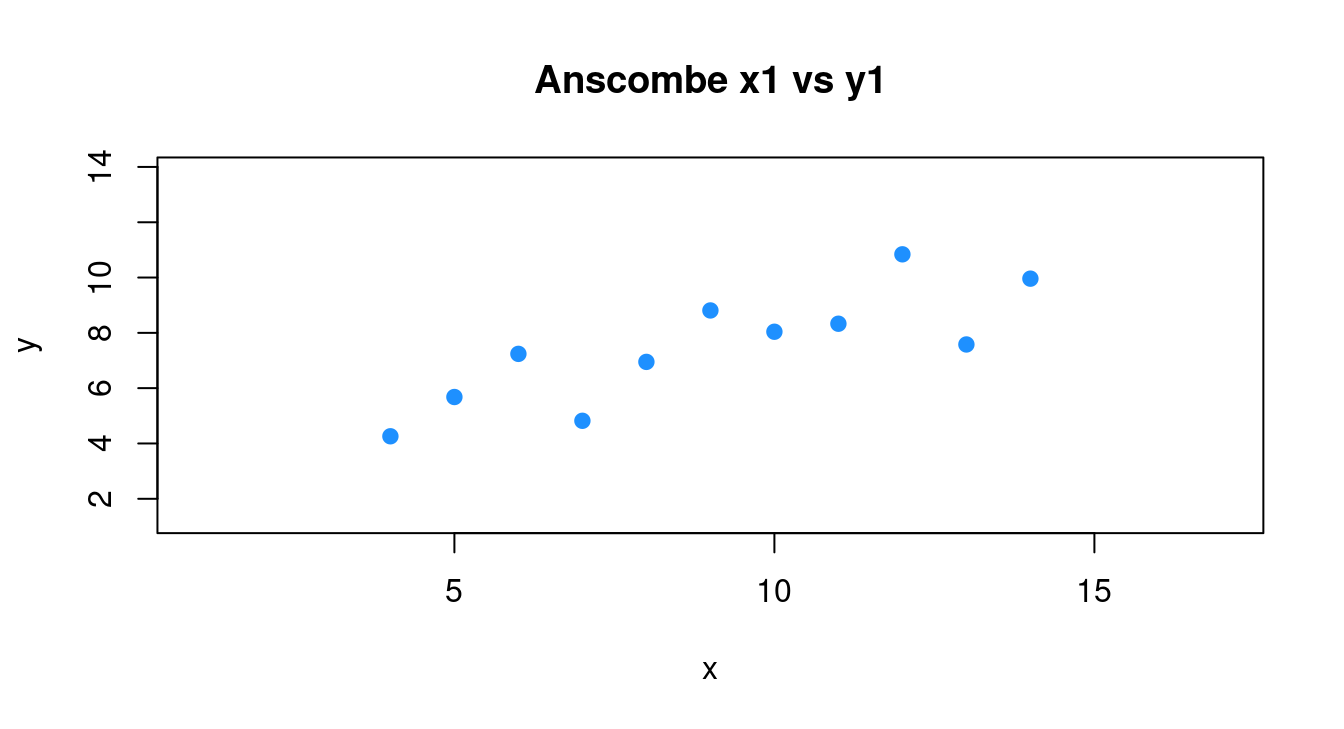
- 建模以及初步檢視模型的零零總總。
m0 <- lm(y ~ x, data = df)
m0 # 簡要報表##
## Call:
## lm(formula = y ~ x, data = df)
##
## Coefficients:
## (Intercept) x
## 3.0001 0.5001summary(m0) # 完整報表##
## Call:
## lm(formula = y ~ x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.92127 -0.45577 -0.04136 0.70941 1.83882
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0001 1.1247 2.667 0.02573 *
## x 0.5001 0.1179 4.241 0.00217 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.237 on 9 degrees of freedom
## Multiple R-squared: 0.6665, Adjusted R-squared: 0.6295
## F-statistic: 17.99 on 1 and 9 DF, p-value: 0.00217SSE <- sum(m0$residuals^2) # 誤差平方和
SSE## [1] 13.76269- 建模成功後為散佈圖加直線「3 + 0.5 x」。
plot(y ~ x, data = df,
xlim = range(df[, "x"]) + c(-3, 3),
ylim = range(df[, "y"]) + c(-3, 3),
col = "dodgerblue",
pch = 20,
cex = 1.5,
main = "Anscombe x1 vs y1")
abline(m0)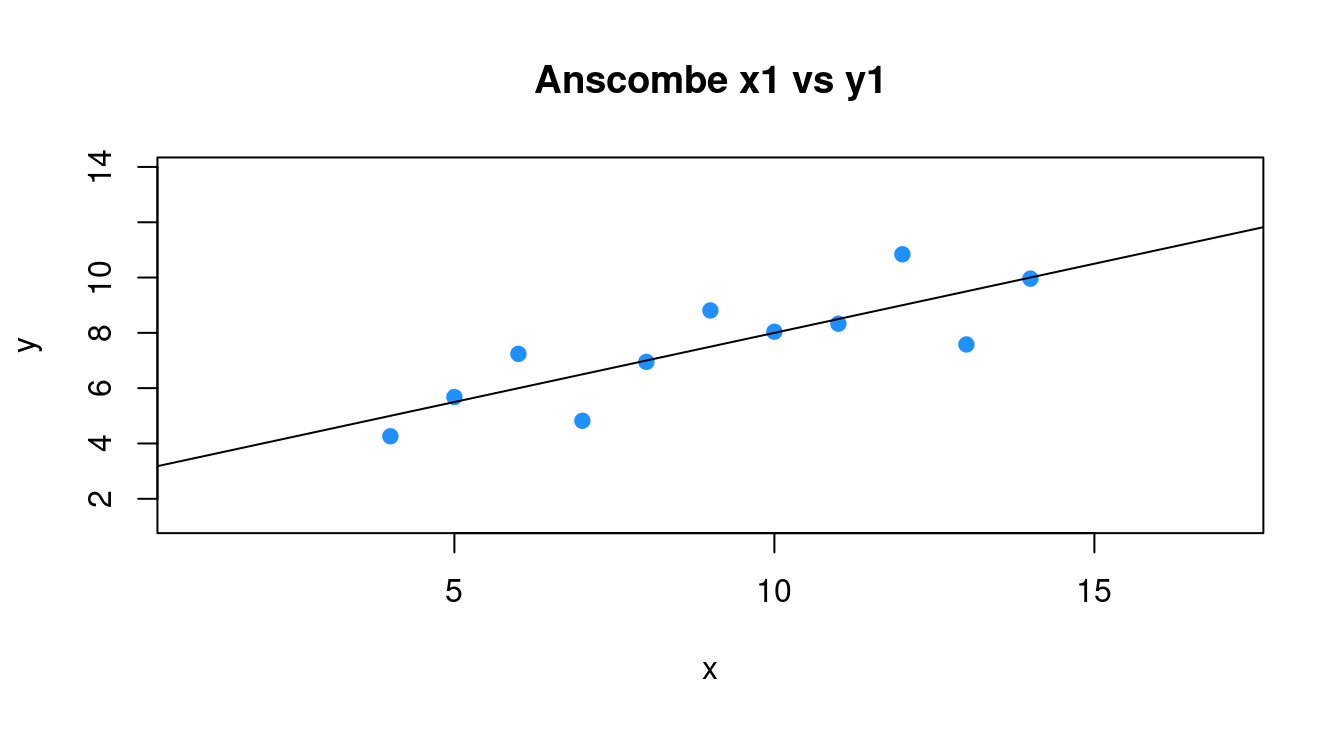
- 萃取模型各式各樣診斷「模型合適性」的特徵值。
require(broom)
m0.diag.metrics <- augment(m0)
m0.diag.metrics## # A tibble: 11 × 8
## y x .fitted .resid .hat .sigma .cooksd .std.resid
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 8.04 10 8.00 0.0390 0.100 1.31 0.0000614 0.0332
## 2 6.95 8 7.00 -0.0508 0.1 1.31 0.000104 -0.0433
## 3 7.58 13 9.50 -1.92 0.236 1.06 0.489 -1.78
## 4 8.81 9 7.50 1.31 0.0909 1.22 0.0616 1.11
## 5 8.33 11 8.50 -0.171 0.127 1.31 0.00160 -0.148
## 6 9.96 14 10.0 -0.0414 0.318 1.31 0.000383 -0.0405
## 7 7.24 6 6.00 1.24 0.173 1.22 0.127 1.10
## 8 4.26 4 5.00 -0.740 0.318 1.27 0.123 -0.725
## 9 10.8 12 9.00 1.84 0.173 1.10 0.279 1.63
## 10 4.82 7 6.50 -1.68 0.127 1.15 0.154 -1.45
## 11 5.68 5 5.50 0.179 0.236 1.31 0.00427 0.166- 繪製迴歸診斷圖。
par(mfrow = c(2, 2))
plot(m0)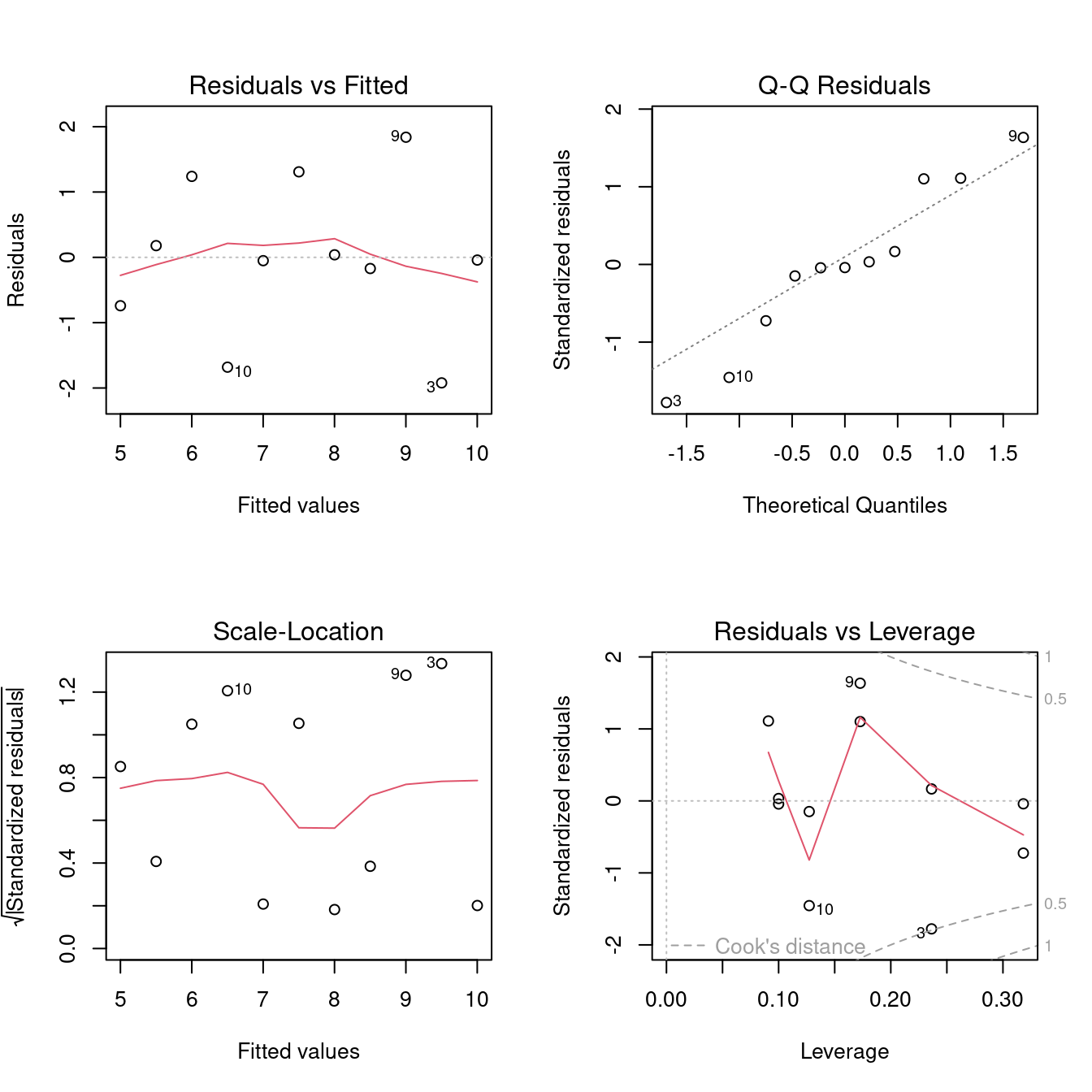
- 迴歸診斷之一。
plot(m0, 1)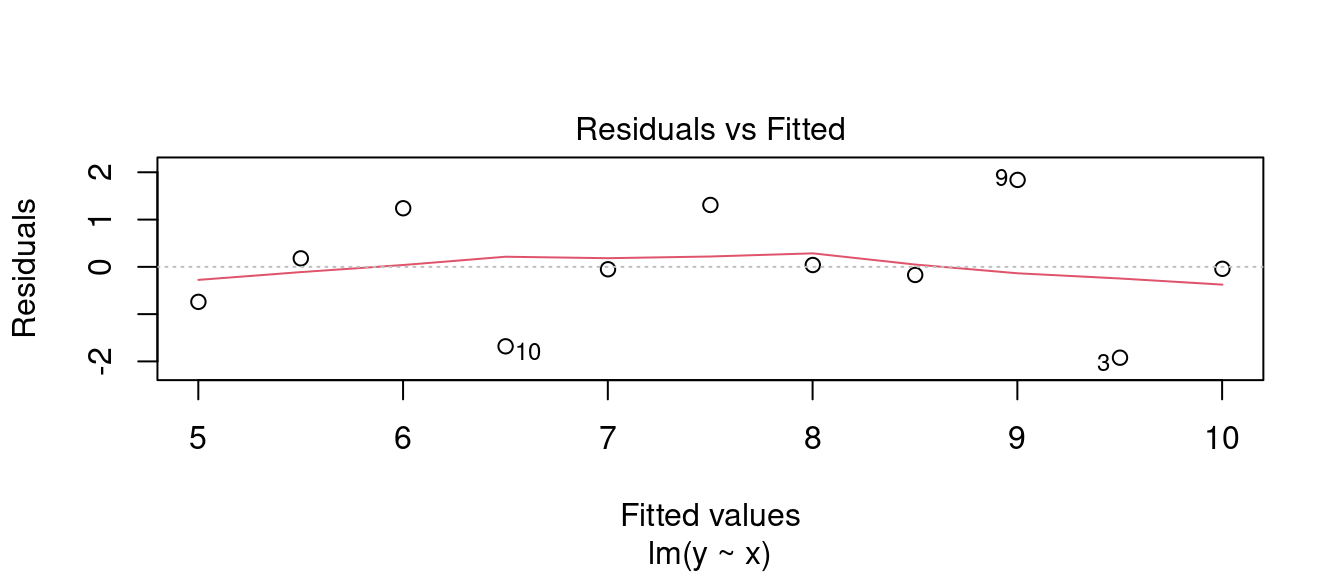
- 迴歸診斷之二。
plot(m0, 3)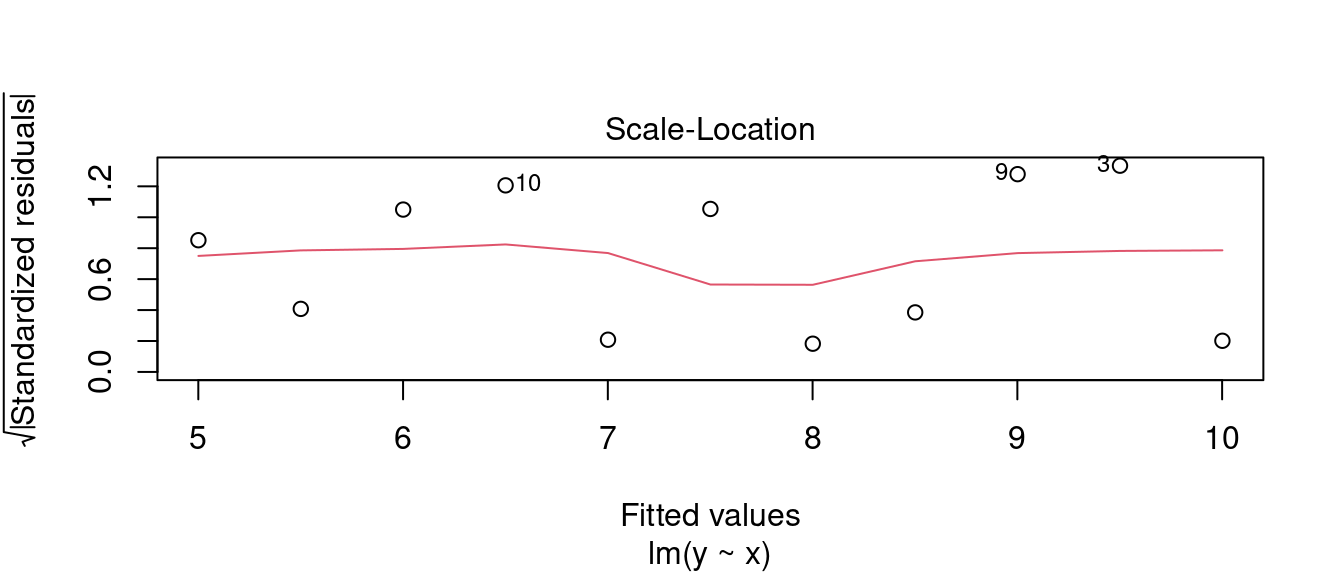
- 迴歸診斷之三。
plot(m0, 2)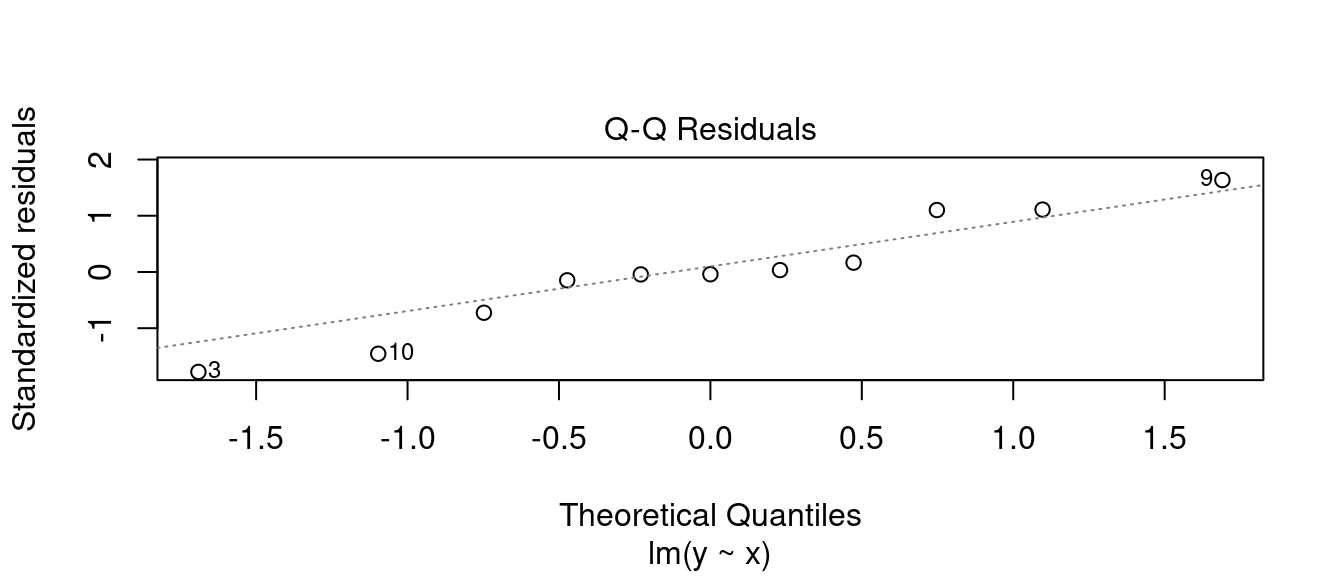
- 迴歸診斷之四。
plot(m0, 5)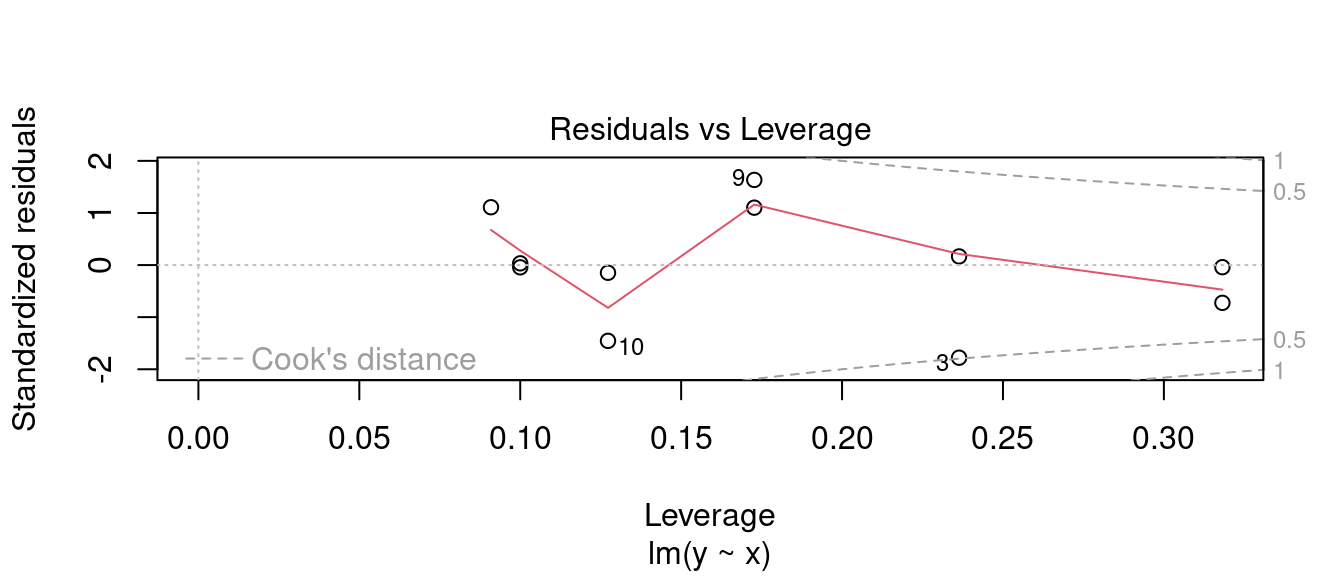
- 迴歸診斷之五。
par(mfrow = c(1,2))
# Cook's distance
plot(m0, 4)
# Residuals vs Leverage
plot(m0, 5)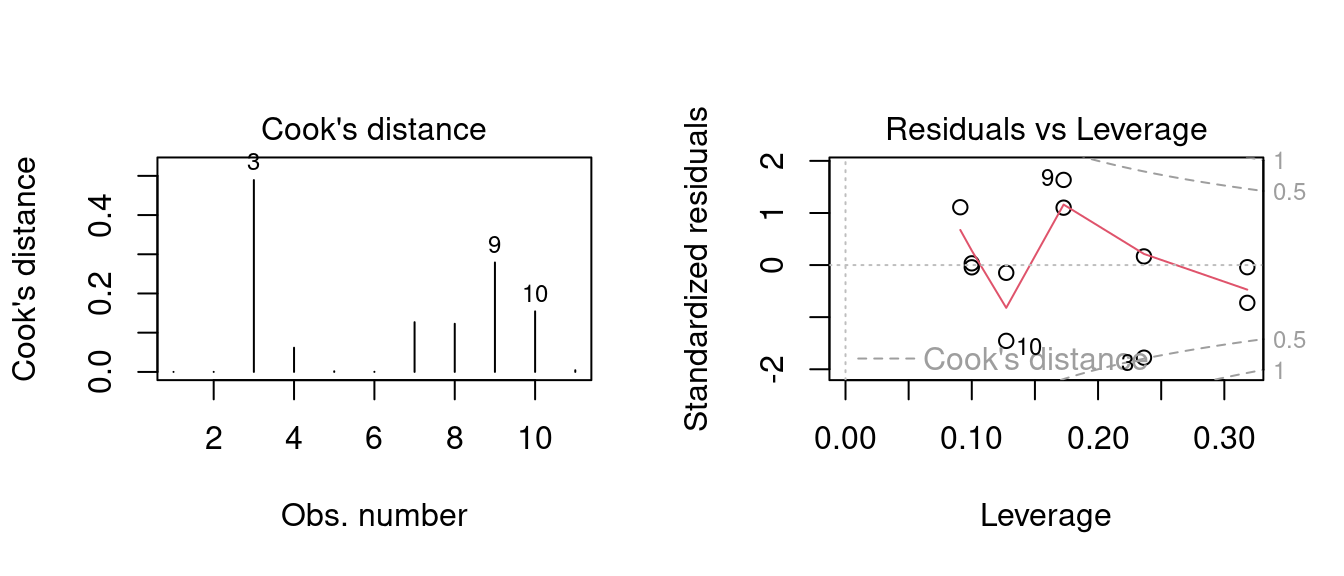
- 迴歸診斷之六。
require(dplyr)
plot(m0, 4, id.n = 5)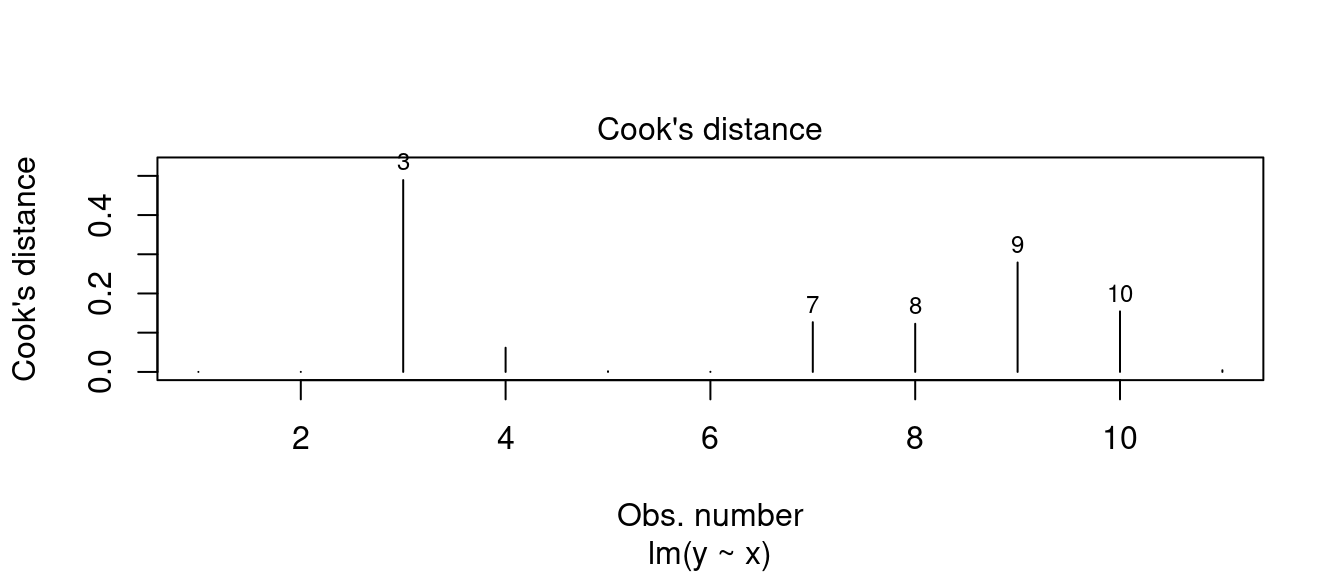
m0.diag.metrics %>%
top_n(5, wt = .cooksd)## # A tibble: 5 × 8
## y x .fitted .resid .hat .sigma .cooksd .std.resid
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 7.58 13 9.50 -1.92 0.236 1.06 0.489 -1.78
## 2 7.24 6 6.00 1.24 0.173 1.22 0.127 1.10
## 3 4.26 4 5.00 -0.740 0.318 1.27 0.123 -0.725
## 4 10.8 12 9.00 1.84 0.173 1.10 0.279 1.63
## 5 4.82 7 6.50 -1.68 0.127 1.15 0.154 -1.4513.9.2 搜尋最小平方法迴歸線一路走來變出多少數字?
在前一節,作者小編攜手R走過了「簡單線性迴歸分析」的全記錄。在這一節,作者小編要進一步從R的報表抓取各種「簡單線性迴歸分析」過程「中」或是成果「內」的數字。為什麼需要學這件事跟需要的R語言呢?
假如我們有許許多多個連續型變數,比如說,在波士頓數據集,我們有「
11」個連續型變數可以用來「解釋、預測」房價中位數,那我們就會有「11」條「簡單線性迴歸分析」後的最小平方法迴歸線,如果一條一條看,然後用手加紙筆作筆記,然後再用文字編輯器寫報告;…;作者小編認為大半的讀者諸君都有過類似的經驗,因為「用程式寫報告」達到「可重複研究」是最近幾年被學術圈倡議的事。
為此,作者小編已經開始在任何課堂上,要求、訓練學生用「.Rmd」格式撰寫作業跟報告。熟悉「.Rmd」格式只是「用程式寫報告」的第一步,學會「抓」肯定是第二步!當然,如果有某一個數字的計算公式、計算演算法,我們不一定要靠「報表」,有R一樣可以完成「用程式寫報告」,所以,在這裡作者小編第一次清楚交代「什麼是『電算』?」跟「什麼是『電算手算』」。請讀者諸君務必學起來。
13.9.2.1 電算手算
「電算手算」,作者小編的本意就是「學習如何寫程式執行手的計算動作」。
- (動作一)呼叫數據集。
df # 原始數據集## x y
## 1 10 8.04
## 2 8 6.95
## 3 13 7.58
## 4 9 8.81
## 5 11 8.33
## 6 14 9.96
## 7 6 7.24
## 8 4 4.26
## 9 12 10.84
## 10 7 4.82
## 11 5 5.68- (動作二)最小平方法迴歸線的斜率的計算公式如下:
\[b = \hat \beta_1 = \frac{\sum xy - \frac{(\sum y)(\sum x)}{n}}{\sum x^2 - \frac{(\sum x)^2}{n}} = \frac{\sum (x - \bar x)(y - \bar y)}{\sum (x - \bar x)^2} = \frac{SSXY}{SSX}\]
這個公式跟「相關係數」的定義有著「熟悉的臉孔」,意味著,當時計算「相關係數」的「SSCP」矩陣,在這裡也是「可用的」。只是,作者小編改了「幾個名字」。
mean(df$x) # 「x」的平均數。## [1] 9mean(df$y) # 「y」的平均數。## [1] 7.500909df$xmod <- df$x - mean(df$x) # 平移到平均數。
df$ymod <- df$y - mean(df$y)
df## x y xmod ymod
## 1 10 8.04 1 0.53909091
## 2 8 6.95 -1 -0.55090909
## 3 13 7.58 4 0.07909091
## 4 9 8.81 0 1.30909091
## 5 11 8.33 2 0.82909091
## 6 14 9.96 5 2.45909091
## 7 6 7.24 -3 -0.26090909
## 8 4 4.26 -5 -3.24090909
## 9 12 10.84 3 3.33909091
## 10 7 4.82 -2 -2.68090909
## 11 5 5.68 -4 -1.82090909df$ssx <- df$xmod^2 # 「x」的平方。
df$ssy <- df$ymod^2 # 「y」的平方。
df## x y xmod ymod ssx ssy
## 1 10 8.04 1 0.53909091 1 0.290619008
## 2 8 6.95 -1 -0.55090909 1 0.303500826
## 3 13 7.58 4 0.07909091 16 0.006255372
## 4 9 8.81 0 1.30909091 0 1.713719008
## 5 11 8.33 2 0.82909091 4 0.687391736
## 6 14 9.96 5 2.45909091 25 6.047128099
## 7 6 7.24 -3 -0.26090909 9 0.068073554
## 8 4 4.26 -5 -3.24090909 25 10.503491736
## 9 12 10.84 3 3.33909091 9 11.149528099
## 10 7 4.82 -2 -2.68090909 4 7.187273554
## 11 5 5.68 -4 -1.82090909 16 3.315709917df$ssxy <- df$xmod*df$ymod # 「x」跟「y」的交叉積。
df## x y xmod ymod ssx ssy ssxy
## 1 10 8.04 1 0.53909091 1 0.290619008 0.5390909
## 2 8 6.95 -1 -0.55090909 1 0.303500826 0.5509091
## 3 13 7.58 4 0.07909091 16 0.006255372 0.3163636
## 4 9 8.81 0 1.30909091 0 1.713719008 0.0000000
## 5 11 8.33 2 0.82909091 4 0.687391736 1.6581818
## 6 14 9.96 5 2.45909091 25 6.047128099 12.2954545
## 7 6 7.24 -3 -0.26090909 9 0.068073554 0.7827273
## 8 4 4.26 -5 -3.24090909 25 10.503491736 16.2045455
## 9 12 10.84 3 3.33909091 9 11.149528099 10.0172727
## 10 7 4.82 -2 -2.68090909 4 7.187273554 5.3618182
## 11 5 5.68 -4 -1.82090909 16 3.315709917 7.2836364SSCP <- apply(df[,c(5,7,7,6)], 2, sum) # 計算總和。
SSCP## ssx ssxy ssxy.1 ssy
## 110.00000 55.01000 55.01000 41.27269SSCP <- matrix(SSCP, 2, 2) # 變成、排成2x2矩陣。
SSCP## [,1] [,2]
## [1,] 110.00 55.01000
## [2,] 55.01 41.27269dimnames(SSCP) <- list(names(df)[1:2], names(df)[1:2]) # 取名字。
SSCP # 這就是「SSCP = sum of squares and cross-product」矩陣。## x y
## x 110.00 55.01000
## y 55.01 41.27269### 「x」跟「y」的相關係數
r <- SSCP[1,2]/sqrt(SSCP[1,1] * SSCP[2,2])
r## [1] 0.8164205- (動作三)取得最小平方法迴歸線的斜率。
### 斜率
b <- SSCP[1,2]/SSCP[1,1]
b## [1] 0.5000909- (動作四)取得最小平方法迴歸線的截距。
### 截距
a <- mean(df$y) - b * mean(df$x)
a## [1] 3.000091- (動作五)取得最小平方法迴歸線的「戴帽子的
y」。
### 配適值
m0fitted <- a + b * df$x
m0fitted## [1] 8.001000 7.000818 9.501273 7.500909 8.501091 10.001364 6.000636
## [8] 5.000455 9.001182 6.500727 5.500545names(m0fitted) <- 1:dim(df)[1]
m0fitted## 1 2 3 4 5 6 7 8
## 8.001000 7.000818 9.501273 7.500909 8.501091 10.001364 6.000636 5.000455
## 9 10 11
## 9.001182 6.500727 5.500545- (動作六)取得最小平方法迴歸線的「殘差」。
### 殘差
m0res <- df$y - (a + b * df$x)
m0res## [1] 0.03900000 -0.05081818 -1.92127273 1.30909091 -0.17109091 -0.04136364
## [7] 1.23936364 -0.74045455 1.83881818 -1.68072727 0.17945455names(m0res) <- 1:dim(df)[1]
m0res## 1 2 3 4 5 6
## 0.03900000 -0.05081818 -1.92127273 1.30909091 -0.17109091 -0.04136364
## 7 8 9 10 11
## 1.23936364 -0.74045455 1.83881818 -1.68072727 0.17945455- (動作七)取得最小平方法迴歸線的「SSE」。
### SSE, MSE
SSE <- sum(m0res^2)
SSE## [1] 13.76269MSE <- SSE/(dim(df)[1] - 2)
MSE## [1] 1.529188sqrt(MSE)## [1] 1.236603- (動作八)取得最小平方法迴歸線的「\(R^2\)」跟「\(\bar R^2\)」。
### R^2
r^2## [1] 0.66654251 - SSE/SSCP[2,2]## [1] 0.66654251 - MSE/(SSCP[2,2]/(dim(df)[1] - 1))## [1] 0.6294916- (動作九)取得最小平方法迴歸線的「殘差的四分位數」。
### 殘差的四分位數與最小值、最大值
quantile(m0res)## 0% 25% 50% 75% 100%
## -1.92127273 -0.45577273 -0.04136364 0.70940909 1.83881818- (動作九)取得最小平方法迴歸線的「係數的t檢定」。
### t test
X <- matrix(c(rep(1,dim(df)[1]), df$x),
dim(df)[1],
2,
byrow = FALSE)
X## [,1] [,2]
## [1,] 1 10
## [2,] 1 8
## [3,] 1 13
## [4,] 1 9
## [5,] 1 11
## [6,] 1 14
## [7,] 1 6
## [8,] 1 4
## [9,] 1 12
## [10,] 1 7
## [11,] 1 5t(X) %*% X## [,1] [,2]
## [1,] 11 99
## [2,] 99 1001C <- solve(t(X) %*% X)
C## [,1] [,2]
## [1,] 0.82727273 -0.081818182
## [2,] -0.08181818 0.009090909sqrt(MSE * C[1,1])## [1] 1.124747t0 <- a/sqrt(MSE * C[1,1])
t0## [1] 2.6673482 * (1 - pt(t0, dim(df)[1] - 2))## [1] 0.02573405sqrt(MSE * C[2,2])## [1] 0.1179055t1 <- b/sqrt(MSE * C[2,2])
t1## [1] 4.2414552 * (1 - pt(t1, dim(df)[1] - 2))## [1] 0.002169629- (動作十)取得最小平方法迴歸線的「迴歸模型的F檢定」。
### F statistics
Fstat <- (SSCP[2,2] - SSE)/MSE
Fstat## [1] 17.989941 - pf(Fstat, 1, dim(df)[1] - 2)## [1] 0.002169629- 驗證上述數字的正確性。
summary(m0)##
## Call:
## lm(formula = y ~ x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.92127 -0.45577 -0.04136 0.70941 1.83882
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0001 1.1247 2.667 0.02573 *
## x 0.5001 0.1179 4.241 0.00217 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.237 on 9 degrees of freedom
## Multiple R-squared: 0.6665, Adjusted R-squared: 0.6295
## F-statistic: 17.99 on 1 and 9 DF, p-value: 0.0021713.9.2.2 電算
先學從「lm的輸出報表」抓,在學從「summary報表」抓。
- (動作一)呼叫數據集。
df # 原始數據集## x y xmod ymod ssx ssy ssxy
## 1 10 8.04 1 0.53909091 1 0.290619008 0.5390909
## 2 8 6.95 -1 -0.55090909 1 0.303500826 0.5509091
## 3 13 7.58 4 0.07909091 16 0.006255372 0.3163636
## 4 9 8.81 0 1.30909091 0 1.713719008 0.0000000
## 5 11 8.33 2 0.82909091 4 0.687391736 1.6581818
## 6 14 9.96 5 2.45909091 25 6.047128099 12.2954545
## 7 6 7.24 -3 -0.26090909 9 0.068073554 0.7827273
## 8 4 4.26 -5 -3.24090909 25 10.503491736 16.2045455
## 9 12 10.84 3 3.33909091 9 11.149528099 10.0172727
## 10 7 4.82 -2 -2.68090909 4 7.187273554 5.3618182
## 11 5 5.68 -4 -1.82090909 16 3.315709917 7.2836364- (動作二)取得「兩張」報表以及相關資訊。
m0 <- lm(y ~ x, data = df)
m0##
## Call:
## lm(formula = y ~ x, data = df)
##
## Coefficients:
## (Intercept) x
## 3.0001 0.5001names(m0)## [1] "coefficients" "residuals" "effects" "rank"
## [5] "fitted.values" "assign" "qr" "df.residual"
## [9] "xlevels" "call" "terms" "model"SUMm0 <- summary(m0)
SUMm0##
## Call:
## lm(formula = y ~ x, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.92127 -0.45577 -0.04136 0.70941 1.83882
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0001 1.1247 2.667 0.02573 *
## x 0.5001 0.1179 4.241 0.00217 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.237 on 9 degrees of freedom
## Multiple R-squared: 0.6665, Adjusted R-squared: 0.6295
## F-statistic: 17.99 on 1 and 9 DF, p-value: 0.00217names(SUMm0)## [1] "call" "terms" "residuals" "coefficients"
## [5] "aliased" "sigma" "df" "r.squared"
## [9] "adj.r.squared" "fstatistic" "cov.unscaled"- (動作三)取得最小平方法迴歸線的斜率。
# 抓斜率跟截距
m0["coefficients"]## $coefficients
## (Intercept) x
## 3.0000909 0.5000909m0$coefficients## (Intercept) x
## 3.0000909 0.5000909SUMm0$coefficients## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0000909 1.1247468 2.667348 0.025734051
## x 0.5000909 0.1179055 4.241455 0.002169629### 斜率
m0["coefficients"]$coefficients[2]## x
## 0.5000909m0$coefficients[2]## x
## 0.5000909SUMm0$coefficients[2]## [1] 0.5000909- (動作四)取得最小平方法迴歸線的截距。
### 截距
m0["coefficients"]$coefficients[1]## (Intercept)
## 3.000091m0$coefficients[1]## (Intercept)
## 3.000091SUMm0$coefficients[1]## [1] 3.000091- (動作五)取得最小平方法迴歸線的「戴帽子的
y」。
### 配適值
m0$fitted.values## 1 2 3 4 5 6 7 8
## 8.001000 7.000818 9.501273 7.500909 8.501091 10.001364 6.000636 5.000455
## 9 10 11
## 9.001182 6.500727 5.500545m0$fitted.values[1]## 1
## 8.001m0$fitted.values[11]## 11
## 5.500545fitted(m0)## 1 2 3 4 5 6 7 8
## 8.001000 7.000818 9.501273 7.500909 8.501091 10.001364 6.000636 5.000455
## 9 10 11
## 9.001182 6.500727 5.500545- (動作六)取得最小平方法迴歸線的「殘差」。
### 殘差
m0$residuals## 1 2 3 4 5 6
## 0.03900000 -0.05081818 -1.92127273 1.30909091 -0.17109091 -0.04136364
## 7 8 9 10 11
## 1.23936364 -0.74045455 1.83881818 -1.68072727 0.17945455m0$residuals[1]## 1
## 0.039m0$residuals[11]## 11
## 0.1794545SUMm0$residuals## 1 2 3 4 5 6
## 0.03900000 -0.05081818 -1.92127273 1.30909091 -0.17109091 -0.04136364
## 7 8 9 10 11
## 1.23936364 -0.74045455 1.83881818 -1.68072727 0.17945455- (動作七)取得最小平方法迴歸線的「SSE」。
### SSE, MSE
SUMm0$sigma## [1] 1.236603SUMm0$sigma^2## [1] 1.529188SUMm0$sigma^2 * (m0$df.residual)## [1] 13.76269- (動作八)取得最小平方法迴歸線的「\(R^2\)」跟「\(\bar R^2\)」。
### R^2
SUMm0$r.squared## [1] 0.6665425SUMm0$adj.r.squared## [1] 0.6294916- (動作九)取得最小平方法迴歸線的「殘差的四分位數」。
### 殘差的四分位數與最小值、最大值
quantile(m0$residuals)## 0% 25% 50% 75% 100%
## -1.92127273 -0.45577273 -0.04136364 0.70940909 1.83881818quantile(SUMm0$residuals)## 0% 25% 50% 75% 100%
## -1.92127273 -0.45577273 -0.04136364 0.70940909 1.83881818- (動作九)取得最小平方法迴歸線的「係數的t檢定」。
### t test
SUMm0$coefficients## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.0000909 1.1247468 2.667348 0.025734051
## x 0.5000909 0.1179055 4.241455 0.002169629### 截距
SUMm0$coefficients["(Intercept)", "Estimate"]## [1] 3.000091SUMm0$coefficients["(Intercept)", "Std. Error"]## [1] 1.124747SUMm0$coefficients["(Intercept)", "t value"]## [1] 2.667348SUMm0$coefficients["(Intercept)", "Pr(>|t|)"]## [1] 0.02573405### 斜率
SUMm0$coefficients["x", "Estimate"]## [1] 0.5000909SUMm0$coefficients["x", "Std. Error"]## [1] 0.1179055SUMm0$coefficients["x", "t value"]## [1] 4.241455SUMm0$coefficients["x", "Pr(>|t|)"]## [1] 0.002169629- (動作十)取得最小平方法迴歸線的「迴歸模型的F檢定」。
### F statistics
SUMm0$fstatistic## value numdf dendf
## 17.98994 1.00000 9.00000- (手算太難的動作十一)取得最小平方法迴歸線「截距跟斜率的變異數-共變異數矩陣」。
# 截距跟斜率的變異數-共變異數矩陣
SUMm0$cov.unscaled## (Intercept) x
## (Intercept) 0.82727273 -0.081818182
## x -0.08181818 0.009090909- (電算才有的動作十二)取得最小平方法迴歸線「呼叫程式碼」。
### 呼叫「lm」的那句話
m0$call## lm(formula = y ~ x, data = df)SUMm0$call## lm(formula = y ~ x, data = df)13.9.3 R怎麼保留最小平方法迴歸線的全部資訊?
- 「
lm()」
x <- sapply(1, function(w){
lm(y ~ x, data = df)
})
x## [,1]
## coefficients numeric,2
## residuals numeric,11
## effects numeric,11
## rank 2
## fitted.values numeric,11
## assign integer,2
## qr qr,5
## df.residual 9
## xlevels list,0
## call expression
## terms y ~ x
## model data.frame,2- 「
summary()」
x <- sapply(1, function(w){
summary(lm(y ~ x, data = df))
})
x## [,1]
## call expression
## terms y ~ x
## residuals numeric,11
## coefficients numeric,8
## aliased logical,2
## sigma 1.236603
## df integer,3
## r.squared 0.6665425
## adj.r.squared 0.6294916
## fstatistic numeric,3
## cov.unscaled numeric,4