Chapter 12 探索式數據分析安可曲

12.1 續

我們從探索式數據分析首部曲開啟「探索式分析波士頓數據集」，先從「房價中位數」開始。走過「莖葉圖」、「次數分配表」、「相對次數分配表」、「累加次數分配表」、「累加相對次數分配表」、「許許多多種摘要統計量」跟「摘要統計量報表」。然後探索式數據分析二部曲把「房價中位數」學到的技術試圖延伸到整張表的全部欄位，繼續走到、「直方圖」、「直方圖陣列」跟整張表的「摘要統計量報表」。也修正了兩個整數變數，一個變成「名目文字」，一個變成「順序文字」，並且順勢帶出「分群、分段的摘要統計量報表」。也把「自製單變量摘要統計量報表」，透過

for迴圈

，變出整張全部連續型變數的「摘要統計量報表」，而且示範了「愛放什麼統計量就放什麼統計量」的

自由自在！

接下來，我們要把「從一到十四一個一個看」的方向，換到「一次兩個」的方向。所謂的「一次兩個」有以下三個意思：

1. 一次看兩個連續型變數
2. 一次看兩個離散型變數
3. 一次看一個連續型變數加一個離散型變數

如果是「一次看兩個連續型變數」，就先來「一個固定在『房價中位數』，十三個取一個的自由變化，嘗試製作並分析這十三張『散佈圖』」。

「散佈圖」到底為何而生啊？

這一套微微書一開始介紹了1900年代的「莖葉圖」，接著「莖葉圖」帶出「次數分配表」，繼續帶出連續型變數的「直方圖」跟離散型變數的「長條圖」等等呈現

分配

的統計技術。看到「莖葉圖」、「直方圖」跟「長條圖」之後，我們開始學習「描述分配的各種特質」。統計學家不只嘗試使用文字，也嘗試使用數字，於是乎，統計學家創造了許許多多描述分配的數字。這些數字，叫做「敘述統計量」，也叫做「摘要統計量」。發展至此，前述提到過的技術都是所謂「單變量摘要技術」。人類不會停下來，統計學家當然也不會停下來！「單(形單影隻)」這個字的下一個就是「雙(成雙成對)」。那

為什麼想要一次看兩個連續型變數呢？

因為我們可能想

…

為了「協助掌握我們辛苦收到的數據集」，「視覺化工具」一向是首選，我們想想1900年代，Arthur Bowley先生發明了「莖葉圖」，作者小編「認為」在當時「莖葉圖」不是第一名就是第二名的統計學發明。很可惜，Arthur Bowley沒有發明「兩個變數一起看的莖葉圖」！

時鐘的秒針繼續往前走！

後來「統計學家」借用了「數學家」在1637年發明、超過380歲的Cartesian coordinate system，變出所謂的「散佈圖(Scatter plot)」這一項「視覺化兩兩變數」的工具。在這一章，作者小編除了介紹「散佈圖(Scatter plot)」，也會介紹統計學家的其他發明，諸如檢視「兩兩連續型變數」的「摘要統計量」。在諸多可能性裡頭，就屬「相關係數(Pearson correlation coefficient)」最搶眼、最流行。作者小編準備介紹R對「相關係數」的諸多支持(計算、視覺化、檢定等等)。

…

如果是「一次看兩個離散型變數」，就先看「兩兩離散型變數」之間的「列聯表」，當然會介紹「列聯表」的「獨立性檢定」跟各種「2x2列聯表」檢視一致性的測度。

…

如果是「一次看一個連續型變數加一個離散型變數」，在波士頓數據集裡，我們有機會看「雙母體的t檢定」、「單向變異數分析的F檢定」以及「雙向變異數分析的F檢定」。

…

請讀者諸君不要轉台！

…

12.2 學習目標

12.3 準備工作

require(MASS) # 用「require」不用「library」，是因為如果R已經將套件MASS載入環境，就不需要再載一次。
data(Boston)
boston <- Boston 
# 「不動」原始數據集，不論它有「多原始」，是R程式設計的一項絕佳習慣。
# 即便一般使用者是無法任意改變套件MASS的內容物！
DISvars <- colnames(boston)[which(sapply(boston, class) == "integer")]
CONvars <- colnames(boston)[which(sapply(boston, class) == "numeric")]
colsBostonFull<-readRDS("/home/fcu/ShinyApps/Textbooks/BOSTON/chapter02/output/data/colsBostonFull.rds")

## Error in gzfile(file, "rb"): 無法開啟連接

colsBostonFull

##                                                                          說明
## CRIM                                            per capita crime rate by town
## ZN           proportion of residential land zoned for lots over 25,000 sq.ft.
## INDUS                        proportion of non-retail business acres per town
## CHAS    Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
## NOX                        nitric oxides concentration (parts per 10 million)
## RM                                       average number of rooms per dwelling
## AGE                    proportion of owner-occupied units built prior to 1940
## DIS                      weighted distances to five Boston employment centres
## RAD                                 index of accessibility to radial highways
## TAX                                  full-value property-tax rate per $10,000
## PTRATIO                                           pupil-teacher ratio by town
## BLACK          1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
## LSTAT                                        % lower status of the population
## MEDV                          Median value of owner-occupied homes in $1000's
##                                 中文翻譯   中文變數名稱  內容物
## CRIM                每個城鎮人均犯罪率。         犯罪率 numeric
## ZN      超過25,000平方呎的住宅用地比例。   住宅用地比例 numeric
## INDUS     每個城鎮非零售業務英畝的比例。   非商業區比例 numeric
## CHAS             是否鄰近Charles River。         河邊宅 integer
## NOX                     氮氧化合物濃度。       空汙指標 numeric
## RM                每個住宅的平均房間數。     平均房間數 numeric
## AGE       1940年之前建造的自用住宅比例。     老房子比例 numeric
## DIS     距波士頓五大商圈的加權平均距離。   加權平均距離 numeric
## RAD             環狀高速公路的可觸指標。     交通便利性 integer
## TAX             財產稅占比(每一萬美元)。       財產稅率 numeric
## PTRATIO                         生師比。         生師比 numeric
## BLACK                       黑人的比例。       黑人指數 numeric
## LSTAT       (比較)低社經地位人口的比例。 低社經人口比例 numeric
## MEDV            以千美元計的房價中位數。     房價中位數 numeric

12.4 散佈圖

作者小編在寫一系列微微書的當下，疫情持續中，但還是有好消息，就是維基百科滿20周年。不論是維基百科中文版，還是維基百科英文版都是作者小編諮詢的對象，因為Wikipedia讓作者小編可以快速回顧數學、統計與資訊相關的專業知識，也借此深入發現數學、統計與資訊相關的專業知識，更可以補充作者小編與時俱增的數學、統計與資訊相關的專業知識。Wikipedia絕對是作者小編一系列微微書的好朋友。那

什麼是「散佈圖」呢？

先看Wikipedia怎麼說？

A scatter plot (also called a scatterplot, scatter graph, scatter chart, scattergram, or scatter diagram) is a type of plot or mathematical diagram using Cartesian coordinates to display values for typically two variables for a set of data.

knitr::include_url("https://en.wikipedia.org/wiki/Scatter_plot")

…

先來幾個簡單的範例：

plot(x = 0:9, y = 0:9)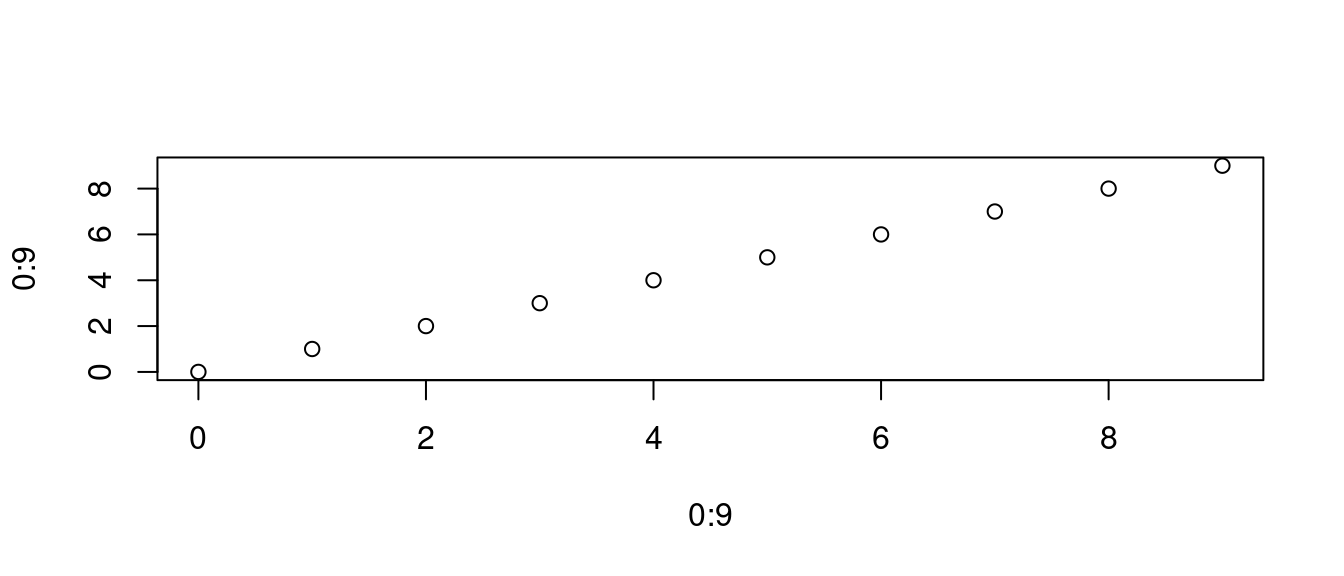

plot(x = 0:9, y = 0:9, xlim = c(-1, 10), ylim = c(-1, 10))

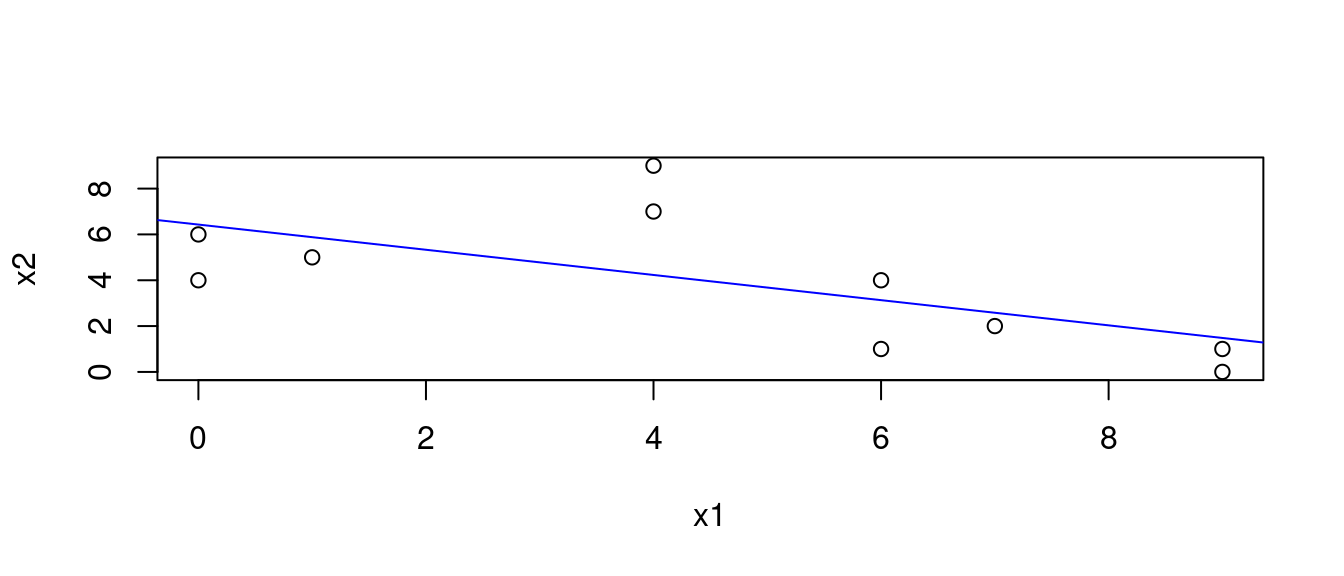
讓作者小編加幾條「輔助線」，協助大家「好看、易看」：

plot(x = 0:9, y = 0:9, xlim = c(-1, 10), ylim = c(-1, 10))
for (i in 0:9) {
  lines(c(i, i), c(-1, i+1), lty = 1)
  lines(c(-1, i+1), c(i, i), lty = 2)
}

這樣，我們就可以確定、保證圖上的「座標」是

data.frame(x = 0:9, y = 0:9)

##    x y
## 1  0 0
## 2  1 1
## 3  2 2
## 4  3 3
## 5  4 4
## 6  5 5
## 7  6 6
## 8  7 7
## 9  8 8
## 10 9 9

「散佈圖」也可以清楚表達數學方程式的部分「圖像」，這是「sin(x)」，一種週期循環的數學方程式：

x <- seq(0,8*pi,length.out=100)
y <- sin(x)
plot(x, y, type = "l")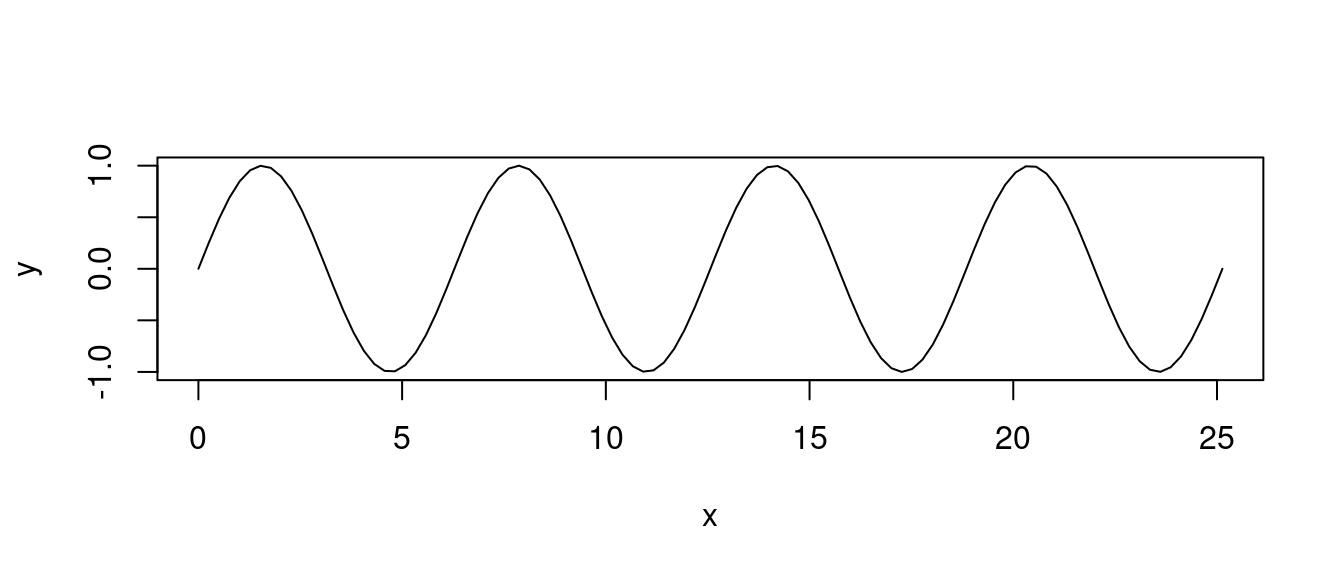

12.4.1 DIY

根據維基百科的定義，基本上，統計學裡的「散佈圖」借用「解析幾何的平面座標技術」。比如說，

1. 抓波士頓數據集的第一個欄位，per capita crime rate by town，當作是「x座標」。再
2. 抓波士頓數據集的房價中位數，Median value of owner-occupied homes in $1000’s，當作是「y座標」。然後，
3. 同一個觀察值編號的「x座標」跟「y座標」形成「二維平面上的點座標(x, y)」，並且打上「二維平面」直到打完全部的點座標。

請看

plot(boston[, "crim"], boston[, "medv"])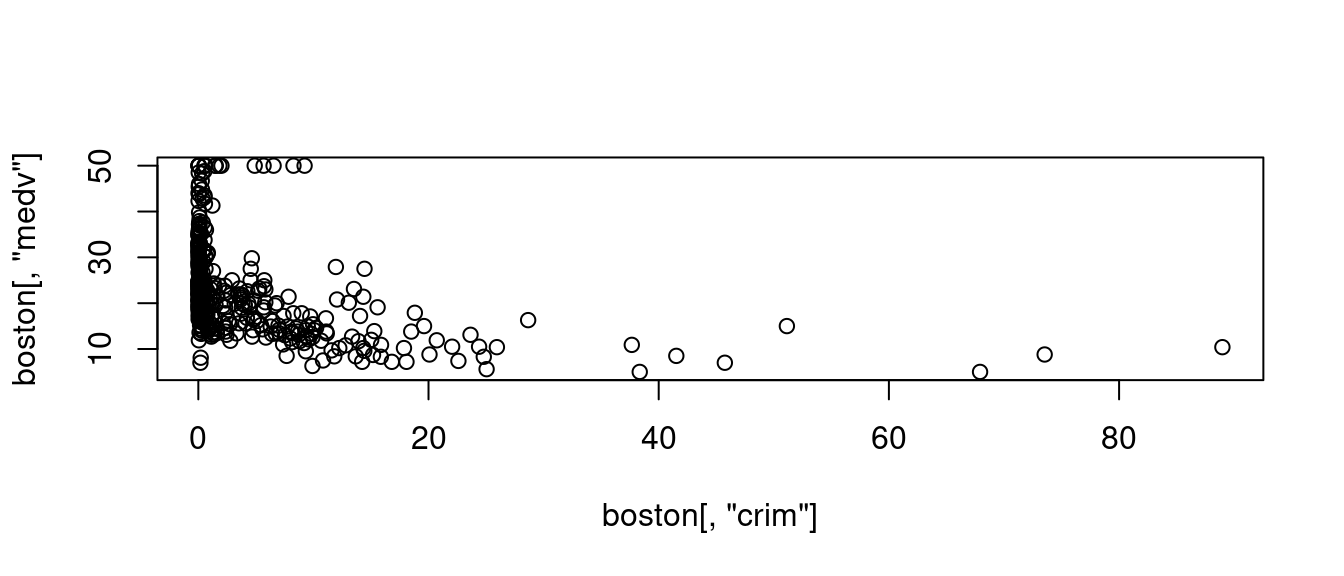

這就是一張「最簡單的散佈圖」。據業界人士的觀察與建議，R是畫圖高手。如果讀者諸君想深入繪圖相關技術，請前進The R Graph Gallery繼續研習、繼續努力、繼續鑽研。接下來，作者小編為上述「最簡單的散佈圖」加味加料：

plot(boston[, "crim"], boston[, "medv"],
     xlab = "犯罪率",
     ylab = "房價中位數",
     main = "犯罪率 vs 房價中位數的散佈圖")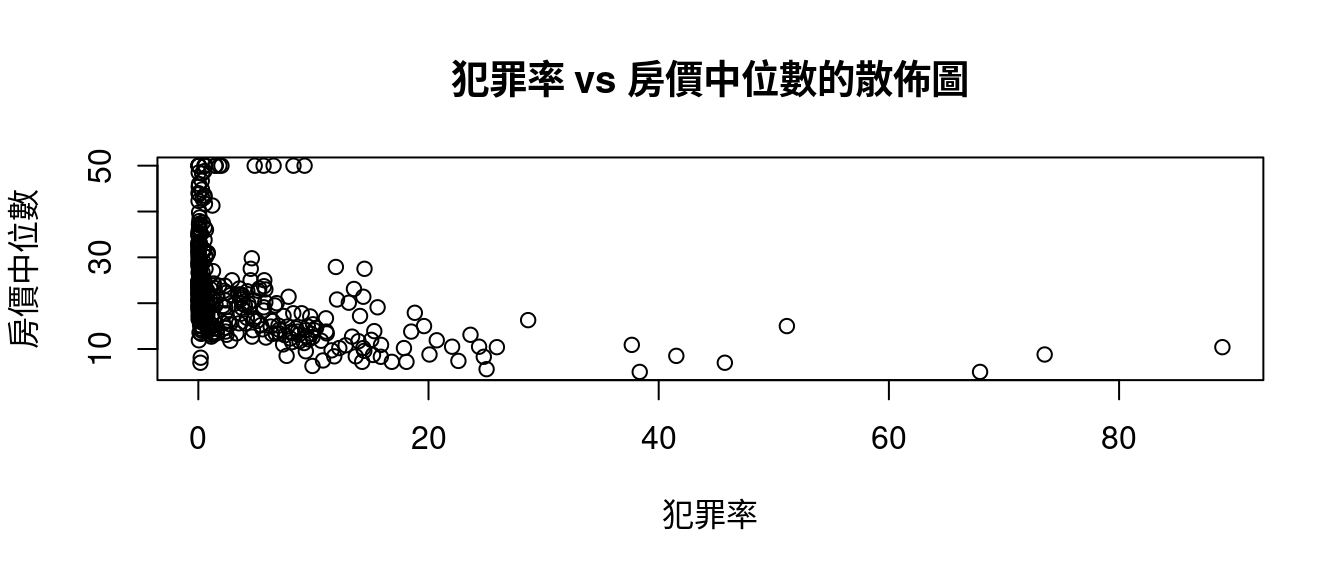

也可以根據「是否『是河岸宅』」加顏色：

plot(boston[, "crim"], boston[, "medv"],
     xlab = "犯罪率",
     ylab = "房價中位數",
     main = "犯罪率 vs 房價中位數的散佈圖",
     col = boston[, "chas"] + 5)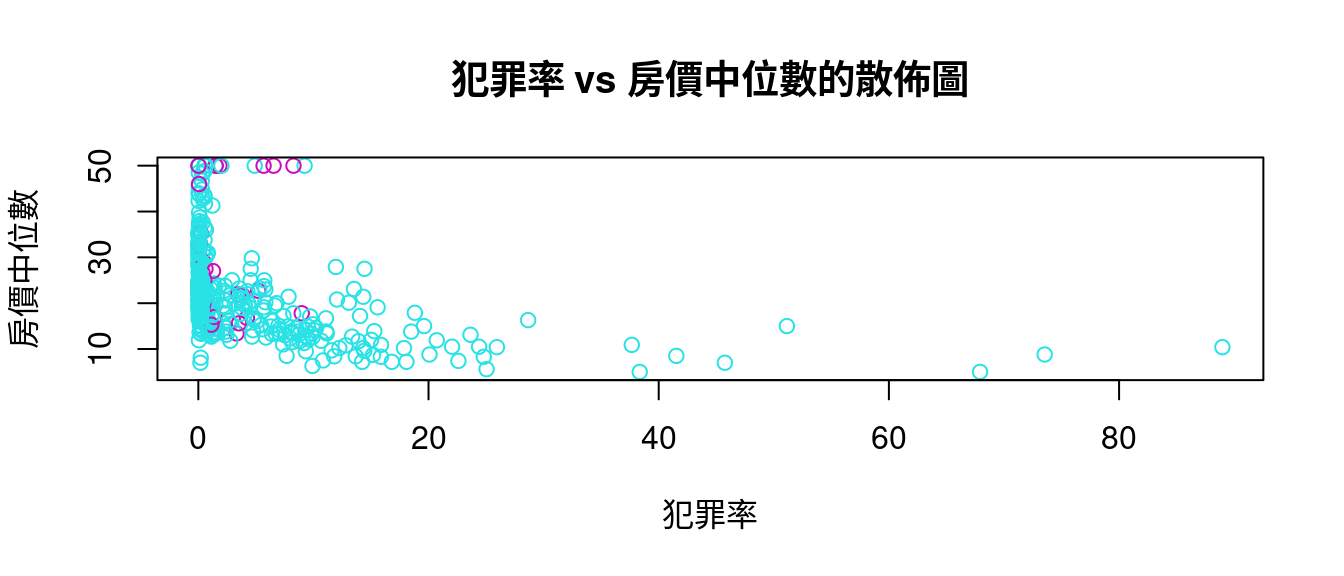

作者小編必須說，R的「圖學」確實是、已經是一門專門的學問了，讀者諸君如果想深入這一門學問，建議前進

1. The R Graph Gallery
2. R Graphics Cookbook
3. ggplot2

…

12.4.2 專家的意見

接下來，作者小編請來專家套件「caret」，讓我們快速取得波士頓數據集全部連續變數對上「房價中位數」的「散佈圖」。

require(caret)

1. 繪製全部連續變數對上「房價中位數」的「散佈圖」。

CONvars

##  [1] "crim"    "zn"      "indus"   "nox"     "rm"      "age"     "dis"    
##  [8] "tax"     "ptratio" "black"   "lstat"   "medv"

featurePlot(x = boston[, CONvars[-12]], 
            y = boston$medv)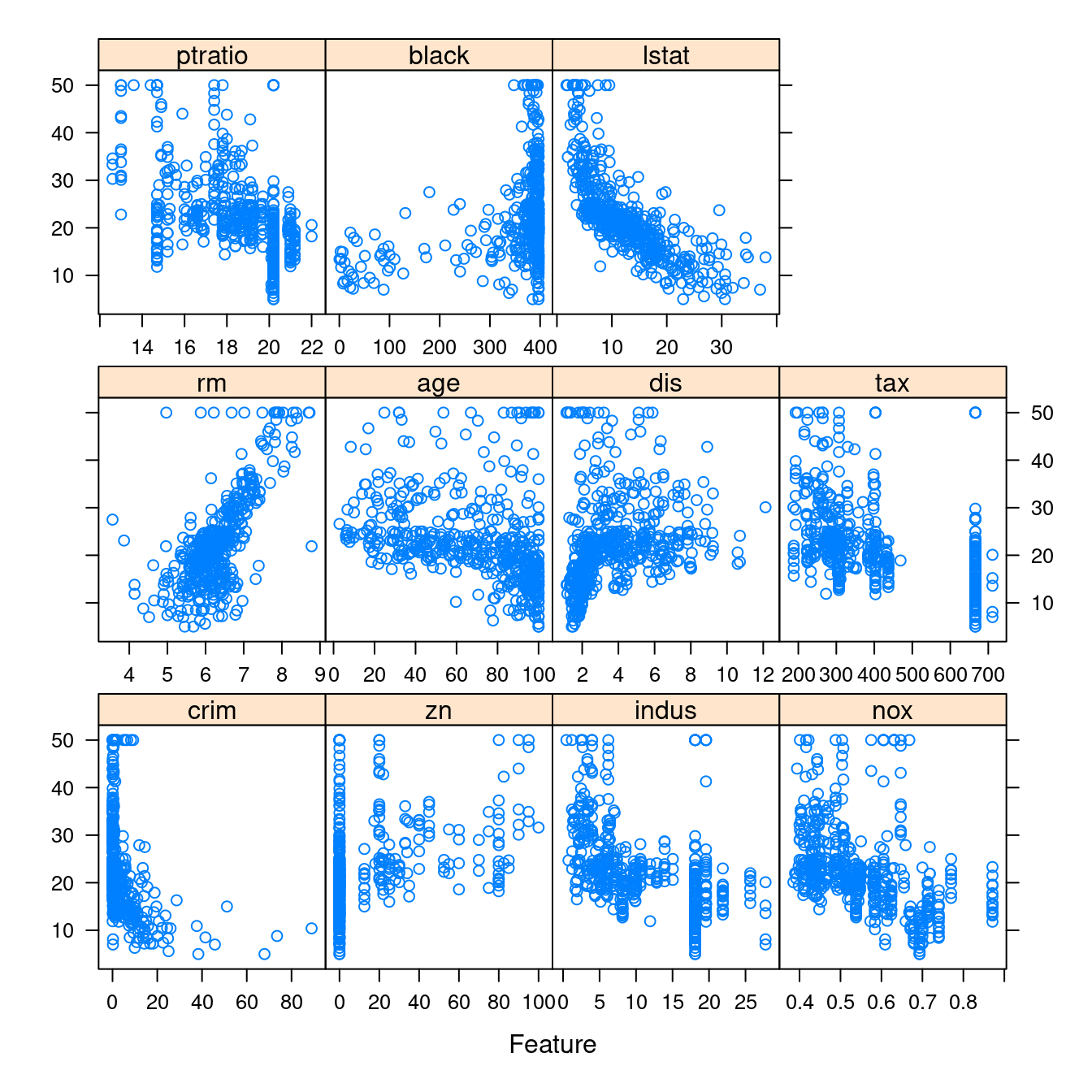

2. 依據是否「是河岸宅」繪製全部連續變數對上「房價中位數」的「散佈圖」。「否」的畫一張、「是」的畫一張。

featurePlot(x = boston[which(boston$chas == 0), CONvars[-12]], 
            y = boston$medv[which(boston$chas == 0)])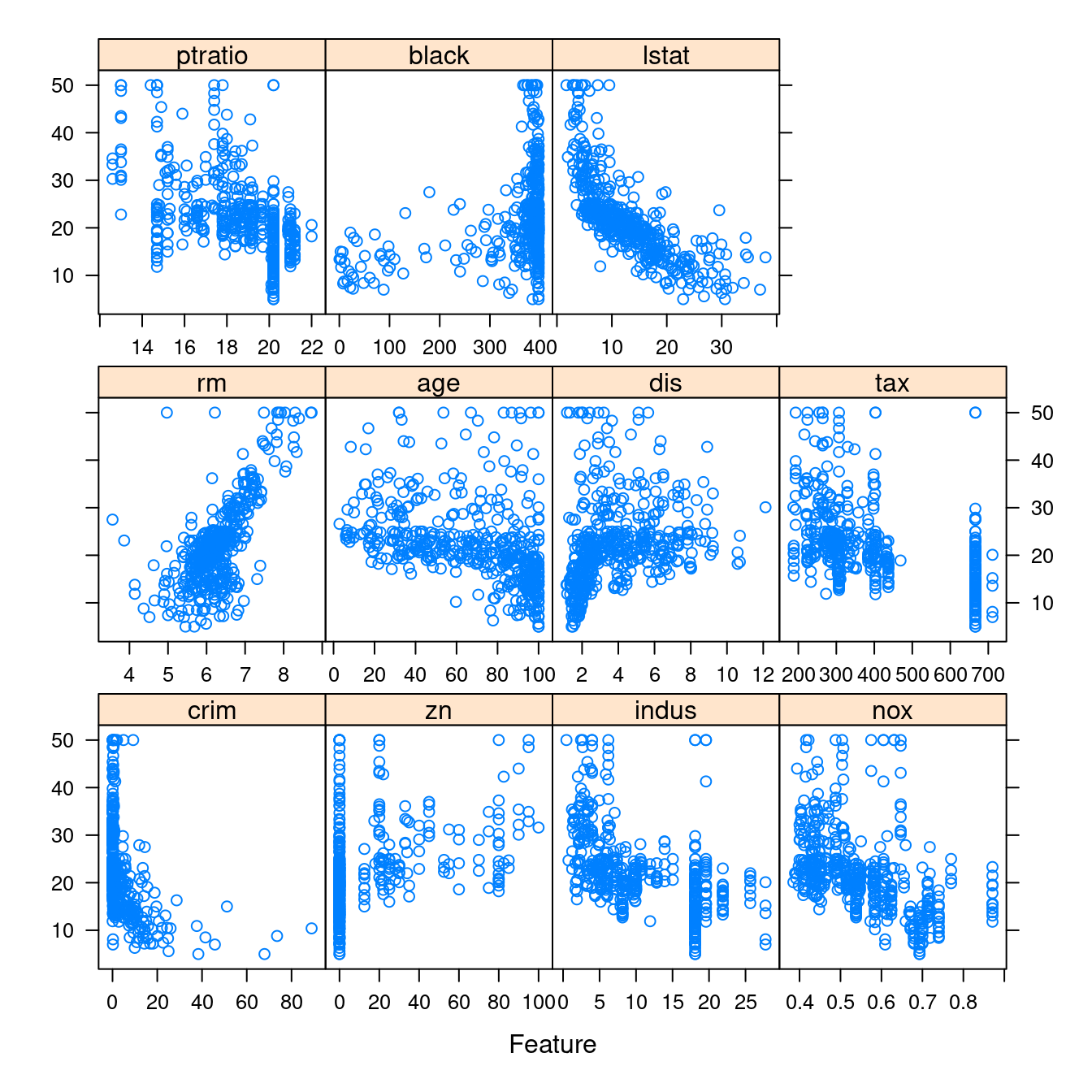

featurePlot(x = boston[which(boston$chas == 1), CONvars[-12]], 
            y = boston$medv[which(boston$chas == 1)])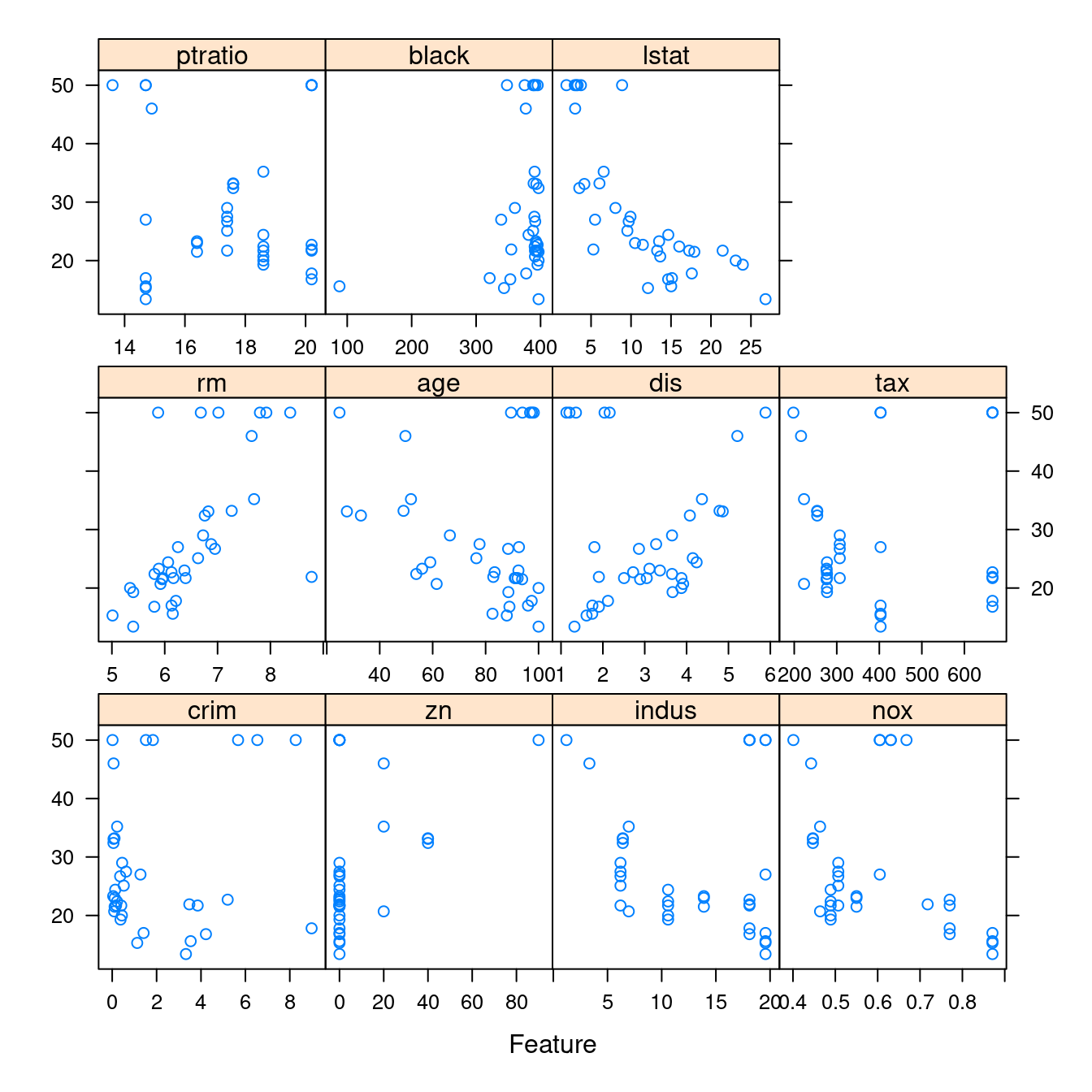

…

12.4.3 抓分群、分段的部分數據集

請讀者諸君再一次注意到

連戲

作者小編在編寫

依據是否「是河岸宅」繪製全部連續變數對上「房價中位數」的「散佈圖」。

時，先抓取了

繪製全部連續變數對上「房價中位數」的「散佈圖」。

的程式碼，下一步，我們一定會面臨這一個問題：

『是河岸宅』的數據在哪裡？『不是河岸宅』的數據在哪裡？

這個問題的答案是「which」，就是「which one」或是「which ones」，請先看官方使用手冊

knitr::include_url("https://www.rdocumentation.org/packages/base/versions/3.6.2/topics/which")

…

作者小編抓官方提供的範例為各位解釋(作者小編加料)「which」的力道：

### 範例一：
which(LETTERS == "R") # R這一個英文字母是第幾個英文字母？

## [1] 18

### 範例二：
which(LL <- c(TRUE, FALSE, TRUE, NA, FALSE, FALSE, TRUE)) # 「TRUE」的位置在哪裡？

## [1] 1 3 7

names(LL) <- letters[seq(LL)] # 命名。
LL # 作者小編加的，呼叫出來看看結果變成什麼樣？

##     a     b     c     d     e     f     g 
##  TRUE FALSE  TRUE    NA FALSE FALSE  TRUE

which(LL)

## a c g 
## 1 3 7

### 範例三：
which((0:9)%%2 == 0) # 哪幾個是偶數？作者小編把「原1:12」改成「0:9」避免把位置誤解為數字。

## [1] 1 3 5 7 9

### 範例四：
which(1:10 > 3, arr.ind = TRUE) # 哪幾個位置的數字大於3？

## [1]  4  5  6  7  8  9 10

### 範例五：
(m <- matrix(1:12, 3, 4)) # 先創造一個3x4的矩陣。在最外圈加上「小括號()」R就會主動把結果顯示在螢幕上。

##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

div.3 <- m %% 3 == 0 # 哪裡有3的倍數？
div.3

##       [,1]  [,2]  [,3]  [,4]
## [1,] FALSE FALSE FALSE FALSE
## [2,] FALSE FALSE FALSE FALSE
## [3,]  TRUE  TRUE  TRUE  TRUE

which(div.3) # 這種位置資訊不清楚，

## [1]  3  6  9 12

which(div.3, arr.ind = TRUE) # 所以，加上「arr.ind = TRUE」這樣可以顯示「列」跟「行」的資訊。

##      row col
## [1,]   3   1
## [2,]   3   2
## [3,]   3   3
## [4,]   3   4

rownames(m) <- paste("Case", 1:3, sep = "_")
m

##        [,1] [,2] [,3] [,4]
## Case_1    1    4    7   10
## Case_2    2    5    8   11
## Case_3    3    6    9   12

which(m %% 5 == 0, arr.ind = TRUE) # 哪裡有5的倍數？

##        row col
## Case_2   2   2
## Case_1   1   4

### 範例六：
dim(m) <- c(2, 2, 3); m # 把原本矩陣m切成三個2x2矩陣。如果想要兩句話寫在同一行，兩句間要加上「;」。

## , , 1
## 
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## 
## , , 2
## 
##      [,1] [,2]
## [1,]    5    7
## [2,]    6    8
## 
## , , 3
## 
##      [,1] [,2]
## [1,]    9   11
## [2,]   10   12

div.3 <- m %% 3 == 0 # 哪裡有3的倍數？為原範例補上這兩句。
div.3

## , , 1
## 
##       [,1]  [,2]
## [1,] FALSE  TRUE
## [2,] FALSE FALSE
## 
## , , 2
## 
##       [,1]  [,2]
## [1,] FALSE FALSE
## [2,]  TRUE FALSE
## 
## , , 3
## 
##       [,1]  [,2]
## [1,]  TRUE FALSE
## [2,] FALSE  TRUE

which(div.3, arr.ind = FALSE) # 記得一定要加上「arr.ind = TRUE」。

## [1]  3  6  9 12

which(div.3, arr.ind = TRUE)

##      dim1 dim2 dim3
## [1,]    1    2    1
## [2,]    2    1    2
## [3,]    1    1    3
## [4,]    2    2    3

### 範例七：
vm <- c(m)
vm

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

dim(vm) <- length(vm) #-- funny thing with  length(dim(...)) == 1
vm

##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

div.3 <- vm %% 3 == 0 # 哪裡有3的倍數？為原範例補上這兩句。
which(div.3, arr.ind = FALSE)

## [1]  3  6  9 12

which(div.3, arr.ind = TRUE) # 這裡不一定需要加上「arr.ind = TRUE」。

##      dim1
## [1,]    3
## [2,]    6
## [3,]    9
## [4,]   12

12.4.4 不分x變數跟y變數的散佈圖

假如「房價中位數」不再是唯一的「y變數」，我們當下「完全沒想法」，那以下的「pairs」就是我們的救星！全部「兩兩連續型變數」之間的散佈圖就靠它了。

pairs(boston[, CONvars])

我們可以慢慢、仔細觀察上述「大圖」，可以深入了解「兩兩連續變數」之間的數學關係，比如說

1. 線性
2. 二次
3. 三次

等等。比如說，

plot(boston[, "dis"], boston[, "nox"])

或是

plot(boston[, "lstat"], boston[, "medv"])

12.5 相關係數

請原諒作者小編「無(多)知(汁)」，讓我先抓維基百科的第一段為各位開場「相關係數」這一段：

In statistics, the Pearson correlation coefficient (PCC, pronounced /ˈpɪərsən/) is also referred to as Pearson’s r, the Pearson product-moment correlation coefficient (PPMCC), or the bivariate correlation.

作者小編喜歡「PPMCC」這一個縮寫，因為它「對稱」加上

which(LETTERS == "R")

## [1] 18

which(LETTERS == "P")

## [1] 16

which(LETTERS == "P")

## [1] 16

which(LETTERS == "M")

## [1] 13

which(LETTERS == "C")

## [1] 3

which(LETTERS == "C")

## [1] 3

…

12.5.1 共變異數

在認識「相關係數」之前，作者小編先介紹一個數字

共變異數

「共變異數」，是「變異數」前面加了一個「共」，統計學家企圖用這一個數字衡量，「兩變數『一起協同共變化』的程度」。為了介紹「共變異數」，我們先借用「鳶尾花數據集(iris)」製作一些假數據，然後用「電算手算」示範如何計算「共變異數」。

12.5.1.1 創造示範數據

data("iris")
x <- iris[,c("Sepal.Length", "Sepal.Width")] # 抓到其中兩個欄位。作者小編相信鳶尾花「sepal」的長跟寬應該有「協同變化」的現象。
head(x, 10)

##    Sepal.Length Sepal.Width
## 1           5.1         3.5
## 2           4.9         3.0
## 3           4.7         3.2
## 4           4.6         3.1
## 5           5.0         3.6
## 6           5.4         3.9
## 7           4.6         3.4
## 8           5.0         3.4
## 9           4.4         2.9
## 10          4.9         3.1

x <- (x*10) %% 10 # 抓第一個小數。
head(x, 10)

##    Sepal.Length Sepal.Width
## 1             1           5
## 2             9           0
## 3             7           2
## 4             6           1
## 5             0           6
## 6             4           9
## 7             6           4
## 8             0           4
## 9             4           9
## 10            9           1

x <- x[!duplicated(x),] # 抓不重複的觀察值(左右各一個加起來)。
head(x, 10)

##    Sepal.Length Sepal.Width
## 1             1           5
## 2             9           0
## 3             7           2
## 4             6           1
## 5             0           6
## 6             4           9
## 7             6           4
## 8             0           4
## 10            9           1
## 11            4           7

x <- x[1:10,] # 抓前十個。
head(x, 10)

##    Sepal.Length Sepal.Width
## 1             1           5
## 2             9           0
## 3             7           2
## 4             6           1
## 5             0           6
## 6             4           9
## 7             6           4
## 8             0           4
## 10            9           1
## 11            4           7

rownames(x) <- 1:dim(x)[1] # 順號「觀察值編號」。
head(x, 10)

##    Sepal.Length Sepal.Width
## 1             1           5
## 2             9           0
## 3             7           2
## 4             6           1
## 5             0           6
## 6             4           9
## 7             6           4
## 8             0           4
## 9             9           1
## 10            4           7

colnames(x) <- c("x1", "x2") # 換名字，避免困擾。
head(x, 10) # 呼叫答案，檢查最後的答案。

##    x1 x2
## 1   1  5
## 2   9  0
## 3   7  2
## 4   6  1
## 5   0  6
## 6   4  9
## 7   6  4
## 8   0  4
## 9   9  1
## 10  4  7

12.5.1.2 喚出散佈圖

plot(x)
abline(lm(x2 ~ x1, data = x), col = "blue")

12.5.1.3 計算SSCP矩陣

mean(x$x1) # 「x1」的平均數。

## [1] 4.6

mean(x$x2) # 「x2」的平均數。

## [1] 3.9

x$x1mod <- x$x1 - mean(x$x1) # 平移到平均數。
x$x2mod <- x$x2 - mean(x$x2)
x

##    x1 x2 x1mod x2mod
## 1   1  5  -3.6   1.1
## 2   9  0   4.4  -3.9
## 3   7  2   2.4  -1.9
## 4   6  1   1.4  -2.9
## 5   0  6  -4.6   2.1
## 6   4  9  -0.6   5.1
## 7   6  4   1.4   0.1
## 8   0  4  -4.6   0.1
## 9   9  1   4.4  -2.9
## 10  4  7  -0.6   3.1

x$ssx1 <- x$x1mod^2 # 「x1」的平方。
x$ssx2 <- x$x2mod^2 # 「x2」的平方。
x

##    x1 x2 x1mod x2mod  ssx1  ssx2
## 1   1  5  -3.6   1.1 12.96  1.21
## 2   9  0   4.4  -3.9 19.36 15.21
## 3   7  2   2.4  -1.9  5.76  3.61
## 4   6  1   1.4  -2.9  1.96  8.41
## 5   0  6  -4.6   2.1 21.16  4.41
## 6   4  9  -0.6   5.1  0.36 26.01
## 7   6  4   1.4   0.1  1.96  0.01
## 8   0  4  -4.6   0.1 21.16  0.01
## 9   9  1   4.4  -2.9 19.36  8.41
## 10  4  7  -0.6   3.1  0.36  9.61

x$scpx1x2 <- x$x1mod*x$x2mod # 「x1」跟「x2」的交叉積。
x

##    x1 x2 x1mod x2mod  ssx1  ssx2 scpx1x2
## 1   1  5  -3.6   1.1 12.96  1.21   -3.96
## 2   9  0   4.4  -3.9 19.36 15.21  -17.16
## 3   7  2   2.4  -1.9  5.76  3.61   -4.56
## 4   6  1   1.4  -2.9  1.96  8.41   -4.06
## 5   0  6  -4.6   2.1 21.16  4.41   -9.66
## 6   4  9  -0.6   5.1  0.36 26.01   -3.06
## 7   6  4   1.4   0.1  1.96  0.01    0.14
## 8   0  4  -4.6   0.1 21.16  0.01   -0.46
## 9   9  1   4.4  -2.9 19.36  8.41  -12.76
## 10  4  7  -0.6   3.1  0.36  9.61   -1.86

SSCP <- apply(x[,c(5,7,7,6)], 2, sum) # 計算總和。
SSCP

##      ssx1   scpx1x2 scpx1x2.1      ssx2 
##     104.4     -57.4     -57.4      76.9

SSCP <- matrix(SSCP, 2, 2) # 變成、排成2x2矩陣。
SSCP

##       [,1]  [,2]
## [1,] 104.4 -57.4
## [2,] -57.4  76.9

dimnames(SSCP) <- list(names(x)[1:2], names(x)[1:2]) # 取名字。
SSCP # 這就是「SSCP = sum of squares and cross-product」矩陣。

##       x1    x2
## x1 104.4 -57.4
## x2 -57.4  76.9

12.5.1.4 取得變異數-共變異數矩陣

S <- SSCP/(NROW(x) - 1) 
S # 呼叫答案檢查答案

##           x1        x2
## x1 11.600000 -6.377778
## x2 -6.377778  8.544444

var(x$x1)

## [1] 11.6

var(x$x2)

## [1] 8.544444

cov(x$x1, x$x2)

## [1] -6.377778

cov(x$x2, x$x1)

## [1] -6.377778

var(x[, c("x1", "x2")])

##           x1        x2
## x1 11.600000 -6.377778
## x2 -6.377778  8.544444

12.5.2 什麼是相關係數？

我們先看「示範數據」的「相關係數」：

cor(x = x$x1, y = x$x2)

## [1] -0.640617

SSCP

##       x1    x2
## x1 104.4 -57.4
## x2 -57.4  76.9

SSCP[1,2]/sqrt(SSCP[1,1] * SSCP[2,2])

## [1] -0.640617

SSCP[2,1]/sqrt(SSCP[1,1] * SSCP[2,2])

## [1] -0.640617

「電算手算」大成功！因為「電算手算」的答案跟「電算」的答案一模一樣！

…

12.5.2.1 性質一：平移變數不會改變相關係數

請看電算程式「cor」的示範：

cor(x$x1, x$x2)

## [1] -0.640617

cor(x$x1mod, x$x2)

## [1] -0.640617

cor(x$x1, x$x2mod)

## [1] -0.640617

cor(x$x1mod, x$x2mod)

## [1] -0.640617

12.5.2.2 性質二：個別變大變小變數不會改變相關係數

請看電算程式「cor」的示範：

cor(x$x1, x$x2)

## [1] -0.640617

cor(x$x1, 3 * x$x2)

## [1] -0.640617

cor(3 * x$x1, x$x2)

## [1] -0.640617

cor(3 * x$x1, 3 * x$x2)

## [1] -0.640617

12.5.2.3 幾組波士頓數據集連續型變數的相關係數

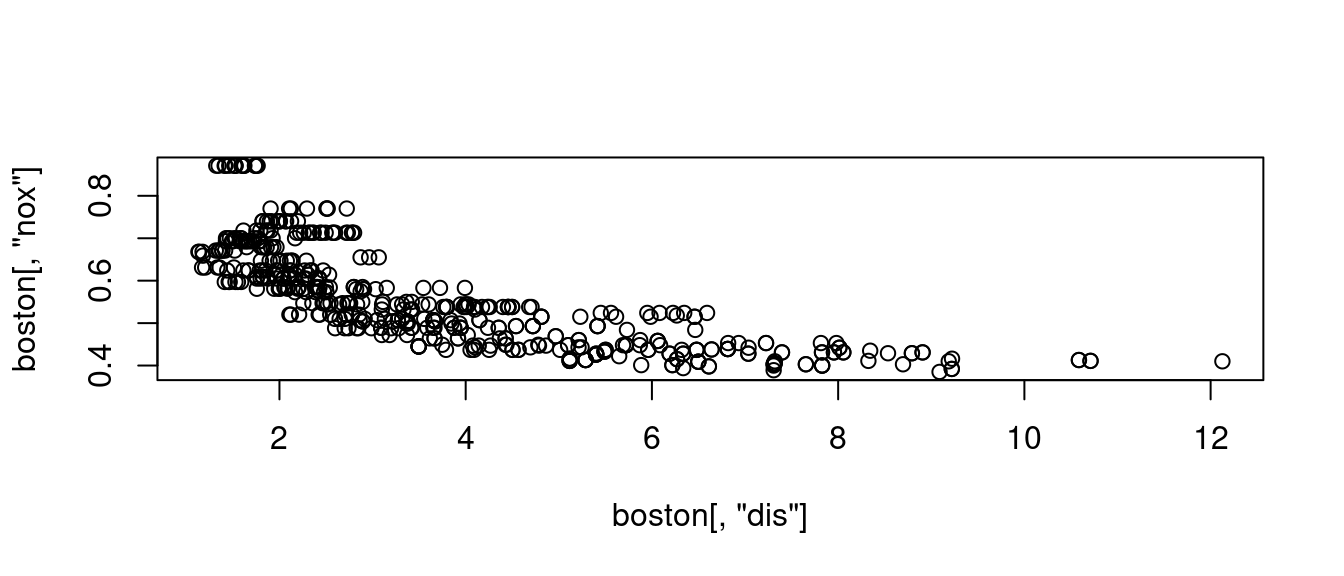
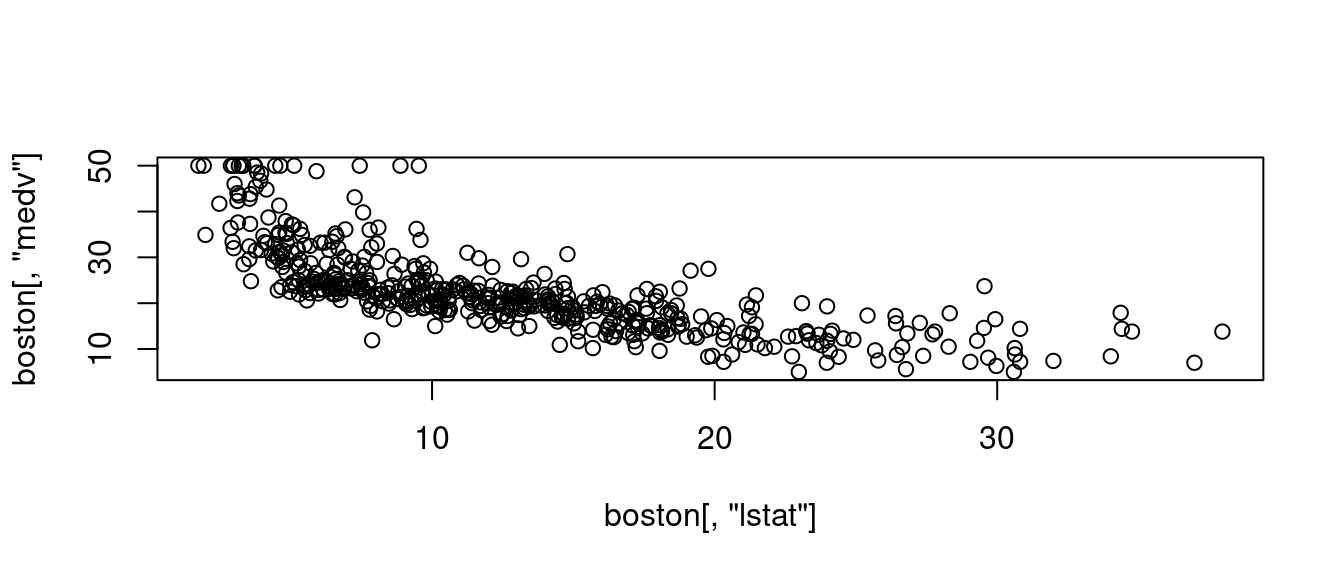
觀察過至少一輪「不分x變數跟y變數的散佈圖」的結果之後，作者小編決定先看看以下這兩組變數的相關係數：

cor(boston[, "dis"], boston[, "nox"])

## [1] -0.7692301

cor(boston[, "lstat"], boston[, "medv"])

## [1] -0.7376627

其中

1. 「負號(-)」代表「x變數越大y變數越小」、
2. 「數字越靠近1」代表「點點越靠近某一條直線」。

接下來，這一張維基百科提供的例子，補充了作者小編想像不到的可能性：

knitr::include_graphics("www/800px-Correlation_examples2.png")

## Error in knitr::include_graphics("www/800px-Correlation_examples2.png"): Cannot find the file(s): "www/800px-Correlation_examples2.png"

看過之後，作者小編再一次確認「相關係數(Pearson correlation coefficient)」這一個數字確實是一個

「衡量」兩連續型變數「線性關係強度」的數字。

那，「相關係數(Pearson correlation coefficient)」怎麼算出來的呢？定義如下：

\[\frac{\sum (x - \bar x)(y - \bar y)}{\sqrt{\sum (x - \bar x)^2 \sum (y - \bar y)^2}}\]

其中「\(\bar x\)」是「x變數」的「平均數」，「\(\bar y\)」是「y變數」的「平均數」。「分子」是「交叉積和」，「分母」是「兩平方和乘積的正方根」。讓我們再抓一組變數來瞧瞧

plot(boston[, "age"], boston[, "dis"])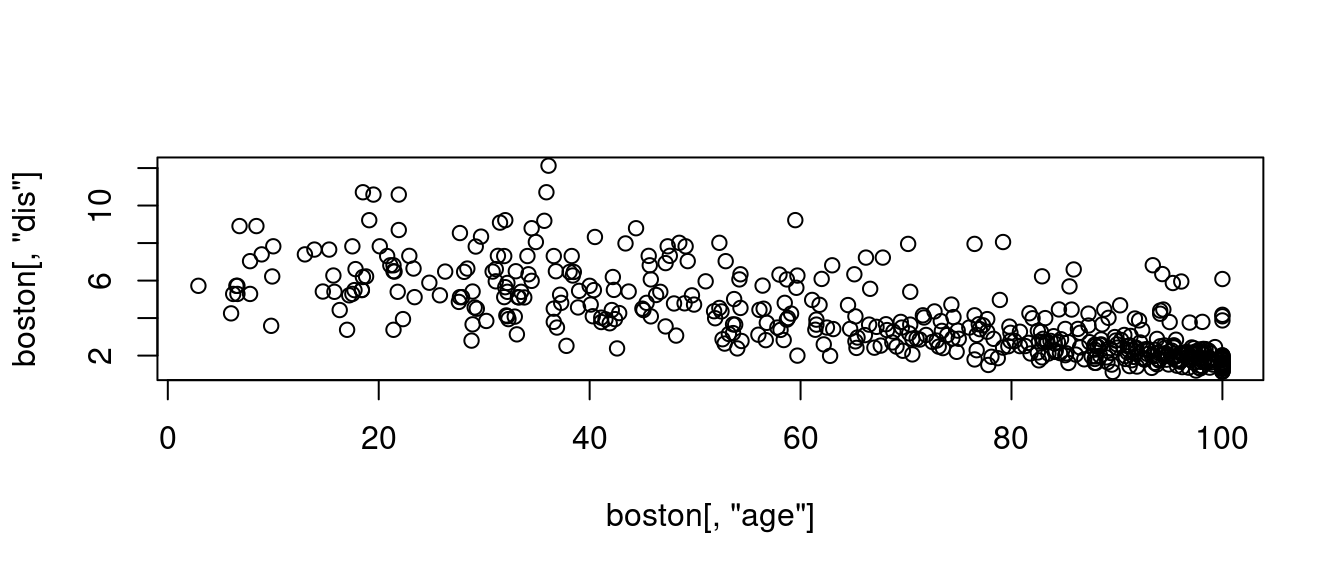

cor(boston[, "age"], boston[, "dis"])

## [1] -0.7478805

很幸運，我們抓到「強度接近」，都是「0.7多」，而且都是「負向」的「相關係數」。作者小編決定把它們放在一起，應該可以「強化」我們對「相關係數」的印象、理解、認識。

par(mfrow = c(1,3))
plot(boston[, "dis"], boston[, "nox"])
title(paste0("相關係數", " = ", cor(boston[, "dis"], boston[, "nox"])))
plot(boston[, "lstat"], boston[, "medv"])
title(paste0("相關係數", " = ", cor(boston[, "lstat"], boston[, "medv"])))
plot(boston[, "age"], boston[, "dis"])
title(paste0("相關係數", " = ", cor(boston[, "age"], boston[, "dis"])))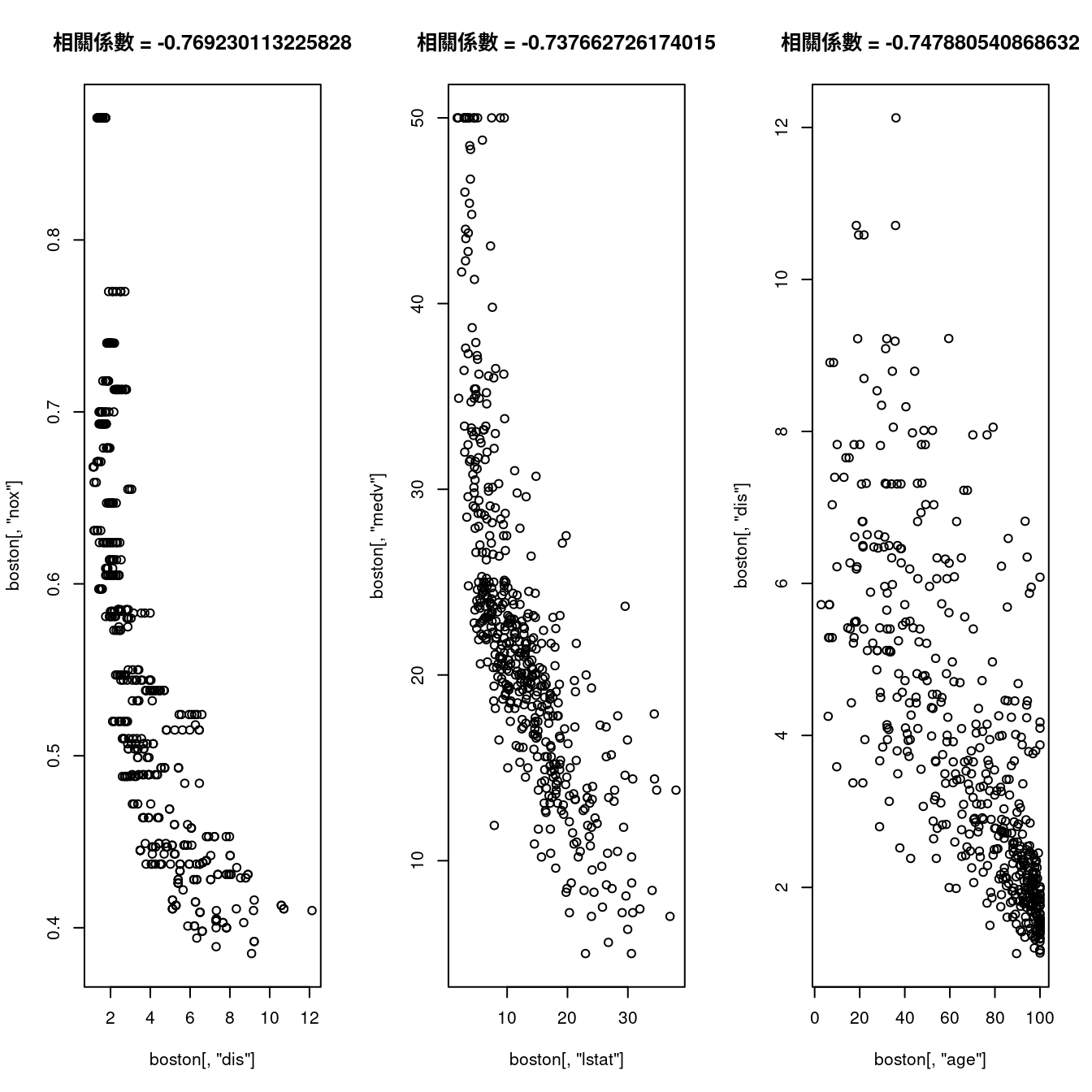

請注意，作者小編正在示範如何透過程式促進我們對某一件事情的理解程度。

12.5.2.4 計算波士頓數據集內11個連續型變數與房價中位數的相關係數

cor(x = boston[, CONvars[-12]], y = boston[, "medv"])

##               [,1]
## crim    -0.3883046
## zn       0.3604453
## indus   -0.4837252
## nox     -0.4273208
## rm       0.6953599
## age     -0.3769546
## dis      0.2499287
## tax     -0.4685359
## ptratio -0.5077867
## black    0.3334608
## lstat   -0.7376627

我們發現(連戲)

CORmedv <- cor(x = boston[, CONvars[-12]], y = boston[, "medv"])
rownames(CORmedv)[which(abs(CORmedv[,1]) <= 0.3)] # 小於0.3。

## [1] "dis"

rownames(CORmedv)[which(abs(CORmedv[,1]) > 0.3 & abs(CORmedv[,1]) <= 0.5)] # 大於0.3且小於0.5。

## [1] "crim"  "zn"    "indus" "nox"   "age"   "tax"   "black"

rownames(CORmedv)[which(abs(CORmedv[,1]) > 0.5 & abs(CORmedv[,1]) <= 0.7)] # 大於0.5且小於0.7。

## [1] "rm"      "ptratio"

rownames(CORmedv)[which(abs(CORmedv[,1]) > 0.7)] # 大於0.7。

## [1] "lstat"

也發現

rownames(CORmedv)[which.max(abs(CORmedv[,1]))] # 最大相關係數發生在哪一個變數？

## [1] "lstat"

因為這個發現，作者小編寫了這一段

maxCOR <- rownames(CORmedv)[which.max(abs(CORmedv[,1]))]
plot(boston[, maxCOR], boston[, "medv"], 
     xlab = maxCOR,
     ylab = "房價中位數")
title(paste0("相關係數", " = ", 
             cor(boston[, maxCOR], 
                 boston[, "medv"])))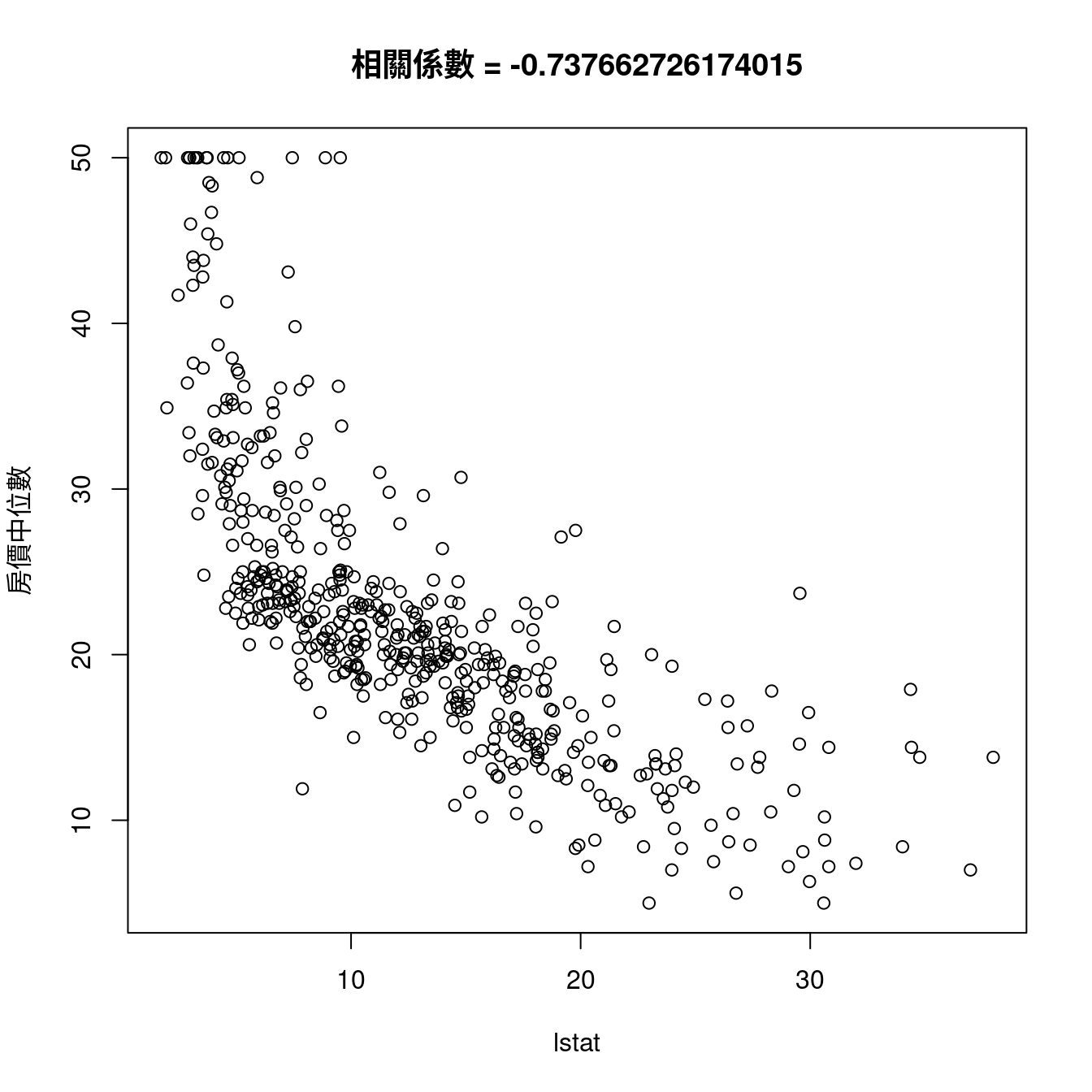

12.5.2.5 幾個相關係數的數學性質

\[\frac{\sum (x - \bar x)(y - \bar y)}{\sqrt{\sum (x - \bar x)^2 \sum (y - \bar y)^2}} = \sum \frac{x - \bar x}{\sqrt{\sum (x - \bar x)^2}}\frac{y - \bar y}{\sqrt{\sum (y - \bar y)^2}} = \frac{1}{n - 1}\sum(\frac{x - \bar x}{s_x})(\frac{y - \bar y}{s_y})\]

探索「相關係數」先停在這裡，

…

12.5.3 相關係數矩陣

以下這張表是波士頓數據集全部連續型變數，「兩兩之間」「cor」算出來的相關係數，比如說

1. 「列名稱 = crim」跟「行名稱 = crim」的相關係數是「1.00」。
2. 「列名稱 = crim」跟「行名稱 = zn」的相關係數是「-0.20」。
3. 「列名稱 = zn」跟「行名稱 = crim」的相關係數是「-0.20」。

as.data.frame.matrix(round(cor(boston[, CONvars]), 2))

##          crim    zn indus   nox    rm   age   dis   tax ptratio black lstat
## crim     1.00 -0.20  0.41  0.42 -0.22  0.35 -0.38  0.58    0.29 -0.39  0.46
## zn      -0.20  1.00 -0.53 -0.52  0.31 -0.57  0.66 -0.31   -0.39  0.18 -0.41
## indus    0.41 -0.53  1.00  0.76 -0.39  0.64 -0.71  0.72    0.38 -0.36  0.60
## nox      0.42 -0.52  0.76  1.00 -0.30  0.73 -0.77  0.67    0.19 -0.38  0.59
## rm      -0.22  0.31 -0.39 -0.30  1.00 -0.24  0.21 -0.29   -0.36  0.13 -0.61
## age      0.35 -0.57  0.64  0.73 -0.24  1.00 -0.75  0.51    0.26 -0.27  0.60
## dis     -0.38  0.66 -0.71 -0.77  0.21 -0.75  1.00 -0.53   -0.23  0.29 -0.50
## tax      0.58 -0.31  0.72  0.67 -0.29  0.51 -0.53  1.00    0.46 -0.44  0.54
## ptratio  0.29 -0.39  0.38  0.19 -0.36  0.26 -0.23  0.46    1.00 -0.18  0.37
## black   -0.39  0.18 -0.36 -0.38  0.13 -0.27  0.29 -0.44   -0.18  1.00 -0.37
## lstat    0.46 -0.41  0.60  0.59 -0.61  0.60 -0.50  0.54    0.37 -0.37  1.00
## medv    -0.39  0.36 -0.48 -0.43  0.70 -0.38  0.25 -0.47   -0.51  0.33 -0.74
##          medv
## crim    -0.39
## zn       0.36
## indus   -0.48
## nox     -0.43
## rm       0.70
## age     -0.38
## dis      0.25
## tax     -0.47
## ptratio -0.51
## black    0.33
## lstat   -0.74
## medv     1.00

請讀者諸君注意，「cor」給我們的成果、輸出，確實是一張「矩陣」，經過作者小編「化了幾筆妝」

1. 四捨五入到兩位小數，「round(, 2)」、
2. 變身為一張表，「as.data.frame.matrix()」。

才讓各位看到上述這一張「美美的樣子」。

12.5.4 相關係數圖

「視覺化」相關係數矩陣是趨勢，原因是，實務上上述「相關係數矩陣」都很大，於是乎，統計學家再度出動，撰寫了套件「corrplot」。讓作者小編告訴大家如何用在波士頓數據集的相關係數矩陣：

1. 呼叫套件「corrplot」。

require(corrplot)

2. 準備波士頓數據集內連續型變數的相關係數矩陣。

corr <- round(cor(boston[, CONvars]), 2)

3. 繪製相關係數圖。把一切都交給corrplot::corrplot決定。如果你關注第一個連續型變數「crim」與其他連續型變數的相關係數之間的「相對大小」與「正負號」，在最左邊類似「觀察值編號」的那一排名字找到「crim」，然後往右看，遇上「紅色圈圈」表示「負的相關係數」，遇上「藍色圈圈」表示「正的相關係數」，「圈圈越大」或是「顏色越深」，表示「數值越大」。

corrplot(corr)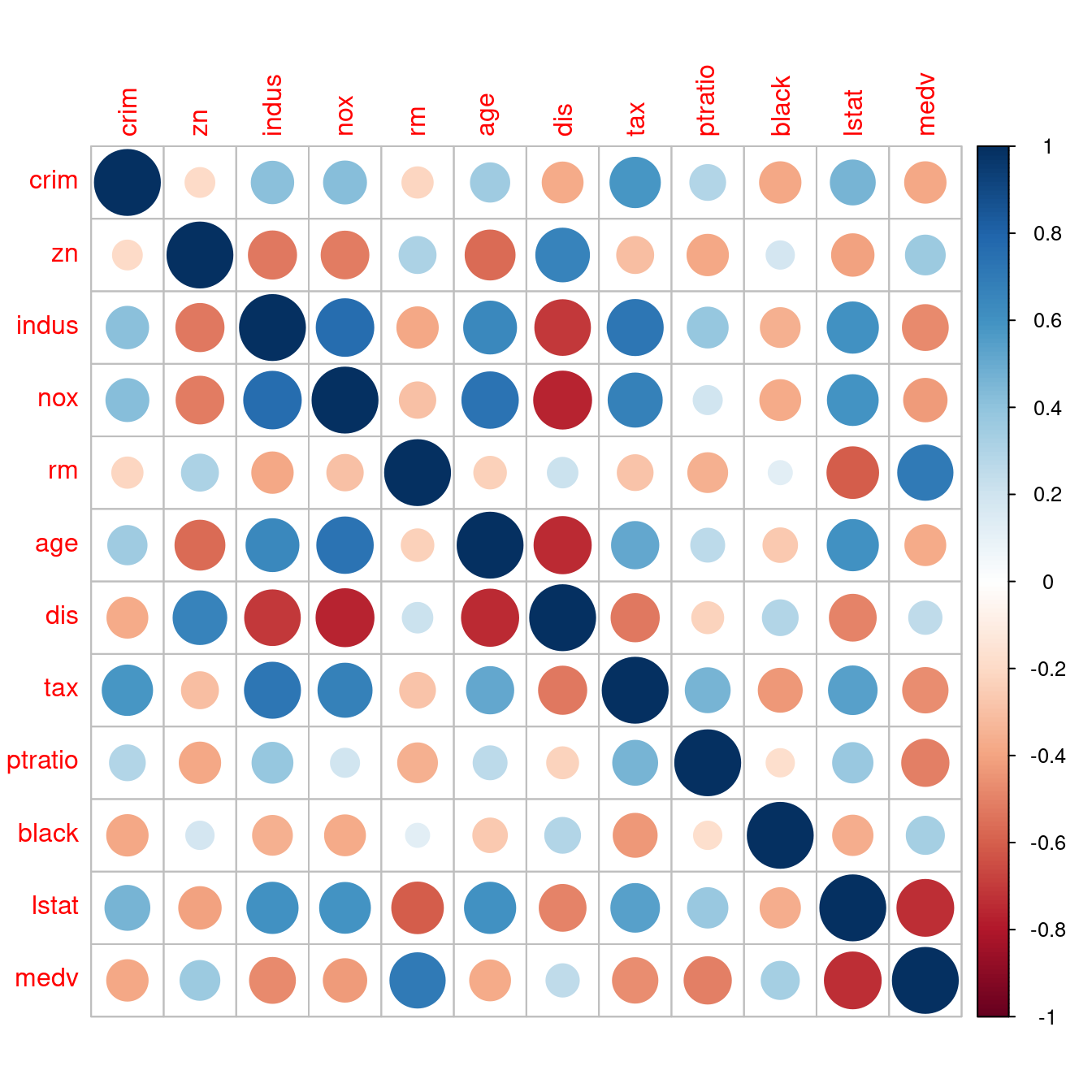

4. 解決問題一：既然相關係數矩陣是對稱的，可以只看一半嗎？corrplot::corrplot讓你加一句「type = "upper"」看「上半矩陣」；如果是「type = "lower"」看「下半矩陣」。

corrplot(corr, type = "upper")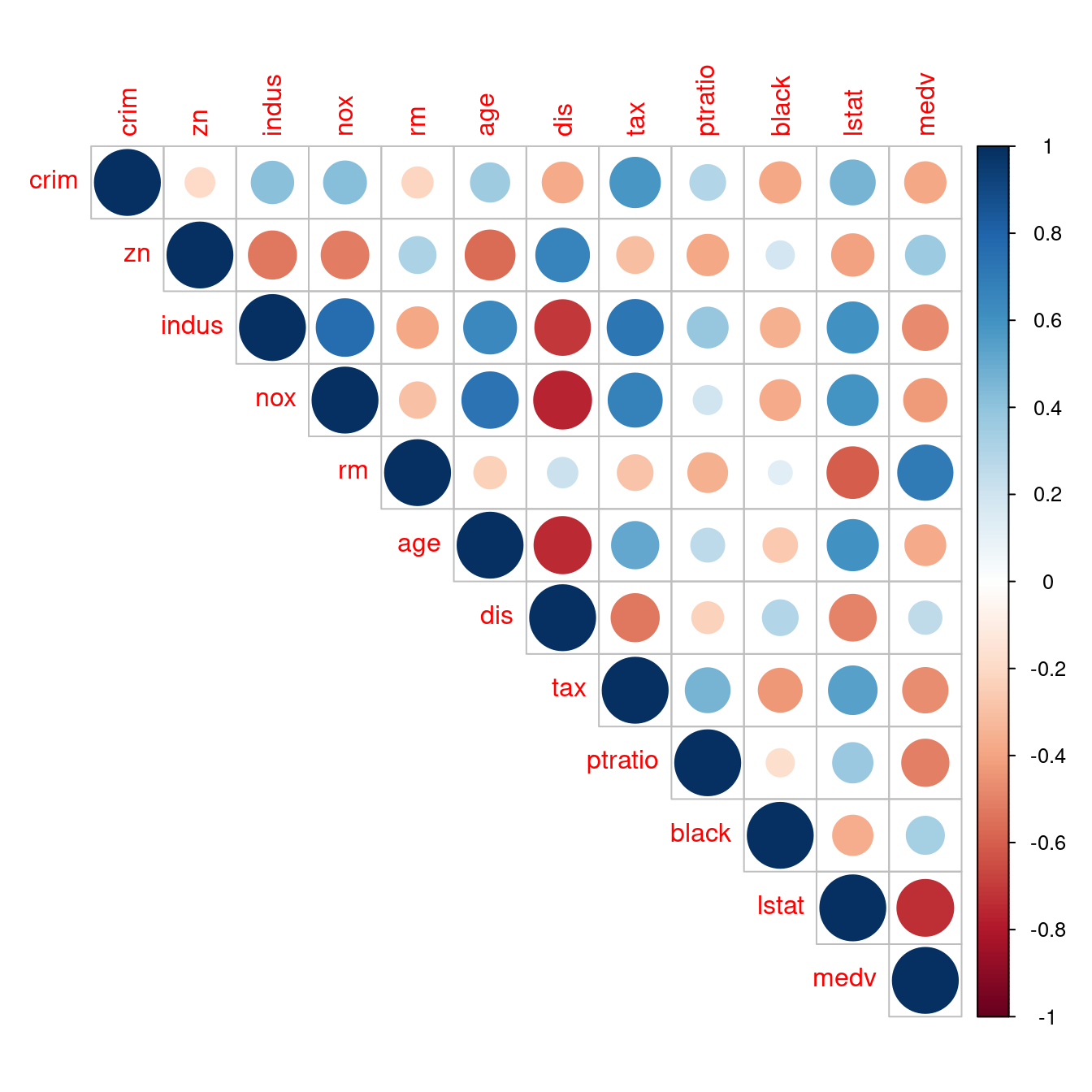

corrplot(corr, type = "lower")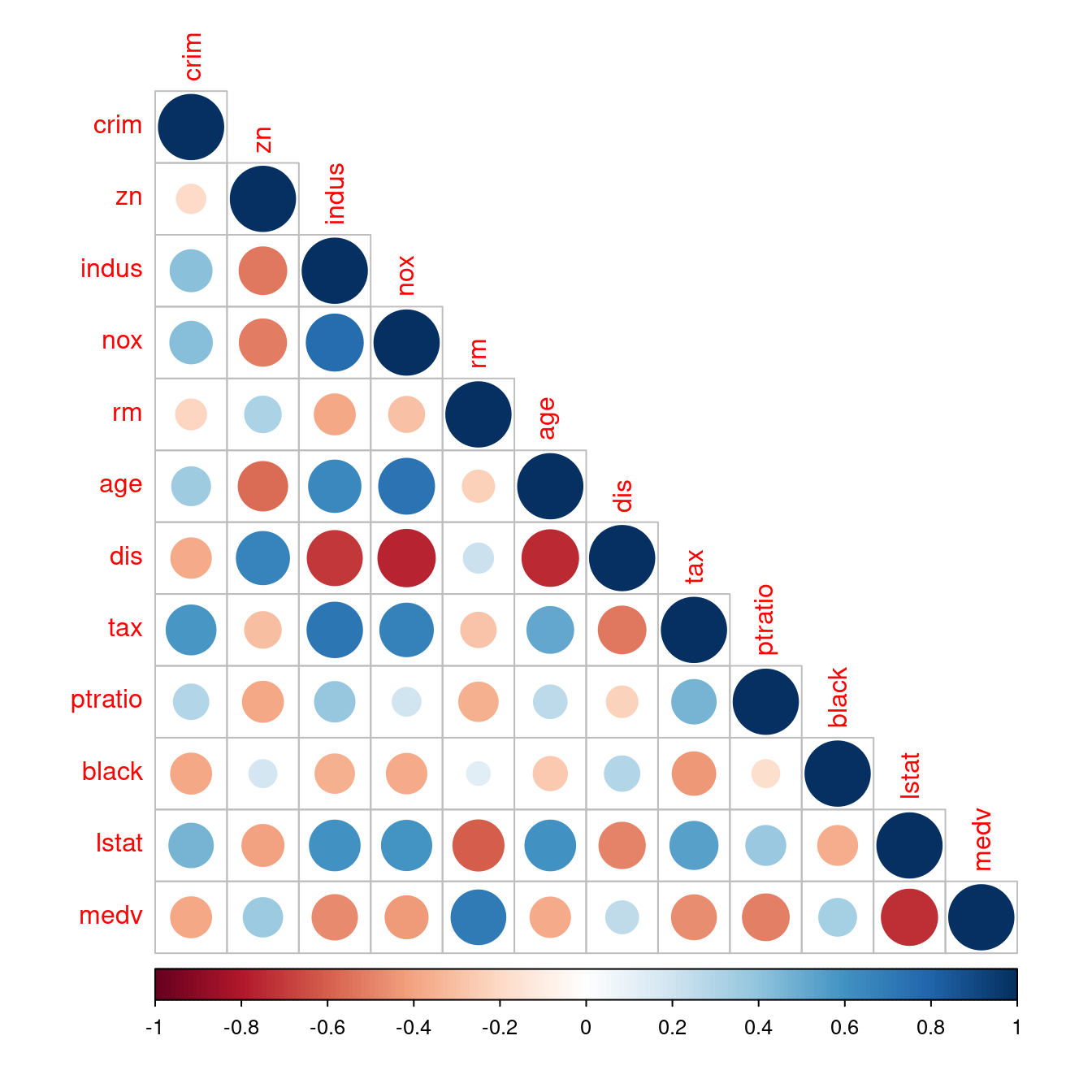

5. 解決問題二：可以根據與房價中位數的相關係數大小排序嗎？因為「房價中位數」是第十二個變數，所以在「列方向」與「行方向」都加一句「order(corr[12,])」，就可以維持「相關係數矩陣是對稱的」這一項性質。請讀者諸君專注在「最後一列」跟「最後一行」。完美！而且我們可以很輕鬆知道「全部連續型變數(lstat, ptratio, indus, tax, nox, crim, age, dis, black, zn, rm, medv)」與「房價中位數」的相關係數的「排行榜」！當然也可以有「按相關係數數值大小的排行榜」！作者小編認為第二個排行榜應該有助於「多個x變數的建模策略」，將在第八章實作、實驗這一項臆測！

corr <- corr[order(corr[12,]), order(corr[12,])]
corrplot(corr)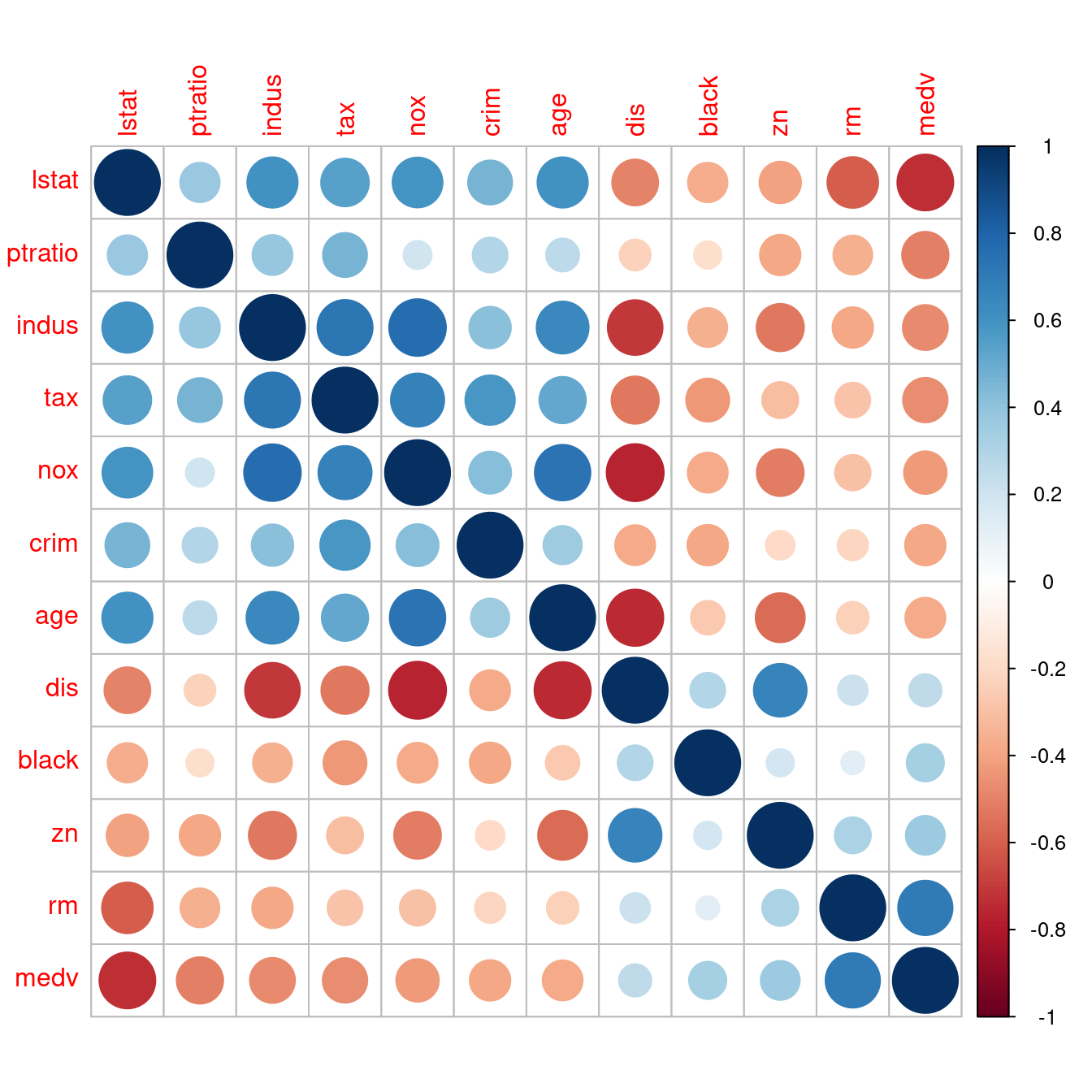

corr <- corr[order(abs(corr[12,])), order(abs(corr[12,]))]
corrplot(corr)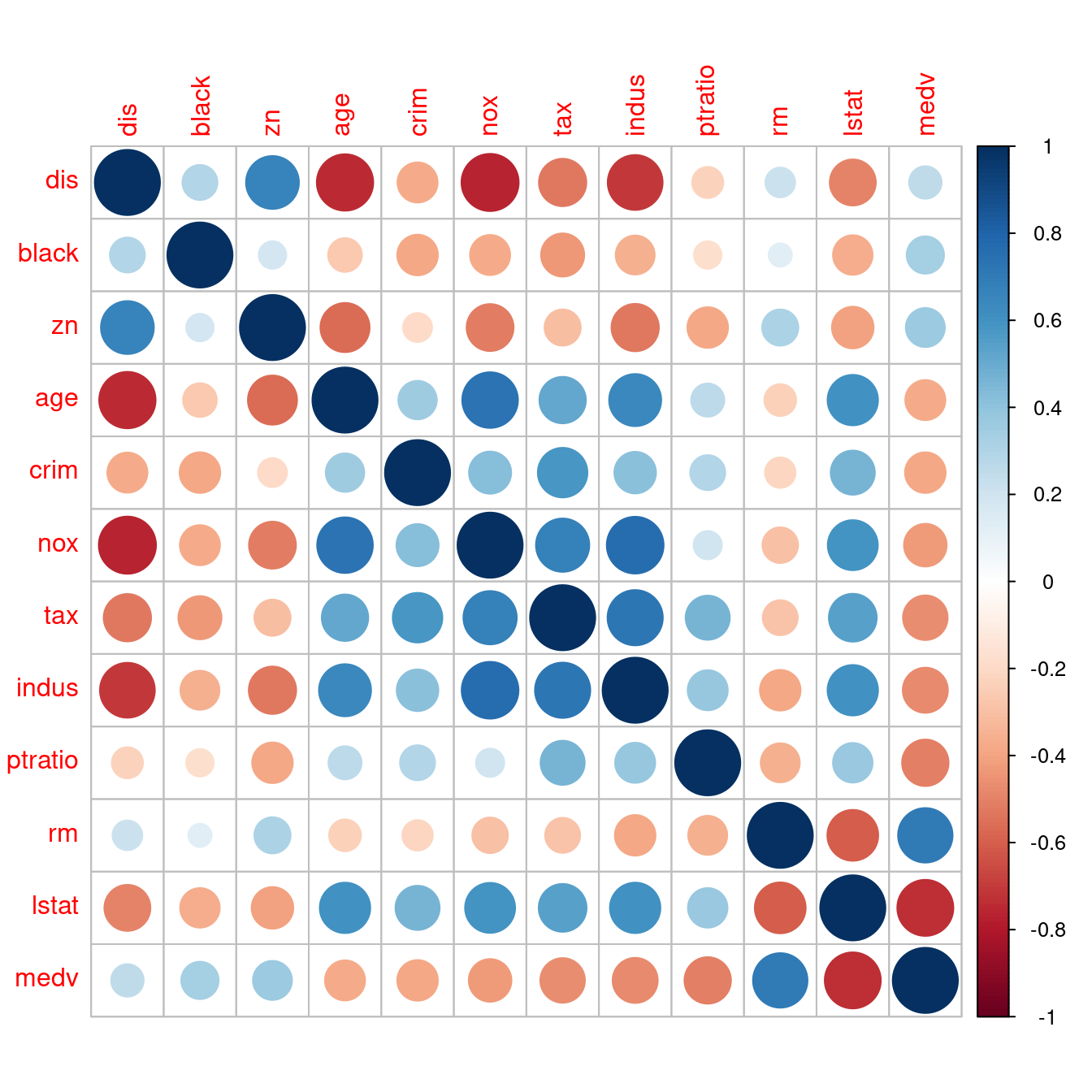

6. 解決問題三：可以把全部變數分類掉、分開來嗎？讓我們一小群一小群觀察嗎？請讀者諸君仔細看，可以發現「四大區塊」，至於「四大區塊」可以為我們在搜尋「1970年代波士頓都會區的最佳『hedonic housing price model』」，幫上什麼忙？就指日可待！！！

corrplot(corr, order = "FPC")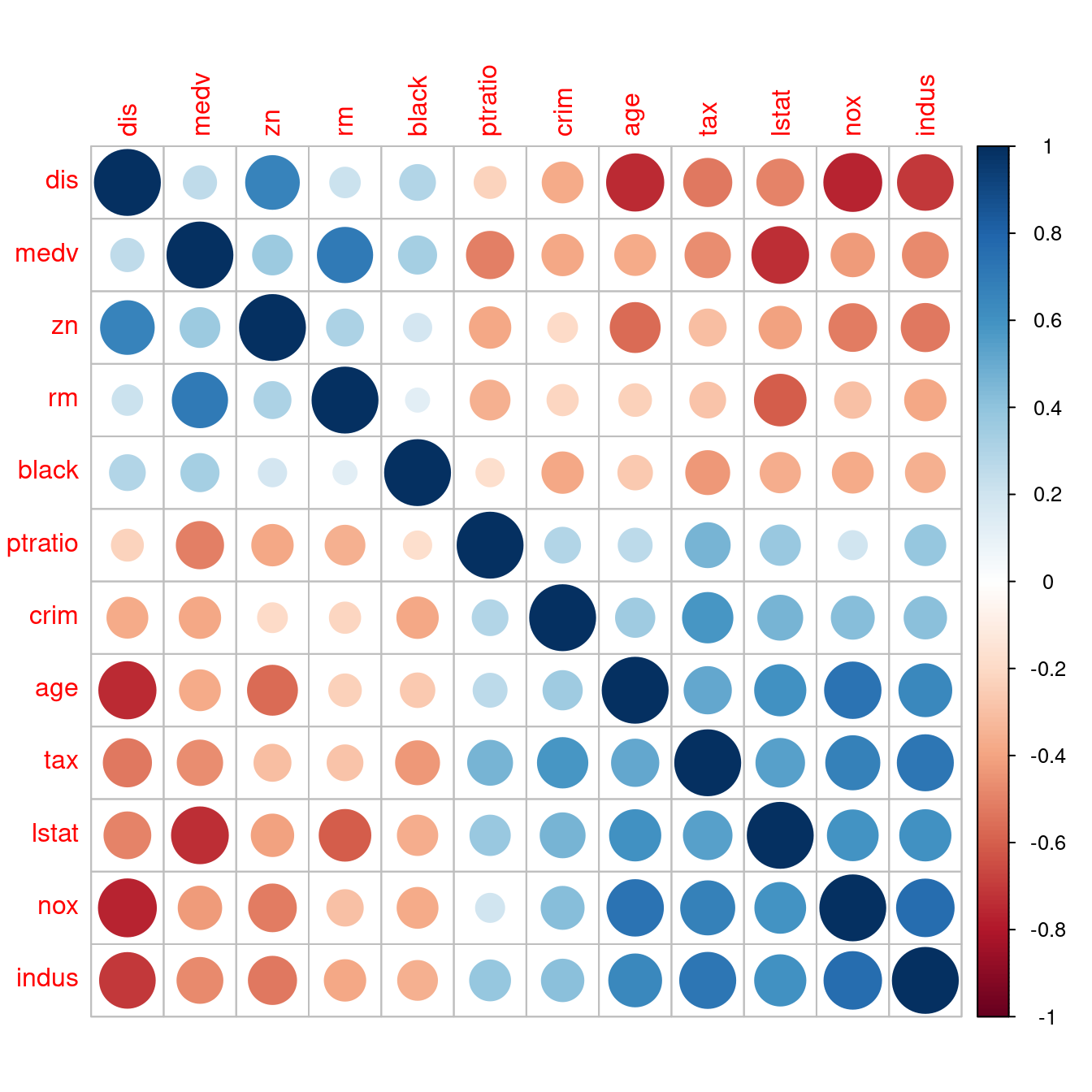

corrplot(corr, order = "hclust")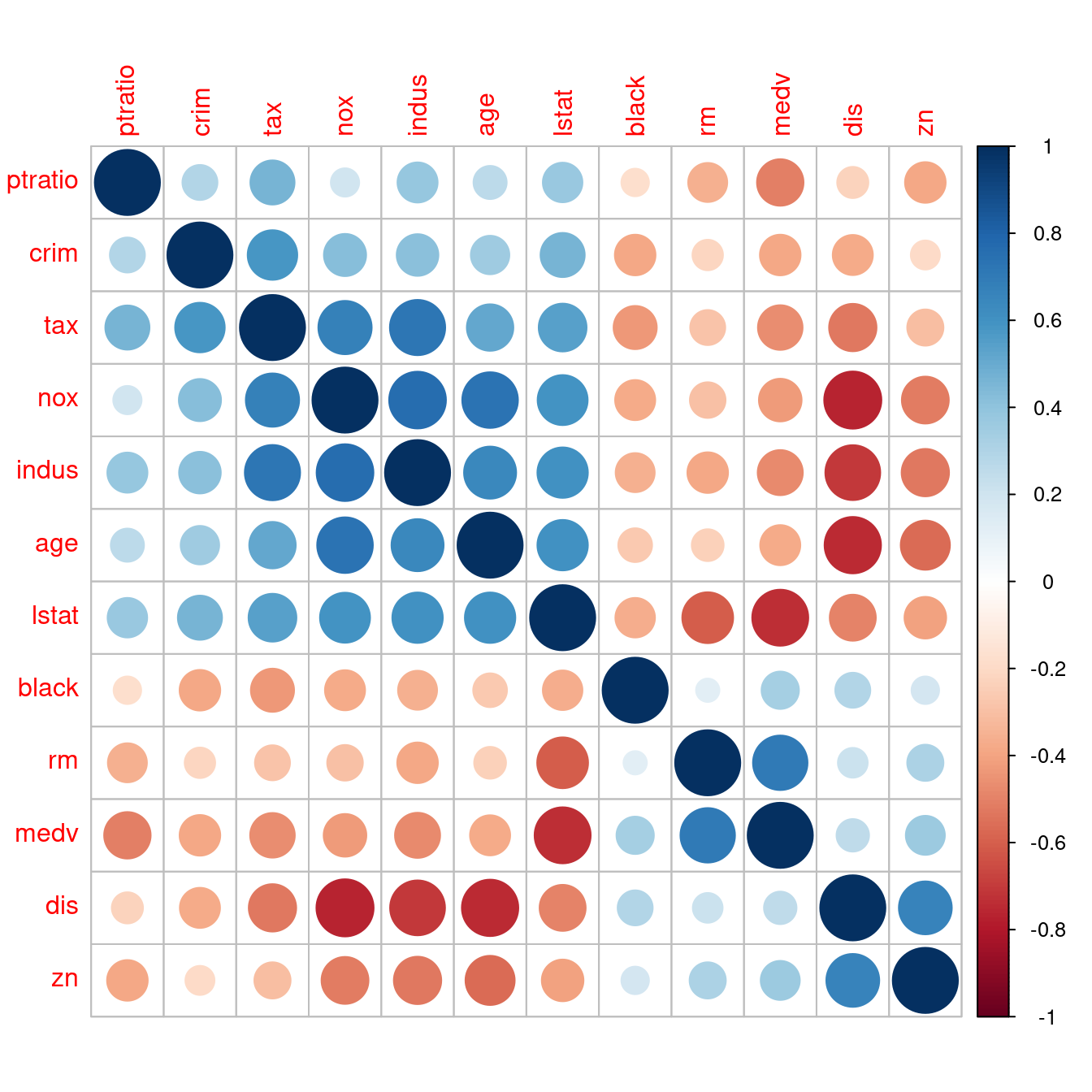

到此，我們已經學過、看過

1. 直方圖
2. 密度圖
3. 散佈圖
4. 相關係數
5. (還缺)相關係數檢定
6. (還缺)修勻

透過下述這一個套件「PerformanceAnalytics」的「chart.Correlation」，可以把這六項技術整合在一張大圖裡。請看…

require(PerformanceAnalytics)
chart.Correlation(boston[, CONvars], 
                  histogram = TRUE, 
                  pch = 8)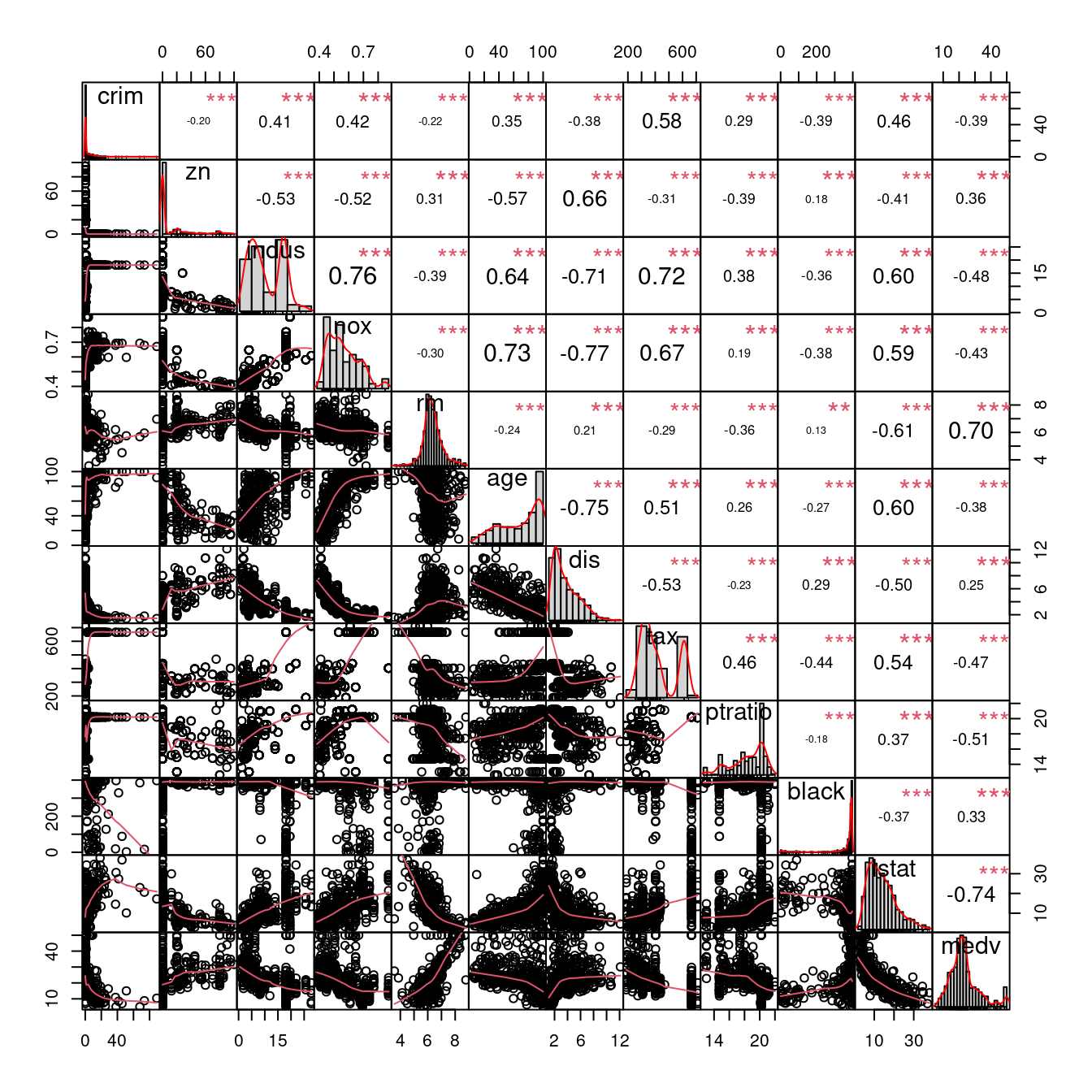

12.5.5 相關係數檢定

我們已經會算「一個兩兩連續型變數的相關係數」，也會算「全部連續型變數的相關係數矩陣」，算完之後，也會交給corrplot::corrplot跟PerformanceAnalytics::chart.Correlation取得相關係數矩陣的視覺化分析輔助圖。接下來，有人問了統計學家一個問題：

這一個相關係數真的不是0嗎？

於是乎，統計學家再度出發，建議了一種「假設檢定」的手法，協助驗證「這一個相關係數真的不是0嗎？」。以下是R提供的使用手冊。

knitr::include_url("https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/cor.test")

12.5.5.1 原始數據之相關係數檢定

我們已經看過，也知道怎麼透過R取得「兩兩連續型變數的相關係數」，或是「多個連續型變數的相關係數矩陣」，我們再一次回顧當時的作法、寫法：

as.data.frame.matrix(round(cor(boston[, CONvars]), 2))

##          crim    zn indus   nox    rm   age   dis   tax ptratio black lstat
## crim     1.00 -0.20  0.41  0.42 -0.22  0.35 -0.38  0.58    0.29 -0.39  0.46
## zn      -0.20  1.00 -0.53 -0.52  0.31 -0.57  0.66 -0.31   -0.39  0.18 -0.41
## indus    0.41 -0.53  1.00  0.76 -0.39  0.64 -0.71  0.72    0.38 -0.36  0.60
## nox      0.42 -0.52  0.76  1.00 -0.30  0.73 -0.77  0.67    0.19 -0.38  0.59
## rm      -0.22  0.31 -0.39 -0.30  1.00 -0.24  0.21 -0.29   -0.36  0.13 -0.61
## age      0.35 -0.57  0.64  0.73 -0.24  1.00 -0.75  0.51    0.26 -0.27  0.60
## dis     -0.38  0.66 -0.71 -0.77  0.21 -0.75  1.00 -0.53   -0.23  0.29 -0.50
## tax      0.58 -0.31  0.72  0.67 -0.29  0.51 -0.53  1.00    0.46 -0.44  0.54
## ptratio  0.29 -0.39  0.38  0.19 -0.36  0.26 -0.23  0.46    1.00 -0.18  0.37
## black   -0.39  0.18 -0.36 -0.38  0.13 -0.27  0.29 -0.44   -0.18  1.00 -0.37
## lstat    0.46 -0.41  0.60  0.59 -0.61  0.60 -0.50  0.54    0.37 -0.37  1.00
## medv    -0.39  0.36 -0.48 -0.43  0.70 -0.38  0.25 -0.47   -0.51  0.33 -0.74
##          medv
## crim    -0.39
## zn       0.36
## indus   -0.48
## nox     -0.43
## rm       0.70
## age     -0.38
## dis      0.25
## tax     -0.47
## ptratio -0.51
## black    0.33
## lstat   -0.74
## medv     1.00

12.5.5.1.1 兩兩連續型變數的相關係數檢定

先看lstat跟medv的相關係數檢定。我們會看到一張統計報表。找到「p-value < 2.2e-16」，這意思是說，「檢定的p值很小」，所以我們有信心「拒絕相關係數是0的虛無假設」。作者小編在這裡測試一下，cor.test的「能耐」，讓它幫我們檢定「自己跟自己的相關係數1是否等於0？」

cor.test(boston[, "lstat"], boston[, "medv"])

## 
##  Pearson's product-moment correlation
## 
## data:  boston[, "lstat"] and boston[, "medv"]
## t = -24.528, df = 504, p-value < 0.00000000000000022
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.7749982 -0.6951959
## sample estimates:
##        cor 
## -0.7376627

cor.test(boston[, "medv"], boston[, "medv"])

## 
##  Pearson's product-moment correlation
## 
## data:  boston[, "medv"] and boston[, "medv"]
## t = Inf, df = 504, p-value < 0.00000000000000022
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  1 1
## sample estimates:
## cor 
##   1

實驗結果告訴我們，「房價中位數自身的相關係數1等於0的檢定p值很小」，p-value < 2.2e-16，所以我們有信心認為「房價中位數自身的相關係數等於1」。

12.5.5.1.2 許多組兩兩連續型變數的相關係數檢定

接下來，我們要面對「11」個相關係數檢定，所以會有剛剛那種報表「11」張，也就是說我們需要「一支程式」整理這「11」張報表。以下這一段程式碼，是作者小編無意間發現一件事後寫出來的，因為意外發現了「相關係數檢定報表」背後的「資料結構」，也就是說，發現了「檢定的相關資料是怎麼擺的？」

1. 無意間的發現。當面對「一變多」的時候，作者小編習慣用「迴圈」重複「一組同樣的動作」，不是用「for」就是用「apply」家族。就像下面這一段，只是用「1:11」而不是用「1」。作者小編編寫這一段的時候，突然發現R的輸出跟前述的「檢定報表」完全不同。說實在的，如果沒有這個發現，各位只會在這裡看到「11」張跟上述報表一樣的報表，只有一個字「慘」！作者小編因為這個發現，燃起「一絲脫離這個『慘』字的希望」！請讀者諸君一定要欣賞這一段的「發展」！

x <- sapply(1, function(w){
  cor.test(boston[, "lstat"], boston[, "medv"])
})
x # 好像是一個「矩陣」？

##             [,1]                                                                                            
## statistic   -24.5279                                                                                        
## parameter   504                                                                                             
## p.value     0.0000000000000000000000000000000000000000000000000000000000000000000000000000000000000005081103
## estimate    -0.7376627                                                                                      
## null.value  0                                                                                               
## alternative "two.sided"                                                                                     
## method      "Pearson's product-moment correlation"                                                          
## data.name   "boston[, "lstat"] and boston[, "medv"]"                                                        
## conf.int    numeric,2

2. 深入檢查。曾經有一位同校的長官問過作者小編一個問題，這位長官問說：「你怎麼知道某一個R物件到底是什麼，R程式碼不像『Fortran』、『C』、『C++』、『JAVA』、『Python』，並沒有『宣告』的區段，不是嗎？」作者小編不假思索地回長官說，「檢查就知道了！」

class(x) # 檢查外觀。

## [1] "matrix" "array"

mode(x) # 檢查內在。

## [1] "list"

typeof(x) # 檢查內在。

## [1] "list"

dim(x) # 矩陣的維度，多少乘以多少？

## [1] 9 1

dimnames(x) # 矩陣的列名稱跟行名稱。

## [[1]]
## [1] "statistic"   "parameter"   "p.value"     "estimate"    "null.value" 
## [6] "alternative" "method"      "data.name"   "conf.int"   
## 
## [[2]]
## NULL

attributes(x) # 檢查「屬性」可以取得上述兩項資訊。

## $dim
## [1] 9 1
## 
## $dimnames
## $dimnames[[1]]
## [1] "statistic"   "parameter"   "p.value"     "estimate"    "null.value" 
## [6] "alternative" "method"      "data.name"   "conf.int"   
## 
## $dimnames[[2]]
## NULL

sapply(x, class) # 檢查內容物。

## [1] "numeric"   "integer"   "numeric"   "numeric"   "numeric"   "character"
## [7] "character" "character" "numeric"

### 因為「x的最後一列」出現作者小編第一次看到的「樣子」，「Numeric,2」。
sapply(x, is.vector) 

## [1]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE

# 是不是向量？請注意最後一列那個「怪怪的東西、物件」不是向量。
# 另外「矩陣(matrix)由向量(vector)構成」，這是「線性代數基本原則」，但是...
sapply(x, is.list) # 所以，作者小編進一步檢查是不是「譜(list)」？

## [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

### 因為統計學的「信賴區間」必須有三項資訊：下界、上界跟顯著水準。
### 於是乎，作者小編決定抓幾個「x矩陣的內容物」來瞧瞧！
x["statistic",1] # [1,1]。似乎有三層的名字！

## $statistic
##        t 
## -24.5279

x["conf.int",1] # [9,1]。兩個數字加一個「attr(,"conf.level")」。似乎有兩層的名字！

## $conf.int
## [1] -0.7749982 -0.6951959
## attr(,"conf.level")
## [1] 0.95

class(x["statistic",1]) # 為了釐清「怪怪的物件」，再一次檢查「class」。

## [1] "list"

class(x["conf.int",1]) # 竟然是「譜(list)」！！！

## [1] "list"

### 到這裡，作者小編就知道怎麼「抓」了！
x["statistic",1]$statistic["t"] # 根據猜測寫三層！

##        t 
## -24.5279

x["conf.int",1]$conf.int[1] # 根據猜測寫兩層加「前一」！

## [1] -0.7749982

x["conf.int",1]$conf.int[2] # 根據猜測寫兩層加「後二」！

## [1] -0.6951959

attr(x["conf.int",1]$conf.int, which = "conf.level") # 抓信賴區間的顯著水準！

## [1] 0.95

3. 既然會抓了，接下來，作者小編開始「創作」自己的報表。根據在前述「相關係數圖」的經驗，也堅持作者小編的「連戲學習法」，我們先依據「相關係數的數值大小」「重排那11個連續型變數的名字」。

CONvars # 先檢視那些名字。

##  [1] "crim"    "zn"      "indus"   "nox"     "rm"      "age"     "dis"    
##  [8] "tax"     "ptratio" "black"   "lstat"   "medv"

corr <- round(cor(boston[, CONvars]), 2) # 取得相關係數矩陣。
CONvars <- CONvars[order(abs(corr[12,]))] # 排序。
CONvars # 呼叫出來再檢視一次。

##  [1] "dis"     "black"   "zn"      "age"     "crim"    "nox"     "tax"    
##  [8] "indus"   "ptratio" "rm"      "lstat"   "medv"

bostonCORtest <- data.frame(statistic = numeric(0),
                            p.value = numeric(0),
                            estimate = numeric(0),
                            L.conf.int = numeric(0),
                            R.conf.int = numeric(0),
                            level = numeric(0),
                            testing = character(0),
                            stringsAsFactors = FALSE) # 準備空表。
for (i in 1:11) {
  x <- sapply(i, function(w){
    cor.test(boston[, CONvars[w]], boston[, "medv"])
    }) # 迴圈「for」內的迴圈「sapply」。
  
  ### 抓各種統計量，並且四捨五入到三位小數。
  statistic <- round(x["statistic",1]$statistic["t"],3)
  p.value <- round(x["p.value",1]$p.value,3)
  estimate <- round(x["estimate",1]$estimate,3)
  L.conf.int <- round(x["conf.int",1]$conf.int,3)[1]
  R.conf.int <- round(x["conf.int",1]$conf.int,3)[2]
  level <- attr(x["conf.int",1]$conf.int, which = "conf.level")
  
  ### 判斷是否拒絕虛無假設 = 相關係數等於0。
  testing <- ifelse(p.value < 1 - level, "Reject", "Not Reject")
  
  ### 裝起來這一次檢定的表。
  bostonCORtest0 <- data.frame(statistic = statistic,
                               p.value = p.value,
                               estimate = estimate,
                               L.conf.int = L.conf.int,
                               R.conf.int = R.conf.int,
                               level = level,
                               testing = testing,
                               stringsAsFactors = FALSE)
  rownames(bostonCORtest0) <- CONvars[i] # 給名字。
  bostonCORtest <- rbind(bostonCORtest, bostonCORtest0) # 疊起來。
}
bostonCORtest # 呼叫檢查結果。

##         statistic p.value estimate L.conf.int R.conf.int level testing
## dis         5.795       0    0.250      0.166      0.330  0.95  Reject
## black       7.941       0    0.333      0.254      0.409  0.95  Reject
## zn          8.675       0    0.360      0.282      0.434  0.95  Reject
## age        -9.137       0   -0.377     -0.449     -0.300  0.95  Reject
## crim       -9.460       0   -0.388     -0.460     -0.312  0.95  Reject
## nox       -10.611       0   -0.427     -0.496     -0.353  0.95  Reject
## tax       -11.906       0   -0.469     -0.534     -0.398  0.95  Reject
## indus     -12.408       0   -0.484     -0.548     -0.414  0.95  Reject
## ptratio   -13.233       0   -0.508     -0.570     -0.440  0.95  Reject
## rm         21.722       0    0.695      0.647      0.738  0.95  Reject
## lstat     -24.528       0   -0.738     -0.775     -0.695  0.95  Reject

• (插曲)作者小編一開始發現「x」之後，以為只要把「1」改成「1:11」，加上把「cor.test」的輸出給「x」，然後按照「步驟二」的抓取動作就能輕鬆造表，但卻一直「鬼打牆」，還花了一個早上四處搜尋幫手跟實驗，雖然最後成功造出美美的表，但是「無法連戲」，「無法用步驟二的抓法抓資訊」！！！作者小編再一次回頭檢視程式碼，才驚覺步驟二的「x」是「sapply」的輸出，並不是「cor.test」的輸出，這才完成「步驟三」的程式碼，並且得到美美的自創表(data.frame)。因為作者小編認為早上的冤枉路，有著不錯的幫手，特別另闢「插曲」，為各位示範一下這幾個有用的套件(package)跟函式(function)。

x <- cor(boston[, c("rm", "lstat", "medv")]) # 取得波士頓數據集的部分相關係數矩陣。
x

##               rm      lstat       medv
## rm     1.0000000 -0.6138083  0.6953599
## lstat -0.6138083  1.0000000 -0.7376627
## medv   0.6953599 -0.7376627  1.0000000

round(x, 2) # 四捨五入到兩位小數。

##          rm lstat  medv
## rm     1.00 -0.61  0.70
## lstat -0.61  1.00 -0.74
## medv   0.70 -0.74  1.00

x <- formatC(x, digits = 2, width = 5, format = "f") 
# 把相關係數用「五個符號，含兩位小數」的文字表示之。
x

##       rm      lstat   medv   
## rm    " 1.00" "-0.61" " 0.70"
## lstat "-0.61" " 1.00" "-0.74"
## medv  " 0.70" "-0.74" " 1.00"

x[lower.tri(x, diag = FALSE)] <- "     " # 換成空白文字讓資訊減半！注意，空白絕不會是數字！
x

##       rm      lstat   medv   
## rm    " 1.00" "-0.61" " 0.70"
## lstat "     " " 1.00" "-0.74"
## medv  "     " "     " " 1.00"

require(gt)
x <- as.data.frame.matrix(x) # 把矩陣變成表。請注意印出來時小數點沒對齊。
x

##          rm lstat  medv
## rm     1.00 -0.61  0.70
## lstat        1.00 -0.74
## medv               1.00

x <- gt(x) # 變出「gt」物件。請注意印出來時小數點沒對齊。
x

rm	lstat	medv
1.00	-0.61	0.70
	1.00	-0.74
		1.00

cols_align(x, align = "right", columns = TRUE) # 右邊靠齊。

rm	lstat	medv
1.00	-0.61	0.70
	1.00	-0.74
		1.00

12.5.5.2 常態轉換數據之相關係數檢定

相關係數檢定的檢定統計量，被R冠上「t」這個名字，根據統計學的習慣，

一定要檢定統計量的抽樣分配服從「t分配」，統計量的名字才會冠上「t」。

作者小編查了一下Wikipedia，找到

knitr::include_url("https://zh.wikipedia.org/wiki/斯皮爾曼等級相關係數")

…

找到了「t」：

\[t = r \times \sqrt{\frac{n - 2}{1 - r^2}}\]

作者小編在這一小節，想要測試「兩兩連續型變數」與「兩兩連續型常態變數」的「可能的差異」，同時介紹一個在「2020-06-08」出版的套件bestNormalize，一個可以讓我們把「非常態分配變數的數據」轉換為「接近常態分配變數的數據」。請讀者諸君繼續看下去，…

1. 載入套件bestNormalize。

require(bestNormalize)

2. 從波士頓數據集取出兩個欄位，medv跟lstat。

medv <- boston[, "medv"]
lstat <- boston[, "lstat"]

3. 檢查medv跟lstat是不是常態變數？

par(mfrow = c(1,2))
qqnorm(medv)
qqline(medv, col = 2)
qqnorm(lstat)
qqline(lstat, col = 2)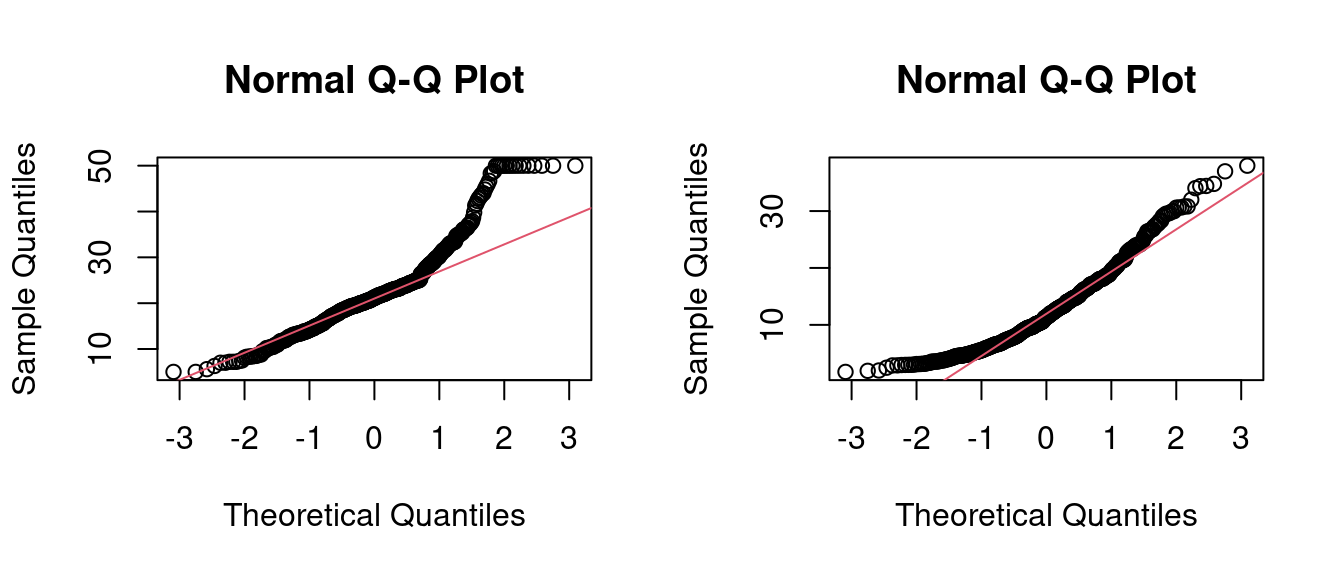

4. 常態變數變換。

medv2 <- bestNormalize(medv)
lstat2 <- bestNormalize(lstat)

5. 檢查常態變數變換後medv跟lstat是不是比較接近常態變數？

par(mfrow = c(1,2))
qqnorm(medv2[["x.t"]])
qqline(medv2[["x.t"]], col = 2)
qqnorm(lstat2[["x.t"]])
qqline(lstat2[["x.t"]], col = 2)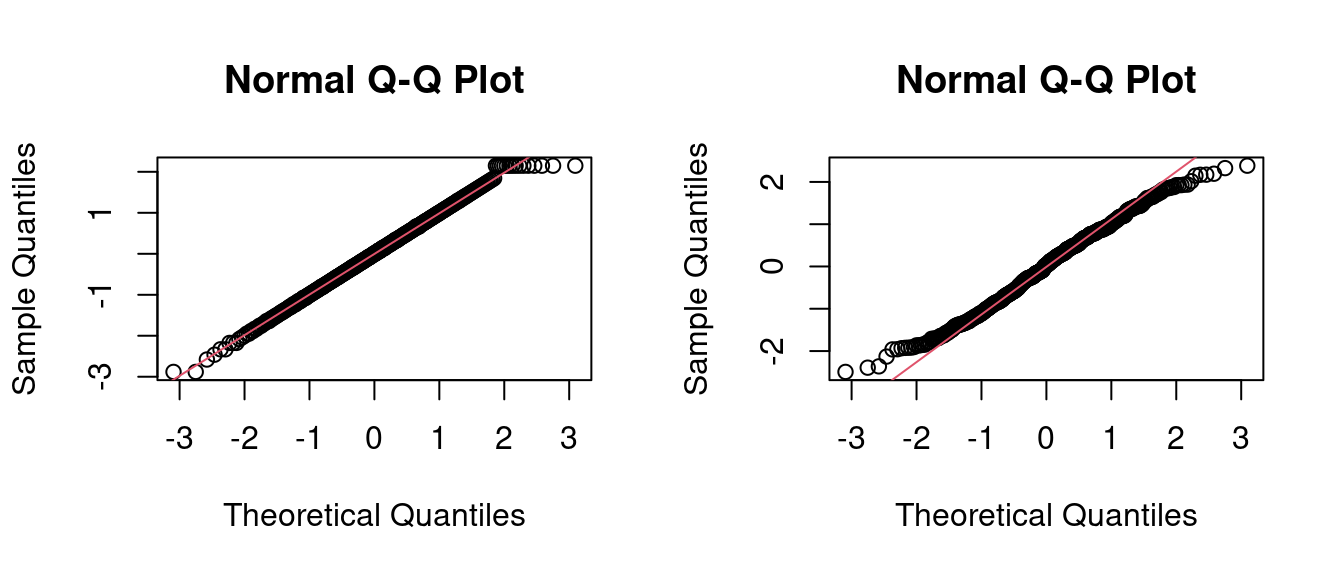

6. 計算四組相關係數。竟然變大了！

cor(lstat, medv)

## [1] -0.7376627

cor(lstat, medv2[["x.t"]])

## [1] -0.81234

cor(lstat2[["x.t"]], medv)

## [1] -0.803444

cor(lstat2[["x.t"]], medv2[["x.t"]])

## [1] -0.8439964

12.6 列聯表

12.6.1 獨立性檢定

12.6.2 2x2列聯表

12.7 雙母體t檢定

12.8 單向變異數分析F檢定

12.9 雙向變異數分析F檢定

12.10 補充資料

為了讓讀者諸君先初步認識什麼是「相關係數(Pearson correlation coefficient)」，作者小編先請Wikipedia幫忙：

knitr::include_url("https://en.wikipedia.org/wiki/Pearson_correlation_coefficient")

…

knitr::include_graphics("www/800px-Correlation_coefficient.png")

## Error in knitr::include_graphics("www/800px-Correlation_coefficient.png"): Cannot find the file(s): "www/800px-Correlation_coefficient.png"

…

12.11 學期小專題

12.12 課後練習題