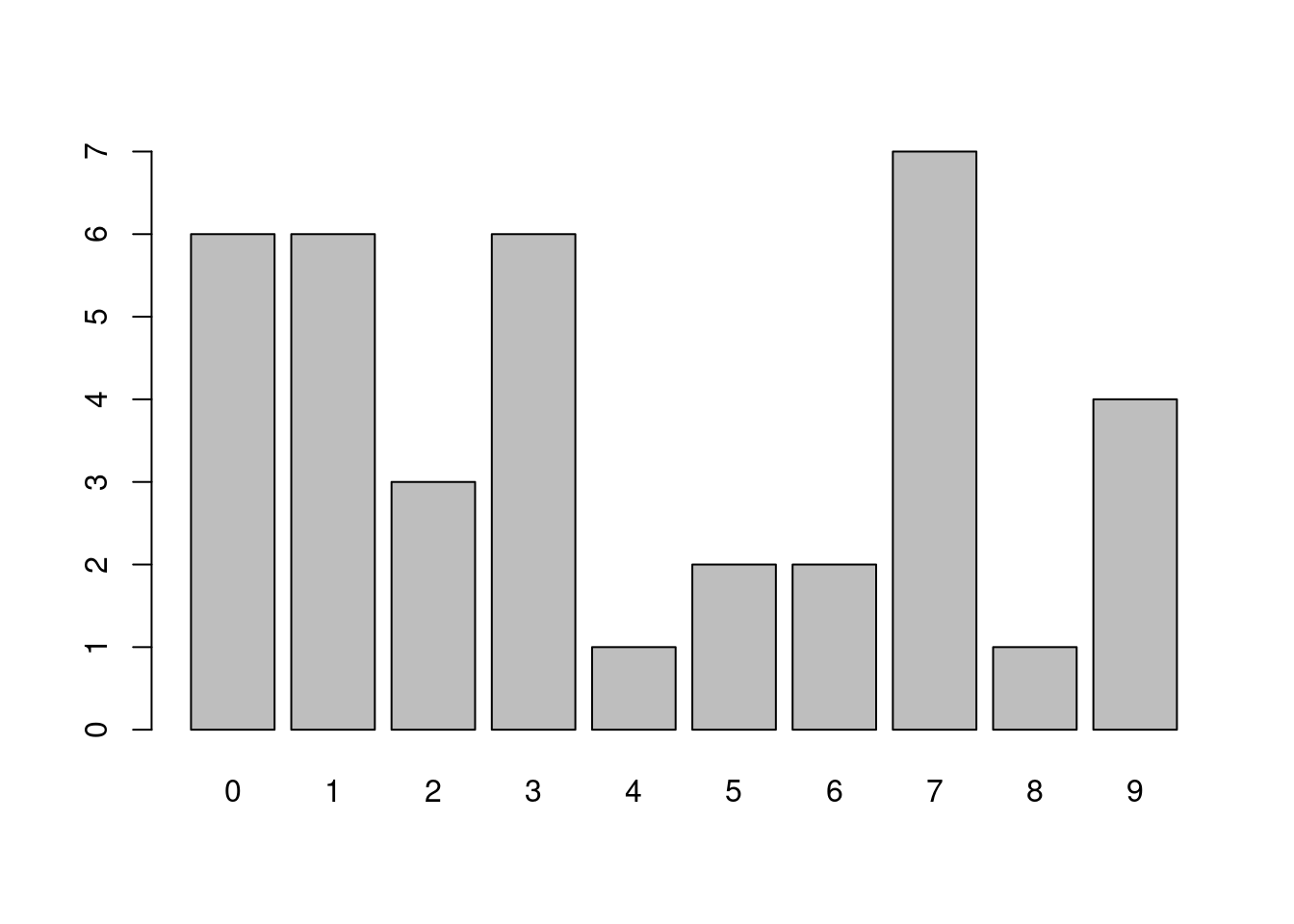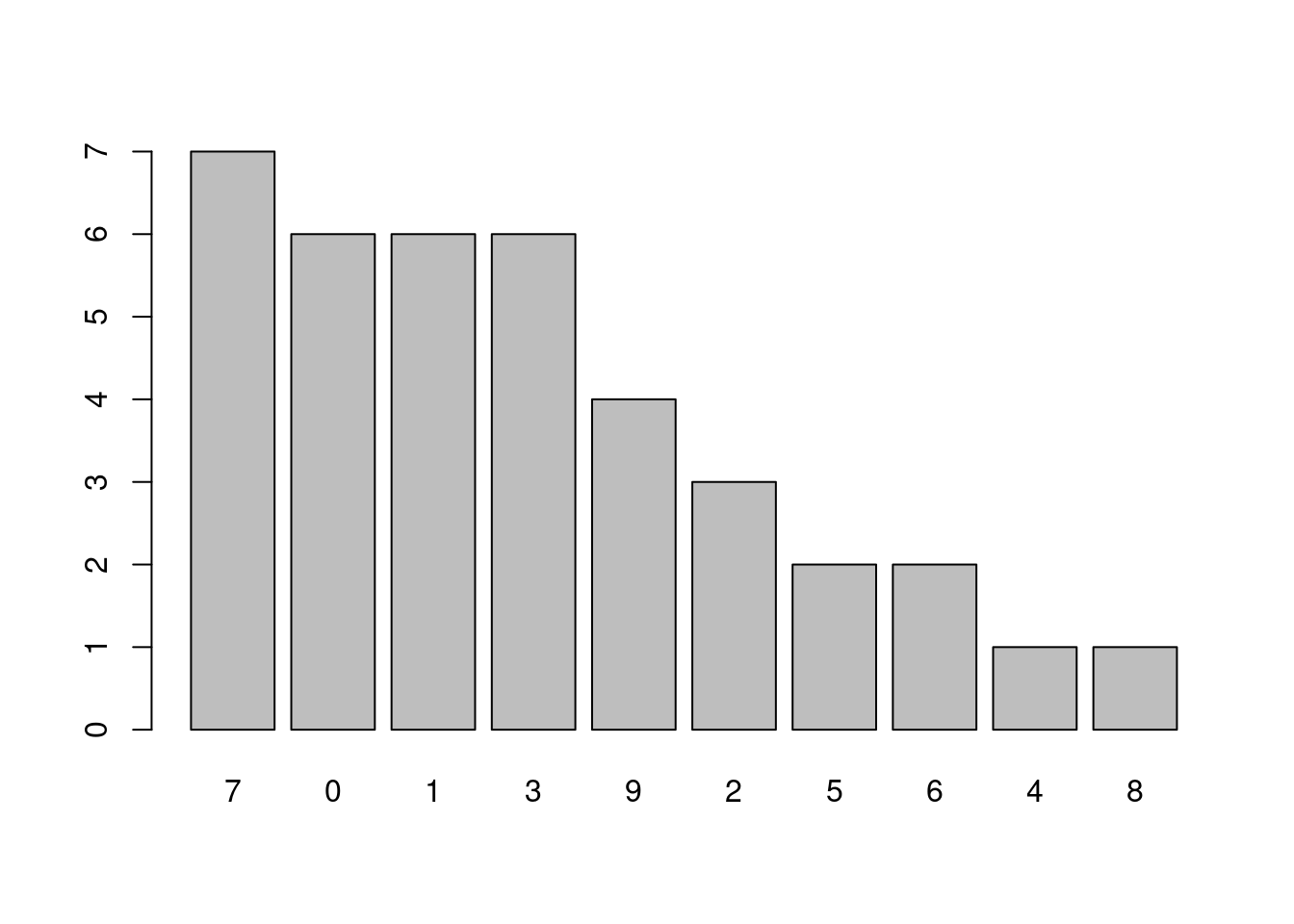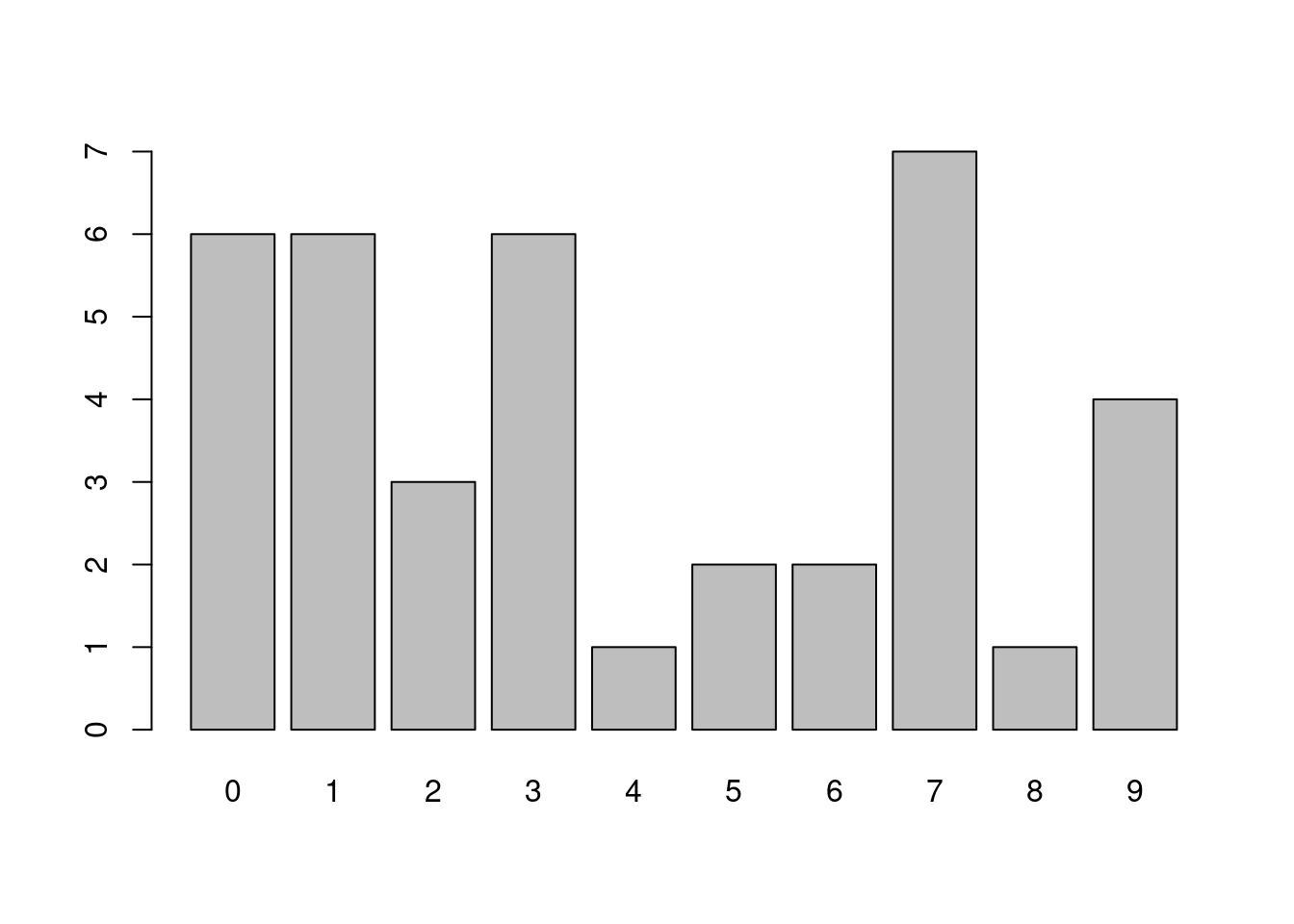Chapter 3 練就基礎統計圖感談分配
一開始,作者「話說統計學從莖葉圖」。當時,作者假設讀者諸君認識印度人發明的「阿拉伯數字」,企圖讓看倌們重新認識「阿拉伯數字」,同時也認識統計學存活超過一百年的「莖葉圖」,『一個「擺放數據」的「圖架」』。作者還企圖透過「莖葉圖」引入統計學的基礎觀念「分配」。接下來,作者安排透過「統計圖」繼續、深入了解、認識「分配」。
3.2 莖葉圖
接續「話說統計學從莖葉圖」的最後一段:
我們如果認真去Wikipedia搜尋,應該很有機會得知以下這幾項技術的時間軸:
- 莖葉圖
- 次數分配表、累加次數分配表
- 排序
- 中位數
- 離群值
- 直方圖
- 長條圖
它們在時間軸上的先後關係,並不是作者在這裡想要回答的問題。作者堅持從「莖葉圖」出發,指導學生經歷一段不一樣的統計學學習之旅,是因為套件「
aplpack」產出的「莖葉圖」可以順勢變出上述六項統計成果,而且顯而易見、直接了當,雖然不是輕而易舉!但,深入了解「莖葉圖」的來龍去脈,就等於一次學到七項技術,至少!
接著,
- 如果「推想、推廣」中位數,可以掌握「平均數」;
- 如果「推想、推廣」中位數,可以創新「四分位數」;
- 如果掌握平均數的理論源頭,可以得知「變異數」與「標準差」;
- 有了標準差,可以推想出「間距」、「四分位數間距」、「十分位數間距」、「百分位數間距」;
- 再加上原始數據,可以掌握「盒型圖」。
- 也可以從「長條圖」變出「圓餅圖」。
- 最後,把時間認為是一種順序很重要的標籤,「長條圖」就會變身為「時間序列圖」。
假如您願意走過一遍又一遍,掌握箇中變化的道理,初等統計學的首篇,「敘述統計學」,也就是「小數據」就被您握在手心了!
我們繼續深入探究「莖葉圖」這一項技術的其他可能性!
…
3.2.1 什麼是莖葉圖?
為了繼續示範1900年代初期,Arthur Bowley提倡的「莖葉圖」,我們依舊需要借用R的套件「aplpack」。
library(aplpack)在大量示範之前,我們先回顧什麼是莖葉圖?請看「38」這一個數字的莖葉圖,
stem.leaf(38, m = 1, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 1
## (1) 3 | 8再看「338」這一個數字的莖葉圖,
stem.leaf(338, m = 1, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 1
## (1) 33 | 8接下來看「3388」這一個數字的莖葉圖,
stem.leaf(3388, m = 1, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 1
## (1) 338 | 8經過、做過「觀察」上述三張圖之後,我們注意到「個位數的『8』」一直留在「|」這一個「半邊絕對值符號」的右邊,而剩下來的「十位數、百位數、千位數」按順序都留在「半邊絕對值符號」的左邊。為了驗證這一項觀察的可靠度,我們搜尋網際網路,找找「什麼是莖葉圖」,也就是找找「莖葉圖的定義」。運氣不錯,找到了Definition of
Stem-and-Leaf Plot。數學定義就怕「失真」,所以我們直接引用,不翻譯。請看
3.2.1.1 莖葉圖的定義
A plot where each data value is split into a “leaf” (usually the last digit) and a “stem” (the other digits). For example “32” is split into “3” (stem) and “2” (leaf). The “stem” values are listed down, and the “leaf” values are listed next to them. This way the “stem” groups the scores and each “leaf” indicates a score within that group.
如果看不懂「英文」,我們請「Google」來幫忙。以下是翻譯上述莖葉圖定義的結果,請參考。
3.2.1.2 莖葉圖定義的Google翻譯
將每個數據值分為“葉子”(通常是最後一位)和“莖”(其他位)的圖。例如,“32”分為“3”(莖)和“2”(葉子)。“stem”值在下方列出,“leaf”值在其旁邊列出。這樣,“stem”將得分分組,每個“leaf”表示該組中的得分。
雖不中亦不遠!
3.2.1.3 莖葉圖的中文定義
請讓作者斗膽嘗試用中文字定義Arthur Bowley提倡的「莖葉圖」:
假設全部數字都是整數,先把第一個數字的個位數切出來形成該數字的葉子,剩下來的位數就是該數字的樹莖。比如說,38這一個數字的葉子是8,而3是樹莖;338的葉子也是8,但是樹莖是33;至於3388的葉子還是8,而樹莖則是338。接下來,根據「數字個數的多跟寡」或是「最大值減去最小值的結果」決定「莖數」,到底用「一株莖」、「兩株莖」、「五株莖」還是「十株莖」?基本原則是「數字多挑莖數少」或是「最大值減去最小值跨越兩位數就選一株莖」。決定後,依序一個數字接著一個數字,先擺「樹莖的數字」,再擺「|」,再擺上「葉子的數字」。如果遇到「空莖」,還是要先擺「樹莖的數字」,再擺「|」,但是不擺「葉子的數字」,因為沒有葉子啊!重複上述動作直到最後一個數字。過程中,往上加「樹莖」,如果看到比圖上最小數字還小的數字;往下加「樹莖」,如果看到比圖上最大數字還大的數字。記得,加之前,該有的「空莖」要先擺上。最後,請按阿拉伯數字,0,1,2,3,4,5,6,7,8,9的順序排序每一株莖的葉子。理論上,我們可以停在這裡,也可以模仿套件「
aplpack」的作法在樹莖的左邊加上「葉數」、「往下累加葉數」、「往上累加葉數」跟「(對半莖的葉數)」。記得加括號。
3.2.1.4 根據定義,如果我們想畫「38,338,3388」等三個數字的莖葉圖,該怎麼畫呢?
請看「aplpack::stem.leaf()」的結果:
stem.leaf(c(38,338,3388))## 1 | 2: represents 1200
## leaf unit: 100
## n: 3
## (2) 0 | 03
## 1 |
## 2 |
## 1 3 | 3這是一張失真的莖葉圖,因為不見任何葉子的數字「8」。所以,我們建議以下這一張莖葉圖:
stem.leaf(c(38,338,3388), m = 1, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 3
## 1 3 | 8
## 4 |
## 5 |
## 6 |
## 7 |
## 8 |
## 9 |
## 10 |
## 11 |
## 12 |
## 13 |
## 14 |
## 15 |
## 16 |
## 17 |
## 18 |
## 19 |
## 20 |
## 21 |
## 22 |
## 23 |
## 24 |
## 25 |
## 26 |
## 27 |
## 28 |
## 29 |
## 30 |
## 31 |
## 32 |
## (1) 33 | 8
## 34 |
## 35 |
## 36 |
## 37 |
## 38 |
## 39 |
## 40 |
## 41 |
## 42 |
## 43 |
## 44 |
## 45 |
## 46 |
## 47 |
## 48 |
## 49 |
## 50 |
## 51 |
## 52 |
## 53 |
## 54 |
## 55 |
## 56 |
## 57 |
## 58 |
## 59 |
## 60 |
## 61 |
## 62 |
## 63 |
## 64 |
## 65 |
## 66 |
## 67 |
## 68 |
## 69 |
## 70 |
## 71 |
## 72 |
## 73 |
## 74 |
## 75 |
## 76 |
## 77 |
## 78 |
## 79 |
## 80 |
## 81 |
## 82 |
## 83 |
## 84 |
## 85 |
## 86 |
## 87 |
## 88 |
## 89 |
## 90 |
## 91 |
## 92 |
## 93 |
## 94 |
## 95 |
## 96 |
## 97 |
## 98 |
## 99 |
## 100 |
## 101 |
## 102 |
## 103 |
## 104 |
## 105 |
## 106 |
## 107 |
## 108 |
## 109 |
## 110 |
## 111 |
## 112 |
## 113 |
## 114 |
## 115 |
## 116 |
## 117 |
## 118 |
## 119 |
## 120 |
## 121 |
## 122 |
## 123 |
## 124 |
## 125 |
## 126 |
## 127 |
## 128 |
## 129 |
## 130 |
## 131 |
## 132 |
## 133 |
## 134 |
## 135 |
## 136 |
## 137 |
## 138 |
## 139 |
## 140 |
## 141 |
## 142 |
## 143 |
## 144 |
## 145 |
## 146 |
## 147 |
## 148 |
## 149 |
## 150 |
## 151 |
## 152 |
## 153 |
## 154 |
## 155 |
## 156 |
## 157 |
## 158 |
## 159 |
## 160 |
## 161 |
## 162 |
## 163 |
## 164 |
## 165 |
## 166 |
## 167 |
## 168 |
## 169 |
## 170 |
## 171 |
## 172 |
## 173 |
## 174 |
## 175 |
## 176 |
## 177 |
## 178 |
## 179 |
## 180 |
## 181 |
## 182 |
## 183 |
## 184 |
## 185 |
## 186 |
## 187 |
## 188 |
## 189 |
## 190 |
## 191 |
## 192 |
## 193 |
## 194 |
## 195 |
## 196 |
## 197 |
## 198 |
## 199 |
## 200 |
## 201 |
## 202 |
## 203 |
## 204 |
## 205 |
## 206 |
## 207 |
## 208 |
## 209 |
## 210 |
## 211 |
## 212 |
## 213 |
## 214 |
## 215 |
## 216 |
## 217 |
## 218 |
## 219 |
## 220 |
## 221 |
## 222 |
## 223 |
## 224 |
## 225 |
## 226 |
## 227 |
## 228 |
## 229 |
## 230 |
## 231 |
## 232 |
## 233 |
## 234 |
## 235 |
## 236 |
## 237 |
## 238 |
## 239 |
## 240 |
## 241 |
## 242 |
## 243 |
## 244 |
## 245 |
## 246 |
## 247 |
## 248 |
## 249 |
## 250 |
## 251 |
## 252 |
## 253 |
## 254 |
## 255 |
## 256 |
## 257 |
## 258 |
## 259 |
## 260 |
## 261 |
## 262 |
## 263 |
## 264 |
## 265 |
## 266 |
## 267 |
## 268 |
## 269 |
## 270 |
## 271 |
## 272 |
## 273 |
## 274 |
## 275 |
## 276 |
## 277 |
## 278 |
## 279 |
## 280 |
## 281 |
## 282 |
## 283 |
## 284 |
## 285 |
## 286 |
## 287 |
## 288 |
## 289 |
## 290 |
## 291 |
## 292 |
## 293 |
## 294 |
## 295 |
## 296 |
## 297 |
## 298 |
## 299 |
## 300 |
## 301 |
## 302 |
## 303 |
## 304 |
## 305 |
## 306 |
## 307 |
## 308 |
## 309 |
## 310 |
## 311 |
## 312 |
## 313 |
## 314 |
## 315 |
## 316 |
## 317 |
## 318 |
## 319 |
## 320 |
## 321 |
## 322 |
## 323 |
## 324 |
## 325 |
## 326 |
## 327 |
## 328 |
## 329 |
## 330 |
## 331 |
## 332 |
## 333 |
## 334 |
## 335 |
## 336 |
## 337 |
## 1 338 | 8大哉問:剛剛往下一路滑過一輪之後,讀者諸君腦門閃過什麼樣的印象呢?
還好,加在,我們活在「開放原始碼」的時代,可以無償地讓「aplpack::stem.leaf()」幫我們,要是活在「只有紙筆」的時代(比如說,作者的孩提時代),就只能「無限想像了」!話,雖然可以這麼說,但是前一張莖葉圖,其實已經顯示了莖葉圖的一項缺失,太大棵了!接著,為了進一步了解莖葉圖的優缺點,讓我們玩玩「阿拉伯數字的莖葉圖」!
3.2.2 阿拉伯數字的莖葉圖
有了「aplpack」相助,我們再一次回顧阿拉伯數字,0, 1, 2, 3, 4, 5, 6, 7, 8, 9的莖葉圖長什麼樣子?
3.2.2.1 如果我們決定把全部阿拉伯數字放在「一株莖(m = 1)」,結果是
stem.leaf(0:9, m = 1, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## (10) 0 | 01234567893.2.2.2 如果我們決定把全部阿拉伯數字放在「兩株莖(m = 2)」,結果是
stem.leaf(0:9, m = 2, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## (5) 0* | 01234
## (5) 0. | 567893.2.2.3 如果我們決定把全部阿拉伯數字放在「五株莖(m = 5)」,結果是
stem.leaf(0:9, m = 5, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## 2 0* | 01
## 4 t | 23
## (2) f | 45
## 4 s | 67
## 2 0. | 893.2.2.4 如果我們決定把全部阿拉伯數字放在「十株莖(m = 10)」,結果是
stem.leaf(0:9, m = 10, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## 1 0 | 0
## 2 0 | 1
## 3 0 | 2
## 4 0 | 3
## (1) 0 | 4
## (1) 0 | 5
## 4 0 | 6
## 3 0 | 7
## 2 0 | 8
## 1 0 | 93.2.2.4.2 計算思維練習題:如果把「unit = 1」從「stem.leaf」拿掉,會看到甚麼樣的莖葉圖呢?
參考答案
stem.leaf(0:9, m = 1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 10
## 1 0 | 0
## 2 1 | 0
## 3 2 | 0
## 4 3 | 0
## (1) 4 | 0
## (1) 5 | 0
## 4 6 | 0
## 3 7 | 0
## 2 8 | 0
## 1 9 | 0stem.leaf(0:9, m = 2)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 10
## 1 0* | 0
## 0. |
## 2 1* | 0
## 1. |
## 3 2* | 0
## 2. |
## 4 3* | 0
## 3. |
## (1) 4* | 0
## 4. |
## (1) 5* | 0
## 5. |
## 4 6* | 0
## 6. |
## 3 7* | 0
## 7. |
## 2 8* | 0
## 8. |
## 1 9* | 0stem.leaf(0:9, m = 5)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 10
## 1 0* | 0
## t |
## f |
## s |
## 0. |
## 2 1* | 0
## t |
## f |
## s |
## 1. |
## 3 2* | 0
## t |
## f |
## s |
## 2. |
## 4 3* | 0
## t |
## f |
## s |
## 3. |
## (1) 4* | 0
## t |
## f |
## s |
## 4. |
## (1) 5* | 0
## t |
## f |
## s |
## 5. |
## 4 6* | 0
## t |
## f |
## s |
## 6. |
## 3 7* | 0
## t |
## f |
## s |
## 7. |
## 2 8* | 0
## t |
## f |
## s |
## 8. |
## 1 9* | 0stem.leaf(0:9, m = 10)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 10
## 1 0 | 0
## 0 |
## 0 |
## 0 |
## 0 |
## 0 |
## 0 |
## 0 |
## 0 |
## 0 |
## 2 1 | 0
## 1 |
## 1 |
## 1 |
## 1 |
## 1 |
## 1 |
## 1 |
## 1 |
## 1 |
## 3 2 | 0
## 2 |
## 2 |
## 2 |
## 2 |
## 2 |
## 2 |
## 2 |
## 2 |
## 2 |
## 4 3 | 0
## 3 |
## 3 |
## 3 |
## 3 |
## 3 |
## 3 |
## 3 |
## 3 |
## 3 |
## (1) 4 | 0
## 4 |
## 4 |
## 4 |
## 4 |
## 4 |
## 4 |
## 4 |
## 4 |
## 4 |
## (1) 5 | 0
## 5 |
## 5 |
## 5 |
## 5 |
## 5 |
## 5 |
## 5 |
## 5 |
## 5 |
## 4 6 | 0
## 6 |
## 6 |
## 6 |
## 6 |
## 6 |
## 6 |
## 6 |
## 6 |
## 6 |
## 3 7 | 0
## 7 |
## 7 |
## 7 |
## 7 |
## 7 |
## 7 |
## 7 |
## 7 |
## 7 |
## 2 8 | 0
## 8 |
## 8 |
## 8 |
## 8 |
## 8 |
## 8 |
## 8 |
## 8 |
## 8 |
## 1 9 | 0請讀者自行解讀。
3.2.2.5 為什麼「m」只能是「1,2,5,10」,這些「均分10個數字的莖數」,難道不能「3」嗎?
stem.leaf(0:9, m = 3, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## 4 0 | 0123
## (3) 0 | 456
## 3 0 | 789「stem.leaf()」絕對可以幫忙,但是…
stem.leaf(rep(0:9, 10), m = 3, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 100
## 40 0 | 0000000000111111111122222222223333333333
## (30) 0 | 444444444455555555556666666666
## 30 0 | 777777777788888888889999999999stem.leaf(rep(0:9, 20), m = 3, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 200
## 80 0 | 00000000000000000000111111111111111111112222222222222222222233333333333333333333
## (60) 0 | 444444444444444444445555555555555555555566666666666666666666
## 60 0 | 777777777777777777778888888888888888888899999999999999999999持續下去,會出現「失衡現象」。這時候,我們需要放手給「stem.leaf()」自己決定「莖數」!
stem.leaf(rep(0:9, 10), unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 100
## 20 0* | 00000000001111111111
## 40 t | 22222222223333333333
## (20) f | 44444444445555555555
## 40 s | 66666666667777777777
## 20 0. | 88888888889999999999結果還不賴!如果把「unit = 1」從「stem.leaf」拿掉,會怎樣?
stem.leaf(rep(0:9, 10))## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 100
## 10 0* | 0000000000
## 0. |
## 20 1* | 0000000000
## 1. |
## 30 2* | 0000000000
## 2. |
## 40 3* | 0000000000
## 3. |
## (10) 4* | 0000000000
## 4. |
## (10) 5* | 0000000000
## 5. |
## 40 6* | 0000000000
## 6. |
## 30 7* | 0000000000
## 7. |
## 20 8* | 0000000000
## 8. |
## 10 9* | 0000000000結果不怎麼樣!所以,「stem.leaf」並非絕對!
3.2.2.5.1 計算思維練習題:繪製並觀察「0:9」跟「19」莖葉圖的各種形狀。
參考答案
stem.leaf(c(0:9,19), unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 11
## 2 0* | 01
## 4 t | 23
## (2) f | 45
## 5 s | 67
## 3 0. | 89
## HI: 19stem.leaf(c(0:9,19), unit = 1, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 11
## 2 0* | 01
## 4 t | 23
## (2) f | 45
## 5 s | 67
## 3 0. | 89
## 1* |
## t |
## f |
## s |
## 1 1. | 9stem.leaf(c(0:9,19), m = 2, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 11
## 5 0* | 01234
## (5) 0. | 56789
## HI: 19stem.leaf(c(0:9,19), m = 2, unit = 1, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 11
## 5 0* | 01234
## (5) 0. | 56789
## 1* |
## 1 1. | 93.2.3 假設阿拉伯數字隨機依序出現體驗莖葉圖的定義
這時候,我們需要借用R官方程式「sample」,中文翻譯為「抽樣」。如果只是把數字丟給她,沒有任何限制、要求,「sample」會回應這些數字的某一種「permutation」。
#set.seed(1233)
# 我們在這裡蓋台set.seed(1233),讓讀者諸君每一次都是新的體驗。
Data <- sample(0:9)
Data## [1] 3 1 7 2 8 6 0 4 5 9再來一個一個看,看阿拉伯數字的莖葉圖如何長大成人?
for (i in 1:length(Data)) {
print(paste0("###", " 第", i, "次 ", "###"))
print(paste0("現在出現數字", Data[i]))
print("莖葉圖到此長這個樣子:")
stem.leaf(Data[1:i], m = 10, unit = 1)
print(paste0(rep("#", 38), collapse = ""))
}## [1] "### 第1次 ###"
## [1] "現在出現數字3"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 1
## (1) 0 | 3
## [1] "######################################"
## [1] "### 第2次 ###"
## [1] "現在出現數字1"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 2
## (1) 0 | 1
## 0 |
## (1) 0 | 3
## [1] "######################################"
## [1] "### 第3次 ###"
## [1] "現在出現數字7"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 3
## 1 0 | 1
## 0 |
## (1) 0 | 3
## 0 |
## 0 |
## 0 |
## 1 0 | 7
## [1] "######################################"
## [1] "### 第4次 ###"
## [1] "現在出現數字2"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 4
## 1 0 | 1
## (1) 0 | 2
## (1) 0 | 3
## 0 |
## 0 |
## 0 |
## 1 0 | 7
## [1] "######################################"
## [1] "### 第5次 ###"
## [1] "現在出現數字8"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 5
## 1 0 | 1
## 2 0 | 2
## (1) 0 | 3
## 0 |
## 0 |
## 0 |
## 2 0 | 7
## 1 0 | 8
## [1] "######################################"
## [1] "### 第6次 ###"
## [1] "現在出現數字6"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 6
## 1 0 | 1
## 2 0 | 2
## (1) 0 | 3
## 0 |
## 0 |
## (1) 0 | 6
## 2 0 | 7
## 1 0 | 8
## [1] "######################################"
## [1] "### 第7次 ###"
## [1] "現在出現數字0"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 7
## 1 0 | 0
## 2 0 | 1
## 3 0 | 2
## (1) 0 | 3
## 0 |
## 0 |
## 3 0 | 6
## 2 0 | 7
## 1 0 | 8
## [1] "######################################"
## [1] "### 第8次 ###"
## [1] "現在出現數字4"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 8
## 1 0 | 0
## 2 0 | 1
## 3 0 | 2
## (1) 0 | 3
## (1) 0 | 4
## 0 |
## 3 0 | 6
## 2 0 | 7
## 1 0 | 8
## [1] "######################################"
## [1] "### 第9次 ###"
## [1] "現在出現數字5"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 9
## 1 0 | 0
## 2 0 | 1
## 3 0 | 2
## 4 0 | 3
## (1) 0 | 4
## 4 0 | 5
## 3 0 | 6
## 2 0 | 7
## 1 0 | 8
## [1] "######################################"
## [1] "### 第10次 ###"
## [1] "現在出現數字9"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## 1 0 | 0
## 2 0 | 1
## 3 0 | 2
## 4 0 | 3
## (1) 0 | 4
## (1) 0 | 5
## 4 0 | 6
## 3 0 | 7
## 2 0 | 8
## 1 0 | 9
## [1] "######################################"3.2.4 手繪莖葉圖為什麼需要先排序呢?
讓我們再一次回顧Wikipedia示範數字的莖葉圖。這一回,我們讓套件「aplpack」的「stem.leaf()」自己決定怎麼畫?
- Wikipedia先把數字按照大小從小往右排到大,會這麼做主要是因為大半的文獻、教科書都說製作莖葉圖的第一個動作,就是「先排序手邊的這些數字」。看起來以下這些數字是按小到大往右一路寫下去:
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)- 但是,如何確定它們「確實從小到大呢?」作者建議這麼做,只要看到最後一句話(R符)的答案是「
0」就表示「Data」確實從小到大排排站了:
diff(Data)## [1] 2 1 2 14 1 2 2 0 4 0 3 1 5 3 4 18diff(Data) < 0## [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [13] FALSE FALSE FALSE FALSEsum(diff(Data) < 0)## [1] 0- 確定後交給
stem.leaf()幫我們製作這些示範數據的莖葉圖:
stem.leaf(Data)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 1 4* | 4
## 4 4. | 679
## 5* |
## 5. |
## 6 6* | 34
## (3) 6. | 688
## 8 7* | 22
## 6 7. | 56
## 4 8* | 14
## 2 8. | 8
## HI: 106觀察過後,我們發現「stem.leaf()」決定用「兩株莖」繪製這一組數字的莖葉圖。而且定調「106」這一個數字是「HI」的離群值。
看似可以接受的結果,但…
3.2.4.1 手繪莖葉圖真的需要先排序嗎?
作者曾經看過幾份參考資料,都提到說「繪製莖葉圖之前要先由小到大排序數字」。但是,如果數字很多,或是很多多,或是現今大數據時代,一般人是無法輕鬆得到「由小到大的排序結果」,但真的需要如此的準備動作嗎 — 「排序」?
- 請看我們的表演:先打亂
set.seed(1233) #這樣,讀者諸君就可以跟朋友討論這一段了!
Data <- sample(Data)
Data## [1] 84 88 68 72 46 44 75 76 68 64 81 49 63 66 106 47 72- 再一個一個看,「stem.leaf()」如何一步步得到最後的答案?
for (i in 1:length(Data)) {
print(paste0("###", " 第", i, "次 ", "###"))
print(paste0("現在出現數字", Data[i]))
print("莖葉圖到此長這個樣子:")
stem.leaf(Data[1:i], m = 1, unit = 1, trim.outliers = FALSE)
}## [1] "### 第1次 ###"
## [1] "現在出現數字84"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 1
## (1) 8 | 4
## [1] "### 第2次 ###"
## [1] "現在出現數字88"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 2
## (2) 8 | 48
## [1] "### 第3次 ###"
## [1] "現在出現數字68"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 3
## 1 6 | 8
## 7 |
## (2) 8 | 48
## [1] "### 第4次 ###"
## [1] "現在出現數字72"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 4
## 1 6 | 8
## (1) 7 | 2
## (2) 8 | 48
## [1] "### 第5次 ###"
## [1] "現在出現數字46"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 5
## 1 4 | 6
## 5 |
## 2 6 | 8
## (1) 7 | 2
## 2 8 | 48
## [1] "### 第6次 ###"
## [1] "現在出現數字44"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 6
## 2 4 | 46
## 5 |
## (1) 6 | 8
## (1) 7 | 2
## 2 8 | 48
## [1] "### 第7次 ###"
## [1] "現在出現數字75"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 7
## 2 4 | 46
## 5 |
## 3 6 | 8
## (2) 7 | 25
## 2 8 | 48
## [1] "### 第8次 ###"
## [1] "現在出現數字76"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 8
## 2 4 | 46
## 5 |
## 3 6 | 8
## (3) 7 | 256
## 2 8 | 48
## [1] "### 第9次 ###"
## [1] "現在出現數字68"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 9
## 2 4 | 46
## 5 |
## 4 6 | 88
## (3) 7 | 256
## 2 8 | 48
## [1] "### 第10次 ###"
## [1] "現在出現數字64"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## 2 4 | 46
## 5 |
## (3) 6 | 488
## (3) 7 | 256
## 2 8 | 48
## [1] "### 第11次 ###"
## [1] "現在出現數字81"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 11
## 2 4 | 46
## 5 |
## 5 6 | 488
## (3) 7 | 256
## 3 8 | 148
## [1] "### 第12次 ###"
## [1] "現在出現數字49"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 12
## 3 4 | 469
## 5 |
## (3) 6 | 488
## (3) 7 | 256
## 3 8 | 148
## [1] "### 第13次 ###"
## [1] "現在出現數字63"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 13
## 3 4 | 469
## 5 |
## (4) 6 | 3488
## 6 7 | 256
## 3 8 | 148
## [1] "### 第14次 ###"
## [1] "現在出現數字66"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 14
## 3 4 | 469
## 5 |
## (5) 6 | 34688
## 6 7 | 256
## 3 8 | 148
## [1] "### 第15次 ###"
## [1] "現在出現數字106"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 15
## 3 4 | 469
## 5 |
## (5) 6 | 34688
## 7 7 | 256
## 4 8 | 148
## 9 |
## 1 10 | 6
## [1] "### 第16次 ###"
## [1] "現在出現數字47"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 16
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 7 7 | 256
## 4 8 | 148
## 9 |
## 1 10 | 6
## [1] "### 第17次 ###"
## [1] "現在出現數字72"
## [1] "莖葉圖到此長這個樣子:"
## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 8 7 | 2256
## 4 8 | 148
## 9 |
## 1 10 | 6我們依序一步步往下看、觀察,發現「絕對不需要」先排序!只要清楚知道阿拉伯數字的大小關係即可,因為「莖內」要「排序」!
3.2.4.2 如果一次擁有全部Wikipedia的示範數字
stem.leaf(Data, m = 1, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 8 7 | 2256
## 4 8 | 148
## 9 |
## 1 10 | 6如果我們想用「兩株莖」繪製示範數字的莖葉圖,結果是
stem.leaf(Data, m = 2, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 1 4* | 4
## 4 4. | 679
## 5* |
## 5. |
## 6 6* | 34
## (3) 6. | 688
## 8 7* | 22
## 6 7. | 56
## 4 8* | 14
## 2 8. | 8
## 9* |
## 9. |
## 10* |
## 1 10. | 6如果我們想用「五株莖」繪製示範數字的莖葉圖,結果是
stem.leaf(Data, m = 5, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 1 f | 4
## 3 s | 67
## 4 4. | 9
## 5* |
## t |
## f |
## s |
## 5. |
## 6* |
## 5 t | 3
## 6 f | 4
## 7 s | 6
## (2) 6. | 88
## 7* |
## 8 t | 22
## 6 f | 5
## 5 s | 6
## 7. |
## 4 8* | 1
## t |
## 3 f | 4
## s |
## 2 8. | 8
## 9* |
## t |
## f |
## s |
## 9. |
## 10* |
## t |
## f |
## 1 s | 6似乎樹越來越扁平!
3.3 次數分配表
為什麼選讀這個主題,基本上,至少三個理由:
- 見證莖葉圖如何得到次數分配表?
- 如何從次數分配表得到相對次數分配表?
- 如何從次數分配表得到累加次數分配表?
- 如何從累加次數分配表得到累加相對次數分配表?
- 學習如何透過次數分配表或是相對次數分配表得知分配的形狀?
- 學習如何透過次數分配表得知某個數線範圍內有多少筆數據?
- 學習如何透過相對次數分配表得知某個數線範圍內的數據佔有多少比例?
3.3.1 建議優先閱讀:莖葉圖
1900年代,Arthur Bowley倡議莖葉圖這一項技術。
…
讓我們回顧以下這一組來自維基百科數據的莖葉圖。請注意,這一組數據在上述網頁是以由小到大的方式呈現,也就是說,已經被「排序」過了!(作者小編並沒有刻意排序後再餵給「stem.leaf」。)
library(aplpack)
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
stem.leaf(Data, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 8 7 | 2256
## 4 8 | 148
## 9 |
## 1 10 | 6Q1:每一株莖到底有幾片葉子呢?
仔細觀察,我們發現,「stem.leaf」用「一株莖(m = 1)」繪製「Data」這一個向量內含的「17」個數字的莖葉圖。接著,最左邊有一排數字從上而下排列,分別是「4, (5), 8, 4, 1」。它們的意義分別是:
第一個「4」的右手邊有「44, 46, 47, 49」,因為圖上記載「
4 | 4679」,所以這一個「4」表示這一株莖有四片葉子,也意味著,「在40到49這一個範圍內,Data有四個數字」。第二個「5」被放在「()」內,它的右手邊有「63, 64, 66, 68, 68」,因為圖上記載「
6 | 34688」,所以這一個「5」表示這一株莖有五片葉子,也意味著,「在50到59這一個範圍內,Data有五個數字」。另外,「()」代表「5前頭的數字4,加上5等於9,已經過半了,超過『length(Data) %/% 2=8』。」第三個「8」的右手邊有「72, 72, 75, 76」,因為圖上記載「
7 | 2256」,但不是「8」個數字,是「4」個,原因是「8」的下面有一個「4」,所以「8」是累加數目,必須「扣掉4等於4」。也就是說這一個「8」扣掉第四個「4」之後得到「4」,表示這一株莖有四片葉子,也意味著,「在70到79這一個範圍內,Data有四個數字」。第四個「4」的右手邊有「81, 84, 88」,因為圖上記載「
8 | 148」,但不是「4」個數字,是「3」個,原因是「4」的下面有一個「1」,所以「4」是累加數目,必須「扣掉1等於3」。也就是說這一個「4」扣掉第五個「1」之後得到「3」,表示這一株莖有三片葉子,也意味著,「在80到89這一個範圍內,Data有三個數字」。第五個「1」的右手邊有「106」,因為圖上記載「
10 | 6」,所以這一個「1」表示這一株莖有一片葉子,也意味著,「在100到109這一個範圍內,Data有一個數字」。
3.3.2 手動整理上述資訊編撰Data的次數分配表
先準備一張「乾淨」、「什麼都沒有」的表:
DF <- data.frame(range = character(0), freq = numeric(0))
DF## [1] range freq
## <0 列> (或零長度的 row.names)- (步驟一) 第一個「4」的右手邊有「44, 46, 47, 49」,因為圖上記載「
4 | 4679」,所以這一個「4」表示這一株莖有四片葉子,也意味著,「在40到49這一個範圍內,Data有四個數字」。
df <- data.frame(range = "40 ~ 49", freq = 4)
DF <- rbind(DF, df)
DF## range freq
## 1 40 ~ 49 4- (步驟二) 第二個「5」被放在「()」內,它的右手邊有「63, 64, 66, 68, 68」,因為圖上記載「
6 | 34688」,所以這一個「5」表示這一株莖有五片葉子,也意味著,「在50到59這一個範圍內,Data有五個數字」。另外,「()」代表「5前頭的數字4,加上5等於9,已經過半了,超過『length(Data) %/% 2=8』。」
df <- data.frame(range = "50 ~ 59", freq = 5)
DF <- rbind(DF, df)
DF## range freq
## 1 40 ~ 49 4
## 2 50 ~ 59 5- (步驟三) 第三個「8」的右手邊有「72, 72, 75, 76」,因為圖上記載「
7 | 2256」,但不是「8」個數字,是「4」個,原因是「8」的下面有一個「4」,所以「8」是累加數目,必須「扣掉4等於4」。也就是說這一個「8」扣掉第四個「4」之後得到「4」,表示這一株莖有四片葉子,也意味著,「在70到79這一個範圍內,Data有四個數字」。
df <- data.frame(range = "70 ~ 79", freq = 4)
DF <- rbind(DF, df)
DF## range freq
## 1 40 ~ 49 4
## 2 50 ~ 59 5
## 3 70 ~ 79 4- (步驟四) 第四個「4」的右手邊有「81, 84, 88」,因為圖上記載「
8 | 148」,但不是「4」個數字,是「3」個,原因是「4」的下面有一個「1」,所以「4」是累加數目,必須「扣掉1等於3」。也就是說這一個「4」扣掉第五個「1」之後得到「3」,表示這一株莖有三片葉子,也意味著,「在80到89這一個範圍內,Data有三個數字」。
df <- data.frame(range = "80 ~ 89", freq = 3)
DF <- rbind(DF, df)
DF## range freq
## 1 40 ~ 49 4
## 2 50 ~ 59 5
## 3 70 ~ 79 4
## 4 80 ~ 89 3- (步驟五) 第五個「1」的右手邊有「106」,因為圖上記載「
10 | 6」,所以這一個「1」表示這一株莖有一片葉子,也意味著,「在100到109這一個範圍內,Data有一個數字」。
df <- data.frame(range = "100 ~ 109", freq = 1)
DF <- rbind(DF, df)
DF## range freq
## 1 40 ~ 49 4
## 2 50 ~ 59 5
## 3 70 ~ 79 4
## 4 80 ~ 89 3
## 5 100 ~ 109 1- 綜合以上:
DF <- data.frame(range = character(0), freq = numeric(0))
# 或是這樣
DF <- data.frame()
df <- data.frame(range = "40 ~ 49", freq = 4)
DF <- rbind(DF, df)
df <- data.frame(range = "50 ~ 59", freq = 5)
DF <- rbind(DF, df)
df <- data.frame(range = "70 ~ 79", freq = 4)
DF <- rbind(DF, df)
df <- data.frame(range = "80 ~ 89", freq = 3)
DF <- rbind(DF, df)
df <- data.frame(range = "100 ~ 109", freq = 1)
DF <- rbind(DF, df)
DF## range freq
## 1 40 ~ 49 4
## 2 50 ~ 59 5
## 3 70 ~ 79 4
## 4 80 ~ 89 3
## 5 100 ~ 109 13.3.3 寫一句R文電動取得Data的次數分配表
table(Data)## Data
## 44 46 47 49 63 64 66 68 72 75 76 81 84 88 106
## 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1答案不一樣。檢視上下結果,看起來似乎是「table(Data)」未定義「range(範圍)」。怎麼辦呢?
3.3.3.1 搜尋網際網路找答案!
我們現在面臨的問題到底是什麼?簡單一句話:
怎麼取得連續數字的次數分配表?
作者用以下這一句英文丟給「Google搜尋引擎」
how to have frequency table of continuous data in r
記住,整句英文一定要用「in r」結束,限制「Google」的搜索範圍。經過一番檢視與閱讀,我們找到了「cut」這個字,讓我們可以定義「數字的範圍」。
table(cut(Data, breaks = c(40, 50, 60, 70, 80, 90, 100, 110)))##
## (40,50] (50,60] (60,70] (70,80] (80,90] (90,100] (100,110]
## 4 0 5 4 3 0 1接下來,我們想變出表格來!
DF <- as.data.frame(table(cut(Data, breaks = c(40, 50, 60, 70, 80, 90, 100, 110))))
DF## Var1 Freq
## 1 (40,50] 4
## 2 (50,60] 0
## 3 (60,70] 5
## 4 (70,80] 4
## 5 (80,90] 3
## 6 (90,100] 0
## 7 (100,110] 1再來,修正表格的「行名稱」,請注意並養成這個撰寫程式的好習慣:欄位名稱一定要前後一致。
colnames(DF) <- c("range", "freq")
DF## range freq
## 1 (40,50] 4
## 2 (50,60] 0
## 3 (60,70] 5
## 4 (70,80] 4
## 5 (80,90] 3
## 6 (90,100] 0
## 7 (100,110] 13.3.4 再論手動整理:莖葉圖裡「4, (5), 8, 4, 1」之間有「空白」
在「手動整理上述資訊編撰Data的次數分配表」這一段得到的次數分配表,跟「寫一句R文電動取得Data的次數分配表」得到的次數分配表並不一樣,除了「range」這一個欄位的表達方式,「freq」也不一樣。「手動」部分少了幾個0!
再認真看一次,
stem.leaf(Data, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 8 7 | 2256
## 4 8 | 148
## 9 |
## 1 10 | 6確認中間的「空白」就是「加0」的意思,也就是說在那個範圍沒有任何數字。所以,我們這樣改程式,也順便修正「range」欄位的表達方式:
DF <- data.frame()
df <- data.frame(range = "(39,49]", freq = 4)
DF <- rbind(DF, df)
df <- data.frame(range = "(49,59]", freq = 0)
DF <- rbind(DF, df)
df <- data.frame(range = "(59,69]", freq = 5)
DF <- rbind(DF, df)
df <- data.frame(range = "(69,79]", freq = 4)
DF <- rbind(DF, df)
df <- data.frame(range = "(79,89]", freq = 3)
DF <- rbind(DF, df)
df <- data.frame(range = "(89,99]", freq = 0)
DF <- rbind(DF, df)
df <- data.frame(range = "(99,109]", freq = 1)
DF <- rbind(DF, df)
DF## range freq
## 1 (39,49] 4
## 2 (49,59] 0
## 3 (59,69] 5
## 4 (69,79] 4
## 5 (79,89] 3
## 6 (89,99] 0
## 7 (99,109] 1現在,手動跟電動的結果已經一樣了!
3.3.5 寫幾句R文電動取得Data的累加次數分配表
讓我們一路觀察每一句R文給了我們什麼?
3.3.5.1 (第一句) 產生「莖葉圖」一致的次數分配表。
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
DF##
## (39,49] (49,59] (59,69] (69,79] (79,89] (89,99] (99,109]
## 4 0 5 4 3 0 13.3.5.2 (第二句) 產生累加次數分配表,並且根據「table」給的次數分配表修正這一張累加次數分配表的外觀。
DF <- cumsum(DF)
DF## (39,49] (49,59] (59,69] (69,79] (79,89] (89,99] (99,109]
## 4 4 9 13 16 16 17請注意看,上下兩句話的輸出結果不一樣,第二句話的輸出少了一行
cat("##", "\n\n") # 失敗,但是意思到了!## ##所以,我們檢查一下前述兩句話之後DF的屬性:
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
class(DF)## [1] "table"DF <- cumsum(DF)
class(DF)## [1] "integer"果然,一前是「table」一後是「integer」,所以我們強迫「integer」的DF變成「table」的DF。
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
DF##
## (39,49] (49,59] (59,69] (69,79] (79,89] (89,99] (99,109]
## 4 0 5 4 3 0 1class(DF)## [1] "table"DF <- as.table(cumsum(DF))
class(DF)## [1] "table"DF## (39,49] (49,59] (59,69] (69,79] (79,89] (89,99] (99,109]
## 4 4 9 13 16 16 17雖然不會變出少掉的那一行空白,但是在下一句,我們看到了「似曾相似」的畫面。
3.3.5.3 (第三句) 強迫累加次數分配表變成「表(data.frame)」。
DF <- as.data.frame(DF)
DF## Var1 Freq
## 1 (39,49] 4
## 2 (49,59] 4
## 3 (59,69] 9
## 4 (69,79] 13
## 5 (79,89] 16
## 6 (89,99] 16
## 7 (99,109] 173.3.5.4 (第四句) 更改欄位名稱,提升名稱的可讀性。
colnames(DF) <- c("range", "cumulative frequency")
DF## range cumulative frequency
## 1 (39,49] 4
## 2 (49,59] 4
## 3 (59,69] 9
## 4 (69,79] 13
## 5 (79,89] 16
## 6 (89,99] 16
## 7 (99,109] 17綜合以上步驟得知以下可以將「次數分配表」得到「累加次數分配表」的程式碼。在這一本書,作者小編將這一類「把手動取得答案的過程換成電腦程式碼取得一樣答案」的手法,暱稱為「電算手算」。
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
DF <- as.table(cumsum(DF))
DF <- as.data.frame(DF)
colnames(DF) <- c("range", "cumulative frequency")
DF## range cumulative frequency
## 1 (39,49] 4
## 2 (49,59] 4
## 3 (59,69] 9
## 4 (69,79] 13
## 5 (79,89] 16
## 6 (89,99] 16
## 7 (99,109] 173.3.6 用「變形金剛」電動取得Data的相對次數分配表與累加相對次數分配表
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
DF <- as.data.frame(DF)
DF <- transform(DF,
cumFreq = cumsum(Freq),
relative = prop.table(Freq),
cumRelative = cumsum(prop.table(Freq)))
colnames(DF)[1:2] <- c("range", "freq")
DF## range freq cumFreq relative cumRelative
## 1 (39,49] 4 4 0.23529412 0.2352941
## 2 (49,59] 0 4 0.00000000 0.2352941
## 3 (59,69] 5 9 0.29411765 0.5294118
## 4 (69,79] 4 13 0.23529412 0.7647059
## 5 (79,89] 3 16 0.17647059 0.9411765
## 6 (89,99] 0 16 0.00000000 0.9411765
## 7 (99,109] 1 17 0.05882353 1.0000000或者用「百分比」報告「累加相對次數」:
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
DF <- as.data.frame(DF)
DF <- transform(DF,
cumFreq = cumsum(Freq),
relative = prop.table(Freq),
cumRelative = cumsum(prop.table(Freq)))
DF$relative <- DF$relative * 100.0
DF$cumRelative <- DF$cumRelative * 100.0
colnames(DF)[1:2] <- c("range", "freq")
DF## range freq cumFreq relative cumRelative
## 1 (39,49] 4 4 23.529412 23.52941
## 2 (49,59] 0 4 0.000000 23.52941
## 3 (59,69] 5 9 29.411765 52.94118
## 4 (69,79] 4 13 23.529412 76.47059
## 5 (79,89] 3 16 17.647059 94.11765
## 6 (89,99] 0 16 0.000000 94.11765
## 7 (99,109] 1 17 5.882353 100.000003.3.7 透過次數分配表如何得知分配的形狀?
3.3.7.1 先看莖葉圖的輸出揣摩分配的形狀
stem.leaf(Data, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 8 7 | 2256
## 4 8 | 148
## 9 |
## 1 10 | 6如果仔細看,我們可以從葉子在每一株莖的數量以及莖與莖之間的上下距離,想像分配的形狀。我們的結論是,數字集中在上方,也就是數線的左邊,然後往下延伸,也就是往右延伸。
3.3.7.2 再看次數分配表的輸出揣摩分配的形狀
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
DF <- as.data.frame(DF)
colnames(DF) <- c("range", "freq")
DF## range freq
## 1 (39,49] 4
## 2 (49,59] 0
## 3 (59,69] 5
## 4 (69,79] 4
## 5 (79,89] 3
## 6 (89,99] 0
## 7 (99,109] 1如果我們用範圍「(69,79]」把整張表格切出上下,會發現上面的「freq」加起來是「9」,而下面加起來是「4」,上面大概是下面的「兩倍多」,所以結論也是數字集中在上方,也就是數線的左邊,然後往下延伸,也就是往右延伸。往右延伸的想像是因為最下方的範圍內只有一片葉子、一個數字。
3.3.8 用R文電動取得任意範圍的次數分配表(最後一段程式碼的一般推廣)
讓我們趁機回顧這一本書之前的內容:
3.3.8.1 取得對應莖葉圖輸出的次數分配表,但是犯了範圍切點的錯誤!
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
DF <- table(cut(Data, breaks = c(40, 50, 60, 70, 80, 90, 100, 110)))
DF <- as.data.frame(DF)
colnames(DF) <- c("range", "freq")
DF## range freq
## 1 (40,50] 4
## 2 (50,60] 0
## 3 (60,70] 5
## 4 (70,80] 4
## 5 (80,90] 3
## 6 (90,100] 0
## 7 (100,110] 13.3.8.2 取得對應莖葉圖輸出的次數分配表,修正範圍切點的錯誤!
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
DF <- table(cut(Data, breaks = c(39, 49, 59, 69, 79, 89, 99, 109)))
DF <- as.data.frame(DF)
colnames(DF) <- c("range", "freq")
DF## range freq
## 1 (39,49] 4
## 2 (49,59] 0
## 3 (59,69] 5
## 4 (69,79] 4
## 5 (79,89] 3
## 6 (89,99] 0
## 7 (99,109] 1請注意,雖然上下表格內的「freq」內容一模一樣,作者相信讀者諸君一定同意「這只是運氣好」!如果讀者諸君正在上班看報表,請注意有沒有上述的現象!?
3.3.8.3 跳脫莖葉圖1-2-5-10的限制,取得任意範圍的次數分配表!
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
DF <- table(cut(Data, breaks = c(19, 39, 59, 79, 99, 119, 139)))
DF <- as.data.frame(DF)
colnames(DF) <- c("range", "freq")
DF## range freq
## 1 (19,39] 0
## 2 (39,59] 4
## 3 (59,79] 9
## 4 (79,99] 3
## 5 (99,119] 1
## 6 (119,139] 0雖然範圍變寬了,但依舊可以得到對「分配形狀」一致的結論。
3.4 直方圖
為什麼選讀這個主題,基本上,至少三個理由:
- 見證如何透過莖葉圖得到絕對次數分配表的直方圖?
- 學習如何繪製相對次數分配表的直方圖?
- 學習如何透過直方圖得知分配的形狀?
- 學習如何透過直方圖得知某個數線範圍內有多少個數字?
- 學習如何透過直方圖得知某個數線範圍內的數據佔有多少比例?
3.4.1 建議優先閱讀:莖葉圖
1900年代,Arthur Bowley倡議莖葉圖這一項技術。
…
讓我們回顧以下這一組數據的莖葉圖:
library(aplpack)
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
stem.leaf(Data, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 8 7 | 2256
## 4 8 | 148
## 9 |
## 1 10 | 6# 數據集Data有幾個數字?
length(Data)## [1] 173.4.2 隨機挑選200個數字的莖葉圖
以下我們用3句R文協助隨機挑來200個數字(超過維基百科示範數據的個數,17):
3.4.2.2 (第二句) 開始抽樣,因為44:198之間不足200個數字,所以設定replace = TRUE讓R可以重複選取。
Data <- sample(44:198, 200, replace = TRUE)3.4.2.3 (第三句) 呼叫Data出來,看看、觀察隨機挑到哪一些數字?
Data## [1] 58 147 173 140 108 86 109 70 196 193 117 191 162 193 165 95 171 163
## [19] 186 92 158 191 55 183 131 194 133 184 109 103 173 190 83 99 156 102
## [37] 183 143 91 127 77 140 184 140 145 151 62 144 130 97 132 113 57 184
## [55] 60 100 121 49 82 85 149 95 81 127 150 158 173 61 145 52 70 140
## [73] 143 77 102 107 77 56 107 52 102 130 90 160 144 167 163 61 134 190
## [91] 97 128 104 74 101 102 98 158 185 179 60 65 144 184 156 147 93 126
## [109] 90 135 57 77 145 120 126 171 120 75 134 173 189 103 115 64 185 73
## [127] 70 116 75 163 133 182 70 175 174 134 190 124 76 71 93 85 154 196
## [145] 113 51 136 162 186 136 189 132 193 46 77 86 69 182 56 119 54 149
## [163] 79 85 55 193 104 163 170 111 48 128 151 68 88 76 148 190 47 125
## [181] 157 49 83 120 195 94 166 102 154 109 72 180 81 195 189 52 66 194
## [199] 136 115這是它們的莖葉圖:
stem.leaf(Data)## 1 | 2: represents 12
## leaf unit: 1
## n: 200
## 5 4 | 67899
## 17 5 | 122245566778
## 27 6 | 0011245689
## 45 7 | 000012345566777779
## 56 8 | 11233555668
## 69 9 | 0012334557789
## 86 10 | 01222223344778999
## 94 11 | 13355679
## (12) 12 | 000145667788
## 94 13 | 00122334445666
## 80 14 | 00003344455577899
## 63 15 | 01144667888
## 52 16 | 0223333567
## 42 17 | 0113333459
## 32 18 | 0223344445566999
## 16 19 | 00001133334455663.4.2.4 如果是300個,莖葉圖會長怎樣?
set.seed(1233)
Data <- sample(44:198, 300, replace = TRUE)
stem.leaf(Data)## 1 | 2: represents 12
## leaf unit: 1
## n: 300
## 7 4 | 5677899
## 24 5 | 01122233455667788
## 38 6 | 00011234556789
## 60 7 | 0000122334555666777779
## 77 8 | 00112233555566788
## 99 9 | 0011233444555777888899
## 120 10 | 001122222334477888999
## 135 11 | 122335556778999
## (21) 12 | 000134455556677888899
## 144 13 | 001122334444455566668
## 123 14 | 0000023333444455577788899
## 98 15 | 0011244666788888
## 82 16 | 00223333335556677
## 65 17 | 00111112333334555679
## 45 18 | 00122334444555667789999
## 22 19 | 00000113333344556666673.4.2.5 如果是800個,莖葉圖會長怎樣?
set.seed(1233)
Data <- sample(44:198, 800, replace = TRUE)
stem.leaf(Data)## 1 | 2: represents 12
## leaf unit: 1
## n: 800
## 17 4 | 56667777778899999
## 70 5 | 00000011111222222223344444455566777777777777788889999
## 107 6 | 0000001122333344444555566667788888899
## 165 7 | 0000000001111222222233333444444555556666667777778889999999
## 210 8 | 000011111122222333344455556666667777778888999
## 263 9 | 00001111122222233344444444455555566777777888888899999
## 310 10 | 00000000011122222222333444444555677777788899999
## 357 11 | 01111222222223333333444445555556666677777778999
## (48) 12 | 000000011111112222223333334455555566677778888899
## 395 13 | 000000011122223333334444444455555555555666666777777888889999
## 335 14 | 0000001112223333334444444455555555566777777788888999999
## 280 15 | 000000011222223444444455555556666666666666777777888888899
## 223 16 | 000000112233333333444445555555566666777799999
## 178 17 | 000000111111122233333344445555555666667777778889999999999
## 121 18 | 00001112222333333333334444444444555555556666677777778888899999
## 59 19 | 00000000000011111122233333333333333444455555566666677778888看起來,每一張莖葉圖內的樹莖大約一般高!
3.4.3 再一次隨機挑選200個數字
3.4.3.1 這200個數字的故事
作者為了設計這一本書(基本上從「初等統計學」出發),參考過一本教科書,發現該書作者群提供的莖葉圖示範數據,是一組診所來客數(來病數)的數字。個人咸信,假設該診所醫生是一位名醫,那這一組數字內「很小(既然是名醫!)」或是「很大(名醫應該不想累倒影響病人權益)」的數字應該是比較少,比較多的數字應該會集中在某一個範圍內。基於這樣的假設,作者試著請「常態分配(相關內容請參考常態分配的章節)」來幫忙定義「數字區間的機率」。
3.4.3.3 (第二句話) 假設我們請平均數121跟標準差等於20的常態分配來幫忙。請讀者諸君注意到,這只是一種可能性,並非絕對的選擇。
p <- dnorm(44:198, mean = mean(44:198), sd = 20)3.4.3.4 (第三句話) 抽樣。一樣需要設定replace = TRUE再加上定義每一個範圍的隨機挑選機率,讓prob = p。
Data <- sample(44:198, 200, replace = TRUE, prob = p)3.4.3.5 (第四句話) 排序。讓我們容易觀察隨機抽樣的結果。
sort(Data)## [1] 49 62 69 81 81 83 84 90 92 93 93 94 95 95 96 96 96 97
## [19] 97 97 97 98 98 99 99 100 102 102 102 102 103 103 103 104 105 105
## [37] 105 105 106 106 107 107 107 108 108 108 109 109 110 110 110 110 111 111
## [55] 111 112 112 112 113 113 113 113 113 113 114 114 114 114 114 115 115 115
## [73] 115 115 116 116 116 116 117 117 117 117 117 117 117 117 118 118 118 120
## [91] 120 120 120 120 120 121 121 122 122 122 122 122 122 122 122 123 123 123
## [109] 123 123 123 124 124 124 125 125 125 126 126 126 127 127 127 128 128 128
## [127] 129 129 129 130 130 130 130 130 130 130 131 131 131 131 131 131 131 131
## [145] 131 132 133 133 133 133 133 133 133 133 134 134 134 134 135 135 135 135
## [163] 135 135 136 137 137 138 139 140 140 141 141 141 142 142 143 143 145 146
## [181] 146 147 148 149 150 151 152 153 153 157 158 160 161 161 165 165 166 170
## [199] 174 1753.4.3.6 (第五句話) 接下來繪製它們的莖葉圖。注意,我們要求stem.leaf不要處理離群值trim.outliers = FALSE,讓我們可以清楚觀察離群值與非離群值之間的大小關係:
stem.leaf(Data, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 200
## 1 4 | 9
## 5 |
## 3 6 | 29
## 7 |
## 7 8 | 1134
## 25 9 | 023345566677778899
## 48 10 | 02222333455556677788899
## 89 11 | 00001112223333334444455555666677777777888
## (40) 12 | 0000001122222222333333444555666777888999
## 71 13 | 0000000111111111233333333444455555567789
## 31 14 | 001112233566789
## 16 15 | 0123378
## 9 16 | 011556
## 3 17 | 045觀察上述「莖葉圖」的形狀確實符合
數字內「很小(既然是名醫!)」或是「很大(名醫應該不想累倒影響病人權益)」的數字應該是比較少,比較多的數字應該會集中在某一個範圍內。
3.4.4 模擬診所數據的直方圖
3.4.4.1 第一次試著繪製等同於「單莖莖葉圖」的直方圖
seq(40, 200, 10)## [1] 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200cut(Data, breaks = seq(40, 200, 10))## [1] (140,150] (110,120] (110,120] (130,140] (130,140] (90,100] (120,130]
## [8] (100,110] (100,110] (120,130] (120,130] (160,170] (130,140] (90,100]
## [15] (150,160] (110,120] (130,140] (110,120] (90,100] (130,140] (110,120]
## [22] (100,110] (120,130] (110,120] (130,140] (90,100] (110,120] (120,130]
## [29] (140,150] (130,140] (110,120] (120,130] (120,130] (140,150] (120,130]
## [36] (110,120] (110,120] (90,100] (120,130] (150,160] (120,130] (160,170]
## [43] (110,120] (110,120] (150,160] (60,70] (120,130] (140,150] (130,140]
## [50] (100,110] (130,140] (80,90] (120,130] (110,120] (110,120] (100,110]
## [57] (120,130] (110,120] (140,150] (120,130] (130,140] (160,170] (120,130]
## [64] (120,130] (110,120] (100,110] (90,100] (120,130] (120,130] (110,120]
## [71] (110,120] (120,130] (90,100] (80,90] (130,140] (140,150] (110,120]
## [78] (130,140] (160,170] (110,120] (140,150] (130,140] (150,160] (140,150]
## [85] (130,140] (140,150] (90,100] (130,140] (100,110] (120,130] (100,110]
## [92] (120,130] (60,70] (120,130] (130,140] (170,180] (120,130] (120,130]
## [99] (120,130] (130,140] (170,180] (110,120] (100,110] (130,140] (100,110]
## [106] (130,140] (110,120] (90,100] (120,130] (90,100] (110,120] (100,110]
## [113] (110,120] (130,140] (110,120] (90,100] (110,120] (160,170] (110,120]
## [120] (140,150] (120,130] (120,130] (130,140] (110,120] (110,120] (110,120]
## [127] (120,130] (110,120] (160,170] (110,120] (80,90] (100,110] (130,140]
## [134] (90,100] (100,110] (110,120] (110,120] (110,120] (80,90] (100,110]
## [141] (120,130] (90,100] (120,130] (130,140] (140,150] (100,110] (140,150]
## [148] (130,140] (90,100] (140,150] (110,120] (100,110] (90,100] (120,130]
## [155] (90,100] (100,110] (40,50] (100,110] (110,120] (100,110] (120,130]
## [162] (100,110] (120,130] (100,110] (120,130] (110,120] (120,130] (90,100]
## [169] (130,140] (110,120] (130,140] (150,160] (130,140] (130,140] (140,150]
## [176] (110,120] (120,130] (130,140] (150,160] (150,160] (110,120] (90,100]
## [183] (100,110] (100,110] (120,130] (120,130] (80,90] (100,110] (130,140]
## [190] (130,140] (130,140] (120,130] (100,110] (100,110] (130,140] (120,130]
## [197] (130,140] (130,140] (110,120] (110,120]
## 16 Levels: (40,50] (50,60] (60,70] (70,80] (80,90] (90,100] ... (190,200]stem.leaf(Data, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 200
## 1 4 | 9
## 5 |
## 3 6 | 29
## 7 |
## 7 8 | 1134
## 25 9 | 023345566677778899
## 48 10 | 02222333455556677788899
## 89 11 | 00001112223333334444455555666677777777888
## (40) 12 | 0000001122222222333333444555666777888999
## 71 13 | 0000000111111111233333333444455555567789
## 31 14 | 001112233566789
## 16 15 | 0123378
## 9 16 | 011556
## 3 17 | 045table(cut(Data, breaks = seq(40, 200, 10)))##
## (40,50] (50,60] (60,70] (70,80] (80,90] (90,100] (100,110] (110,120]
## 1 0 2 0 5 18 26 43
## (120,130] (130,140] (140,150] (150,160] (160,170] (170,180] (180,190] (190,200]
## 41 35 14 7 6 2 0 0hist(Data, breaks = seq(40, 200, 10))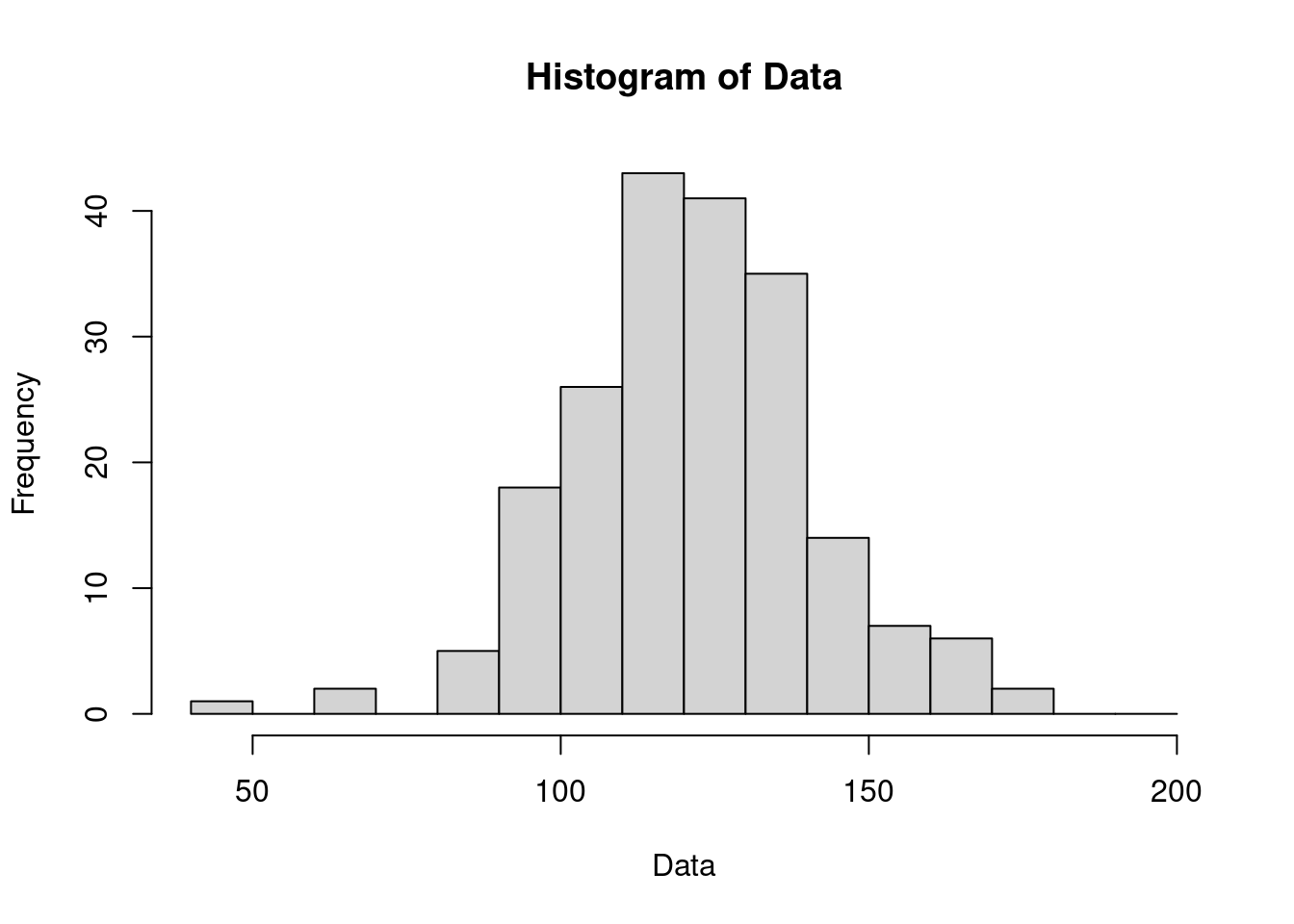
眼尖的讀者一定發現了,上述五句話裡哪個部分跟「莖葉圖」以及「次數分配表」有衝突?所以,我們修正後,再來一次。
3.4.4.2 第二次試著繪製等同於「單莖莖葉圖」的直方圖
seq(39, 200, 10) # 取得切點。## [1] 39 49 59 69 79 89 99 109 119 129 139 149 159 169 179 189 199cut(Data, breaks = seq(39, 200, 10)) # 取得切點定義出來的範圍。## [1] (139,149] (109,119] (109,119] (129,139] (129,139] (89,99] (119,129]
## [8] (99,109] (109,119] (119,129] (119,129] (159,169] (129,139] (89,99]
## [15] (149,159] (119,129] (129,139] (109,119] (89,99] (129,139] (109,119]
## [22] (99,109] (129,139] (109,119] (129,139] (89,99] (109,119] (129,139]
## [29] (139,149] (129,139] (109,119] (119,129] (119,129] (139,149] (129,139]
## [36] (109,119] (109,119] (89,99] (129,139] (149,159] (119,129] (159,169]
## [43] (109,119] (109,119] (149,159] (59,69] (119,129] (139,149] (139,149]
## [50] (99,109] (129,139] (79,89] (119,129] (109,119] (109,119] (99,109]
## [57] (119,129] (109,119] (139,149] (119,129] (129,139] (159,169] (119,129]
## [64] (119,129] (109,119] (99,109] (89,99] (119,129] (119,129] (109,119]
## [71] (119,129] (119,129] (89,99] (89,99] (129,139] (139,149] (109,119]
## [78] (129,139] (159,169] (109,119] (139,149] (129,139] (149,159] (139,149]
## [85] (129,139] (139,149] (89,99] (129,139] (99,109] (119,129] (99,109]
## [92] (129,139] (59,69] (119,129] (129,139] (169,179] (119,129] (119,129]
## [99] (119,129] (129,139] (169,179] (119,129] (99,109] (129,139] (99,109]
## [106] (129,139] (109,119] (99,109] (119,129] (89,99] (109,119] (99,109]
## [113] (119,129] (139,149] (119,129] (89,99] (109,119] (169,179] (109,119]
## [120] (149,159] (119,129] (129,139] (129,139] (109,119] (109,119] (109,119]
## [127] (119,129] (109,119] (159,169] (109,119] (79,89] (109,119] (129,139]
## [134] (89,99] (99,109] (109,119] (109,119] (119,129] (79,89] (99,109]
## [141] (119,129] (89,99] (119,129] (129,139] (139,149] (99,109] (139,149]
## [148] (129,139] (89,99] (139,149] (109,119] (109,119] (89,99] (119,129]
## [155] (89,99] (99,109] (39,49] (109,119] (109,119] (99,109] (119,129]
## [162] (99,109] (119,129] (99,109] (119,129] (109,119] (119,129] (89,99]
## [169] (129,139] (109,119] (129,139] (149,159] (129,139] (129,139] (139,149]
## [176] (109,119] (119,129] (129,139] (149,159] (159,169] (109,119] (89,99]
## [183] (99,109] (99,109] (119,129] (129,139] (79,89] (99,109] (129,139]
## [190] (129,139] (129,139] (119,129] (99,109] (99,109] (129,139] (119,129]
## [197] (129,139] (129,139] (109,119] (109,119]
## 16 Levels: (39,49] (49,59] (59,69] (69,79] (79,89] (89,99] ... (189,199]stem.leaf(Data, trim.outliers = FALSE) # 繪製莖葉圖。## 1 | 2: represents 12
## leaf unit: 1
## n: 200
## 1 4 | 9
## 5 |
## 3 6 | 29
## 7 |
## 7 8 | 1134
## 25 9 | 023345566677778899
## 48 10 | 02222333455556677788899
## 89 11 | 00001112223333334444455555666677777777888
## (40) 12 | 0000001122222222333333444555666777888999
## 71 13 | 0000000111111111233333333444455555567789
## 31 14 | 001112233566789
## 16 15 | 0123378
## 9 16 | 011556
## 3 17 | 045table(cut(Data, breaks = seq(39, 200, 10))) # 取得次數分配表。##
## (39,49] (49,59] (59,69] (69,79] (79,89] (89,99] (99,109] (109,119]
## 1 0 2 0 4 18 23 41
## (119,129] (129,139] (139,149] (149,159] (159,169] (169,179] (179,189] (189,199]
## 40 40 15 7 6 3 0 0hist(Data, breaks = seq(39, 200, 10)) # 繪製直方圖。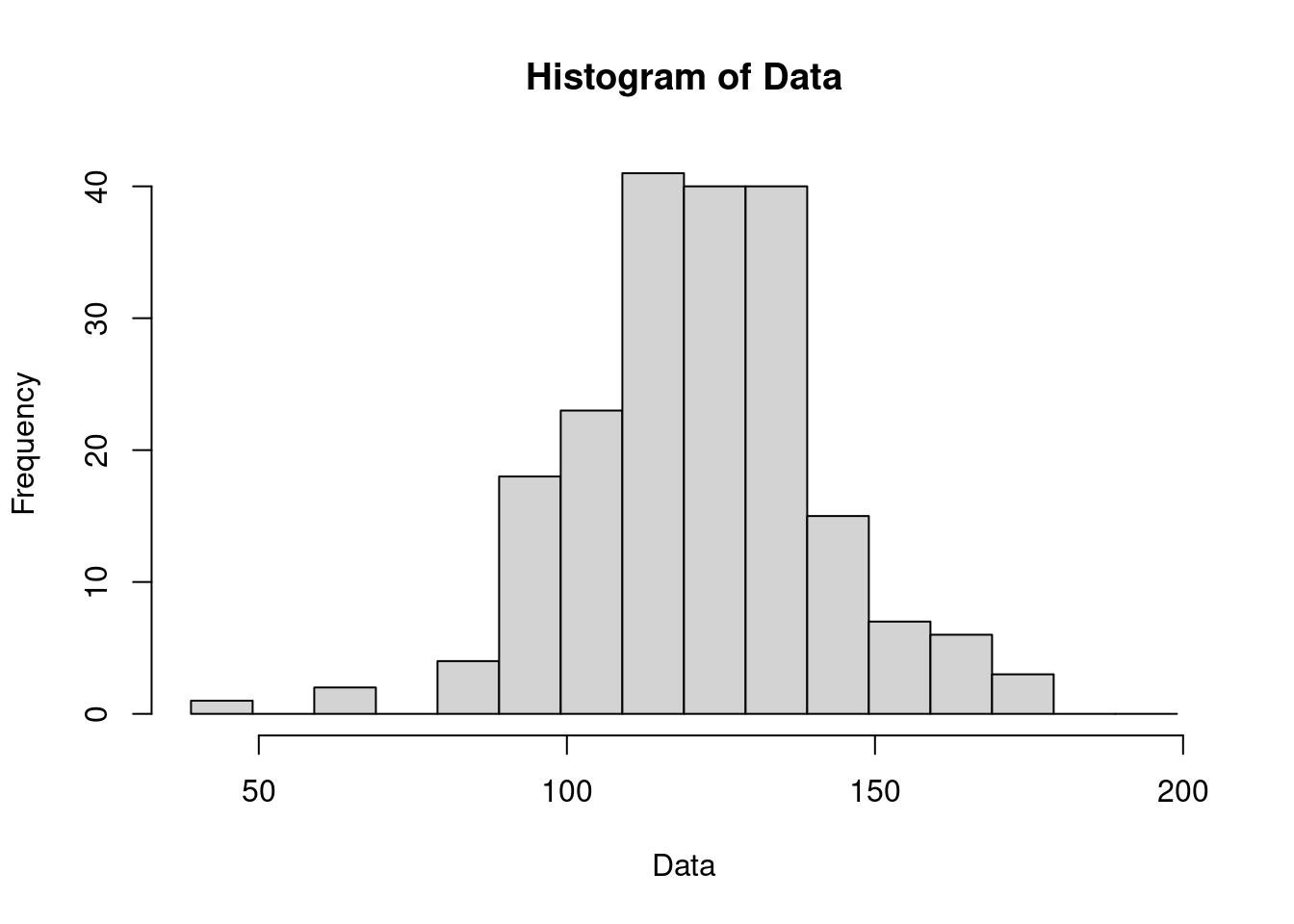
3.4.4.3 第一次試著繪製等同於「雙莖莖葉圖」的直方圖
seq(39, 200, 5)## [1] 39 44 49 54 59 64 69 74 79 84 89 94 99 104 109 114 119 124 129
## [20] 134 139 144 149 154 159 164 169 174 179 184 189 194 199cut(Data, breaks = seq(39, 200, 5))## [1] (139,144] (114,119] (109,114] (129,134] (129,134] (94,99] (119,124]
## [8] (104,109] (109,114] (124,129] (119,124] (159,164] (134,139] (89,94]
## [15] (154,159] (119,124] (129,134] (109,114] (89,94] (129,134] (109,114]
## [22] (99,104] (129,134] (114,119] (129,134] (94,99] (109,114] (129,134]
## [29] (144,149] (134,139] (109,114] (124,129] (124,129] (144,149] (129,134]
## [36] (114,119] (109,114] (89,94] (129,134] (149,154] (119,124] (164,169]
## [43] (114,119] (109,114] (149,154] (64,69] (119,124] (144,149] (139,144]
## [50] (104,109] (129,134] (79,84] (119,124] (114,119] (114,119] (104,109]
## [57] (124,129] (114,119] (139,144] (119,124] (134,139] (159,164] (119,124]
## [64] (124,129] (109,114] (104,109] (94,99] (124,129] (119,124] (109,114]
## [71] (119,124] (119,124] (94,99] (89,94] (134,139] (139,144] (114,119]
## [78] (129,134] (164,169] (114,119] (139,144] (129,134] (154,159] (139,144]
## [85] (134,139] (144,149] (94,99] (129,134] (99,104] (119,124] (104,109]
## [92] (129,134] (59,64] (124,129] (129,134] (174,179] (119,124] (124,129]
## [99] (124,129] (134,139] (169,174] (119,124] (99,104] (129,134] (99,104]
## [106] (134,139] (114,119] (99,104] (124,129] (94,99] (109,114] (104,109]
## [113] (119,124] (139,144] (119,124] (89,94] (114,119] (169,174] (114,119]
## [120] (149,154] (124,129] (129,134] (129,134] (109,114] (114,119] (109,114]
## [127] (119,124] (114,119] (164,169] (109,114] (79,84] (109,114] (129,134]
## [134] (94,99] (104,109] (109,114] (114,119] (119,124] (79,84] (104,109]
## [141] (124,129] (94,99] (119,124] (134,139] (139,144] (99,104] (144,149]
## [148] (129,134] (94,99] (139,144] (114,119] (109,114] (94,99] (124,129]
## [155] (94,99] (99,104] (44,49] (109,114] (114,119] (104,109] (119,124]
## [162] (104,109] (124,129] (99,104] (119,124] (114,119] (119,124] (94,99]
## [169] (134,139] (109,114] (129,134] (149,154] (129,134] (129,134] (144,149]
## [176] (114,119] (124,129] (129,134] (149,154] (159,164] (109,114] (94,99]
## [183] (99,104] (104,109] (119,124] (129,134] (79,84] (104,109] (129,134]
## [190] (134,139] (129,134] (119,124] (104,109] (104,109] (129,134] (119,124]
## [197] (134,139] (129,134] (114,119] (109,114]
## 32 Levels: (39,44] (44,49] (49,54] (54,59] (59,64] (64,69] (69,74] ... (194,199]stem.leaf(Data, m = 2, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 200
## 1 4. | 9
## 5* |
## 5. |
## 2 6* | 2
## 3 6. | 9
## 7* |
## 7. |
## 7 8* | 1134
## 8. |
## 12 9* | 02334
## 25 9. | 5566677778899
## 34 10* | 022223334
## 48 10. | 55556677788899
## 69 11* | 000011122233333344444
## 89 11. | 55555666677777777888
## (25) 12* | 0000001122222222333333444
## 86 12. | 555666777888999
## 71 13* | 00000001111111112333333334444
## 42 13. | 55555567789
## 31 14* | 001112233
## 22 14. | 566789
## 16 15* | 01233
## 11 15. | 78
## 9 16* | 011
## 6 16. | 556
## 3 17* | 04
## 1 17. | 5table(cut(Data, breaks = seq(39, 200, 5)))##
## (39,44] (44,49] (49,54] (54,59] (59,64] (64,69] (69,74] (74,79]
## 0 1 0 0 1 1 0 0
## (79,84] (84,89] (89,94] (94,99] (99,104] (104,109] (109,114] (114,119]
## 4 0 5 13 9 14 21 20
## (119,124] (124,129] (129,134] (134,139] (139,144] (144,149] (149,154] (154,159]
## 25 15 29 11 9 6 5 2
## (159,164] (164,169] (169,174] (174,179] (179,184] (184,189] (189,194] (194,199]
## 3 3 2 1 0 0 0 0hist(Data, breaks = seq(39, 200, 5))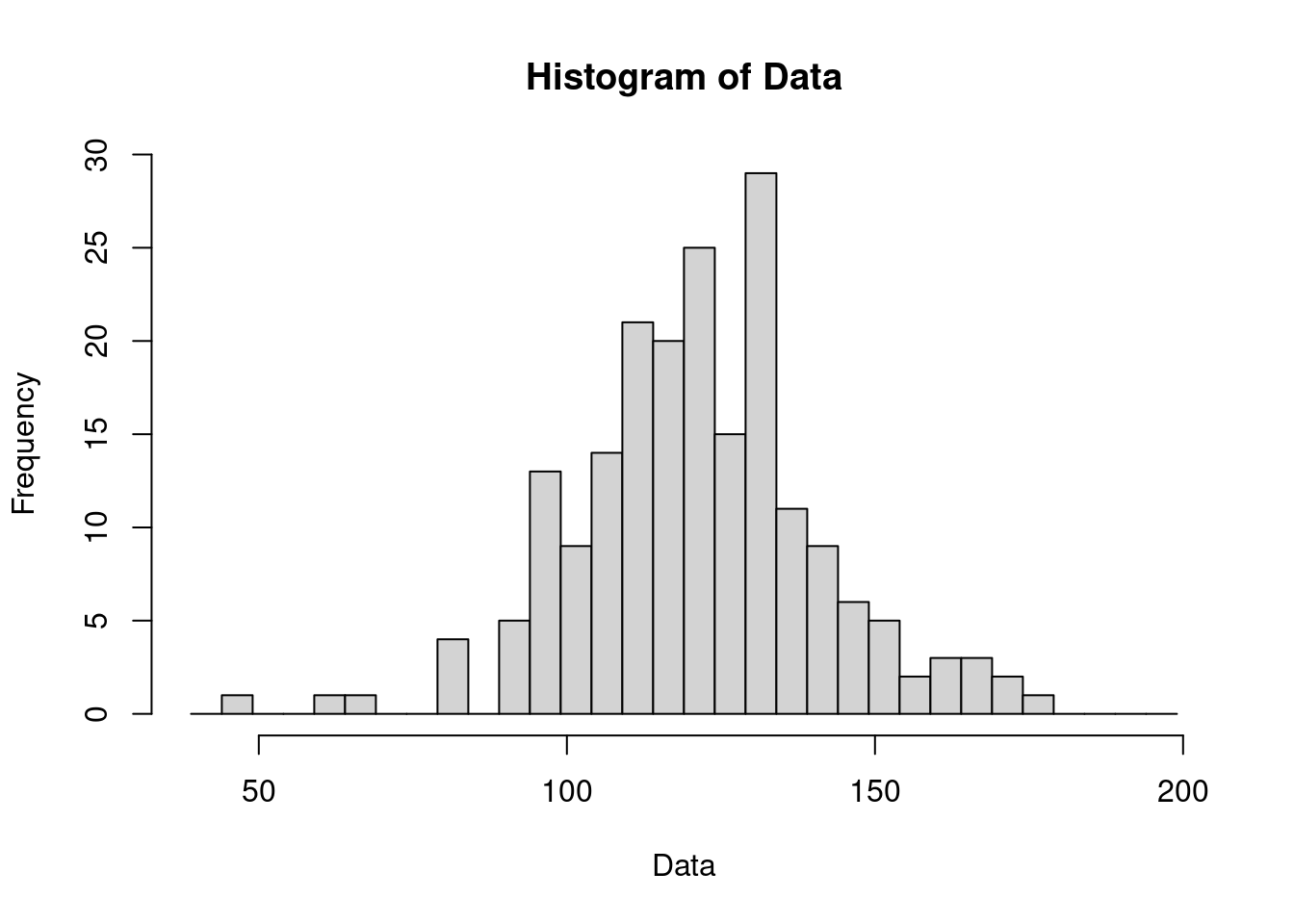
3.4.5 直方圖總論
3.4.5.1 「seq(39, 200, 10)」的直方圖 = 單莖莖葉圖
p <- hist(Data, breaks = seq(39, 200, 10))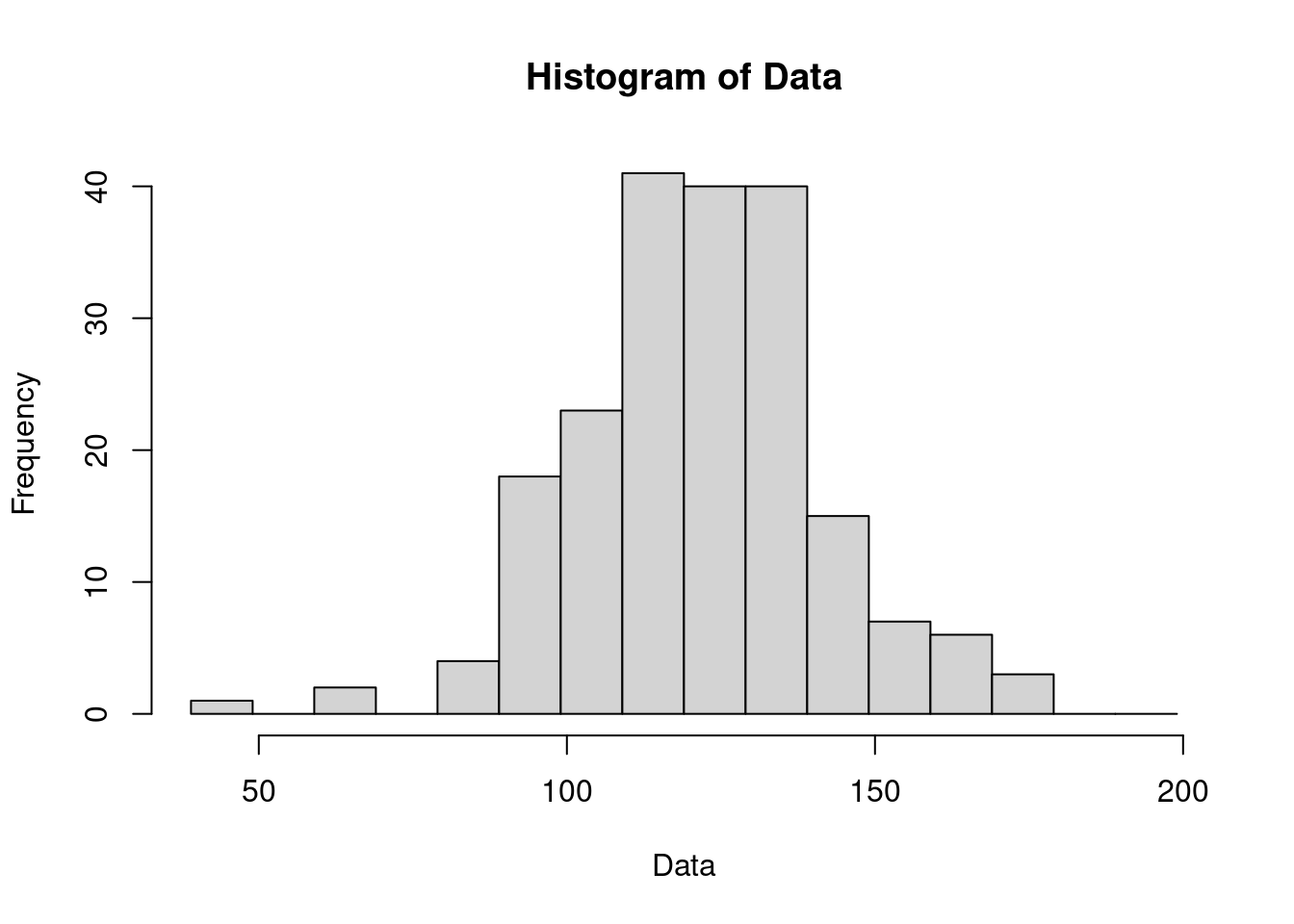
p## $breaks
## [1] 39 49 59 69 79 89 99 109 119 129 139 149 159 169 179 189 199
##
## $counts
## [1] 1 0 2 0 4 18 23 41 40 40 15 7 6 3 0 0
##
## $density
## [1] 0.0005 0.0000 0.0010 0.0000 0.0020 0.0090 0.0115 0.0205 0.0200 0.0200
## [11] 0.0075 0.0035 0.0030 0.0015 0.0000 0.0000
##
## $mids
## [1] 44 54 64 74 84 94 104 114 124 134 144 154 164 174 184 194
##
## $xname
## [1] "Data"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"3.4.5.2 「seq(39, 200, 5)」的直方圖 = 雙莖莖葉圖
p <- hist(Data, breaks = seq(39, 200, 5))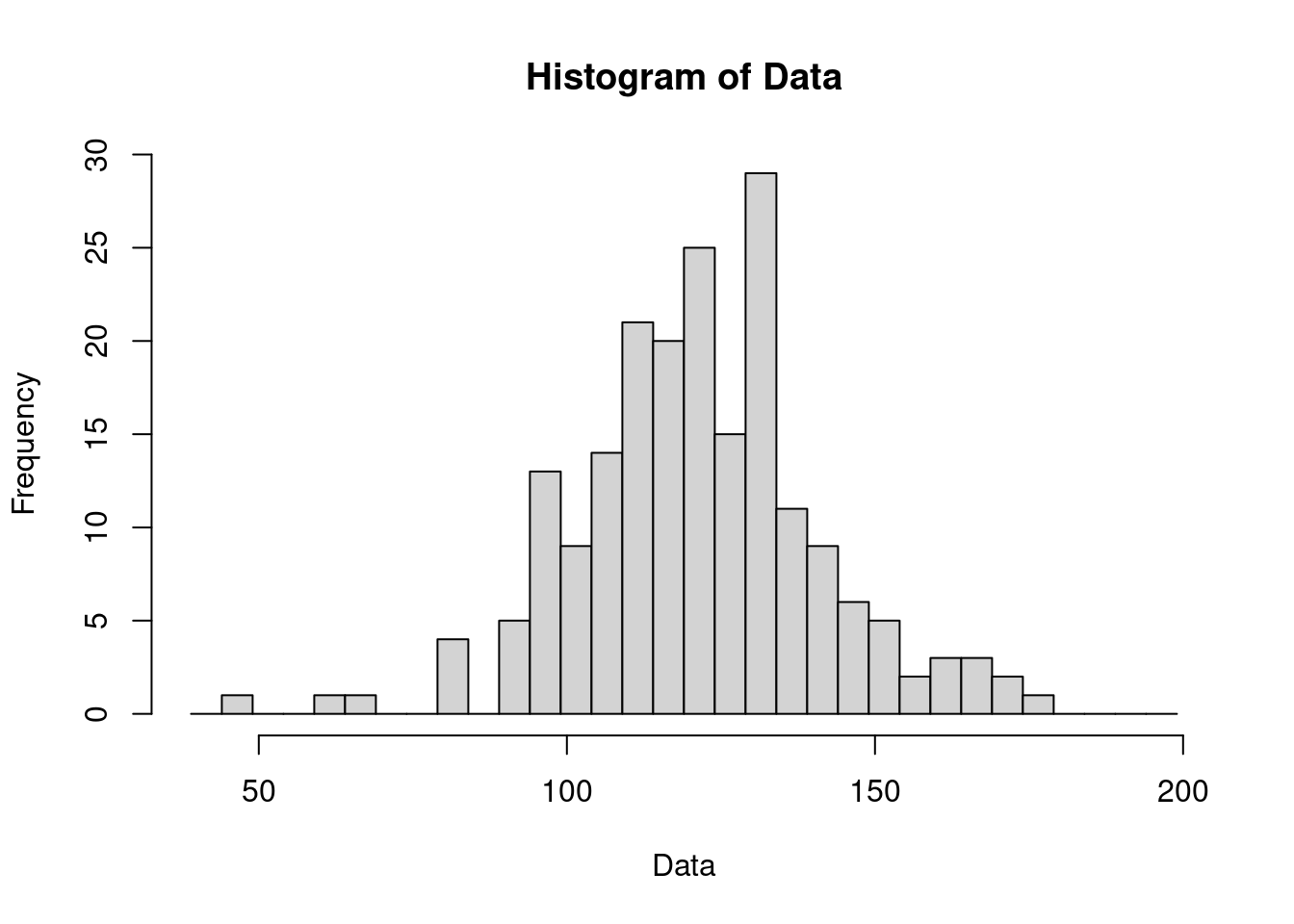
p## $breaks
## [1] 39 44 49 54 59 64 69 74 79 84 89 94 99 104 109 114 119 124 129
## [20] 134 139 144 149 154 159 164 169 174 179 184 189 194 199
##
## $counts
## [1] 0 1 0 0 1 1 0 0 4 0 5 13 9 14 21 20 25 15 29 11 9 6 5 2 3
## [26] 3 2 1 0 0 0 0
##
## $density
## [1] 0.000 0.001 0.000 0.000 0.001 0.001 0.000 0.000 0.004 0.000 0.005 0.013
## [13] 0.009 0.014 0.021 0.020 0.025 0.015 0.029 0.011 0.009 0.006 0.005 0.002
## [25] 0.003 0.003 0.002 0.001 0.000 0.000 0.000 0.000
##
## $mids
## [1] 41.5 46.5 51.5 56.5 61.5 66.5 71.5 76.5 81.5 86.5 91.5 96.5
## [13] 101.5 106.5 111.5 116.5 121.5 126.5 131.5 136.5 141.5 146.5 151.5 156.5
## [25] 161.5 166.5 171.5 176.5 181.5 186.5 191.5 196.5
##
## $xname
## [1] "Data"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"3.4.5.3 「seq(39, 200, 2)」的直方圖 = 五莖莖葉圖
p <- hist(Data, breaks = seq(39, 200, 2))
p## $breaks
## [1] 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75
## [20] 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113
## [39] 115 117 119 121 123 125 127 129 131 133 135 137 139 141 143 145 147 149 151
## [58] 153 155 157 159 161 163 165 167 169 171 173 175 177 179 181 183 185 187 189
## [77] 191 193 195 197 199
##
## $counts
## [1] 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 2 1 1 0 0
## [26] 1 3 3 7 4 1 7 5 5 5 7 9 10 12 3 8 14 6 6 6 16 9 10 3 2
## [51] 5 4 1 3 2 2 3 0 1 1 3 0 2 1 0 1 0 2 0 0 0 0 0 0 0
## [76] 0 0 0 0 0
##
## $density
## [1] 0.0000 0.0000 0.0000 0.0000 0.0025 0.0000 0.0000 0.0000 0.0000 0.0000
## [11] 0.0000 0.0025 0.0000 0.0000 0.0025 0.0000 0.0000 0.0000 0.0000 0.0000
## [21] 0.0050 0.0025 0.0025 0.0000 0.0000 0.0025 0.0075 0.0075 0.0175 0.0100
## [31] 0.0025 0.0175 0.0125 0.0125 0.0125 0.0175 0.0225 0.0250 0.0300 0.0075
## [41] 0.0200 0.0350 0.0150 0.0150 0.0150 0.0400 0.0225 0.0250 0.0075 0.0050
## [51] 0.0125 0.0100 0.0025 0.0075 0.0050 0.0050 0.0075 0.0000 0.0025 0.0025
## [61] 0.0075 0.0000 0.0050 0.0025 0.0000 0.0025 0.0000 0.0050 0.0000 0.0000
## [71] 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000
##
## $mids
## [1] 40 42 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76
## [20] 78 80 82 84 86 88 90 92 94 96 98 100 102 104 106 108 110 112 114
## [39] 116 118 120 122 124 126 128 130 132 134 136 138 140 142 144 146 148 150 152
## [58] 154 156 158 160 162 164 166 168 170 172 174 176 178 180 182 184 186 188 190
## [77] 192 194 196 198
##
## $xname
## [1] "Data"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"3.4.5.4 「任意範圍、任意切割」的直方圖 != 任何莖葉圖
p <- hist(Data, breaks = seq(40, 200, 8))
p## $breaks
## [1] 40 48 56 64 72 80 88 96 104 112 120 128 136 144 152 160 168 176 184
## [20] 192 200
##
## $counts
## [1] 0 1 1 1 0 4 10 17 24 37 31 39 13 9 5 5 3 0 0 0
##
## $density
## [1] 0.000000 0.000625 0.000625 0.000625 0.000000 0.002500 0.006250 0.010625
## [9] 0.015000 0.023125 0.019375 0.024375 0.008125 0.005625 0.003125 0.003125
## [17] 0.001875 0.000000 0.000000 0.000000
##
## $mids
## [1] 44 52 60 68 76 84 92 100 108 116 124 132 140 148 156 164 172 180 188
## [20] 196
##
## $xname
## [1] "Data"
##
## $equidist
## [1] TRUE
##
## attr(,"class")
## [1] "histogram"3.4.6 透過200個常態數字的直方圖揣摩分配的形狀
常態分配是往後許多章節的常客。之前,我們認識了dnorm,現在我們又認識了rnorm(往下看程式碼)。dnorm幫我計算某個範圍、某種常態分配下的機率;而rnorm幫我們從某一個常態分配抽樣。
set.seed(1233) # 設定隨機種子。
# 常態抽樣。並且位移(+4.3)加形變(*30),最後再四捨五入(round)到整數(0)。
DataNorm <- round((rnorm(200) + 4.3) * 30, 0)
stem.leaf(DataNorm, m = 1, unit = 1, trim.outliers = FALSE) # 不厭其煩,再一次看看莖葉圖。## 1 | 2: represents 12
## leaf unit: 1
## n: 200
## 1 0 | 8
## 1 |
## 2 |
## 3 |
## 2 4 | 4
## 5 5 | 088
## 8 6 | 456
## 17 7 | 033677999
## 27 8 | 0012357779
## 38 9 | 12224456679
## 60 10 | 0011222233455566777899
## 85 11 | 0001123345556666677788889
## (27) 12 | 000012334445666667777777899
## 88 13 | 000111334445567779999
## 67 14 | 001122333556677888
## 49 15 | 000111223344556678899
## 28 16 | 2455677788
## 18 17 | 13467
## 13 18 | 0115677
## 6 19 | 68
## 4 20 | 12
## 2 21 | 0
## 22 |
## 1 23 | 4hist(DataNorm) # 讓R決定怎麼畫直方圖。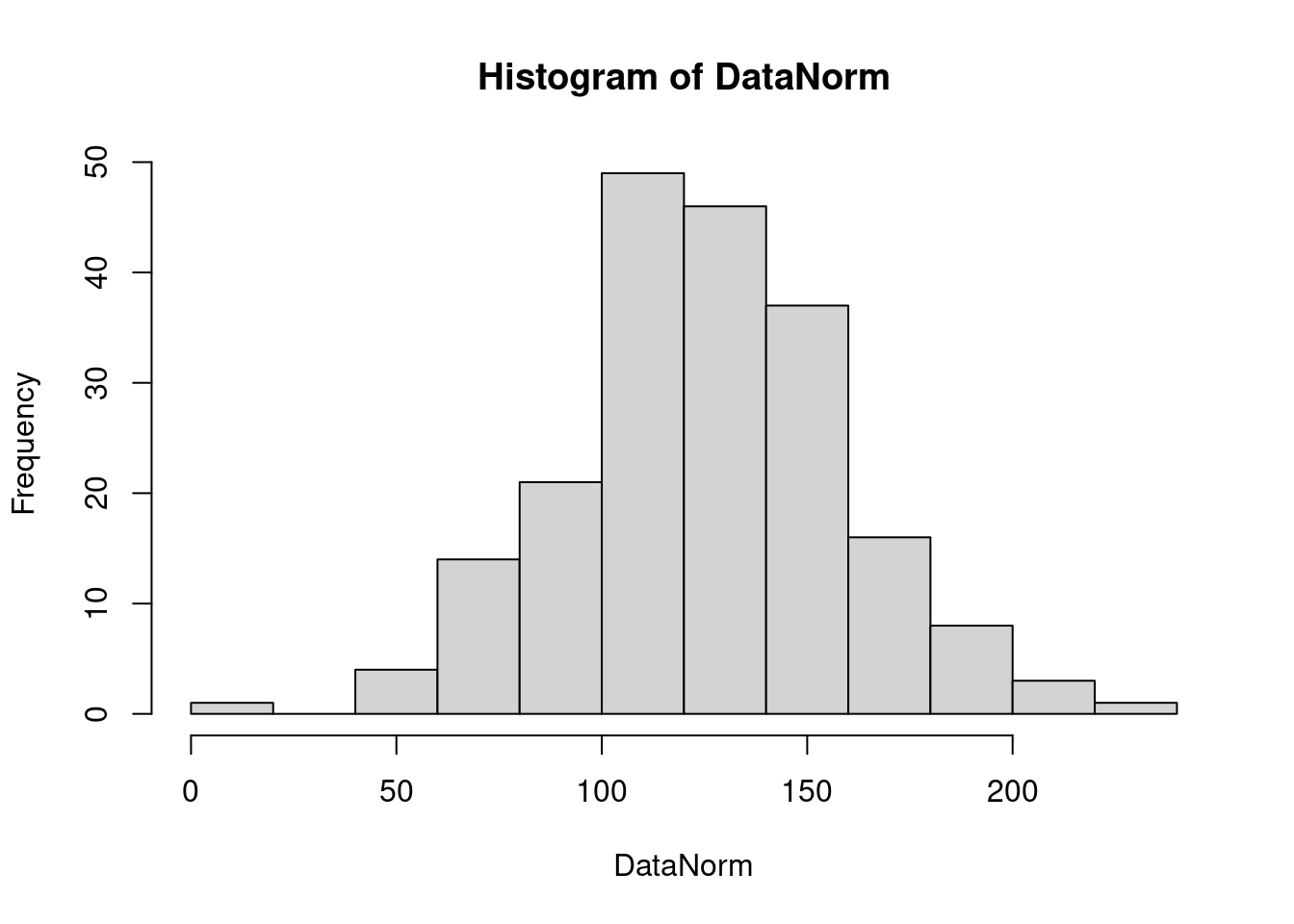
hist(DataNorm, breaks = 10) # 讓我們決定怎麼切範圍。
hist(DataNorm, breaks = 10, col = "blue") # 讓我們也決定顏色。
hist(DataNorm, breaks = 20, col = "blue") # 繼續實驗切點。
hist(DataNorm, breaks = 50, col = "blue") # 繼續實驗切點。
hist(DataNorm, breaks = 100, col = "blue") # 繼續實驗切點。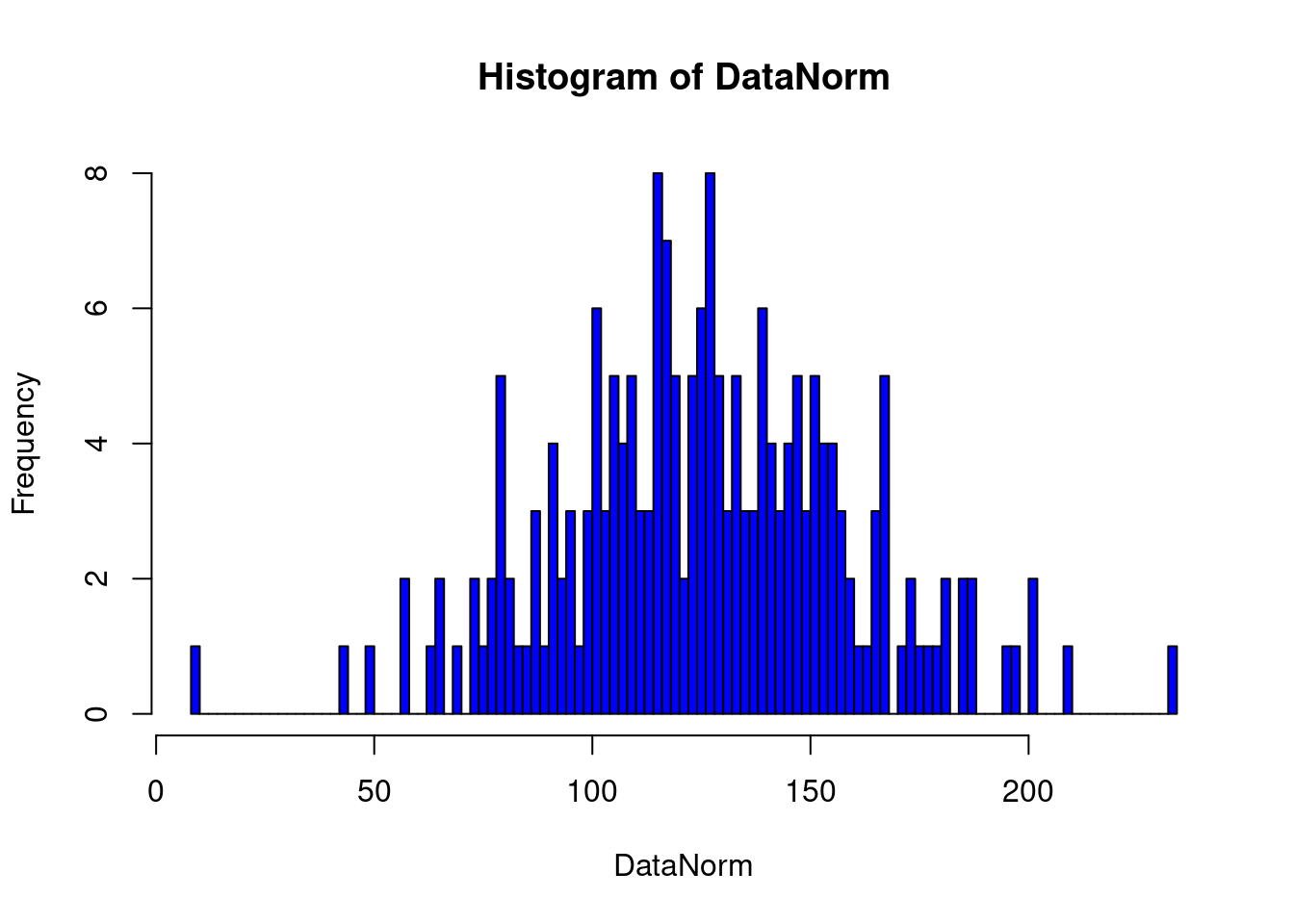
hist(DataNorm, breaks = 100, freq = FALSE) # 讓R顯示相對次數。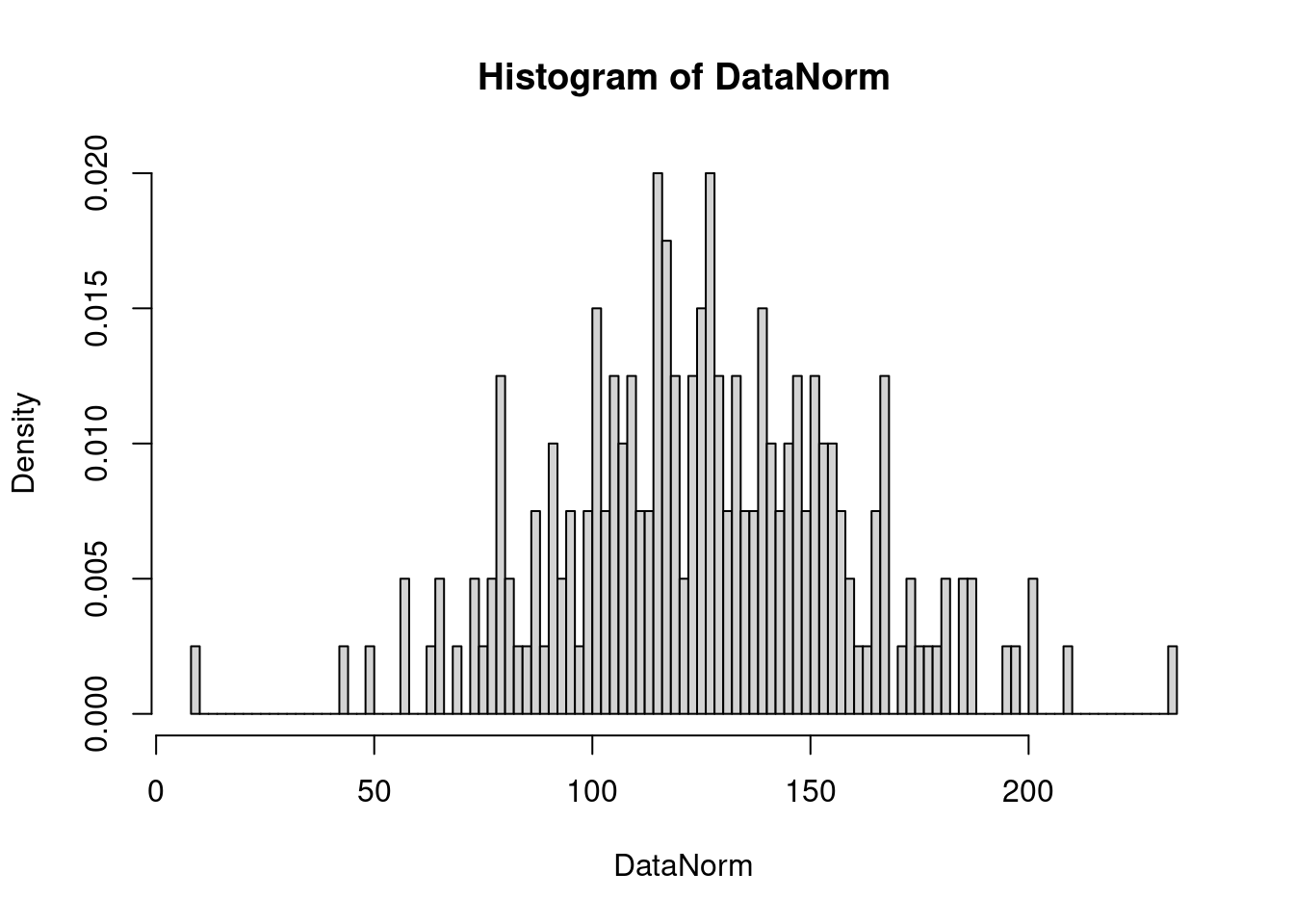
請讀者諸君試著揣摩上述200個常態數字直方圖的形狀,也就是常態分配的形狀,並回答以下問題:
- 一座山,還是兩座山,還是多座山?
- 左右對稱嗎?
- 有很小的數字嗎?
- 有很大的數字嗎?
- 很小的數字很多嗎?
- 很大的數字很多嗎?
回答問題時,請特別注意:上述常態數字直方圖是隨機種子1233的,當我們換了種子,上述的直方圖就會改變。再則,切很細,比如說,「breaks = 100」對於判斷分配的形狀並不利。所以作者個人從以下這一張直方圖
hist(DataNorm) # 讓R決定怎麼畫直方圖。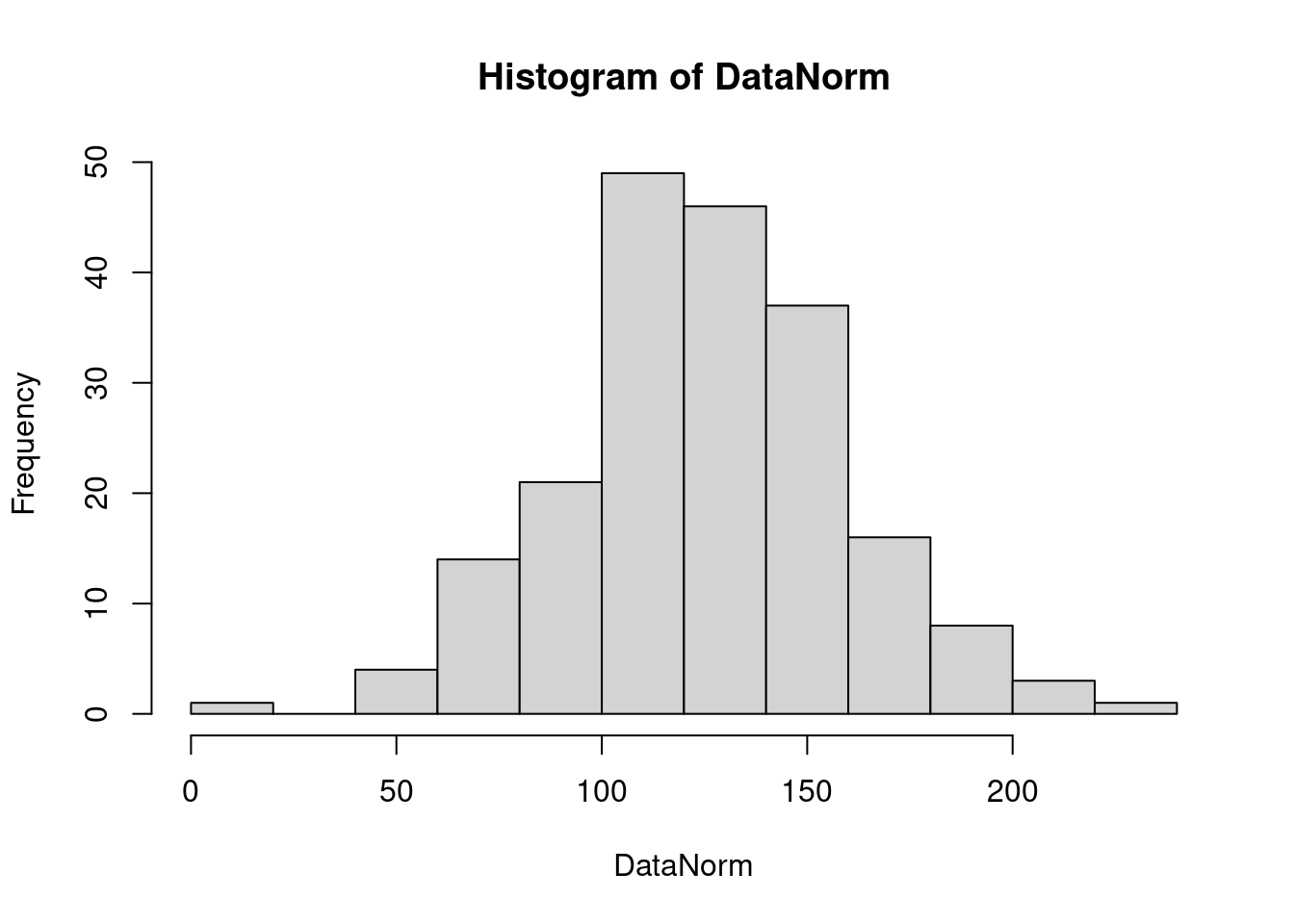
認為:
- 一座山,還是兩座山,還是多座山? —> 一座山。
- 左右對稱嗎? —> 是。
- 有很小的數字嗎? —> 有。
- 有很大的數字嗎? —> 沒有。
- 很小的數字很多嗎? —> 沒有。
- 很大的數字很多嗎? —> 沒有。
以上見解提供給各位參考。
3.5 長條圖
為什麼選讀這個主題,基本上,至少三個理由:
- 見證莖葉圖如何得到長條圖?
- 學習如何透過長條圖得知分配的形狀?
- 學習如何透過長條圖得知某個標籤出現過多少次?
3.5.1 建議優先閱讀:莖葉圖
1900年代,Arthur Bowley倡議莖葉圖這一項技術。
…
讓我們回顧以下這一組數據的莖葉圖:
library(aplpack)
Data <- c(44,46,47,49,63,64,66,68,68,72,72,75,76,81,84,88,106)
stem.leaf(Data, trim.outliers = FALSE)## 1 | 2: represents 12
## leaf unit: 1
## n: 17
## 4 4 | 4679
## 5 |
## (5) 6 | 34688
## 8 7 | 2256
## 4 8 | 148
## 9 |
## 1 10 | 6注意:數字
44跟46同時落入40這一株莖,是因為它們都屬於「40 ~ 49」這一個範圍內的整數。
3.5.2 再看一次阿拉伯數字的莖葉圖
有了「aplpack」相助,我們再一次看看(雖然已經不知道看了多少次了)阿拉伯數字,0,1,2,3,4,5,6,7,8,9的莖葉圖長什麼樣子?
3.5.2.1 如果我們決定把全部阿拉伯數字放在「一株莖(m = 1)」,結果是
stem.leaf(0:9, m = 1, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## (10) 0 | 01234567893.5.2.2 如果我們決定把全部阿拉伯數字放在「兩株莖(m = 2)」,結果是
stem.leaf(0:9, m = 2, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## (5) 0* | 01234
## (5) 0. | 567893.5.3 假如每一個阿拉伯數字都代表著某一家超市某件商品
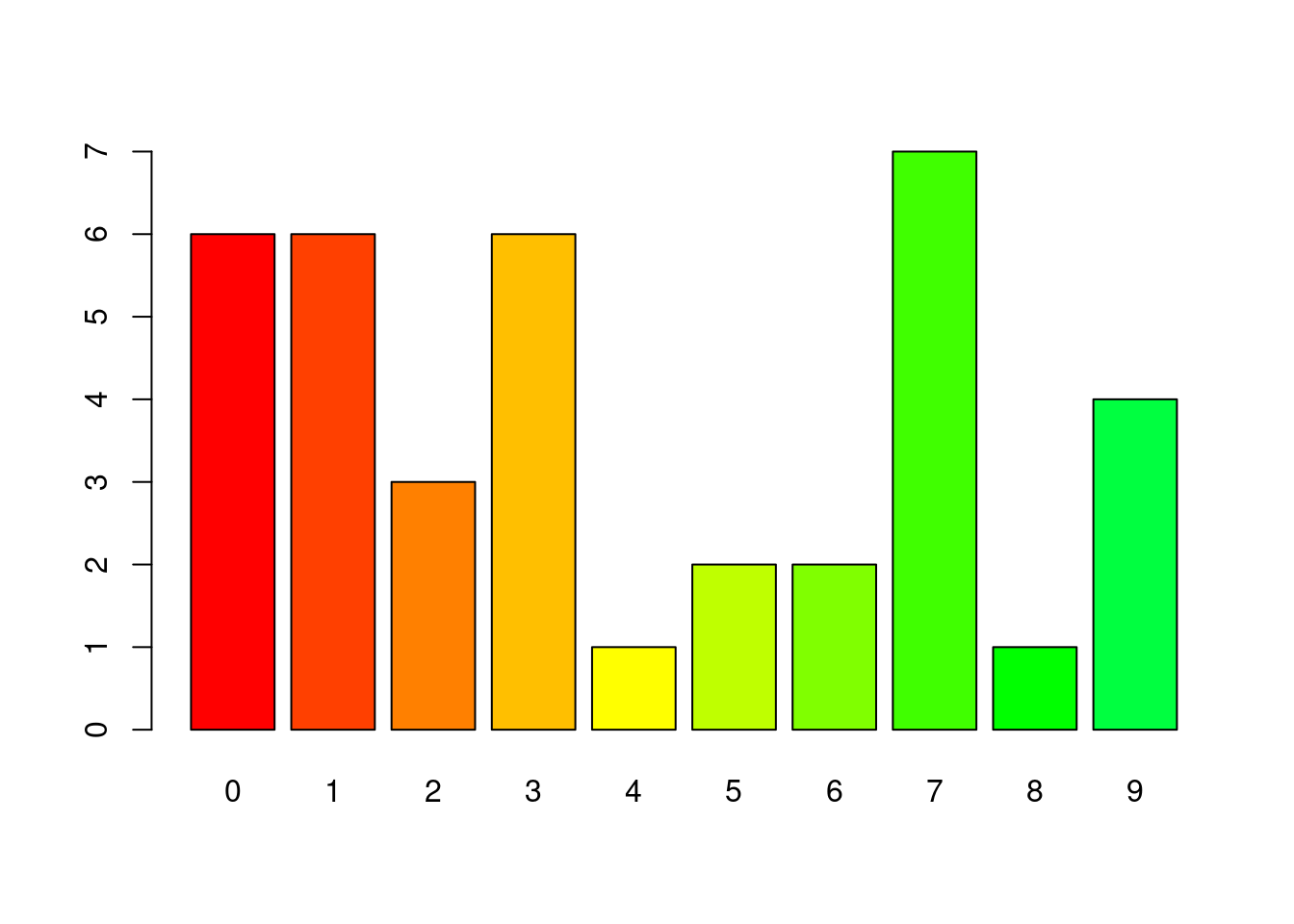
3.5.3.1 第一張莖葉圖
stem.leaf(0:9, m = 1, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## (10) 0 | 01234567893.5.3.2 第二張莖葉圖
stem.leaf(0:9, m = 2, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## (5) 0* | 01234
## (5) 0. | 567893.5.3.3 第三張莖葉圖
stem.leaf(0:9, m = 5, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## 2 0* | 01
## 4 t | 23
## (2) f | 45
## 4 s | 67
## 2 0. | 893.5.3.4 第四張莖葉圖
stem.leaf(0:9, m = 10, unit = 1)## 1 | 2: represents 12
## leaf unit: 1
## n: 10
## 1 0 | 0
## 2 0 | 1
## 3 0 | 2
## 4 0 | 3
## (1) 0 | 4
## (1) 0 | 5
## 4 0 | 6
## 3 0 | 7
## 2 0 | 8
## 1 0 | 93.5.3.5 哪一張才是正確的莖葉圖?
上面哪一張都不對,只有這一張才對!
為什麼?
stem.leaf(0:9, m = 1, unit = 0.1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 10
## 1 0 | 0
## 2 1 | 0
## 3 2 | 0
## 4 3 | 0
## (1) 4 | 0
## (1) 5 | 0
## 4 6 | 0
## 3 7 | 0
## 2 8 | 0
## 1 9 | 0因為
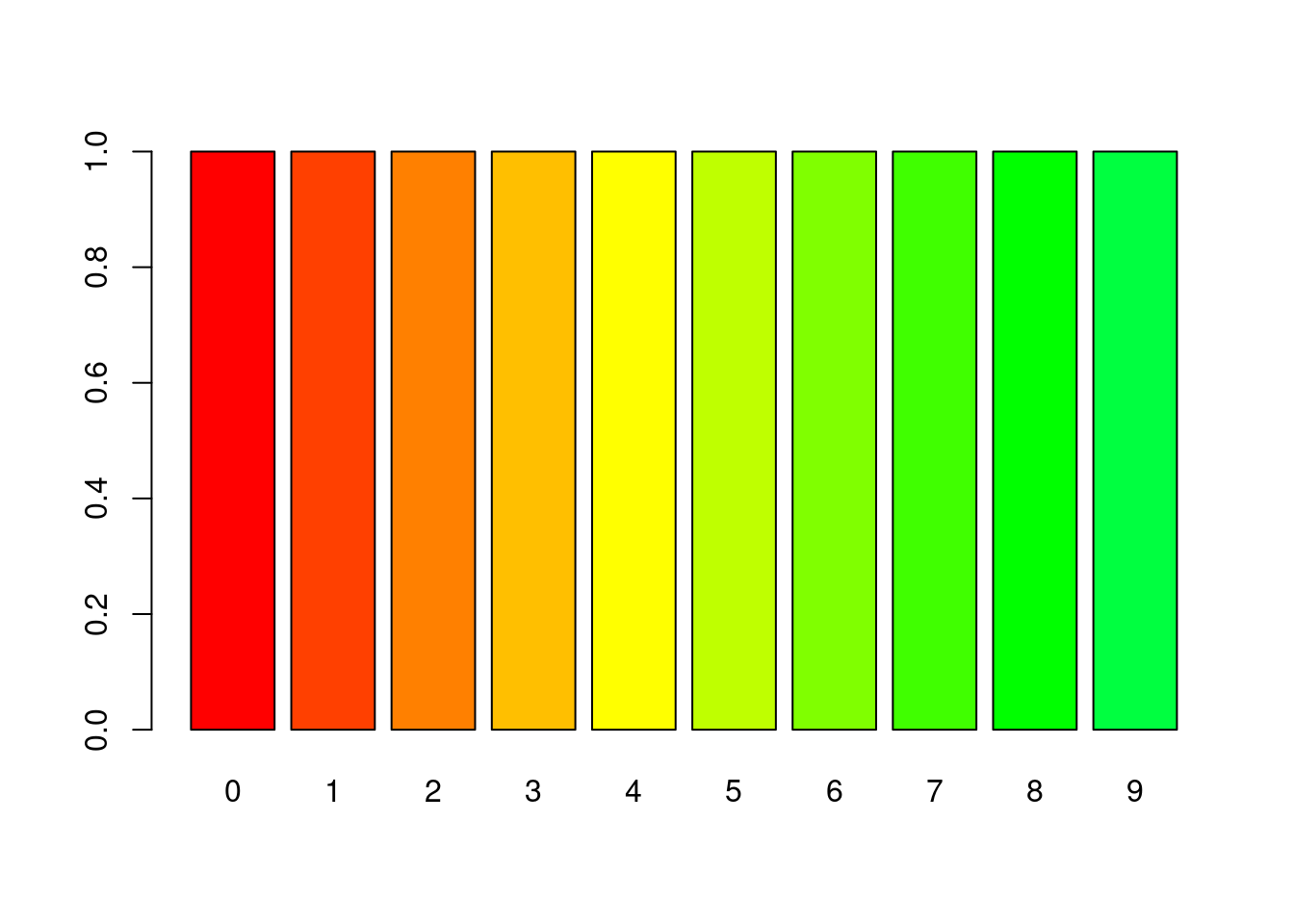
這時候,只有上面這一張圖是對的。因為,阿拉伯數字,0, 1, 2, 3, 4, 5, 6, 7, 8, 9都是商品的代號,它們之間的順序這時候或許有意義、或許沒意義,但無論如何都不應該被放入同一株莖裡。現在,莖放代號、葉子都是以0表示,非常寫意!因為幾個0就代表該商品有幾個!請繼續看這一個例子:
set.seed(1233)
stem.leaf(sample(0:9, 38, replace = TRUE), m = 1, unit = 0.1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 38
## 6 0 | 000000
## 12 1 | 000000
## 15 2 | 000
## (6) 3 | 000000
## 17 4 | 0
## 16 5 | 00
## 14 6 | 00
## 12 7 | 0000000
## 5 8 | 0
## 4 9 | 0000如果這時候「
stem.leaf」可以給我們「次數分配」而不是「上下累加次數分配」就更棒了!
3.5.4 隨機挑38個阿拉伯數字的長條圖
3.5.4.2 (第二句)先看過莖葉圖
stem.leaf(x, m = 1, unit = 0.1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 38
## 6 0 | 000000
## 12 1 | 000000
## 15 2 | 000
## (6) 3 | 000000
## 17 4 | 0
## 16 5 | 00
## 14 6 | 00
## 12 7 | 0000000
## 5 8 | 0
## 4 9 | 00003.5.5 更多商品的長條圖
set.seed(1233)
x <- sample(0:19, 38, replace = TRUE)
stem.leaf(x, m = 1, unit = 0.1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 38
## 4 0 | 0000
## 9 1 | 00000
## 2 |
## 11 3 | 00
## 4 |
## 5 |
## 6 |
## 15 7 | 0000
## 8 |
## 17 9 | 00
## 18 10 | 0
## (4) 11 | 0000
## 16 12 | 00
## 14 13 | 0
## 13 14 | 00
## 11 15 | 0
## 10 16 | 00
## 8 17 | 0
## 7 18 | 000
## 4 19 | 0000barplot(table(x))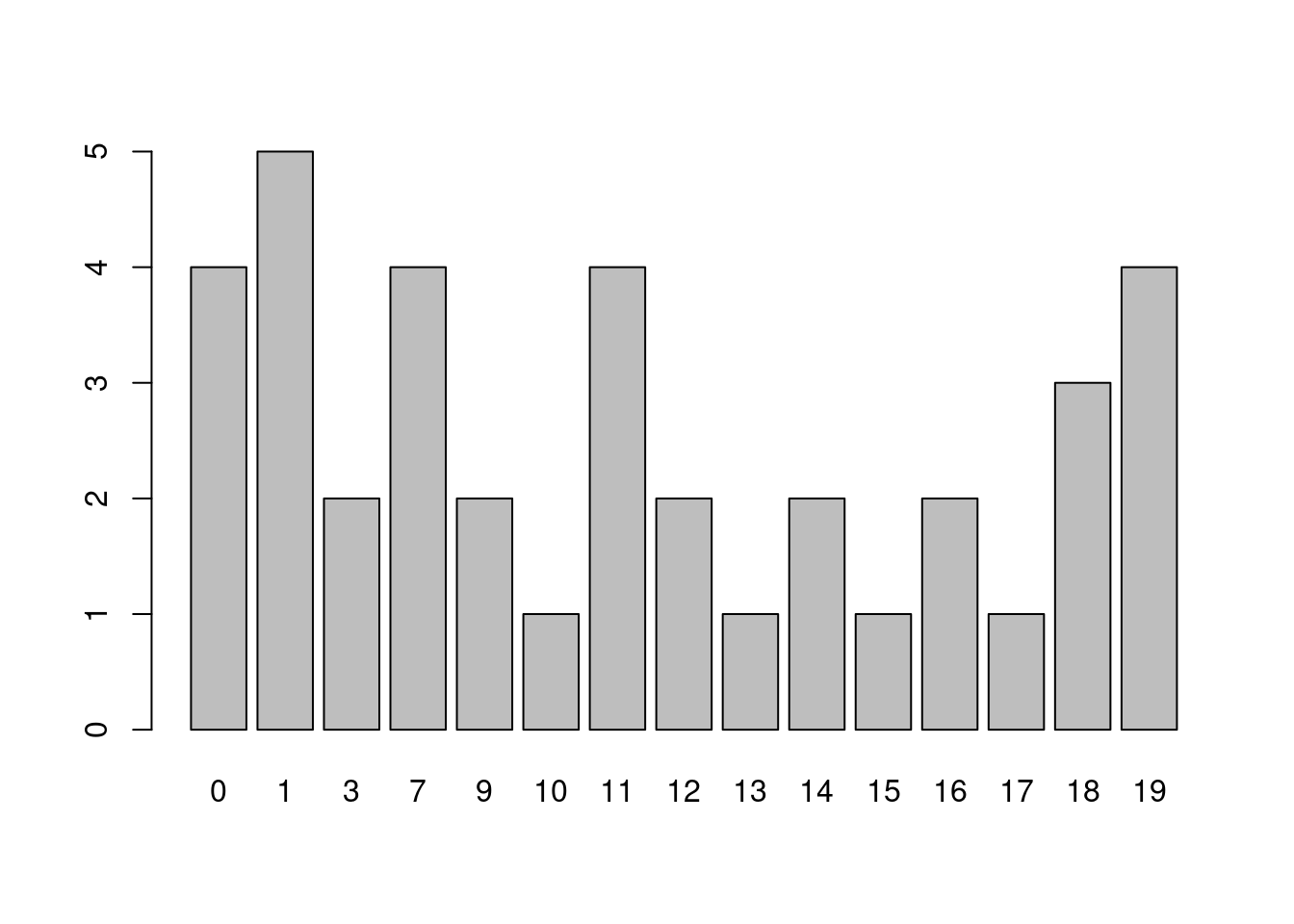
3.5.5.1 長條圖無法複刻莖葉圖了!缺了那些沒葉子的樹莖,怎麼辦?
stem.leaf(x, m = 1, unit = 0.1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 38
## 4 0 | 0000
## 9 1 | 00000
## 2 |
## 11 3 | 00
## 4 |
## 5 |
## 6 |
## 15 7 | 0000
## 8 |
## 17 9 | 00
## 18 10 | 0
## (4) 11 | 0000
## 16 12 | 00
## 14 13 | 0
## 13 14 | 00
## 11 15 | 0
## 10 16 | 00
## 8 17 | 0
## 7 18 | 000
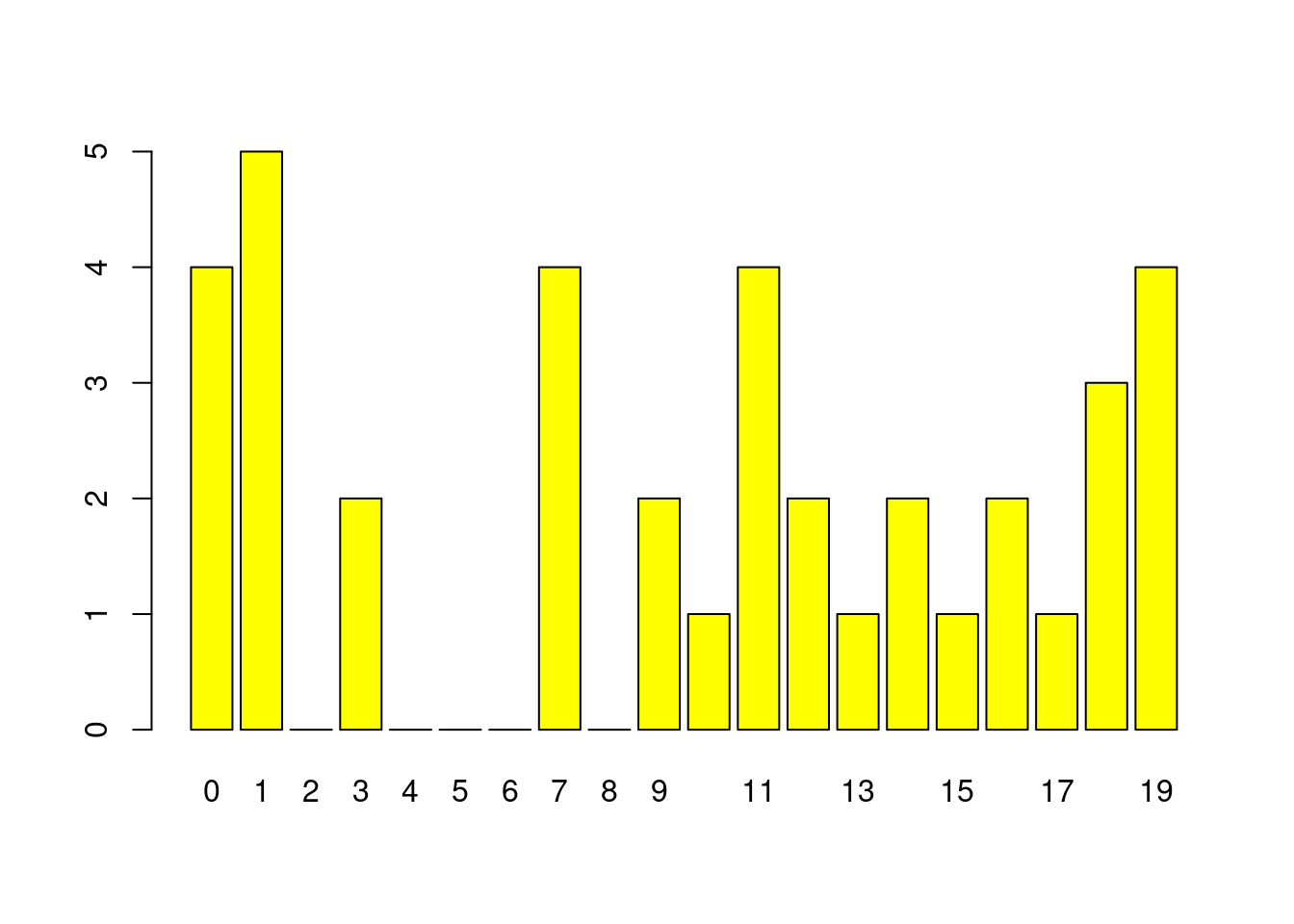
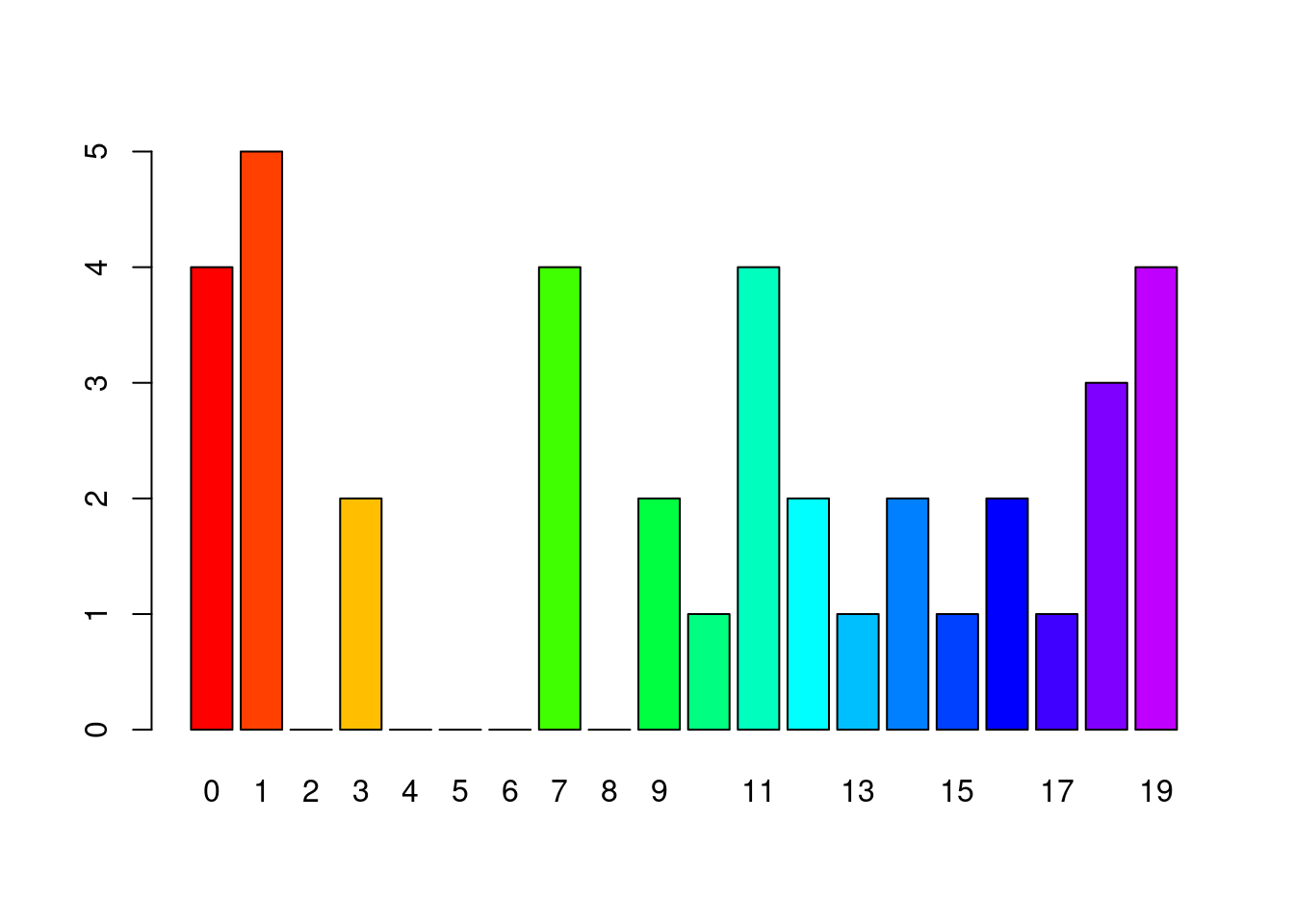
## 4 19 | 0000barplot(table(factor(x, levels = 0:19)))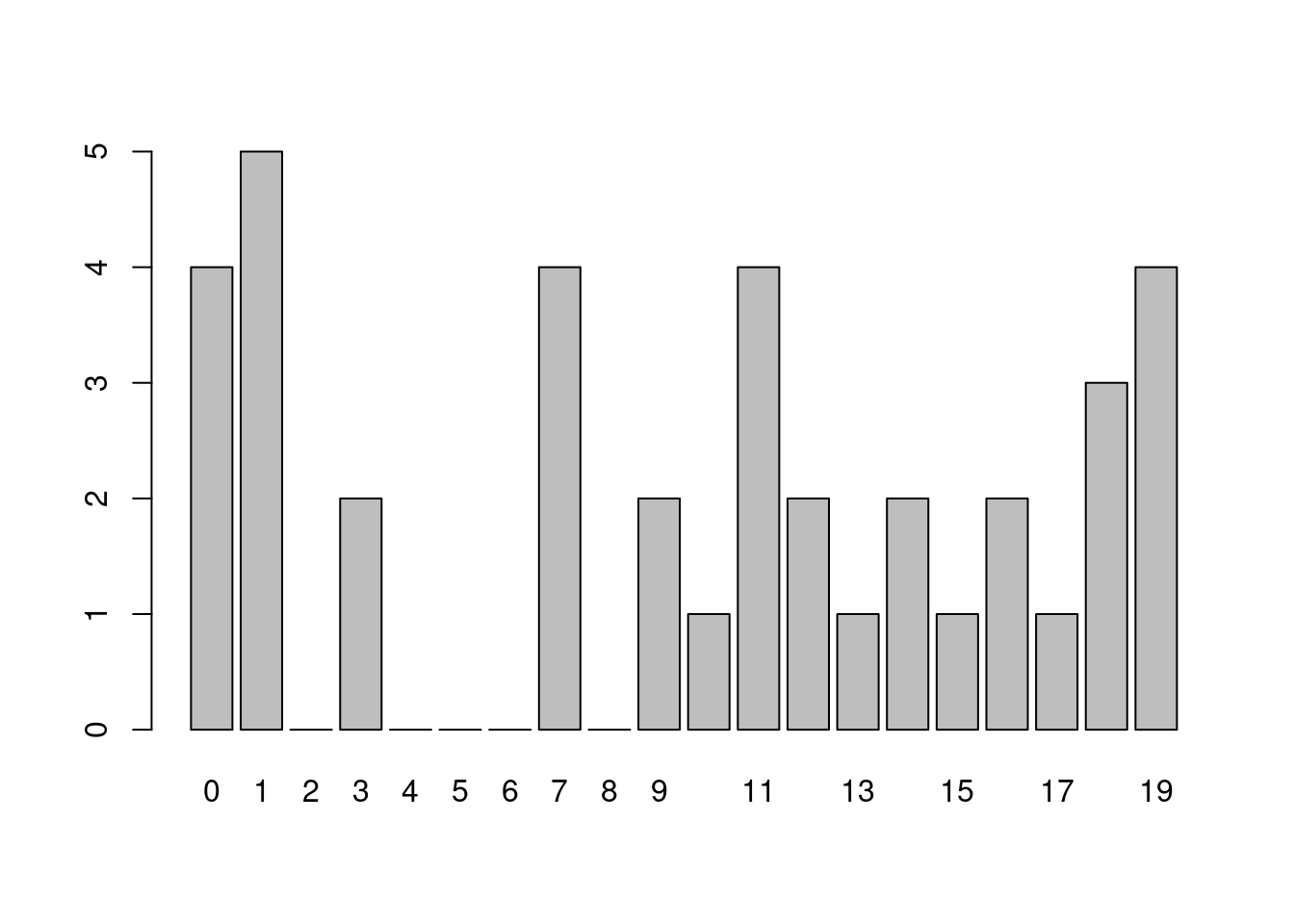
這時候「factor(x, levels = 0:19)」就非常好用,因為把x的數字本質修為文字,而且定義文字的範圍(levels = 0:19)。請讀者諸君持續關注「factor」的魅力。
3.6 圓餅圖
為什麼選讀這個主題,基本上,至少三個理由:
- 見證長條圖如何得到圓餅圖?
- 學習如何透過圓餅圖得知分配的形狀?
- 學習如何透過圓餅圖得知某個數線範圍內有多少個數字?
3.6.1 建議優先閱讀:莖葉圖與長條圖
1900年代,Arthur Bowley倡議莖葉圖這一項技術。
…
讓我們回顧以下這一組38個阿拉伯數字的莖葉圖跟長條圖:
3.6.1.2 (第二步) 準備數字
set.seed(1233)
x <- sample(0:9, 38, replace = TRUE)
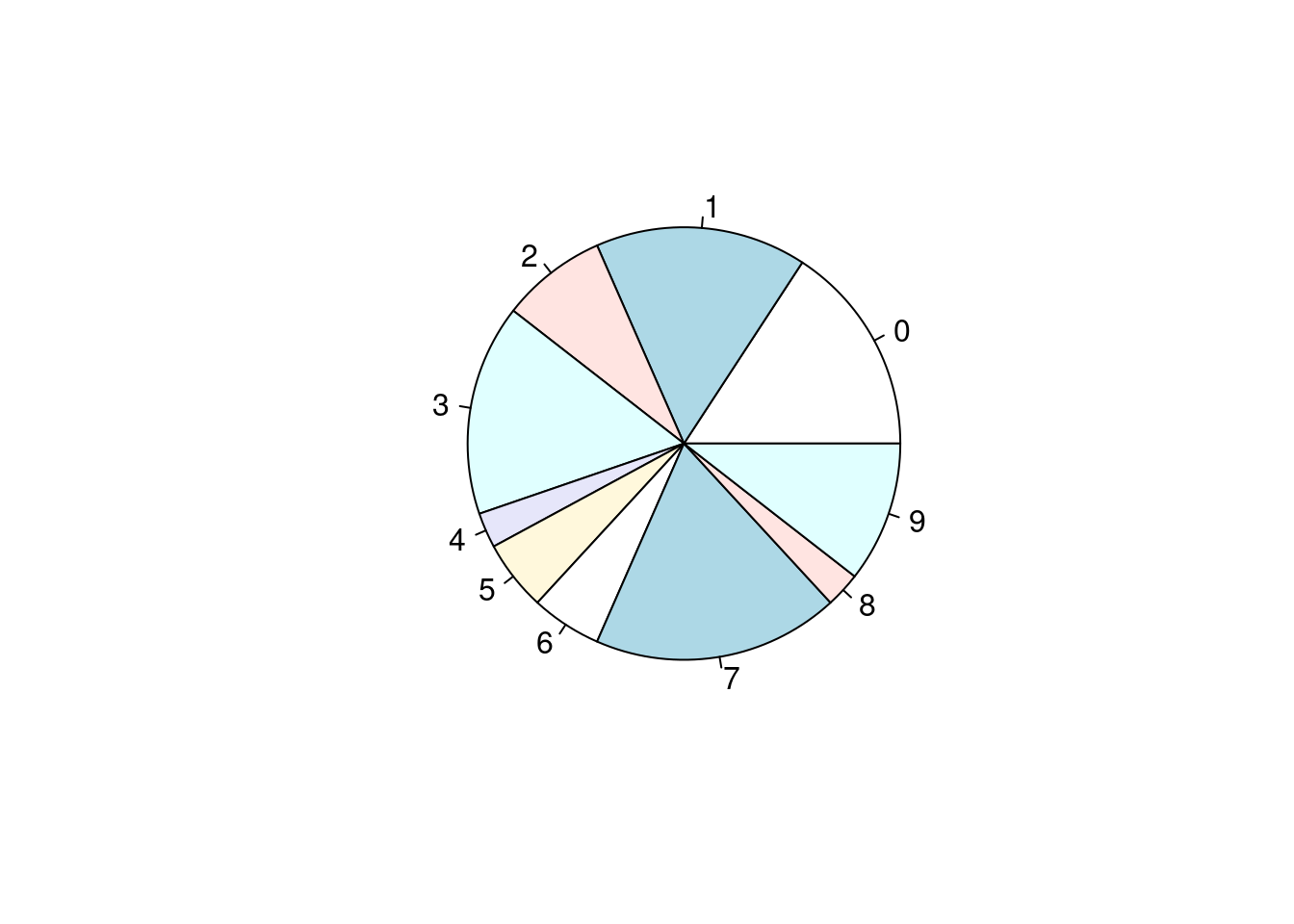
x## [1] 7 9 1 0 0 1 8 5 9 3 6 7 5 9 3 7 2 0 0 2 3 7 4 7 6 9 3 1 1 2 7 7 0 3 1 0 3 13.6.2 這一組38個阿拉伯數字的圓餅圖
3.6.3 甜甜圈:另一種圓餅圖
3.6.3.1 第一層的圓餅圖
# 第一層。
pie(table(x),
clockwise = TRUE,
radius = 0.8,
border = "white",
col = rainbow(24))
3.6.3.2 靜止同一張畫布
# 第一層。
pie(table(x),
clockwise = TRUE,
radius = 0.8,
border = "white",
col = rainbow(24))
# 加這一句R文。
par(new = TRUE)3.6.3.3 疊第二層
# 第一層。
pie(table(x),
clockwise = TRUE,
radius = 0.8,
border = "white",
col = rainbow(24))
# 加這一句R文。
par(new = TRUE)
# 第二層。
pie(1,
clockwise = TRUE,
radius = 0.6,
border = "white",
col = "white",
labels = "")
3.7 時間序列圖
為什麼選讀這個主題,基本上,至少三個理由:
3.7.1 建議優先閱讀:長條圖
先看隨機挑38個阿拉伯數字的長條圖。
- 準備數字
set.seed(1233)
x <- sample(0:9, 38, replace = TRUE)- 先看過莖葉圖
library(aplpack)
stem.leaf(x, m = 1, unit = 0.1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 38
## 6 0 | 000000
## 12 1 | 000000
## 15 2 | 000
## (6) 3 | 000000
## 17 4 | 0
## 16 5 | 00
## 14 6 | 00
## 12 7 | 0000000
## 5 8 | 0
## 4 9 | 0000- 再看過長條圖
barplot(table(x))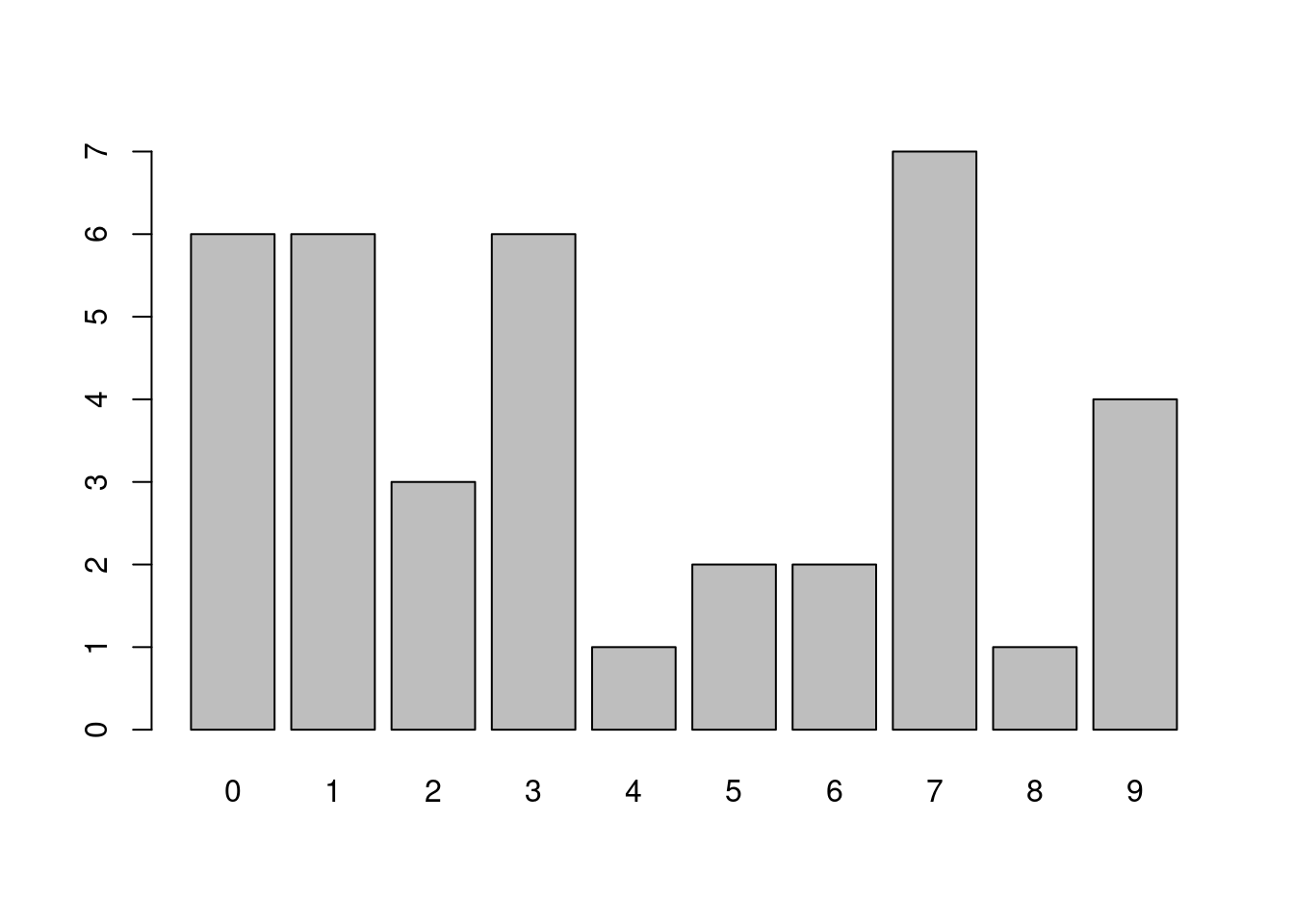
各位請看,跟莖葉圖一模一樣,只是視角不一樣。莖葉圖從上而下、長條圖從左而右。
3.7.2 時間序列範例:AirPassengers
3.7.2.1 時間序列圖
library(datasets)data("AirPassengers")length(AirPassengers)## [1] 144str(AirPassengers)## Time-Series [1:144] from 1949 to 1961: 112 118 132 129 121 135 148 148 136 119 ...head(AirPassengers)## [1] 112 118 132 129 121 135tail(AirPassengers)## [1] 622 606 508 461 390 432AirPassengers[1]## [1] 112plot(AirPassengers)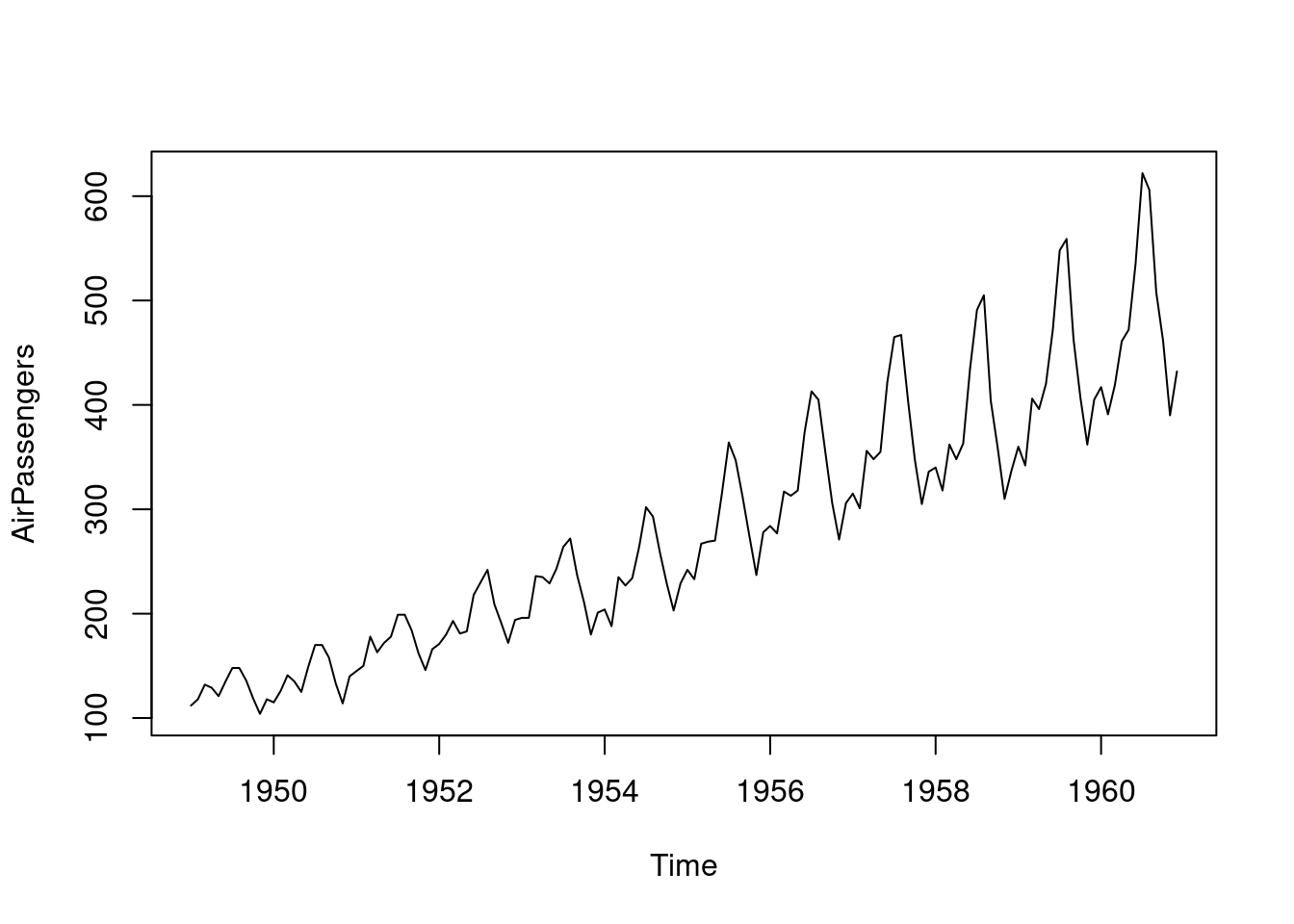
3.7.2.2 另一種視角:時間序列的基本資料
x <- AirPassengers
x## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 112 118 132 129 121 135 148 148 136 119 104 118
## 1950 115 126 141 135 125 149 170 170 158 133 114 140
## 1951 145 150 178 163 172 178 199 199 184 162 146 166
## 1952 171 180 193 181 183 218 230 242 209 191 172 194
## 1953 196 196 236 235 229 243 264 272 237 211 180 201
## 1954 204 188 235 227 234 264 302 293 259 229 203 229
## 1955 242 233 267 269 270 315 364 347 312 274 237 278
## 1956 284 277 317 313 318 374 413 405 355 306 271 306
## 1957 315 301 356 348 355 422 465 467 404 347 305 336
## 1958 340 318 362 348 363 435 491 505 404 359 310 337
## 1959 360 342 406 396 420 472 548 559 463 407 362 405
## 1960 417 391 419 461 472 535 622 606 508 461 390 432class(x)## [1] "ts"is.ts(x)## [1] TRUEnames(x)## NULLtime(x)## Jan Feb Mar Apr May Jun Jul Aug
## 1949 1949.000 1949.083 1949.167 1949.250 1949.333 1949.417 1949.500 1949.583
## 1950 1950.000 1950.083 1950.167 1950.250 1950.333 1950.417 1950.500 1950.583
## 1951 1951.000 1951.083 1951.167 1951.250 1951.333 1951.417 1951.500 1951.583
## 1952 1952.000 1952.083 1952.167 1952.250 1952.333 1952.417 1952.500 1952.583
## 1953 1953.000 1953.083 1953.167 1953.250 1953.333 1953.417 1953.500 1953.583
## 1954 1954.000 1954.083 1954.167 1954.250 1954.333 1954.417 1954.500 1954.583
## 1955 1955.000 1955.083 1955.167 1955.250 1955.333 1955.417 1955.500 1955.583
## 1956 1956.000 1956.083 1956.167 1956.250 1956.333 1956.417 1956.500 1956.583
## 1957 1957.000 1957.083 1957.167 1957.250 1957.333 1957.417 1957.500 1957.583
## 1958 1958.000 1958.083 1958.167 1958.250 1958.333 1958.417 1958.500 1958.583
## 1959 1959.000 1959.083 1959.167 1959.250 1959.333 1959.417 1959.500 1959.583
## 1960 1960.000 1960.083 1960.167 1960.250 1960.333 1960.417 1960.500 1960.583
## Sep Oct Nov Dec
## 1949 1949.667 1949.750 1949.833 1949.917
## 1950 1950.667 1950.750 1950.833 1950.917
## 1951 1951.667 1951.750 1951.833 1951.917
## 1952 1952.667 1952.750 1952.833 1952.917
## 1953 1953.667 1953.750 1953.833 1953.917
## 1954 1954.667 1954.750 1954.833 1954.917
## 1955 1955.667 1955.750 1955.833 1955.917
## 1956 1956.667 1956.750 1956.833 1956.917
## 1957 1957.667 1957.750 1957.833 1957.917
## 1958 1958.667 1958.750 1958.833 1958.917
## 1959 1959.667 1959.750 1959.833 1959.917
## 1960 1960.667 1960.750 1960.833 1960.917timestamp(x)## ##------ 112 ------##
## ##------ 118 ------##
## ##------ 132 ------##
## ##------ 129 ------##
## ##------ 121 ------##
## ##------ 135 ------##
## ##------ 148 ------##
## ##------ 148 ------##
## ##------ 136 ------##
## ##------ 119 ------##
## ##------ 104 ------##
## ##------ 118 ------##
## ##------ 115 ------##
## ##------ 126 ------##
## ##------ 141 ------##
## ##------ 135 ------##
## ##------ 125 ------##
## ##------ 149 ------##
## ##------ 170 ------##
## ##------ 170 ------##
## ##------ 158 ------##
## ##------ 133 ------##
## ##------ 114 ------##
## ##------ 140 ------##
## ##------ 145 ------##
## ##------ 150 ------##
## ##------ 178 ------##
## ##------ 163 ------##
## ##------ 172 ------##
## ##------ 178 ------##
## ##------ 199 ------##
## ##------ 199 ------##
## ##------ 184 ------##
## ##------ 162 ------##
## ##------ 146 ------##
## ##------ 166 ------##
## ##------ 171 ------##
## ##------ 180 ------##
## ##------ 193 ------##
## ##------ 181 ------##
## ##------ 183 ------##
## ##------ 218 ------##
## ##------ 230 ------##
## ##------ 242 ------##
## ##------ 209 ------##
## ##------ 191 ------##
## ##------ 172 ------##
## ##------ 194 ------##
## ##------ 196 ------##
## ##------ 196 ------##
## ##------ 236 ------##
## ##------ 235 ------##
## ##------ 229 ------##
## ##------ 243 ------##
## ##------ 264 ------##
## ##------ 272 ------##
## ##------ 237 ------##
## ##------ 211 ------##
## ##------ 180 ------##
## ##------ 201 ------##
## ##------ 204 ------##
## ##------ 188 ------##
## ##------ 235 ------##
## ##------ 227 ------##
## ##------ 234 ------##
## ##------ 264 ------##
## ##------ 302 ------##
## ##------ 293 ------##
## ##------ 259 ------##
## ##------ 229 ------##
## ##------ 203 ------##
## ##------ 229 ------##
## ##------ 242 ------##
## ##------ 233 ------##
## ##------ 267 ------##
## ##------ 269 ------##
## ##------ 270 ------##
## ##------ 315 ------##
## ##------ 364 ------##
## ##------ 347 ------##
## ##------ 312 ------##
## ##------ 274 ------##
## ##------ 237 ------##
## ##------ 278 ------##
## ##------ 284 ------##
## ##------ 277 ------##
## ##------ 317 ------##
## ##------ 313 ------##
## ##------ 318 ------##
## ##------ 374 ------##
## ##------ 413 ------##
## ##------ 405 ------##
## ##------ 355 ------##
## ##------ 306 ------##
## ##------ 271 ------##
## ##------ 306 ------##
## ##------ 315 ------##
## ##------ 301 ------##
## ##------ 356 ------##
## ##------ 348 ------##
## ##------ 355 ------##
## ##------ 422 ------##
## ##------ 465 ------##
## ##------ 467 ------##
## ##------ 404 ------##
## ##------ 347 ------##
## ##------ 305 ------##
## ##------ 336 ------##
## ##------ 340 ------##
## ##------ 318 ------##
## ##------ 362 ------##
## ##------ 348 ------##
## ##------ 363 ------##
## ##------ 435 ------##
## ##------ 491 ------##
## ##------ 505 ------##
## ##------ 404 ------##
## ##------ 359 ------##
## ##------ 310 ------##
## ##------ 337 ------##
## ##------ 360 ------##
## ##------ 342 ------##
## ##------ 406 ------##
## ##------ 396 ------##
## ##------ 420 ------##
## ##------ 472 ------##
## ##------ 548 ------##
## ##------ 559 ------##
## ##------ 463 ------##
## ##------ 407 ------##
## ##------ 362 ------##
## ##------ 405 ------##
## ##------ 417 ------##
## ##------ 391 ------##
## ##------ 419 ------##
## ##------ 461 ------##
## ##------ 472 ------##
## ##------ 535 ------##
## ##------ 622 ------##
## ##------ 606 ------##
## ##------ 508 ------##
## ##------ 461 ------##
## ##------ 390 ------##
## ##------ 432 ------##start(x)## [1] 1949 1end(x)## [1] 1960 12window(x)## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 112 118 132 129 121 135 148 148 136 119 104 118
## 1950 115 126 141 135 125 149 170 170 158 133 114 140
## 1951 145 150 178 163 172 178 199 199 184 162 146 166
## 1952 171 180 193 181 183 218 230 242 209 191 172 194
## 1953 196 196 236 235 229 243 264 272 237 211 180 201
## 1954 204 188 235 227 234 264 302 293 259 229 203 229
## 1955 242 233 267 269 270 315 364 347 312 274 237 278
## 1956 284 277 317 313 318 374 413 405 355 306 271 306
## 1957 315 301 356 348 355 422 465 467 404 347 305 336
## 1958 340 318 362 348 363 435 491 505 404 359 310 337
## 1959 360 342 406 396 420 472 548 559 463 407 362 405
## 1960 417 391 419 461 472 535 622 606 508 461 390 4323.7.2.3 另一種視角:抓前面十二個數字
x <- AirPassengers[1:12]
x## [1] 112 118 132 129 121 135 148 148 136 119 104 118class(x)## [1] "numeric"is.ts(x)## [1] FALSEnames(x)## NULLtime(x)## [1] 1 2 3 4 5 6 7 8 9 10 11 12
## attr(,"tsp")
## [1] 1 12 1timestamp(x)## ##------ 112 ------##
## ##------ 118 ------##
## ##------ 132 ------##
## ##------ 129 ------##
## ##------ 121 ------##
## ##------ 135 ------##
## ##------ 148 ------##
## ##------ 148 ------##
## ##------ 136 ------##
## ##------ 119 ------##
## ##------ 104 ------##
## ##------ 118 ------##start(x)## [1] 1 1end(x)## [1] 12 1window(x)## [1] 112 118 132 129 121 135 148 148 136 119 104 118
## attr(,"tsp")
## [1] 1 12 13.7.2.4 另一種視角:抓前面十二個數字
x <- window(AirPassengers, c(1949,1), c(1949,12))
x## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 112 118 132 129 121 135 148 148 136 119 104 118class(x)## [1] "ts"is.ts(x)## [1] TRUEnames(x)## NULLtime(x)## Jan Feb Mar Apr May Jun Jul Aug
## 1949 1949.000 1949.083 1949.167 1949.250 1949.333 1949.417 1949.500 1949.583
## Sep Oct Nov Dec
## 1949 1949.667 1949.750 1949.833 1949.917timestamp(x)## ##------ 112 ------##
## ##------ 118 ------##
## ##------ 132 ------##
## ##------ 129 ------##
## ##------ 121 ------##
## ##------ 135 ------##
## ##------ 148 ------##
## ##------ 148 ------##
## ##------ 136 ------##
## ##------ 119 ------##
## ##------ 104 ------##
## ##------ 118 ------##start(x)## [1] 1949 1end(x)## [1] 1949 12window(x)## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 112 118 132 129 121 135 148 148 136 119 104 1183.7.3 比較時間序列的莖葉圖與時間序列圖
x <- window(AirPassengers, c(1949,1), c(1949,12)) - 100
x## Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1949 12 18 32 29 21 35 48 48 36 19 4 18y <- rep(1:12, x)
y## [1] 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2
## [26] 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
## [51] 3 3 3 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4 4 4 4 4
## [76] 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 5 5 5 5 5
## [101] 5 5 5 5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 6 6 6 6
## [126] 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 7 7 7
## [151] 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7
## [176] 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 8 8 8 8 8
## [201] 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8
## [226] 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 9 9 9 9 9 9 9
## [251] 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
## [276] 9 9 9 9 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 11 11
## [301] 11 11 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12 12stem.leaf(y, m = 1, unit = 0.1)## 1 | 2: represents 1.2
## leaf unit: 0.1
## n: 320
## 12 1 | 000000000000
## 30 2 | 000000000000000000
## 62 3 | 00000000000000000000000000000000
## 91 4 | 00000000000000000000000000000
## 112 5 | 000000000000000000000
## 147 6 | 00000000000000000000000000000000000
## (48) 7 | 000000000000000000000000000000000000000000000000
## 125 8 | 000000000000000000000000000000000000000000000000
## 77 9 | 000000000000000000000000000000000000
## 41 10 | 0000000000000000000
## 22 11 | 0000
## 18 12 | 000000000000000000plot(x, type = "b", ylim = c(0, 55))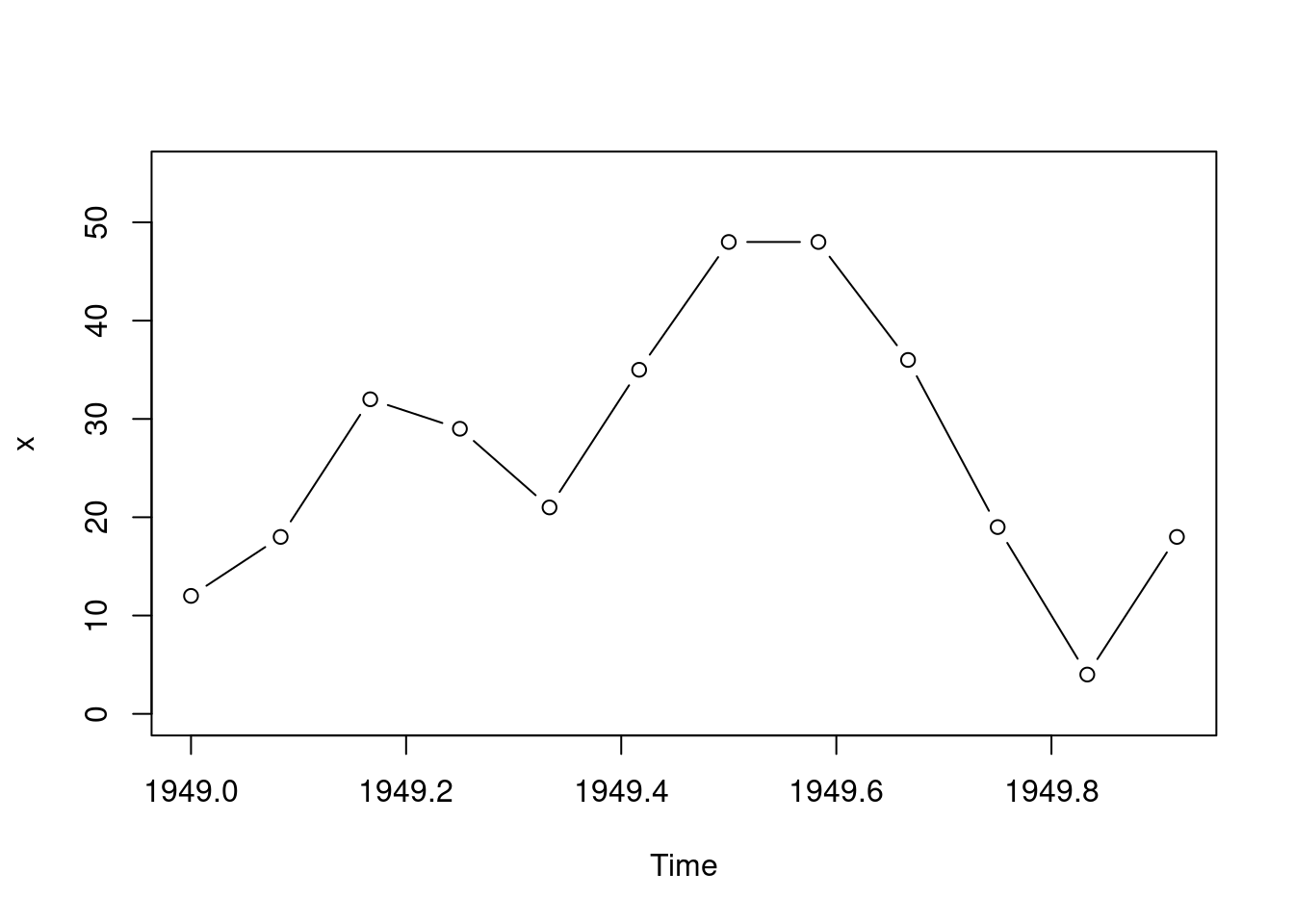
請注意,觀察時的視角。