Chapter 8 發現常態機率模型談抽樣分配
我們繼續談「分配」。
說到「分」,最簡單的「分」就是「一分為二」。為此,人類發明了最簡單的「伯努利分配」。「伯努利分配」定義了「二取一」的機率分配。這裡的「二」,只要給「兩個足以區分彼此的符號」即可,諸如,「H、T」、「人頭、梅花」、「成功、失敗」、「Success、Failure」。有了「伯努利分配」,人類想知道「成功幾次的機率」,於是乎「把許許多多個獨立的伯努利分配加起來」得到了「二項分配」,只要這些「伯努利分配」彼此之間是「獨立的」。有了「二項分配」,數學家發現如果把「許許多多」一直放大,直到「無限大」,「二項分配」變出「常態分配」。數學家還發現,「把許許多多個彼此獨立的常態分配加起來」還是「常態分配」。有了這一個數學上的性質、定理,我們可以得到
把許許多多個彼此獨立的常態分配加起來之後取平均的機率分配是「常態分配」。
後來,更多數學家研究「各種許許多多個機率分配加起來之後取平均的機率分配」,造就了最重要的里程碑「中央極限定理」。有了這個橋梁式的「中央極限定理」,讓我們「猜測某一個分配的平均數」變成可能!基本上,「中央極限定理」的樣子是
\[\bar X \sim N(\mu, (\frac{\sigma}{\sqrt{n}})^2)\]
有了「中央極限定理」之後,有一位好奇心非常強烈的啤酒工廠工程師,找到了「學生t分配」,解決了「因為無法得知\(\sigma\)的真實值,而無法得知標準化\(\bar X\)之後的機率分配」這一項世紀難題。所謂標準化\(\bar X\)是這個意思:
\[\frac{\bar X - \mu}{\frac{\sigma}{\sqrt{n}}}\]
或是這個意思
\[\frac{\bar X - \mu}{\frac{s}{\sqrt{n}}}\]
到此,我們知道了最重要的「機率分配演變史」,也讓我們可以從「敘述統計學逃脫」,繼續往前,進入「推論統計學」的世界。我們現在,在「發現常態機率模型談理論分配」這一章,這一章是「橋梁」,走過、從這一頭走到那一頭是必須的、必要的。
請讀者諸君繼續往推論統計學邁進!
8.1 暫停!喝杯水!
先說壞消息。
現實裡,我們經常只會有一組數據集,統計學叫做「樣本」,也就是說,我們只會有一個「平均數」。「平均數」壓縮了所有數據集擁有的資訊,會把讀者諸君可能擁有的「大數據」變成「小數據」。也因為只有一個,「無法分」,當然就沒有「分配」,所以我們必須仰賴數據集背後的專業知識,判斷「樣本」背後的「機率分配」,這個機率分配叫做「母體機率分配」,比如說,「伯努利分配」、「二項分配」、「布瓦松分配」、「常態分配」、「指數分配」、「對數常態分配」等等。這一項知識將給我們引用「中央極限定理」的信心,並且判斷「是否需要新增樣本」,雖然新增樣本就是增加成本,但我們不是也常說「加碼」、「超前佈署」嗎!
至於好消息是:
「中央極限定理」的研究實際上不斷推陳出新,讀者諸君有興趣當然可以加入。但,無論如何,R提供了許許多多、非常豐富的「統計推論套件」,絕對足以應付各種已知的難題。請讀者諸君拭目以待。
8.3 二項分配
為什麼選讀這個主題,基本上,至少有以下這些理由:
- 學習如何從伯努利分配得到二項分配?
- 學習如何描述某一個二項分配?
- 學習如何用R整理描述某一個二項分配?
- 學習如何用R取得某一個二項分配?
- 學習如何電算二項分配的期望值。
- 學習如何手算二項分配的期望值。
- 學習如何電算二項分配的變異數。
- 學習如何手算二項分配的變異數。
8.3.1 建議優先閱讀:伯努利分配
8.3.1.1 抽樣一枚公平銅板的成功次數五十次
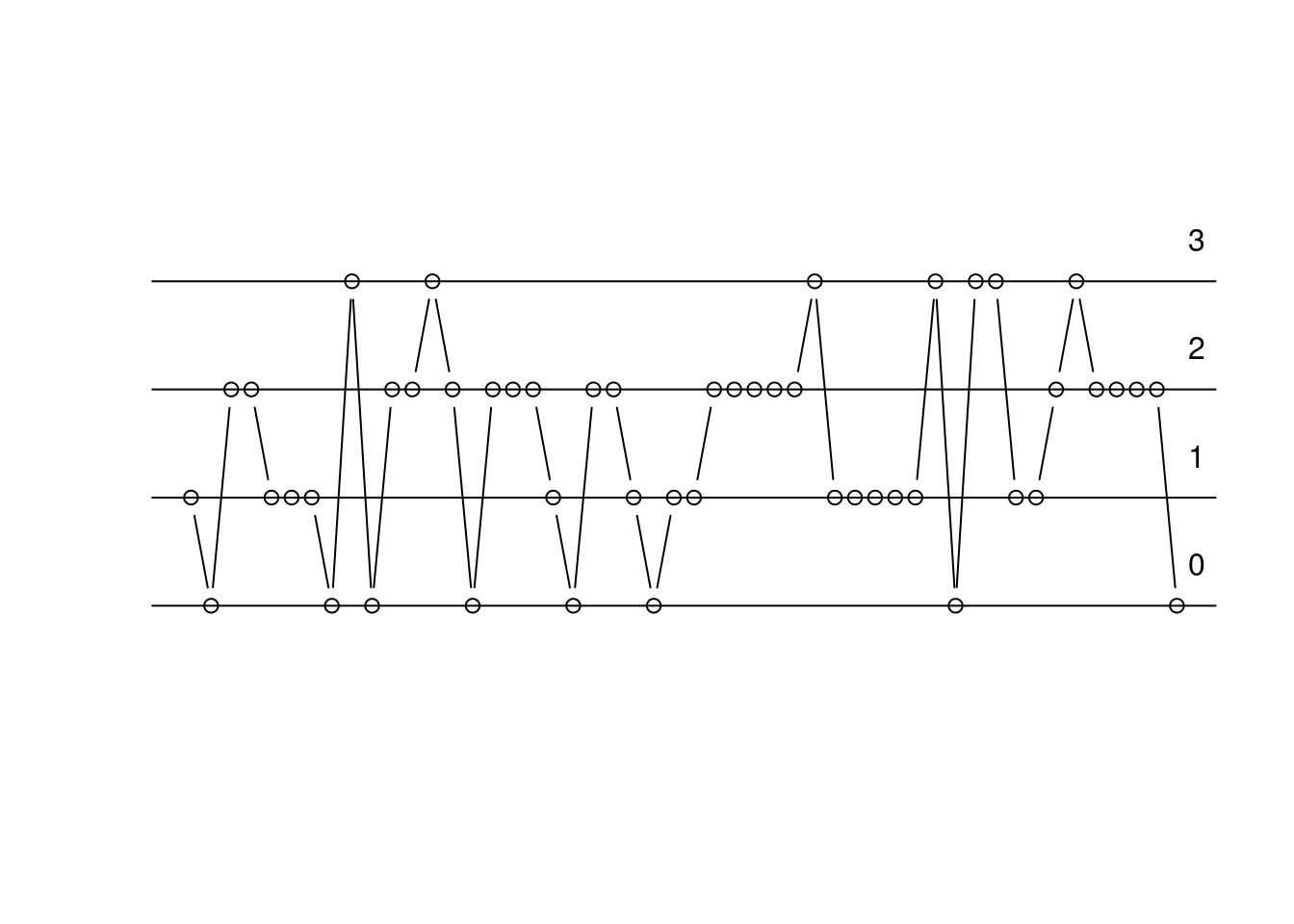
在伯努利分配的時候,我們用長條圖整理30次「二取一試驗」的次數分配,當時並沒有用R程式碼示意「一次又一次試驗的結果」。接下來,我們一句一句解釋R程式碼,學學怎麼畫簡單的示意圖?
- 事前準備
SUM <- numeric(0)- 設定隨機種子,讓我們可以重複同樣的「二取一試驗過程」。
set.seed(1288)- 引用
for迴圈持續「二取一」50次。每一次都計算全部樣本的總和。
for (i in 1:50) {
Data <- sample(0:1, 1, replace = TRUE)
SUM <- c(SUM, sum(Data))
}SUM這一個向量收集到全部「二取一」50次的總和。因為每一次不是看到「0」就是「1」,所以總和也是『不是看到「0」就是「1」』。依序往右打點加點跟點之間的線段。
plot(SUM,
type = "b",
ylim = c(-1,2),
axes = FALSE,
xlab = "",
ylab = "")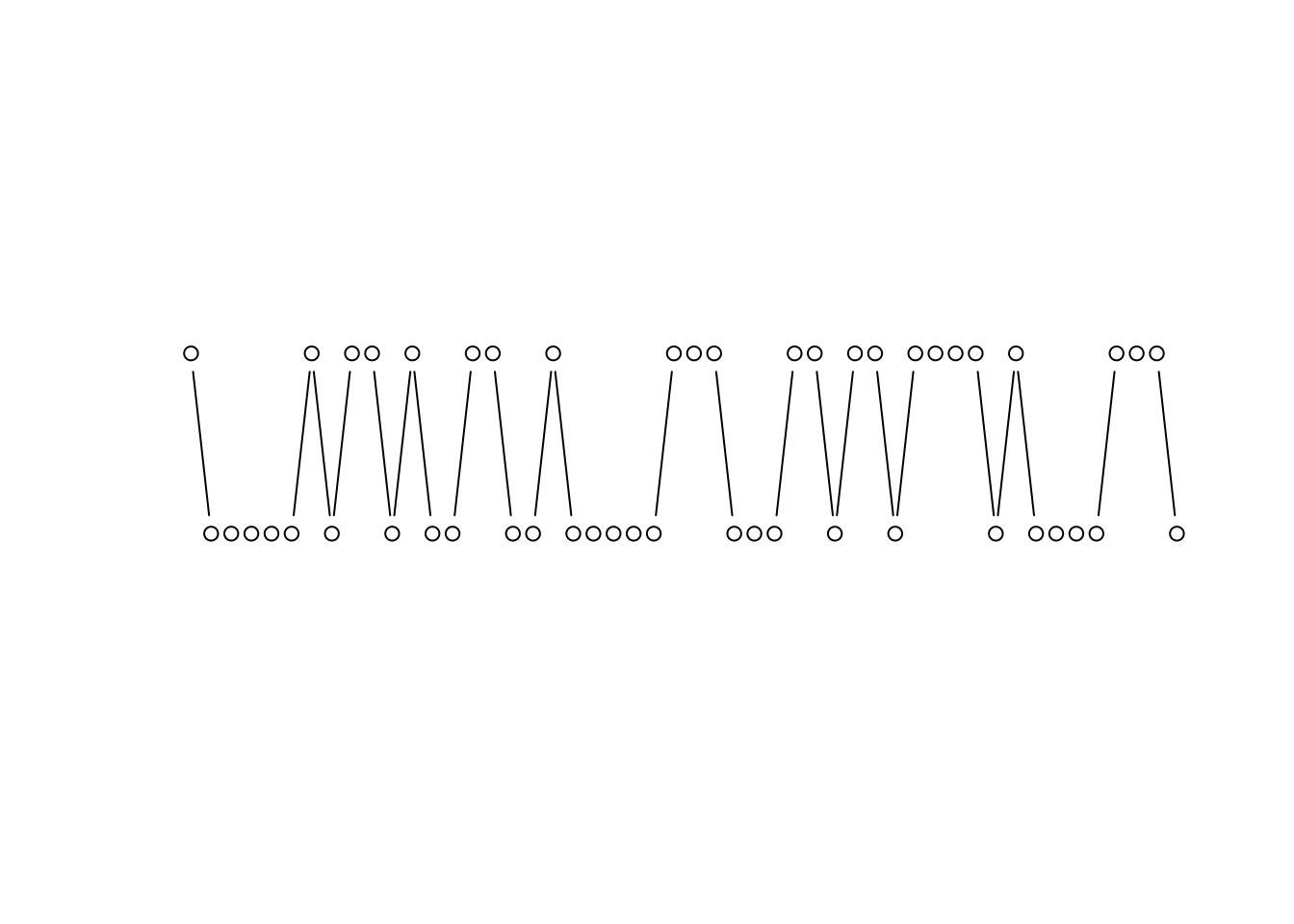
- 加兩條水平線,分別在「
y = 0」跟「y = 1」。
plot(SUM,
type = "b",
ylim = c(-1,2),
axes = FALSE,
xlab = "",
ylab = "")
abline(h = 0)
abline(h = 1)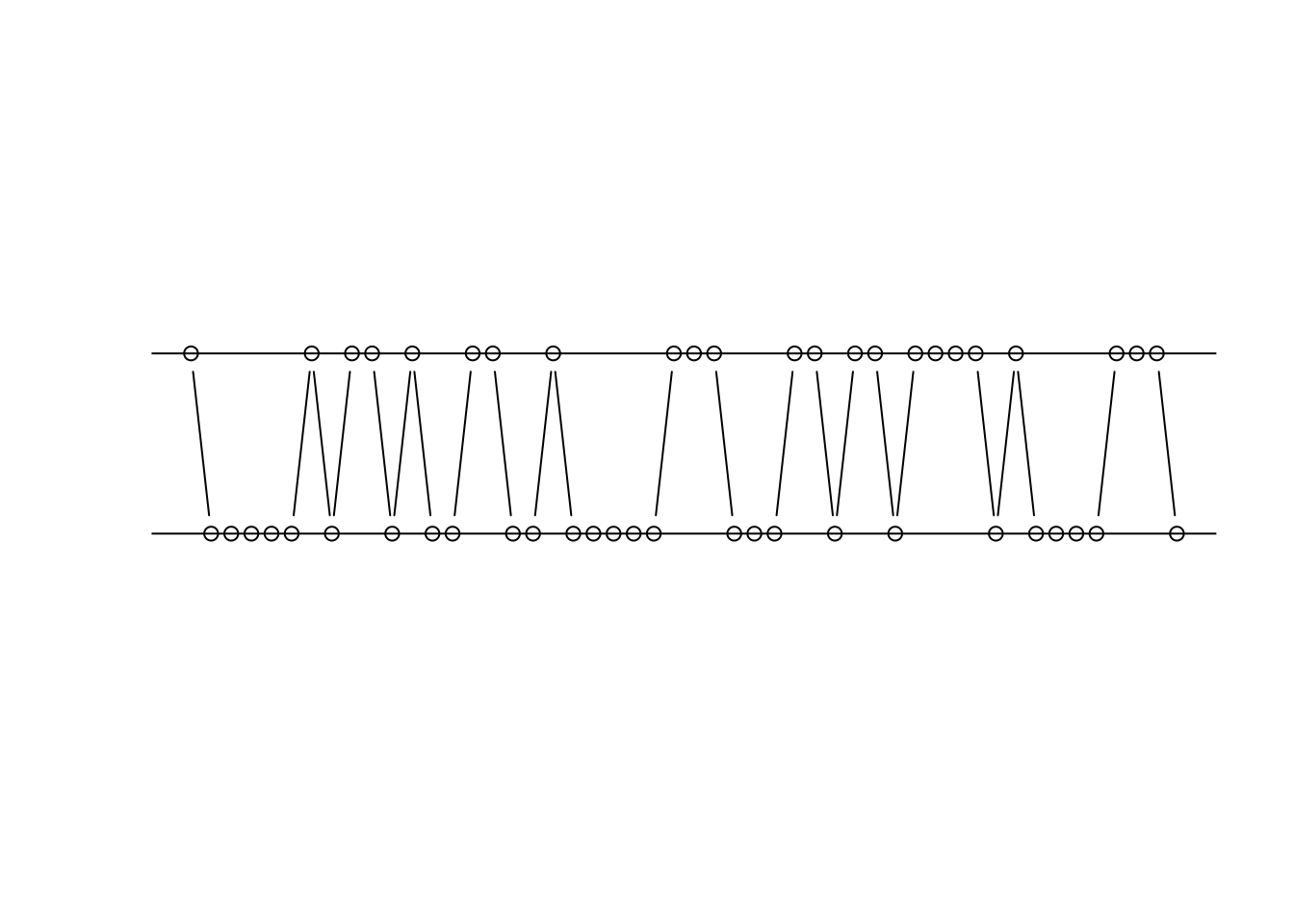
- 在水平線上註記「
0」跟「1」。
plot(SUM,
type = "b",
ylim = c(-1,2),
axes = FALSE,
xlab = "",
ylab = "")
abline(h = 0)
abline(h = 1)
text(51, 0.3, "0")
text(51, 1.3, "1")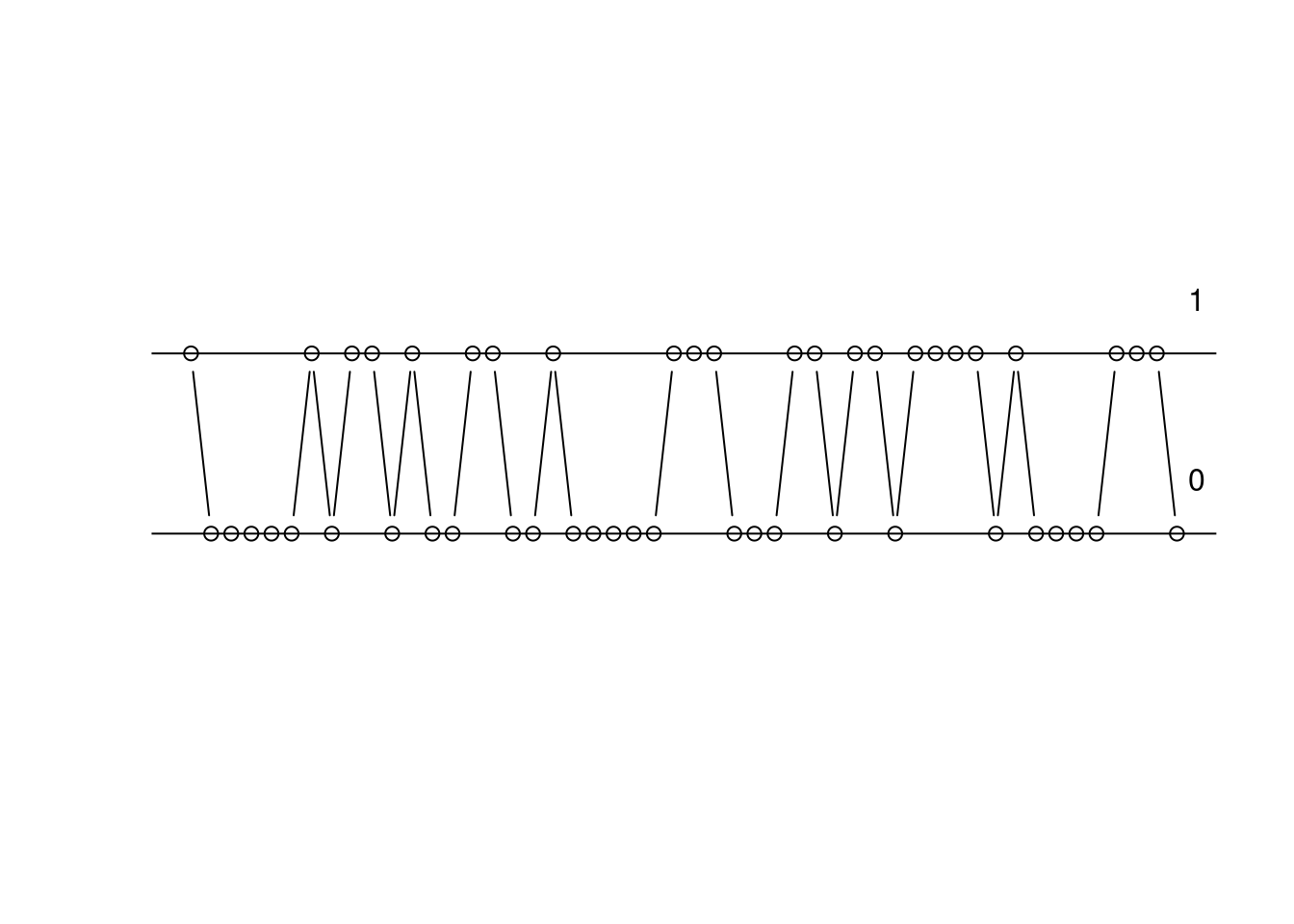
8.3.2 丟擲數枚公平銅板的成功次數
8.3.2.2 兩枚時代的有跡可循
我們先看「抽樣兩枚公平銅板的成功次數五十次」,可能會看到的結果、景象。
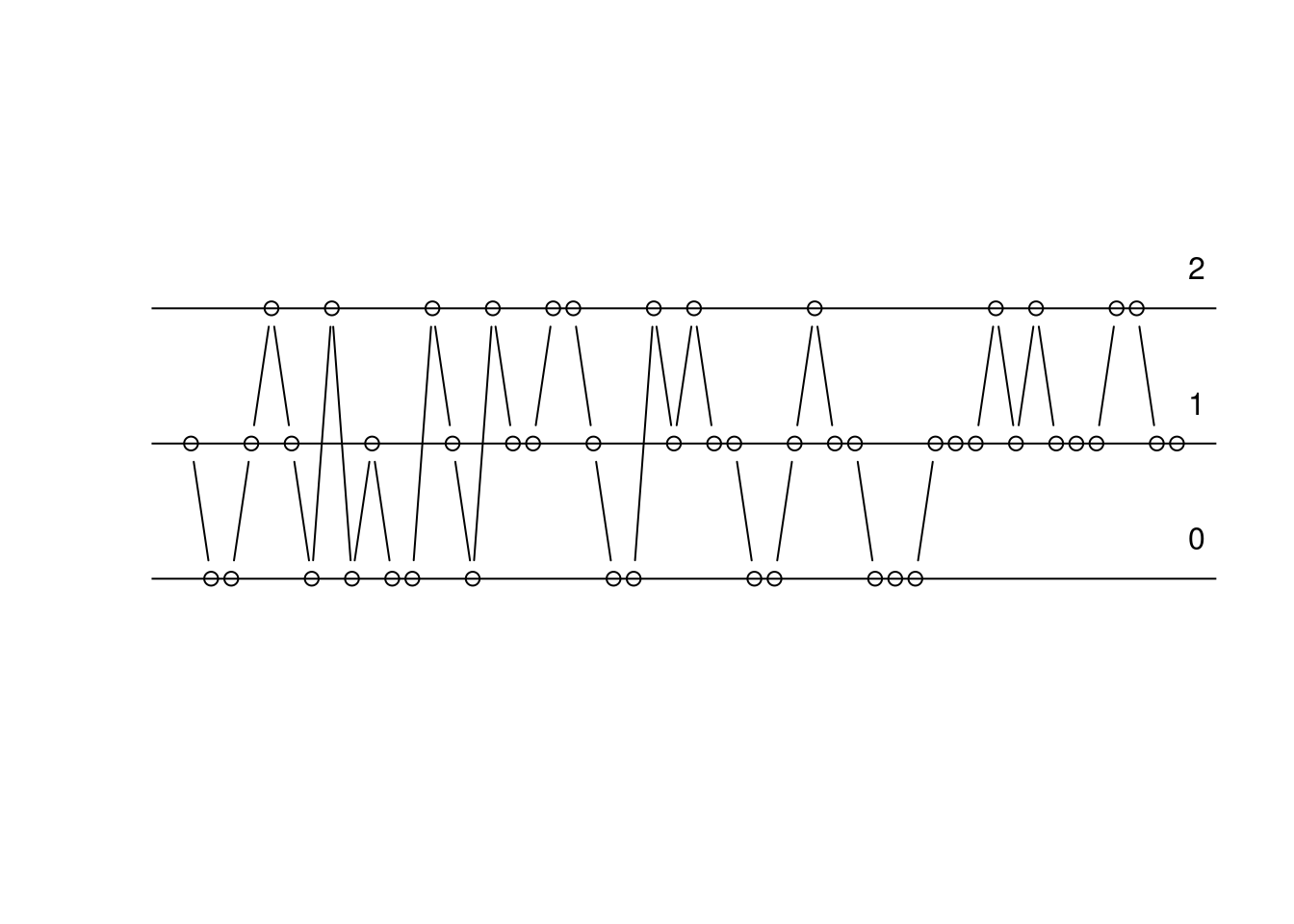
我們準備兩枚銅板,一次丟一枚、連續丟兩次,結果應該是以下其中一種情形:
- 第一枚反面朝上、第二枚反面朝上,得到的成功次數是「
0」,機率是
\[第一枚反面朝上的機率0.5 * 第二枚反面朝上的機率0.5 = 0.25\]
- 第一枚正面朝上、第二枚反面朝上,得到的成功次數是「
1」,機率是
\[第一枚正面朝上的機率0.5 * 第二枚反面朝上的機率0.5 = 0.25\]
- 第一枚反面朝上、第二枚正面朝上,得到的成功次數是「
1」,機率是
\[第一枚反面朝上的機率0.5 * 第二枚正面朝上的機率0.5 = 0.25\]
- 第一枚正面朝上、第二枚正面朝上,得到的成功次數是「
2」,機率是
\[第一枚正面朝上的機率0.5 * 第二枚正面朝上的機率0.5 = 0.25\]
8.3.2.2.1 檢驗上述四點是否定義了一種機率分配?
- 每一個0.25都是大於0的數字、
- 四個0.25加起來等於1.0。
但是,我們發現「丟擲兩枚公平銅板的成功次數」只會有「0, 1, 2」三種情形,所以前述四點描述的機率分配必須改寫為
- 丟擲兩枚公平銅板的成功次數等於0,機率是0.25、
- 丟擲兩枚公平銅板的成功次數等於1,機率是0.50、
- 丟擲兩枚公平銅板的成功次數等於2,機率是0.25、
8.3.2.2.2 將上述手算成果用R整理成表格
- 請
expand.grid幫我們把所有可能的情況羅列在一張表裡。
DM2 <- expand.grid(0:1, 0:1)
DM2## Var1 Var2
## 1 0 0
## 2 1 0
## 3 0 1
## 4 1 1- 修改欄位名稱、行名稱。
colnames(DM2) <- c("第一枚銅板的正反面","第二枚銅板的正反面")
DM2## 第一枚銅板的正反面 第二枚銅板的正反面
## 1 0 0
## 2 1 0
## 3 0 1
## 4 1 1- 換符號再示意一次。
DM2 <- expand.grid(c("T","H"), c("T","H"))
colnames(DM2) <- c("第一枚銅板的正反面","第二枚銅板的正反面")
DM2## 第一枚銅板的正反面 第二枚銅板的正反面
## 1 T T
## 2 H T
## 3 T H
## 4 H H- 換符號再示意一次。
DM2 <- expand.grid(c("反面","正面"), c("反面","正面"))
colnames(DM2) <- c("第一枚銅板的正反面","第二枚銅板的正反面")
DM2## 第一枚銅板的正反面 第二枚銅板的正反面
## 1 反面 反面
## 2 正面 反面
## 3 反面 正面
## 4 正面 正面- 把符號換回
0跟1之後繼續編寫。
DM2 <- expand.grid(0:1, 0:1)
colnames(DM2) <- c("第一枚銅板的正反面","第二枚銅板的正反面")
DM2## 第一枚銅板的正反面 第二枚銅板的正反面
## 1 0 0
## 2 1 0
## 3 0 1
## 4 1 1- 計算成功次數。
DM2$`成功次數` <- apply(DM2, 1, sum)
DM2## 第一枚銅板的正反面 第二枚銅板的正反面 成功次數
## 1 0 0 0
## 2 1 0 1
## 3 0 1 1
## 4 1 1 2- 設定機率。
DM2$`成功次數的機率` <- 0.5^2
DM2## 第一枚銅板的正反面 第二枚銅板的正反面 成功次數 成功次數的機率
## 1 0 0 0 0.25
## 2 1 0 1 0.25
## 3 0 1 1 0.25
## 4 1 1 2 0.25- 透過「加總」整併同樣成功次數的機率,得到「丟擲兩枚公平銅板成功次數的機率分配」。
BIN2 <- aggregate(DM2$`成功次數的機率`, by = list(DM2$`成功次數`), sum)
colnames(BIN2) <- c("成功次數", "成功次數的機率")
BIN2## 成功次數 成功次數的機率
## 1 0 0.25
## 2 1 0.50
## 3 2 0.25- (另一招)請R的官方函式
dbinom幫我們計算成功的機率。
DM2$`成功次數的機率` <- dbinom(DM2$`成功次數`, 2, 0.5)
DM2## 第一枚銅板的正反面 第二枚銅板的正反面 成功次數 成功次數的機率
## 1 0 0 0 0.25
## 2 1 0 1 0.50
## 3 0 1 1 0.50
## 4 1 1 2 0.25- (另一招)捨棄重複項目,一樣可以得到「丟擲兩枚公平銅板成功次數的機率分配」。因為這樣做會得到原表的子表,所以必須重新命名「列名稱」。
BIN2 <- DM2[,c(3,4)]
BIN2 <- BIN2[!duplicated(BIN2),]
rownames(BIN2) <- 1:dim(BIN2)[1]
BIN2## 成功次數 成功次數的機率
## 1 0 0.25
## 2 1 0.50
## 3 2 0.258.3.2.3 三枚時代的有跡可循
跟之前一樣的歷程、一樣的研究方法,我們先看「抽樣三枚公平銅板的成功次數五十次」,可能會看到的結果、景象。
我們準備三枚銅板,一次丟一枚、連續丟三次,結果應該是以下其中一種情形:
- 第一枚反面、第二枚反面、第三枚反面,得到的成功次數是「
0」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
- 第一枚正面、第二枚反面、第三枚反面,得到的成功次數是「
1」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
- 第一枚反面、第二枚正面、第三枚反面,得到的成功次數是「
1」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
- 第一枚正面、第二枚正面、第三枚反面,得到的成功次數是「
2」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
- 第一枚反面、第二枚反面、第三枚正面,得到的成功次數是「
1」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
- 第一枚正面、第二枚反面、第三枚正面,得到的成功次數是「
2」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
- 第一枚反面、第二枚正面、第三枚正面,得到的成功次數是「
2」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
- 第一枚正面、第二枚正面、第三枚正面,得到的成功次數是「
3」,機率是
\[0.5 * 0.5 * 0.5 = 0.125\]
8.3.2.3.1 檢驗上述八點是否定義了一種機率分配?
- 每一個0.125都是大於0的數字、
- 八個0.25加起來等於1.0。
但是,我們發現「丟擲三枚公平銅板的成功次數」只會有「0, 1, 2, 3」四種情形,所以前述八點描述的機率分配必須改寫為
- 丟擲三枚公平銅板的成功次數等於0,機率是0.125、
- 丟擲三枚公平銅板的成功次數等於1,機率是0.375、
- 丟擲三枚公平銅板的成功次數等於2,機率是0.375、
- 丟擲三枚公平銅板的成功次數等於3,機率是0.125、
接下來,仿「丟擲兩枚公平銅板的歷程」,一樣可以請R幫我們整理出「丟擲三枚公平銅板成功次數的機率分配」。
DM3 <- expand.grid(0:1, 0:1, 0:1)
colnames(DM3) <- c("第一枚銅板的正反面","第二枚銅板的正反面","第三枚銅板的正反面")
DM3## 第一枚銅板的正反面 第二枚銅板的正反面 第三枚銅板的正反面
## 1 0 0 0
## 2 1 0 0
## 3 0 1 0
## 4 1 1 0
## 5 0 0 1
## 6 1 0 1
## 7 0 1 1
## 8 1 1 1DM3$`成功次數` <- apply(DM3, 1, sum)
DM3## 第一枚銅板的正反面 第二枚銅板的正反面 第三枚銅板的正反面 成功次數
## 1 0 0 0 0
## 2 1 0 0 1
## 3 0 1 0 1
## 4 1 1 0 2
## 5 0 0 1 1
## 6 1 0 1 2
## 7 0 1 1 2
## 8 1 1 1 3DM3$`成功次數的機率` <- 0.5^3
DM3## 第一枚銅板的正反面 第二枚銅板的正反面 第三枚銅板的正反面 成功次數
## 1 0 0 0 0
## 2 1 0 0 1
## 3 0 1 0 1
## 4 1 1 0 2
## 5 0 0 1 1
## 6 1 0 1 2
## 7 0 1 1 2
## 8 1 1 1 3
## 成功次數的機率
## 1 0.125
## 2 0.125
## 3 0.125
## 4 0.125
## 5 0.125
## 6 0.125
## 7 0.125
## 8 0.125BIN3 <- aggregate(DM3$`成功次數的機率`, by = list(DM3$`成功次數`), sum)
colnames(BIN3) <- c("成功次數", "成功次數的機率")
BIN3## 成功次數 成功次數的機率
## 1 0 0.125
## 2 1 0.375
## 3 2 0.375
## 4 3 0.125DM3$`成功次數的機率` <- dbinom(DM3$`成功次數`, 3, 0.5)
DM3## 第一枚銅板的正反面 第二枚銅板的正反面 第三枚銅板的正反面 成功次數
## 1 0 0 0 0
## 2 1 0 0 1
## 3 0 1 0 1
## 4 1 1 0 2
## 5 0 0 1 1
## 6 1 0 1 2
## 7 0 1 1 2
## 8 1 1 1 3
## 成功次數的機率
## 1 0.125
## 2 0.375
## 3 0.375
## 4 0.375
## 5 0.375
## 6 0.375
## 7 0.375
## 8 0.125BIN3 <- DM3[,c(4,5)]
BIN3 <- BIN3[!duplicated(BIN3),]
rownames(BIN3) <- 1:dim(BIN3)[1]
BIN3## 成功次數 成功次數的機率
## 1 0 0.125
## 2 1 0.375
## 3 2 0.375
## 4 3 0.1258.3.3 二項分配
8.3.3.3 三枚銅板時代的有跡可循
在三枚時代,機率分配其實就是「『伯努利分配』加『伯努利分配』加『伯努利分配』」,也就是說,三枚時代的二項分配等於「加總三個伯努利分配」,記為「BIN(3, 0.5)」。
8.3.3.4 一般情形的有跡可循
假設我們連續丟了「n」顆公平銅板,也就是說,機率分配會是「加了『伯努利分配』n次」,得到的二項分配記為「BIN(n, 0.5)」。
8.3.3.5 「更」一般情形的有跡可循
假設我們連續丟了「n」顆成功機率等於「p」的銅板,也就是說,機率分配會是「加了『成功機率等於「p」的伯努利分配』n次」,得到的二項分配記為「BIN(n, p)」。
8.3.6 二項分配的期望值與變異數
「分配」,不論是「次數分配」還是「機率分配」,都會有「期望值」,也就是「平均數」與「變異數」,甚至更高階的動差,還有其他在「敘述統計學」相關微微書介紹過的統計量。關於「伯努利分配的期望值」,請讀者諸君回頭、回顧伯努利分配。在這裡,我們想示範幾種可能性:
- 電算。請R幫我們算,只要一句話,只要我們把「輸入」準備好。
- 手算。在這裡,這一本微微書沒有黑板,要手算談而容易,所以,作者準備一張樹狀圖模擬一張黑板,再加上「手寫」模擬看倌的手、的手算過程。
- 電算手算。一樣請R幫忙,只是這一回寫程式模擬手從製作機率分配表到得到期望值或是變異數的動作與過程。
8.3.6.1 伯努利分配的期望值
8.3.6.1.1 一枚公平銅板的伯努利分配期望值
所謂「一枚公平銅板」這一句話,等同於「銅板停止不動後人頭朝上的機率等於0.5」。一般的統計學教科書會用
\[p = 0.5\]
取代如此冗長的一句話。
- 電算。既然
\[p = 0.5 = \frac{1}{2} = \frac{1}{1 + 1}\]
最後分母的「\(1 + 1\)」,意味著,「人頭(H)」與「梅花(T)」的比例是「1:1」。所以,我們在準備mean的「輸入」時,「1」跟「0」的比例就得是「1:1」。
rep(c(0,1), c(1,1))## [1] 0 1所以,「一枚公平銅板的伯努利分配期望值」的電算就這麼寫:
mean(rep(c(0,1), c(1,1)))## [1] 0.5- 電算手算。歷程如下所示:
DM1 <- expand.grid(0:1)
colnames(DM1) <- c("第一枚銅板的正反面")
DM1## 第一枚銅板的正反面
## 1 0
## 2 1DM1$`成功次數` <- apply(DM1, 1, sum)
DM1## 第一枚銅板的正反面 成功次數
## 1 0 0
## 2 1 1DM1$`成功次數的機率` <- dbinom(DM1$`成功次數`, 1, 0.5)
DM1## 第一枚銅板的正反面 成功次數 成功次數的機率
## 1 0 0 0.5
## 2 1 1 0.5BIN1 <- DM1[,c("成功次數","成功次數的機率")]
BIN1 <- BIN1[!duplicated(BIN1),]
BIN1## 成功次數 成功次數的機率
## 1 0 0.5
## 2 1 0.5EXP1 <- sum(BIN1$`成功次數` * BIN1$`成功次數的機率`)
EXP1## [1] 0.5- 手算。步驟一:手繪樹狀圖。
# libraries
require(ggraph)
require(igraph)
require(tidyverse)
# create an edge list data frame giving the hierarchical structure of your individuals
d1 <- data.frame(from="origin", to=paste("group", seq(1,2), sep=""))
edges <- rbind(d1)
# Create a graph object
mygraph <- graph_from_data_frame(edges)
# Basic tree
ggraph(mygraph, layout = 'dendrogram', circular = FALSE) +
geom_edge_diagonal() +
geom_node_point() +
theme_void()
開始手算:
\[\frac{0 + 1}{2} = 0.5\]
8.3.6.1.2 一枚不公平銅板的伯努利分配期望值
- 電算。假設
\[p = 0.2 = \frac{1}{5} = \frac{1}{1 + 4}\]
最後分母的「\(1 + 4\)」,意味著,「人頭(H)」與「梅花(T)」的比例是「1:4」。所以,我們在準備mean的「輸入」時,「1」跟「0」的比例就得是「1:4」。
mean(rep(c(0,1), c(4,1)))## [1] 0.2- 電算手算。一樣的歷程,請讀者諸君再看一次。
DM1 <- expand.grid(0:1)
colnames(DM1) <- c("第一枚銅板的正反面")
DM1## 第一枚銅板的正反面
## 1 0
## 2 1DM1$`成功次數` <- apply(DM1, 1, sum)
DM1## 第一枚銅板的正反面 成功次數
## 1 0 0
## 2 1 1DM1$`成功次數的機率` <- dbinom(DM1$`成功次數`, 1, 0.2)
DM1## 第一枚銅板的正反面 成功次數 成功次數的機率
## 1 0 0 0.8
## 2 1 1 0.2BIN1 <- DM1[,c("成功次數","成功次數的機率")]
BIN1 <- BIN1[!duplicated(BIN1),]
BIN1## 成功次數 成功次數的機率
## 1 0 0.8
## 2 1 0.2EXP1 <- sum(BIN1$`成功次數` * BIN1$`成功次數的機率`)
EXP1## [1] 0.2- 手算。步驟一:一樣先手繪樹狀圖。這裡的R技巧,要把
seq(1,2)改成seq(1,5)。
開始手算:
\[\frac{0 + 0 + 0 + 0 + 1}{5} = 1/5 = 0.2\]
8.3.6.2 二項分配的期望值
我們已經知道「二項分配」等於「加總數個彼此獨立的伯努利分配」。然後,再根據「期望值的性質」可以得知
\[固定幾次試驗的二項分配的期望值就等於加總幾次伯努利分配的期望值。\]
讓我們舉幾個例子看看,並且從中學習一些R技巧。
8.3.6.2.1 連續丟擲兩枚公平銅板的二項分配期望值
8.3.6.2.2 連續丟擲三枚公平銅板的二項分配期望值
8.3.6.2.3 連續丟擲三枚不公平銅板的二項分配期望值
- 手算。
\[0.2 + 0.2 + 0.2 = 0.2 * 3 = 3 * 0.2 = 0.6\]
- 電算手算。
DM3 <- expand.grid(0:1, 0:1, 0:1)
colnames(DM3) <- c("第一枚銅板的正反面","第二枚銅板的正反面","第三枚銅板的正反面")
DM3$`成功次數` <- apply(DM3, 1, sum)
DM3$`成功次數的機率` <- dbinom(DM3$`成功次數`, 3, 0.2)
DM3## 第一枚銅板的正反面 第二枚銅板的正反面 第三枚銅板的正反面 成功次數
## 1 0 0 0 0
## 2 1 0 0 1
## 3 0 1 0 1
## 4 1 1 0 2
## 5 0 0 1 1
## 6 1 0 1 2
## 7 0 1 1 2
## 8 1 1 1 3
## 成功次數的機率
## 1 0.512
## 2 0.384
## 3 0.384
## 4 0.096
## 5 0.384
## 6 0.096
## 7 0.096
## 8 0.008BIN3 <- DM3[,c("成功次數","成功次數的機率")]
BIN3 <- BIN3[!duplicated(BIN3),]
BIN3## 成功次數 成功次數的機率
## 1 0 0.512
## 2 1 0.384
## 4 2 0.096
## 8 3 0.008EXP3 <- sum(BIN3$`成功次數` * BIN3$`成功次數的機率`)
EXP3## [1] 0.63 * 0.2## [1] 0.6sum(BIN3$`成功次數` * dbinom(BIN3$`成功次數`, 3, 0.2))## [1] 0.6sum(DM3$`成功次數` * DM3$`成功次數的機率`)## [1] 1.7528.3.6.3 二項分配的變異數
我們已經知道「二項分配」等於「加總數個彼此獨立的伯努利分配」。然後,再根據「變異數的性質」可以得知
\[固定幾次試驗的二項分配的變異數就等於加總幾次伯努利分配的變異數。\]
我們用「連續丟擲三枚公平銅板的二項分配」為例,示範兩種手算:
8.3.6.3.1 第一種手算:取得母體數字,再用變異數公式,或是變異數的動差公式。
- 手繪樹狀圖。
- 開始手算。
DM3 <- expand.grid(0:1, 0:1, 0:1) # 把樹狀圖表格化。
apply(DM3, 1, sum) # 加總三層樹狀圖之後,每一片葉子上面的數字。## [1] 0 1 1 2 1 2 2 3sjstats::var_pop(apply(DM3, 1, sum)) # 計算母體變異數。這也是一種電算。## [1] 0.75mean((apply(DM3, 1, sum))^2) - (mean(apply(DM3, 1, sum)))^2 # 利用動差性質計算母體變異數。## [1] 0.758.4 Galton board
8.4.1 先看一張圖
quincunx(n = 1, seed = 1233)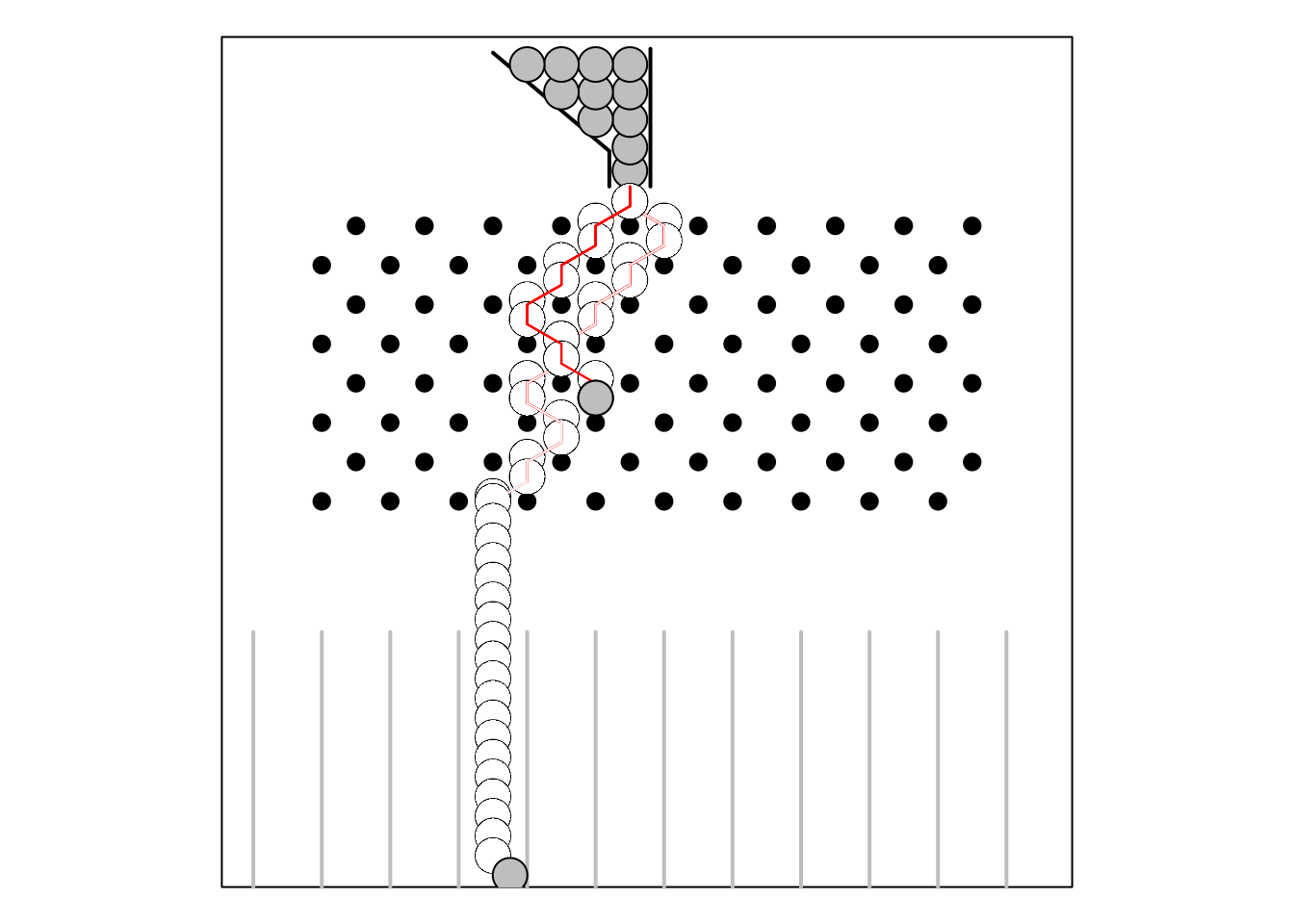
## Mean= 3.5
## SD= NA
## Bins:
## 0 0 0 1 0 0 0 0 0 0 0## $file
## [1] "Q1233.WMF"
##
## $seed
## [1] 1233
##
## $bins
## [1] 0 0 0 1 0 0 0 0 0 0 08.4.2 再看一張圖
quincunx(n = 1, seed = 1288)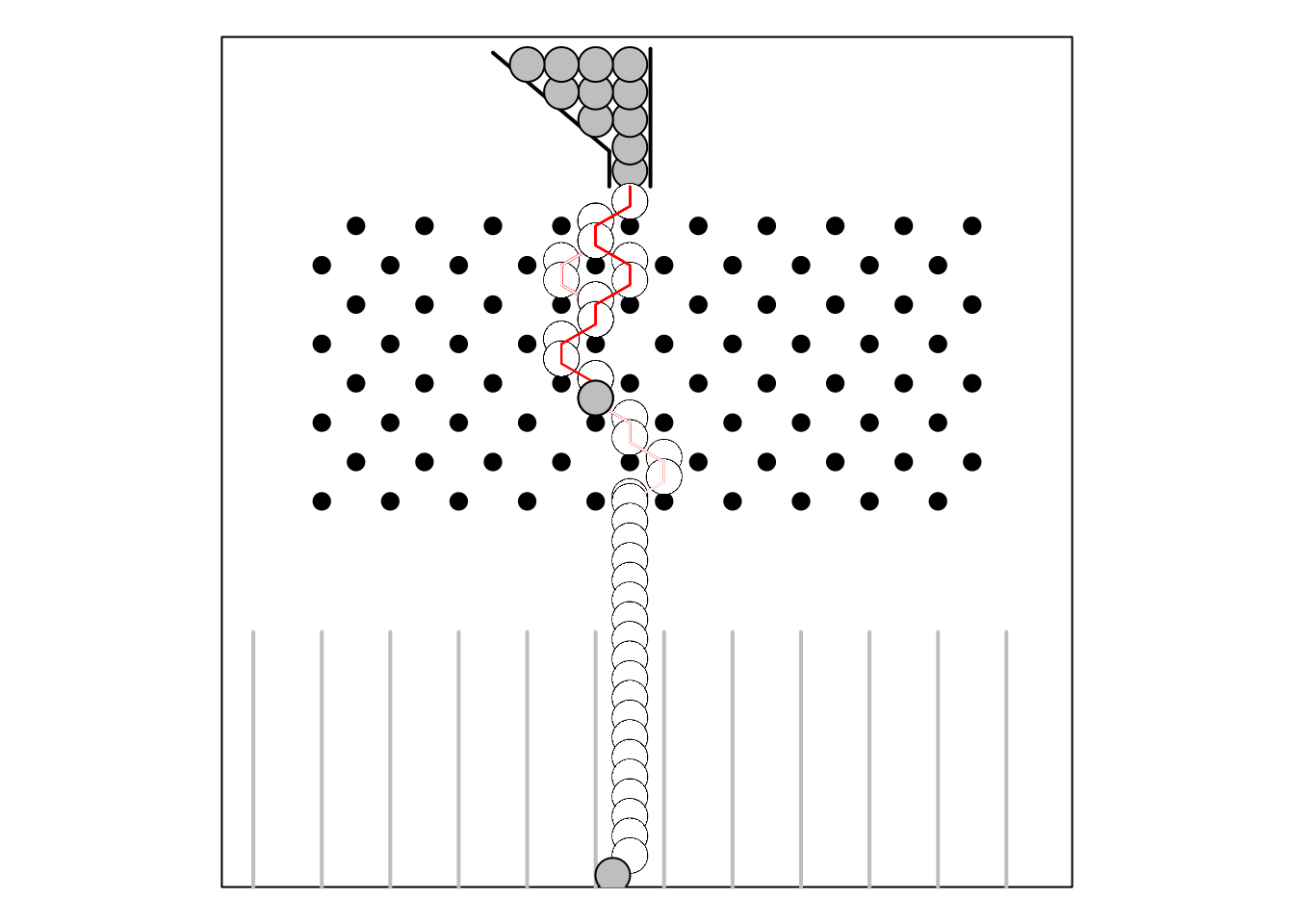
## Mean= 5.5
## SD= NA
## Bins:
## 0 0 0 0 0 1 0 0 0 0 0## $file
## [1] "Q1288.WMF"
##
## $seed
## [1] 1288
##
## $bins
## [1] 0 0 0 0 0 1 0 0 0 0 08.4.3 甚麼是「Galton Board」?
The Galton Board is a 7.5” by 4.5” desktop probability machine. This delightful little device brings to life the statistical concept of normal distribution. As you rotate the Galton Board on its axis, you set into motion a flow of steel beads that bounce with equal probability to the left or right through several rows of pegs. As the beads accumulate in the bins, they approximate the bell curve, as shown by the yellow line on the front of the Galton board. This hands-on Galton Board allows you to visualize the order embedded in the chaos of randomness.
8.5 常態分配
統計界(statistical universe)的「黃金比例」分配,非「常態分配」莫屬。
常態分配,它的機率密度曲線,
\[\frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{1}{2}(\frac{x - \mu}{\sigma})^2}\]
被暱稱為「鐘形曲線」具備
- 單峰
- 左右對稱
- 單位長度處曲線翻轉
x <- seq(-4, 4, 0.1)
y <- 1 / sqrt(2 * pi) * exp(-0.5 * x^2)
par(mfrow = c(2,2))
plot(x, y,
type = "l",
xlim = c(-4, 4),
xlab = "",
ylab = "",
axes = FALSE)
#axis(1, at = seq(-4, 4, 1))
axis(1, labels = FALSE)
abline(v = 0)
###
plot(x[x >= 0], y[x >= 0],
type = "l",
lwd = 3,
col = "red",
xlim = c(-4, 4),
xlab = "",
ylab = "",
axes = FALSE)
axis(1, at = seq(-4, 4, 1))
abline(v = 0)
points(-x[x <= 0], y[x <= 0])
###
plot(x[x <= 0], y[x <= 0],
type = "l",
lwd = 3,
col = "red",
xlim = c(-4, 4),
xlab = "",
ylab = "",
axes = FALSE)
axis(1, at = seq(-4, 4, 1))
abline(v = 0)
points(-x[x >= 0], y[x >= 0])
###
plot(x, y,
type = "l",
lwd = 3,
col = "red",
xlim = c(-4, 4),
xlab = "",
ylab = "",
axes = FALSE)
axis(1, at = seq(-4, 4, 1))
abline(v = 0)
points(-x, y)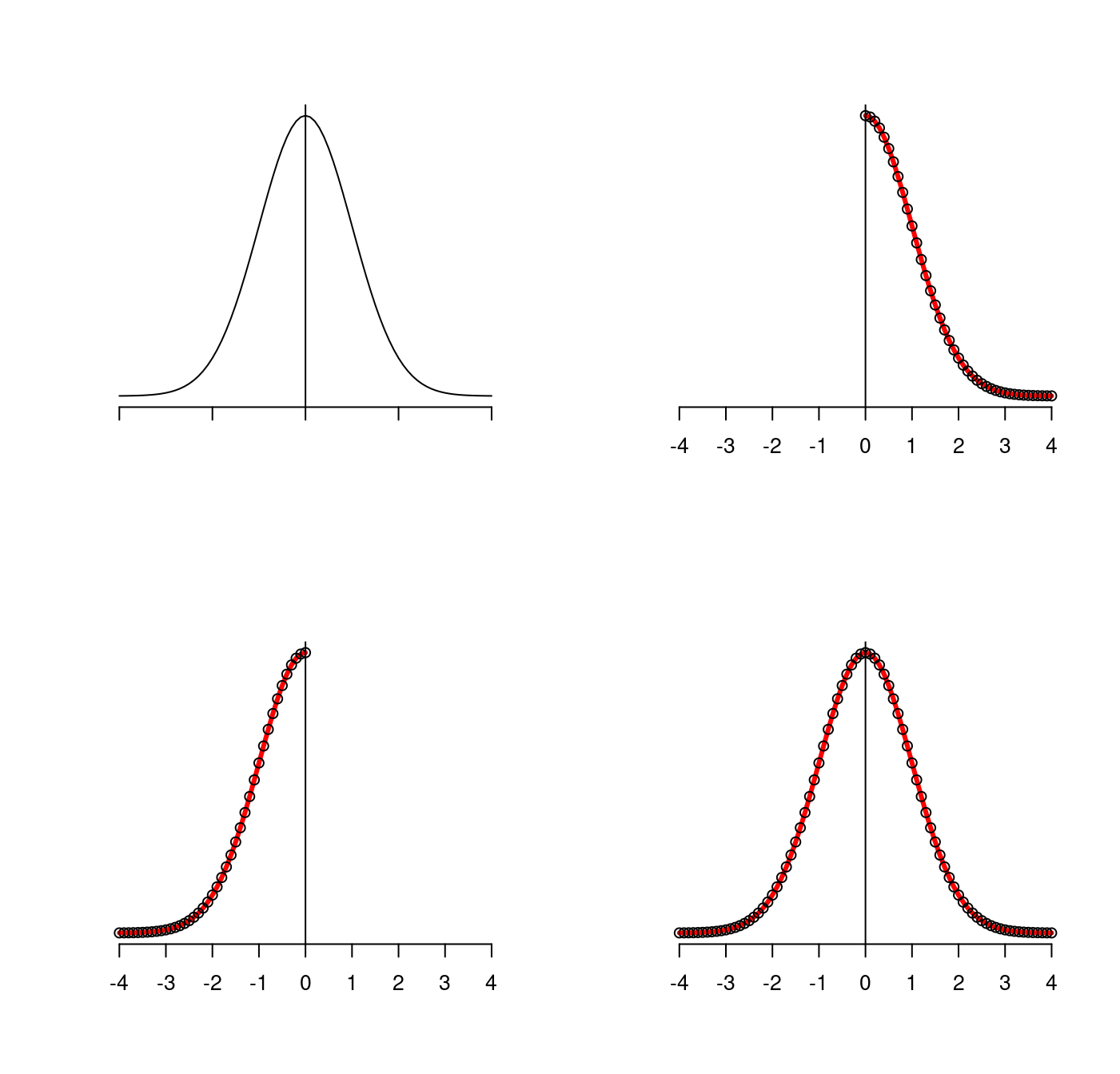
常態分配,也叫做高斯分配,當然是為了紀念高斯這一號人物。這一套微微書庫,從超過百年歷史的「莖葉圖」談起,而「常態分配」這一項機率學理的成就已經接近300年了。
8.5.1 建議優先閱讀:Galtonsboard
當時這一本微微書,Galtonsboard,作者曾經提醒各位看倌許許多多(彈珠在經過)一連串的「左右彈跳」之後,跌入像「直方圖」,也像「長條圖」的建築物、的方塊裡。只要彈珠夠多,一顆疊過一顆,最後這些彈珠的上簷會創造出非常接近「常態曲線」的曲線。雖然在「Galtonsboard」這一本微微書,因為計算資源有限,再加上模擬「Galton’s Board」的程式碼仍需進一步優化,我們只示範一顆彈珠的印象,無法讓讀者諸君線上玩電子版的「Galton’s Board」。非常可惜!直到目前為止,作者還是不會寫模擬「Galton’s Board」的程式,但無論如何,作者確實可以寫一段R示意「Galton’s Board」最後的印象,不論用了幾顆彈珠。
…
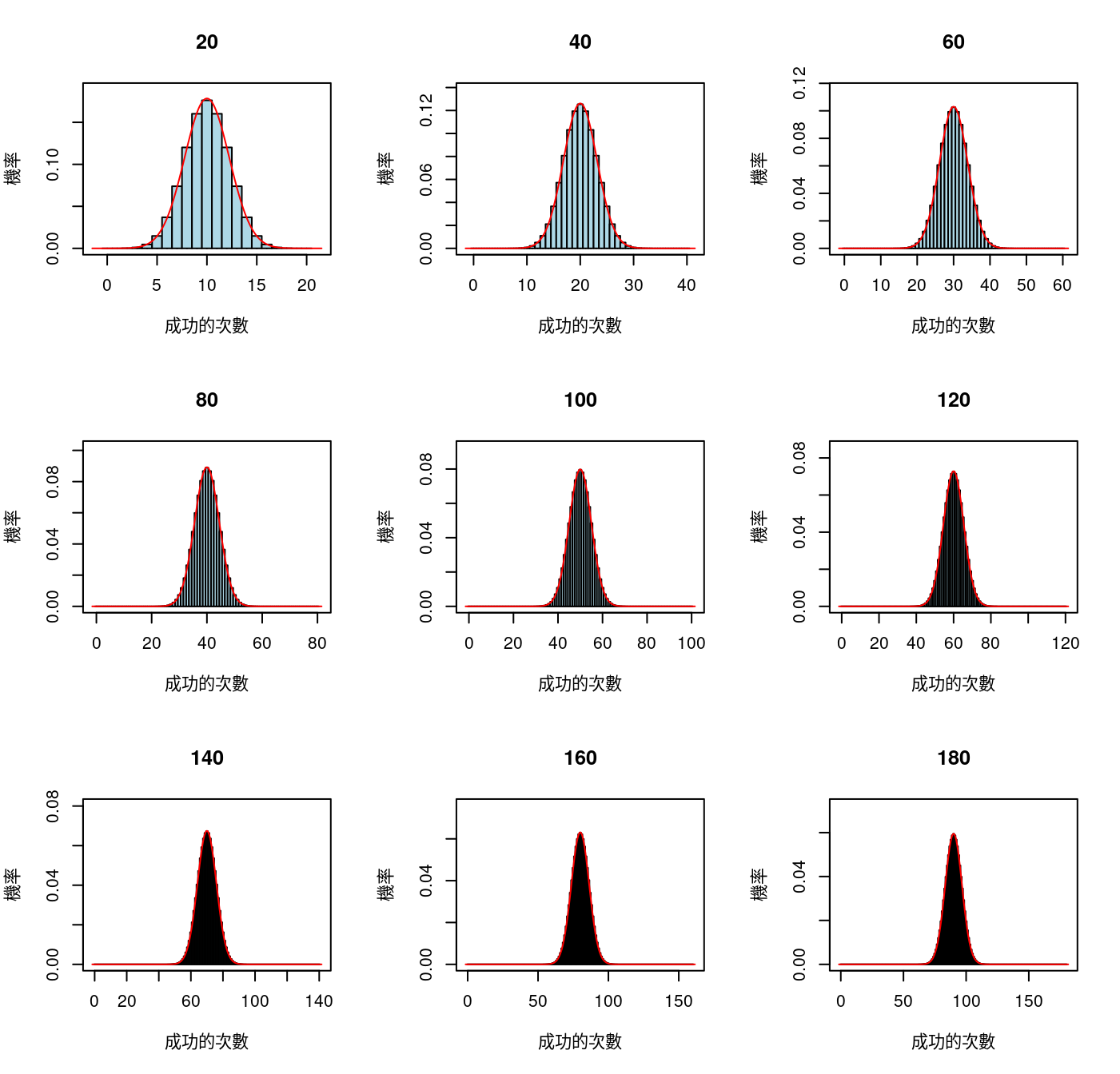
8.5.2 當試驗次數(n)不斷增加看二項分配的走向
注意這句話,『許許多多一連串的「左右彈跳」之後』,如果彈珠往左邊跳,表示為「失敗」,並且「減一」,它會往「Galton’s Board」的左邊(x軸的左邊)掉;如果彈珠往右邊跳,表示為「成功」,並且「加一」,它會往「Galton’s Board」的右邊(x軸的右邊)掉。現實裡的「Galton’s Board」,有許多層、有許多跳針,針針左左右右直到底層,就像丟銅板許多次、許多次撞地,次次不是「人頭」就是「梅花」,次次相加最後得到一個「成功次數」。許多次「同樣的銅板」、「同樣的試驗次數」,次次不同的結果被同時一起看,就是一張「直方圖」或是「長條圖」。在這裡,我們只準備示範成功機率等於0.5的二項分配如何順著樣本數、試驗次數越來越多而改變,至於其他可能的成功機率,諸如,0.1, 0.2, 0.3, …會有什麼樣的結局與印象,請讀者諸君把作者提供的參考碼帶回自己的計算環境裡,如法炮製,換個成功機率就可以輕鬆感受、目睹到這本書無法提供的其他故事了。
8.5.2.1 怎麼看作者準備的示意圖
作者先畫一張二項分配的機率密度圖來說說「怎麼看?」
- 先準備試驗次數跟二項分配成功次數的所有可能性
n <- 2
success <- 0:n
success## [1] 0 1 2- 再來計算每一種成功次數的機率
y <- dbinom(success, size = n, prob = 0.5)
y## [1] 0.25 0.50 0.25- 畫圖了。
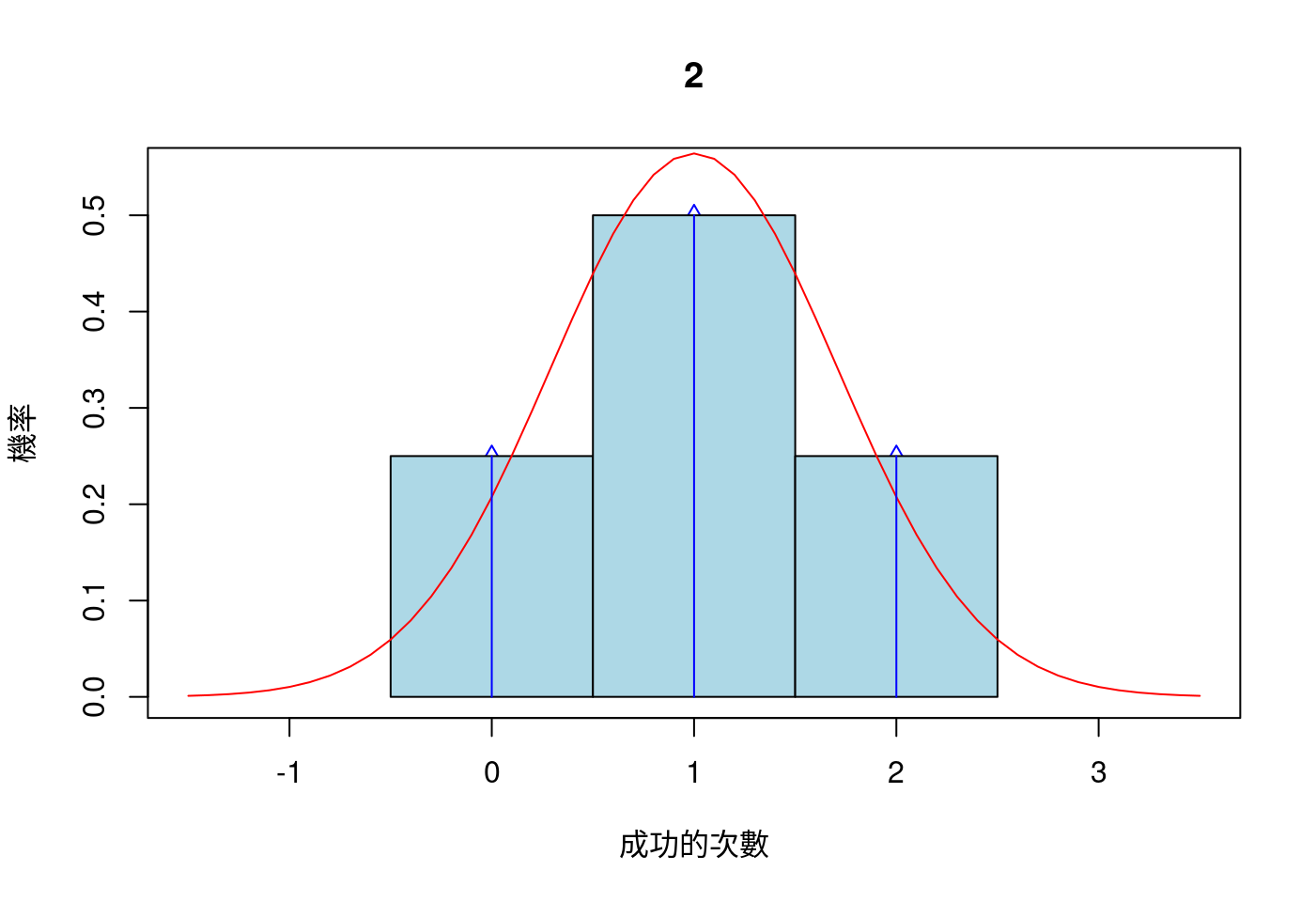
觀察,是每一次、每一隻程式碼之後,必要的動作。以下是作者的意思:
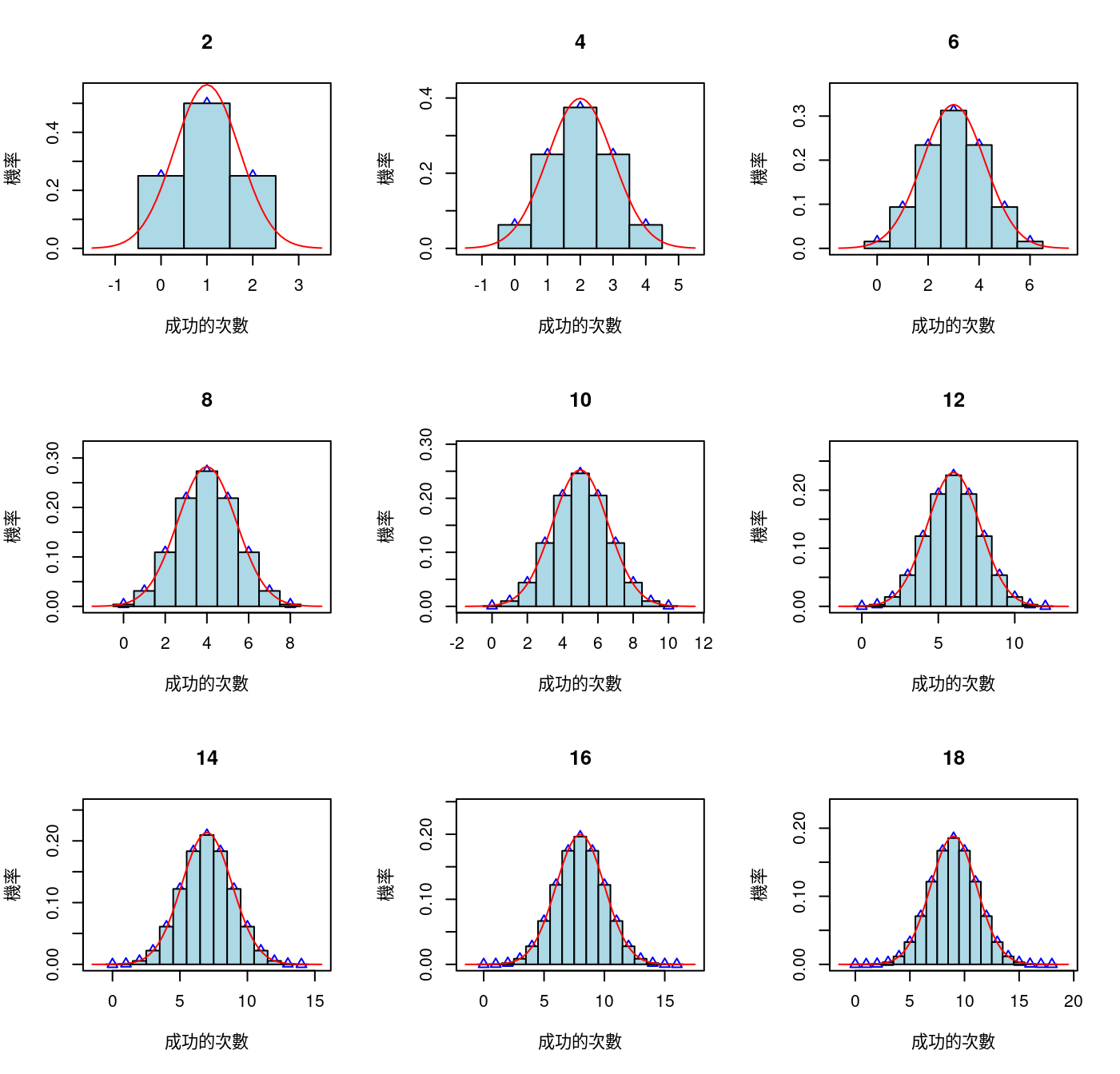
- 每一棟淺藍色方塊的高度代表方塊x軸中點數字,也就是成功次數的機率。
- 紅色的曲線是常態曲線。
- 藍色茅的長度(不含尖尖的厚度)代表茅所在x軸數字,也就是成功次數的機率。
- 如果茅穿越紅色曲線表示同一個位置、同一個成功次數,二項機率高過常態機率。
- 如果茅未穿越紅色曲線表示同一個位置、同一個成功次數,二項機率低於常態機率。
- 穿過越多或是處於越下方,表示差距越大。
- 反之,表示差距越小。
- 照說,樣本數、試驗次數越多,這一類的差距會越來越小。
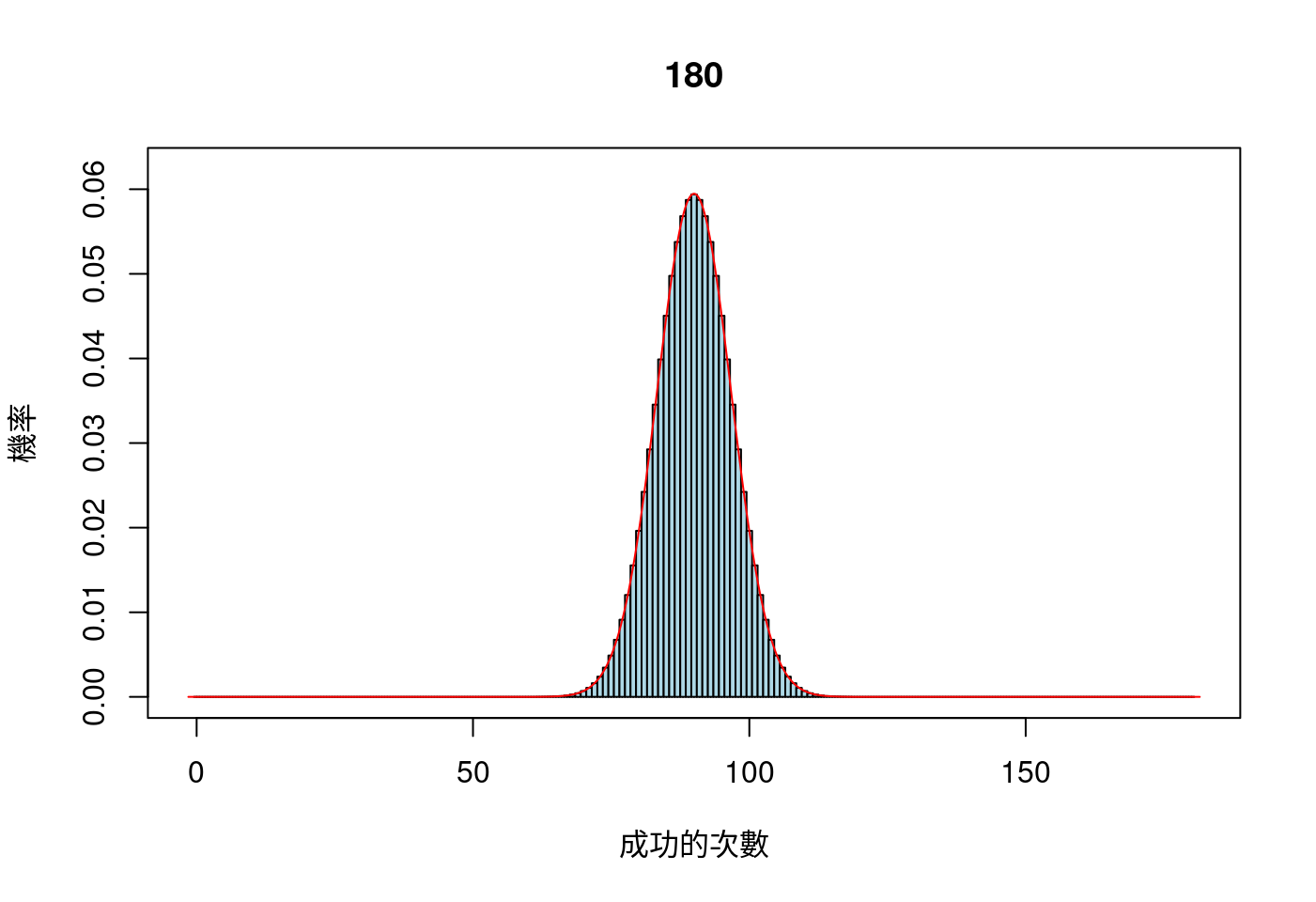
8.5.2.2 一次看個夠:n in c(2, 4, 6, 8, 10, 12, 14, 16, 18)
# 1. 把畫布切成九小塊。
par(mfrow = c(3,3))
# 2. 九種試驗次數,用迴圈一次畫一張。
for (n in c(2, 4, 6, 8, 10, 12, 14, 16, 18)) {
# 3. 準備座標(x, y)。
success <- 0:n
y <- dbinom(success, size = n, prob = 0.5)
# 4. 畫二項分配圖,但是plot只給一根一根柱子,不是方塊。
plot(success,
dbinom(success, size = n, prob = 0.5),
type = 'p',
pch = 2,
col = "blue",
ylim = c(0, max(y) + 0.048),
xlim = c(-1.5, n + 1.5),
xlab = "成功的次數",
ylab = "機率",
main = n)
# 5. 多少種成功次數的可能性,就畫幾個方塊,底座就是成功次數加減0.5。
for (i in 1:length(success)) {
lb <- success[i] - 0.5
ub <- success[i] + 0.5
x.values <- seq(lb, ub, 0.1)
polygon(c(lb, x.values, ub),
c(0, rep(y[i], length(x.values)), 0),
col = "lightblue")
}
# 6. 計算二項分配的期望值跟標準差,然後給常態分配用。
m <- n * 0.5
s <- sqrt(n * 0.5 * 0.5)
# 6. 為二項分配的方塊加上常態曲線。
lines(seq(-1.5, (n + 1.5), 0.1),
dnorm(seq(-1.5, (n + 1.5), 0.1), mean = m, sd = s),
col = "red")
}
8.5.3 常態分配的歷史沿革
一般的統計學教科書,不會特別重視統計學歷史,如果想知道,作者會試著問問維基百科。用
normal distribution wiki
就會找到常態分配的英文維基。找找是不是有紀錄常態分配的發展史呢?常態分配在整個統計學發展上,佔有一席之地,應該會有…。作者往下滑動網頁,找到了。
8.5.3.1 請注意這一段
Some authors attribute the credit for the discovery of the normal distribution to de Moivre, who in 1738 published in the second edition of his “The Doctrine of Chances” the study of the coefficients in the binomial expansion of \((a + b)^n\).
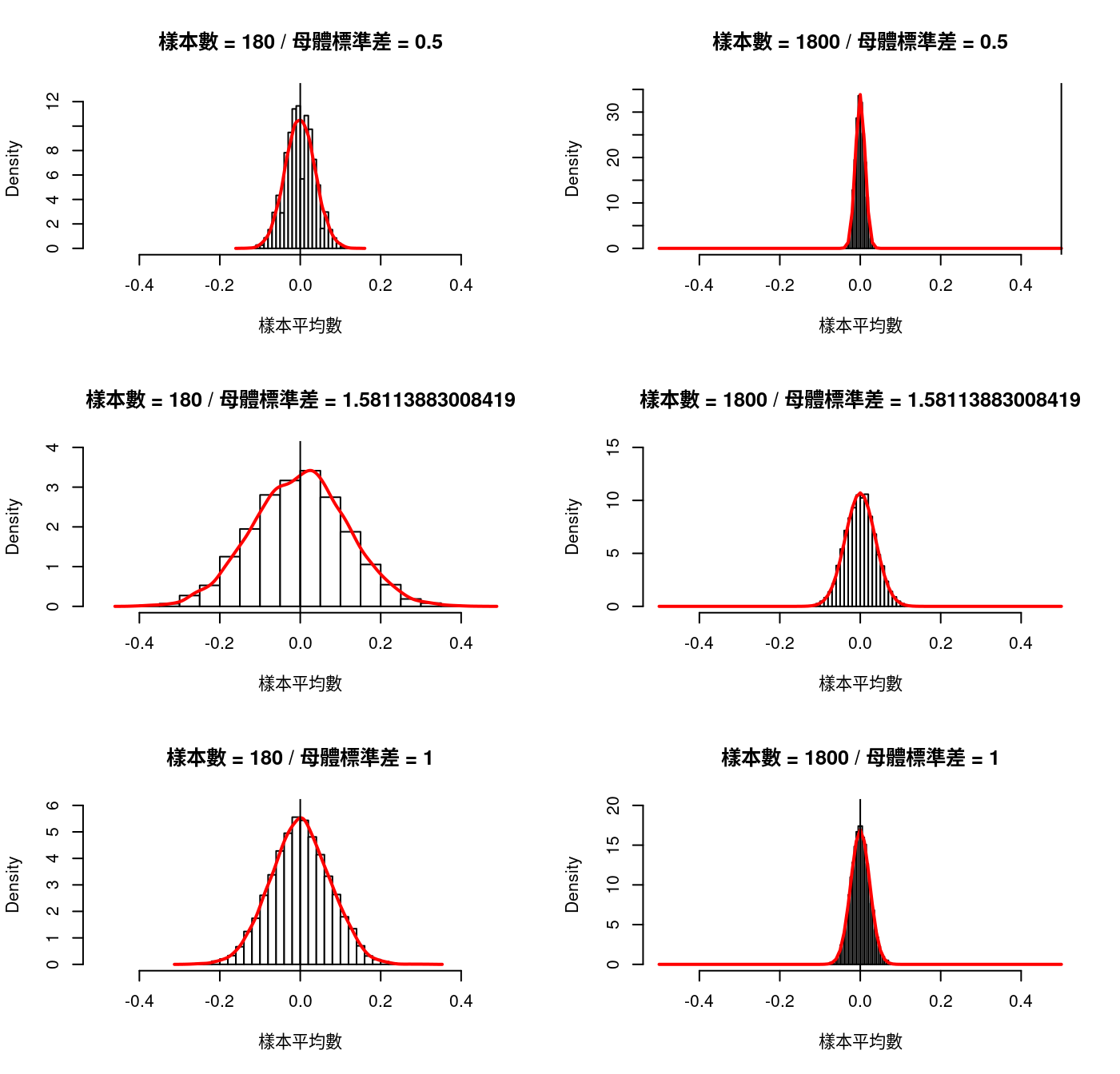
這一段也是支持作者撰寫開頭示意圖程式碼的力量,或許作者無力證明二項分配與常態分配之間的數學關係,或許無法撰寫「Galton’s Board」的模擬程式碼,雖然如此,…。作者確實用了程式示意二項分配,只要試驗次數夠大,二項分配會等於某一個常態分配,雖然只實驗到試驗次數等於180。
8.5.4 常態分配的基本面
8.5.4.1 常態分配的記號
\[N(\mu, \sigma^2)\] 比如說,
\[N(0, 1^2), N(0, 2^2), N(0, \sqrt{2}^2)\]
請注意,作者如何表達\(\sigma^2\),跟著做,準備「標準差」,然後用「指數」,「平方」,也就是,「標準差的平方」表達「變異數」。絕對不要,把「平方的結果算出來」。因為這樣的表達方式,有幾層意義:
- 表達標準差的大小。
- 親自手算或是心算變異數的大小。
- 標準差一定大於0。
8.5.4.2 常態分配的機率密度函數
\[f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}}\exp(-\frac{1}{2}(\frac{x - \mu}{\sigma})^2)\]
8.5.4.3 標準常態分配圖
所謂的標準常態是
\[\mu = 0\] ,也就是平均數等於0,以及
\[\sigma = 1\] ,也就是標準差等於1的常態分配。至於怎麼畫這一張圖呢?
- 準備我們想畫標準常態曲線圖的\(x\)範圍(機率密度函數內的那個\(x\))
x.values <- seq(-4, 4, 0.1)- 繪製常態曲線圖。我們請
dnorm幫忙。dnorm包含兩個字,第一個是d,代表density,第二個字是norm,代表normal distribution。dnorm可以幫我們算出上述\(f(x)\)的答案。
plot(x = x.values,
y = dnorm(x.values, mean = 0, sd = 1),
type = "l",
ylim = c(0,.4),
xlab = "",
ylab = "",
axes = FALSE,
main = "標準常態分配")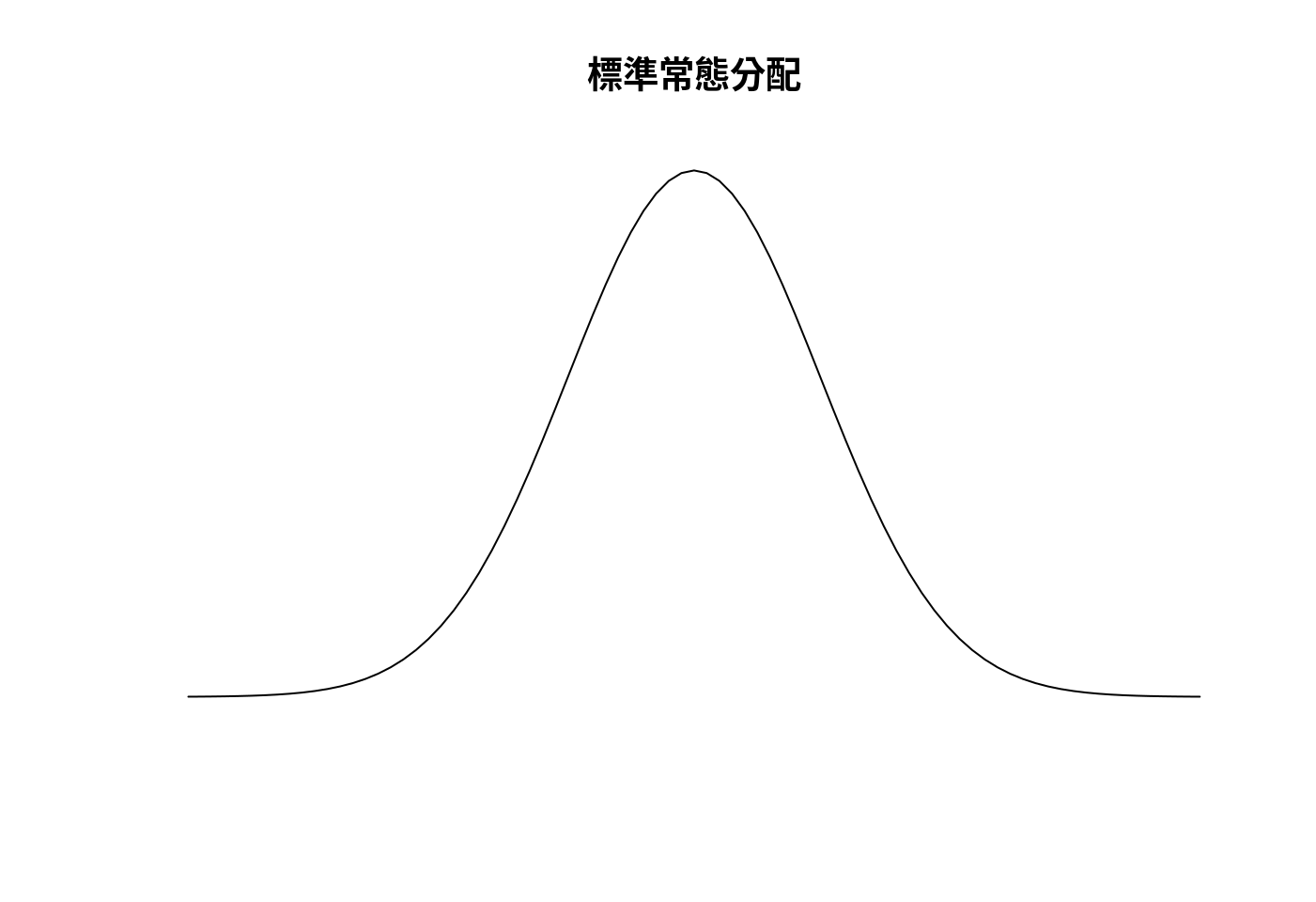
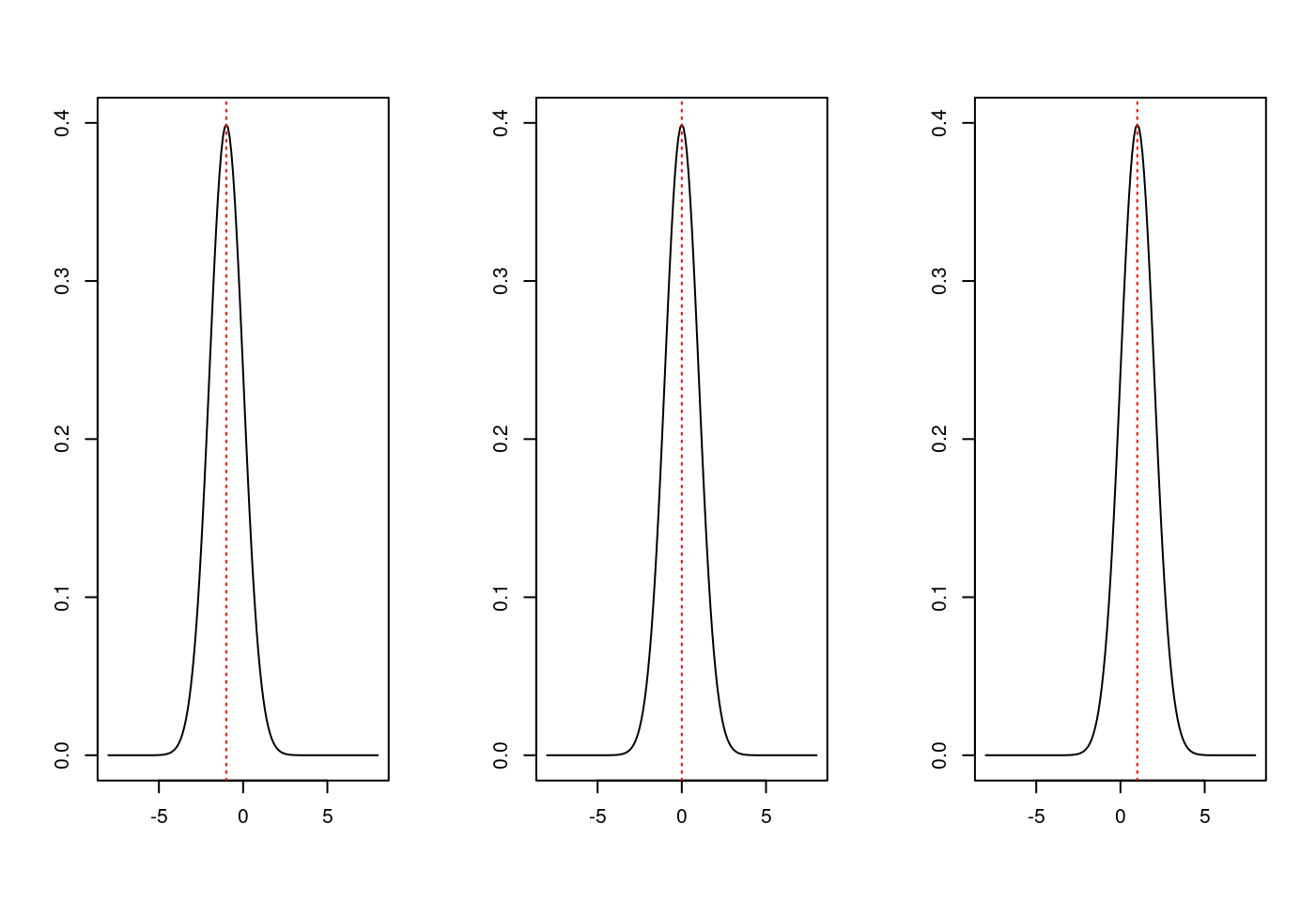
- 加上三條垂直線,中間那一條虛線示意平均數所在的位置,旁邊兩條紅色垂直線段個別在
1跟-1,整個\(x\)範圍代表「一倍標準差的範圍」。最後,畫上x軸。
plot(x = x.values,
y = dnorm(x.values, mean = 0, sd = 1),
type = "l",
ylim = c(0,.4),
xlab = "",
ylab = "",
axes = FALSE,
main = "標準常態分配")
abline(v = 0, lty = "dashed")
lines(c(1, 1), c(0, dnorm(1)), col = "blue")
lines(c(-1, -1), c(0, dnorm(-1)), col = "blue")
axis(1, at = seq(-4, 4, 1), pos = 0)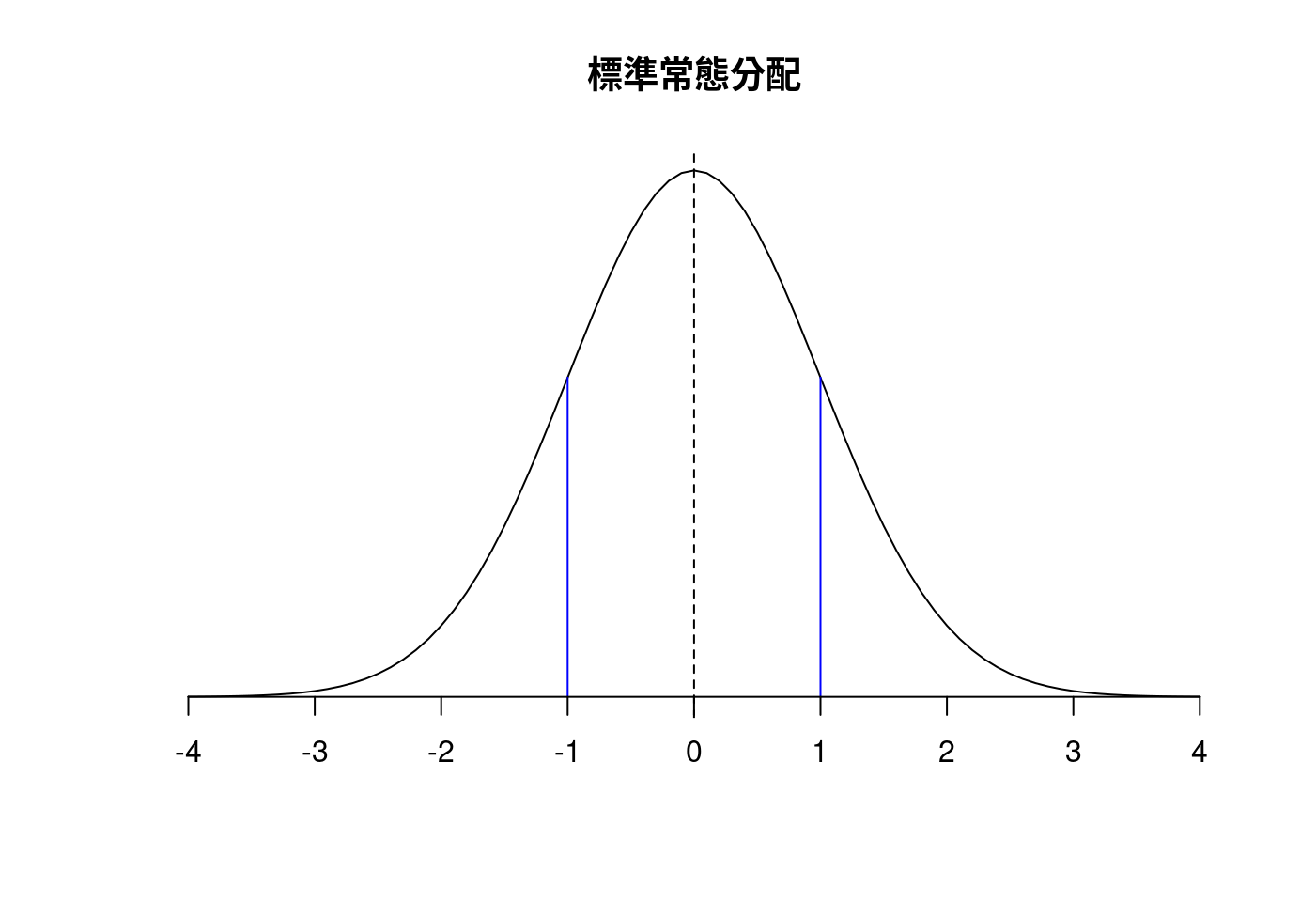
接下來,讓我們看看數個常態分配之間的關係。
8.5.4.3.4 計算思維練習題:畫出維基百科的常態分配示意圖。
8.5.5 常態分配的大小事
這裡作者想談論常態分配的理論,並且嘗試示範程式跟理論的一致性。雖然談理論,但是這裡沒有證明,沒有處處都是符號,只用例子示範理論的結果。
8.5.5.1 期望值
\[\mu\]
integrand <- function(x) {x * dnorm(x, mean = 0, sd = 1)}
integrate(integrand, -Inf, Inf) ## works## 0 with absolute error < 0integrand <- function(x) {x * dnorm(x, mean = 1, sd = 1)}
integrate(integrand, -Inf, Inf) ## works## 1 with absolute error < 0.00000044integrand <- function(x) {x * dnorm(x, mean = 1, sd = 2)}
integrate(integrand, -Inf, Inf) ## works## 1 with absolute error < 0.0000000318.5.5.2 變異數與標準差
8.5.5.2.2 變異數
\[\sigma^2\]
integrand <- function(x) {(x - 0)^2 * dnorm(x, mean = 0, sd = 1)}
integrate(integrand, -Inf, Inf) ## works## 1 with absolute error < 0.00000012integrand <- function(x) {(x - 1)^2 * dnorm(x, mean = 1, sd = 1)}
integrate(integrand, -Inf, Inf) ## works## 1 with absolute error < 0.00000054integrand <- function(x) {(x - 1)^2 * dnorm(x, mean = 1, sd = 2)}
integrate(integrand, -Inf, Inf) ## works## 4 with absolute error < 0.000000178.5.5.3 偏度與扁度
8.5.5.4 常態分配之形變
比如說,根據變異數的定義與相關定理,可以證明以下結果。還有一件事很重要,標準常態分配形變之後是某一種常態分配。
\[N(0, 1^2)/2 = N(0, (1/2)^2)\]
8.5.5.4.1 如果不會推導、如果不知道\(N(0, 1^2)/2\)的機率密度函數。
integrand <- function(x) {x/2 * dnorm(x, mean = 0, sd = 1)}
integrate(integrand, -Inf, Inf) ## works## 0 with absolute error < 0integrand <- function(x) {(x/2 - 0)^2 * dnorm(x, mean = 0, sd = 1)}
integrate(integrand, -Inf, Inf) ## works## 0.25 with absolute error < 0.0000000298.5.5.4.2 如果會推導、如果知道\(N(0, 1^2)/2\)的機率密度函數。
integrand <- function(x) {x * dnorm(x, mean = 0, sd = 1/2)}
integrate(integrand, -Inf, Inf) ## works## 0 with absolute error < 0integrand <- function(x) {(x - 0)^2 * dnorm(x, mean = 0, sd = 1/2)}
integrate(integrand, -Inf, Inf) ## works## 0.25 with absolute error < 0.000000248.5.5.5 兩獨立之常態分配相加
比如說,獨立的常態分配相加還是常態分配,新的分配的平均數等於原始分配的平均數全部加起來,至於變異數也一樣,所以標準差的結果就很明顯了。還有一件事很重要,只要獨立成立,再多個常態分配相加,結果都會是某一個常態分配。
\[N(1, 1^2) + N(1, 1^2) = N(2, \sqrt{2}^2)\]
8.5.6 我要更常態!
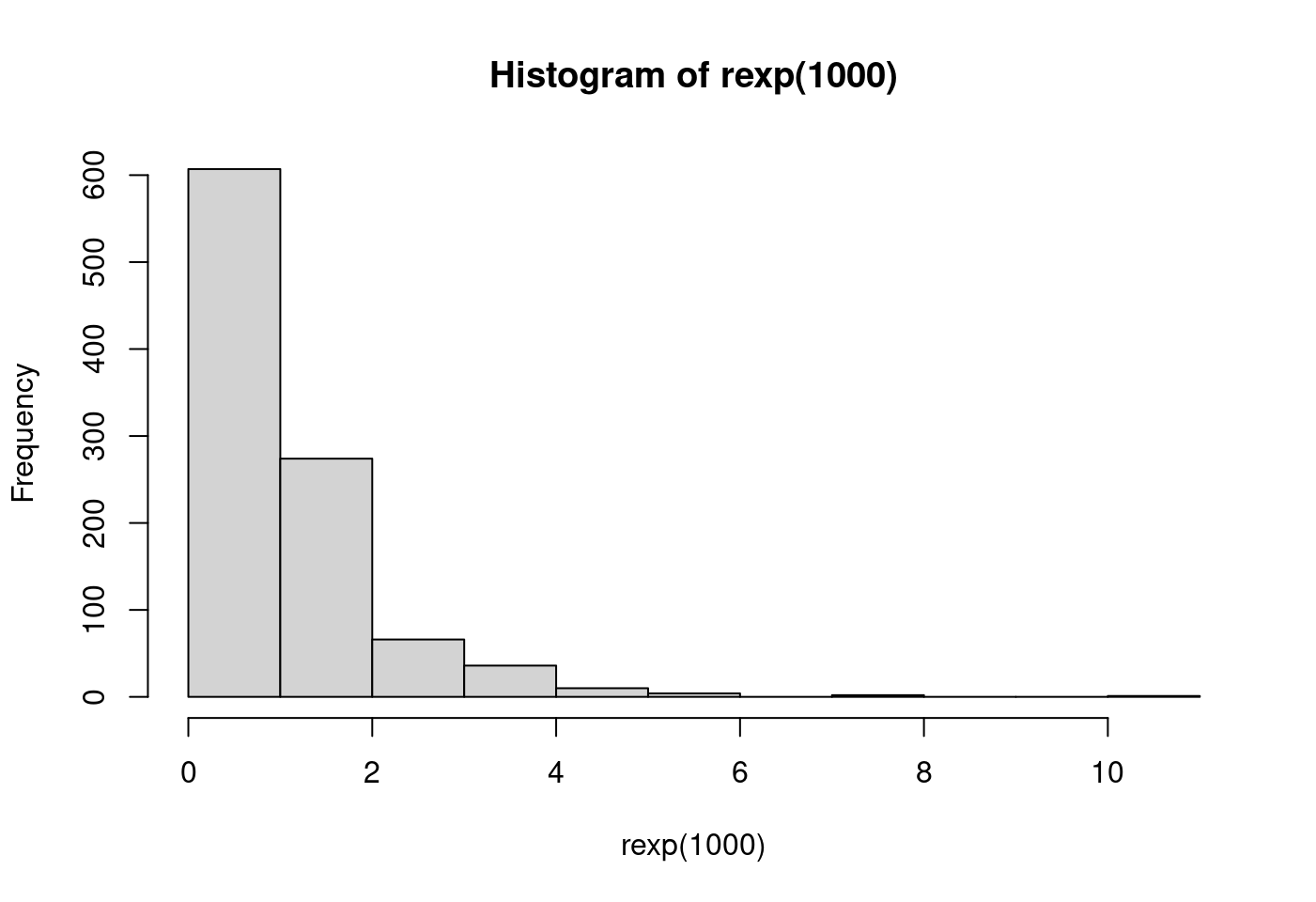
set.seed(1233)
x <- rexp(1000)
moments::skewness(x)## [1] 2.528778hist(log(x))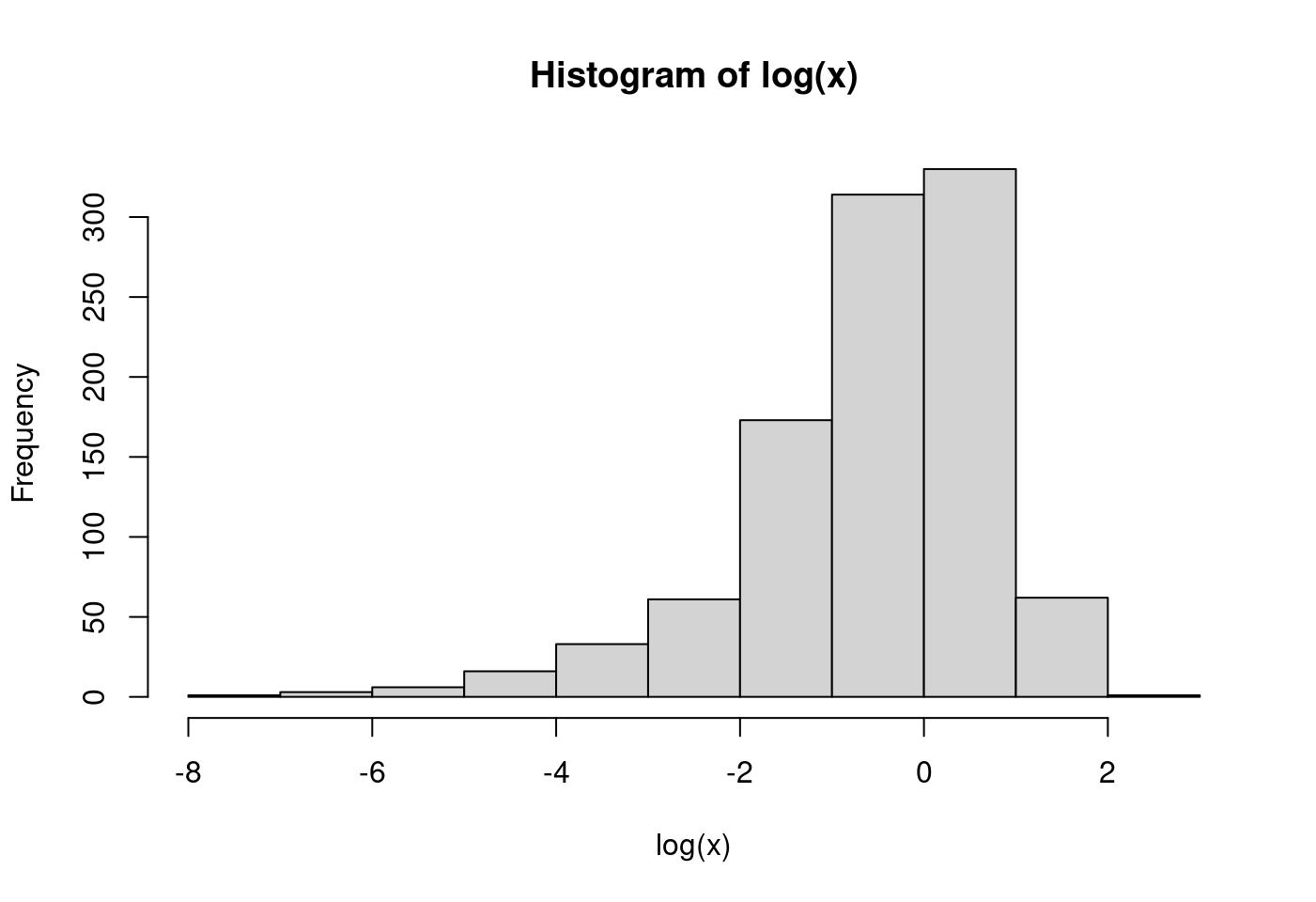
moments::skewness(log(x))## [1] -1.365378moments::skewness(sqrt(x))## [1] 0.6361516moments::skewness(x^(1/3))## [1] 0.0792358moments::skewness(1/x)## [1] 21.2052hist(x^(1/3))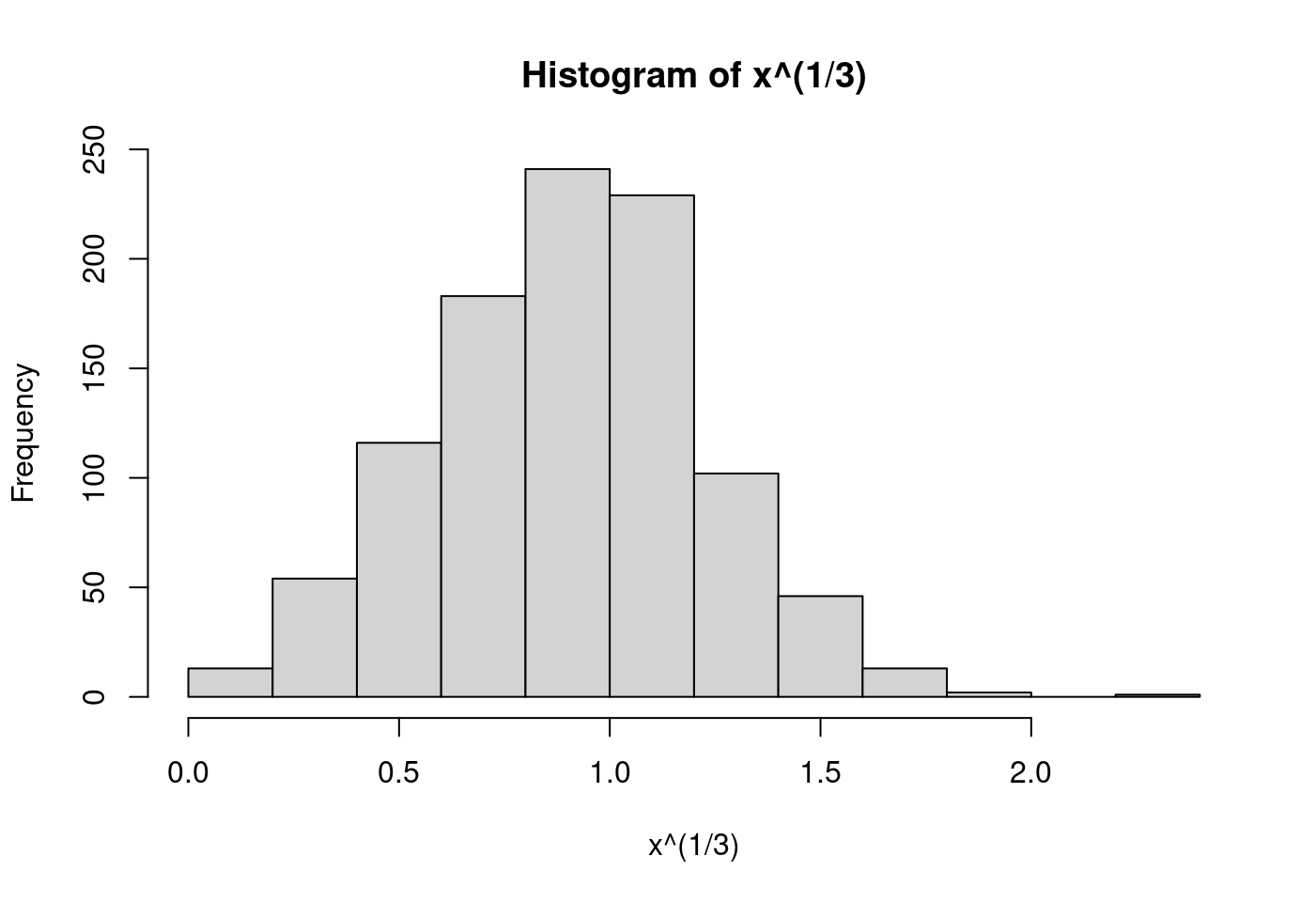
df <- data.frame(x = x,
logx = log(x),
sqrtx = sqrt(x),
cubex = x^(1/3),
invx = 1/x)
ggdensity(df, x = "cubex", fill = "lightgray", title = "x^(1/3)") +
scale_x_continuous(limits = c(-3, 3)) +
stat_overlay_normal_density(color = "red", linetype = "dashed")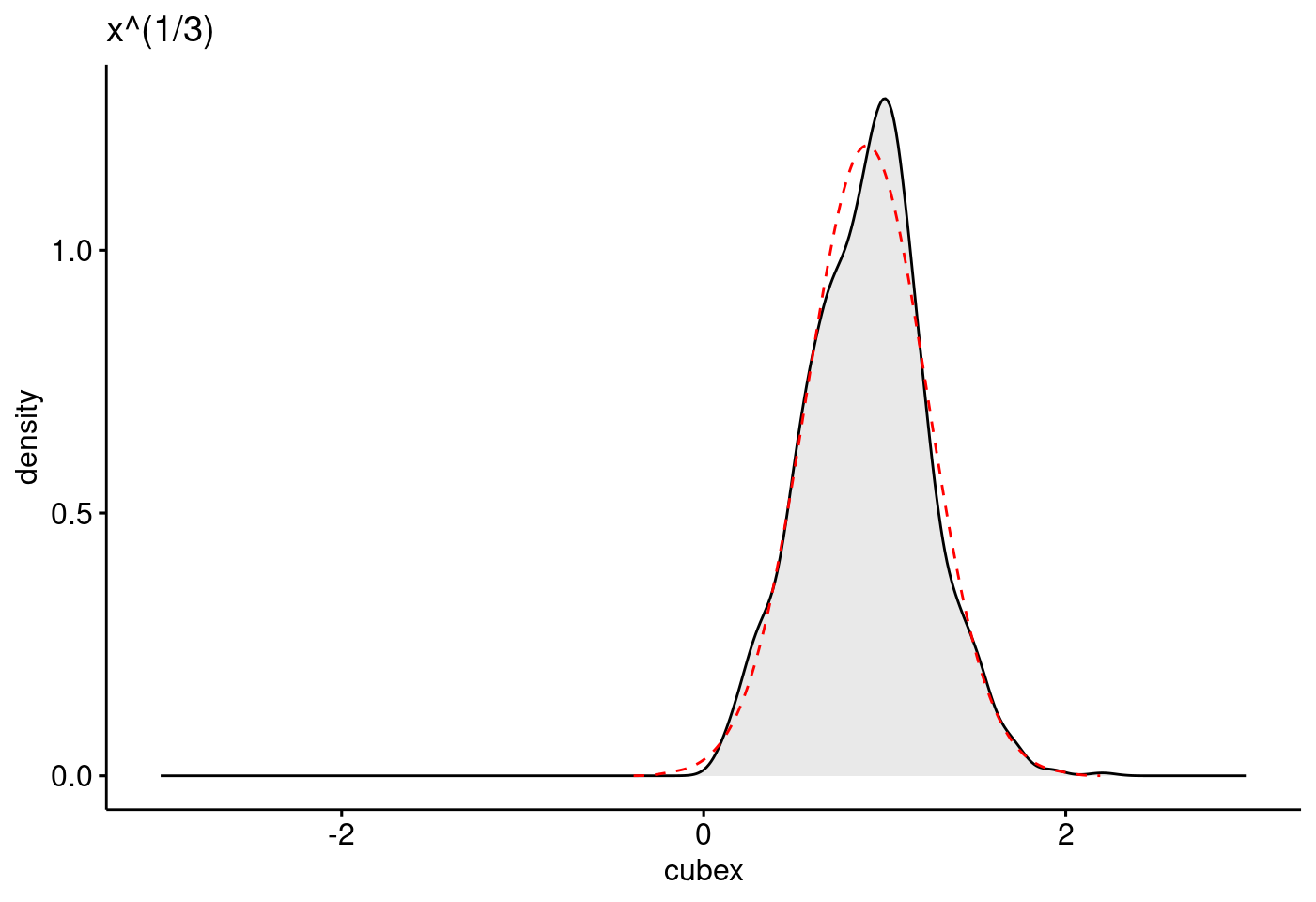
8.5.7 選讀:繪製常態分配圖
在這裡,特別提出來討論繪製常態分配圖,除了作者想談談R的圖學,也希望讀者看倌可以學到繪製常態分配圖的技術,有助於深化撰寫統計報告的能力,因為許許多多統計技術都牽扯常態分配。基本上,畫常態分配圖就是畫常態分配的\(f(x)\)。我們稱呼\(f(x)\)為常態曲線。
8.5.7.1 傳統做法
基本技術有:
- 取範圍。我們沒有無限大的畫圖紙、螢幕,所以要限制範圍。雖然常態密度函數處處大於0,哪裏都是常態機率的一部分,但是一般我們還是「畫重點」,也就是只畫可以涵蓋絕大部分機率的範圍。對於標準常態而言,這一個範圍大概是「正負4」。
- 先劃一條常態曲線。傳統的作法就是呼叫「
plot」幫忙。 - 再加其他常態曲線。由於在同一張畫布上加線,所以我們請「
lines」幫忙。 - 示意每一條常態曲線的特殊意義。在畫布上註記足以分辨彼此的文字,要請「
legend」幫忙。 - 當然,畫圖就是要準備座標,\((x, y)\),其中的\(x\)就是第一個動作的成果,而\(y = f(x)\)就是請「
dnorm」來幫忙。
看程式碼時,只要一步一步往下看,看出段落就看出想得到什麼需要什麼程式碼?
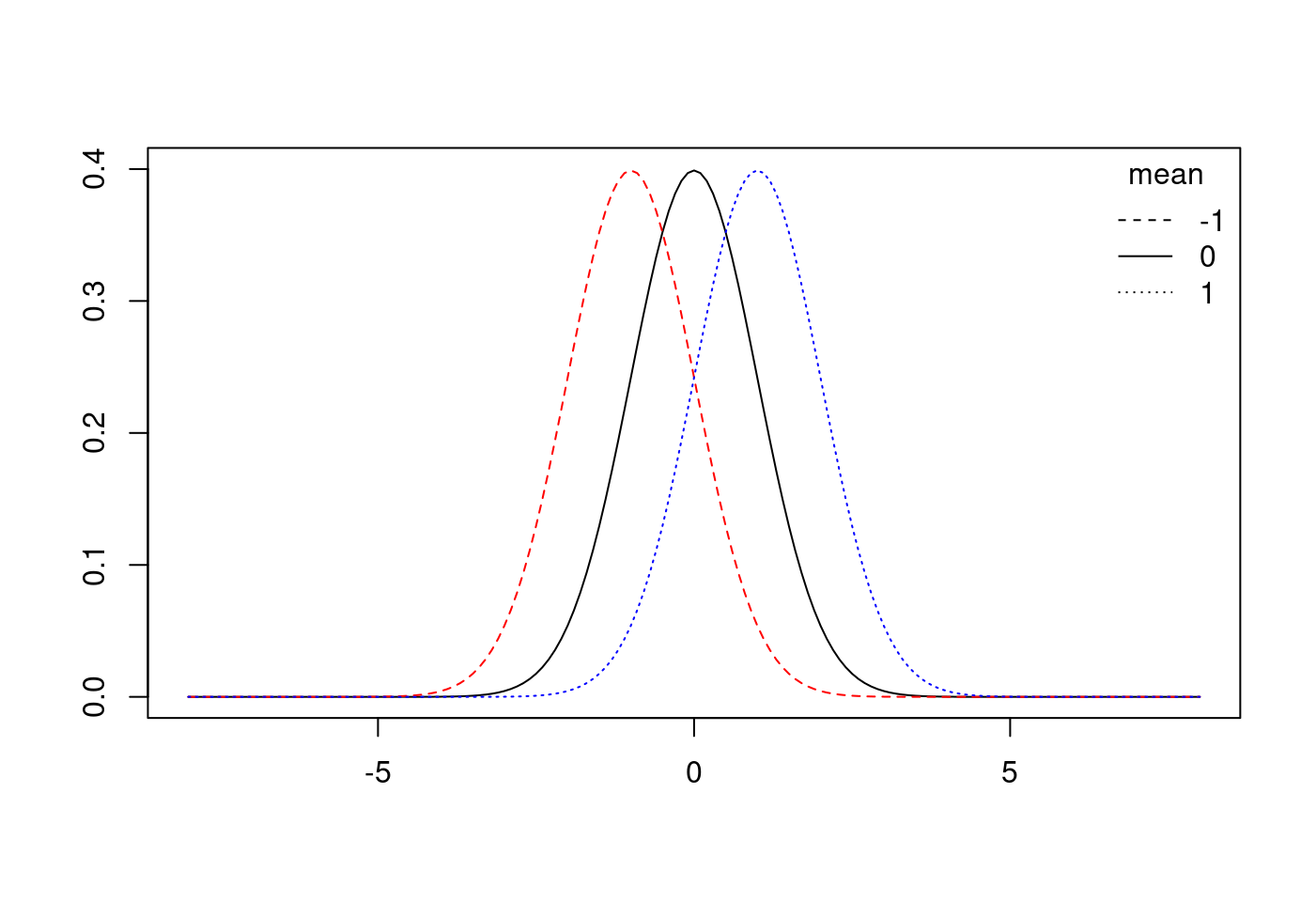
8.5.7.1.1 標準常態分配往右或是往左移動
# 1.
x.values <- seq(-8, 8, 0.1)
# 2.
plot(x = x.values,
y = dnorm(x.values, mean = 0, sd = 1),
type = "l",
ylim = c(0,.4),
xlab = "",
ylab = "")
# 3.
lines(x.values,
dnorm(x.values, mean = -1, sd = 1),
col = "red")
# 4.
lines(x.values,
dnorm(x.values, mean = 1, sd = 1),
col = "blue")
# 5.
legend("topright",
title = "mean",
legend = c("-1","0","1"),
lty = c("solid","solid","solid"),
col = c("red","black","blue"),
bty = "n")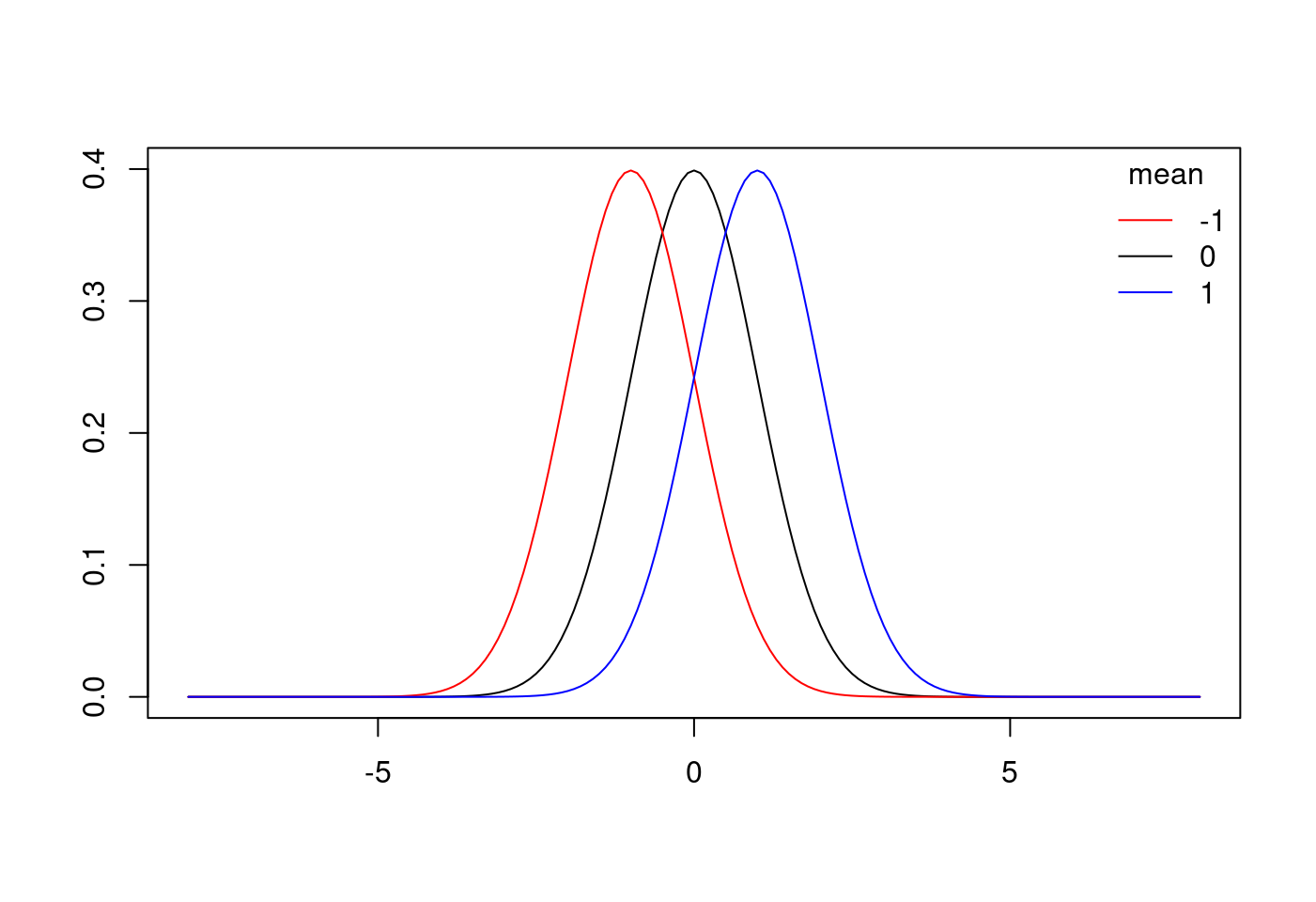
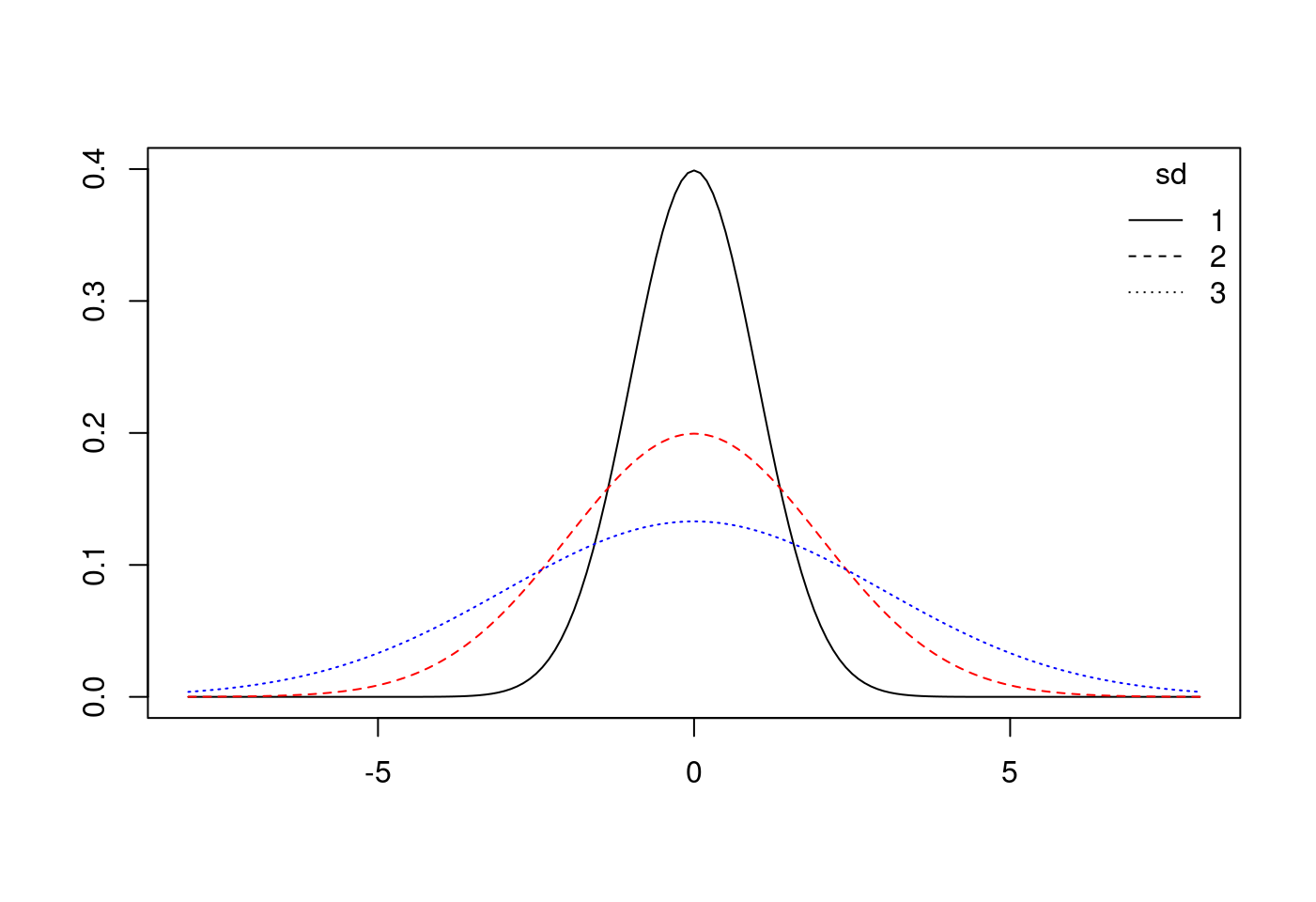
8.5.7.1.2 標準常態分配會變胖
x.values <- seq(-8, 8, 0.1)
plot(x = x.values,
y = dnorm(x.values, mean = 0, sd = 1),
type = "l",
ylim = c(0,.4),
xlab = "",
ylab = "")
lines(x.values,
dnorm(x.values, mean = 0, sd = 2),
col = "red")
lines(x.values,
dnorm(x.values, mean = 0, sd = 3),
col = "blue")
legend("topright",
title = "sd",
legend = c("1","2","3"),
lty = c("solid","solid","solid"),
col = c("black","red","blue"),
bty = "n")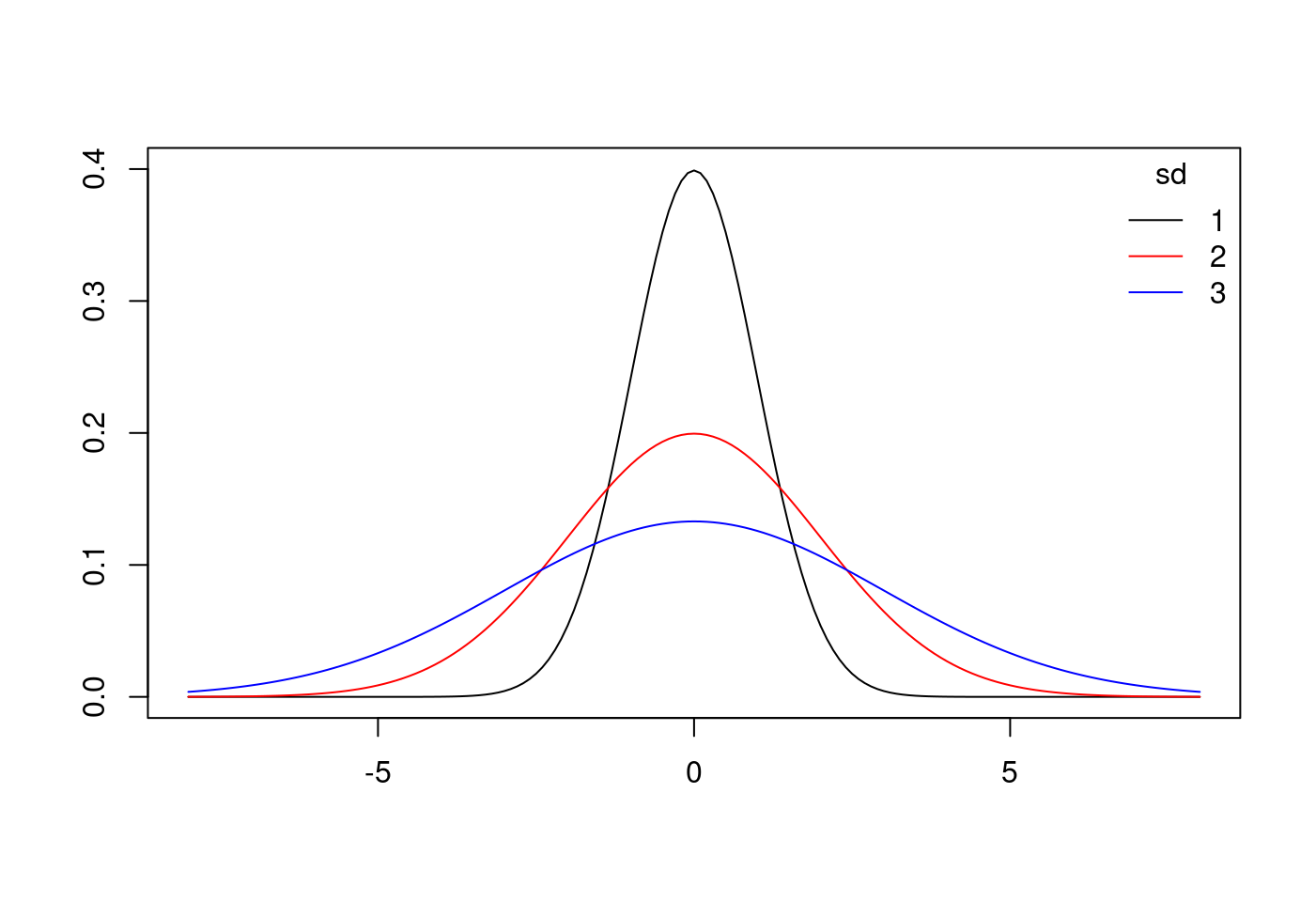
8.5.7.2 ggplot2的作法
8.5.7.2.3 標準常態分配
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black")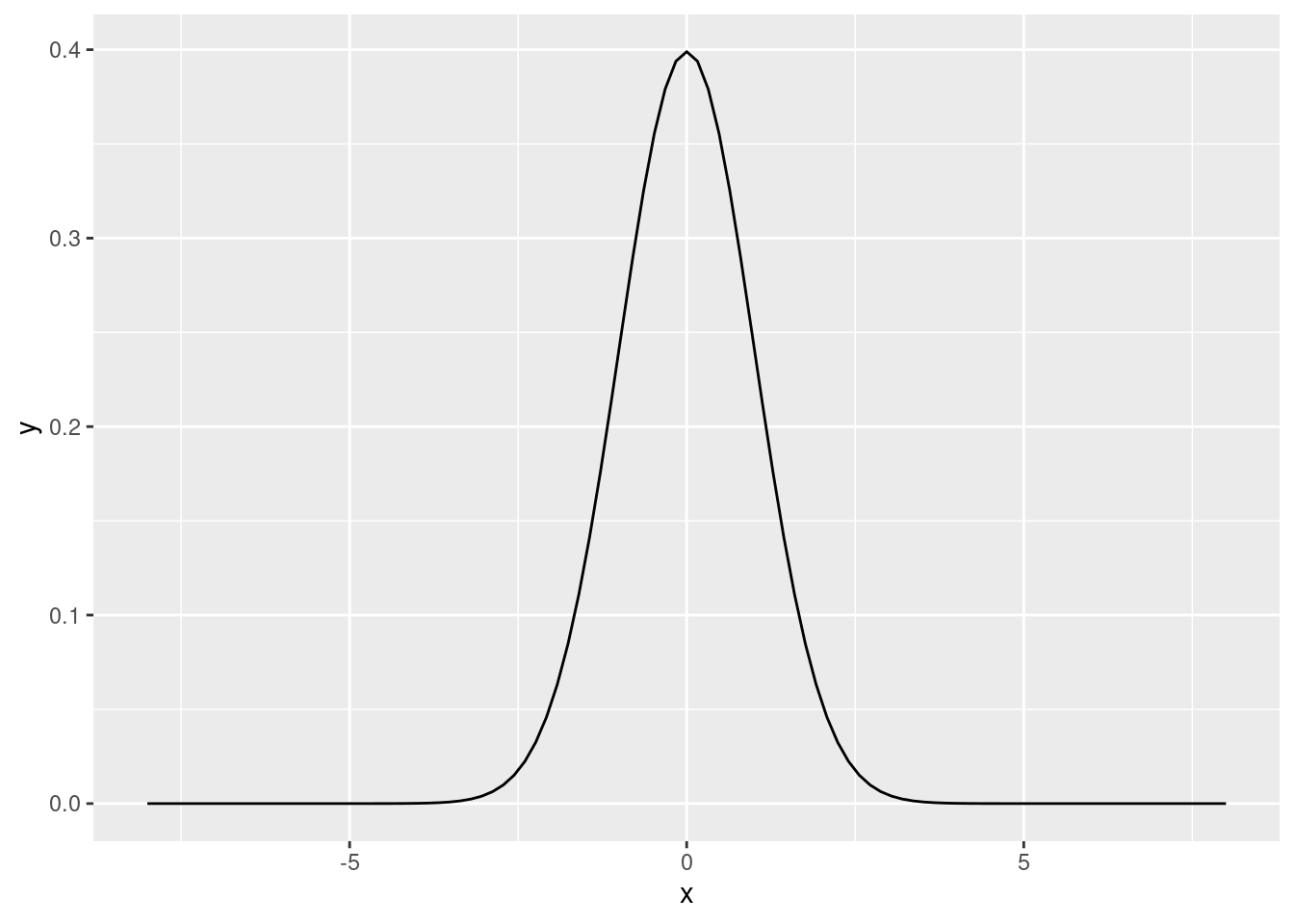
8.5.7.2.4 標準常態分配往右或是往左移動
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black") +
stat_function(fun = dnorm, args = list(1, 1), colour = "blue") +
stat_function(fun = dnorm, args = list(-1, 1), colour = "red")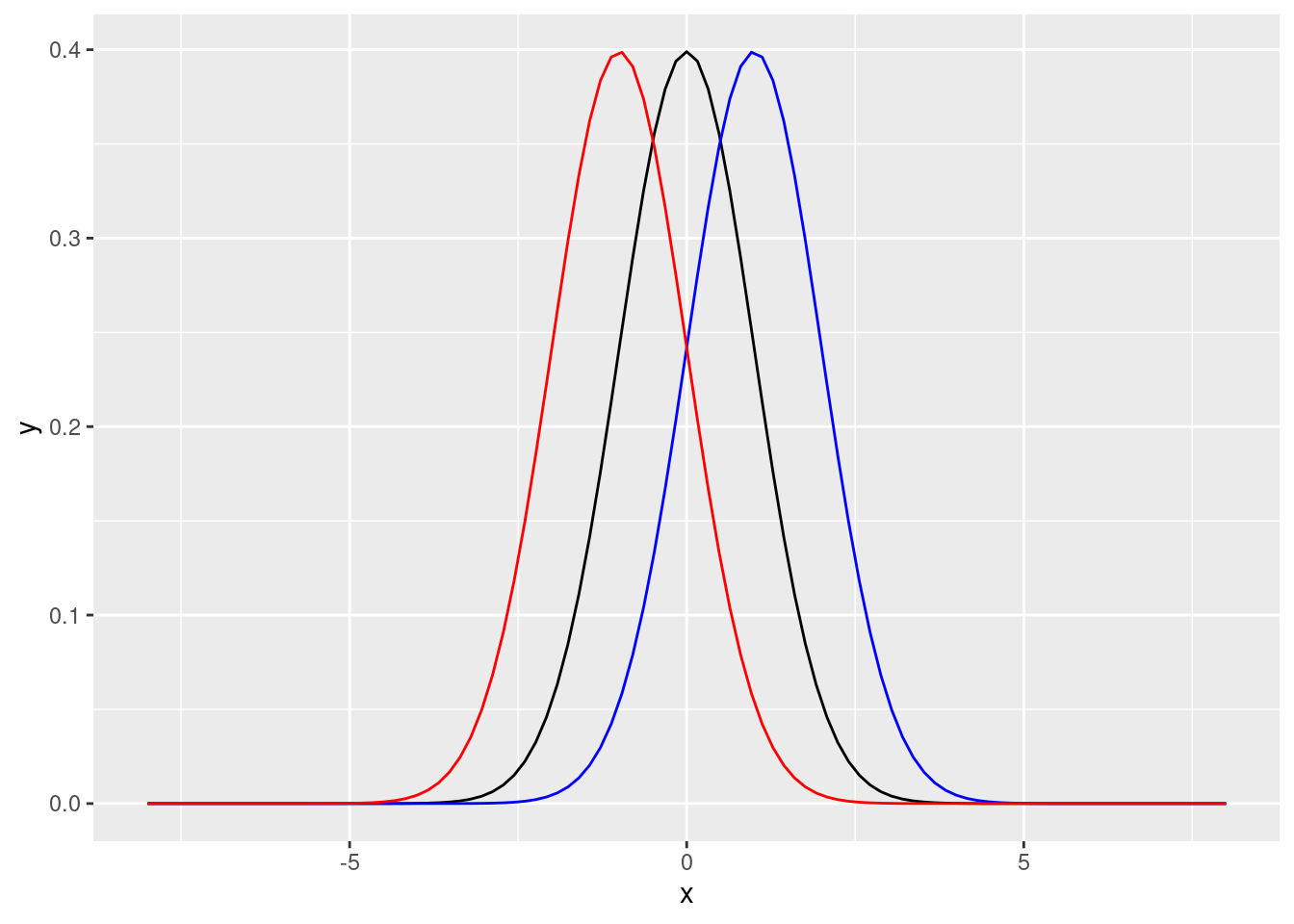
8.5.7.2.5 標準常態分配會變胖
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black") +
stat_function(fun = dnorm, args = list(0, 2), colour = "red") +
stat_function(fun = dnorm, args = list(0, 3), colour = "blue")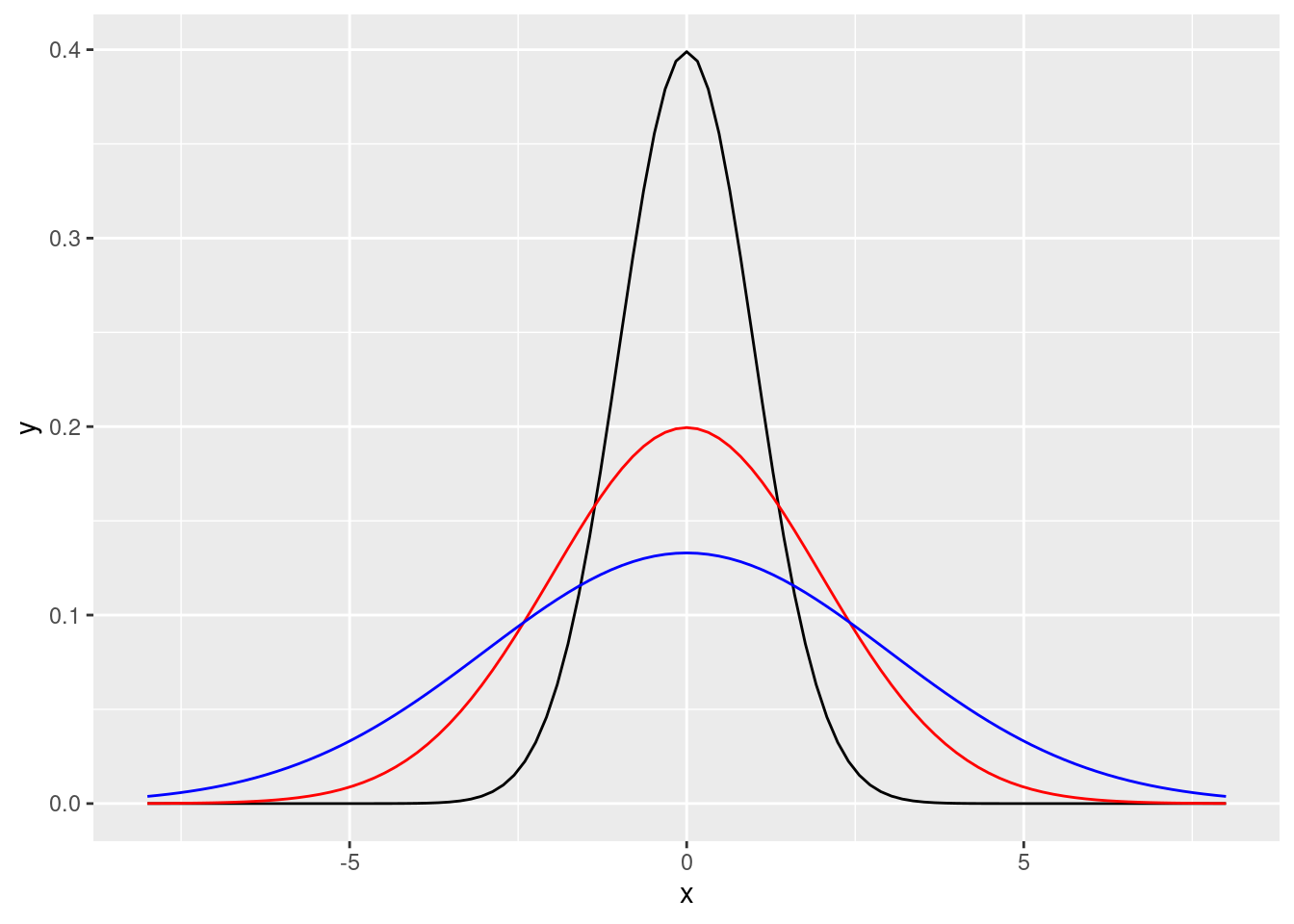
8.5.7.2.6 標準常態分配位移加形變
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black") +
stat_function(fun = dnorm, args = list(-1, 1), colour = "red") +
stat_function(fun = dnorm, args = list(1, 2), colour = "blue")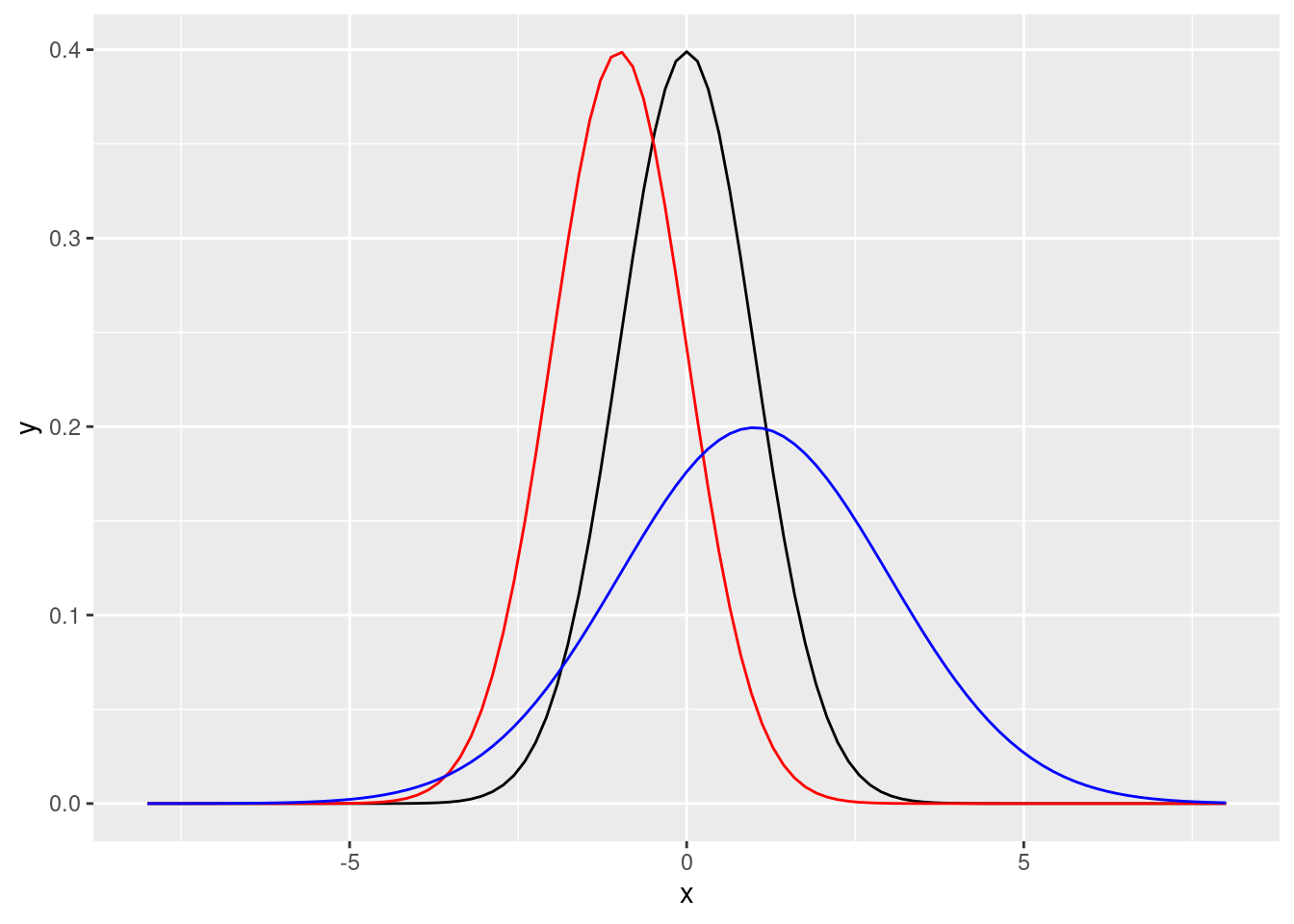
8.5.7.2.7 加上x軸標籤跟y軸標籤
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black") +
stat_function(fun = dnorm, args = list(-1, 1), colour = "red") +
stat_function(fun = dnorm, args = list(1, 2), colour = "blue") +
scale_x_continuous(name = "x value") +
scale_y_continuous(name = "Density")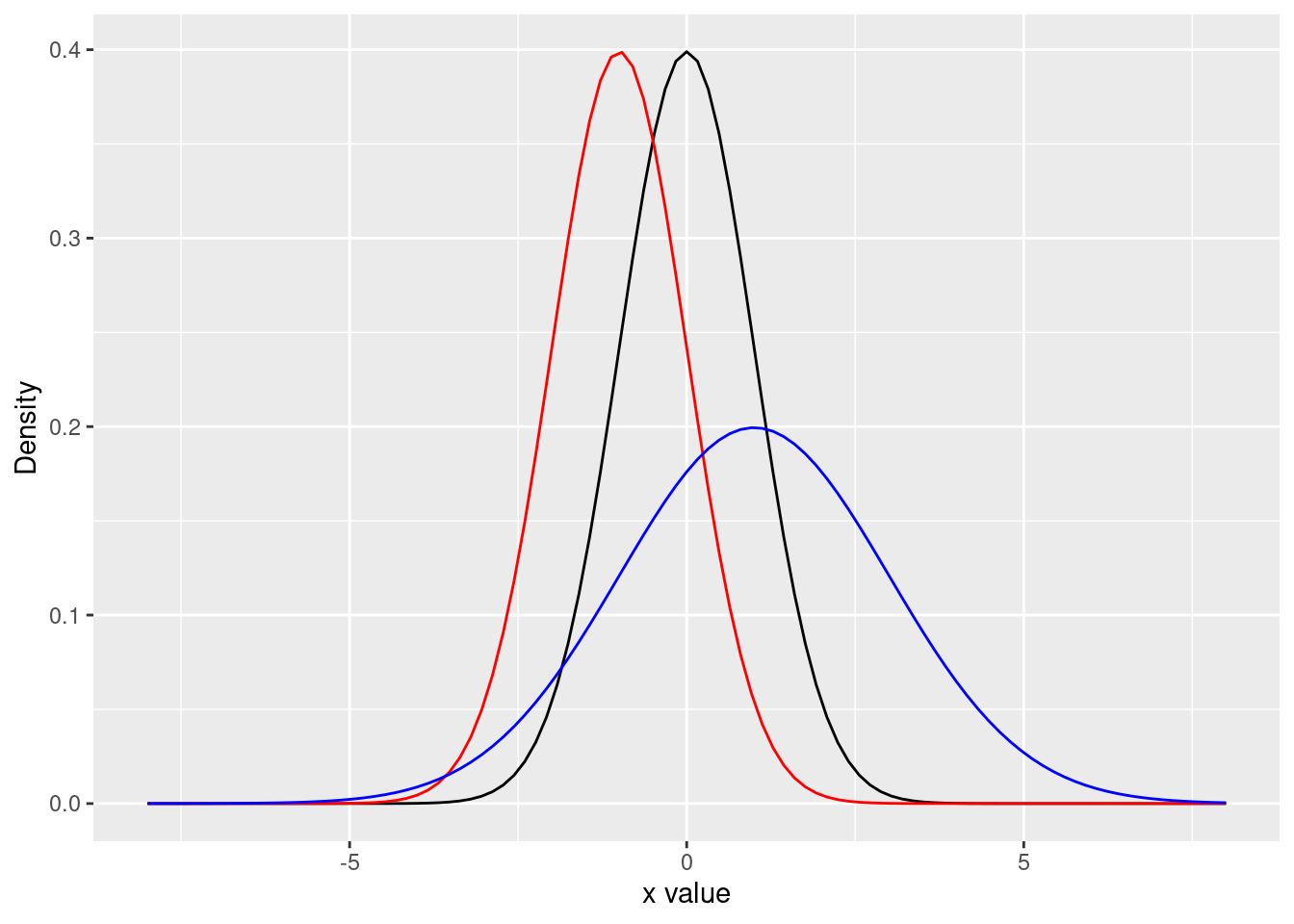
8.5.7.2.8 再加上圖標
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black") +
stat_function(fun = dnorm, args = list(-1, 1), colour = "red") +
stat_function(fun = dnorm, args = list(1, 2), colour = "blue") +
scale_x_continuous(name = "x value") +
scale_y_continuous(name = "Density") +
ggtitle("Normal function curves of probabilities")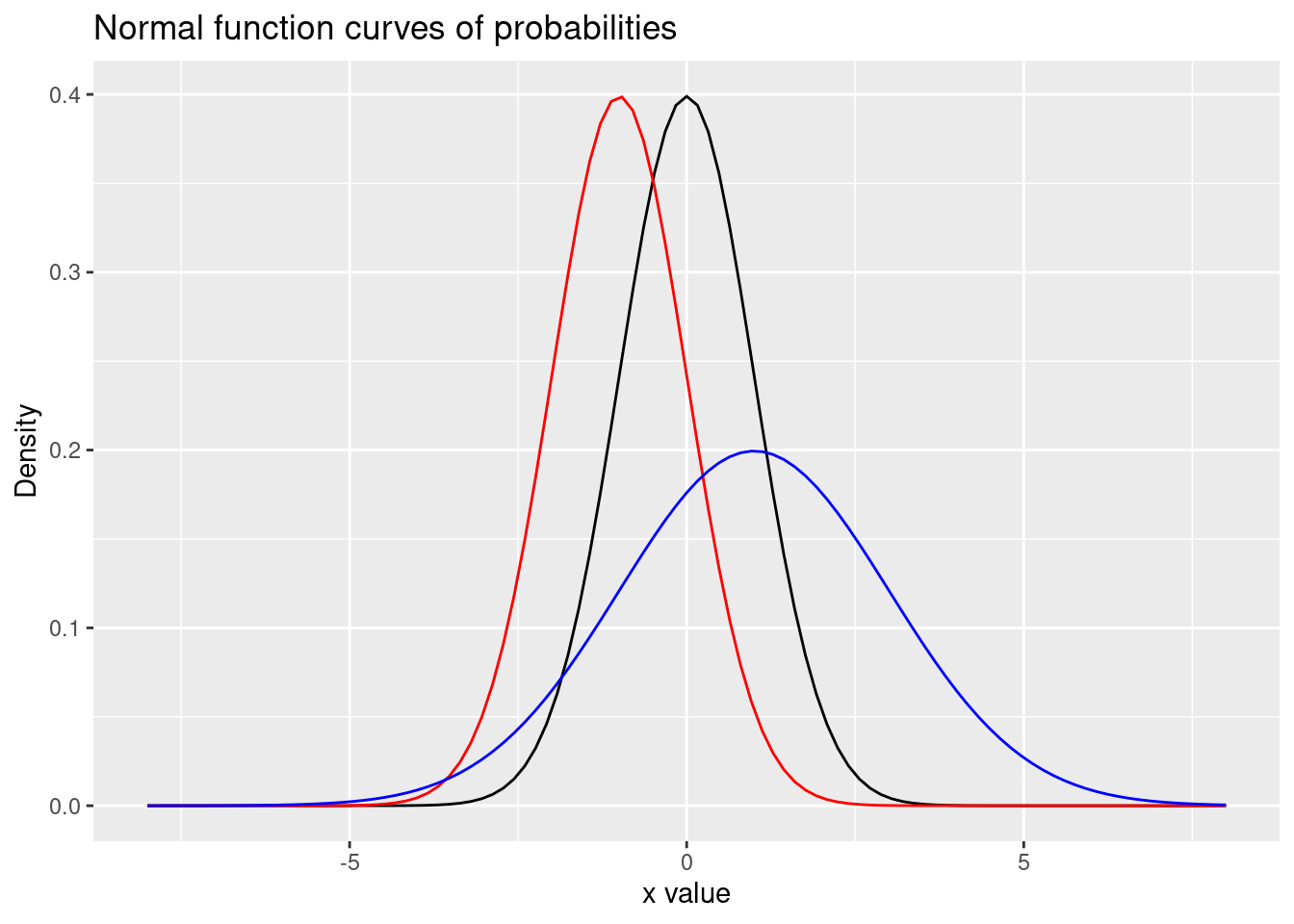
8.5.7.2.9 換成中文
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black") +
stat_function(fun = dnorm, args = list(-1, 1), colour = "red") +
stat_function(fun = dnorm, args = list(1, 2), colour = "blue") +
scale_x_continuous(name = "x") +
scale_y_continuous(name = "密度") +
ggtitle("常態機率分配")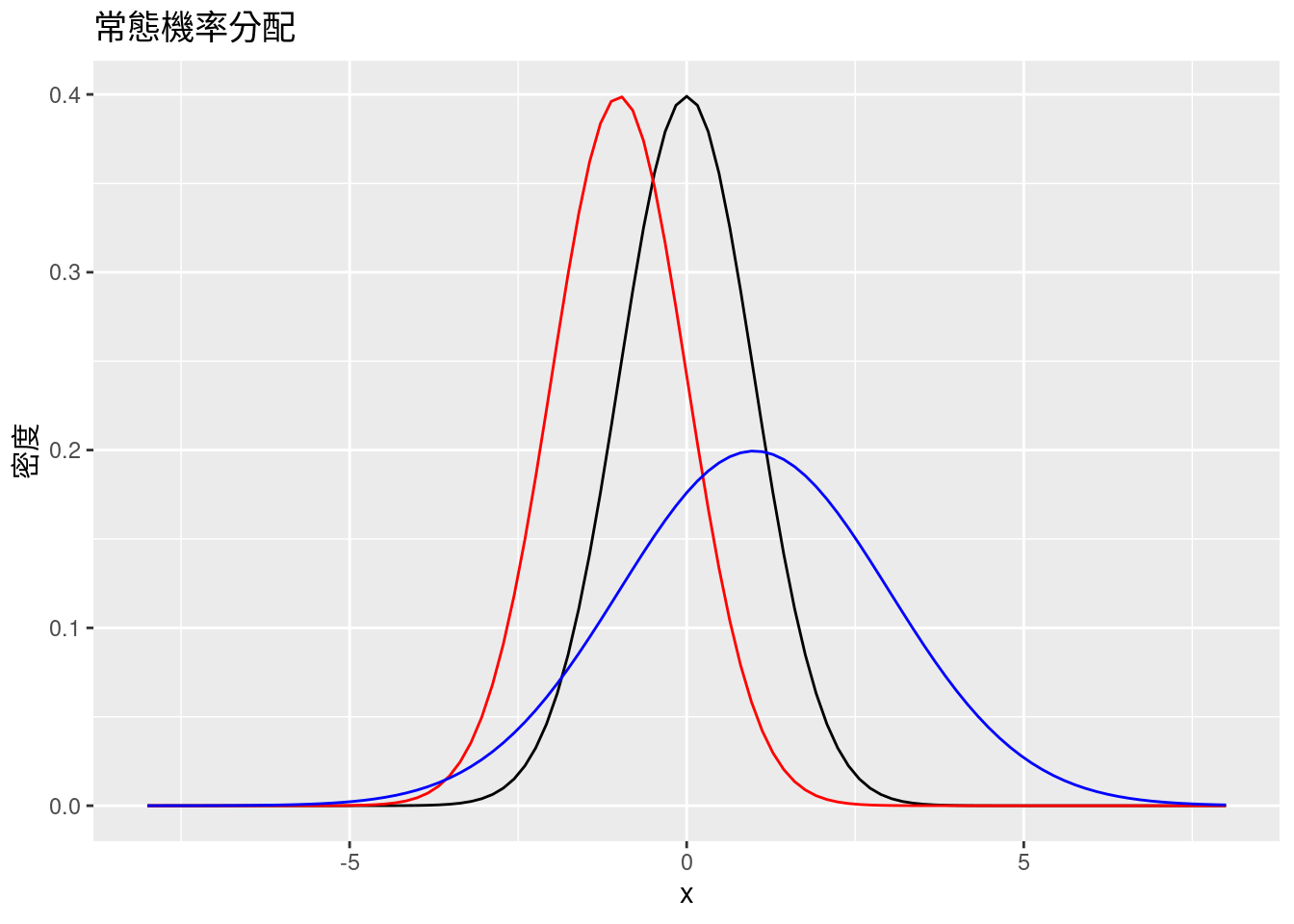
8.5.7.2.10 換x軸範圍並且把圖標置中
DF <- data.frame(x = c(-6, 8))
ggplot(DF, aes(x = x)) +
stat_function(fun = dnorm, args = list(0, 1), colour = "black") +
stat_function(fun = dnorm, args = list(-1, 1), colour = "red") +
stat_function(fun = dnorm, args = list(1, 2), colour = "blue") +
scale_x_continuous(name = "x") +
scale_y_continuous(name = "密度") +
ggtitle("常態機率分配") +
theme(plot.title = element_text(hjust = 0.5))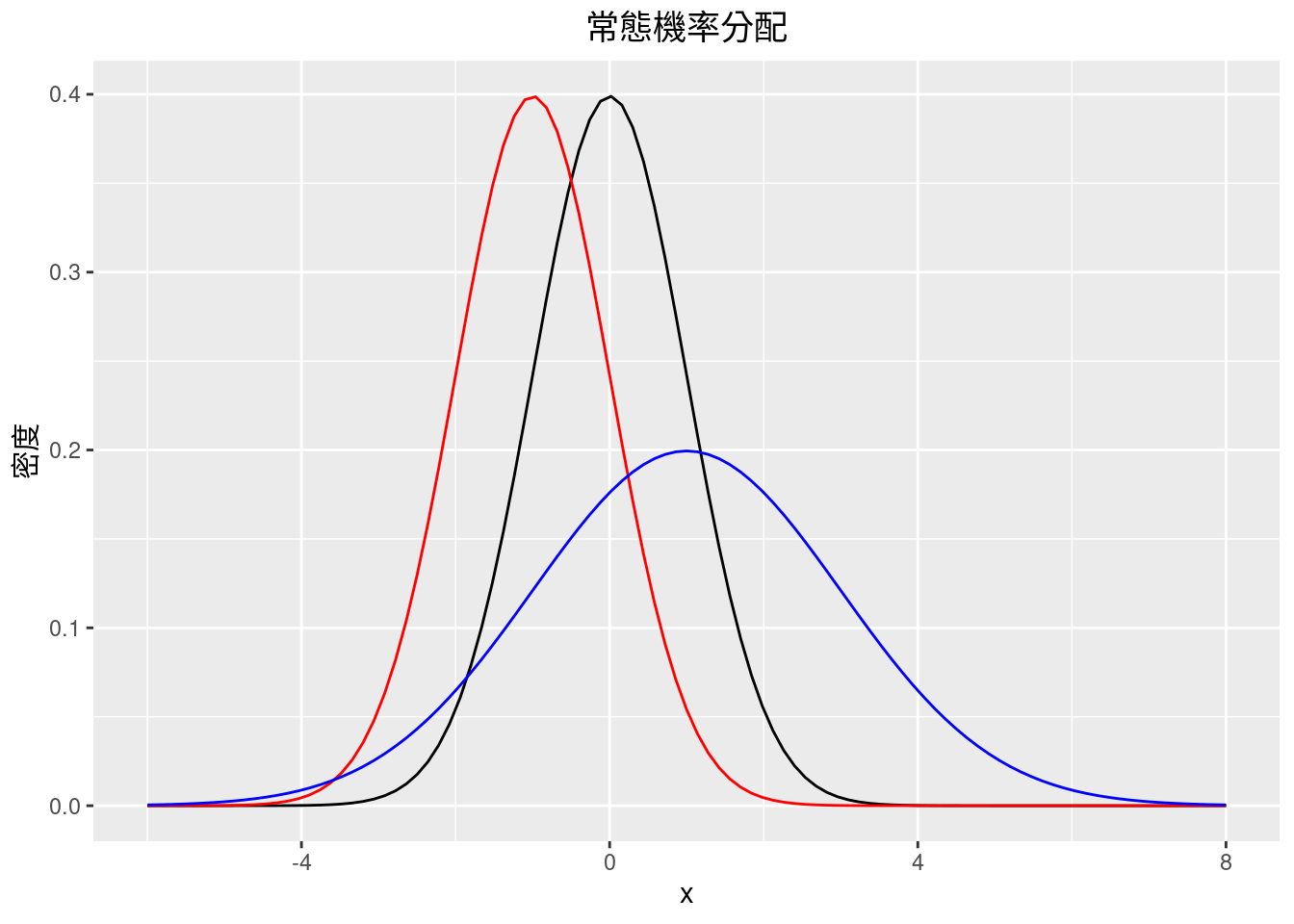
8.5.7.3 繪製常態機率密度函數下的面積
我們一樣請套件ggplot2來幫忙。這裡要學習自訂函式的本事,自訂函式如何加入stat_function,就是以下這一個funcShaded函式要加入stat_function並且以綠色示意面積的範圍。
8.5.7.3.1 標準常態機率密度函數小於1.0的面積
score <- 1
m <- 0
std <- 1
funcShaded <- function(x, lower_bound) {
y = dnorm(x, mean = m, sd = std)
y[x > lower_bound] <- NA
return(y)
}
ggplot(data.frame(x = c(-4, 4)), aes(x = x)) +
stat_function(fun = dnorm, args = list(mean = m, sd = std)) +
stat_function(fun = funcShaded,
args = list(lower_bound = score),
geom = "area",
fill = "green",
alpha = .2) +
scale_x_continuous(name = "Score", breaks = seq(-4, 4, std))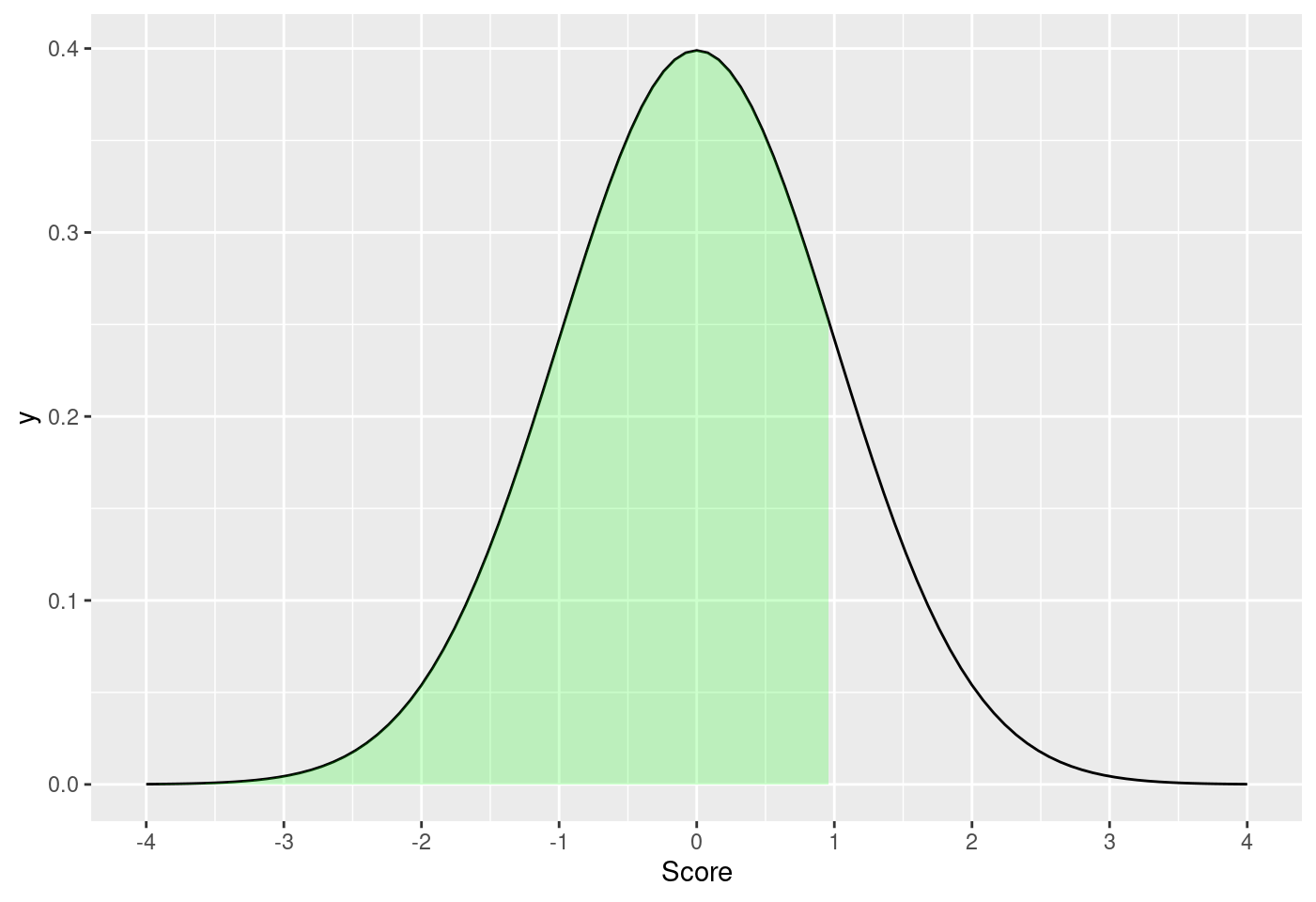
8.5.7.3.2 標準常態機率密度函數大於1.0的面積
score <- 1
m <- 0
std <- 1
funcShaded <- function(x, lower_bound) {
y = dnorm(x, mean = m, sd = std)
y[x < lower_bound] <- NA
return(y)
}
ggplot(data.frame(x = c(-4, 4)), aes(x = x)) +
stat_function(fun = dnorm, args = list(mean = m, sd = std)) +
stat_function(fun = funcShaded,
args = list(lower_bound = score),
geom = "area",
fill = "green",
alpha = .2) +
scale_x_continuous(name = "Score", breaks = seq(-4, 4, std))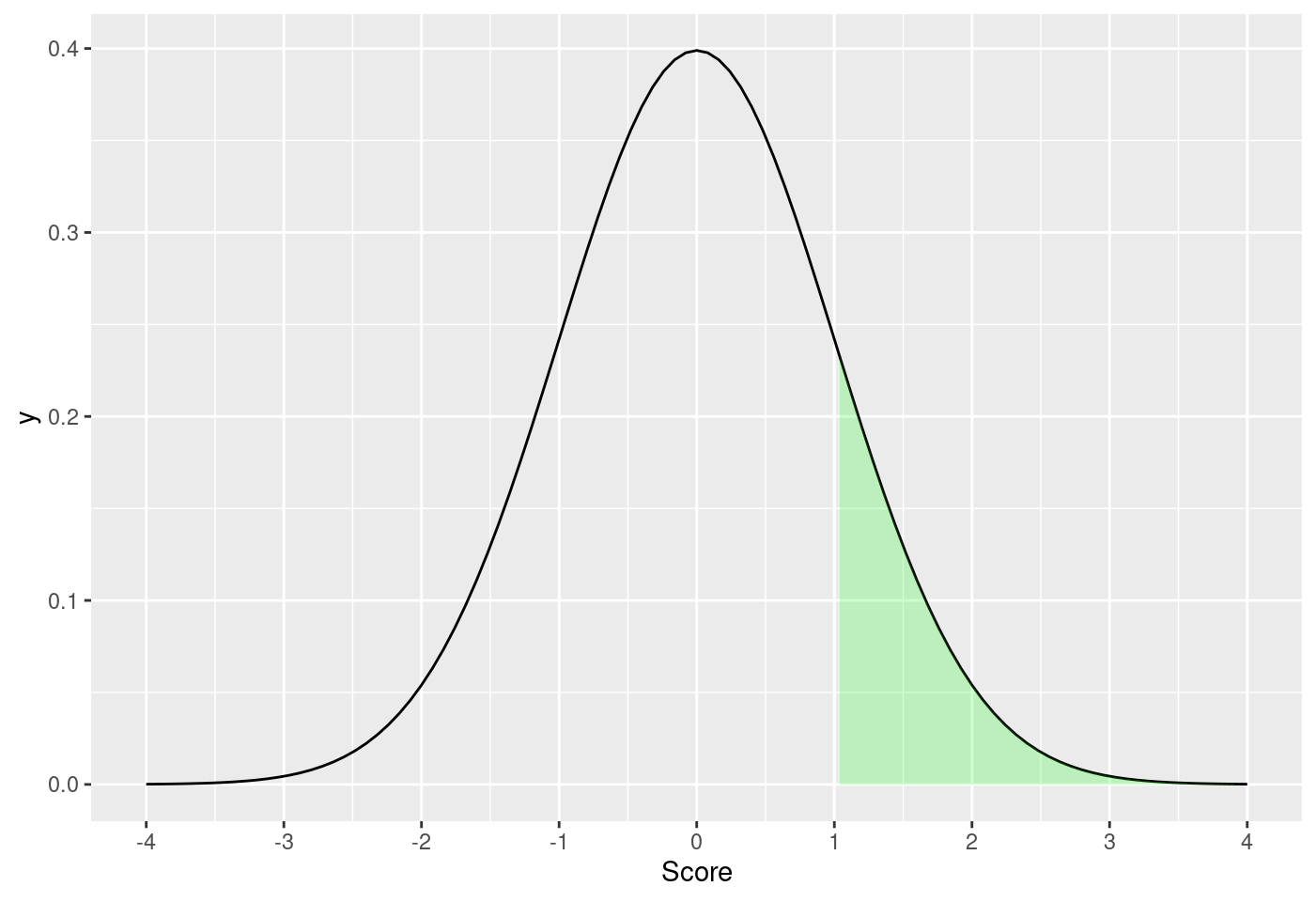
8.5.7.3.3 標準常態機率密度函數小於-1.0或大於1.0的面積
Lscore <- -1
Uscore <- 1
m <- 0
std <- 1
funcShaded <- function(x, lower_bound, up_bound) {
y = dnorm(x, mean = m, sd = std)
y[x > lower_bound & x < up_bound] <- NA
return(y)
}
ggplot(data.frame(x = c(-4, 4)), aes(x = x)) +
stat_function(fun = dnorm, args = list(mean = m, sd = std)) +
stat_function(fun = funcShaded,
args = list(lower_bound = Lscore, up_bound = Uscore),
geom = "area",
fill = "green",
alpha = .2) +
scale_x_continuous(name = "Score", breaks = seq(-4, 4, std))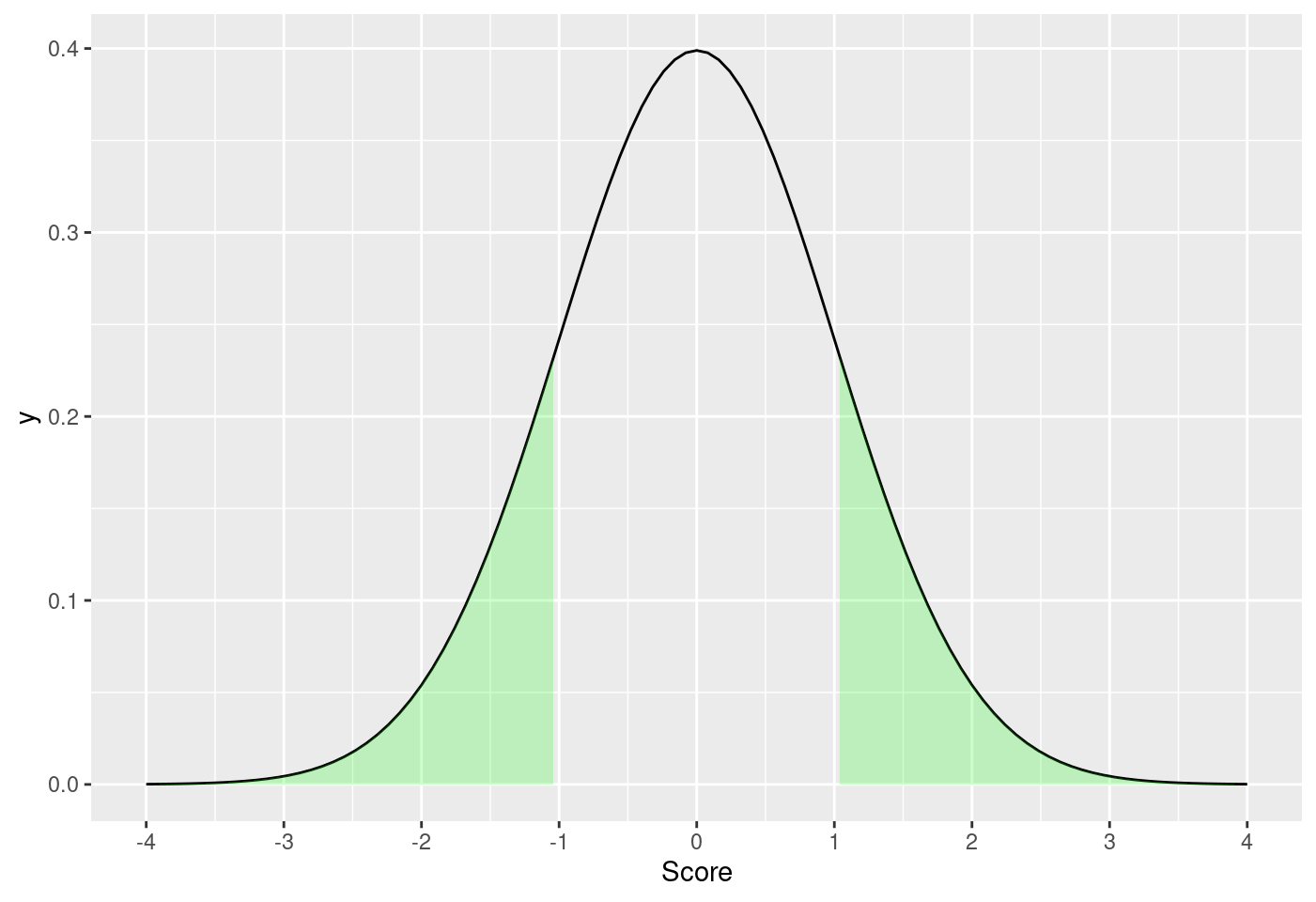
8.5.7.3.4 標準常態機率密度函數大於-1.0且小於1.0的面積
Lscore <- -1
Uscore <- 1
m <- 0
std <- 1
funcShaded <- function(x, lower_bound, up_bound) {
y = dnorm(x, mean = m, sd = std)
y[x < lower_bound | x > up_bound] <- NA
return(y)
}
ggplot(data.frame(x = c(-4, 4)), aes(x = x)) +
stat_function(fun = dnorm, args = list(mean = m, sd = std)) +
stat_function(fun = funcShaded,
args = list(lower_bound = Lscore, up_bound = Uscore),
geom = "area",
fill = "green",
alpha = .2) +
scale_x_continuous(name = "Score", breaks = seq(-4, 4, std))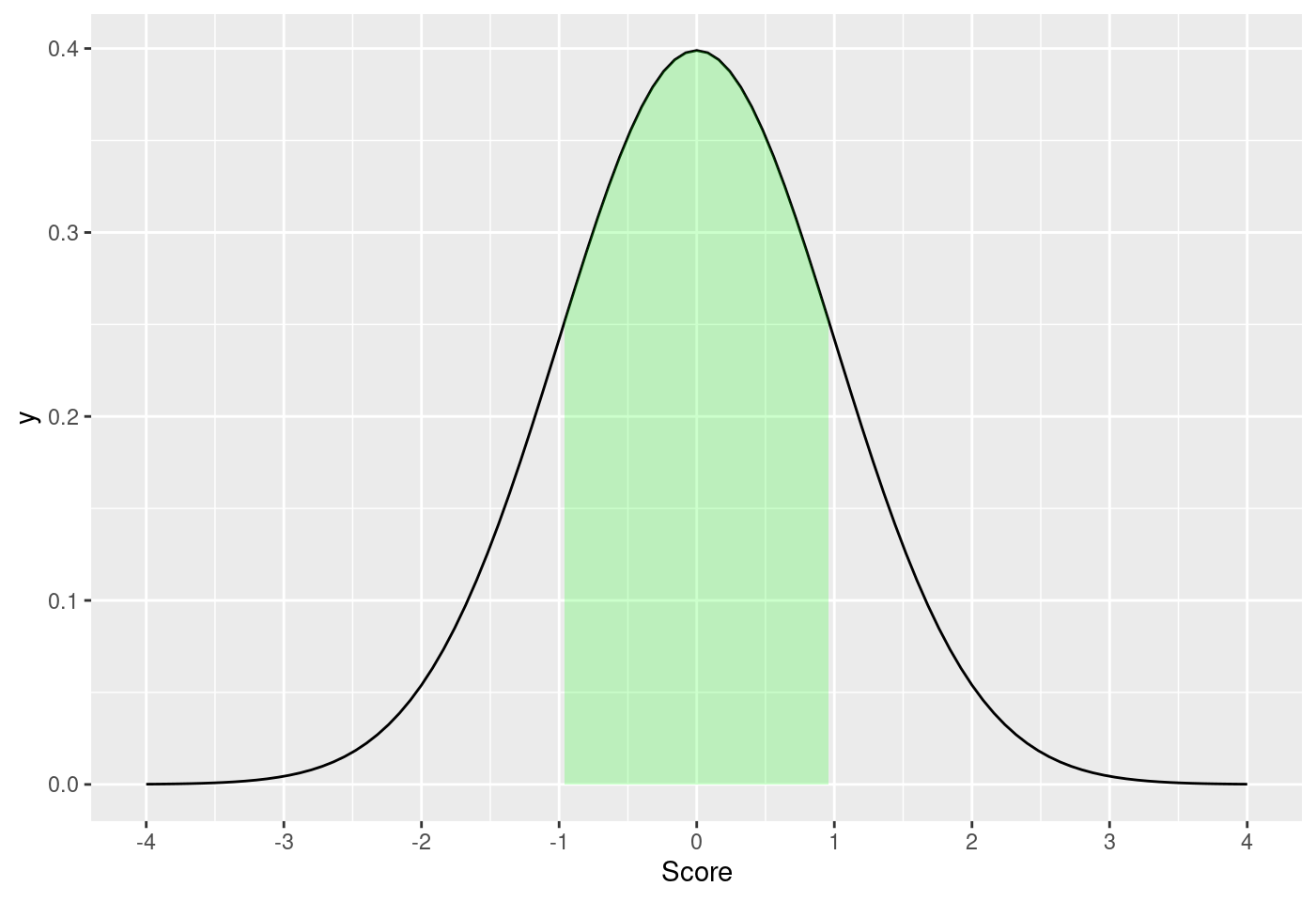
8.6 中央極限定理
繼續談「抽樣分配」。
我們已經知道
- 「把許許多多個獨立的伯努利分配加起來」得到了「二項分配」。
- 「把許許多多個獨立的二項分配加起來」得到了「二項分配」。
- 「二項分配會越來越像常態分配」只要試驗次數越來越多。
- 「把許許多多個彼此獨立的常態分配加起來」還是「常態分配」。
我們還可以得到
把許許多多個彼此獨立的常態分配加起來之後取平均的機率分配是「常態分配」。
後來,更多數學家研究
- 各種許許多多個機率分配加起來之後取平均的機率分配,
造就了最重要的里程碑「中央極限定理」。有了中央極限定理,我們知道
- 可以用常態分配近似樣本平均數的抽樣分配。
有了這個橋梁式的「中央極限定理」,讓我們「猜測某一個分配的平均數」變成可能! </div”>
8.6.1 什麼是中央極限定理?
8.6.1.1 中央極限定理
如果樣本一個接著一個來,每來一個我們就重新計算一次「樣本平均數」,最後那一筆「樣本平均數」的機率分配會是哪一種機率分配呢?
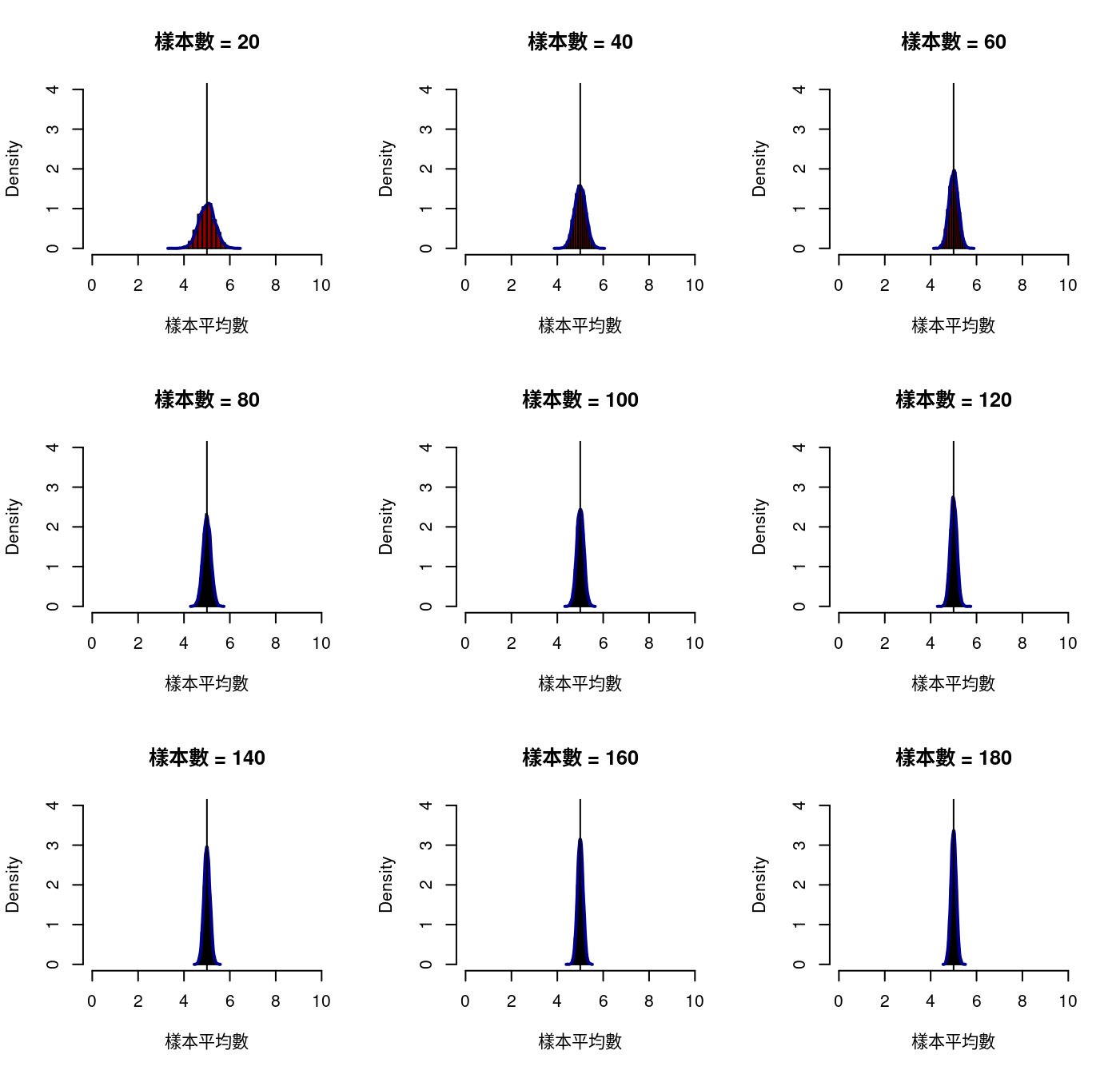
作者必須承認這是一個很難的數學、機率問題。所以,作者回過神來,想請R幫幫忙,為我們示範在「『許許多多次』樣本一個接著一個來,最後那一個『樣本』平均數」之後的「『樣本的(sampling)』次數分配」會長什麼樣子?先讓我們「預知」中央極限定理的數學結果:
\[\bar X_n \overset{d}{\sim} N(\mu, (\frac{\sigma}{\sqrt{n}})^2)\]
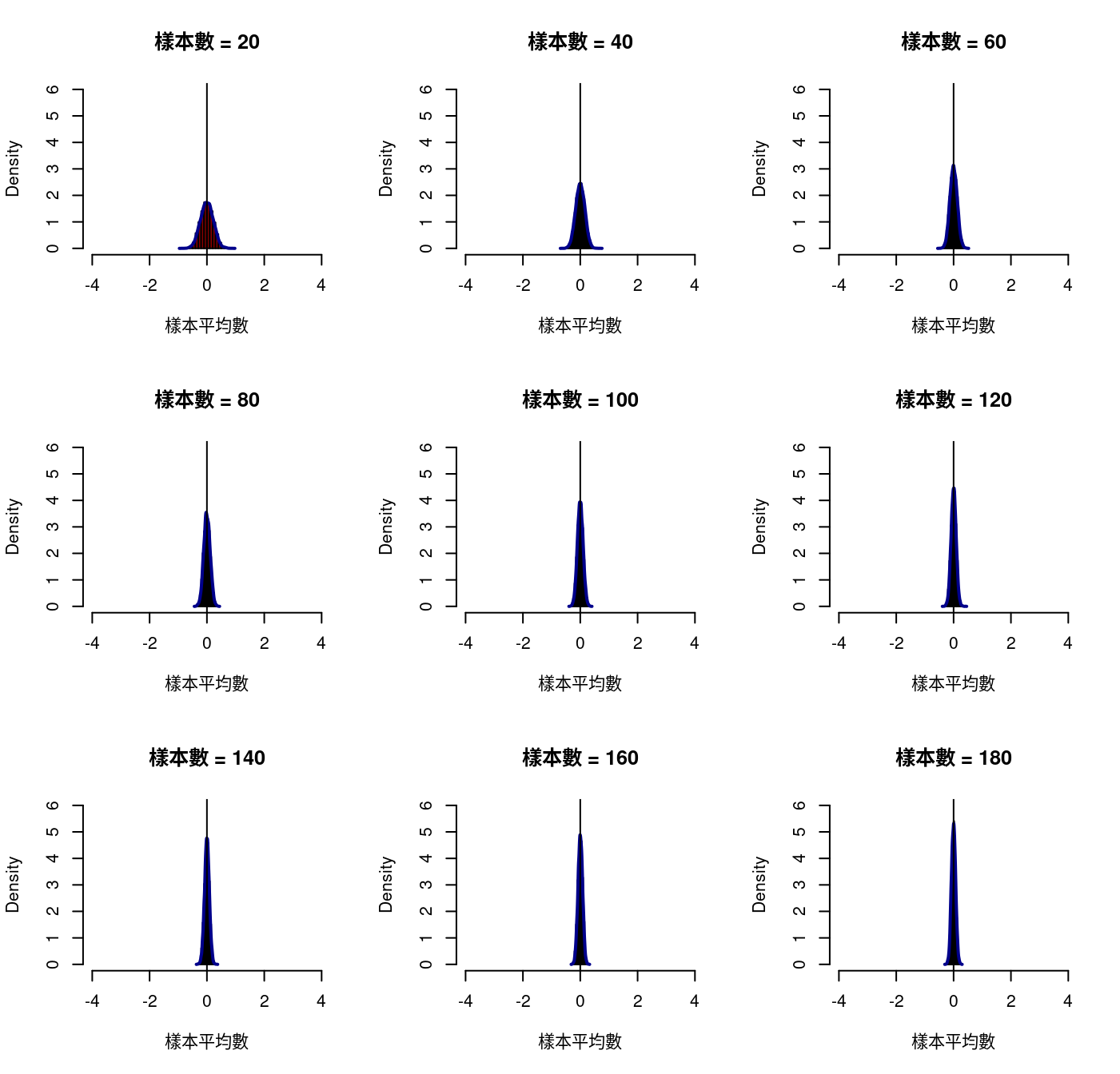
或者是
\[\sqrt{n}(\bar X_n - \mu) \overset{d}{\sim} N(0, \sigma^2)\]
其中,\(n\)是樣本一個接著一個來之後,當我們在計算樣本平均數的時候,手上到底有多少個數字?\(\mu\)是母體的平均數,\(\sigma\)是母體的標準差。\(\overset{d}{\sim}\)表示最後樣本平均數的「『樣本的(sampling)』次數分配」會「收斂」到某一個機率分配函數。
8.6.1.2 『樣本的(sampling)』次數分配 = 『樣本的(sampling)』抽樣分配
我們先回顧「抽樣分配」,透過R程式碼的協助,可以一次看到許許多多、各種樣本數的「模擬的樣本平均數次數分配」。如果嫌不夠,就把程式碼「撿走」,回家(放在自己的筆電),再加自己想看的「樣本數」,跑過一次,就可以「任君挑選了」!
我們順著微微書的發展邏輯,各挑一個
- 伯努利分配
- 二項分配
- 常態分配
為讀者諸君示範各種樣本數下,來自上述分配,樣本平均數的抽樣分配,也就是『樣本的(sampling)』次數分配。
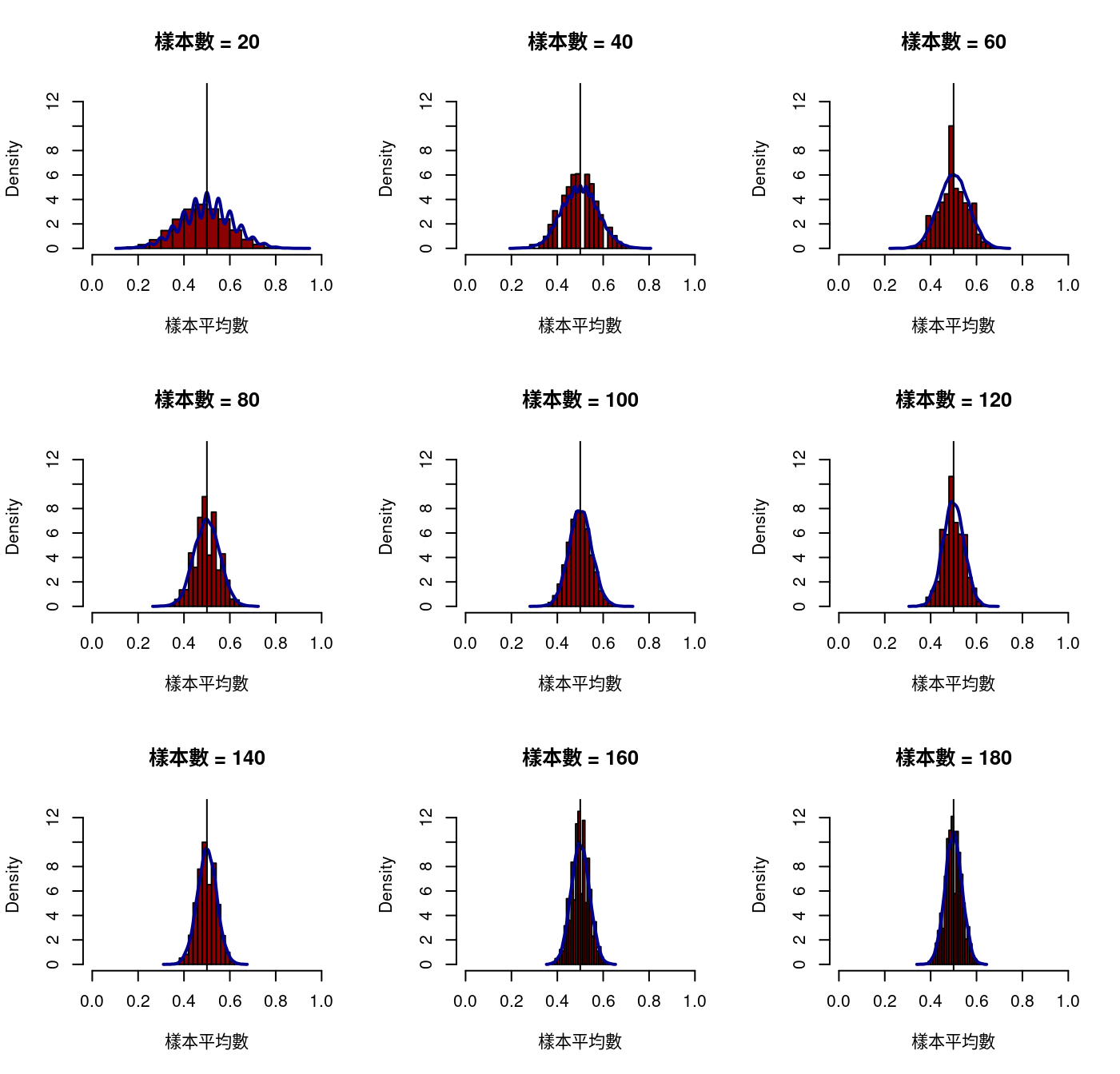
8.6.1.2.1 來自成功機率等於0.5的伯努利分配
先設定我們的模擬環境:
- 母體:伯努利分配、
- 成功機率:0.5、
- 每一次看多少次,也就是「統計學」專稱的「樣本數」:一共9個。「20, 40, 60, 80, 100, 120, 140, 160, 180」、
- 每一種上述狀況的組合都重複10000次。也就是會有10000個樣本平均數。
set.seed(1233)
# 1. 把畫布切成九小塊。
par(mfrow = c(3,3))
# 2. 九種試驗次數,用迴圈一次畫一張。
for (n in c(20, 40, 60, 80, 100, 120, 140, 160, 180)) {
x <- numeric(0)
for (i in 1:10000) {
x0 <- rbinom(n = n, size = 1, prob = 0.5)
x <- c(x, mean(x0))
}
hist(x,
breaks = 20,
xlim = c(0, 1),
ylim = c(0, 13),
main = "",
xlab = "樣本平均數",
prob = T,
col = "darkred")
lines(density(x),
col = "darkblue",
lwd = 2)
abline(v = 0.5)
title(paste0("樣本數 = ", n))
}