9 September 15
9.1 Announcements
- Go over assignment #2
- Oppportunity to redo the assignment #2
- Why you may want to come to office hours
- Common issues
- New resource
9.2 Extreme precipitation in Kansas
- What we will need to learn
- How to use R as a geographic information system
- New general tools from statistics
- Gaussian process
- Metropolis and Metropolis–Hastings algorithms
- Gibbs sampler
- How to use the hierarchical modeling framework to describe Kriging
- Hierarchical Bayesian model vs. “empirical” hierarchical model
- Specialized language used in spatial statistics (e.g., range, nugget, variogram)
9.3 Gaussian process
- See bottom of pg. 139 in Wikle et al. (2019)
- A Gaussian process is a probability distribution over functions
- If the function is observed at a finite number of points or “locations,” then the vector of values follows a multivariate normal distribution.
9.3.1 Multivariate normal distribution
- Multivariate normal distribution
- \(\boldsymbol{\eta}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{R})\)
- Definitions
- Correlation matrix – A positive semi-definite matrix whose elements are the correlation between observations
- Correlation function – A function that describes the correlation between observations
- Example correlation matrices
- Compound symmetry \[\mathbf{R}=\left[\begin{array}{cccccc} 1 & 1 & 0 & 0 & 0 & 0\\ 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 1 & 1 \end{array}\right]\]
- AR(1) \[\mathbf{R(\phi})=\left[\begin{array}{ccccc} 1 & \phi^{1} & \phi^{2} & \cdots & \phi^{n-1}\\ \phi^{1} & 1 & \phi^{1} & \cdots & \phi^{n-2}\\ \phi^{2} & \phi^{1} & 1 & \vdots & \phi^{n-3}\\ \vdots & \vdots & \vdots & \ddots & \ddots\\ \phi^{n-1} & \phi^{n-2} & \phi^{n-3} & \ddots & 1 \end{array}\right]\:\]
Example simulating from \(\boldsymbol{\eta}\sim\text{N}(\mathbf{0},\sigma^{2}\mathbf{R})\) in R
n <- 200 x <- 1:n I <- diag(1, n) sigma2 <- 1 library(MASS) set.seed(2034) eta <- mvrnorm(1, rep(0, n), sigma2 * I) cor(eta[1:(n - 1)], eta[2:n])## [1] -0.06408623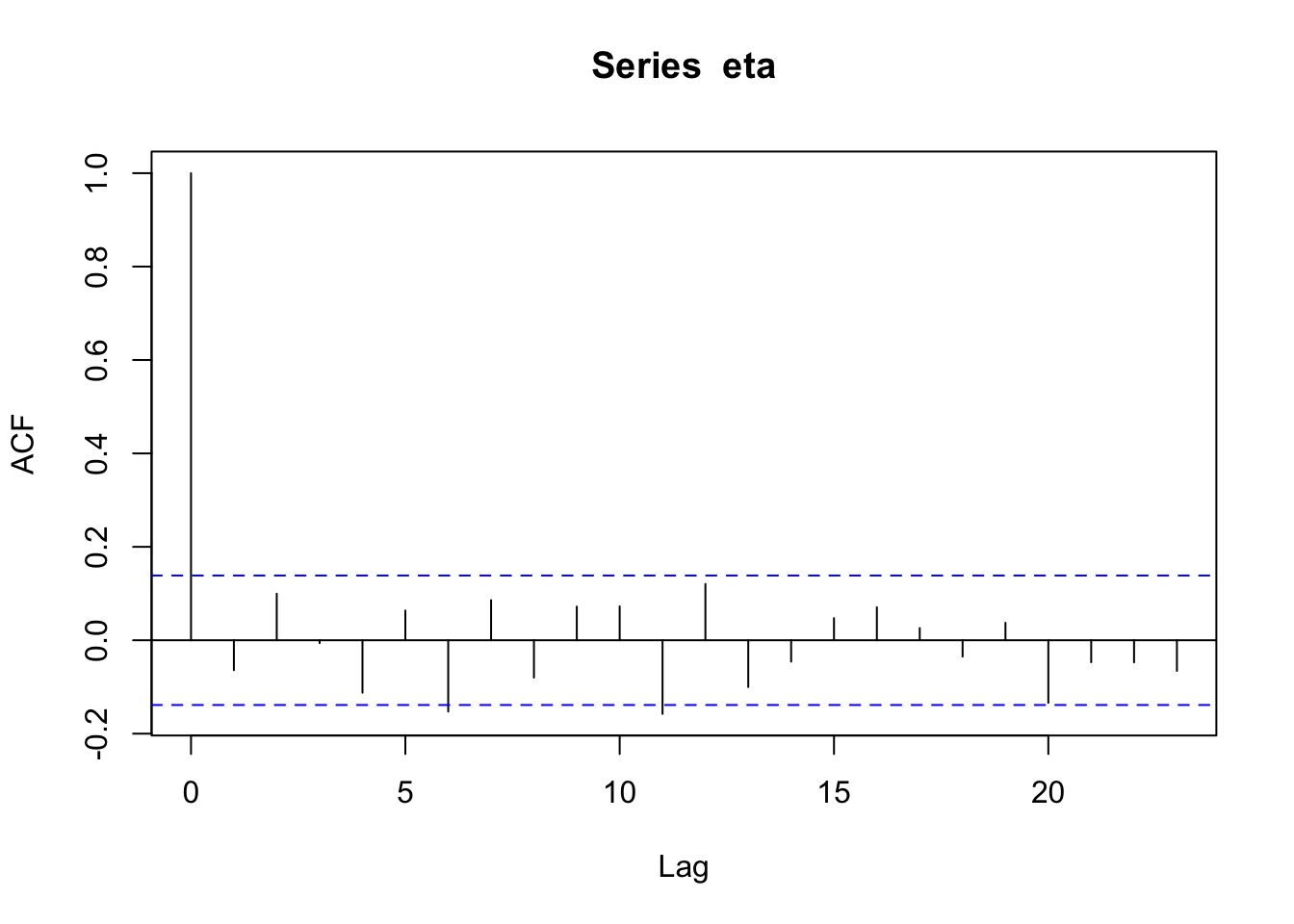
par(mfrow = c(2, 1)) par(mar = c(0, 2, 0, 0), oma = c(5.1, 3.1, 2.1, 2.1)) plot(x, eta, typ = "l", xlab = "", xaxt = "n") abline(a = 0, b = 0) n <- 200 x <- 1:n # Must be equally spaced phi <- 0.7 R <- phi^abs(outer(x, x, "-")) sigma2 <- 1 set.seed(1330) eta <- mvrnorm(1, rep(0, n), sigma2 * R) cor(eta[1:(n - 1)], eta[2:n])## [1] 0.7062142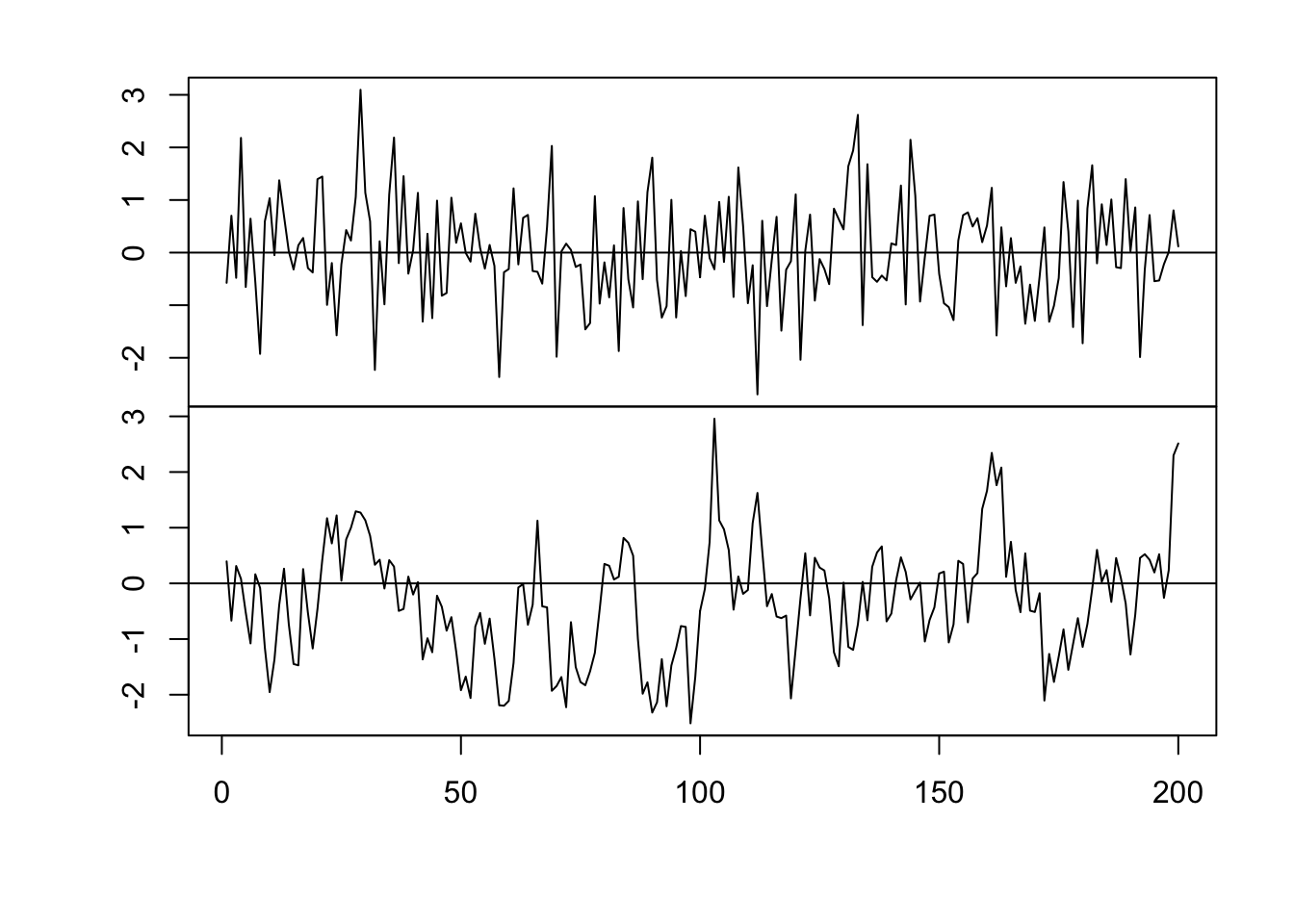
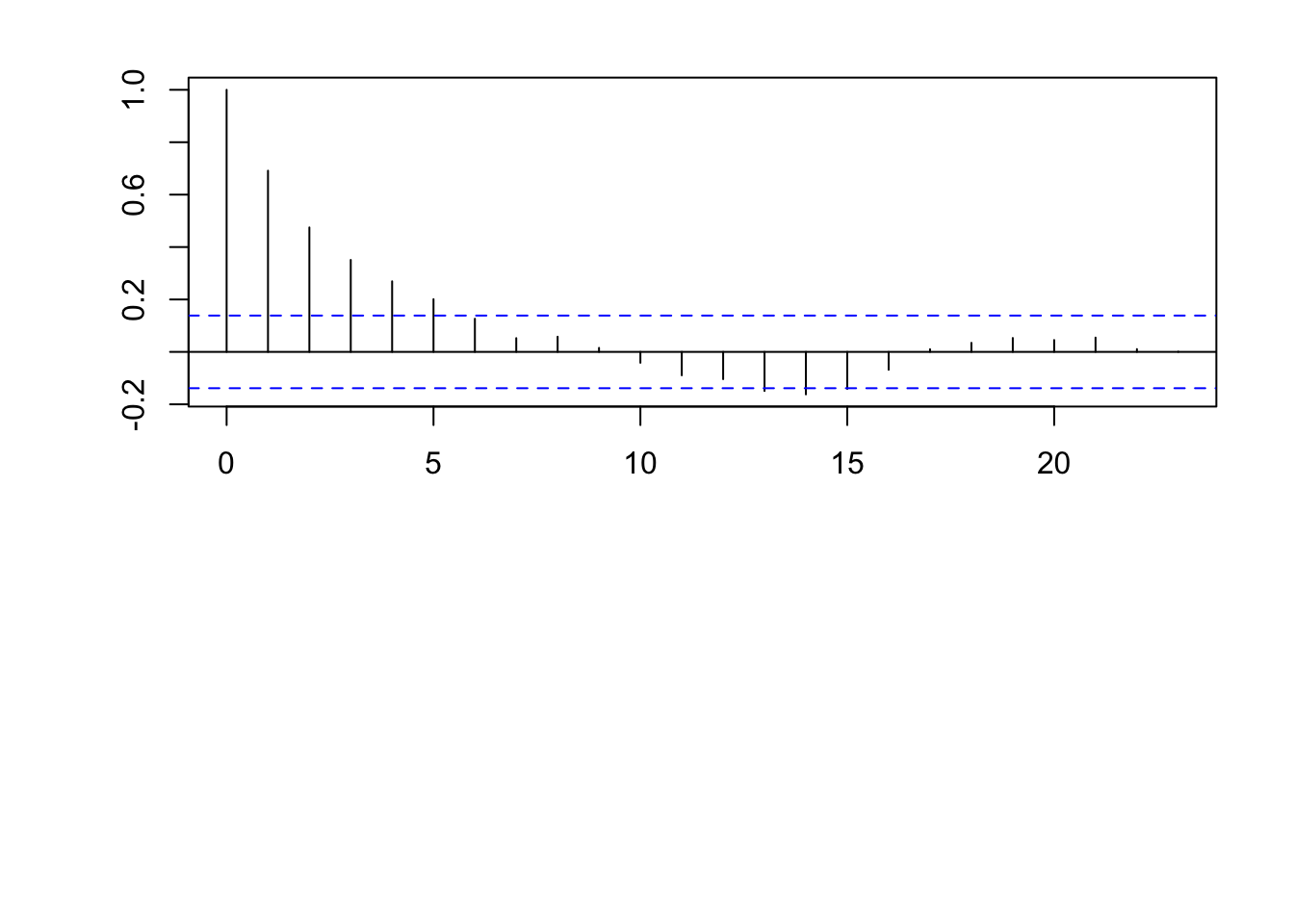
- Example correlation functions
- Gaussian correlation function \[r_{ij}(\phi)=e^{-\frac{d_{ij}^{2}}{\phi}}\] where \(d_{ij}\) is the “distance” between locations i and j (note that \(d_{ij}=0\) for \(i=j\)) and \(r_{ij}(\phi)\) is the element in the \(i^{\textrm{th}}\) row and \(j^{\textrm{th}}\) column of \(\mathbf{R}(\phi)\).
library(fields) n <- 200 x <- 1:n phi <- 40 d <- rdist(x) R <- exp(-d^2/phi) sigma2 <- 1 set.seed(4673) eta <- mvrnorm(1, rep(0, n), sigma2 * R) plot(x, eta, typ = "l") abline(a = 0, b = 0)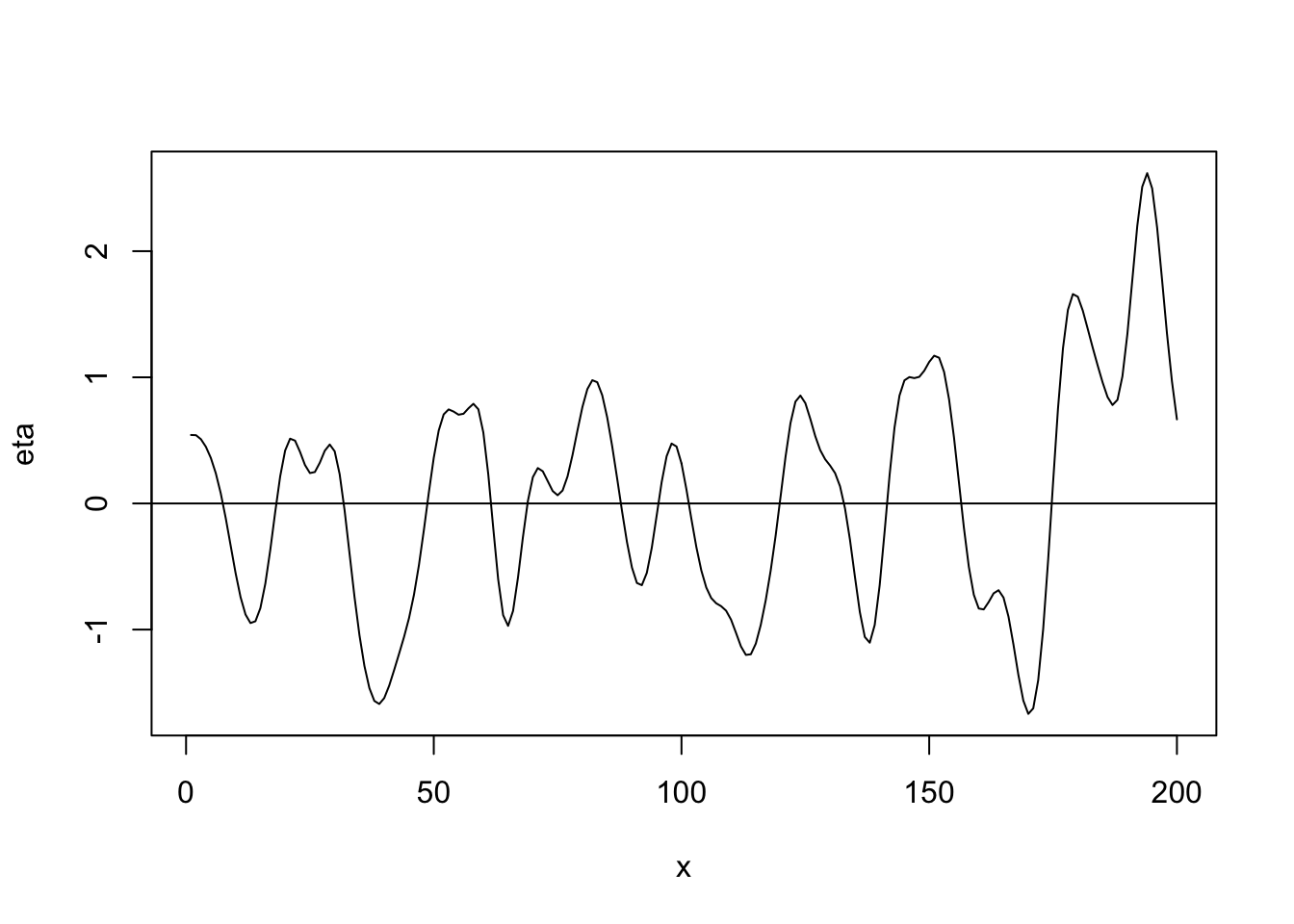
## [1] 0.9717695- Linear correlation function \[r_{ij}(\phi)=\begin{cases} 1-\frac{d_{ij}}{\phi} &\text{if}\ d_{ij}<0\\ 0 &\text{if}\ d_{ij}>0 \end{cases}\]
library(fields) n <- 200 x <- 1:n phi <- 40 d <- rdist(x) R <- ifelse(d < phi, 1 - d/phi, 0) sigma2 <- 1 set.seed(4803) eta <- mvrnorm(1, rep(0, n), sigma2 * R) plot(x, eta, typ = "l") abline(a = 0, b = 0)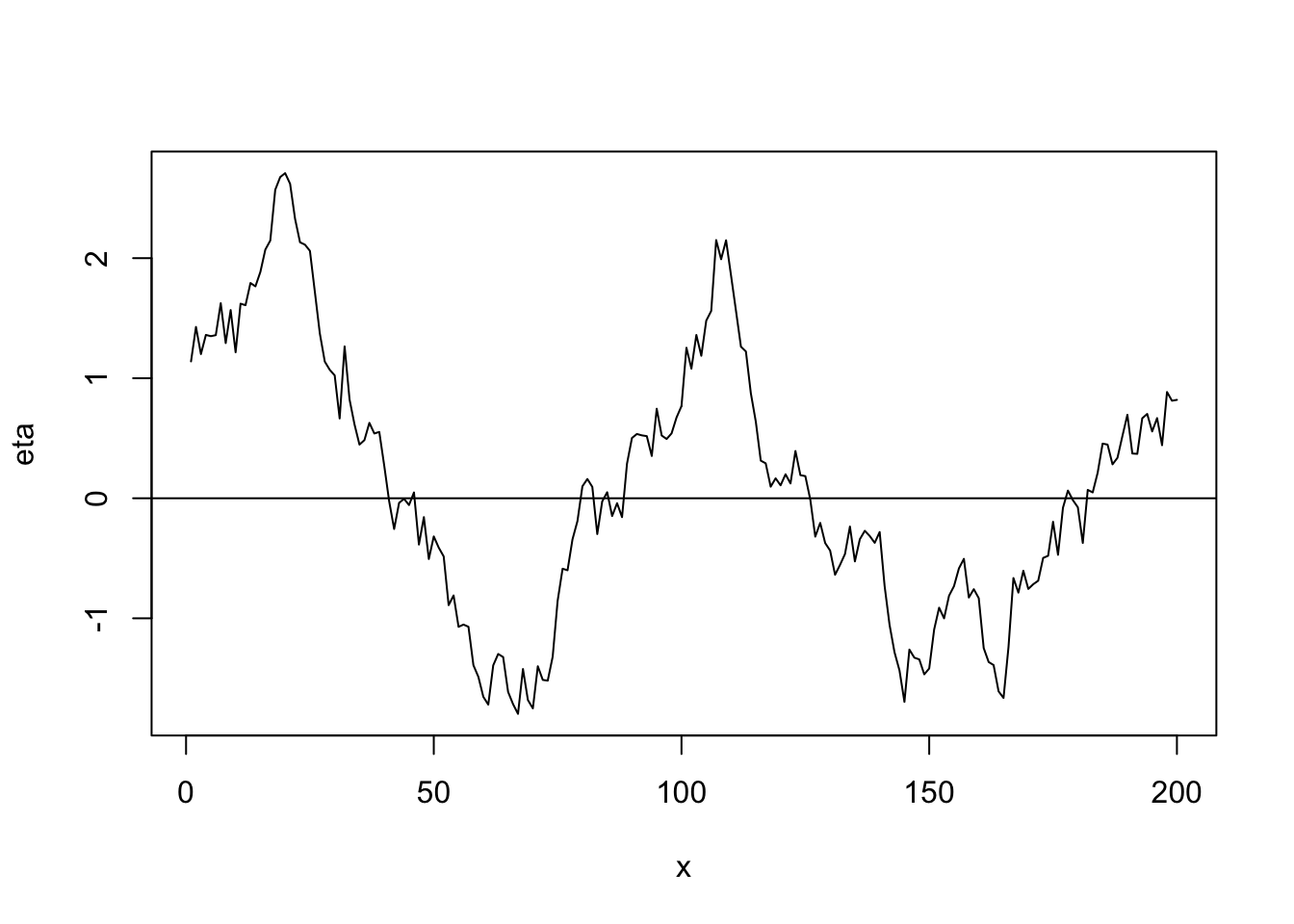
## [1] 0.9779363- Example correlation functions