Kapitel 1 Deskriptive Statistik
Lernziele:
- Arithmetisches Mittel, Median und Modalwert berechnen und interpretieren
- Varianz und Standardabweichung berechnen und interpretieren
- Quantile bestimmen
- Datensätze im Histogramm grafisch darstellen
- Empirische Verteilungsfunktion grafisch darstellen
- Zusammenhänge zwischen zwei Variablen erkennen und quantifizieren
- Regressionsschätzung einer Geraden mit der Methode der Kleinsten Quadrate durchführen und Schätzergebnisse interpretieren
Die deskriptive Statistik dient dazu, Informationen aus Daten zu extrahieren und zu verstehen, insbesondere wenn der Datensatz groß und eine direkte Betrachtung schwierig ist. Lagemaße wie das arithmetische Mittel helfen, die zentrale Tendenz der Daten zu charakterisieren, während Streuungsmaße wie Varianz und Standardabweichung die Variabilität der Daten quantifizieren. Grafische Darstellungen wie Histogramme und empirische Verteilungsfunktionen veranschaulichen die Verteilung der Daten. Statistische Methoden, wie Regression, ermöglichen die Modellierung von Zusammenhängen zwischen Variablen.
1.1 Lagemaße
Lagemaße sind Kennzahlen, die die Lage einer Verteilung erfassen. Sie geben an, wie weit sich die Verteilung links oder rechts auf der horizontalen Achse (Abszisse) befindet. Das gebräuchlichste Lagemaß ist das arithmetische Mittel, auch bekannt als Durchschnitt oder Mittelwert.
Beispiel 1.1 (Arithmetischer Mittelwert)
Formal ausgedrückt definieren wir
\[\overline{𝑥} = \frac{1}{𝑛} \sum^𝑛_{𝑖=1} 𝑥_𝑖\] wobei \(\overline{𝑥}\) unser Mittelwert ist.
Der Mittelwert kann für eine komplette Grundgesamtheit oder nur für eine Auswahl aus der Grundgesamtheit, der sogenannten Stichprobe, berechnet werden. Normalerweise arbeiten wir mit Stichproben, da es oft nicht möglich ist, die Grundgesamtheit zu untersuchen. So werden z.B. Wahlumfragen (“Wie viele Bürger würden eine Partei A wählen, wenn morgen Bundestagswahl wäre?”) auf Basis einer Stichprobe ermittelt, die als möglichst repräsentativer Ausschnitt aus der Grundgesamtheit aller Wähler ausgewählt wird.
In jedem Fall wird der Mittelwert berechnet, indem alle Beobachtungen aufsummiert und durch die Anzahl der Beobachtungen geteilt werden. In der Stichprobe wird der Mittelwert mit \(\overline{𝑥}\) bezeichnet, während für die Grundgesamtheit der Buchstabe μ verwendet wird. Die Anzahl der Beobachtungen in der Stichprobe wird meist mit \(𝑛\) und in der Grundgesamtheit mit \(𝑁\) bezeichnet. Für den Mittelwert der Grundgesamtheit ergibt sich also:
\[μ = \frac{1}{𝑁} \sum^𝑁_{𝑖=1} 𝑥_𝑖\]
Bei gruppierten Daten, bei denen nur Informationen über die Verteilung der Beobachtungen in Intervallen vorliegen, müssen Annahmen getroffen werden, um den Mittelwert zu berechnen. In der Regel geht man davon aus, dass die Beobachtungen innerhalb eines Intervalls gleichmäßig verteilt sind und der Mittelpunkt des Intervalls eine geeignete Näherung für die unbekannte Beobachtung darstellt.
Beispiel 1.2 (Mittelwert für gruppierte Daten)
Bei der Berechnung von Mittelwerten ist es wichtig, zu beachten, welche Angaben die Beobachtungen repräsentieren (z. B. Alter) und welche die Anzahl oder Häufigkeit. Die Gruppierung von Daten führt zu einem Verlust von Informationen und macht das Ergebnis ungenauer als bei exakten Beobachtungen.
Der Mittelwert kann als Schwerpunkt der Verteilung betrachtet werden. Wenn man sich die Verteilung als Modell vorstellt und es auf einem Stift balanciert, würde der Mittelwert genau dort liegen, wo der Stift platziert werden müsste, um das Modell im Gleichgewicht zu halten. Wir kommen darauf in Kapitel 3 zurück.
Aufgabe 1.1 Es gibt 10 Familien mit einem Fernsehgerät, 12 Familien mit 2 Fernsehgeräten und 3 Familien mit 3 Fernsehgeräten. Wie viele Fernsehgeräte besitzt eine Familie im Durchschnitt?
Aufgabe 1.2 Ein Autofahrer notiert seine Benzinkäufe während einer längeren Reise:
| Tankstelle | 1 | 2 | 3 |
| Anzahl Liter | 33 | 40 | 25 |
| Preis pro Liter | 1,6 | 1,5 | 1,6 |
Berechnen Sie den durchschnittlichen Preis pro Liter.
Aufgabe 1.3 (Schultypen) Gegeben sind die Kosten pro Schüler nach Schultyp:
| Grundschule | Sekundarstufe I | Sekundarstufe II | |
|---|---|---|---|
| Kosten pro Schüler und Jahr in GBP | 1.750 | 3.100 | 3.820 |
| Anzahl der Schüler | 8.000 | 7.000 | 3.000 |
| Anteil der Schüler | ? | ? | ? |
Wie viel Geld wird im Durchschnitt über die Stufen pro Schüler ausgegeben?
Hinweis: Aus der Tabelle ist unmittelbar ersichtlich, dass die Anteile der Schüler über die Stufen nicht gleich sind. Berechnen Sie zunächst die Anzahl der Schüler insgesamt. Damit ermitteln Sie die Anteile der Schüler, die auf die drei Stufen entfallen. Diese Anteile sind dann die Gewichte, mit denen Sie die Kosten in jeder Stufe multiplizieren müssen, um den gewichteten Durchschnitt zu berechnen. Die Summe der Gewichte ergibt immer 1.
Ergebnis zur Kontrolle: 2.620 Pfund.
Neben dem Mittelwert existieren weitere Lagemaße wie Median und Modalwert:
Der Median ist der Wert, der die Verteilung in zwei gleiche Teile teilt, wenn die Beobachtungen nach Größe sortiert sind. Er ist sinnvoll, wenn die Verteilung stark asymmetrisch ist und Ausreißer vorhanden sind. Im Falle einer symmetrischen Verteilung liegen Mittelwert und Median aufeinander.
Beispiel 1.3 (Median)
Während der Median gegen einzelne Ausreißer, also extreme Beobachtungen, robust ist, reagiert das arithmetische Mittel sehr sensitiv. Im Extremfall kann eine einzelne extreme Beobachtung den arithmetischen Mittelwert beliebig beeinflussen.
Dieser Effekt ist oftmals unerwünscht. Bei Beobachtungen mit starken Ausreißern ist dann der Median als Lagemaß aussagekräftiger und oftmals repräsentativer für den Großteil der Beobachtungen einer Gruppe.
Im echten Leben wird der Unterschied zwischen Mittelwert und Median bei der Vermögensverteilung deutlich. Diese ist in westlichen Ländern zumeist stark asymmetrisch: Viele Menschen haben ein vergleichsweise geringes Vermögen, während einige wenige Personen enorm viel Geld haben. Wenn Sie über alle Personen das durchschnittliche Vermögen ausrechnen, erhalten Sie einen überraschend hohen Wert. Das liegt daran, dass der Mittelwert sensitiv auf Ausreißer reagiert, d. h. durch die wenigen Reichen nach oben „verzerrt“ wird. Hier eignet sich der Median besser als Lagemaß, um das Vermögen eines typischen Durchschnittsbürgers zu beschreiben.
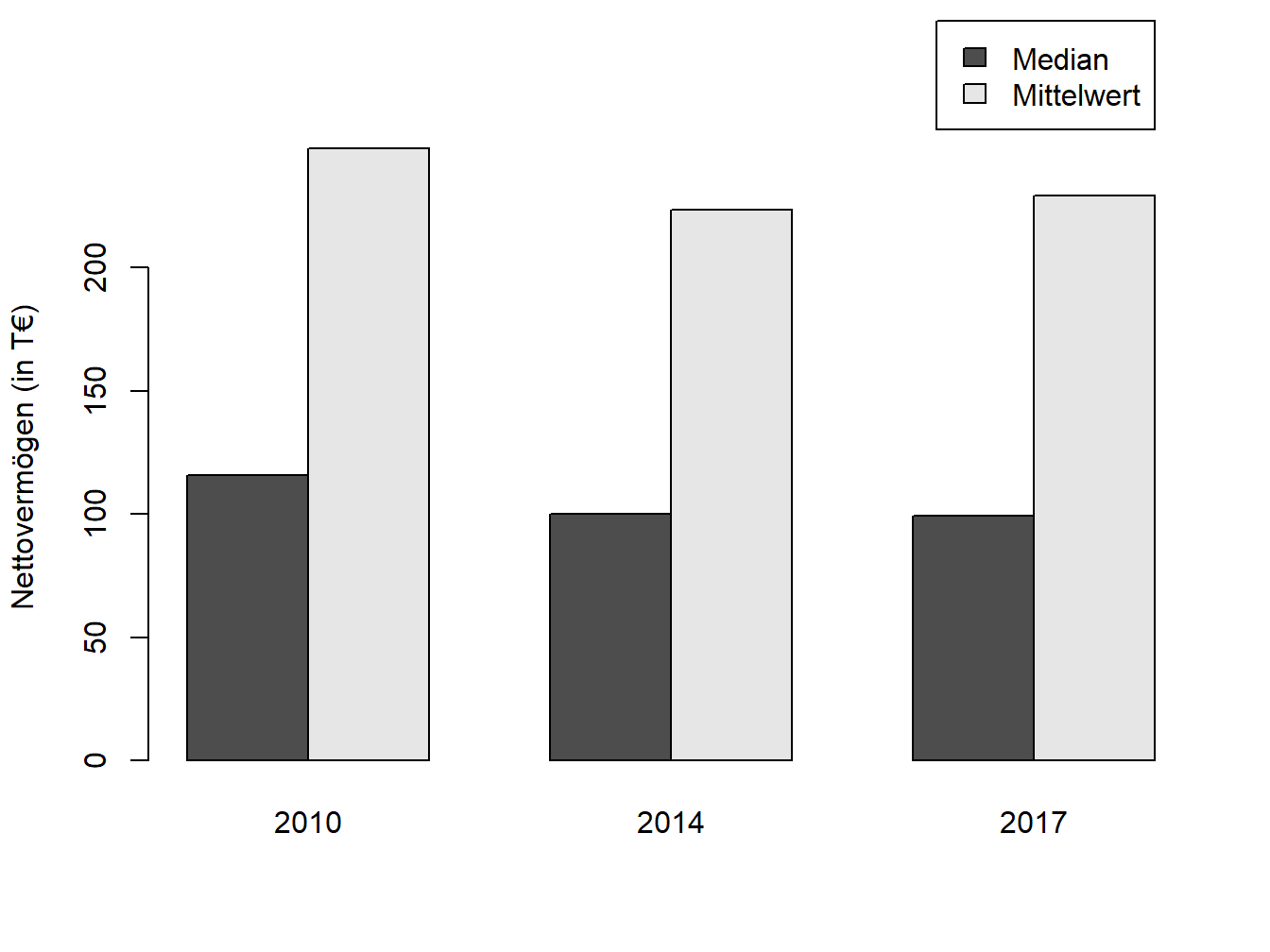
Abbildung 1.1: Mediane und arithmetische Mittel zur Vermögensverteilung im Euroraum; Daten-Quelle: HFCS.
Household Finance and Consumption Survey (HFCS)

Seit 2010 hat die europäische Zentralbank in mehreren Wellen eine Untersuchung zur Lage der Haushalte in den Euro-Ländern veranlasst. Ergebnisse zum Nettovermögen der privaten Haushalte, aufgeschlüsselt nach teilnehmenden Ländern, sind den Berichten zu entnehmen. Dort werden sowohl der Median als auch das arithmetische Mittel als Lagemaße verwendet.
Der Modalwert – auch Modus genannt – ist der am häufigsten vorkommende Wert in einer Verteilung oder Stichprobe. Daher wird er auch als typischer Wert einer Verteilung bzw. einer Stichprobe bezeichnet.
Bei der Bestimmung des Modalwerts für gruppierte Daten ist es wichtig zu beachten, dass breitere Intervalle häufig mehr Beobachtungen enthalten als schmalere Intervalle. Daher kann man bei unterschiedlichen Klassenbreiten nicht einfach die am häufigsten vorkommende Klasse zählen. Stattdessen muss man die Häufigkeitsdichte für jedes Intervall berechnen. Diese Dichte berücksichtigt den Effekt der Klassenbreite, indem die Anzahl der Personen im Intervall durch die Klassenbreite dividiert wird. Je breiter das Intervall ist, desto niedriger ist die Häufigkeitsdichte bei konstanter Personenzahl.
Im folgenden Beispiel werden der Mittelwert, Median und Modalwert am Beispiel der Vermögensverteilung in Großbritannien im Jahr 1979 berechnet und interpretiert:
Beispiel 1.4 (Median)
Aufgabe 1.4 Gegeben ist die Anzahl der Betriebe im produzierenden Gewerbe in Großbritannien im Jahr 1991/1992, geordnet nach Anzahl der Beschäftigten.
| Anzahl der Beschäftigten | Anzahl der Betriebe |
|---|---|
| 1 bis 9 | 95.409 |
| 10 bis 19 | 15.961 |
| 20 bis 49 | 16.688 |
| 50 bis 99 | 7.229 |
| 100 bis 199 | 4.504 |
| 200 bis 499 | 2.949 |
| 500 bis 999 | 790 |
| 1.000 bis 3.000 | 332 |
| Gesamt | ? |
Berechnen Sie arithmetisches Mittel, Median und Modalwert zu den Daten und interpretieren Sie die Ergebnisse.
1.2 Quantile
Quantile sind Aufteilungen einer Verteilung in gleich große Teile, basierend auf der Anzahl der Beobachtungen. Der Median teilt die Verteilung in zwei Hälften. Quartile, Quintile, Dezile und Perzentile teilen die Verteilung in vier, fünf, zehn und hundert gleiche Teile auf. Beim Ermitteln der Quantile schneidet man einen bestimmten Prozentsatz der Verteilung ab und sucht die Stelle, an der der Schnitt erfolgt.
Beispiel 1.5 (Quantile der Vermögensverteilung in Großbritannien)
Aufgabe 1.5 Wie viel Vermögen haben die oberen 25 % mindestens? (Vermögensverteilung von 1979)
Wir kommen auf die Quantile erneut zu sprechen, wenn wir konkrete Wahrscheinlichkeitsverteilungen kennenlernen. Auch das Risikomaß Value at Risk, welches in anderen Modulen eine größere Rolle spielen wird, ist im Grunde genommen ein Quantil; beim Value at Risk schneiden wir ebenfalls eine gegebene Fläche unter der Verteilung ab und interessieren uns für die Stelle, an der zu schneiden ist.
1.3 Streuungsmaße
Die Streuung ist ein wesentliches Charakteristikum einer Verteilung, welches die Breite einer Verteilung erfasst. Ein sehr einfaches Beispiel für ein Streuungsmaß ist die Streubreite, d.h. die Differenz zwischen der größten und kleinsten Beobachtung. Wesentlich gebräuchlicher und auch aussagekräftiger sind jedoch die Varianz und die Standardabweichung. Die Varianz misst den Abstand jeder Beobachtung vom Mittelwert, indem die quadrierten Abweichungen aufsummiert und durch die Anzahl der Beobachtungen dividiert werden. Die Standardabweichung ist die Quadratwurzel der Varianz und wird in regulären Einheiten gemessen. Für die Stichprobe werden angepasste Formeln verwendet, bei denen durch die Anzahl der Beobachtungen minus eins dividiert wird. Die Formeln in Excel unterscheiden zwischen Grundgesamtheit (VAR.P) und Stichprobe (VAR.S). Es ist wichtig zu wissen, welche Formel in welchem Fall anzuwenden ist. Die Varianz wird mit \(\sigma^2\) (Grundgesamtheit) bzw. \(𝑠^2\) (Stichprobe) bezeichnet.
Formel für die Varianz:
\[\sigma^2 = \frac{1}{𝑁} \sum_{𝑖=1}^𝑁 (𝑥_𝑖 −\mu)^2\]
Sie erkennen unmittelbar, dass Sie für die Varianzberechnung zunächst den Mittelwert \(\mu\) kennen bzw. ermitteln müssen. Sie berechnen dann für jede Beobachtung \(𝑥_𝑖\) die Differenz zum Mittelwert. Diese Differenz müssen Sie quadrieren. Was würde passieren, wenn Sie die Differenzen nicht quadrieren? Es gibt sowohl positive als auch negative Abweichungen, denn es gibt Beobachtungen, die größer als der Mittelwert sind und andere, die kleiner als der Mittelwert sind. Wenn Sie diese positiven und negativen Abweichungen dann aufsummieren, könnten Sie bei null landen! Das Quadrieren hat außerdem den Effekt, dass Abweichungen, die betragsmäßig kleiner als eins sind, (noch) kleiner werden, während solche, die betragsmäßig größer als eins sind, größer werden. Insofern reagiert die Varianz, ebenso wie der Mittelwert, sensitiv auf extreme Beobachtungen. Nachdem Sie die quadrierten Abweichungen aufsummiert haben, müssen Sie die Summe noch durch die Anzahl der Beobachtungen, d. h. durch die Anzahl der quadrierten Abweichungen, dividieren. Sie erhalten dadurch eine durchschnittliche quadrierte Abweichung.
Da dies ein quadriertes Maß ist, wird sie auch in einer quadrierten Einheit gemessen: Jahre2, Pfund2 usw. Dies ist natürlich nicht interpretierbar, gibt aber einen Eindruck davon, wie breit die Beobachtungen streuen (daher „Streuungsmaß“).
Um zu einem interpretierbaren, nicht-quadrierten Streuungsmaß zu gelangen, ziehen wir die Quadratwurzel aus der Varianz und erhalten die Standardabweichung:
\[\sigma = \sqrt{\sigma^2}\]
Die Standardabweichung wird in regulären Einheiten gemessen (Jahre, Pfund usw.) und kann unmittelbar interpretiert werden. Sie benötigen für die Berechnung der Standardabweichung immer erst die Varianz und dafür immer erst den Mittelwert.
Wenn Sie sich für das Durchschnittsalter der deutschen Bevölkerung interessieren, dieses aber für die Grundgesamtheit nicht kennen, würden Sie eine Stichprobe ziehen, das Durchschnittsalter für die Stichprobe berechnen und hoffen, dass Sie möglichst nahe am wahren Wert für die Grundgesamtheit liegen.
Der wahre Mittelwert für die Grundgesamtheit heißt \(\mu\), die dazugehörige Varianz \(\sigma^2\) und die Standardabweichung entsprechend \(\sigma\). Für die Stichprobe sind es \(\overline{x}\) für den Mittelwert, \(𝑠^2\) für die Varianz und s für die Standardabweichung.
Die Formel für die Stichprobe lautet entsprechend:
\[𝑠^2 = \frac{1}{𝑛 − 1} \sum_{𝑖=1}^{𝑛} (𝑥_𝑖 − \overline{x})^2\]
bzw.
\[𝑠 = \sqrt{𝑠^2}\]
Wenn Sie die Varianz für die Stichprobe berechnen und zuvor den Mittelwert ebenfalls aus der Stichprobe ermitteln, also den wahren Wert \(\mu\) nicht kennen, sollten Sie bei der Berechnung von \(𝑠^2\) nicht durch \(n\) dividieren, sondern durch \((n-1)\).
Die Formel (sie heißt auch „Schätzer“) für \(𝑠^2\) trifft im Mittel den wahren Wert der Grundgesamtheit, also \(s^2\), wenn wir durch \((n-1)\) dividieren, während der Schätzer, der durch \(n\) dividiert, im Mittel neben (unter) dem wahren Wert liegt. Schätzer, die im Mittel den wahren Wert treffen, heißen „erwartungstreu“ oder „unverzerrt“ (auf Englisch: unbiased). Entsprechend liegen verzerrte Schätzer im Mittel daneben. Sie haben trotzdem ihre Existenzberechtigung: Dies ist besonders dann der Fall, wenn sie zwar im Mittel daneben liegen, aber nur wenig vom wahren Wert abweichen, während andere Schätzer zwar im Mittel richtig liegen, aber mit einer recht hohen Wahrscheinlichkeit weit daneben landen (also breit streuen).
In dem Tabellenkalkulationsprogramm Microsoft Excel sind deshalb jeweils zwei Formeln für die Varianz und die Standardabweichung hinterlegt: Einmal die für die Grundgesamtheit (VAR.P) – hier kennen Sie \(\mu\) – und einmal die für die Stichprobe – hier schätzen Sie \(\mu\) durch \(\overline{x}\) –, die dann erwartungstreu ist (VAR.S). Auf Englisch ist „population“ die Grundgesamtheit und „sample“ die Stichprobe, daher die Abkürzungen in Excel. Sie sollten wissen, wann Sie welche Formel anzuwenden haben.
Aufgabe 1.6 Berechnen Sie für die Vermögensverteilung in Großbritannien die Standardabweichung. Benutzen Sie als Mittelwert \(\overline{x}=16.399\) Pfund (Beispiel oben). Sie haben hier gruppierte Daten, so dass Sie den Intervallmittelpunkt zugrunde legen müssen.
| Vermögen in GBP | Anzahl in Tausend |
|---|---|
| 0 bis | 1.606 |
| 1.000 bis | 2.927 |
| 3.000 bis | 2.562 |
| 5.000 bis | 3.483 |
| 10.000 bis | 2.876 |
| 15.000 bis | 1.916 |
| 20.000 bis | 3.425 |
| 50.000 bis | 621 |
| 100.000 bis | 170 |
| 200.000 bis 400.000 | 59 |
| Summe |
Aufgabe 1.7 Berechnen Sie die Standardabweichung für die Betriebsgröße in Großbritannien. Der Mittelwert \(\overline{x}\) wurde in Aufgabe 1.4 aus der Stichprobe geschätzt. Runden Sie auf ganze Mitarbeiter.
1.4 Histogramm
Das Histogramm ist - im Gegensatz zu den bisher besprochenen numerischen Methoden - eine grafische Methode zur Darstellung von Daten, wie in Abb. 1.2 und 1.3 gezeigt.
Die Daten werden hierfür in Klassen eingeteilt, die eine konstante oder variable Breite haben können. Rechtecke von der Breite der jeweiligen Klasse werden direkt nebeneinander gezeichnet; dabei wird die Höhe der Rechtecke so gewählt, dass die jeweiligen Flächeninhalte die Häufigkeiten der Beobachtungen in den Klassen darstellen.
Wahlweise können dabei entweder die relativen oder absoluten Häufigkeiten dargestellt werden. Die absolute Häufigkeit einer Klasse ist die Anzahl der Beobachtungen in dieser Klasse (\(f_i\)). Die relative Häufigkeit ist der Anteil der Beobachtungen in dieser Klasse, d. h. der Quotient aus \(f_i\) und der Anzahl der Beobachtungen insgesamt. Die Höhe der Säulen ist die Häufigkeitsdichte, d.h. die relative oder absolute Häufigkeit geteilt durch die Klassenbreite. Die Summe der Rechtecksflächen beträgt deshalb 1, wenn relative Häufigkeiten zugrunde gelegt werden, d.h. die relativen Häufigkeiten müssen sich zu 1 aufaddieren. Wird stattdessen mit den absoluten Häufigkeiten gearbeitet, so entspricht die Flächensumme der Anzahl der Beobachtungen insgesamt.
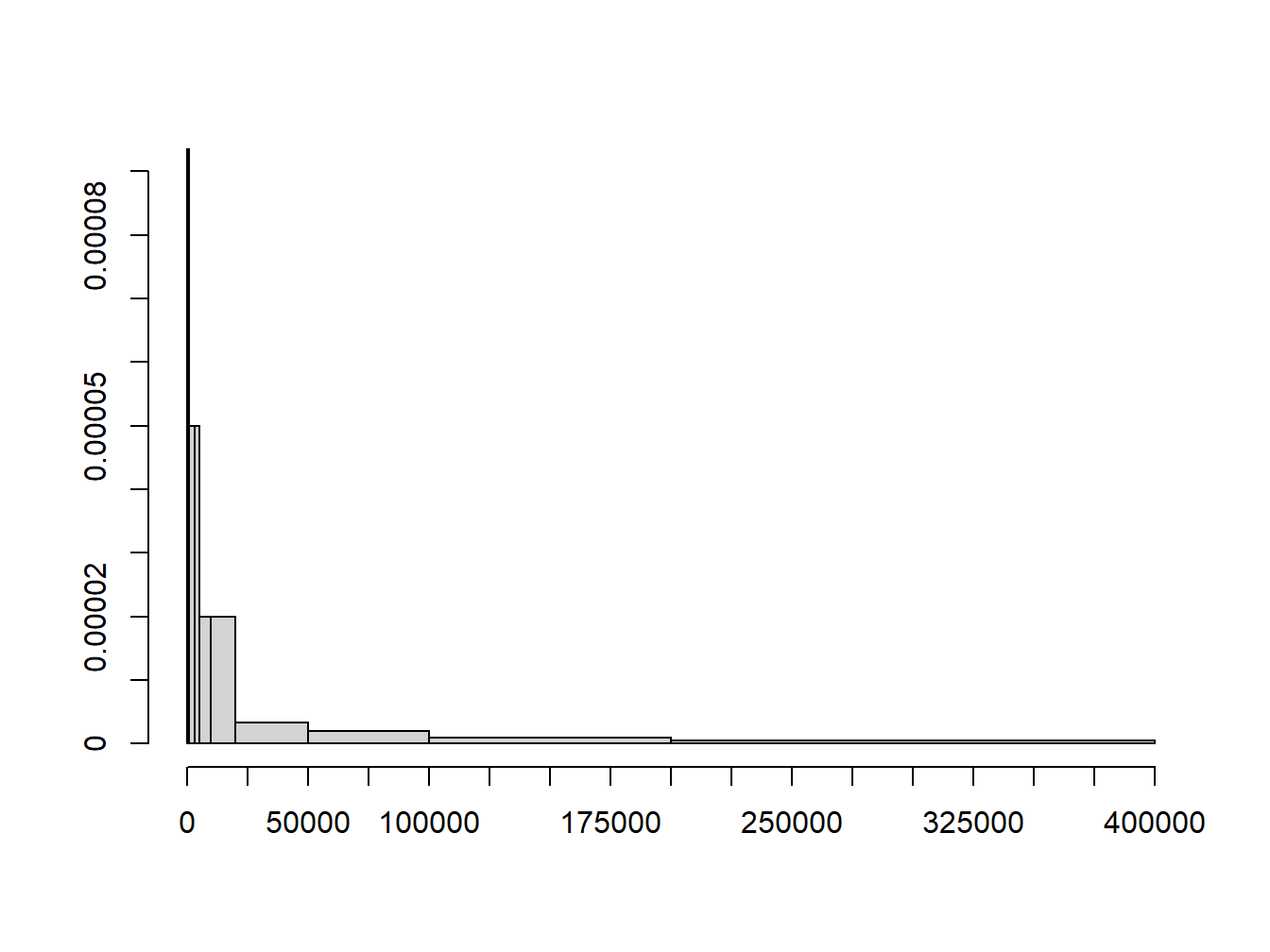
Abbildung 1.2: Histogramm der Vermögensverteilung in Großbritannien im Jahr 1979
Beispiel 1.6 (Berechnung der Balkenhöhen)
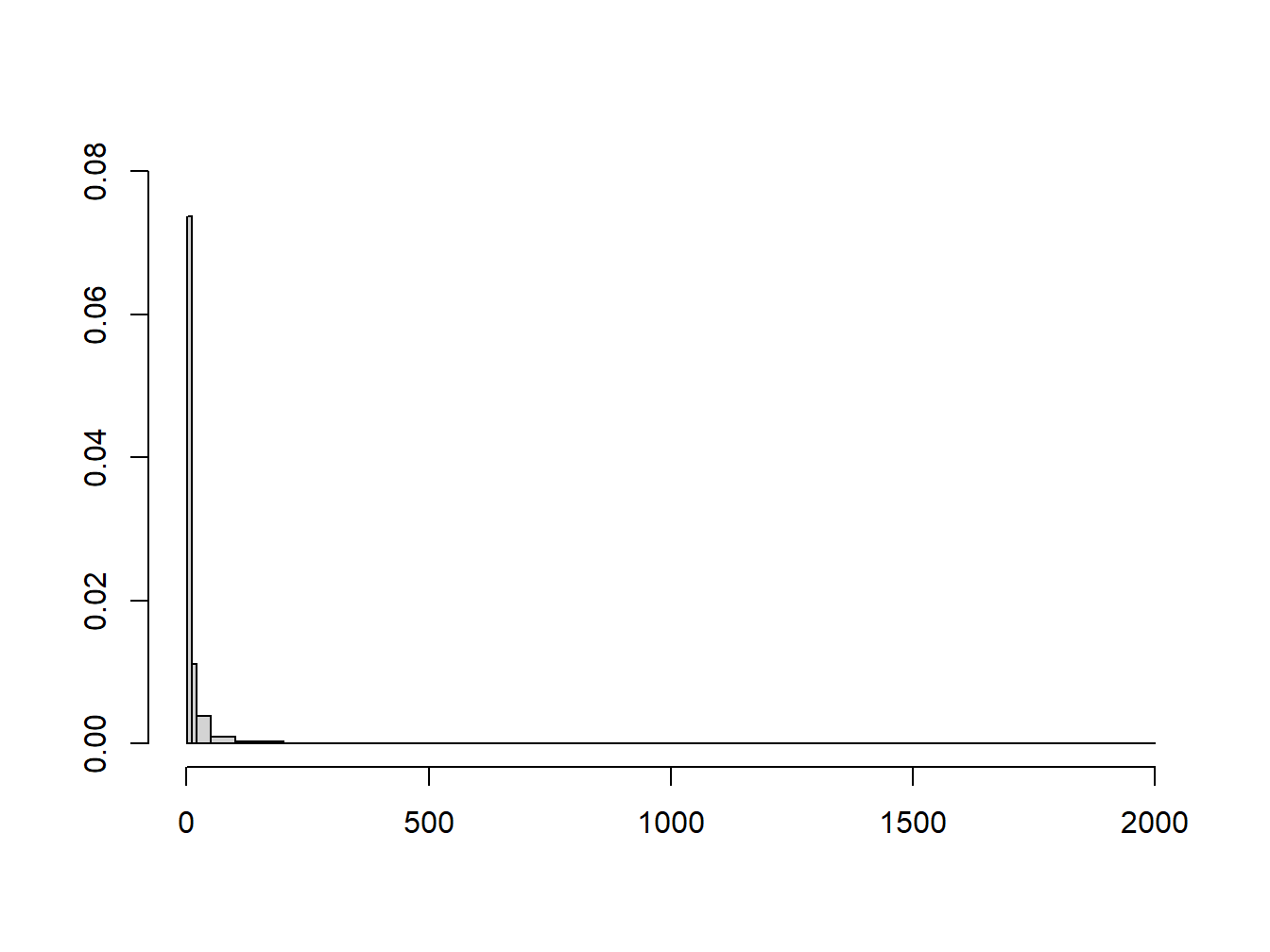
Abbildung 1.3: Histogramm der Beschäftigtenzahl pro Betrieb in Großbritannien 1991/1992 (produzierendes Gewerbe)
Das Verständnis darüber, wie Histogramme erzeugt werden, ermöglicht es Diagramme richtig zu interpretieren. Mit Histogrammen können Informationen aus einem Datensatz auf manipulative Weise dargestellt werden. Es ist wichtig, solche Täuschungen zu erkennen. Eine offensichtliche Möglichkeit, die Darstellung zu manipulieren, ist die Wahl der Klassenanzahl und -breite. Eine zu große Anzahl an Klassen macht die Darstellung unübersichtlich, während zu wenige Klassen zu grobe Informationen liefern. Ein zu breites Intervall kann Balken so flach machen, dass sie kaum erkennbar sind. Bei der Betrachtung von Grafiken sollte man sich immer fragen, welche Botschaft der Autor mit der Grafik vermitteln möchte und wie er dies erreicht. Es ist wichtig zu hinterfragen, ob die Informationen tatsächlich in den Daten stecken oder ob sie nur durch die Art und Weise der Darstellung aufgedrängt werden.
1.5 Empirische Verteilungsfunktion
Mit Histogrammen wurden zuletzt Häufigkeiten in den einzelnen Klassen dargestellt. Manchmal liegt jedoch das Interesse darin, den Anteil der Beobachtungen zu kennen, die unterhalb eines bestimmten Werts liegen. Dazu werden kumulierte relative Häufigkeiten schrittweise durch die Addition der relativen Häufigkeiten für jedes Intervall erzeugt.
Beispiel 1.7 (Berechnung der empirischen Verteilungsfunktion)
Die kumulierten relativen Häufigkeiten können grafisch als stetig kumuliertes Histogramm oder als Treppenkurve, die die empirische Verteilungsfunktion zeigt, dargestellt werden. Ein stetig kumuliertes Histogramm, in welchem die kumulativen relativen Häufigkeiten als fortlaufende Linie gezeigt werden, ist in Abb. 1.4 zu sehen.
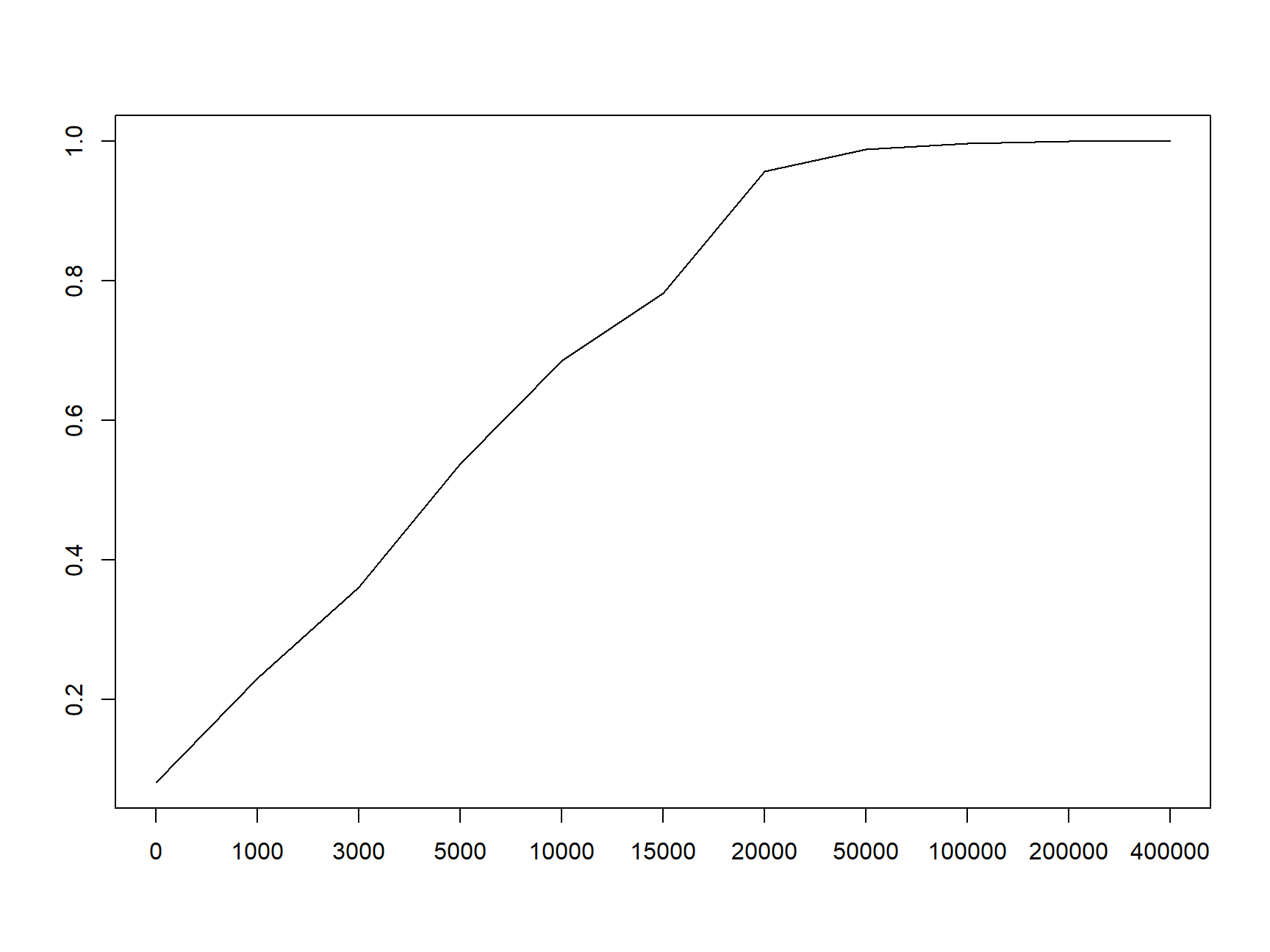
Abbildung 1.4: Empirische Verteilungsfunktion am Beispiel der Vermögensverteilung in Großbritannien 1979
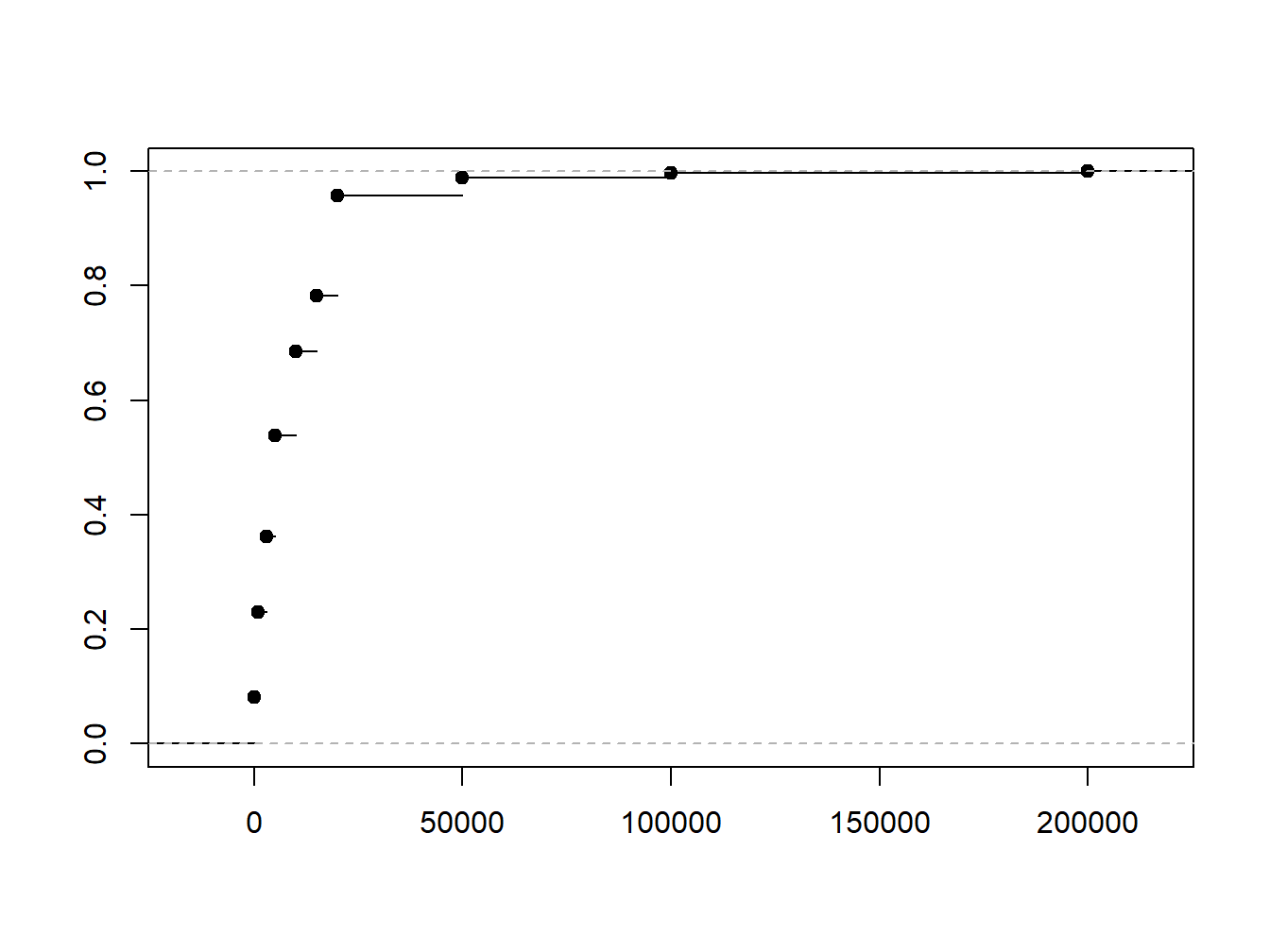
Abbildung 1.5: Treppenkurve aus den kumulierten relativen Häufigkeiten am Beispiel der Vermögensverteilung in Großbritannien 1979
Die Alternative Darstellung als Treppenkurve ist in Abb. 1.5 zu sehen. Sie zeigt den Verlauf der kumulierten relativen Häufigkeiten von 0 bis 1 und steigt mit jedem Intervall um den entsprechenden Anteil an. Die gezeigte Treppenfunktion ist die empirische Verteilungsfunktion. Da eine Verteilungsfunktion nicht fallen kann und die Kurve zwischen den Intervallgrenzen konstant verläuft, entsteht das typische Treppenmuster.
In den weiteren Kapiteln zur statistischen Analyse werden diese Konzepte aufgegriffen. Die relativen Häufigkeiten werden dann zu Wahrscheinlichkeiten; das kumulierte Histogramm wird zur Verteilungsfunktion. Da die Verteilungsfunktion hier aus dem vorliegenden Datensatz abgeleitet wurde und nicht theoretisch aus einer statistischen Verteilung, handelt es sich um eine empirische Verteilungsfunktion.
1.6 Empirische Korrelation
Bisher haben wir uns mit der Beschreibung einer einzelnen Variable beschäftigt. In Beispielen wurden die Verteilung des Alters, des Vermögens in der Bevölkerung oder der Beschäftigtenzahl in Betrieben betrachtet. Häufig interessiert allerdings auch der Zusammenhang zwischen zwei Variablen, z.B. zwischen:
- Naturkatastrophen und Prämienentwicklung der Gebäudeversicherung
- Bruttoinlandsprodukt und Unternehmensinsolvenzen (Kreditvergabe der Banken)
- Rendite und Risiko einer Aktienanlage
Der Korrelationskoeffizient \(\rho\) dient als Maß für den linearen Zusammenhang zwischen zwei Variablen und wird auch als Pearsons Korrelationskoeffizient bezeichnet. Der \(\rho\)-Wert ist standardisiert, so dass er nur Werte von -1 bis +1 annehmen kann. Das Vorzeichen gibt dabei Richtung und der Betrag die Stärke des linearen Zusammenhangs an. Ein positiver Wert \(\rho\) weist auf eine positive Korrelation, also einen gleichgerichteten Zusammenhang, hin (wenn die eine Variable steigt, dann steigt auch die andere). Ein negativer Wert dagegen deutet auf eine negative Korrelation, d.h. einen entgegengesetzten Zusammenhang hin (wenn die eine Variable steigt, fällt die andere). Bei \(\rho=0\) liegt kein linearer Zusammenhang vor, d.h. die Variablen sind unkorreliert. Liegt \(\rho\) betragsmäßig nahe an 1, dann sprechen wir von einem stark ausgeprägten Zusammenhang. Bei einem Betrag gleich 1 haben wir perfekte Korrelation: In diesem Fall liegen die Punkte für die Wertepaare der beiden Variablen auf einer Geraden.
Der Korrelationskoeffizient beschreibt lediglich den linearen Zusammenhang zwischen zwei Variablen. Da auch nicht-lineare Abhängigkeiten zwischen zwei Variablen bestehen können, lässt sich aus Unkorreliertheit nicht auf Unabhängigkeit schließen. Aus Unabhängigkeit folgt allerdings umgekehrt die Unkorreliertheit zweier Variablen.
Berechnung des Korrelationskoeffizienten
Um den Korrelationskoeffizienten für zwei Variablen \(x\) und \(y\) berechnen zu können, benötigen wir zunächst die Kovarianz. Die Kovarianz ist ein Zwischenschritt zur Berechnung des Korrelationskoeffizienten. Sofern der wahre Mittelwert der Grundgesamtheit für beide Variable bekannt ist, berechnet sich die Kovarianz nach dieser Formel:
\[Cov(x,y) =\sigma_{xy}=\frac{1}{N} \sum_{i=1}^N (x_i-\mu_x)(y_i-\mu_y)\] Vergleicht man die Formel für die Kovarianz mit der Formel für die Varianz (vgl. 1.3), so ist zu erkennen, dass die Kovarianz einer Variablen \(x\) mit sich selbst gleich der Varianz von \(x\) ist. Da bei der Arbeit mit Stichproben die wahren Mittelwerte meist unbekannt sind, wird für die Stichprobenkovarianz – oder auch empirische Kovarianz – wieder wie bei der Varianz ein Korrekturfaktor verwendet, um einen erwartungstreuen Schätzer für die Kovarianz zu erhalten. Damit ergibt sich dann folgende Formel.
Definition 1.1 (korrigierte Stichprobenkovarianz) Für eine gemeinsame Datenreihe \((x_1,y_1),\dots,(x_n,y_n)\) zweier statistischer Variablen \(x\) und \(y\) ist die korrigierte Stichprobenkovarianz
\[s_{xy}=\frac{1}{n-1} \sum_{i=1}^n (x_i-\overline{x})(y_i- \overline{y})\]
wobei \(\overline{x}\) und \(\overline{y}\) die arithmetischen Mittel (siehe 1.1) der Datenreihen \((x_1),\dots,(x_N)\) und \((y_1),\dots,(y_N)\) sind.
Aus der Kovarianz lässt sich ablesen, ob die beiden Variablen tendenziell gleich (positives Vorzeichen der Kovarianz) oder entgegengesetzt verlaufen (negatives Vorzeichen der Kovarianz). Da die Kovarianz nicht normiert ist, kann man aus ihr allerdings nicht unmittelbar auf die Stärke des linearen Zusammenhanges schließen. Durch eine geeignete Normierung erhält man daraus jedoch den Korrelationskoeffizienten:
\[\rho_{xy}=\frac{s_{xy}}{s_x s_y}\] Durch die Division durch das Produkt aus den beiden Standardabweichungen ist der Korrelationskoeffizient so normiert, dass er zwischen -1 und 1 liegt.
Beispiel 1.8 (Korrelationskoeffizient für zwei Aktienkurse)
Wir schließen diesen Abschnitt mit einem Anwendungsbeispiel ab: Wir berechnen die Zusammensetzung des varianzminimalen Portfolios.
Beispiel 1.9 (Varianzminimales Portfolio)
1.7 Regression
Das Ziel der Regression in der deskriptiven Statistik besteht darin, eine Gerade an eine Punktwolke anzupassen. Dabei betrachten wir Wertepaare \((x, y)\) und möchten eine Regressionsgerade der Form \(y = mx + n\) finden, die sich den Daten möglichst gut annähert. Eine solche Gerade durch eine Punktwolke ist am Beispiel der fiktiven Aktienkuse aus den vorigen Beispielen in Abb. 1.6 dargestellt.
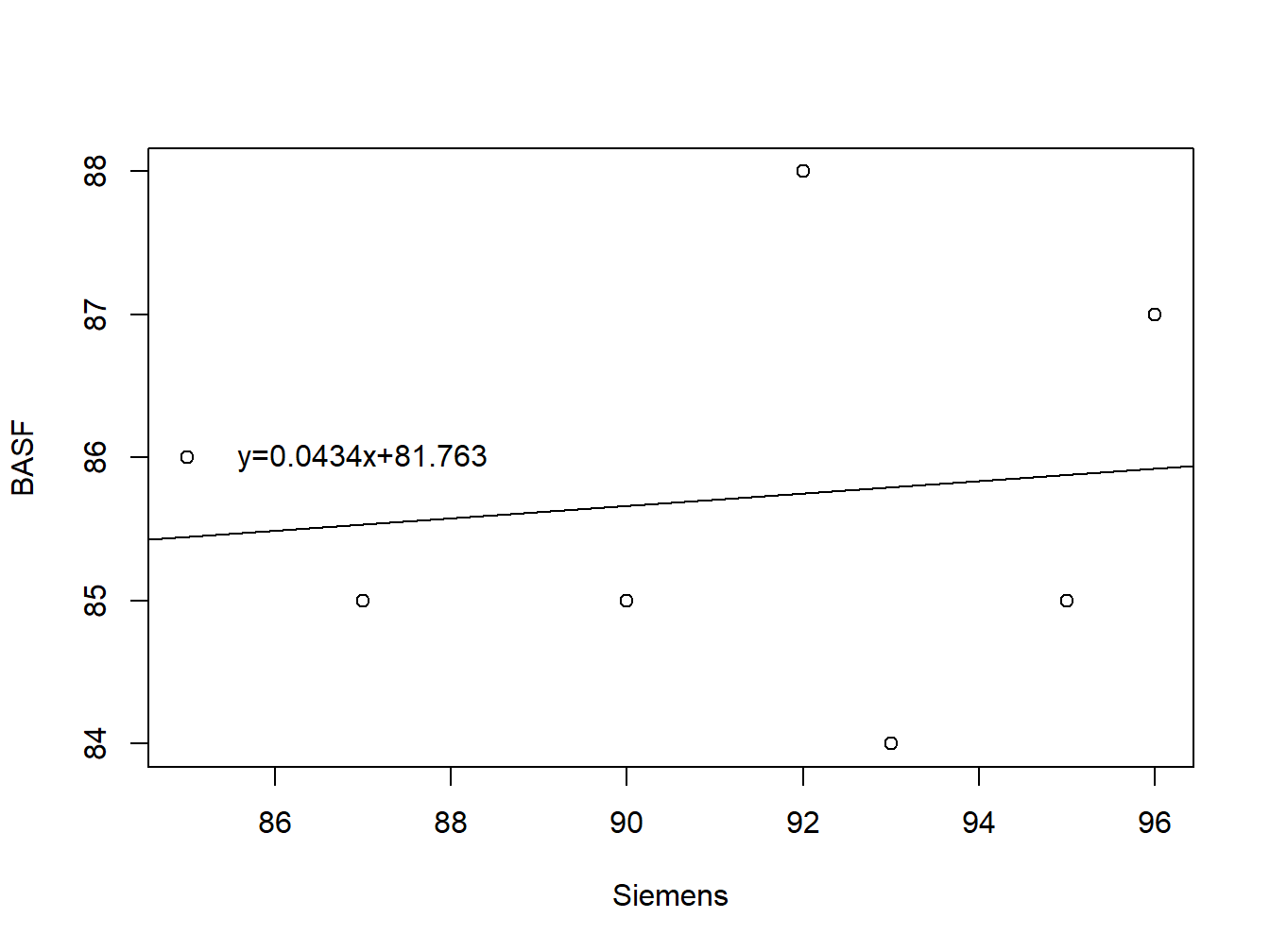
Abbildung 1.6: Fiktive Aktienkurse von Siemens und BASF mit geschätzter Regressionsgerade
Um die Gerade zu finden, nutzen wir die Methode der kleinsten Quadrate, bei der wir die quadrierten Abweichungen zwischen den tatsächlichen \(y\)-Werten und den berechneten \(y\)-Werten minimieren. Das Verfahren geht auf Carl Friedrich Gauss (1777-1855) zurück. Wie schon vorher bei der Berechnung der Varianz erfolgt das Quadrieren der Differenzen, weil sich ansonsten beim Aufsummieren negative und positive Differenzen gegenseitig auslöschen würden. Regressionsschätzer, die nach der Methode der kleinsten Quadrate ermittelt werden, haben vorteilhafte Eigenschaften (z.B. Erwartungstreue) und sind deshalb sehr gebräuchlich. Auf Englisch heißt das Schätzverfahren „ordinary least squares“ – kurz „OLS“.
Herleitung der Kleinste-Quadrate-Schätzer
Zu schätzen ist eine Regressionsgerade der Form \(y=m\cdot x+n\). Jede Beobachtung \(y_i\) lässt sich dann interpretieren als Summe aus einem deterministischen Teil, \(y_i=m \cdot x_i+n\), und einer stochastischen Fehlerkomponente, dem Residuum \(e_i\). Ziel ist es, die quadrierten Residuen \(e_i\) zu minimieren. Statt mit Quadraten könnte man auch mit Absolutbeträgen arbeiten, aber die Formeln würden dann komplizierter werden.
Die zu minimierende Zielfunktion ist also die Summe der quadrierten Abweichungen zwischen tatsächlich beobachteten Kursen und dem durch die Regressionsgleichung erklärten deterministischen Teil:
\[F(m,n)=\sum_{i=1}^n e_i^2=∑_{i=1}^n(y_i-m\cdot x_i-n)^2 \to min.!\] Zunächst folgt die partielle Ableitung nach \(n\):
\[\frac{\partial F(m,n)}{\partial n}=(-2) \cdot \sum_{i=1}^n (y_i-n-m \cdot x_i)\]
Nun die partielle Ableitung nach \(m\):
\[\frac{\partial F(m,n)}{\partial m}=(-2)\cdot \sum_{i=1}^n (y_i-n-m \cdot x_i) \cdot x_i\] Die Ableitungen müssen gleich null gesetzt werden, so dass die \((-2)\) entfallen darf. Daraus entsteht ein Gleichungssystem mit zwei Unbekannten, \(m\) und \(n\), und zwei Gleichungen. Dieses können wir lösen und so Formeln für die Schätzer der Regressionskoeffizienten finden:
\[\hat m=\frac{∑ x_i y_i-n\cdot \overline{x}\cdot \overline{y}}{∑ x_i^2-n\cdot \overline{x}^2}\]
\[\hat n=\overline{y}-\hat m\cdot \overline{x}\] Die geschätzten Werte bekommen ein Dach, um zu zeigen, dass es sich um Schätzer handelt, nicht etwa um die uns unbekannten wahren Werte. Die Methode der Kleinsten Quadrate lässt sich nicht nur für Geraden anwenden, sondern auch für anders spezifizierte Modelle (beispielsweise quadratische Funktionen).
Interpretation des geschätzten Regressionsmodells
Bei der Interpretation der Schätzergebnisse ist Vorsicht geboten. Am Beispiel der Aktienkurse stellt sich die Frage, welche Aussagekraft einer Regression von BASF auf Siemens liegt. Womöglich könnte man meinen, damit sei ein kausaler Zusammenhang impliziert: Wenn der Siemens-Kurs um 1 Euro steigt, dann steigt der BASF-Kurs um 4 Cent. Einen kausalen Zusammenhang können Sie aber aus statistischen Modellen nicht ableiten; dieser muss vielmehr aus der ökonomischen Theorie entstehen. Dort gibt es natürlich Modelle, die Faktoren benennen, die die Entwicklung von Aktienkursen treiben. Das einfachste Modell ist das Capital Asset Pricing Model (CAPM), das Sie auch empirisch überprüfen können – mit Regressionsanalyse!
Oftmals wird ein kausaler Zusammenhang „vorgetäuscht“, indem eine ausgeprägte Korrelation statistisch nachgewiesen wird. Wenn Sie beispielsweise den Zusammenhang zwischen „Wert des Autos“ und „Größe der Wohnung bzw. des Hauses“ statistisch untersuchen, dann werden Sie feststellen, dass beide Variablen eng miteinander korrelieren: Wer ein großes Haus hat, fährt tendenziell auch ein großes Auto. Das heißt aber nicht, dass Sie auch ein großes Haus hätten, wenn Sie nur ein teures Auto kauften! Vielmehr beruht der „vorgetäuschte“ Zusammenhang auf der Höhe des verfügbaren Einkommens. Ein kausaler Zusammenhang zwischen Autos und Häusern ist deshalb nur vorgetäuscht. Eine solche Korrelation ist deshalb nicht echt – auf Englisch: spurious correlation.
Website: Spurious correlations

Zur Veranschaulichung von spurious correlation gibt es allerhand kuriose Beispiele. Einige davon sind hier zusammengestellt, z.B. die Korrelation zwischen US-Rohölimporten aus Norwegen und der Anzahl an Verkehrstoten durch Kollision mit einem Zug.
Darüber hinaus bleibt offen, wie gut die Anpassung der Geraden an die Punktwolke überhaupt ist: Wenn die Anpassung nur mangelhaft gelingt, dann sollten aus den geschätzten Werten für \(m\) und \(n\) natürlich keinerlei Schlüsse gezogen werden. Sie könnten beispielsweise untersuchen, welcher Anteil der Schwankung („Variation“) der einen Variablen, hier der BASF-Kurse, durch die Schwankung in der anderen Variablen, hier der Siemens-Kurse, erklärt wird. Dieser Anteil wird mit \(R^2\) bezeichnet, es ist das Bestimmtheitsmaß und eine sehr gebräuchliche Maßzahl für die Anpassungsgüte eines Modells.
In Kapitel 8 werden wir statistische Testverfahren behandeln, mit denen auch überprüft werden kann, ob die Schätzer überhaupt statistisch signifikant sind. Um dieses Testverfahren zu verstehen, benötigen Sie Kenntnisse über statistische Verteilungen; deshalb können wir an dieser Stelle noch keine Tests durchführen. Wesentlich ist im Moment jedoch die Erkenntnis, dass Schlüsse aus den geschätzten Werten \(\hat m=0{,}04\) bzw. \(\hat n=81{,}76\) auf der Grundlage der uns bisher verfügbaren Informationen nicht fundiert möglich sind.
Aufgabe 1.8 Ein Versicherer interessiert sich für den Zusammenhang zwischen der Prämienhöhe und dem Schadenaufkommen in den vergangenen 15 Jahren. Führen Sie hierzu eine Regressionsanalyse durch und interpretieren Sie das Ergebnis.
| Jahr i | Prämien \(x_i\) in Mio. € | Schäden \(y_i\) in Mio. € |
|---|---|---|
| 1 | 4,903 | 2,200 |
| 2 | 4,754 | 2,095 |
| 3 | 4,618 | 3,377 |
| 4 | 4,479 | 2,455 |
| 5 | 4,388 | 2,121 |
| 6 | 4,435 | 2,100 |
| 7 | 4,638 | 2,336 |
| 8 | 4,790 | 2,816 |
| 9 | 5,011 | 2,418 |
| 10 | 5,250 | 2,855 |
| 11 | 5,349 | 2,901 |
| 12 | 5,805 | 2,715 |
| 13 | 5,929 | 2,634 |
| 14 | 6,122 | 2,822 |
| 15 | 6,542 | 3,270 |
Schlüsselbegriffe
Arithmetisches Mittel; Median und Modalwert; Varianz und Standardabweichung; Quantile; Histogramm; Empirische Verteilungsfunktion; Zusammenhänge zwischen zwei Variablen; Regressionsschätzung einer Geraden; Methode der Kleinsten Quadrate (OLS)
Literatur: