Kapitel 4 Gesetz der Großen Zahlen, Zentraler Grenzwertsatz
Lernziele
- Numerische Stabilisierung des arithmetischen Mittels erklären können
- Gesetz der Großen Zahlen erläutern können
- Stichprobenmittelwert als Zufallsvariable erkennen und interpretieren können
- Verteilung des Stichprobenmittelwerts bei Normalverteilung als Ausgangsverteilung
- Verteilung des Stichprobenmittelwerts bei beliebiger Ausgangsverteilung: Zentraler Grenzwertsatz
- Bedeutung und Anwendungsbeispiele des Zentralen Grenzwertsatzes erklären können
4.1 Gesetz der Großen Zahlen
Das Gesetz der Großen Zahlen ist ein wesentliches Gesetz der Wahrscheinlichkeitsrechnung. Wir lernen es unter zwei Blickwinkeln kennen:
Stellen Sie sich vor, Sie wiederholen dasselbe Zufallsexperiment sehr oft und notieren das jeweilige Ergebnis. Wenn Sie die Liste dieser Ausgänge betrachten, werden Sie eine gewisse Tendenz feststellen: Beim Münzwurf werden Sie in etwa hälftig „Kopf“ und „Zahl“ beobachten. Wenn Sie würfeln und fortlaufend das arithmetische Mittel der Augenzahlen bilden, wird sich dieser Mittelwert auf 3,5 einpendeln (numerische Stabilisierung des arithmetischen Mittels). Dieses Phänomen heißt „Gesetz der großen Zahlen“. Wir wollen uns im Folgenden mit diesen beiden Aspekten des Gesetzes beschäftigen:
- Der Mittelwert einer Stichprobe konvergiert mit wachsender Beobachtungszahl gegen den Erwartungswert der Zufallsvariable.
- Die relativen Häufigkeiten konvergieren mit wachsender Beobachtungszahl gegen die Wahrscheinlichkeiten.
Zum ersten Phänomen: In Abschnitt 1.1 haben wir den Mittelwert als Schwerpunkt der Verteilung kennengelernt. Angenommen die Wahrscheinlichkeitsfunktion sieht wie folgt aus:
| k | P(X=k) |
|---|---|
| k=1 | 1/6 |
| k=2 | 1/6 |
| k=3 | 1/6 |
| k=4 | 1/6 |
| k=5 | 1/6 |
| k=6 | 1/6 |
bzw. als Grafik
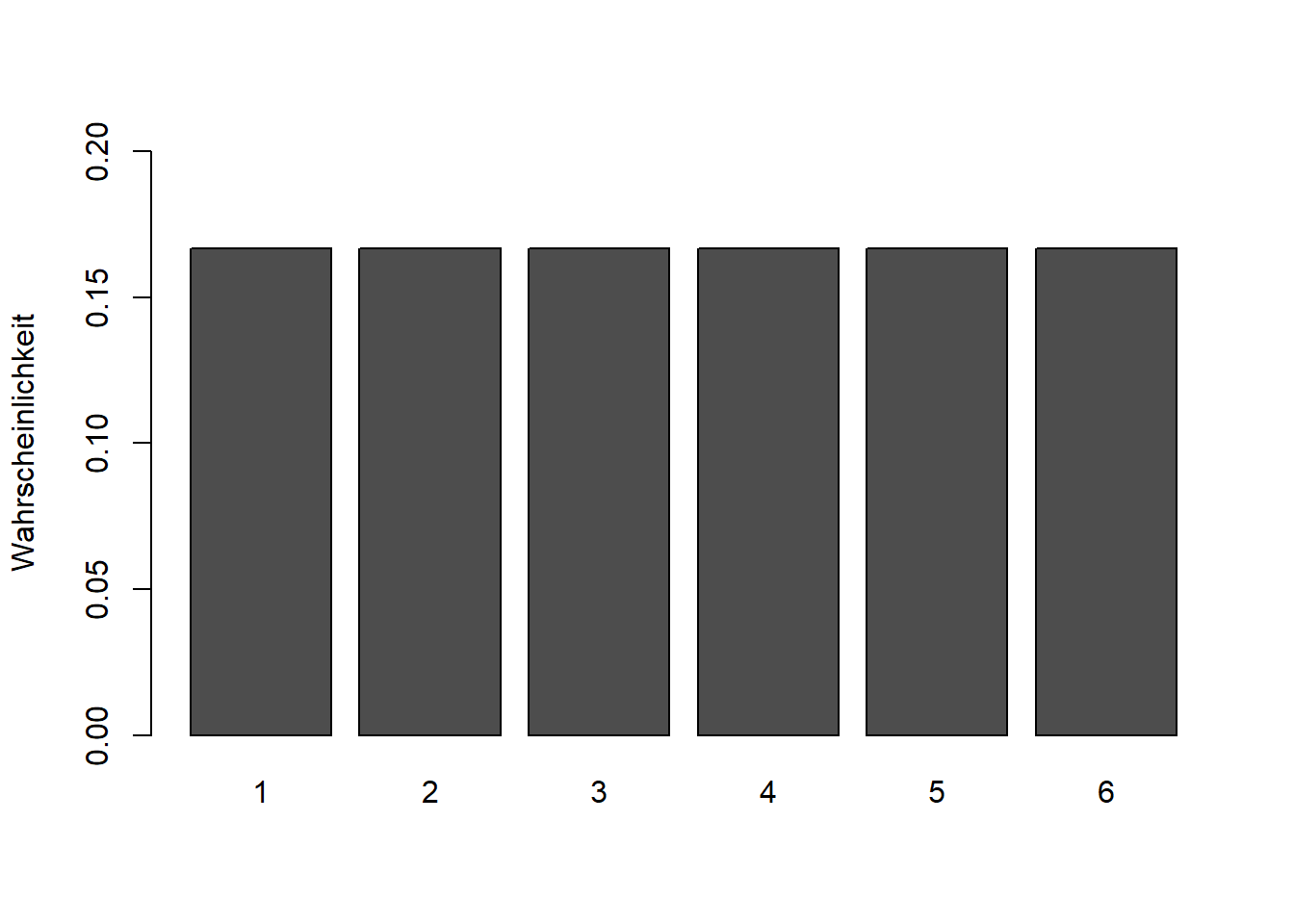
Abbildung 4.1: Wahrscheinlichkeitsfunktion beim Würfelwurf
Dann müssten Sie den Stift bei 3,5 ansetzen, um die Verteilung darauf zu balancieren. Somit ist 3,5 der Schwerpunkt der Verteilung und der Erwartungswert. Auf diesen Wert wird sich der Mittelwert langfristig stabilisieren.
Diese Beobachtung lässt sich mit den Ungleichungen von Markov und Chebyshev beweisen. Wenn Sie den mathematischen Beweis nachvollziehen möchten, sei Ihnen hier der Griff zur Literatur empfohlen.
Genauso wie sich der fortlaufend berechnete Mittelwert auf den Erwartungswert der Verteilung stabilisiert, so pendeln sich auch die relativen Häufigkeiten auf die Wahrscheinlichkeiten ein (unser „zweites Phänomen“). Wenn Sie beim Würfelwurf nicht etwa fortlaufend den Mittelwert der Augenzahlen berechnen, sondern nur die (relative) Häufigkeit notieren, mit der eine 6 erscheint, dann wird sich diese relative Häufigkeit auf \(1/6=0{,}167\) stabilisieren. Dies ist eine weitere Facette des Gesetzes der Großen Zahlen.
Bei den Wiederholungen des Zufallsexperimentes ist es wesentlich, dass die Wiederholungen (Versuche) stochastisch unabhängig sind und die Wiederholungen unter gleichen Bedingungen stattfinden.
Ziel dieses Abschnittes war es, Ihnen ein Grundverständnis über das Gesetz der Großen Zahlen zu vermitteln. Eng verwandt mit dieser Gesetzmäßigkeit ist der Zentrale Grenzwertsatz, den wir als Anwendung der Normalverteilung im folgenden Abschnitt kennenlernen.
4.2 Zentraler Grenzwertsatz
Der Zentrale Grenzwertsatz ist einer der bedeutendsten Anwendungen der Normalverteilung. Wir betrachten nun nicht mehr eine „einfache“ Variable als Zufallsvariable, sondern vielmehr deren Mittelwert. Nehmen Sie an: Sie haben eine Zufallsvariable, die einer bestimmten Verteilung folgt, und Sie ziehen aus dieser Verteilung mehrere Stichproben nacheinander, berechnen aus diesen Stichproben jeweils den Mittelwert und notieren diesen. Sie werden dann feststellen, dass der Stichprobenmittelwert wiederum eine Zufallsvariable darstellt, die einer Verteilung folgt. Nach dem Zentralen Grenzwertsatz ist dies immer zumindest approximativ eine Normalverteilung – unabhängig von der Ausgangsverteilung! Wir wollen uns im Folgenden mit diesem Phänomen beschäftigen.
Im ersten Schritt gehen wir von einer normalverteilten Zufallsvariable aus. Beispielsweise sei unsere Ausgangsverteilung die Körpergröße erwachsener Männer, die wir bereits im Abschnitt 3.2.1 untersucht haben. Aus dieser Normalverteilung ziehen wir mehrere zufällige Stichproben nacheinander und unabhängig voneinander. Für jede Stichprobe berechnen wir das arithmetische Mittel und legen dann die „gezogenen“ Männer für die Folgestichprobe zurück in die Verteilung. Diese Stichprobenmittelwerte sind wieder eine Zufallsvariable. Die Frage ist nun, welcher statistischen Verteilung sie folgen.
\[\overline{x}=\frac 1 n (x_1+x_2+x_3+x_4+⋯+x_n)\]
Jede Beobachtung \(x_i\) ist eine normalverteilte Zufallsvariable. \(\overline{x}\) ist eine Linearkombination normalverteilter Zufallsvariable und deshalb selbst wieder normalverteilt.
Welche Parameter hat nun diese Normalverteilung der Stichprobenmittelwerte?
\[ E(\overline{x})=\frac 1 n \left(E(x_1 )+E(x_2 )+E(x_3 )+E(x_4 )+⋯+E(x_n )\right)= \frac 1 n (\mu+\mu+\mu+\dots+\mu)\\ =\frac{1}{n}\cdot n\cdot \mu =\mu \]
Demnach ist der erste Parameter der Normalverteilung der Stichprobenmittelwerte gleich dem ersten Parameter der Ausgangsverteilung, also unser \(\mu\). Im obigen Beispiel der Körpergröße ist dies 1,74 m.
\[ \begin{aligned} Var(\overline{x})=Var\left(\frac 1 n (x_1+x_2+x_3+⋯+x_n )\right)\\ =\frac 1 {n^2} \left(Var(x_1 )+Var(x_2 )+Var(x_3 )+⋯+Var(x_n )\right)\\ =\frac 1 {n^2} (\sigma^2+\sigma^2+\sigma^2+\dots+\sigma^2 )=\frac 1 {n^2} \cdot n\cdot \sigma^2=\frac 1 n \sigma^2 \end{aligned} \]
Dies ist der zweite Parameter der Normalverteilung der Stichprobenmittelwerte. Im Vergleich zur Ausgangsverteilung ist die Varianz der Stichprobenmittelwerte kleiner: statt \(\sigma^2\) in der Ausgangsverteilung ist die Varianz nun \(\frac 1 n \sigma^2\). Dies ist plausibel, denn die Stichprobenmittelwerte werden weniger streuen als die ursprüngliche Zufallsvariable.
Beispiel 4.1 (Normalverteilung der Körpergröße) Nehmen wir wiederum die Normalverteilung der Körpergröße erwachsener Männer aus Beispiel 3.5 als Ausgangsverteilung: Mittelwert 174 cm, Standardabweichung 9,6 cm, Varianz 92,16 cm². Die Stichprobenmittelwerte aus dieser Verteilung sind wieder normalverteilt mit Mittelwert 174 cm und Varianz \(\frac{92{,}16}{n}\) (\(n\) ist der Stichprobenumfang). Wenn wir aus der Ausgangsverteilung einige Männer herausziehen, kann es durchaus vorkommen, dass diese Männer entweder sehr klein oder sehr groß sind. Bei den Mittelwerten ist dies recht unwahrscheinlich: Dass ein Mittelwert bei 160 cm oder 190 cm liegt, ist schwer vorstellbar, aber ein einzelner „gezogener“ Mann könnte durchaus eine dieser Größen haben. Deshalb schwanken die Mittelwerte wesentlich weniger als die Ausgangszufallsvariable.
Nehmen wir an, wir ziehen eine Stichprobe vom Umfang \(n=9\). Wie hoch ist die Wahrscheinlichkeit, dass die Stichprobenmittelwerte größer als 180 cm sind?
Sie erinnern sich, wir hatten dies bereits für die Ausgangsverteilung ermittelt, es waren 26,4 %. Wir berechnen nun die Wahrscheinlichkeit für den Stichprobenmittelwert:
\[z=\frac{180-174}{\sqrt{\frac{92{,}16}{9}}}=1{,}88\]
Dies schlagen wir in der Tabelle für die Standardnormalverteilung nach und erhalten 3 % – also wesentlich weniger als für die Ausgangsverteilung. Dies ist plausibel, denn die Normalverteilung der Stichprobenmittelwerte liegt zwar an derselben Stelle wie die Ausgangsverteilung, sie ist aber wesentlich schmaler als die Ausgangsverteilung. Deshalb muss die Fläche in der rechten Flanke rechts von 180 cm auch geringer sein als für die Ausgangsverteilung.
Wir halten fest: Wenn die Ausgangsverteilung eine Normalverteilung ist, dann sind die Stichprobenmittelwerte wieder normalverteilt mit demselben Mittelwert der Ausgangsverteilung und mit kleinerer Varianz (\(\frac{\sigma^2}{n}\)). Je größer die Stichprobe, desto stabiler sind die Stichprobenmittelwerte und umso schmaler deren Verteilung.
Wie ist dies, wenn die Ausgangsverteilung keine Normalverteilung ist? Hier nutzen wir den Zentralen Grenzwertsatz (ZGWS, englisch: Central Limit Theorem CLT):
Die Stichprobenmittelwerte \(\overline{x}\) aus einer Grundgesamtheit mit Mittelwert \(\mu\) und Varianz \(\sigma^2\) folgen näherungsweise einer Normalverteilung mit Mittelwert \(\mu\) und Varianz \(\frac{\sigma^2}{n}\), wobei die Annäherung an die Normalverteilung mit steigendem Stichprobenumfang \(n\) besser wird.
Wir wollen diese Erkenntnis auf die Vermögensverteilung anwenden, da wir von dieser Verteilung bereits wissen, dass sie stark asymmetrisch ist, so dass in diesem Beispiel die Ausgangsverteilung keineswegs eine Normalverteilung ist.
Aufgabe 4.1 Wir erinnern uns:
Mittelwert \(\mu\) = 16.399 Pfund
Varianz \(\sigma^2\) = 652.915.569 Pfund2
Stichprobenumfang \(n = 50\)
Wie hoch ist die Wahrscheinlichkeit von \(\overline{x}\)>20.000 Pfund?
Aufgabe 4.2 Wie hoch ist die Wahrscheinlichkeit von \(x\) > 20.000 Pfund?
Ein Versicherer teilt das Risiko, dass er auszahlen muss, im Versichertenkollektiv auf. Dies funktioniert bei einem großen Kollektiv (\(n\) groß) besonders gut; die Streuung der Stichprobenmittelwerte (Auszahlung durch den Versicherer) ist dann gering. In der Tarifierung werden üblicherweise prozentuale Aufschläge auf eine theoretisch berechnete faire Prämie ermittelt. Diese Aufschläge können entweder fest sein oder proportional zur Streuung des Risikos.
Der Zentrale Grenzwertsatz kann mathematisch formal aus dem Gesetz der Großen Zahlen hergeleitet werden. Wichtig sind für uns zwei Erkenntnisse:
- unabhängig von der Form der Ausgangsverteilung sind die Stichprobenmittelwerte zumindest approximativ normalverteilt und
- die Normalverteilung der Stichprobenmittelwerte hat als Mittelwert wieder denselben wie die Ausgangsverteilung, die Varianz ist aber wesentlich geringer, da die Stichprobenmittelwerte stabiler sind (\(\frac{\sigma^2}{n}\)).
Schlüsselbegriffe:
Numerische Stabilisierung des arithmetischen Mittels; Gesetz der Großen Zahlen; Stichprobenmittelwert als Zufallsvariable; Verteilung des Stichprobenmittelwerts; Zentraler Grenzwertsatz
Literatur: