Kapitel 8 Statistische Testverfahren

---

Lernziele

• Nullhypothesen aufstellen und testen können
• Einseitige und zweiseitige Tests
• Prüfgröße mit passender Verteilung auswählen können (Auswahl fundiert begründen können)
• Irrtumswahrscheinlichkeit erklären können (\(\alpha\)- und \(\beta\)-Fehler)
• Ablehnungsbereich ermitteln können
• Aussage des P-Wertes erklären können
• Verbindung zwischen Konfidenzintervallen und Signifikanztests erklären können
• Präzise Formulierung zum Verwerfen von Nullhypothesen kennen und begründen können
• Signifikanztests mit Prüfgrößen folgender Verteilungen durchführen und erläutern können: Binomial-, Normal-, t- und Chi-Quadrat-Verteilung
• Gemeinsamkeiten und Unterschiede von Chi-Quadrat-Anpassungstest und Chi-Quadrat-Unabhängigkeitstest erklären können
• Q-Q-Plots einordnen können

---

Statistische Testverfahren sind das Herzstück der Statistik. Sie beinhalten nicht nur die zentrale Schlussfolgerung von der Stichprobe auf die unbekannte Grundgesamtheit, sondern sie quantifizieren auch die Unsicherheit, die mit diesem Schluss einhergeht, indem Hypothesen (beispielsweise „Das Klima hat sich in den letzten 20 Jahren verändert“ oder „Nichtraucher leben länger“) statistisch getestet werden. Wir haben in den vorangegangenen Kapiteln die Grundlagen gelegt, die wir für dieses „Königskapitel“ benötigen. Wir lernen mehrere Testverfahren kennen, die auf unterschiedlichen statistischen Verteilungen beruhen, die zum Teil noch neu für uns sind. Am Ende des Kapitels können Sie selbstständig Hypothesen aufstellen und testen: Oftmals sind wir mit Hypothesen über eine Grundgesamtheit konfrontiert. Ob diese statistisch haltbar sind, werden Sie fundiert auf der Basis einer Stichprobe beurteilen können.

8.1 Einführung in statistische Signifikanztests

Zunächst wollen wir das Prinzip von statistischen Signifikanztests und ein paar grundlegende Begriffe erarbeiten.

Hypothesen beziehen sich immer auf die Grundgesamtheit. Wir akzeptieren oder verwerfen eine Hypothese auf der Grundlage der Informationen in einer Stichprobe. Mit der Entscheidung, die Hypothese zu akzeptieren oder zu verwerfen, können wir richtig oder falsch liegen, genauso wie unsere Konfidenzintervalle den wahren Wert überdecken oder im Einzelfall weit von ihm entfernt liegen können. Wir begehen dabei zwei Arten von Fehlern:

1. den Fehler, eine wahre Hypothese fälschlicherweise zu verwerfen (\(\alpha\)-Fehler oder Fehler 1. Art, mit Wahrscheilichkeit \(\alpha\)) und
2. den Fehler, eine falsche Hypothese versehentlich zu akzeptieren (\(\beta\)-Fehler oder Fehler 2. Art, mit Wahrscheilichkeit \(\beta\)).

Es ist nicht möglich, beide Fehlertypen gleichzeitig zu minimieren. Wir halten die Wahrscheinlichkeit eines \(\alpha\)-Fehlers gering und nehmen eine große Wahrscheinlichkeit für einen \(\beta\)-Fehler in Kauf. Die Hypothese, welche die zu überprüfende Annahme über die Wahrscheinlichkeitsverteilung einer bzw. mehrerer Zufallsvariablen definiert, bezeichnet man als Nullhypothese \(H_{0}\). Wird die Nullhypothese verworfen, so nehmen wir an, dass stattdessen eine Alternativhypothese \(H_1\) gelten muss.

Typ-I- und Typ-II-Fehler ergänzen sich nicht etwa zu 100 %, sondern sind Flächen unter zwei unterschiedlichen Verteilungen. Der Typ-II-Fehler (\(\beta\)) liegt unter der Verteilung der Prüfgröße unter der \(H_1\)-Hypothese, während der Typ-I-Fehler (\(\alpha\)) unter der Verteilung unter der Nullhypothese \(H_0\) liegt (und zwar in Richtung \(H_1\), d. h. in Richtung des Ablehnungsbereiches) (vgl. Abbildung 8.1). Häufig ist die exakte Lage des Mittelwerts unter der Alternativhypothese jedoch nicht näher bestimmt, sodass in der Regel die Wahrscheinlichkeit eines Typ-II-Fehlers nicht vorab bestimmt werden kann.

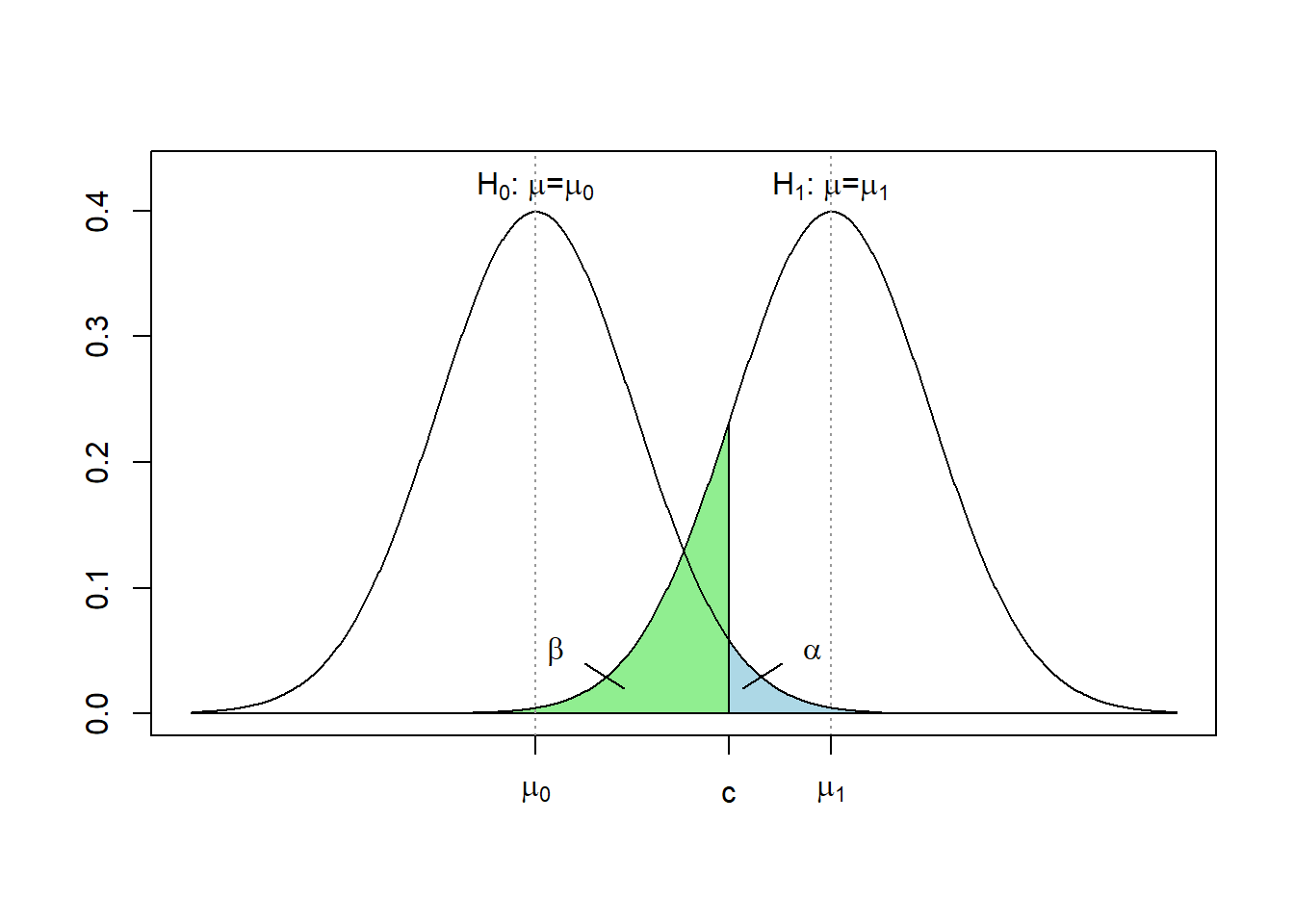
Abbildung 8.1: Veranschaulichung der Wahrscheinlichkeit eines Fehlers 1. Art \(\alpha\) und eines Fehlers 2. Art \(\beta\) am Beispiel eines einseitigen Signifikanztests über den Erwartungswert \(\mu\). \(c\) ist hier der kritische Wert des Tests.

Die Fehler von Typ-I und Typ-II stehen in direktem Zusammenhang mit zwei weiteren Begriffen:

1. die richtige Entscheidung, eine wahre Hypothese nicht zu verwerfen (Spezifität, mit Wahrscheinlichkeit \(1-\alpha\)) und
2. die richtige Entscheidung, eine falsche Hypothese zu verwerfen (Power, Mächtigkeit oder auch Trennschärfe des Tests, mit Wahrscheinlichkeit \(1-\beta\)).

Beispiel 8.1 (Polit-Umfrage: Aufstellen von Hypothesen) Bei einer Polit-Umfrage behauptet ein Kandidat, dass er mindestens 50 % der Wähler hinter sich hätte. Wir formulieren auf dieser Grundlage die Nullhypothese:

\[H_0: \pi≥0{,}5, \text{d. h. }\pi_0=0{,}5\]

und die Alternativhypothese:

\[H_1: \pi<0{,}5\]

Als Eselsbrücke können Sie sich merken, dass das Gleichheitszeichen immer in die Nullhypothese sollte. Die beiden Hypothesen müssen einander ausschließen.

Wir ziehen nun eine Stichprobe vom Umfang 10 und fragen, welche Anzahl an Personen in der Stichprobe den Kandidaten unterstützt. Diese Anzahl ist eine Zufallsvariable und in einer großen Grundgesamtheit approximativ binomialverteilt.

Bei welcher Anzahl X der Unterstützer in der Stichprobe sollen wir die Nullhypothese annehmen, bei welcher Anzahl verwerfen?

Beim klassischen Signifikanztest verwenden wir folgende Entscheidungsregel: Wir verwerfen die Nullhypothese nur dann, wenn es sehr unwahrscheinlich ist, dass sie wahr ist. Umgekehrt ist es unwahrscheinlich, dass X klein ist, wenn die Nullhypothese wahr ist. Falls also X sehr klein ist, verwerfen wir die Nullhypothese. Die Werte von X, für die wir die Nullhypothese verwerfen, heißen Verwerfungs- oder Ablehnungsbereich.

Beispiel 8.2 (Polit-Umfrage: Signifikanzniveau und Hypothesentest) Im nächsten Schritt wählen wir die maximale Wahrscheinlichkeit eines \(\alpha\)-Fehlers, also die Wahrscheinlichkeit, eine wahre Nullhypothese versehentlich zu verwerfen. Diese Wahrscheinlichkeit heißt Signifikanzniveau des Tests und wird mit \(\alpha\) bezeichnet, weil es die Wahrscheinlichkeit des \(\alpha\)-Fehlers ist. Wie beim Konfidenzniveau wählt man üblicherweise 1 %, 5 % oder 10 % als Signifikanzniveau.

Das Signifikanzniveau legt den Ablehnungsbereich fest. Wir wählen immer den größtmöglichen Ablehnungsbereich, der das Signifikanzniveau gerade noch einhält:

Prüfgröße X	\(P(X)=\dbinom{10}{x} 0{,}5^x 0{,}5^{10-x}\)	P(X≤x)
0	0,00098	0,00098
1	0,0098	0,01
2	0,044	0,05
3	0,12	0,17
4	0,21	0,38
5	0,25	0,62
6	0,21	0,83
7	0,12	0,95
8	0,044	0,989
9	0,0098	0,999
10	0,00098	1,0

Die Tabelleneinträge können Sie selbstständig anhand der Binomialverteilung nachvollziehen.

Bei einem Signifikanzniveau von 0,1 = 10 % haben wir einen Ablehnungsbereich von \(\{0,1,2\}\), denn bei \(x=3\) übersteigt die kumulierte Wahrscheinlichkeit die 10 %-Marke. Somit ist \(A=\{0,1,2\}\) der größtmögliche Ablehnungsbereich. Wenn in unserer Stichprobe nur weniger als 3 Personen den Kandidaten unterstützen, verwerfen wir die Nullhypothese.

Aufgabe 8.1 (Polit-Umfrage: weiterer Signifikanztest) Wie wäre der Ablehnungsbereich für das Signifikanzniveau von 5 %?

Wie schon bei den Konfidenzintervallen sollten wir auch hier auf exakte Formulierungen achten. Da die Wahrscheinlichkeit eines \(\beta\)-Fehlers im Einzelfall sehr hoch werden kann, sagen wir nie, dass wir eine Nullhypothese „annehmen“ oder „akzeptieren“. Wir können entweder eine Nullhypothese verwerfen oder nicht verwerfen. Wenn wir die Nullhypothese verwerfen, begehen wir einen kleinen Fehler, nämlich maximal \(\alpha\). Wenn wir die Nullhypothese nicht verwerfen, kann die Wahrscheinlichkeit, dass wir falsch liegen, recht hoch werden (\(\beta\)). In diesem Fall sind wir uns nicht sicher, ob die Nullhypothese tatsächlich richtig ist. Deshalb nehmen wir sie nicht an, sondern verwerfen sie nur nicht.

Beispiel 8.3 (Polit-Umfrage: zweiseitiger Hypothesentest) Wir unterscheiden zwischen einseitigen und zweiseitigen Hypothesentests. Wenn der Ablehnungsbereich wie im obigen Beispiel nur auf einer Seite der Wahrscheinlichkeitsverteilung liegt, ist es ein einseitiger Test. Beim zweiseitigen Test befindet sich der (halbe!) Ablehnungsbereich auf beiden Seiten der Verteilung; dies ist analog zu den Konfidenzintervallen, die wir im Kapitel 7 kennengelernt haben. Bei zweiseitigen Tests ist die Nullhypothese

\[H_0: \pi=0,5\]

und entsprechend die Alternativhypothese

\[H_1: \pi≠0,5\]

Der Ablehnungsbereich wird zwischen linker und rechter Flanke aufgeteilt, d. h. \(A=\{0,1,2,7,8,9,10\}\) mit gerundeten Werten (aus der Tabelle in Beispiel 8.2). Wenn wir in der Stichprobe eine Anzahl aus dem Ablehnungsbereich \(A\) beobachten, verwerfen wir die Nullhypothese. Dies ist intuitiv plausibel, denn wenn beispielsweise 9 von 10 Personen den Kandidaten unterstützen, sollten wir nicht daran festhalten, dass der Kandidat „nur“ 50 % Unterstützer hinter sich vereint.

Wir haben in diesem Abschnitt bereits mehrfach auf Konfidenzintervalle Bezug genommen. Der wesentliche Unterschied zu Konfidenzintervallen besteht darin, dass wir bei den Konfidenzintervallen die Informationen aus der Stichprobe vorliegen haben und eine Aussage über die unbekannte Grundgesamtheit treffen wollen. Beim Hypothesentest hingegen liegt uns eine Vermutung zur Grundgesamtheit vor, die wir anhand der Informationen in der Stichprobe überprüfen.

Der zweiseitige Hypothesentest und das Konfidenzintervall müssen bei gleichem Konfidenz- bzw. Signifikanzniveau zum selben Ergebnis führen. Die Werte des Parameters, die außerhalb des Konfidenzintervalls liegen, können mit dem Signifikanztest verworfen werden.

Fassen wir die Grundidee des Signifikanztests noch einmal zusammen. Es wird eine Prüfgröße berechnet (im obigen Beispiel ist X die Prüfgröße), deren statistische Verteilung bekannt ist. Wir legen eine Irrtumswahrscheinlichkeit fest und schneiden diese einseitig oder zweiseitig von den Flanken der Verteilung ab. Die Stelle, wo die Flanken abgeschnitten werden, wird als kritischer Wert bezeichnet und meist mit dem Buchstaben \(c\) (für critical value) angegeben. Wenn der Wert der Prüfgröße für eine konkrete Stichprobe jenseits eines kritischen Wertes, d. h. in einer „abgeschnittenen“ Flanke liegt, verwerfen wir die Nullhypothese mit einer Irrtumswahrscheinlichkeit \(\alpha\).

Ein moderneres Verfahren des Signifikanztests wurde möglich, als Softwarepakete die Fläche in den Flanken der Verteilung der Prüfgröße an jeder Stelle berechnen konnten. Seither ist es nicht mehr sinnvoll, die kritischen Werte für eine fix vorgegebene Irrtumswahrscheinlichkeit festzulegen. Stattdessen wird im Test der sogenannte P-Wert ausgegeben. Dies ist die Wahrscheinlichkeit, unter der Nullhypothese einen mindestens so extremen Wert für die Prüfgröße zu erhalten wie in der konkreten Stichprobe. Falls der P-Wert (noch) kleiner ist als ein klassisches Signifikanzniveau, fällt die Prüfgröße in den Ablehnungsbereich. Der Vorteil des P-Wertes gegenüber dem Signifikanzniveau besteht darin, dass der Leser beim P-Wert selbst entscheiden kann, bei welcher Irrtumswahrscheinlichkeit er die Nullhypothese verwerfen möchte. Seine Aussage ist genauer, weil sie nicht nur bestimmt, ob die Prüfgröße in den Ablehnungsbereich fällt oder nicht, sondern vielmehr ihre Position innerhalb der statistischen Verteilung der Prüfgröße angibt. Der P-Wert ist demnach generell informativer als das Ergebnis des klassischen Signifikanztests.

Wir haben uns jetzt das Grundprinzip des klassischen Signifikanztests erarbeitet. Im obigen Beispiel der Polit-Umfrage haben wir sogar unbewusst bereits einen Binomialtest durchgeführt, denn unsere Prüfgröße war binomialverteilt. Wir werden im Folgenden die gebräuchlichsten Signifikanztests systematisch kennenlernen.

8.2 Binomialtest

Der Binomialtest wird für Hypothesen über den Anteil in einer Grundgesamtheit angewendet; dieser Anteil in der Grundgesamtheit wird mit \(\pi\) bezeichnet. Wir haben im obigen Beispiel einer Polit-Umfrage bereits einen solchen Binomialtest kennengelernt. Wenn Sie die Tabelle in Beispiel 8.2) händisch nachvollzogen haben, ist Ihnen aufgefallen, dass die Ermittlung des Ablehnungsbereichs mit der Binomialverteilung recht aufwändig sein kann. Dies hatten wir bereits im Abschnitt 3.1.1 festgestellt und gelernt, dass wir die Binomialverteilung durch eine Normalverteilung annähern können. Dies gilt insbesondere dann, wenn \(n\) groß ist und die Erfolgswahrscheinlichkeit möglichst nahe an 0,5 liegt. Die Parameter dieser angenäherten Normalverteilung lauten:

\[\mu=n\cdot\pi\]

\[\sigma^2=n\cdot\pi\cdot(1-\pi)\]

Sie kennen diesen Zusammenhang nicht nur aus Abschnitt 3.1.1, sondern auch von den Konfidenzintervallen im Kapitel 7.

Nach dem Zentralen Grenzwertsatz ergibt sich für den Signifikanztest die Prüfgröße

\[Z=\frac{X-n\cdot\pi}{\sqrt{n\cdot\pi\cdot(1-\pi)}},\]

die einer Standardnormalverteilung folgt, so dass wir den P-Wert aus der uns vertrauten Tabelle 8.1 für die Standardnormalverteilung ablesen können. Dieser Test ist ein approximativer Binomialtest, weil wir die Binomialverteilung durch eine Normalverteilung annähern.

Nachdem wir uns eingangs der Mühe unterzogen haben, den exakten Binomialtest durchzuführen, wollen wir ihn nun approximativ mit der Normalverteilung vornehmen und die Ergebnisse vergleichen.

Beispiel 8.4 (Polit-Umfrage: approximativer Binomialtest) Zur Erinnerung: \(n=10\), \(\pi=0{,}5\) somit \(\mu=10\cdot 0,5=5\) und \(\sigma^2=10\cdot 0,5\cdot 0,5=2,5\).

Wir betrachten zur Übung zwei Fälle: \(X=5\) und \(X=8\).

Für den Wert der Prüfgröße: \[Z=\frac{X-5}{\sqrt{2{,}5}}\] erhält man

• im Fall \(X=5\): Z = 0
  
• im Fall \(X=8\): Z = 1,9

Die P-Werte lauten

• für \(Z=0\): 0,5 und
• für \(Z=1{,}9\): 0,0287

Demnach würden wir für \(X=5\) die Nullhypothese nicht verwerfen, für \(X=8\) mit einem P-Wert von 2,9 % aber schon. Dies ist intuitiv plausibel, denn bei 80 % Unterstützung des Kandidaten in der Stichprobe ist die Vermutung schwer haltbar, er hätte nur 50 % Unterstützung in der Grundgesamtheit.

Alternativ können wir beispielsweise für eine Irrtumswahrscheinlichkeit von 10 % und einen zweiseitigen Test die Stellen der Standardnormalverteilung aus der Tabelle 8.1 ablesen, an denen wir die Nullhypothese beginnen zu verwerfen. Diese Stellen kennen wir bereits von den Konfidenzintervallen (Kapitel 7): \(\pm 1,64\). Somit ist \(Z=0\) nicht zu verwerfen, \(Z=1{,}9\) aber schon.

Wir haben nunmehr den klassischen Signifikanztest verstanden und können ihn für eine binomial- und eine normalverteilte Zufallsvariable anwenden. Wir können sowohl einen Ablehnungsbereich festlegen oder aber den P-Wert zum Wert einer Prüfgröße angeben. Demnach können wir zweifelsfrei entscheiden, ob wir eine Hypothese bezüglich der Grundgesamtheit verwerfen oder nicht.

Aufgabe 8.2 (Binomialtest der Pünktlichkeitsquote) Eine Reiseversicherung zahlt aus, wenn sich eine Flugverbindung um mindestens 2 Stunden verspätet. Es gibt für Flüge auf einer bestimmten Route eine allgemeine Pünktlichkeitsquote. Wir nehmen an, dass diese bei 80 % liegt und betrachten 200 Flüge, von denen 140 pünktlich waren. Können wir auf dieser Grundlage die Hypothese verwerfen, dass der Anteil der pünktlichen Flüge bei 0,8 liegt? Sie dürfen den approximativen Binomialtest verwenden.

8.3 Gauß-Test

In Kapitel 7 haben wir Konfidenzintervalle für Mittelwerte berechnet. In diesem Abschnitt lernen wir das Pendant dazu unter den Hypothesentests kennen.

Die Prüfgröße folgt unmittelbar aus dem Zentralen Grenzwertsatz (Abschnitt 4.2) und ist standardnormalverteilt, wenn wir die Varianz der Grundgesamtheit kennen:

\[Z=\frac{\overline{X}-\mu}{\sigma⁄\sqrt{n}} \sim N(0,1)\]

Bei Kenntnis der Varianz der Grundgesamtheit ist diese Prüfgröße exakt normalverteilt. Da die Normalverteilung von Carl Friedrich Gauß entdeckt wurde, wird sie auch Gauß-Verteilung genannt. Der Signifikanztest mit dieser Prüfgröße heißt deshalb auch Gauß-Test. Der Ablehnungsbereich dieser Prüfgröße hängt ausschließlich vom Signifikanzniveau ab. Wir lesen ihn in der Tabelle 8.1 für die Standardnormalverteilung ab.

Da Sie das Verfahren auch aus Kapitel 7 kennen, können Sie die folgende Aufgabe direkt im Selbststudium lösen:

Aufgabe 8.3 (Test auf angegebenen Mittelwert bei bekannter Varianz)) Eine Maschine füllt Mehl in Tüten ab. Da die Maschine nicht exakt arbeitet, sind manche Tüten etwas schwerer als 1 kg und manche etwas leichter. Wir prüfen das Gewicht von 80 Tüten; hier liegt das durchschnittliche Gewicht bei 1.001,6 g. Zu testen ist die Vermutung, dass die Mehltüten ein Gewicht von genau 1 kg aufweisen. Legen Sie ein Signifikanzniveau von 10 % zugrunde. Die Varianz sei aus früheren Untersuchungen bekannt und betrage 8,0.

Wir sind jetzt vertraut mit Signifikanztests über den Mittelwert, wenn die Varianz bekannt ist. Wir wollen dies nun erweitern auf den Fall, dass die Varianz nicht bekannt ist, sondern aus der Stichprobe erwartungstreu geschätzt werden muss.

8.4 t-Test

Wir betrachten in diesem Abschnitt grundsätzlich den gleichen Signifikanztest wie in Abschnitt 8.3, allerdings ist hier die Varianz unbekannt und muss erwartungstreu aus der Stichprobe geschätzt werden (siehe Abschnitt 1.3). Dadurch ist die Prüfgröße jetzt nicht mehr normalverteilt, sondern t-verteilt. Deshalb heißt der Test jetzt t-Test.

Die t-Verteilung kennen wir noch nicht. Sie ist wie die Standardnormalverteilung symmetrisch um den Mittelwert, hat aber einen Verteilungsparameter, die sogenannten Freiheitsgrade. Die Anzahl der Freiheitsgrade bei der Verteilung der Prüfgröße ist die Anzahl der Beobachtungen \(n-1\). Bei einer kleinen Anzahl an Freiheitsgraden ist die t-Verteilung in der Mitte etwas schmaler als die Standardnormalverteilung und hat dafür breitere Flanken („Enden“). Bei einer größeren Anzahl an Freiheitsgraden nähert sich die t-Verteilung immer mehr der Standardnormalverteilung.

Für den Signifikanztest behalten wir die Prüfgröße aus dem Abschnitt 8.3 bei, verwenden statt \(\sigma\) nun \(s\), und die Prüfgröße folgt einer t-Verteilung mit \((n-1)\) Freiheitsgraden. Wir nennen deshalb die Prüfgröße nicht mehr Z, sondern T:

\[T=\frac{\overline{x}-\mu}{s⁄\sqrt{n}} \sim t(n-1)\]

Die Grenzen des Ablehnungsbereiches sind hier nicht mehr nur abhängig vom Signifikanzniveau und davon, ob der Test einseitig oder zweiseitig ist, sondern zusätzlich noch vom Stichprobenumfang n, der die Anzahl der Freiheitsgrade festlegt. Die kritischen Werte der t-Verteilung sind aus einer entsprechenden Tabelle abzulesen, oder sie werden von Softwarepaketen berechnet.

Da das Vorgehen beim t-Test sehr ähnlich dem beim Gauß-Test ist, können Sie direkt die Tabelle 8.2 für die t-Verteilung verwenden, um die folgende Aufgabe zu lösen.

Aufgabe 8.4 (Test auf Mittelwert bei unbekannter Varianz) Der Vorstand eines Versicherungsunternehmens möchte die Hypothese getestet haben, dass die Sturmfrequenzen in den vergangenen 15 Jahren kleiner als 1,25 sind. Die Sturmfrequenzen lauten:

Jahr i	Anzahl Sturmereignisse
1	0
2	1
3	2
4	0
5	1
6	0
7	3
8	0
9	0
10	1
11	0
12	2
13	1
14	0
15	1

Führen Sie den Hypothesentest zu 95 % Konfidenzniveau durch.

Als nächstes wenden wir uns einer anderen Gruppe von Signifikanztests zu. Wir halten fest, dass wir Prüfgrößen konstruieren und berechnen können, die einer uns bekannten Verteilung folgen. Damit lassen sich Wahrscheinlichkeiten für bestimmte Werte der Prüfgröße ermitteln. Wenn unsere Prüfgröße einen unwahrscheinlichen Wert annimmt, verwerfen wir die Nullhypothese.

8.5 Chi-Quadrat-Anpassungstest

Bisher haben wir Signifikanztests durchgeführt, bei denen eine Hypothese über die Grundgesamtheit überprüft wurde. Diese Hypothese bezog sich auf eine Kennzahl, mit der die Grundgesamtheit charakterisiert werden kann, beispielsweise auf den Mittelwert.

Wir passen nun ein Modell an unsere Daten an und wollen überprüfen, ob das Modell gut passt. Dies ist ein umfassenderer Ansatz als „nur“ eine Kennzahl. Die Nullhypothese bezieht sich nicht auf eine Kennzahl, sondern auf ein ganzes Modell. Hierzu werden die theoretisch aus dem Modell ermittelten Daten mit den tatsächlich beobachteten ins Verhältnis gesetzt. Dieses Verhältnis ist eine Prüfgröße, die einer Chi-Quadrat-Verteilung folgt. Der Signifikanztest heißt deshalb Chi-Quadrat-Anpassungstest: Er testet mit einer Chi-Quadrat-verteilten Prüfgröße die Anpassungsgüte unseres Modells. Wir lernen dieses Testverfahren im Folgenden anhand eines Beispiels näher kennen (angelehnt an Zucchini et al. (2009)).

Beispiel 8.5 (Anpassungstest zur Betrugsdetektion I) Die Häufigkeiten von Ziffern, die beispielsweise in einer Buchhaltung vorkommen, folgen gewissen statistischen Regelmäßigkeiten. Wir wollen davon ausgehen, dass die zehn Ziffern von 0 bis 9 jeweils gleich häufig vorkommen, und zwar mit jeweils 1/10 Wahrscheinlichkeit. Sollten sich bei den tatsächlich beobachteten Häufigkeiten deutliche Abweichungen von dieser gleichen Verteilung ergeben, könnte dies ein Anhaltspunkt für die Vermutung sein, dass die Zahlen in der Buchhaltung manipuliert wurden. Mit dem Signifikanztest kann festgestellt werden, ob es sich um „deutliche Abweichungen“ handelt, also die Zahlen möglicherweise manipuliert wurden, oder aber ob es einfach zufällige Schwankungen sind, die zu den Abweichungen führen. Solche Tests werden beispielsweise von Finanzämtern angewendet, um Steuerbetrug auf die Spur zu kommen.

Erste Nachkommastelle in Kasseneinträgen	Erwartete Häufigkeit bei 1.000 Kasseneinträgen (\(f_{ie}\))	Beobachtete Häufigkeit in 1.000 Kasseneinträgen (\(f_{io}\))
0	100	114
1	100	97
2	100	95
3	100	100
4	100	96
5	100	104
6	100	88
7	100	97
8	100	99
9	100	110

Weichen erwartete und beobachtete Häufigkeiten statistisch signifikant voneinander ab?

Hypothesen:

\(H_0\): Das vorgeschlagene Modell trifft zu, d. h. in jeder der zehn Klassen 1/10 der Beobachtungen
\(H_1\): Das vorgeschlagene Modell trifft nicht zu.

Als nächstes muss die Prüfgröße das Chi-Quadrat-Tests bestimmt werden…

Wir betrachten Beobachtungen eines Merkmals \(X\), welche in \(K\) verschiedene Kategorien fallen. Die Anzahl der Beobachtungen, die in die \(i\)-te Kategorie fallen, wird mit \(f_{io}\) bezeichnet. Diese Anzahl soll anhand der Chi-Quadrat-Prüfgröße verglichen werden mit der Anzahl \(f_{ie}\), welche unter der Nullhypothese zu erwarten wäre:

\[X^2=∑_{i=1}^K \frac{(f_{io}-f_{ie})^2}{f_{ie}}\]

Wir gehen also von der quadrierten Differenz zwischen beobachteter („observed“) und theoretisch errechneter („expected“) Häufigkeit in jeder Klasse aus und setzen dies zur errechneten, erwarteten Häufigkeit ins Verhältnis. Je kleiner die erwartete Häufigkeit ist, desto mehr Gewicht erhält die Abweichung im Zähler der Prüfgröße.

Unter der Nullhypothese ist die Prüfgröße Chi-Quadrat-verteilt mit einem Parameter \(\nu\), der Anzahl der Freiheitsgrade:

\(\nu\) = Anzahl Klassen – Anzahl zu schätzender Parameter – 1

Beispiel 8.6 (Anpassungstest zur Betrugsdetektion II) Da wir keine Parameter schätzen, sondern von einer Gleichverteilung der Ziffern in den Kasseneinträgen ausgehen, ist die Anzahl der Freiheitsgrade:

\(\nu=10-0-1 = 9\)

Damit schlagen wir den kritischen Wert in Tabelle 8.3 nach und erhalten 16,92 (einseitiger Test, 5 % Irrtumswahrscheinlichkeit). Wenn die theoretischen Häufigkeiten stark von den beobachteten abweichen, wird die Prüfgröße einen großen Wert annehmen. In diesem Fall verwerfen wir die Nullhypothese.

Wir berechnen die Prüfgröße in einer Arbeitstabelle:

Erste Nach-kom-ma-stel-le	Erwartete Häufigkeit \(f_{ie}\)	Beobachtete Häufigkeit \(f_{io}\)	\((f_{io}-f_{ie})\)	\((f_{io}-f_{ie})^2\)	\(\frac{(f_{io}-f_{ie})^2}{f_{ie}}\)
0	100	114	14	196	1,96
1	100	97	-3	9	0,09
2	100	95	-5	25	0,25
3	100	100	0	0	0,00
4	100	96	-4	16	0,16
5	100	104	4	16	0,16
6	100	88	-12	144	1,44
7	100	97	-3	9	0,09
8	100	99	-1	1	0,01
9	100	110	10	100	1,00
				Summe	5,16

Der Wert der Prüfgröße beträgt 5,16 und liegt weit unterhalb des kritischen Wertes von 16,92. Die Nullhypothese kann somit nicht verworfen werden. Die Beobachtungen widersprechen nicht der Vermutung, dass die Ziffern gleich häufig vorkommen. Wir sehen deshalb keinen Anhaltspunkt für eine Manipulation der Kasseneinträge.

Aufgabe 8.5 In der folgenden Tabelle sind beobachtete und erwartete Häufigkeiten für die erste Stelle von 1.000 Kasseneinträgen gegeben. Die Ziffern an der ersten Stelle sollen dem Benford’schen Gesetz (\(f(d)=log_{10} (1+1/d)\)) folgen. Überprüfen Sie diese Nullhypothese. Die Prüfgröße ist Chi-Quadrat-verteilt mit \(9-0-1=8\) Freiheitsgraden (jetzt nur 9 Klassen, da die erste Stelle keine 0 sein kann) und hat bei einer Irrtumswahrscheinlichkeit von 10 % einen kritischen Wert von 13,36. Verwenden Sie die folgende Arbeitstabelle.

Erste Stelle	Erwartete Häufigkeit \(f_{ie}\)	Beobachtete Häufigkeit \(f_{io}\)	\((f_{io}-f_{ie})\)	\((f_{io}-f_{ie})^2\)	\(\frac{(f_{io}-f_{ie})^2}{f_{ie}}\)
1	301	284
2	176	197
3	125	132
4	97	98
5	79	69
6	67	67
7	58	47
8	51	62
9	46	44
				Summe

Aufgabe 8.6 Ein Versicherer deckt Schäden aus Erdbeben ab und interessiert sich für die monatliche Anzahl starker Beben. Hier erhalten Sie die erwarteten Werte nicht aus einem theoretischen Modell, sondern aus einem Modell, das aus den Daten geschätzt wird. Wir beobachten die Anzahl der Erdbeben in 420 Monaten und erhalten als geschätzten Mittelwert 1,2 pro Monat; dies entspricht dem Schätzer für den Parameter \(\lambda\) bzw. \(\mu\) der Poissonverteilung. Überprüfen Sie mit einem statistischen Signifikanztest, ob die Poissonverteilung ein geeignetes Modell für die Erdbebendaten ist. Verwenden Sie die Arbeitstabelle.

Anzahl Erdbeben	Erwartete Häufigkeit \(f_{ie}\)	Beobachtete Häufigkeit \(f_{io}\)	\((f_{io}-f_{ie})\)	\((f_{io}-f_{ie})^2\)	\(\frac{(f_{io}-f_{ie})^2}{f_{ie}}\)
0		127
1		142
2		96
3		38
4 oder mehr		17
Summe		420

Aufgabe 8.7 Ein Versicherer möchte überprüfen, ob eine Poissonverteilung geeignet ist, um die Sturmfrequenz zu modellieren. Die Sturmfrequenzen der letzten 15 Jahre lauten:

Jahr i	Anzahl Sturmereignisse \(X_i\)
1	0
2	1
3	2
4	0
5	1
6	0
7	3
8	0
9	0
10	1
11	0
12	2
13	1
14	0
15	1

Schätzen Sie zunächst den Parameter der Poissonverteilung aus diesen Daten und testen Sie danach die Hypothese (95 %), dass die Daten an diese Poissonverteilung passen.

Abschließend sei erwähnt, dass dieses Verfahren durchaus auch für stetige Verteilungen angewendet wird. Beispielsweise ist in der empirischen Kapitalmarktforschung die Frage interessant, welcher Verteilung die Aktienrenditen folgen. Es gibt Hinweise darauf, dass die Verteilung von Aktienrenditen nicht eine Normalverteilung ist, sondern dass die Renditeverteilung in der Mitte spitzer verläuft als die Normalverteilung. Dafür sind die Flanken breiter. Man kann mit einem Chi-Quadrat-Anpassungstest untersuchen, ob die Normalverteilung geeignet ist, um Aktienrenditen abzubilden (und vorherzusagen). Die Berechnung der erwarteten Häufigkeiten folgt im Verfahren den obigen Beispielen, ist aber durch das Standardisieren recht aufwendig. Wir wollen es daher hier nicht im Einzelnen nachvollziehen, sondern zur Kenntnis nehmen, dass die Nullhypothese der Normalverteilung von Renditen im Allgemeinen und bei gebräuchlichen Signifikanzniveaus zu verwerfen ist.

Mit dem Chi-Quadrat-Anpassungstest überprüfen wir, ob ein bestimmtes Modell geeignet ist, um die beobachteten Daten zu beschreiben (und vorherzusagen). Wir wenden uns nun einer weiteren Anwendung des Chi-Quadrat-Tests zu. Dabei wird getestet, ob zwei Zufallsvariablen statistisch unabhängig sind.

8.6 Chi-Quadrat-Unabhängigkeitstest

Ausgangspunkt ist eine Stichprobe über zwei Merkmale. Mit dem Chi-Quadrat-Unabhängigkeitstest soll geprüft werden, ob die beiden Merkmale in der Grundgesamtheit unabhängig sind. Falls dies zutrifft, gilt:

\(P(x,y)=P(x)\cdot P(y)\) (diskreter Fall, Randwahrscheinlichkeiten)

\(f(x,y)=f(x)\cdot f(y)\) (stetiger Fall, Randdichten)

Da es in der Stichprobe zufällige Schwankungen gibt, können die Merkmale in der Grundgesamtheit auch dann unabhängig sein, wenn die Produktregel nicht vollständig erfüllt ist. Dieses Phänomen wird mit dem Hypothesentest erfasst. Wir erarbeiten ihn an einem Beispiel (Zucchini et al. (2009)).

Beispiel 8.7 (Polit-Umfrage: Unabhängigkeitstest) Betrachtet wird eine Polit-Umfrage unter 383 Befragten. Sie geben jeweils an, ob sie den Kandidaten unterstützen und welches Geschlecht sie haben. Es entstehen demnach 2 Zufallsvariablen:

\(X\): Geschlecht, weiblich =0, männlich=1

\(Y\): Wahlentscheidung, pro = 0, contra = 1

Daraus ergibt sich die folgende Kontingenztafel:

	Pro	Contra	Gesamt
Weiblich	73	144	217
Männlich	73	93	166
Gesamt	146	237	383

Hängt die Unterstützung des Kandidaten vom Geschlecht der Wähler ab?

Die Nullhypothese lautet:

\(H_0\) : Die beiden Merkmale sind unabhängig verteilt.

Zur Überprüfung der Nullhypothese werden zunächst die Anteile berechnet, indem der Eintrag in jedem Feld durch 383 dividiert wird:

	Pro	Contra	Gesamt
Weiblich	0,1906	0,3760	0,5666
Männlich	0,1906	0,2428	0,4334
Gesamt	0,3812	0,6188	1

Wir sehen diese Anteile als gemeinsame Wahrscheinlichkeiten an; die Einträge unter „Gesamt“ sind demnach die Randwahrscheinlichkeiten. Beispielsweise waren 57 % der befragten Personen Frauen und 38 % der Befragten unterstützen den Kandidaten.

Die unter der Nullhypothese erwartete Häufigkeit wird berechnet, indem die Randwahrscheinlichkeiten miteinander multipliziert und danach mit der Anzahl der insgesamt Befragten multipliziert wird:

	Pro	Contra	Gesamt
Weiblich	\(0,2160\cdot 383=83\)	134	217
Männlich	63	103	166
Gesamt	146	237	383

Die Prüfgröße ergibt sich in Analogie zum Abschnitt 8.5 wie folgt:

	Pro	Contra	Gesamt
Weiblich	\(\frac{(73-83)^2}{83}=1,2\)	\(\frac{(144-134)^2}{134}=0,75\)
Männlich	\(\frac{(73-63)^2}{63}=1,6\)	\(\frac{(93-103)^2}{103}=0,97\)
Gesamt			4,52

Die Anzahl der Freiheitsgrade in der Chi-Quadrat-Verteilung ergibt sich aus:

\(\nu=(\text{Zeilen}-1)\cdot (\text{Spalten}-1) = (2-1)\cdot (2-1)=1\)

Bei einem Signifikanzniveau von 5 % ist der kritische Wert 3,84. Da die Prüfgröße 4,26 größer ist, wird die Annahme der Unabhängigkeit bei einem Signifikanzniveau von 5% abgelehnt. Der dazugehörige P-Wert liegt bei ca. 3 % (diesen können wir aus der Tabelle 8.3 nicht ablesen!). Hinweis: die Berechnung in dieser Darstellung verwendet an mehreren Stellen gerundete Werte - bei genauer Berechnung weichen Prüfgröße und P-Wert leicht ab.

Aufgabe 8.8 Ein Unfallversicherer führt eine Studie zur Wirksamkeit von Sicherheitsgurten bei Autounfällen durch. Die beobachteten Häufigkeiten lauten:

	Gurt benutzt	Gurt nicht benutzt	Gesamt
Fahrer unverletzt	12.813	65.963	78.776
Fahrer minimal verletzt	647	4.000	4.647
Fahrer mittel verletzt	359	2.642	3.001
Fahrer schwer/tödlich verletzt	42	303	345
Gesamt	13.861	72.908	86.769

Muss der Versicherer bei Verwendung von Sicherheitsgurten seltener auszahlen? In diesem Fall könnte er einen Rabatt auf die Prämie gewähren, wenn konsequent ein Sicherheitsgurt verwendet wird. Untersuchen Sie den Zusammenhang mit einem Chi-Quadrat-Unabhängigkeitstest.

Wir betrachten beim Chi-Quadrat-Unabhängigkeitstest also Beobachtungen zweier Merkmale \(X\) und \(Y\). \(X\) kann \(I\) verschiedene Kategorien (\(i=1,\dots,I\)) annehmen und \(Y\) hat \(J\) mögliche Kategorien (\(j=1,\dots,J\)). Mit \(n_{i\,\cdot}\) bezeichnen wir die beobachtete Häufigkeit, dass \(X\) die Kategorie \(i\) annimmt und analog mit \(n_{\cdot\,j}\) die beobachtete Häufigkeit für Kategorie \(j\) in Merkmal \(X\). \(n\) ist die Anzahl der Beobachtungen insgesamt. Die beobachteten Häufigkeiten für das gemeinsame Auftreten von Kategorie \(i\) in Merkmal \(X\) und Kategorie \(j\) in Merkmal \(Y\) bezeichnen wir mit \(n_{ij}\). Die unter der Annahme der Unabhängigkeit von \(X\) und \(Y\) erwarteten Häufigkeiten dafür, dass Merkmal \(X\) in die Kategorie \(i\) fällt und \(Y\) in die Kategorie \(j\), werden entsprechend als \(n^*_{ij}\) bezeichnet. Dabei ergibt sich unter Unabhängigkeit von X und Y \(n^*_{ij} = \frac{n_{i\,\cdot} \cdot n_{\cdot\,j}}{n}\). Dann lautet die Teststatistik für den \(\chi^2\)-Test auf Unabhängigkeit der Merkmale \(X\) und \(Y\):

\[X^2 = \sum_{i=1}^I\sum_{j=1}^J \frac{(n_{ij}- n^*_{ij})^2}{n^*_{ij}}\]

Unter Annahme der Unabhängigkeit von X und Y ist diese Prüfgröße Chi-Quadrat-verteilt mit \(\nu = (I-1)(J-1)\) Freiheitsgraden.

Wir haben in den Abschnitten 8.5 und 8.6 Testverfahren kennengelernt, mit denen wir überprüfen können, ob die beobachteten Daten aus einem bestimmten Modell generiert werden. Dieses Modell kann entweder eine konkrete Verteilung oder einfach „Unabhängigkeit“ sein. Beide Tests können wir nun anwenden. Wir haben Beispiele bearbeitet, die sich auf Aktienrenditen oder Versicherer beziehen, so dass uns die Relevanz der Testverfahren unmittelbar klar ist. Der Vollständigkeit halber wenden wir uns abschließend noch Q-Q-Plots zu.

8.7 Q-Q-Plots

In einem Q-Q-Plot (Quantil-Quantil-Diagramm) wird die empirische (d. h. beobachtete) Verteilung einer theoretischen Verteilung gegenübergestellt; meist ist die theoretische Verteilung eine Normalverteilung, weil die statistische Inferenz in den meisten Fällen auf der Normalverteilungsannahme beruht. Wenn sich die Wertepaare (theoretisches Quantil, beobachtetes Quantil) auf der 45-Grad-Linie aufreihen und davon nicht oder kaum abweichen, dann ist davon auszugehen, dass die Beobachtungen der angenommenen theoretischen Verteilung folgen. Kommt es hingegen zu nennenswerten Abweichungen von der 45-Grad-Linie, so ist die Annahme nicht haltbar, die Beobachtungen wären dieser theoretischen Verteilung entnommen. Üblicherweise werden die theoretischen Quantile auf der horizontalen Achse abgetragen, während die aus der Stichprobe an der vertikalen Achse stehen.

Die Ausführungen in diesem Abschnitt sind teilweise wörtlich aus Cottin and Döhler (2013) entnommen.

Hierbei ist es dem Analysten überlassen zu entscheiden, wann eine Abweichung von der Winkelhalbierenden als nennenswert einzustufen ist. Deshalb ist dieses grafische Verfahren, mit dem die Verteilung der Daten festgelegt werden soll, subjektiv. Wir haben mit den Anpassungstests objektive Verfahren kennengelernt, bei denen auf der Grundlage einer Prüfgröße und eines vor dem Test festgelegten kritischen Wertes entschieden wird. Deshalb sollten Konfidenzbänder um die Punkte im Q-Q-Plot gelegt werden.

Die folgende Abbildung zeigt den Q-Q-Plot einer Normalverteilung. Die Quantil-Punkte befinden sich weitgehend auf einer Linie, jedoch nicht auf der 45-Grad-Linie. Die dargestellte Normalverteilung hat daher andere Parameter als die theoretisch angenommene.

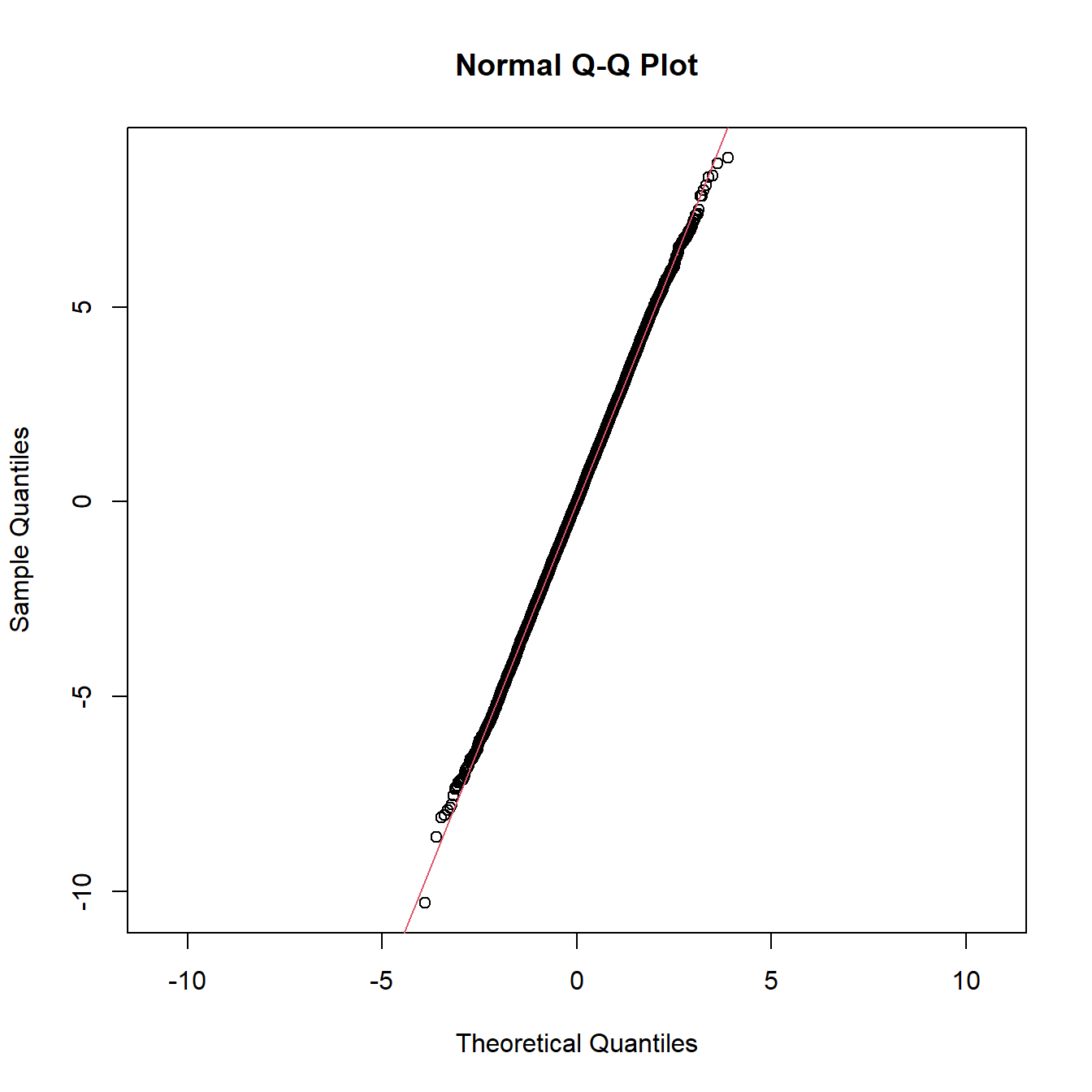
Abbildung 8.2: Q-Q-Plot einer Normalverteilung, die nicht der theoretisch angenommenen Normalverteilung entspricht (abweichende Parameterwerte)

Wenn die theoretische Verteilung eine Standardnormalverteilung ist, die Daten aber in Wirklichkeit einer anderen Normalverteilung entstammen, dann liegen die Wertepaare im Q-Q-Plot zwar auf einer Geraden, jedoch nicht auf der Winkelhalbierenden. Die Geradengleichung würde lauten: \(y_i=\mu+\Phi^{-1} (i⁄n)\sigma\), wobei mit \(i\) die Quantile nummeriert werden (\(i\) läuft von 1 bis n; dies sind die Beobachtungen in der Stichprobe), und \(\Phi\) ist die Verteilungsfunktion der Normalverteilung. Da \(\Phi^{-1}(1)=∞\), wird die Quantilfunktion nicht exakt an den Stellen \(i⁄\)n berechnet, sondern an etwas modifizierten Stellen.

Q-Q-Plots werden nicht nur benutzt, um Verteilungsannahmen zu überprüfen, sondern auch, um Informationen über die Flanken der empirischen Verteilung zu erhalten. Wenn die Linie (Verlauf der Punkte) im Q-Q-Plot links unten nach unten gebogen ist und rechts oben nach oben, dann ist bei der empirischen Verteilung von breiteren Flanken (heavy tails) auszugehen als die theoretische Verteilung aufweist. Die Verteilungen, denen die Daten aus dem Risikomanagement entstammen, haben grundsätzlich breitere Flanken als die Normalverteilung, so dass dies die Form des Q-Q-Plots sein wird, die Sie am häufigsten beobachten werden.

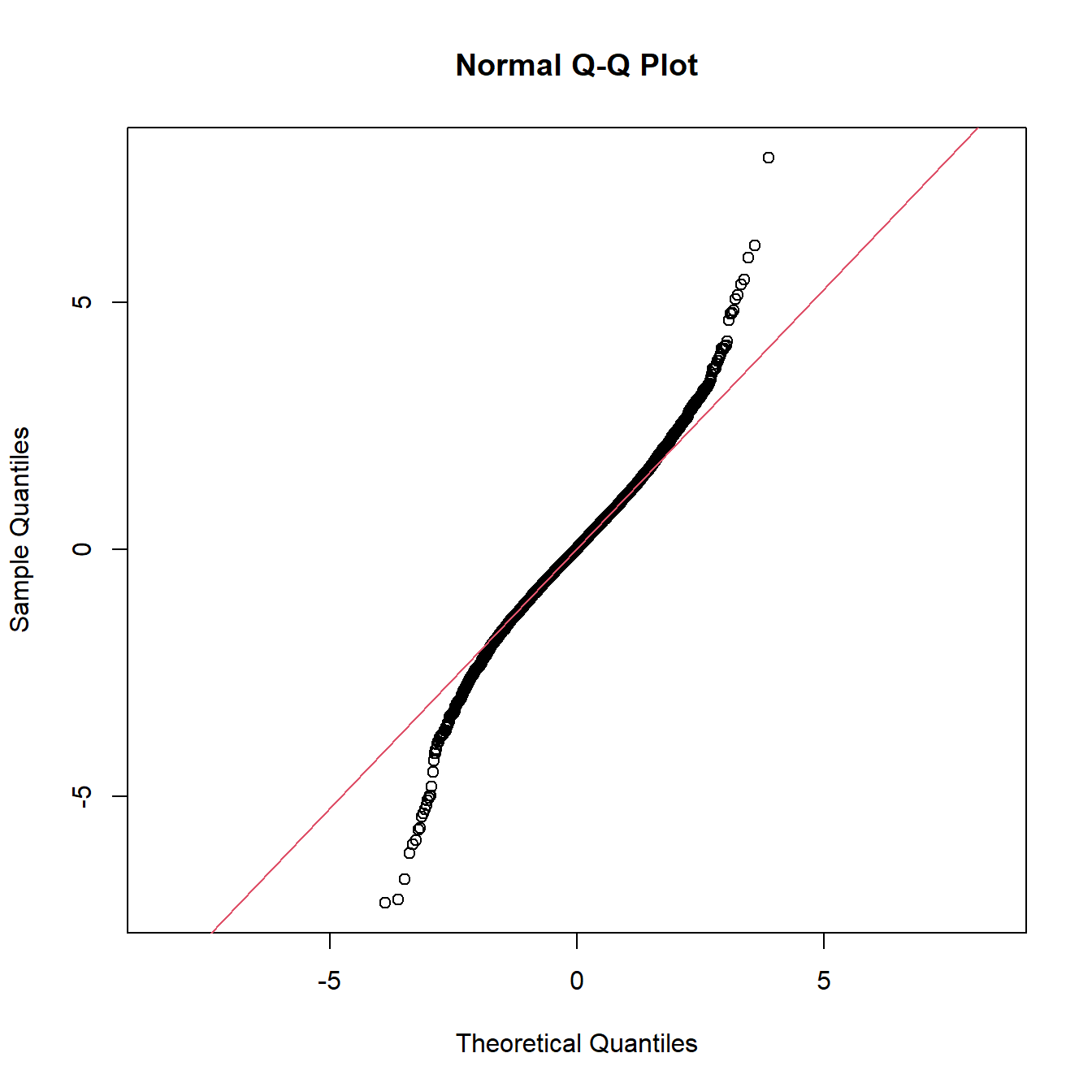
Abbildung 8.3: Q-Q-Plot einer empirischen Verteilung mit breiteren Flanken als bei der theoretisch angenommenen Normalverteilung

Gleichermaßen lässt der Q-Q-Plot Aussagen zur Schiefe der empirischen Verteilung zu. Falls die Verteilung symmetrisch ist, liegen die Punkte im mittleren Bereich auf einer Geraden; die Ränder im Q-Q-Plot werden von den Flanken der empirischen Verteilung bestimmt. Bei einer rechtsschiefen Verteilung verlaufen die Punkte im Q-Q-Plot konvex, während sie bei einer linksschiefen Verteilung konkav liegen.

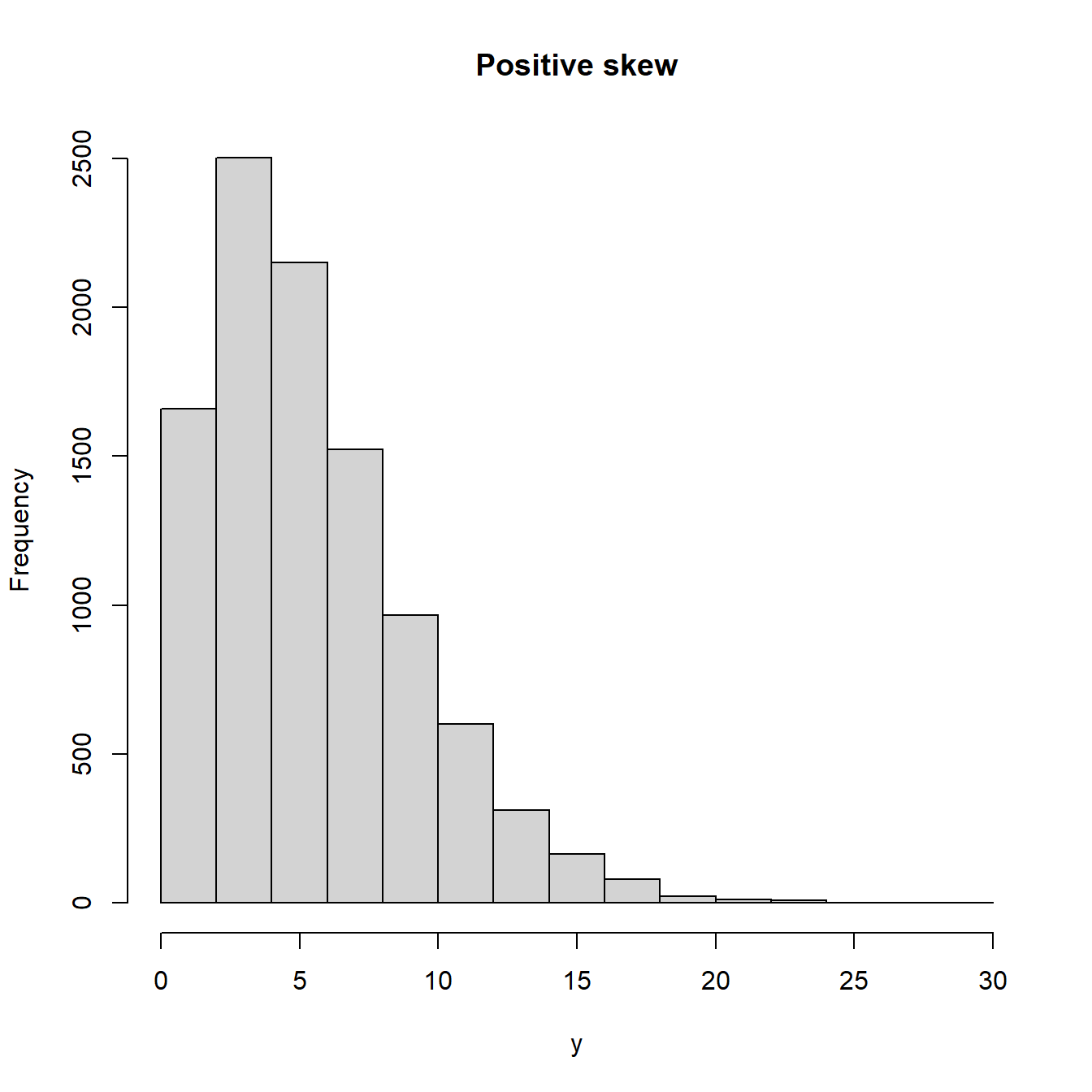
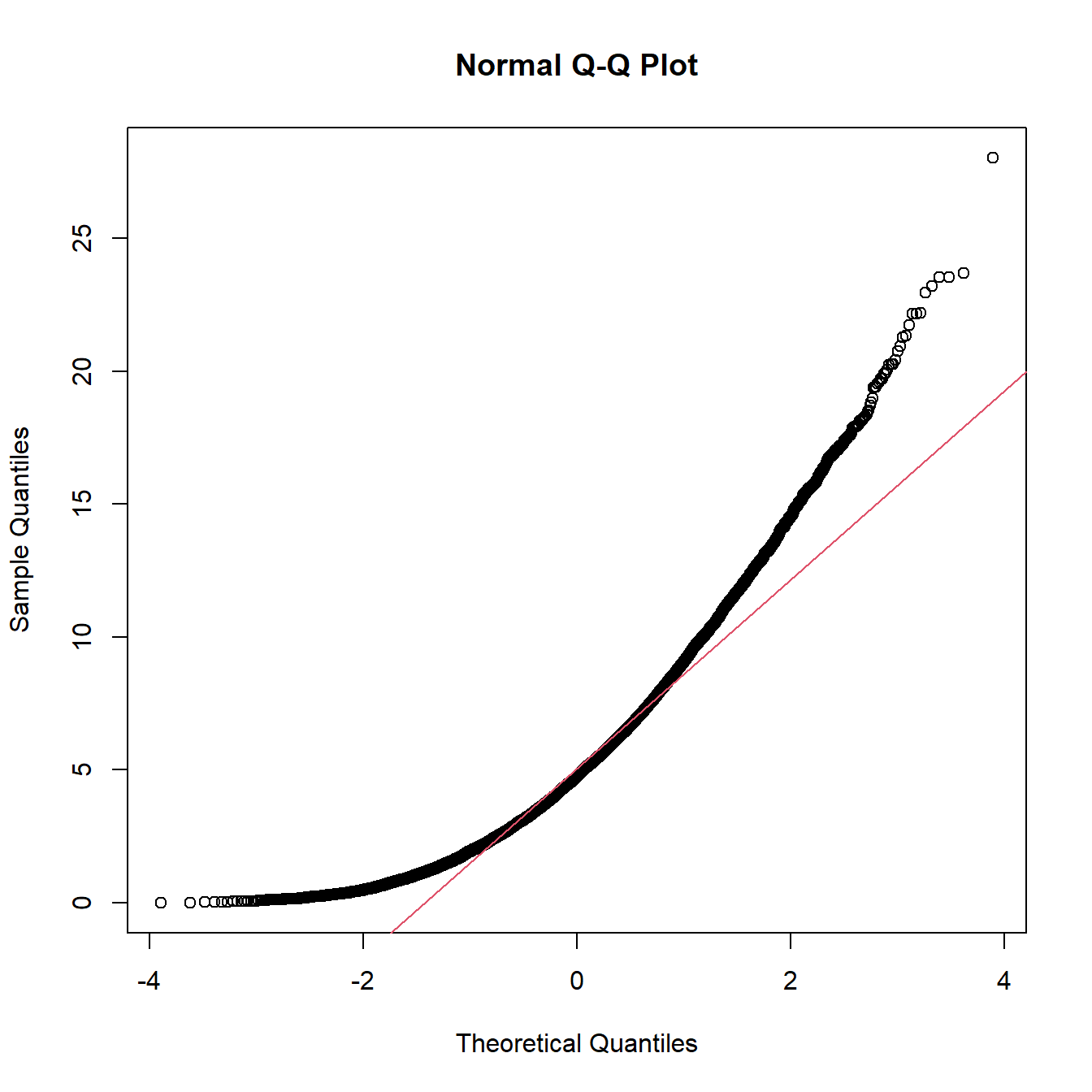
Abbildung 8.4: Q-Q-Plots für schiefe Verteilungen (positive skew= rechtsschief)

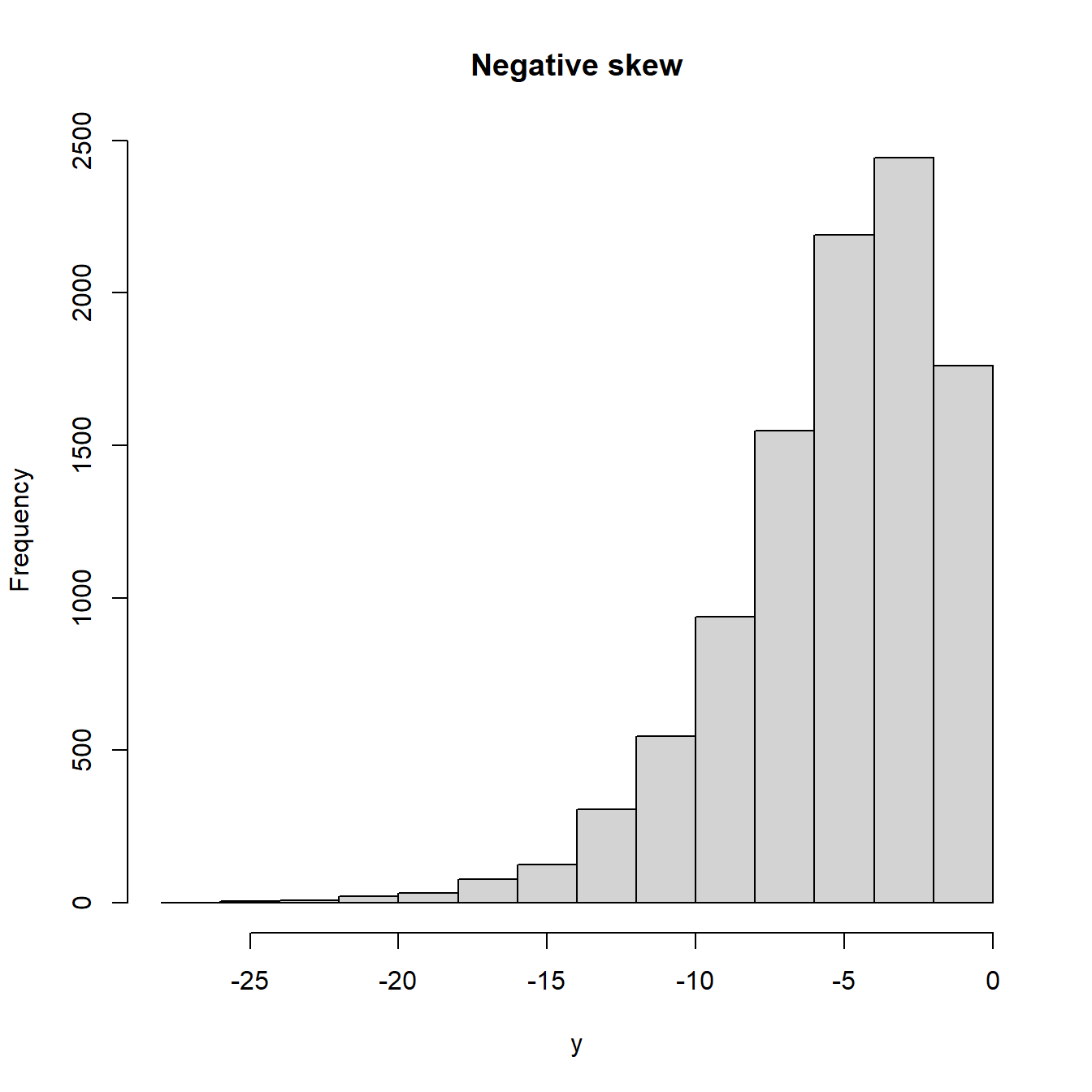
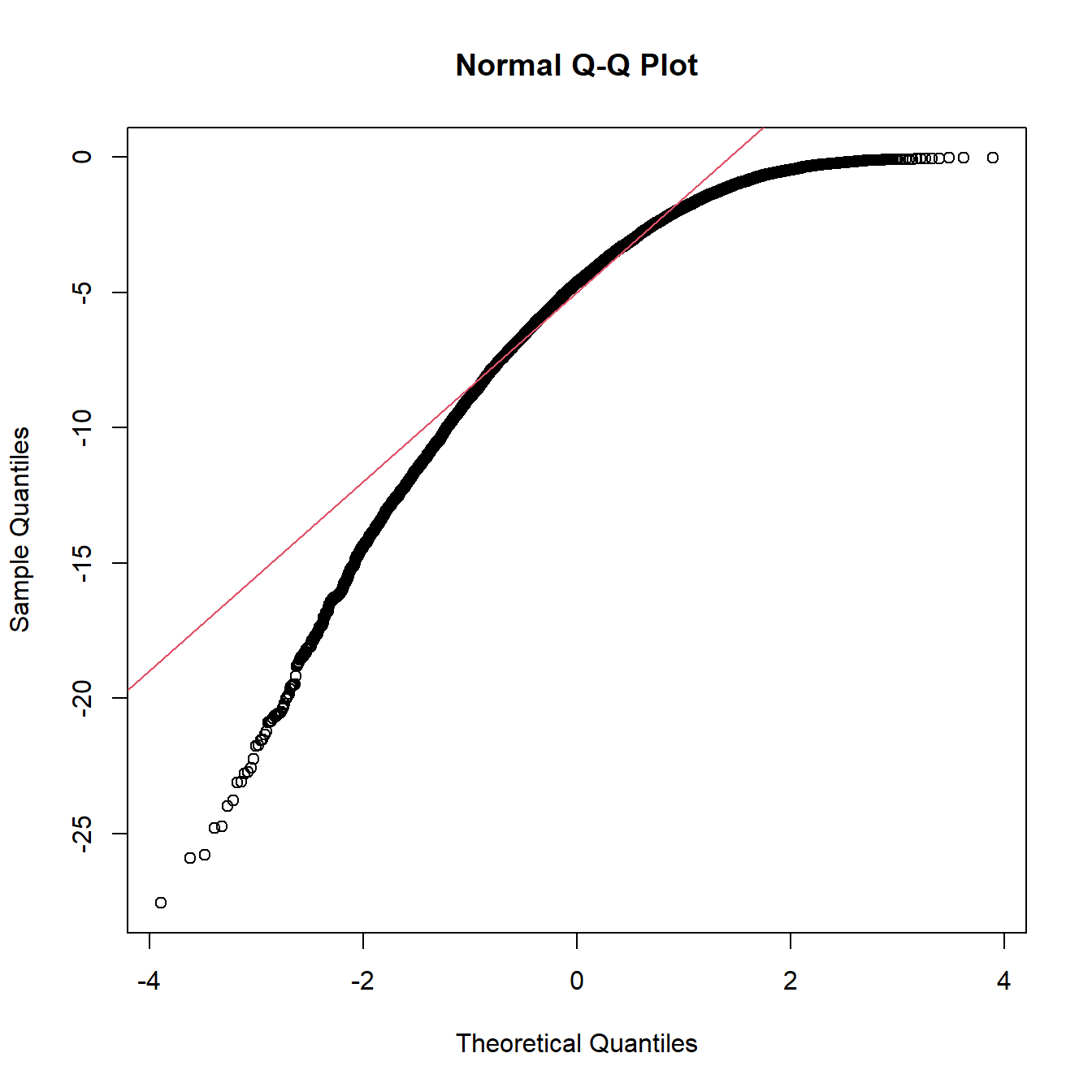
Abbildung 8.5: Q-Q-Plots für schiefe Verteilungen (negative skew= linksschief)

Die meisten Statistik-Software-Pakete beinhalten das Erstellen von Q-Q-Plots gegen die Standardnormalverteilung. Da das grafische Instrument dieser Plots die statistischen Signifikanztests nicht ersetzen kann oder soll, behandeln wir diese Diagramme hier nicht weiter. Stattdessen überlasse ich Ihnen zum Selbststudium eine Excel-Datei auf der Online-Lernplattform, in der Sie das Erstellen von Q-Q-Plots demonstriert bekommen. Damit können Sie auch die Parameter der theoretischen Verteilung variieren und sich den Effekt auf den Q-Q-Plot anschauen.

Excel: Q-Q-Plots zur Analyse der DAX-Renditen

 

Im Excel-Sheet wird die empirische Verteilung der DAX-Renditen mit einer Normalverteilung verglichen. Wir stellen fest, dass sich die Quantile auf einer Linie befinden, die allerdings nicht der 45-Grad-Linie im Diagramm entspricht. Daraus schließen wir, dass die DAX-Renditen zwar einer Normalverteilung folgen, allerdings nicht der Standardnormalverteilung. Sie können die Parameter der Normalverteilung verändern, was lediglich den Anstieg und die Lage der Geraden beeinflusst, nicht aber die Form des Q-Q-Plots. Können Sie Aussagen zu den Flanken der Rendite-Verteilung treffen, z. B. ob diese breiter als jene der Normalverteilung sind? Ist die Verteilung symmetrisch?

Das 8. Kapitel macht Sie mit statistischen Signifikanztests vertraut. Hierfür wird zunächst das Konzept der statistischen Signifikanz eingeführt und danach die grundlegende Verfahrensweise bei Signifikanztests erläutert: Wir konstruieren eine Prüfgröße, die die zu testende Fragestellung erfasst und einer bekannten statistischen Verteilung folgt. Wir legen eine akzeptable Irrtumswahrscheinlichkeit fest (meist 5 % oder 10 %) oder geben den P-Wert an. Damit kann entschieden werden, ob die Prüfgröße einen sehr unwahrscheinlichen Wert angenommen hat, so dass wir die Nullhypothese verwerfen, oder ob die Prüfgröße einen häufigeren Wert aufweist, so dass wir die Nullhypothese nicht verwerfen.

Sie können nunmehr statistische Signifikanztests mit binomialverteilter, t-verteilter, normalverteilter und Chi-Quadrat-verteilter Prüfgröße selbstständig durchführen. Da Sie das grundlegende Prinzip der Signifikanztests verstanden haben, sind Sie darüber hinaus in der Lage, Tests mit anders verteilten Prüfgrößen umzusetzen.

---

Schlüsselbegriffe:

Nullhypothesen; Einseitige und zweiseitige Tests; Prüfgröße; Irrtumswahrscheinlichkeit (\(\alpha\)- und \(\beta\)-Fehler); Ablehnungsbereich; P-Wert; Verbindung zwischen Konfidenzintervallen und Signifikanztests; Verwerfen von Nullhypothesen; Signifikanztests mit Prüfgrößen folgender Verteilungen: Binomial-, Normal-, t- und Chi-Quadrat-Verteilung; Chi-Quadrat-Anpassungstest und Chi-Quadrat-Unabhängigkeitstest; Q-Q-Plots

Literatur:

Barrow (2017)

Barrow, Michael. 2017. Statistics for Economics, Accounting and Business Studies. Pearson Education Limited. https://plus.orbis-oldenburg.de/permalink/f/126s6ph/JBElbs881838667.

Cottin, Claudia, and Sebastian Döhler. 2013. Risikoanalyse. Springer Fachmedien Wiesbaden. https://doi.org/10.1007/978-3-658-00830-7.

Dehling, Herold, and Beate Haupt. 2004. Einführung in Die Wahrscheinlichkeits-Theorie Und Statistik. Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-35117-5.

Fahrmeir, Ludwig, Christian Heumann, Rita Künstler, Iris Pigeot, and Gerhard Tutz. 2016. Statistik. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-50372-0.

Zucchini, Walter, Andreas Schlegel, Oleg Nenadić, and Stefan Sperlich. 2009. Statistik Für Bachelor- Und Masterstudenten. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-540-88987-8.