Kapitel 5 Abhängigkeitsmaße: Rangkorrelation und Copulas
Lernziele
- Spearman Rangkorrelation berechnen und interpretieren können
- Vergleich mit Pearson Korrelationskoeffizient
- Grundverständnis für Copulas entwickeln
Im Abschnitt 1.7 haben wir uns bereits mit empirischer Korrelation beschäftigt und Kovarianz und Korrelationskoeffizienten kennengelernt. In diesem Kapitel bauen wir auf unsere Erkenntnisse aus dem Abschnitt 1.7 auf. Vor allem benötigen wir aber unser Wissen über Dichte- und Verteilungsfunktionen. Bisher haben wir diese jeweils für eine Zufallsvariable kennengelernt. In diesem Kapitel erweitern wir die Dichte- und Verteilungsfunktionen auf mehrere Zufallsvariablen zugleich, d. h. innerhalb einer Verteilung.
5.1 Rangkorrelation
Es gibt Szenarien, in denen die Beobachtungen nicht einzeln vorliegen, um den Korrelationskoeffizienten zu berechnen, jedoch sind die Daten zumindest sortiert. Beispielsweise könnten Sie sich dafür interessieren, wie gut Schüler einer Schule in zentralen Prüfungen abschneiden. Der Anteil der Schüler, die bestanden haben, wird nicht für jede Schule veröffentlicht, aber die Schulen werden nach dem Abschneiden ihrer Schüler sortiert (gerankt). Gleichermaßen wird nicht publiziert, wieviel Geld die Schulbehörde für jede einzelne Schule ausgibt, aber wir können die Schulen nach ihren Kosten sortieren bzw. aufreihen. Wenn mehr Geld dazu führt, dass die Schüler einer Schule besser bei zentralen Prüfungen abschneiden, dann sollten höher gerankte Schulen nach dem Abschneiden ihrer Schüler auch bei den Kosten höher gerankt sein.
Die Rangkorrelation ist auch dann aussagekräftig, wenn zwar die einzelnen Beobachtungen vorliegen, diese aber extreme Werte beinhalten oder die Verteilungen schief sind. Der Korrelationskoeffizient, den Sie bereits kennen, beruht auf der Normalverteilungsannahme, die bei einer stark schiefen Verteilung verletzt ist. Dann wäre der Korrelationskoeffizient nicht aussagekräftig und man würde stattdessen die Rangkorrelation verwenden.
Natürlich gehen in die Rangkorrelation weniger Informationen ein als in den Korrelationskoeffizienten – insofern ist letzterer aussagekräftiger. Die Rangkorrelation ist jedoch robuster, da weniger anfällig für extreme Beobachtungen oder schiefe Verteilungen.
Wenn Ränge doppelt vorkommen (so genannte Ties oder Knoten), dann werden die Durchschnittsränge benutzt. Dies wollen wir an einem Beispiel verdeutlichen.
Beispiel 5.1 (Durchschnittsränge bei der Rangbildung zweier Aktienkurse) Wir kommen zurück auf unser Beispiel 1.8 aus Abschnitt 1.7, in dem wir Aktienkurse von Siemens und BASF betrachten und fügen die Ränge hinzu:
| Kurs | Siemens | Rang Siemens | BASF | Rang BASF |
|---|---|---|---|---|
| 1 | 85 | 7 | 86 | 3 |
| 2 | 87 | 6 | 85 | 5 |
| 3 | 92 | 4 | 88 | 1 |
| 4 | 96 | 1 | 87 | 2 |
| 5 | 90 | 5 | 85 | 5 |
| 6 | 93 | 3 | 84 | 7 |
| 7 | 95 | 2 | 85 | 5 |
Der höchste Aktienkurs ist in diesem Beispiel jeweils Rang 1 usw. Wenn zwei oder mehr Beobachtungen identisch sind (wie beispielsweise bei BASF die zweite, fünfte und siebente Beobachtung, alle drei 85), dann bekommen sie auch alle denselben Rang, allerdings ist dieser das arithmetische Mittel der eigentlich zu vergebenen Ränge. Im Beispiel wären die Ränge 4, 5 und 6, das arithmetische Mittel ist 5, also bekommen alle drei den Rang 5. Der nächste Kurs (84, 6. Beobachtung) muss dann den Rang 7 bekommen, d. h., 4 und 6 entfallen. In Excel können Sie dies mit der Funktion RANG.MITTELW erreichen.
Die Spearman Rangkorrelation
Der Rangkorrelationskoeffizient nach Spearman ist eine weit verbreitete Methode, um die Rangkorrelationen zu quantifizieren. Um die Rangkorrelation für die paarweisen Beobachtungen zweier Variablen \(X\) und \(Y\) zu bestimmen, werden zunächst die Ränge der Beobachtungen \(x_i\), \(y_i\) gebildet, also \(R(x_i)\) und \(R(y_i)\). Üblicherweise wird hier der kleinsten Beobachtung einer Variablen der Rang 1 vergeben, der zweitkleinsten der Rang 2 und so weiter. Dann ist der Spearman Rangkorrelationskoeffizient gleich dem uns bekannten Pearson Korrelationskoeffizienten aus Abschnitt 1.6, angewendet auf die Ränge der Variablen \(R(x_i)\) und \(R(y_i)\):
\[r_S= \rho_{R(X),R(X)}=\frac{s_{R(X),R(y)}}{s_{R(X)}s_{R(Y)}}\]
Wie herum die Ränge gebildet werden, ist für die Berechnung der Spearman Korrelation unerheblich, solange man für beide Beobachtungsreihen gleich vorgeht.
Beispiel 5.2 (Spearman Rangkorrelation am Beispiel zweier Aktienrenditen) Wir betrachten nun die diskreten Renditen aus Beispiel 1.8 und berechnen hierfür die Rangkorrelation, d. h. die Korrelation der gerankten Renditen der Aktien von Siemens und BASF. Der Pearson Korrelationskoeffizient lag im Beispiel 1.8 für die Renditen bei 61 %.
| Kurstag | Rendite Siemens | Rendite BASF |
|---|---|---|
| 1 | 0,02 | -0,01 |
| 2 | 0,06 | 0,04 |
| 3 | 0,04 | -0,01 |
| 4 | -0,06 | -0,02 |
| 5 | 0,03 | -0,01 |
| 6 | 0,02 | 0,01 |
| Kurstag | Siemens Rang | BASF Rang |
|---|---|---|
| 1 | 2,5 | 3 |
| 2 | 6 | 6 |
| 3 | 5 | 3 |
| 4 | 1 | 1 |
| 5 | 4 | 3 |
| 6 | 2,5 | 5 |
Seien x die Renditen von Siemens und y die Renditen von BASF. Die Spearman-Rangkorrelation wird dann als Pearson-Korrelation der Ränge von x und y berechnet:
\[r_s=\frac{n \sum_{i=1}^6 R(x_i)R(y_i)-(\sum_{i=1}^6R(x_i))(\sum_{i=1}^6R(y_i))}{\sqrt{\left(n \sum_{i=1}^6R(x_i)^2-(\sum_{i=1}^6R(x_i))^2\right)\left(n\sum_{i=1}^6R(y_i)^2-(\sum_{i=1}^6R(y_i))^2\right)}}\]
Es ergibt sich eine Rangkorrelation von 60 %; dies ist nicht wesentlich anders als das Pearson-Maß von 61 % für die Renditen.
Mit einem statistischen Signifikanztest könnte nun die Hypothese überprüft werden, ob die wenigen Beobachtungen Anhaltspunkte geben für eine Korrelation oder doch nicht. Wir können solche Tests im Moment noch nicht durchführen und wenden uns deshalb nun Copulas zu, mit denen ebenfalls Abhängigkeiten erfasst und abgebildet werden.
5.2 Copulas
Stellen Sie sich nun eine Verteilungsfunktion vor, die nicht eindimensional ist, sondern wie ein Gebirge über zwei Zufallsvariablen X und Y steht wie in Abb. 5.1 (siehe Abschnitt 3.5). Im Prinzip können es auch mehrere Zufallsvariablen sein, damit wir uns dies besser vorstellen können, beschränken wir uns im Beispiel auf zwei Zufallsvariablen.
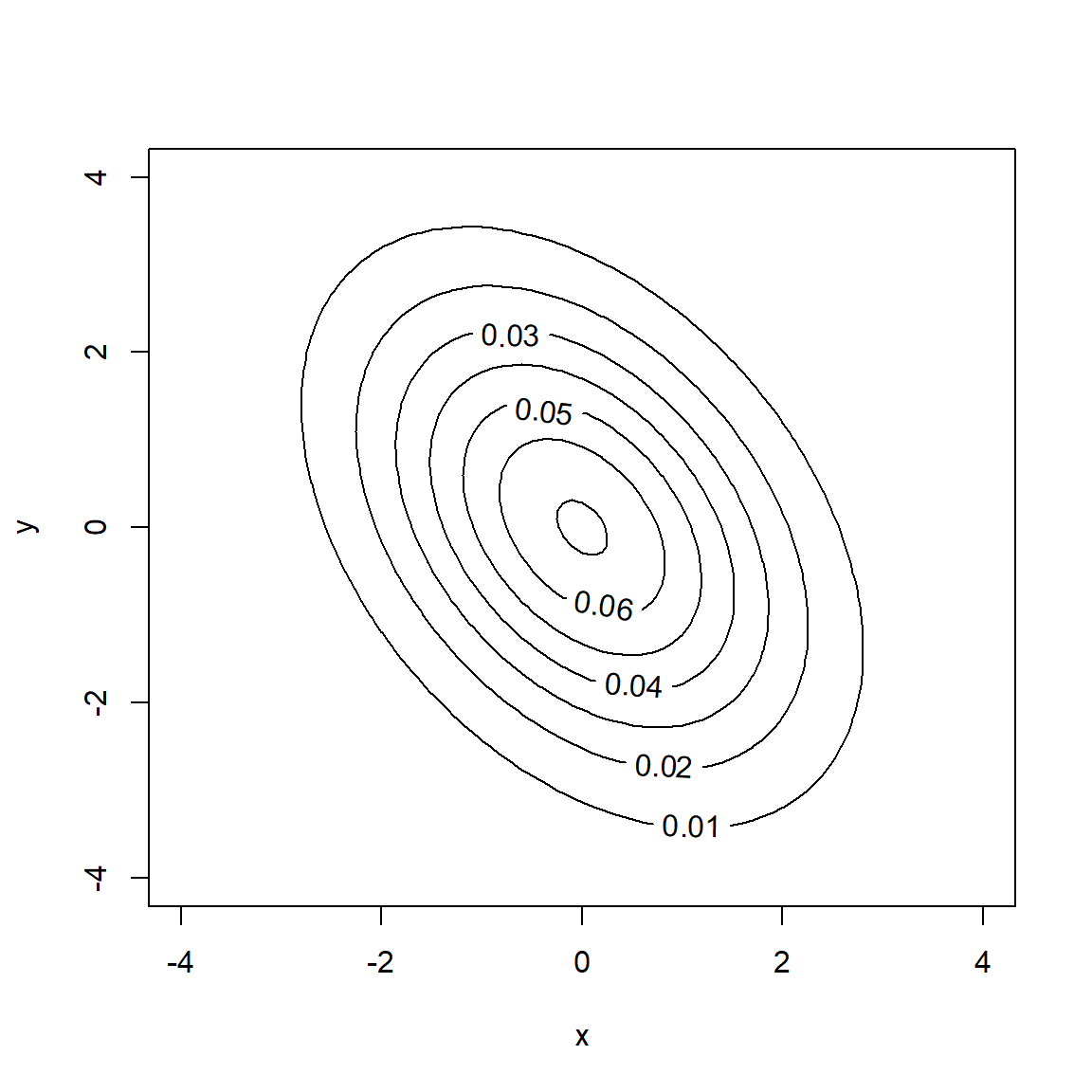
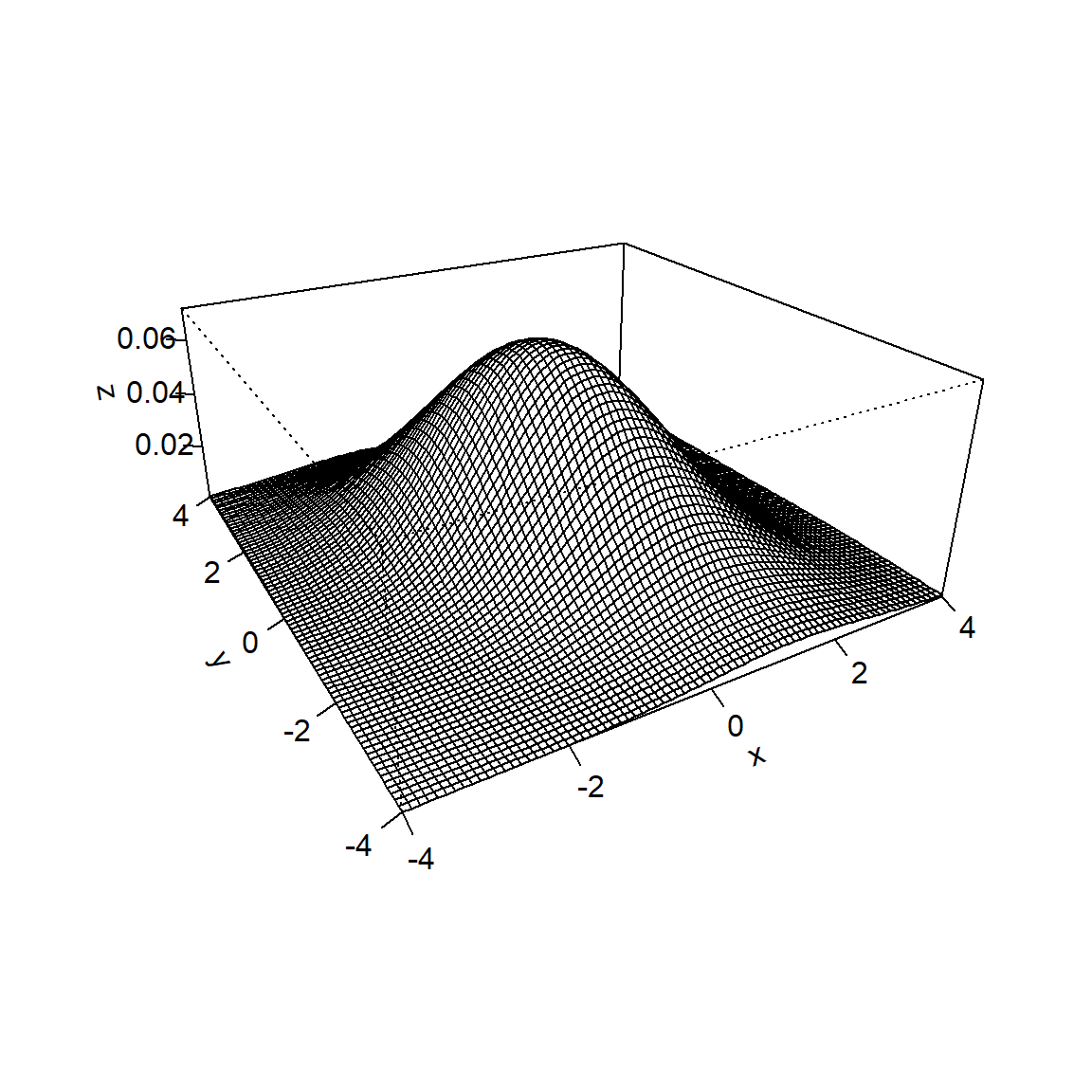
Abbildung 5.1: Dichte einer bivariaten Normalverteilung als Kontur-Plot (links) und 3D-Plot (rechts)
Aus Abschnitt 3.5 wissen wir, dass in der zweidimensionalen (auch mehrdimensionalen) Verteilung auch die Information über die eindimensionalen Verteilungen der einzelnen Zufallsvariablen steckt und dass wir diese durch Bilden der entsprechenden Randdichte erhalten. Im Beispiel der bivariaten Normalverteilung sind die Randverteilungen ebenfalls Normalverteilungen (vgl. Abb. 5.2).
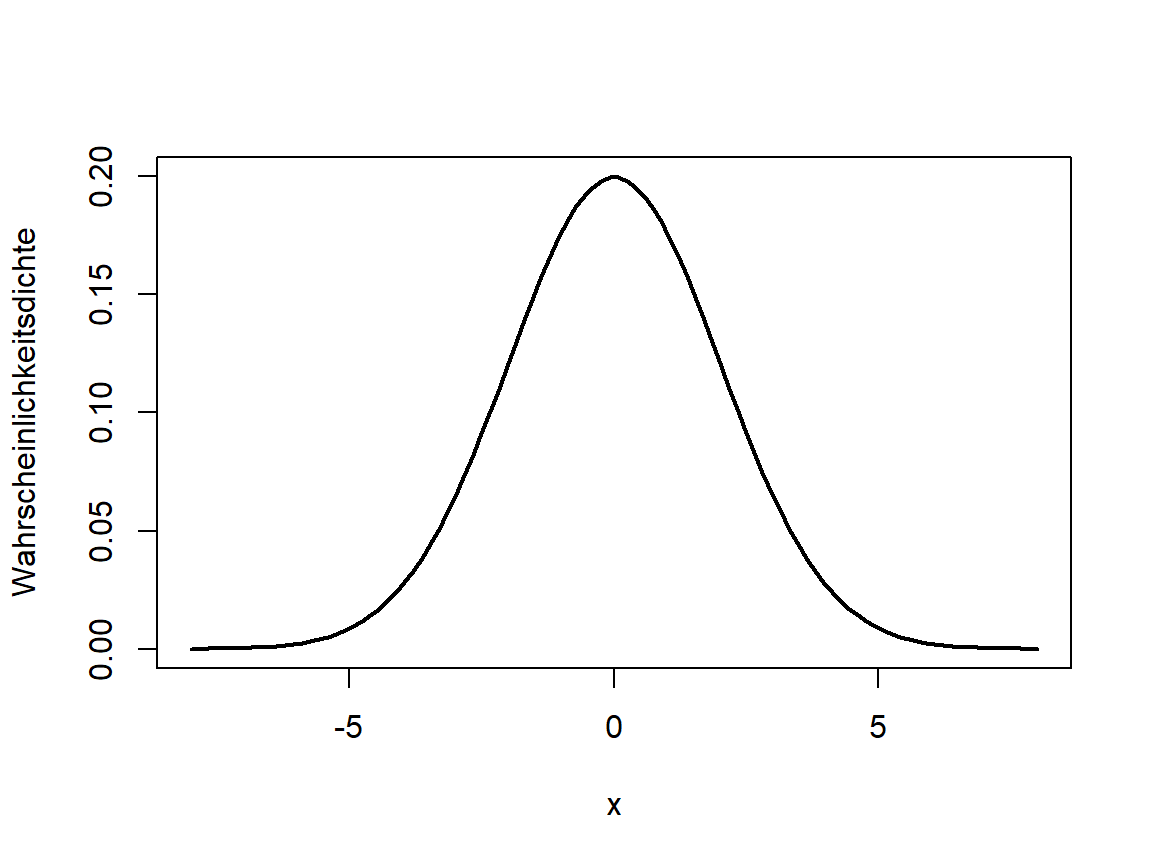
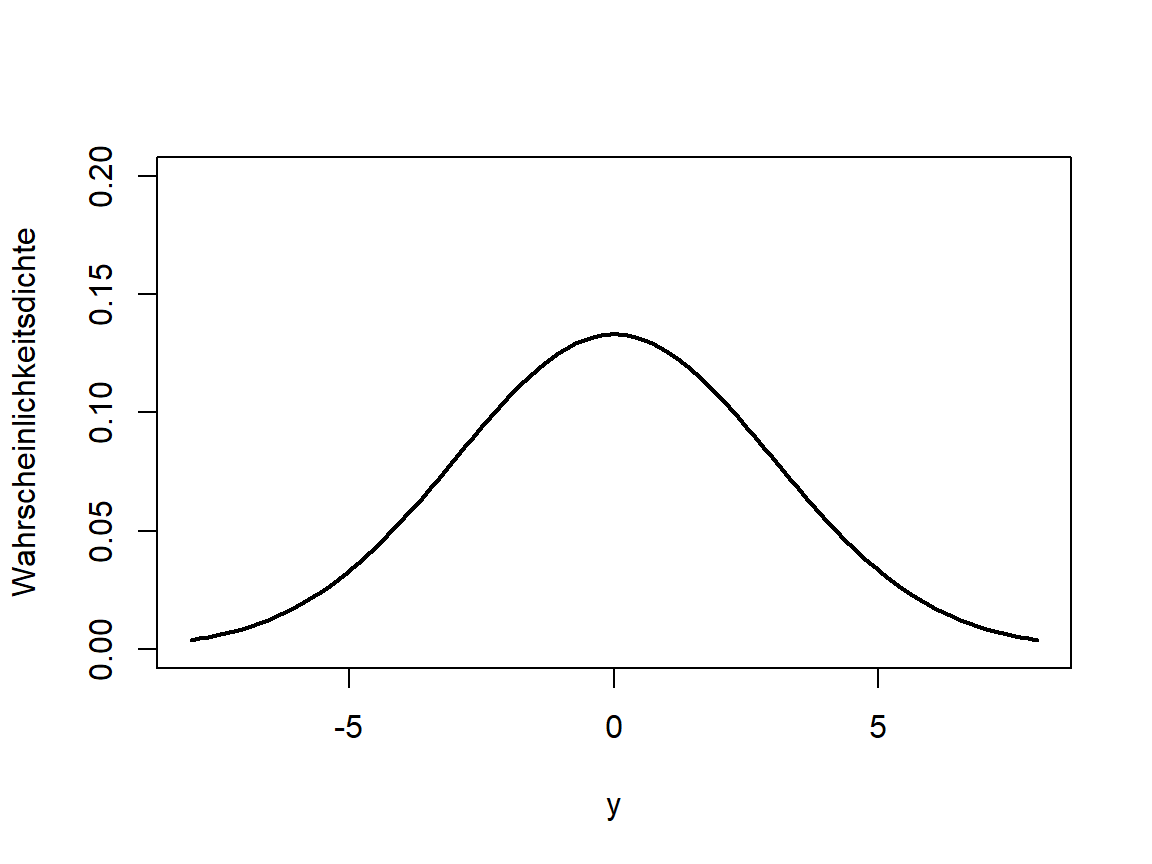
Abbildung 5.2: Dichten der zugehörigen univariaten Normalverteilungen für X (links) und Y (rechts)
Der für Copulas zentrale Satz von Sklar sagt aus, dass jede mehrdimensionale Verteilungsfunktion in die jeweils eindimensionalen Randverteilungsfunktionen (Abb. 5.2) und eine Copula (Abb. 5.3 links) zerlegt werden kann:
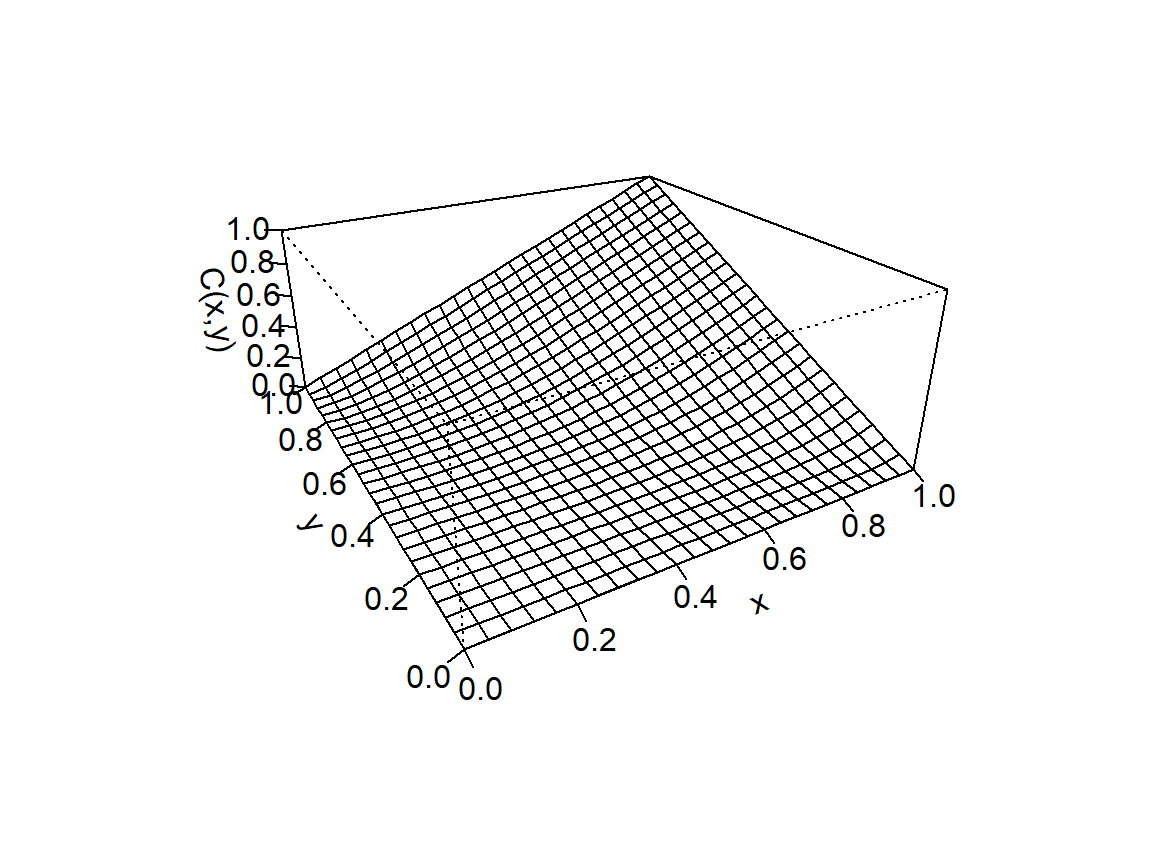
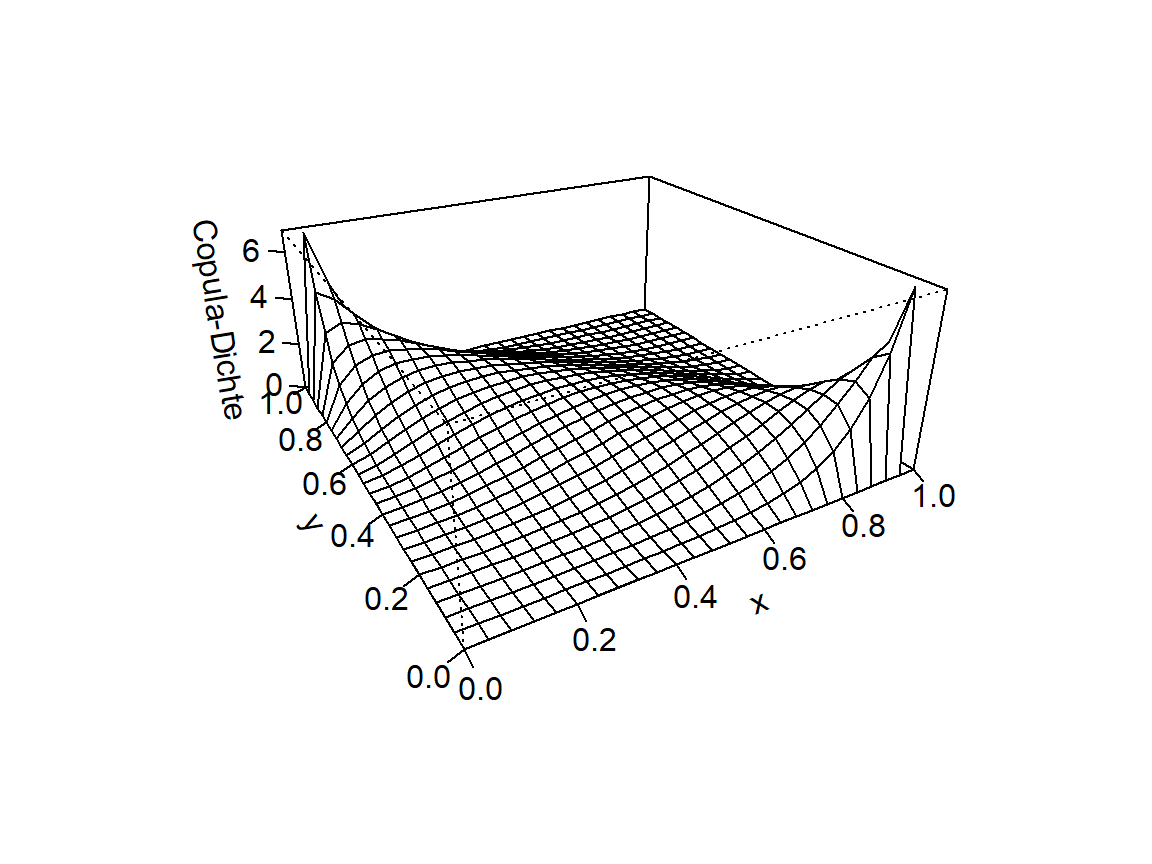
Abbildung 5.3: Copula für X und Y (links) und zugehörige Dichte (rechts)
Definition 5.1 (Satz von Sklar) Sei \(F: \overline{\mathbb R}^n, \, \overline{\mathbb{R}}:=\mathbb{R} \cap \{-\infty,+\infty\}\) eine \(n\)-dimensionale Verteilungsfunktion mit eindimensionalen Randverteilungen \(F_1,\dots,F_n: \overline{\mathbb{R}}\to [0,1]\). Dann existiert eine \(n\)-dimensionale Copula \(C\), sodass für alle \((x_1,\dots,x_n) \in \overline{\mathbb{R}}^n\) gilt: \[F(x_1,\dots,x_n)=C(F_1(x_1),\dots,F_n(x_n))\] Wenn alle \(F_i\) stetig sind, so ist die Copula eindeutig.
Anschaulich gesagt ist eine Copula das, was wir bekommen, wenn wir aus einer multivariaten Verteilungsfunktion die Information über die Randverteilung durch Transformation zu einer Gleichverteilung entfernen. Die Transformation erfolgt durch Anwenden der Quantilfunktion (verallgemeinerte inverse Verteilungsfunktion) auf die einzelnen Ränder der Verteilung (Anwenden von \(F_i^{-1}\) auf die \(x_i\)). Dies führt mit dem Satz von Sklar zur Copula: \[F(F_1^{-1}(x_1),\dots,F_n^{-1}(x_n))=C(x_1,\dots,x_n)\] Diese neu entstehende Verteilungsfunktion namens Copula enthält nun keine Informationen über die eindimensionalen Randverteilungen der Ursprungsverteilung mehr, behält aber die weiteren umfassenden Informationen über die Abhängigkeiten zwischen den Zufallsvariablen bei.
Der Vorteil von Copulas ist nun einerseits, dass wesentlich komplexere Abhängigkeiten damit abgebildet werden können, als es mit Korrelationskoeffizienten bzw. einer Korrelationsmatrix möglich ist. Andererseits ermöglicht der Copula-Ansatz flexibel neue Verteilungen zusammenzubauen: Man kann zum Beispiel die Copula aus einer multivariate Normalverteilung bilden und diese mit komplett anderen Randverteilungen kombinieren, z.B. einer Gumbel-Verteilung für die erste Zufallsvariable und einer Exponentialverteilung für die zweite Zufallsvariable. Diese Flexibilität wird in anderen Modulen nützlich sein, um Risiken angemessen modellieren zu können.
Schlüsselbegriffe:
Spearman Rangkorrelation; Pearson Korrelationskoeffizient; Copulas
Literatur: