Kapitel 2 Zufall und Wahrscheinlichkeit

Lernziele

  • Begriffe aus der Wahrscheinlichkeitstheorie anwenden können
  • Eigenschaften von Wahrscheinlichkeiten kennen
  • Rechenregeln für Wahrscheinlichkeiten anwenden können
  • Bedingte Wahrscheinlichkeiten ermitteln können
  • Konzept der stochastischen Unabhängigkeit verstehen und anwenden können

Haben Sie sich schon einmal gefragt, wie wahrscheinlich es ist, dass Sie im Lotto gewinnen? Oder wenn Sie ein Kind erwarten, mit welcher Wahrscheinlichkeit es ein Junge oder ein Mädchen wird? Oder wenn Sie einen Kredit vergeben, mit welcher Wahrscheinlichkeit der Kreditnehmer ausfällt? Oder wenn Sie eine Versicherung verkaufen, mit welcher Wahrscheinlichkeit der Schadenfall eintritt und Sie auszahlen müssen? All diese Fragen thematisieren Wahrscheinlichkeiten, mit denen wir uns in diesem Kapitel und in den folgenden beschäftigen.

Zunächst werden wir die wesentlichen Begriffe aus der Wahrscheinlichkeitstheorie zusammentragen.

2.1 Zufallsexperimente

Beginnen wir mit einer Frage: Was ist Stochastik? Eine mögliche Antwort wäre: Stochastik ist die Lehre vom Zufall.
Dann stellt sich die Frage: Was ist Zufall?
Eine richtige Antwort auf diese Frage gibt es wohl nicht. Es gibt Menschen, die bezweifeln, dass es überhaupt Zufall gibt. Andererseits gehen viele Physiker davon aus, dass es zumindest in der Quantenphysik echten Zufall gibt.
Wir können aber die Frage, was ein Zufallsexperiment ist, beantworten:

  1. Ein Zufallsexperiment ist ein Experiment mit unbekanntem Ergebnis, aber fester Ergebnismenge.
  2. Diese Ergebnismenge wird in der Wahrscheinlichkeitsrechnung häufig mit \(\Omega\) bezeichnet.
  3. Ein Zufallsexperiment kann (unter gleichen Bedingungen) wiederholbar sein, muss es aber nicht.

Beispiel 2.1 (Zufallsexperimente)

  1. Das Werfen einer Münze; die möglichen Ausgänge in der Ergebnismenge sind „Kopf“ und „Zahl“.
  2. Das Würfelexperiment mit \(\Omega := \{1;2;3;4;5;6\}=\mathbb N_6\) ist ein wiederholbares Zufallsexperiment.
  3. Der Kurs einer Aktie zu einem bestimmten Zeitpunkt in der Zukunft mit \(\Omega :={\mathbb R}^+_0\) ist ein nicht wiederholbares Zufallsexperiment.
  4. Die Befragung irgendeiner Person, nach ihrem Beruf ist ein Zufallsexperiment mit \(\Omega:=\mbox{Menge aller Berufe} \cup \{\mbox{kein Beruf}\}\).

Wenn Sie ein Zufallsexperiment ein Mal durchführen, dann ist dies ein Versuch.

Ein weiterer wichtiger Begriff ist das Ereignis. In der Stochastik wird genau zwischen Ergebnissen und Ereignissen unterschieden. Wenn von Wahrscheinlichkeiten die Rede ist, dann beziehen Sie sich immer auf ein Ereignis.

Definition 2.1 (Wichtige Begriffe zum Zufall)

  1. Sei \(\Omega\) die Menge der Ergebnisse eines Zufallsexperimentes, dann wird \(\Omega\) Ergebnismenge oder der Ergebnisraum genannt.
  2. “Geeignete” Teilmengen von \(\Omega\) werden Ereignisse genannt.
  3. Die einelementigen Teilmengen heißen Elementarereignisse.
  4. Sei \(\omega \in \Omega\), dann ist \(\omega\) ein Ergebnis, aber \(\{\omega\}\) ein (Elementar-)ereignis!
  5. Wenn \(\mathcal A\) die Menge der Ereignisse ist, wird \((\Omega,\mathcal A)\) Ereignisraum genannt.

Im Beispiel des Münzwurfs ist die Ergebnismenge \(\Omega=\{ \mathrm{Kopf}, \mathrm{Zahl} \}\). Diese Ausgänge müssen sich gegenseitig ausschließen, d. h., wenn ein Ergebnis eintritt, können die anderen nicht gleichzeitig eintreten. Wenn Sie „Kopf“ erhalten, kann die Münze nicht zugleich auf „Zahl“ landen. Die Ergebnismenge beinhaltet alle möglichen Ausgänge, d. h., sie ist erschöpfend.

Merken Sie sich:

  • Ergebnisse sind Elemente von \(\Omega\).
  • Ereignisse sind Teilmengen von \(\Omega\).

Für Ereignisse gelten alle aus der Mengenlehre bekannten Regeln und Eigenschaften!

OMB+: Logik und Mengenlehre

 

Wenn Wiederholungsbedarf zu den Grundlagen der Mengenlehre besteht, sollten Sie dies an dieser Stelle nachholen. Arbeiten Sie hierzu das Themengebiet Logik und Mengenlehre in OMB+ durch.

Beispiel 2.2 (Ergebnismengen von Zufallsexperimenten)

  1. \(\Omega :=\{1,2,3,4,5,6\}\) ist die Ergebnismenge für die möglichen Augenzahlen beim Würfelexperiment. \(A:=\{2;4;6\}\) ist zum Beispiel das Ereignis, eine gerade Zahl zu werfen.
  2. \(\Omega :=\{\mathrm{Kopf},\mathrm{Zahl}\}\) ist die Ergebnismenge für einen Münzwurf.
  3. \(\Omega :={\mathbb R}^+_0\) ist die Ergebnismenge für das mögliche Gehalt eines Mitarbeiters. \(I=[0;1000]\) ist dann das Ereignis, dass der Mitarbeiter höchstens \(1000\) verdient.
  4. \(\Omega :={\mathbb R}^+_0\) ist auch die Ergebnismenge für die mögliche Lebensdauer eines elektronischen Bauteils.
  5. \(\Omega :=\{A\subset \mathbb N_{49}: |A|=6 \}\) ist die Ergebnismenge für die Ziehung der Lottozahlen. Mögliche Ereignisse sind 4 Richtige, 5 Richtige etc. Man beachte: Ergebnisse sind hier Mengen, Ereignisse Mengen von Mengen!

Das Beispiel mit dem Münzwurf motiviert die folgende Definition:

Definition 2.2 (Bernoulli-Experiment) Enthält der Ereignisraum \(\Omega\) eines Zufallsexperimentes nur zwei Elemente, dann wird es ein Bernoulli-Experiment genannt.

Bernoulli-Experimente treten in der Praxis häufig auf:

Beispiel 2.3 (Bernoulli-Experimente)

  1. \(\Omega :=\{\mathrm{intakt};\mathrm{defekt}\}\)
  2. \(\Omega :=\{\mathrm{krank};\mathrm{gesund}\}\)
  3. \(\Omega :=\{\mathrm{männlich};\mathrm{weiblich}\}\)
  4. \(\Omega :=\{0;1\}\)
  5. \(\Omega :=\{\mathrm{Misserfolg};\mathrm{Erfolg}\}\)

In der Praxis betrachtet man oft Wiederholungen von Bernoulliexperimenten und interessiert sich zum Beispiel für die Anzahl der Erfolge.

Ereignisse sind Teilmengen von \(\Omega\), das heißt, dass für Ereignisse alle aus der Mengenlehre bekannten Regeln gelten!
In der Stochastik weichen aber die Bezeichnungen von denen der Mengenlehre ab:

Definition 2.3 (Mengensymbole in der Stochastik)

  1. \(\Omega\): Das sichere Ereignis
  2. \(\emptyset\): Das unmögliche Ereignis
  3. \(A \cap B\): Das Ereignis “\(A\) und \(B\)”
  4. \(A \cup B\): Das Ereignis “\(A\) oder \(B\)”
  5. \(A \backslash B\): Das Ereignis “\(A\) und nicht \(B\)”
  6. \(\overline{A}=\Omega \backslash A\): Das Ereignis, dass \(A\) nicht eintritt (“nicht \(A\)”)
  7. \(A \subseteq B\). Die Aussage “Aus dem Ereignis \(A\) folgt das Ereignis \(B\)” (kurz: Aus \(A\) folgt \(B\))
  8. \(A \cap B=\emptyset\): Die Ereignisse \(A\) und \(B\) sind disjunkt oder schließen sich aus

Wichtig: \(A\) Ereignis \(\Rightarrow\) \(A \subseteq \Omega\), aber die Umkehrung gilt nicht unbedingt. Aber Durchschnitt, Vereinigung und Komplement von Ereignissen müssen wieder Ereignisse sein!
Frage: Welche Teilmengen von \(\Omega\) sind keine Ereignisse?

2.2 Wahrscheinlichkeitsmodelle

Der wichtigste Begriff in der Wahrscheinlichkeitrechnung ist natürlich der der Wahrscheinlichkeit. Aber es stellt sich die Frage: Was ist Wahrscheinlichkeit? Eine verbreitete umgangssprachliche Definition ist folgende:

Wahrscheinlichkeit ist die Einstufung von Aussagen nach dem Grad ihrer Gewissheit.

Um zu einer mathematischen Definition zu gelangen, lernen wir ein weiteres wichtiges Konzept in der Wahrscheinlichkeitsrechnung kennen: das Konzept der Wahrscheinlichkeitsmodelle. Ein Wahrscheinlichkeitsmodell bestimmt, wie Wahrscheinlichkeiten von Ereignissen festgelegt werden.

Jeder wird zustimmen, wenn man sagt, die Wahrscheinlichkeit, eine Sechs zu würfeln, betrage \(\frac16\).
Wie kommt man zu dieser Aussage bzw. was bedeutet sie?
Wir betrachten zwei Modelle, um diese Frage zu beantworten. Dabei wird die Wahrscheinlichkeit für ein Ereignis mit \(\mathbb P\) für probability bezeichnet.

  • Laplace-Modell: Es wird angenommen, dass alle Elementarereignisse gleich wahrscheinlich sind. Es ist besonders nützlich bei endlichen Ergebnismengen.
  • Frequentistisches Wahrscheinlichkeitsmodell: Es basiert auf der Häufigkeit von Ereignissen bei wiederholten Experimenten.

Definition 2.4 (Laplace-Modell) Es sei \(|\Omega|=n\) und alle Elementarereignisse haben die gleiche Wahrscheinlichkeit (\(\mathbb P(\{\omega_i\})=\frac{1}{n}\) für alle \(i=1, \ldots , n\)). Dann gilt für alle Ereignisse \(A\subset \Omega\): \[\mathbb P(A):=\frac{|A|}{|\Omega|}=\frac{\text{Anzahl der für A günstigen Ausgänge}}{\text{Anzahl aller möglichen Ausgänge}}\]

Bei dem Würfelexperiment gibt es sechs Ergebnisse. Aus Symmetriegründen kann davon ausgegangen werden, dass alle Elemtarereignisse die gleiche Wahrscheinlichkeit haben. Es gilt also: \[\mathbb P(\{6\})=\frac{|\{6\}|}{|\Omega|}=\frac16\] Bei diesem Modell sind keine Experimente nötig; man geht von Symmetrieeigenschaften aus und leitet daraus die Wahrscheinlichkeiten ab. Da bei Würfel z.B. alle Seiten gleich sind, sollten auch die entsprechenden Wahrscheinlichkeiten gleich sein.

Beispiel 2.4 (Laplace-Modell)

  1. Beim Würfeln (Augenzahlen) wird von gleichen Wahrscheinlichkeiten ausgegangen, da alle Seiten gleich sind, wenn der Würfel fair ist.
  2. Beim Münzwurf (Kopf oder Zahl) wird ebenfalls von gleichen Wahrscheinlichkeiten ausgegangen, wenn die Münze fair ist.

Leider gelten oft keine Symmetrien oder sind zumindest nicht erkennbar, aber viele Wahrscheinlichkeitsverteilungen lassen sich auf ein Laplace-Modell zurückführen und sind damit berechenbar.

Video: Laplacescher Wahrscheinlichkeitsraum

 

In diesem Video werden der Laplacesche Wahrscheinlichkeitsraum sowie historische Kontroversen darüber, was gleich wahrscheinlich sei, vorgestellt. Anhand eines Beispiels wird gezeigt, dass die Behandlung von Laplace-Modellen Kenntnisse der Kombinatorik erfordert.

Definition 2.5 (Frequentistisches Wahrscheinlichkeitsmodell) Ein zufälliges Experiment mit dem Ergebnisraum \(\Omega\) werde \(n\)-mal wiederholt und \(h_n(A)\) sei die Häufigkeit mit der das Ereignis \(A \subseteq \Omega\) eintritt. Dann wird mit \[\mathbb P(A):=\lim_{n \rightarrow \infty} \frac{h_n(A)}n = \lim_{n \rightarrow \infty} f_n(A)\] die Wahrscheinlichkeit, dass das Ereignis \(A\) eintritt, bestimmt.

Intuitiv gehen viele Menschen davon aus, dass sich die relative Häufigkeit \(f_n\) mit wachsendem \(n\) einem Grenzwert nähert. Der Grenzwert in dieser Form existiert zwar nicht, aber mit dem schwachen Gesetz der großen Zahlen gilt etwas Ähnliches. Die genaue Formulierung folgt später.

Video: Das frequentistische Wahrscheinlichkeitsmodell

 

Obwohl bei jedem Zufallsexperiment der Zufall darüber entscheidet, ob ein Ereignis A eintritt oder nicht, stabilisiert sich erfahrungsgemäß bei oftmaliger Wiederholung des Vorgangs die relative Häufigkeit des Eintretens von A. Das Video illustriert dieses Phänomen anhand des wiederholten Wurfs einer Reißzwecke und sensibilisiert für die frequentistische Definition der Wahrscheinlichkeit nach Richard von Mises. Schließlich werden die Axiome eines endlichen Wahrscheinlichkeitsraumes nach A.N. Kolmogorov motiviert.

Excel-Dateien: Bernoulli- und Laplace-Experiment

 

Simulationen zur Veranschaulichung des Beroulli-Experiments und des Würfelwurfs. Hier kann man erkennen, wie sich nach mehreren Experimenten die relativen Häufigkeiten stabilisieren.

2.3 Das Kolmogoroffsche Axiomensystem

Andrei Kolmogoroff formulierte in den 1930er Jahren eine axiomatische Begründung der Wahrscheinlichkeitstheorie. Demnach muss ein Wahrscheinlichkeitsmaß drei Axiome erfüllen. Wir geben hier direkt das verallgemeinerte Axiomensystem wieder, welches nicht nur für endliche und abzählbare sondern auch für überabzählbare Ergebnisräume geeignet ist:

Definition 2.6 (Verallgemeinertes Axiomensystem nach Kolmogoroff) Axiom 1: Sei \(\Omega\) die Menge der möglichen Ergebnisse eines Experimentes (Ergebnisraum). Dann ist einigen (nicht notwendigerweise allen) Ereignissen \(A\subset \Omega\) eine reelle Zahl \(\mathbb P(A) \geq 0\) als Wahrscheinlichkeit zugeordnet, die den Grad der Sicherheit angibt, mit der \(A\) eintritt.

Axiom 2 \(\mathbb P(\Omega)=1\)

Axiom 3 (\(\sigma\)-Additivität von \(\mathbb P\)) Für eine Folge \(A_1,A_2,\dots\) paarweise disjunkter Teilmengen \(\Omega\) gilt: \(\mathbb P(\cup_{n \in \mathbb N} A_n)=\sum_{n \in \mathbb N} \mathbb P(A_n)\). (Das heißt eine Verallgemeinerung von \(\mathbb P(A\cup B)=\mathbb P(A)+\mathbb P(B)\) für alle \(A,B\in \mathcal A\) mit \(A\cap B=\emptyset\) soll für abzählbare Mengen von disjunkten Ereignissen gelten.).

Für den Definitionsbereich für das Wahrscheinlichkeitsmaß fordern wir, dass bestimmten Ereignissen Wahrscheinlichkeiten zugeordnet werden können.

  • Dem Ergebnisraum \(\Omega\) wird eine Wahrscheinlichkeit zugeordnet.
  • Wenn dem Ereignis \(A\) eine Wahrscheinlichkeit zugeordnet ist, dann hat auch das Komplementärereignis eine Wahrscheinlichkeit.
  • Wenn den Ereignissen \(A\) und \(B\) eine Wahrscheinlichkeit zugeordnet ist, dann auch dem Durchschnitt der beiden.
  • Wenn abzählbar vielen disjunkten Ereignissen jeweils eine Wahrscheinlichkeit zugeordnet ist, dann ist auch deren Vereinigung eine Wahrscheinlichkeit zugeordnet.

Ein solches Mengensystem von Ereignissen nennen wir \(\sigma\)-Algebra:

Definition 2.7 (σ-Algebra über Ω) Sei \(\Omega\) eine nichtleere Menge. Dann ist \(\mathcal{A} \subset \mathcal{P}(\Omega)=\{A : A \subset \Omega\}\) (Potenzmenge von \(\Omega\), d.h. Menge aller Teilmengen von \(\Omega\)) genau dann eine \(\sigma\)-Algebra, wenn gilt:

  1. \(\Omega \in \mathcal{A}\)
  2. \(A \in \mathcal{A} \Rightarrow A^c \in \mathcal{A}\)
  3. \(A,B \in \mathcal{A} \Rightarrow A\cap B \in \mathcal{A}\)
  4. \(A_i \in \mathcal{A}, i \in \mathbb N, A_i \cap A_j = \emptyset\) für \(i\neq j \Rightarrow \bigcup_{i\in \mathbb N} A_i \in \mathcal{A}\)

Somit können wir schließlich das Wahrscheinlichkeitsmaß definieren:

Definition 2.8 (Wahrscheinlichkeitsmaß) Sei \(\Omega\) nichleer und \(\mathcal A\) eine \(\sigma\)-Algebra. Dann nennen wir \((\Omega,\mathcal A)\) einen messbaren Raum. Eine Abbildung \(\mathbb P:\mathcal A\rightarrow [0,1]\), welche die Axiome 2 (‘normiert’) und 3 (‘\(\sigma\)-additiv’) erfüllt, heißt Wahrscheinlichkeitsmaß.

Das Tripel \((\Omega, \mathcal A, \mathbb P)\) wird dann Wahrscheinlichkeitsraum genannt.

Zur exakten Bestimmung von Wahrscheinlichkeiten für Experimente mit endlichen Ergebnisräumen eignet sich das einfachere Laplace-Modell. Die Verwendung von \(\sigma\)-Algebren ermöglicht es Ihnen, auch mit allgemeineren Ergebnisräumen arbeiten zu können, denen Sie in anderen Modulen begegnen werden.

Beispiel 2.5 (Lotto) Beim Lotto mit \[\Omega :=\{A\subset \mathbb N_{49}: |A|=6 \}\] werden 6 Kugeln aus 49 ausgewählt, das heißt \[|\Omega|={49 \choose 6}=13983816.\] Sei \(A\) das Ereignis 5 Richtige im Lotto zu haben, dann gilt \(|A|={6 \choose 5} \cdot {43 \choose 1}=6\cdot 43\), also \[\mathbb P(A)=\mathbb P(\{5 \mbox{ Richtige}\})=258/13983816=0,000018449...\]

Die kleinste mögliche \(\sigma\)-Algebra, welche dieses Ereignis enthält, ist \(\mathcal A= \{ \emptyset, A, A^{\mathsf c}, \Omega \}\).

Wenn wir die Abbildung \(\mathbb P\) für alle Teilmengen aus \(\mathcal A\) definiert haben (also auch \(\mathbb P(\emptyset)=0\), \(\mathbb P(\Omega)=1\), \(\mathbb P(A^{\mathsf c})=1-\mathbb P(A)\)), so bekommen wir mit dem Tripel \((\Omega, \mathcal A, \mathbb P)\) einen geeigneten Wahrscheinlichkeitsraum.

Beispiel 2.6 (Würfelexperiment) Für alle \(k \in \Omega:=\mathbb N_6\) ist \[\mathbb P(\{k\})=\frac16\] Als \(\sigma\)-Algebra eignet sich hier die Potenzmenge, \(\mathcal{A} = \mathcal{P}(\Omega)\).

Beispiel 2.7 (Würfeln im abzählbar unendlichen Wahrscheinlichkeitsraum) Es werde wiederholt ein Würfel geworfen. Ergebnis sei die Anzahl der Würfe bis zur ersten “6”. Dann ist \(\Omega:=\mathbb N_0\) und \(p_i=\mathbb P(\{i\})=\frac16 \cdot (\frac56)^i\) für alle \(i \in \mathbb N_0\).

2.4 Rechenregeln im Wahrscheinlichkeitsraum

Für die Wahrscheinlichkeiten in einem Wahrscheinlichkeitsraum gelten folgende wesentliche Regeln.

  1. Werte im Intervall zwischen 0 und 1: Die Wahrscheieinlichkeiten beliebiger Ereignisse liegen immer zwischen 0 und 1. Das unmögliche Ereignis hat die Wahrscheinlichkeit \(\mathbb P(\emptyset)=0\). Das sichere Ereignis hat die Wahrscheinlichkeit \(\mathbb P(\Omega)=1\)

  2. Das Komplement (nicht: Kompliment!) eines Ereignisses: \(A\) umfasst alles in der Ergebnismenge außer dem Ereignis \(A\). Die gängige Notation für das Komplement von \(A\) ist \(\overline{A}\), manchmal auch \(A^c\). Beispielsweise ist das Komplement von „Kopf“ beim Münzwurf „Zahl“. Es gilt: P\((A) + P(\overline{A}) = 1\). Bei manchen Aufgaben ist es einfacher, die Wahrscheinlichkeit des Komplements zu berechnen als direkt die gefragte Wahrscheinlichkeit. In diesem Fall berechnen Sie das Komplement und die Differenz zu eins ist dann das gesuchte Ergebnis.

  3. Additivität disjunkter Mengen: Die Wahrscheinlichkeit, dass ein Ereignis A oder ein Ereignis B eintritt, ist die Summe der beiden Wahrscheinlichkeiten („Additionsregel“): \(P(A\text{ oder }B) = P(A \cup B) = P(A) + P(B)\). Beispielsweise könnten Sie beim Würfelwurf nach der Wahrscheinlichkeit gefragt werden, eine 5 oder 6 zu erhalten: \(P(5\text{ oder }6) = P(5 \cup 6) = P(5) + P(6) = 1/6 + 1/6 = 1/3\). Hierbei schließen die Ausgänge A bzw. 5 und B bzw. 6 einander aus, siehe Abb. 2.1

  4. Prinzip von Inklusion und Exklusion: Es ist aber auch denkbar, dass die beiden Kreise einander überdecken wie in Abb. 2.2, d. h., sie haben eine nicht-leere Schnittmenge: Wenn Sie in diesem Fall die beiden Kreise addieren, zählen Sie die überlappende Fläche die zu A und zugleich zu B gehört doppelt, nämlich ein Mal als Bestandteil von A und ein Mal als Teil von B. Wenn sich also die beiden Ausgänge des Zufallsexperimentes nicht ausschließen, dann müssen Sie beim Summieren der Einzelwahrscheinlichkeiten die Wahrscheinlichkeit der Schnittmenge subtrahieren: \[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

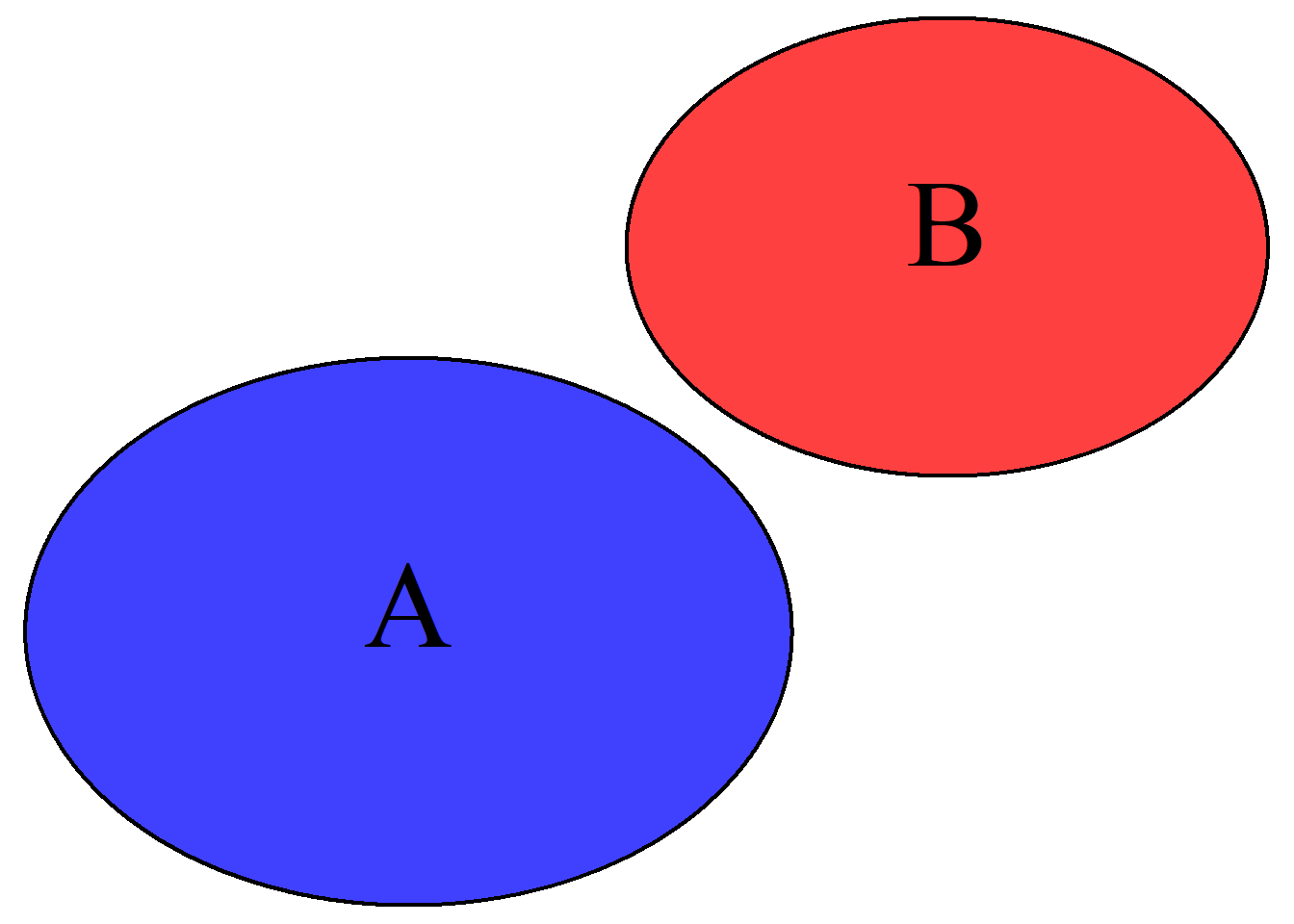
Additionsregel mit leerer Schnittmenge

Abbildung 2.1: Additionsregel mit leerer Schnittmenge

Additionsregel mit nicht-leerer Schnittmenge

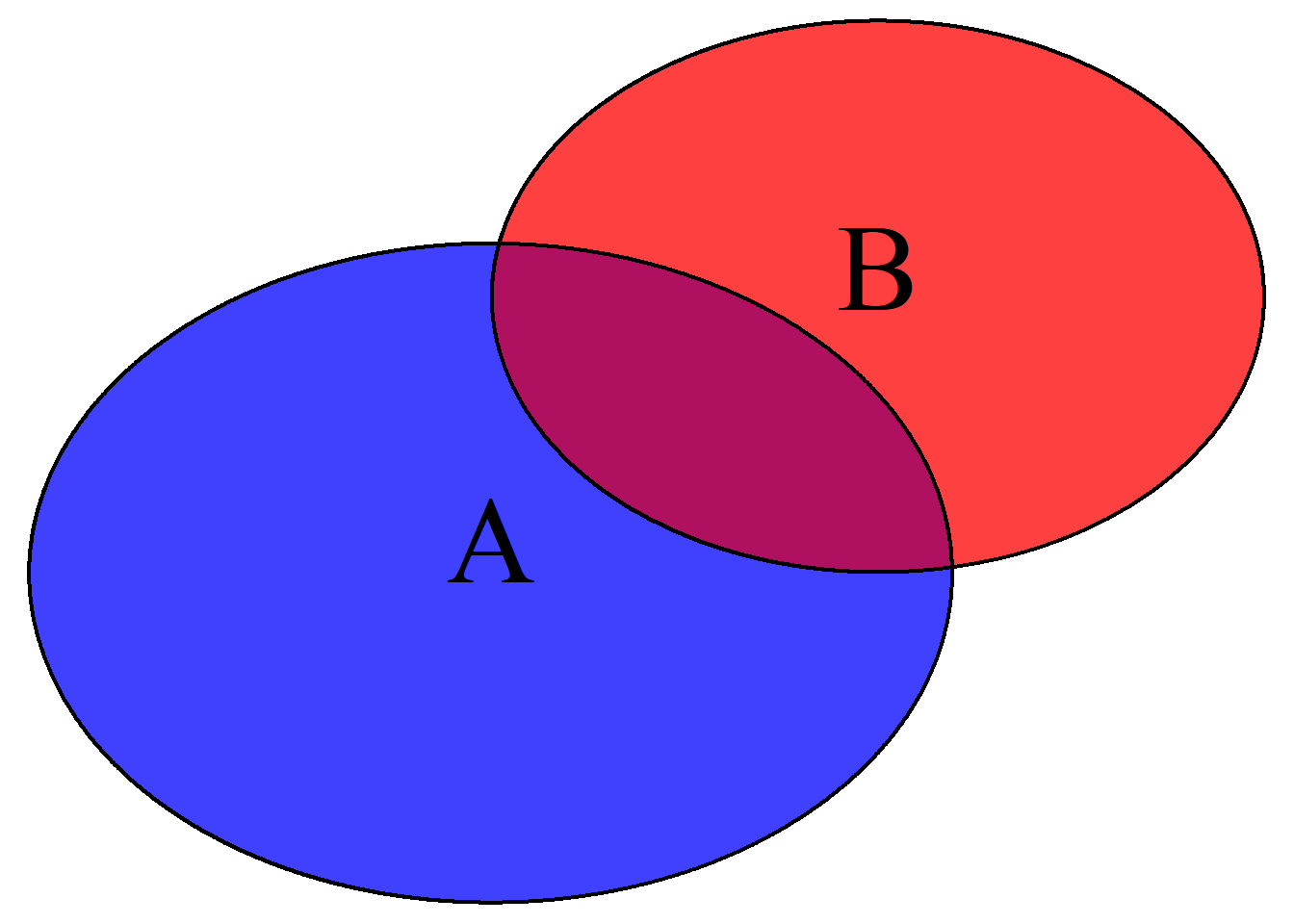
Abbildung 2.2: Additionsregel mit nicht-leerer Schnittmenge

Nach diesen mengentheoretischen Überlegungen sollten Ihnen die Rechenregeln in folgendem Satz intuitiv nachvollziehbar sein:

Satz 2.1 (Rechenregeln für Wahrscheinlichkeitsmaße) Sei \(\mathbb P\) ein Wahrscheinlichkeitsmaß auf \(\Omega\), dann gilt

  1. Werte im Intervall von 0 bis 1: \(0≤P(A)≤1\) für ein beliebiges Ereignis \(A\).
  2. Komplement: \(\mathbb P(\overline{A})=1-\mathbb P(A)\) für alle \(A\in \mathcal A\).
  3. Endliche Additivität: \(\mathbb P(\bigcup_{n=1}^m A_n)=\sum_{n=1}^m \mathbb P(A_n)\) für paarweise disjunkte \(A_1,\dots,A_m \in \mathcal A\).
  4. Prinzip von Inklusion und Exklusion: \(\mathbb P(A\cup B)=\mathbb P(A)+\mathbb P(B)-\mathbb P(A\cap B)\) für alle \(A,B\in \mathcal A\).
  5. Subtraktivität: \(\mathbb P(A\setminus B)=\mathbb P(A)-\mathbb P(B)\) für alle \(A,B\in \mathcal A\) mit \(B\subset A\).
  6. Monotonie: \(A,B\in \mathcal A\) mit \(B\subset A \Rightarrow \mathbb P(B) \le \mathbb P(A)\) (Monotonie von \(\mathbb P\)).

2.5 Kombinatorik

Erinnern wir uns an das Laplace-Modell, wo Wahrscheinlichkeiten als \(\mathbb P=|A|/|\Omega|\) bestimmt werden. Um mit Hilfe des Laplace-Ansatzes Wahrscheinlichkeiten zu berechnen, ist es notwendig die Elemente einer Menge zu zählen. Betrachten wir zunächst die Anzahl der Elemente im kartesischen Produkt.

Satz 2.2 (Das kartesische Produkt) Für das kartesische Produkt von Mengen \(A_1\), \(A_2\),…,\(A_n\), \[A_1 \times A_2 \times ... \times A_n := \{(a_1,a_2,...,a_n)|\; a_i\in A_i \mbox{ für alle } i \in \mathbb N_n\}\] gilt: \[|A_1 \times A_2 \times ... \times A_n| = |A_1|\cdot|A_2| \cdots |A_n|\]

Wenn alle \(n\) Mengen gleich sind, führt dies zu folgendem Spezialfall.

Definition 2.9 (Das kartesische Produkt) Für das kartesische Produkt \(A^n:=\underbrace{A\times\dots\times A}_{k\text{-mal}}\) von Mengen \(A\) mit \(k \in \mathbb N\) gilt: \[|A^k|= |A|^k\]

In vielen Fällen lassen sich die Zählvorgänge anhand von Urnenmodellen veranschaulichen. Im Folgenden stelle man sich eine Urne (Menge) mit \(n\) nummerierten Kugeln (Elementen) vor, aus der jeweils \(k\)-mal eine Kugel (Element) gezogen (zufällig gewählt) wird. In Abhängigkeit davon, ob die Kugel zurückgelegt wird oder nicht, bzw. die Reihenfolge berücksichtigt wird oder nicht, ergeben sich folgende 4 Fälle:

Satz 2.3 (Geordnete Probe mit Wiederholung) Für die Ziehung von \(k\) Kugeln aus einer Urne mit \(n\) nummerierten Kugeln (\(\mathbb N_n:=\{1,2,\dots,n\}\)) mit Zurücklegen und mit Berücksichtigung der Reihenfolge gibt es \(n^k\) Möglichkeiten.

Dies ergibt sich, da für die Ergebnismenge \[\Omega:=\{(\omega_1,\omega_2,...,\omega_k)|\omega_i \in \mathbb N_n\}=\mathbb N_n \times \mathbb N_n \times ... \times \mathbb N_n=(\mathbb N_n)^k\] gilt: \[|\Omega|=|\mathbb N_n^k|=|\mathbb N_n|^k=n^k.\]

Beispiel 2.8 (8-malige Wiederholung eines Würfelexperimentes) Die Ergebnismenge ist \[\Omega:=\{(\omega_1,\omega_2,...,\omega_8)|\omega_i \in \mathbb N_6\}=(\mathbb N_6)^8\] und es ergibt sich: \[|\Omega|=|\mathbb N_6|^8=6^8=1679616\]

Satz 2.4 (Geordnete Probe ohne Wiederholung) Für die Ziehung von \(k\) Kugeln aus einer Urne mit \(n\) nummerierten Kugeln (\(\mathbb N_n\)) Zurücklegen und Berücksichtigung der Reihenfolge gibt es \(n \cdot (n-1) \cdot ... \cdot (n-k+1)\) Möglichkeiten.

Dies ergibt, da für die Ergebnismenge \[\Omega:=\{(\omega_1,\omega_2,...,\omega_k)|\omega_i \in \mathbb N_n \wedge (i \ne j \Rightarrow \omega_i\ne \omega_j) \}\] gilt: \[|\Omega|=n \cdot (n-1) \cdot ... \cdot (n-k+1)=\frac{n!}{(n-k)!}\]

Beispiel 2.9 (Rangfolge der Bundesligamannschaften) Wie viele Möglichkeiten gibt es von den 18 Bundesligamannschaften 5 auf die ersten Plätze zu verteilen: \[\Omega:=\{(\omega_1,\omega_2,...,\omega_5)|\omega_i \in \mathbb N_{18} \wedge (i \ne j \Rightarrow \omega_i\ne \omega_j) \}\] und \[|\Omega|=18 \cdot 17 \cdot ... \cdot (18-5+1)=\frac{18!}{13!}=1028160\]

Satz 2.5 (Permutationen) \(n\) verschiedene Elemente können auf \(n!\) verschiedene Arten angeordnet werden. Es existieren also \(n!\) Permutationen einer \(n\)-elementigen Menge.

Dies ergibt sich aus dem vorigen Satz als Sonderfall von \(n=k\), da dann gilt: \[|\Omega|=n \cdot (n-1) \cdot ... \cdot (n-n+1)=\frac{n!}{0!}=n!\]

Beispiel 2.10 (Bundesligatabelle) Es gibt dann \[18!=6,402... \cdot 10^{15}\] Möglichkeiten für eine komplette Bundesligatabelle.

Satz 2.6 (Ungeordnete Probe ohne Wiederholung) Für die Ziehung von \(k\) Kugeln aus einer Urne mit \(n\) Kugeln Wiederholung (Zurücklegen) und Berücksichtigung der Reihenfolge gibt es \({n \choose k}\) Möglichkeiten.

Dies ergibt sich aus der geordneten Probe ohne Wiederholung, indem die geordneten Proben, die sich nur in der Reihenfolge unterscheiden, identifiziert werden. Dies entspricht einer k-elementigen Teilmenge einer n-elementigen Grundmenge \(\{1,2,3,...,n\}\). Für die Ergebnismenge \[\Omega:=\{A \subseteq \{1,2,3,...,n\}: |A|=k \}\] gilt \[|\Omega|=\frac{n!}{k!(n-k)!}=:{n \choose k}\] Da hier die Reihenfolge nicht berücksichtigt wird, müssen jeweils \(k!\) Ergebnisse des vorherigen Modells zu einem Ergebnis zusammengefasst werden.

Beispiel 2.11 (Lottospiel) Sei \(U\) die Menge der Zahlen 1 bis 49, also \(U:=\{1,2,...,49\}\). Dann gilt für das Lotto-Spiel mit \(|U|=49\) \[\Omega:=\{A \subseteq U: |A|=6 \}\] und \[|\Omega|=\frac{49!}{6!(49-6)!}={49 \choose 6}=13983816\]

Satz 2.7 (Ungeordnete Probe mit Wiederholung) Für die Ziehung von \(k\) Kugeln aus einer Urne mit \(n\) Kugeln mit Zurücklegen und ohne Berücksichtigung der Reihenfolge gibt es \[{n+k-1 \choose k}\] Möglichkeiten.

Hier ohne Beweis.

Beispiel 2.12 (Häufigkeiten beim Würfelwurf) Es werde 20 mal ein Würfel geworfen und es wird nur gezählt, wie oft eine Zahl vorkommt. Wie viele Häufigkeitstabellen gibt es?

\[|\Omega|= {6+20-1 \choose 20}=\frac{25 \cdot 24 \cdot 23 \cdot 22 \cdot 21}{5!}=53130\]

Bemerkung. Sind keine Wiederholungen erlaubt, muss natürlich \(k\le n\) gelten.

2.6 Bedingte Wahrscheinlichkeiten

Bevor die Definition für die bedingte Wahrscheinlichkeit gegeben wird, wollen wir uns der bedingte Wahrscheinlichkeit zunächst auf eine heuristische Weise nähern.

Wir betrachten zwei Ergebnisse \(A\) und \(B\) in einem Wahrscheinlichkeitsraum \((\Omega,\mathcal{A},\mathbb P)\) mit \(\mathbb P(B)>0\). Nun sei bekannt, dass das Ereignis \(B\) eingetreten ist. Wie wahrscheinlich ist es nun, dass \(A\) eintritt?

Aufgrund der zusätzlichen Information, dass bereits \(B\) eingetreten ist, schrumpft unser Ergebnisraum. Statt wie bisher \(\Omega\), ist der neue Ergebnisraum für die bedingte Wahrscheinlichkeit nun \(\Omega':=B\). Dies ist grafisch in Abb. 2.3 veranschaulicht. Wir beziehen also die gemeinsame Wahrscheinlichkeit \(P(A \cap B)\) auf \(P(B)\).

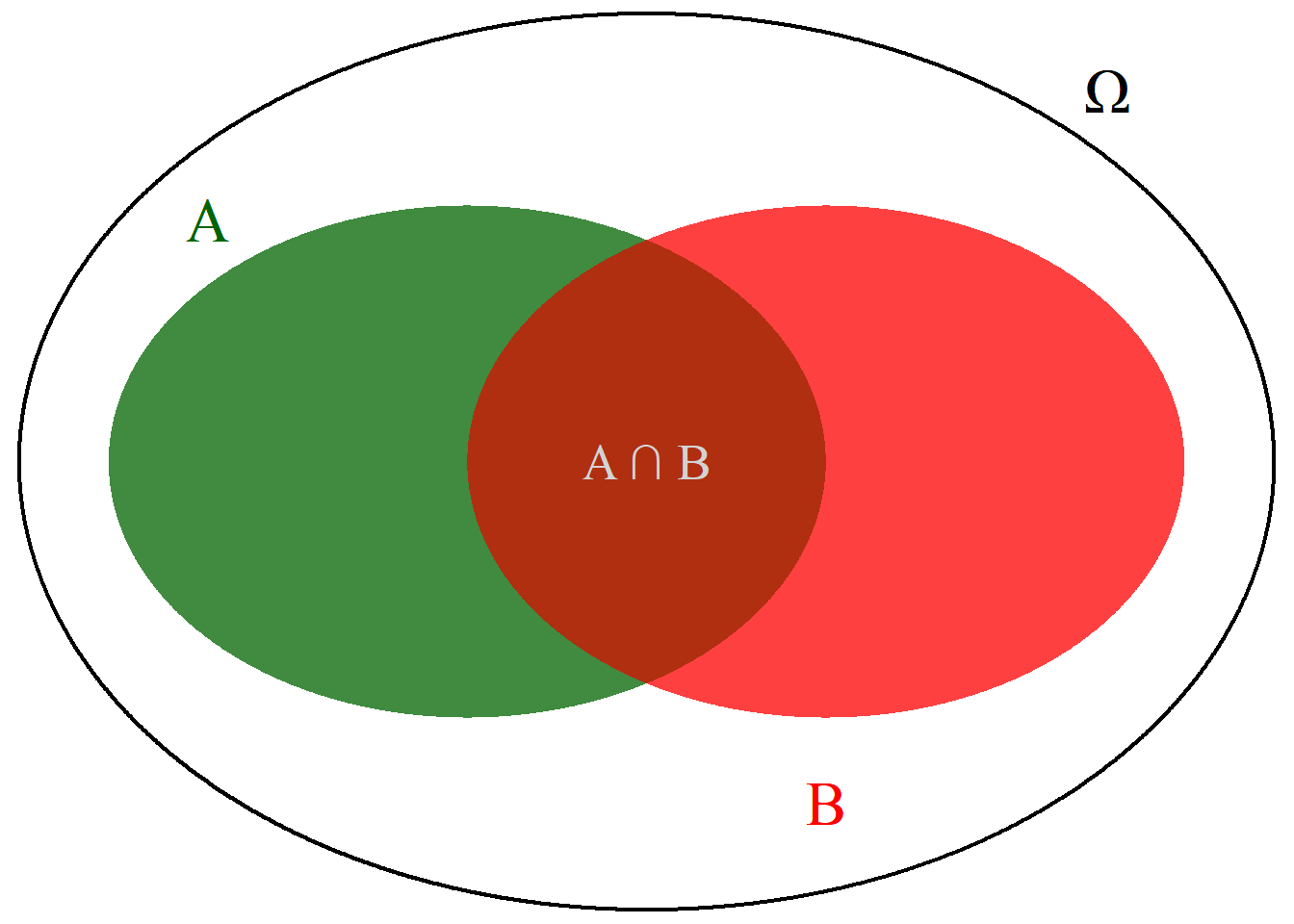
Bedingte Wahrscheinlichkeiten

Abbildung 2.3: Bedingte Wahrscheinlichkeiten

Definition 2.10 (Bedingte Wahrscheinlichkeit) Für zwei Ereignisse \(A\) und \(B\) zwei Ereignisse mit \(\mathbb P(B)\neq0\), heißt \[\mathbb P(A|B):=\frac{\mathbb P(A\cap B)}{\mathbb P(B)} \mbox{ falls } \mathbb P(B)\ne 0\] die bedingte Wahrscheinlichkeit für das Eintreten von \(A\) unter (der Bedingung) \(B\).

Achtung: Dies ist eine Definition und kein Gesetz!

Beispiel 2.13 (Mittelwert für gruppierte Daten)

2.7 Stochastische Unabhängigkeit

Die Überlegungen zur bedingten Wahrscheinlichkeit helfen dabei, das Konzept der Unabhängigkeit zu formalisieren:

Zwei Ereignisse \(A\) und \(B\) heißen (stochastisch) unabhängig, wenn gilt: \[\mathbb P(A|B)=\mathbb P(A) \quad {\mbox oder } \quad \mathbb P(B|A)=\mathbb P(B)\] In diesem Fall beeinflusst das Eintreten von B nicht die Eintrittswahrscheinlichkeit von A (bzw. das Eintreten von A beeinflusst nicht die Eintrittswahrscheinlichkeit von B).

Aus dieser vorläufigen Definition, also \(\mathbb P(A│B)=\frac{\mathbb P(A∩B)}{\mathbb P(B)}=\mathbb P(A)\) bzw. \(\mathbb P(B│A)=\frac{\mathbb P(A∩B)}{\mathbb P(A)}=\mathbb P(B)\), folgt, dass \(P(A∩B)=P(A)\cdot P(B)\). Diese letztere Gleichung ist allgemeiner, weil sie auch für \(\mathbb P(B)=0\) oder \(\mathbb P(A)=0\) gilt. Daher benutzen wir diese Gleichung für die formale Definition der stochastischen Unabhängigkeit:

Definition 2.11 (Unabhängigkeit von Ereignissen) Zwei Ereignisse \(A\) und \(B\) heißen (stochastisch) unabhängig, wenn gilt: \[\mathbb P(A\cap B)=\mathbb P(A) \cdot \mathbb P(B)\]

Achtung: Die stochastische Unabhängigkeit hat nichts mit der linearen oder kausalen Unabhängigkeit zu tun. Solange es keine Missverständnisse gibt, wird oft auch nur von Unabhängigkeit gesprochen.

Aufgabe 2.1 Nehmen Sie an, Sie würfeln mit zwei Würfeln jeweils ein Mal. Sind die Ergebnisse, die jeder Würfel anzeigt, unabhängig?

Aufgabe 2.2 Sie sollen mit einem Würfel drei Mal werfen. Bei den ersten beiden Würfen haben Sie eine 5 und eine 6 gewürfelt. Wie wahrscheinlich ist es, dass Sie beim 3. Wurf eine 6 erhalten?

Beispiel 2.14

  • Sei \(\Omega:=\{1;2;3;4;5;6\}\) (Laplacewürfel) und
  • \(A:=\{2;4;6\}\), \(B:=\{1;2;3\}\) und \(C:=\{2;5\}\), dann ist
  • \(\mathbb P(A)=\frac{1}{2}\) und
  • \(\mathbb P(A|B)=\frac{1/6}{1/2}=\frac{1}{3}\), aber
  • \(\mathbb P(A|C)=\frac{1/6}{1/3}=\frac{1}{2}\).
  • \(A\) und \(B\) sind also nicht unabhängig, wohl aber \(A\) und \(C\).

Das Konzept der Unabhängigkeit lässt sich nicht nur auf zwei Ereignisse A und B anwenden, sondern auch auf mehrere. Diese beliebigen Ereignisse sind gemeinsam stochastisch unabhängig, wenn beispielsweise \(P(A \cap B \cap C) = P(A) \cdot P(B) \cdot P(C)\), d. h., die paarweise Unabhängigkeit \((A \cap B)\), \((A \cap C)\) und \((B \cap C)\) reicht bei der Erweiterung auf mehrere Ereignisse nicht aus.

Video: Stochastische Unabhängigkeit

 

Ausgehend von bedingten Wahrscheinlichkeiten wird die Begriffsbildung der stochastischen Unabhängkeit von zwei Ereignissen motiviert.

Beispiel 2.15 (Multiplikationsregel bei stochastischer Unabhängigkeit)

2.8 Multiplikationssatz

Eine allgemeine Multiplikationsregel für zwei Ereignisse A und B, welche auch gilt wenn A und B nicht unabhängig sind, ist folgender Satz.

Satz 2.8 (Multiplikationssatz) Für zwei Ereignisse mit \(\mathbb P(A)>0\) und \(\mathbb P(B)>0\) gilt: \[\mathbb P(A \cap B) = \mathbb P(B) \cdot \mathbb P(A|B) = \mathbb P(A) \cdot \mathbb P(B|A)\]

Daraus folgt \[\frac{\mathbb P(A)}{\mathbb P(B)}=\frac{\mathbb P(A|B)}{\mathbb P(B|A)}.\] Aus dieser Gleichung geht klar hervor, dass \(A\) und \(B\) in der bedingten Wahrscheinlichkeit nicht vertauscht werden dürfen!

Beispiel 2.16 (Multiplikationssatz) Bedingte Wahrscheinlichkeiten dürfen nicht einfach vertauscht werden:

  • Aus der Aussage “`Nahezu jeder Heroinabhängige hat Marihuana konsumiert.”’ lässt sich keine Schlussfolgerung über die Wahrscheinlichkeit, dass ein Marihuanakonsument heroinabhängig wird treffen.
  • Aus der Aussage, “`Die meisten Raucher trinken auch Kaffee”’ lässt sich nicht schließen, ob unter Kaffeetrinkern besonders viele Raucher sind.

Satz 2.9 (Multiplikationssatz, allgemein) Für Ereignisse \(A_1,A_2,...,A_n\) mit \(\mathbb P(A_1 \cap A_2 \cap ... \cap A_n)>0\) folgt: \[\mathbb P(A_1 \cap A_2 \cap ... \cap A_n)=\] \[\mathbb P(A_1) \cdot \mathbb P(A_2|A_1) \cdot \mathbb P(A_3|A_1 \cap A_2) \cdot ... \cdot \mathbb P(A_n|A_1 \cap A_2 \cap ... \cap A_{n-1}).\]

Dieser Satz ist eine Grundlage für die sogenannten Pfadregeln in Wahrscheinlichkeitsbäumen.

Beispiel 2.17 (Zug von Pik aus Skatbatt) Es werden zwei Karten aus einem Laplace-Skatblatt mit 32 Karten gezogen. \(A_1\) sei das Ereignis im ersten Zug ein Pik zu ziehen, \(A_2\) das gleiche für den zweiten und so weiter.

  \(A_1 \cap A_2\) ist dann das Ereignis zwei Pik zu ziehen und es gilt
  \[\mathbb P(A_1 \cap A_2) = \mathbb P(A_1) \cdot \mathbb P(A_2|A_1) = \frac8{32} \cdot \frac7{31} = \frac7{124}\]
  sowie
  \[\mathbb P(A_1 \cap A_2 \cap A_3) = \mathbb P(A_1) \cdot \mathbb P(A_2|A_1) \cdot \mathbb P(A_3|A_1 \cap A_2)\]
  \[= \frac8{32} \cdot \frac7{31} \cdot \frac6{30} = \frac7{620}\]
  etc.

2.9 Satz von der totalen Wahrscheinlichkeit

Mit dem Satz der totalen Wahrscheinlichkeit lässt sich die Wahrscheinlichkeit für ein Ereignis A berechnen, wenn nur bedingte Wahrscheinlichkeiten abhängig von einem zweiten Ergebnis B gegeben sind.

Satz 2.10 (Totale Wahrscheinlichkeit) In einem Wahrscheinlichkeitsraum \((\Omega,\mathcal{A},\mathbb P)\) seien \(B_1,\ldots, B_n\) disjunkte Ereignisse mit \(\Omega = \bigcup_{i=1}^n B_i.\) mit \(P(B_i)>0, i=1,\dots,n\). Wir bezeichnen dann \(B_1,\ldots, B_n\) als Partition von \(\Omega\). Dann gilt für ein beliebiges Ereignis \(A \in \mathcal{A}\): \[\mathbb P(A) = \sum_{i=1}^n \mathbb P(B_i) \cdot \mathbb P(A|B_i).\]

Ein Spezialfall davon ist für Ereignisse \(A,B\): \[\mathbb P(A) = \mathbb P(B) \cdot \mathbb P(A|B) + \mathbb P(\overline{B}) \cdot \mathbb P(A|\overline{B}).\]

Beispiel 2.18 (Partition nach Blutgruppen und Rhesusfaktor)

2.10 Satz von Bayes

Satz 2.11 (Bayessche Formel) In einem Wahrscheinlichkeitsraum \((\Omega,\mathcal{A},\mathbb P)\) seien \(B_1,\ldots, B_n\) disjunkte Ereignisse mit \(\Omega = \bigcup_{i=1}^n B_i.\) mit \(P(B_i)>0, i=1,\dots,n\). Dann gilt für \(A\in \mathcal{A}\), \(P(A)>0\): \[\mathbb P(B_i|A)=\frac{\mathbb P(A|B_i)\mathbb P(B_i)}{\sum_{i=1}^n \mathbb P(B_i) \mathbb P(A|B_i)}.\] Hinweis: Der Nenner entspricht der Wahrscheinlichkeit \(\mathbb P(A)=\sum_{i=1}^n \mathbb P(B_i) \mathbb P(A|B_i)\).

Im Spezialfall einer disjunkten Zerlegung in ein Ereignis \(B\) und sein Gegenereignis \(\overline{B}\), bekommen wir also:

Für zwei Ereignisse \(A\) und \(B\) mit \(\mathbb P(A)>0\) und \(\mathbb P(B)>0\) gilt: \[\mathbb P(B|A)=\frac{\mathbb P(B) \cdot \mathbb P(A|B)}{\mathbb P(A)} =\frac{\mathbb P(B) \cdot \mathbb P(A|B)}{\mathbb P(B) \cdot \mathbb P(A|B)+\mathbb P(\overline{B}) \cdot \mathbb P(A|\overline{B})}.\]

Beispiel 2.19 (Blutgruppen bei gegebenem Rhesusfaktor)

Excel: Beispiele zum Satz von Bayes

 

Im vorigen Beispiel war \(\mathbb P(A|R_+)\approx\mathbb P(A)\).
Dass das nicht so sein muss, zeigen die Beispiele Medizinischer Test.xlsx und Corona.xlsx.

Video: Simpson-Paradoxon

 

Das nach dem britischen Statistiker Edward Hugh Simpson (1922-2019) benannte Paradoxon besagt, dass in einer Population eine bestimmte Aussage zutreffen kann, die aber bei Aufteilung der Population in Teilpopulationen innerhalb jeder der Teilpopulationen nicht gilt. In diesem Video wird das Simpson-Paradoxon anhand von Beispielen vorgestellt, und es wird geklärt, was dieses Paradoxon mit der Formel von der totalen Wahrscheinlichkeit zu tun hat.

Schlüsselbegriffe

Zufallsexperiment, Versuch, Ausgang, Ergebnis, Ereignis, Ergebnismenge, Komplement; Additionsregel, Multiplikationsregel; Bedingte Wahrscheinlichkeit; Stochastische Unabhängigkeit

Literatur:

Barrow, Michael. 2017. Statistics for Economics, Accounting and Business Studies. Pearson Education Limited. https://plus.orbis-oldenburg.de/permalink/f/126s6ph/JBElbs881838667.
Cottin, Claudia, and Sebastian Döhler. 2013. Risikoanalyse. Springer Fachmedien Wiesbaden. https://doi.org/10.1007/978-3-658-00830-7.
Dehling, Herold, and Beate Haupt. 2004. Einführung in Die Wahrscheinlichkeits-Theorie Und Statistik. Springer Berlin Heidelberg. https://doi.org/10.1007/3-540-35117-5.
Fahrmeir, Ludwig, Christian Heumann, Rita Künstler, Iris Pigeot, and Gerhard Tutz. 2016. Statistik. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-50372-0.
Zucchini, Walter, Andreas Schlegel, Oleg Nenadić, and Stefan Sperlich. 2009. Statistik Für Bachelor- Und Masterstudenten. Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-540-88987-8.