Beispiel: Bedingte Wahrscheinlichkeit
Beispiel: Geburtsgeschlecht
Bei der ersten Geburt betrage die Wahrscheinlichkeit für Mädchen und Jungen je 50 %:
\(\mathsf{P(B_1)=P(\text{,,Erstgeburt ist Junge''})=}\) 0,5
\(\mathsf{P(\overline{B_1})=P(\text{,,Erstgeburt ist Mädchen''})=}\) 0,5
Bei der zweiten Geburt sei die Wahrscheinlichkeit für einen Jungen 60 %, falls die erste Geburt ein Junge wurde:
\(\mathsf{P(B_2 | B_1) = P(\text{,,Zweites ist Junge''} | \text{,,Erstes ist Junge''}) =}\) 0,6
\(\mathsf{P(\overline{B_2} | B_1) = P(\text{,,Zweites ist Mädchen''} | \text{,,Erstes ist Junge''}) =}\) 0,4
und analog für Mädchen \(\mathsf{P(\overline{B_2}|\overline{B_1})=}\) 0,6 und damit \(\mathsf{P(B_2 | \overline{B_1})=}\) 0,4
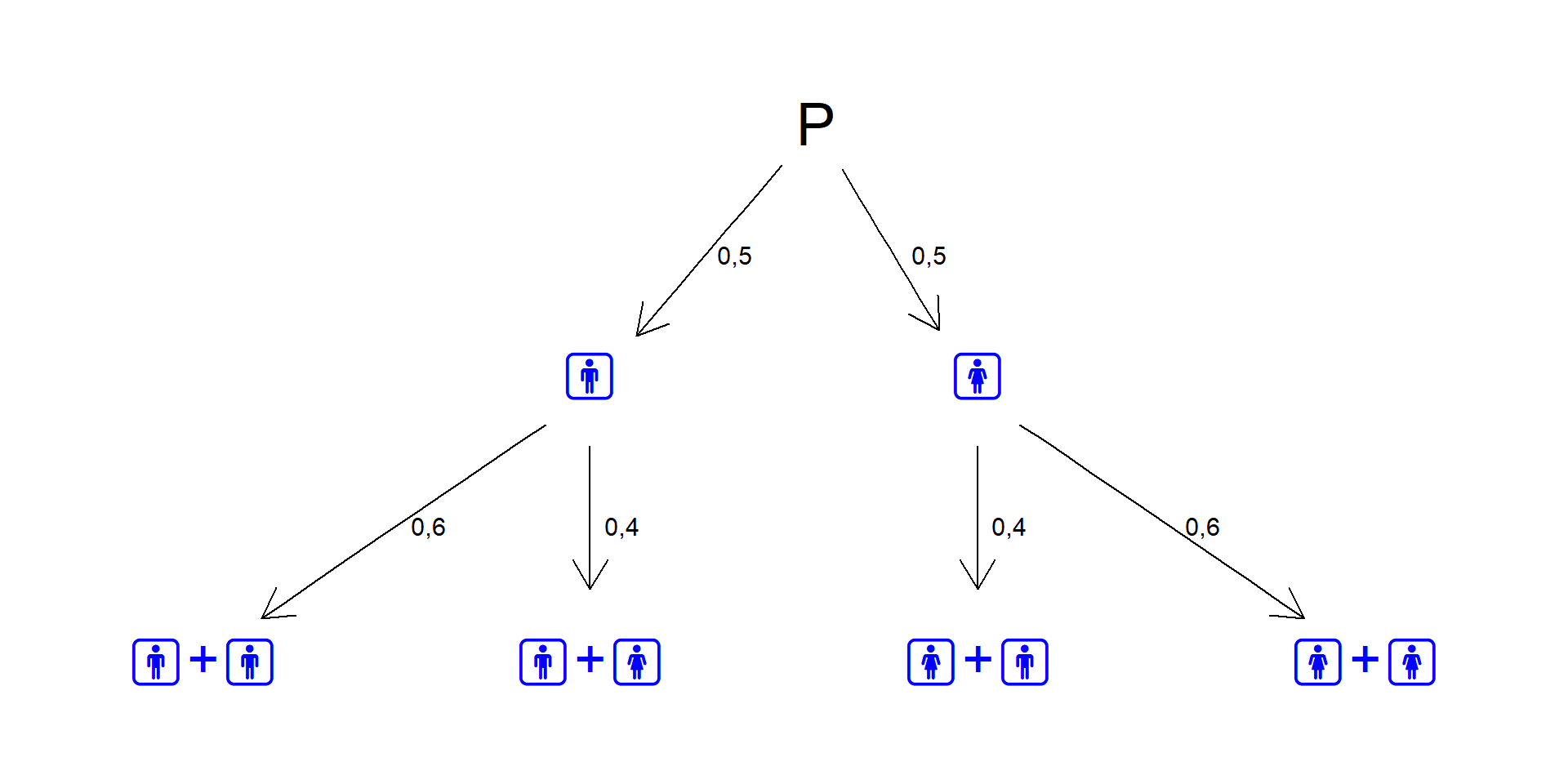
Im Wahrscheinlichkeitsbaum sind die möglichen Ausgänge mit ihren bedingten Wahrscheinlichkeiten dargestellt.
Ergebnis
Durch Multiplikation der Äste im Wahrscheinlichkeitsbaum erhält man Wahrscheinlichkeiten für alle möglichen Ausgänge, z.B. \(\mathsf{P(B_1 \cap B_2) = P(B_1) \cdot P(B_2|B_1) =}\) 0,5 \(\cdot\) 0,6 = 0,3
| Ergebnis | Rechenweg | Wahrscheinlichkeit |
|---|---|---|
| 2 Jungen | 0,5 \(\cdot\) 0,6 | 0,3 |
| 2 Mädchen | 0,5 \(\cdot\) 0,6 | 0,3 |
| 1 Junge und 1 Mädchen | 0,5 \(\cdot\) 0,4 | 0,2 |
| 1 Mädchen und 1 Junge | 0,5 \(\cdot\) 0,4 | 0,2 |
| Summe | 1 |